Geometallurgical Cluster Creation in a Niobium Deposit Using Dual-Space Clustering and Hierarchical Indicator Kriging with Trends
Abstract
1. Introduction
2. Theoretical Background
2.1. Cluster Analysis
2.1.1. Agglomerative Hierarchical Clustering
2.1.2. K-Means
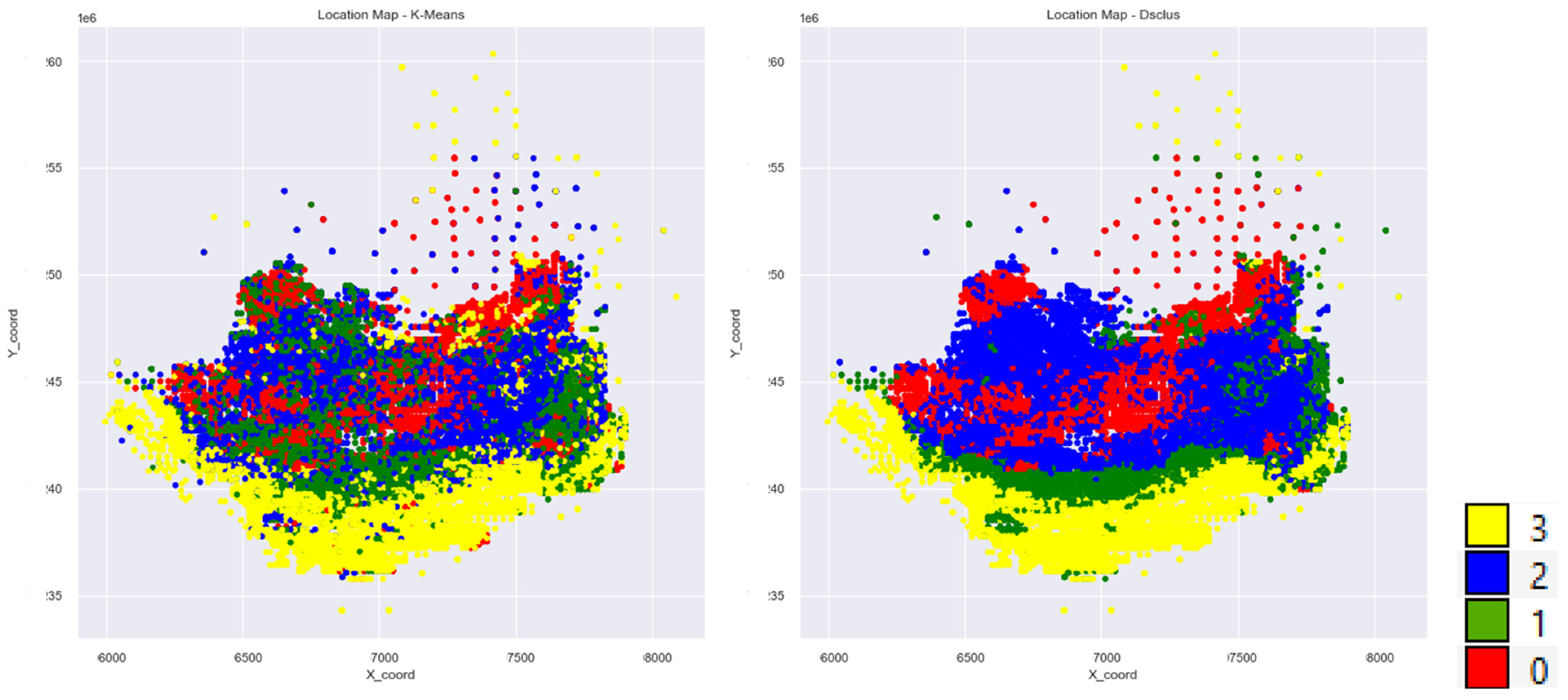
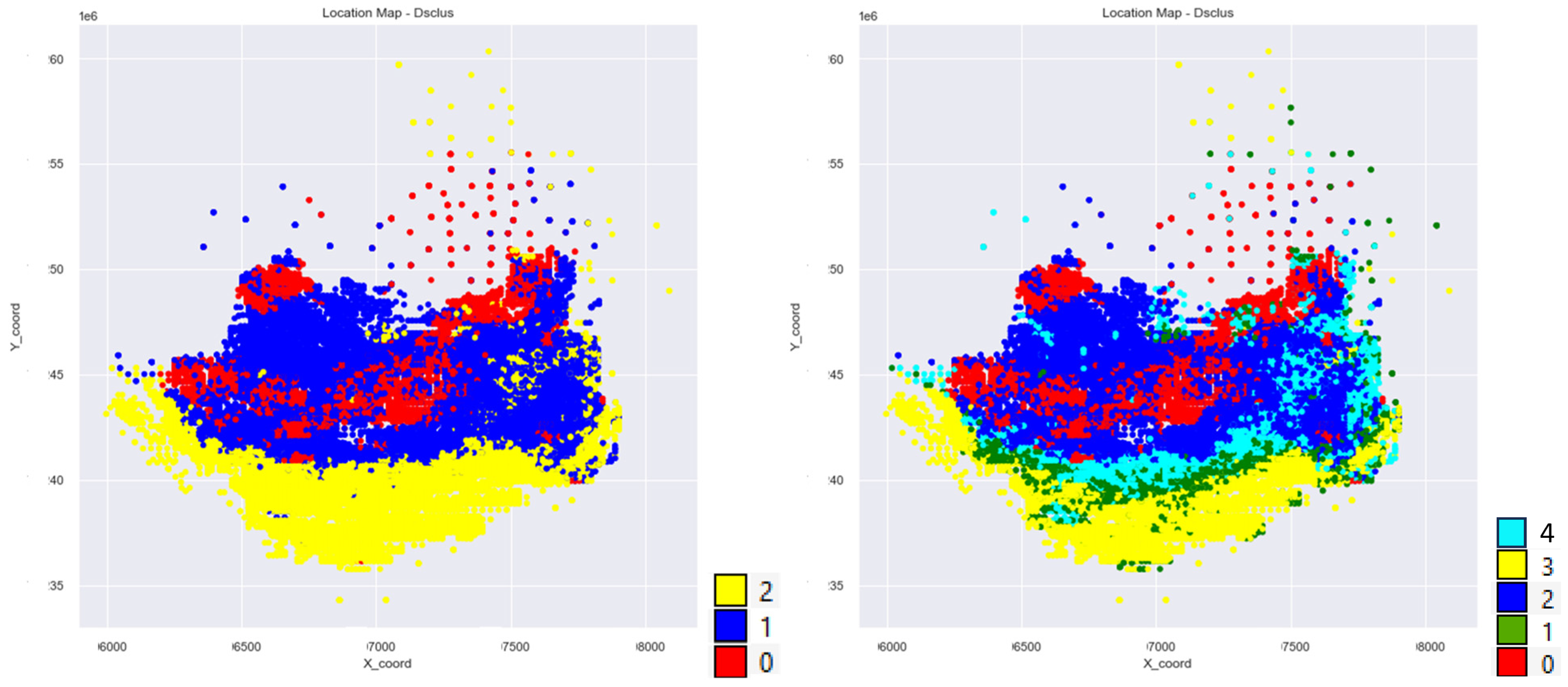
2.1.3. Dual-Space Clustering
2.1.4. Spatial Autocorrelation
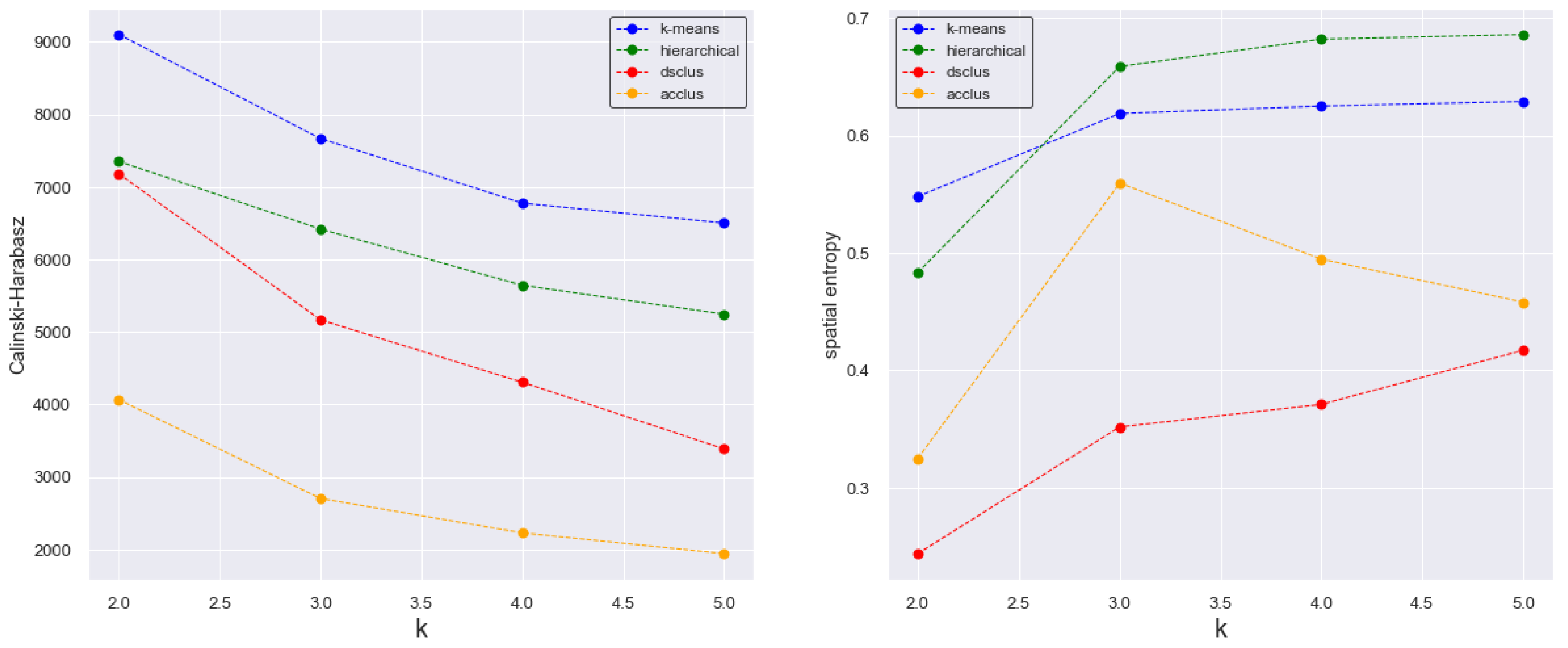
2.1.5. Metrics to Evaluate the Ideal Number of Clusters
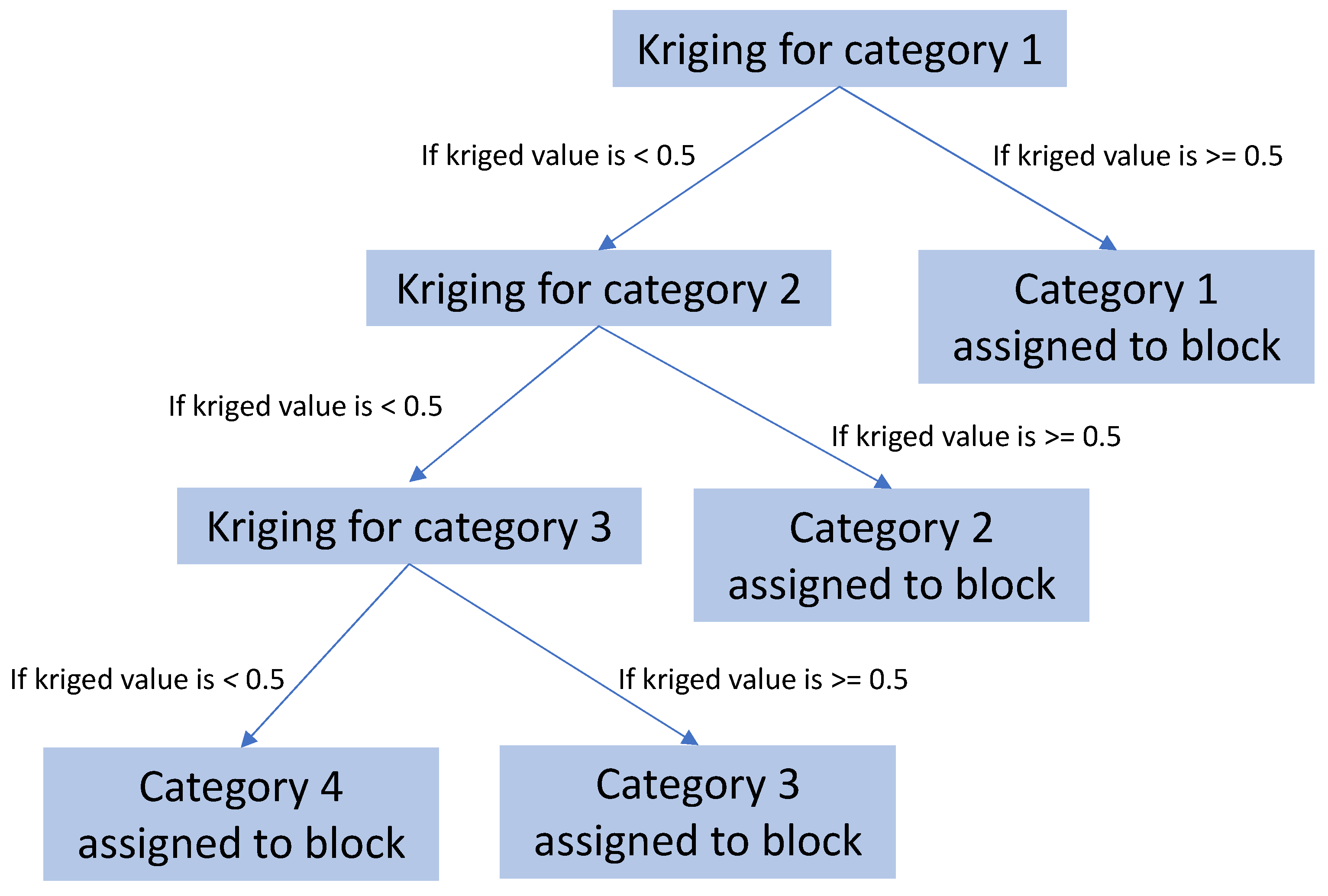
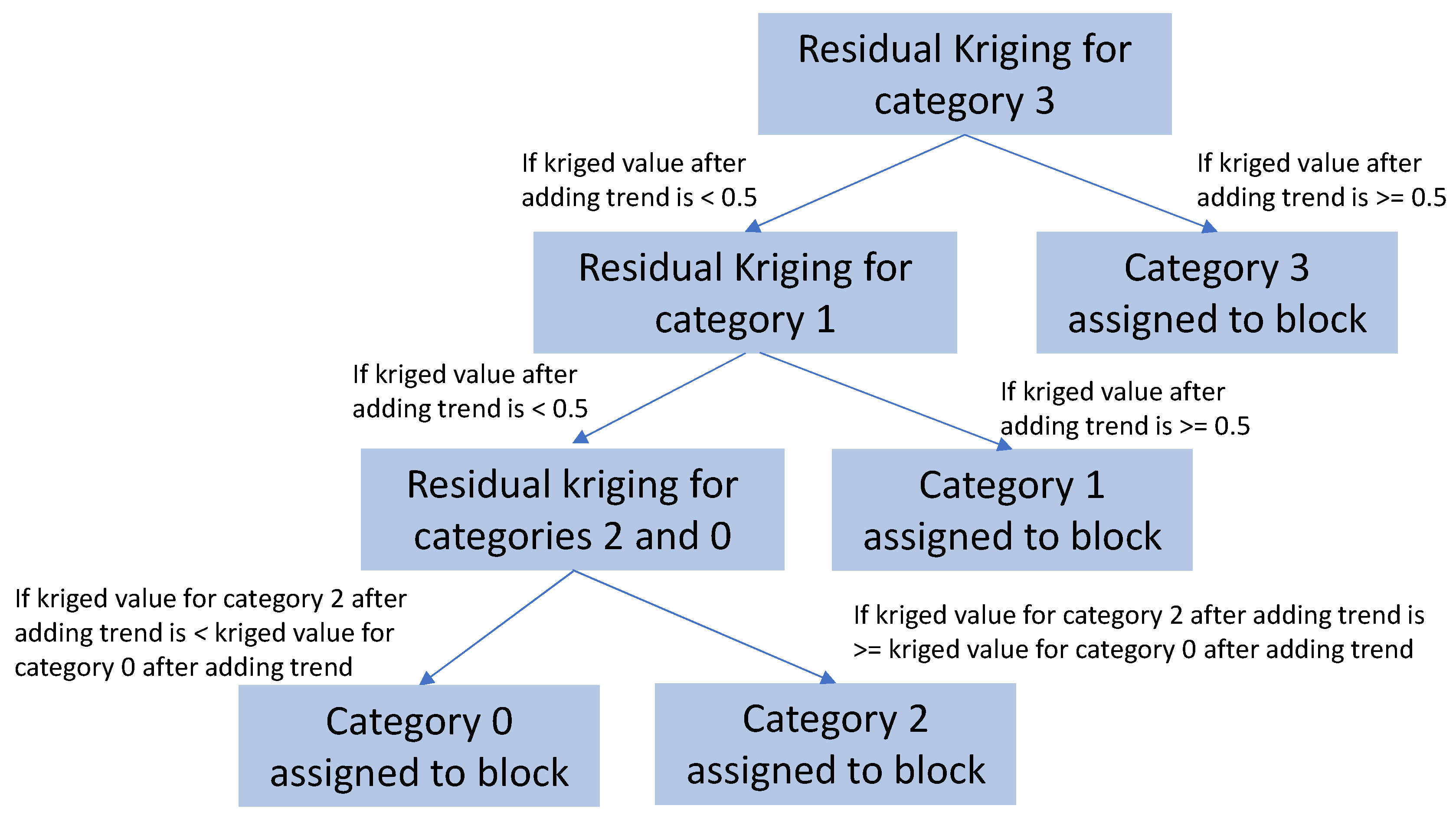
2.2. Hierarchical Indicator Kriging
- The authors of [39] demonstrate how different tree structures impact the realizations generated by Pluri-Gaussian Simulations. The authors state that building the tree structure for complex cases is not simple. The authors also emphasize that spatial and temporal relationships between different categories should be considered to build the tree.
- The authors of [40] highlight that both Sequential Indicator Simulation (SIS) and HIK depend heavily on hierarchical decisions. Poorly defined hierarchies can lead to artifacts such as extreme weights or unrealistic spatial transitions.
- The authors of [41] demonstrate that grouping similar rock types or materials in early hierarchical splits produces more geologically realistic boundaries, while poorly structured hierarchies compromise spatial continuity.
- Insights from [42] regarding hierarchical Truncated Pluri-Gaussian models further emphasize that incorrect truncation trees—or by analogy, partitioning trees in HIK—negatively impact the spatial distribution and proportions of categories.
Best Practices for Hierarchy Definition in HIK
- Start by splitting major geological or material groups, specifically those with the greatest dissimilarity in terms of physical properties, genesis, or economic value. Examples include
- ○
- Geotechnical modeling: dividing soft and hard rock;
- ○
- Mineral resource estimation: distinguishing ore from waste;
- ○
- Geometallurgical modeling: separating oxide ore from sulfide or primary ore.
- After this first split, subsequent divisions progressively refine the hierarchy, ideally grouping categories with greater internal similarity at each stage. The process continues until each individual category or rock type is isolated.
- Early splits influence large-scale spatial patterns;
- Later splits refine finer-scale heterogeneity;
- The order of splits governs how uncertainty and continuity propagate through the model, with different hierarchies producing distinct spatial realizations, even with identical input data.
2.3. Trend Model
- (1)
- Build the trend model with an appropriate technique. Thus, for each block in the model, there will be a probability of belonging or not belonging to a category, given the block location;
- (2)
- Assign a trend value to each sample by migrating the trend from the closest block;
- (3)
- Subtract the category indicator from the migrated trend value to compute the residual for each sample;
- (4)
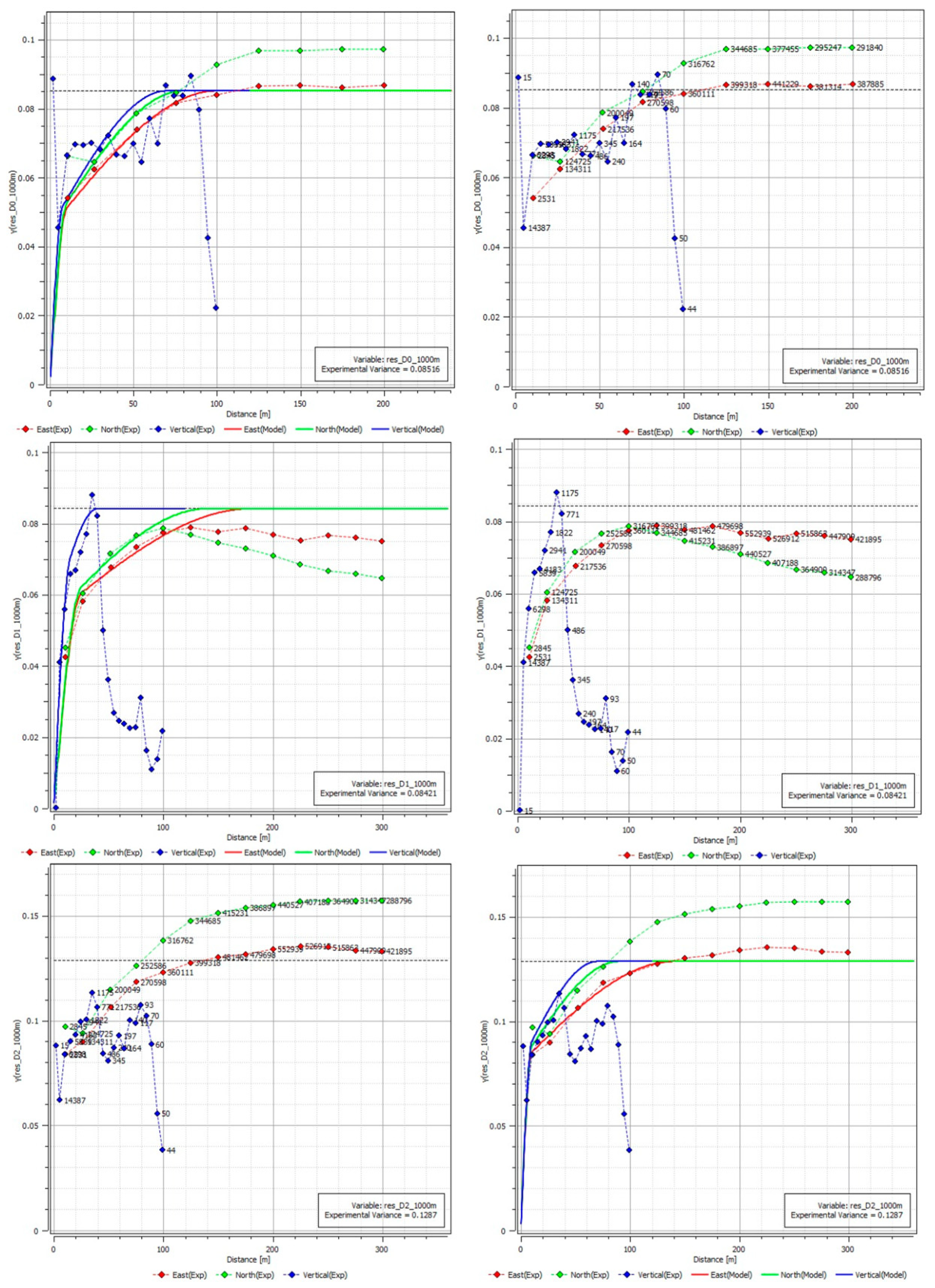
- Build the residual variogram model;
- (5)
- Krige the residual or simulate it;
- (6)
- For each block, add the kriged (or simulated) residual to the trend value, ensuring the final probability remains within the 0 to 1 range;
- (7)
- Validate the results.
SPDE
3. Materials and Methods
3.1. Geological Aspects
3.2. Processing Flowsheet
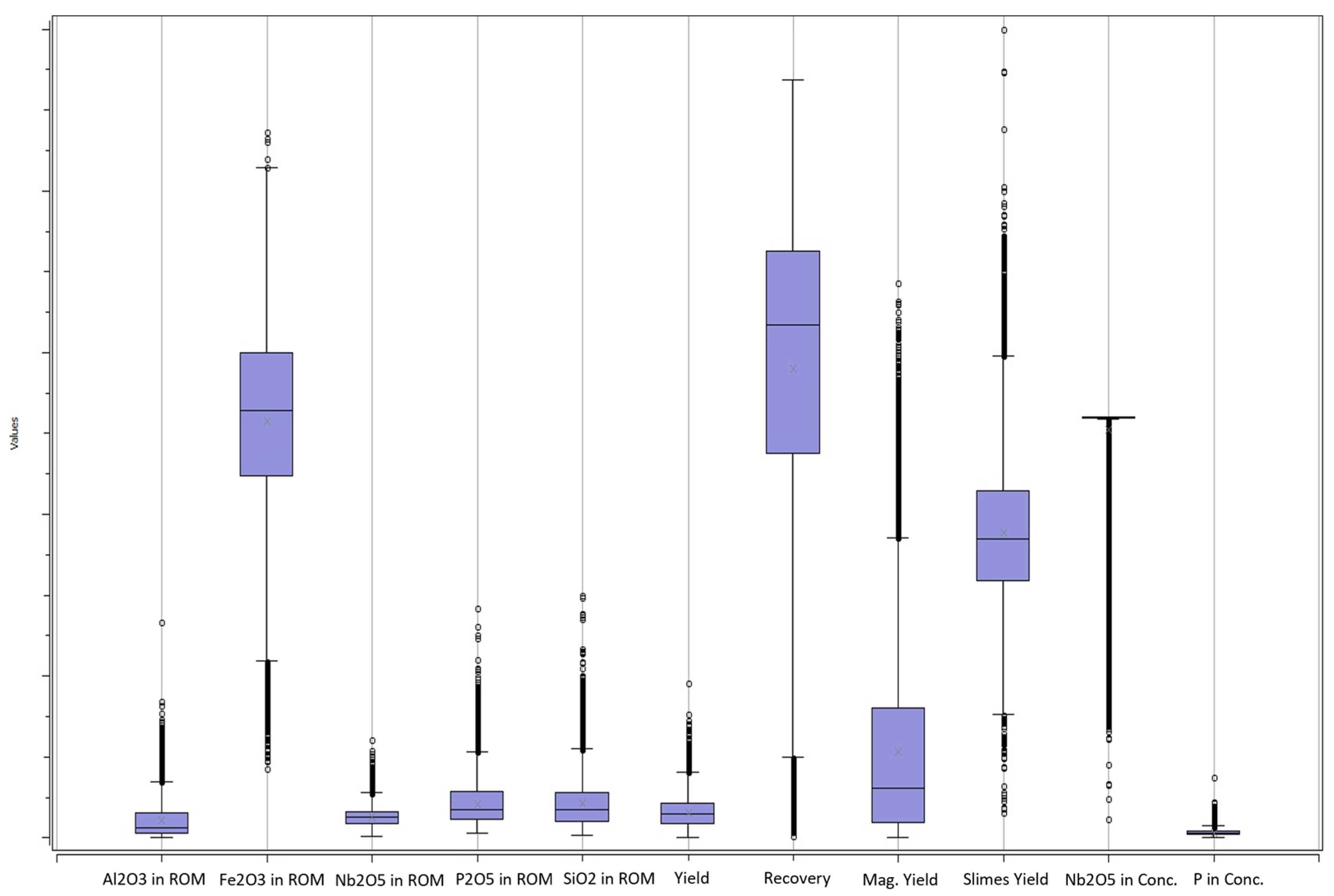
3.3. Database Information
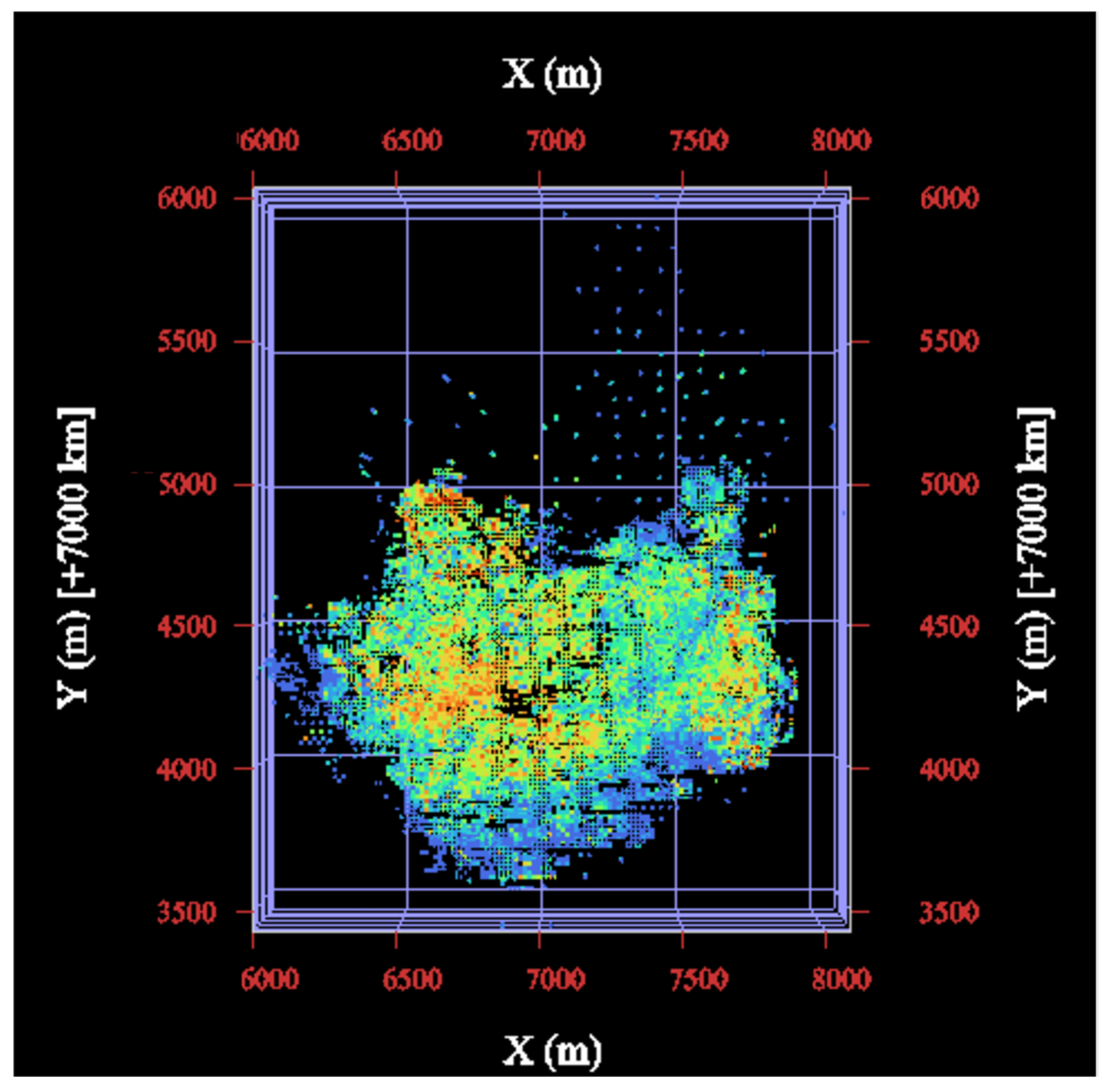
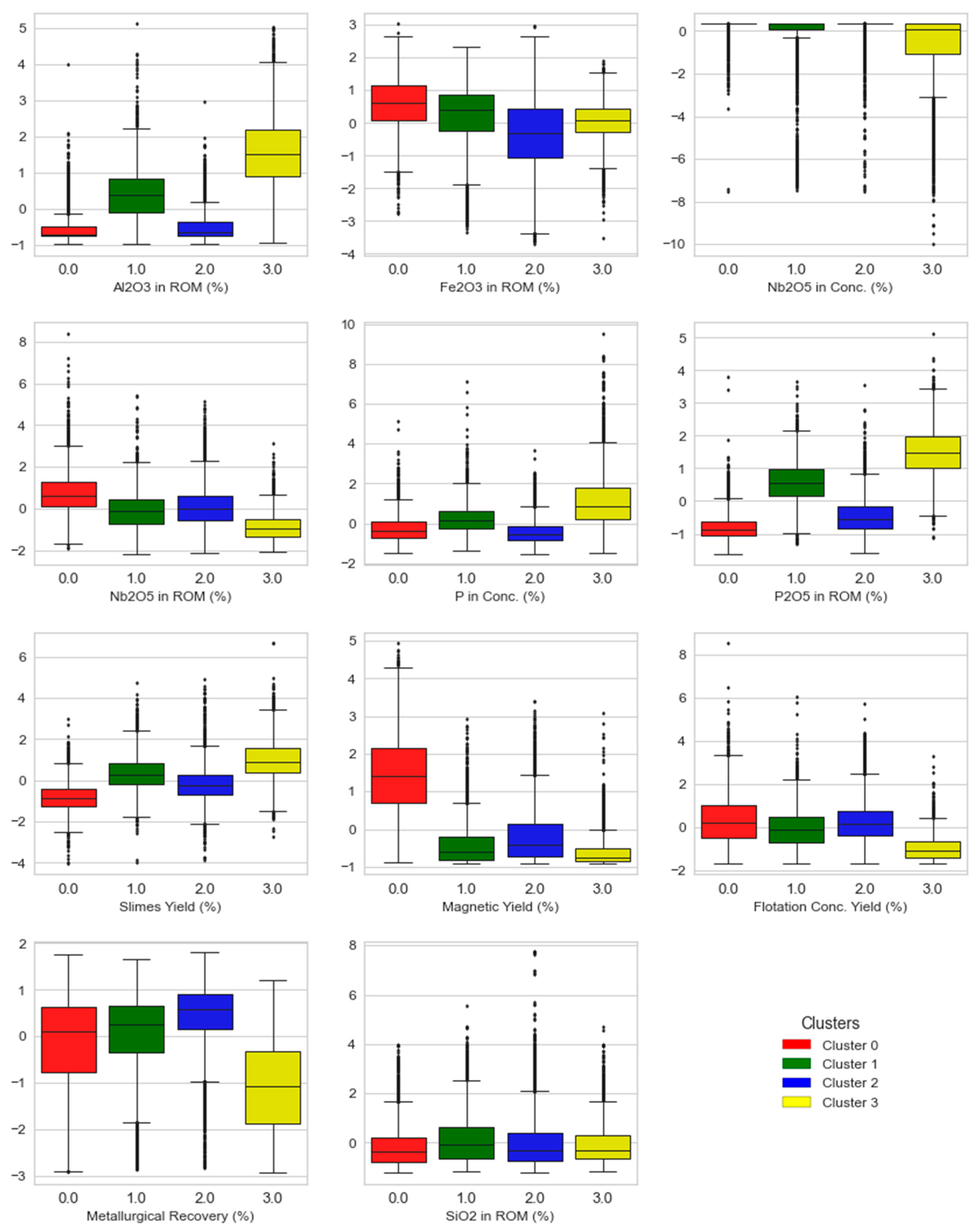
3.4. Cluster Analysis
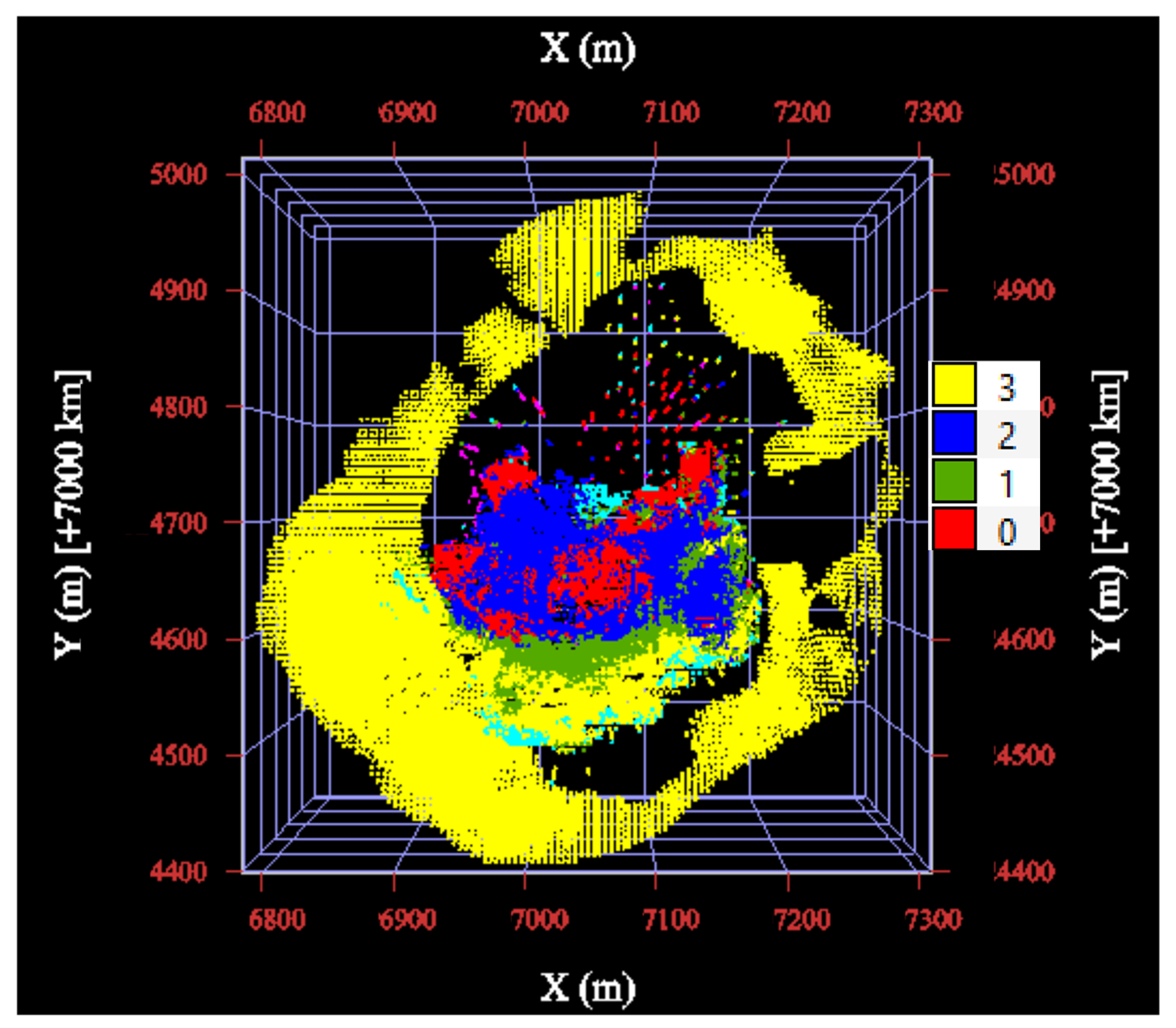
3.5. Hierarchical Indicator Kriging
3.6. Mineralogical Interpretation of the Clusters
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Niquini, F.G.F.; Costa, J.F.C.L.; Schneider, C.L.; Pereira, M.A.S. Economical definition of ore: Grade cutoffs or geo metallurgical response? In Proceedings of the 12th International Geostatistics Congress, Ponta Delgada, Portugal, 2–6 September 2024. [Google Scholar]
- Lemos, M.G.; Valente, T.; Marinho-Reis, A.P.; Fonseca, R.; Dumont, J.M.; Ferreira, G.M.M.; Delbem, I.D. Geoenvironmental study of gold mining tailings in a circular economy context: Santa Barbara, Minas Gerais, Brazil. Mine Water Environ. 2021, 40, 257–269. [Google Scholar] [CrossRef]
- Lemos, M.G.; Valente, T.M.; Reis, A.P.M.; Fonseca, R.M.F.; Guabiroba, F.; Mata Filho, J.G.; Magalhães, M.F.; Delbem, I.D.; Diório, G.R. Adding value to mine waste through recovery of Au, Sb, and As: The case of auriferous tailings in the Iron Quadrangle, Brazil. Minerals 2023, 13, 863. [Google Scholar] [CrossRef]
- Louwrens, E.; Napier-Munn, T.; Keeney, L. Geometallurgical characterisation of a tailings storage facility—A novel approach. In Proceedings of the Tailings and Mine Waste Management for the 21st Century, Sydney, NSW, Australia, 27–28 July 2015. [Google Scholar]
- Knight, R.; Olson Hoal, K.; Abraham, A.P.G. Three-dimensional geometallurgical data integration for predicting concentrate quality and tailings composition in a massive sulfide deposit. In Proceedings of the First AUSIMM International Geometallurgy Conference, Brisbane, QLD, Australia, 5–7 September 2011; pp. 227–232. [Google Scholar]
- Niquini, F.G.F.; Branches, A.M.B.; Costa, J.F.C.L.; Moreira, G.d.C.; Schneider, C.L.; de Araújo, F.C.; Capponi, L.N. Recursive feature elimination and neural networks applied to the forecast of mass and metallurgical recoveries in a Brazilian phosphate mine. Minerals 2023, 13, 748. [Google Scholar] [CrossRef]
- Niquini, F.G.F.; Costa, J.F.C.L. Mass and Metallurgical Balance Forecast for a Zinc Processing Plant Using Artificial Neural Networks. Nat. Resour. Res. 2020, 29, 3569–3580. [Google Scholar] [CrossRef]
- Boisvert, J.B.; Rossi, M.E.; Ehrig, K.; Deutsch, C.V. Geometallurgical modeling at Olympic Dam Mine, South Australia. Math. Geosci. 2013, 45, 901–925. [Google Scholar] [CrossRef]
- Montoya, P.A.; Keeney, L.; Jahoda, R.; Hunt, J.; Berry, R.; Drews, U.; Chamberlain, V.; Leichliter, S. Techniques applicable to prefeasibility projects—La Colosa case study. In Proceedings of the First AUSIMM International Geometallurgy Conference, Brisbane, QLD, Australia, 5–7 September 2011; pp. 103–111. [Google Scholar]
- Niquini, F.G.F.; Andrade, I.A.; Costa, J.F.C.L.; Silva, V.M.; Marcelino, R.S. A workflow to create geometallurgical clusters without looking directly at geometallurgical variables. Miner. Eng. 2025, 222, 109171. [Google Scholar] [CrossRef]
- Faouzi, R.; Oumesaoud, H.; Naji, K.; Benzakour, I.; Aboulhassan, M.A.; Faqir, H.; Tahari, H. Predictive geometallurgical modeling for flotation performance in mixed copper ores using discriminatory methods. Arab. J. Sci. Eng. 2024, 49, 8057–8078. [Google Scholar] [CrossRef]
- Siddiqui, M.U.; Erwin, K.; Khan, S.; Chandramohan, R.; Meinke, C. An efficient sample selection methodology for a geometallurgy study utilizing statistical analysis techniques. Min. Metall. Explor. 2024, 41, 2193–2201. [Google Scholar] [CrossRef]
- Mu, Y.; Salas, J.C. Data-driven synthesis of a geometallurgical model for a copper deposit. Processes 2023, 11, 1775. [Google Scholar] [CrossRef]
- Bhuiyan, M.; Esmaieli, K.; Ordóñez-Calderón, J.C. Application of data analytics techniques to establish geometallurgical relationships to bond work index at the Paracutu Mine, Minas Gerais, Brazil. Minerals 2019, 9, 302. [Google Scholar] [CrossRef]
- Rajabinasab, B.; Asghari, O. Geometallurgical domaining by cluster analysis: Iron ore deposit case study. Nat. Resour. Res. 2018, 28, 665–684. [Google Scholar] [CrossRef]
- Sepúlveda, E.; Dowd, P.A.; Xu, C. Fuzzy clustering with spatial correction and its application to geometallurgical domaining. Math. Geosci. 2018, 50, 895–928. [Google Scholar] [CrossRef]
- Manfrino, A. Unravelling the factors impacting on concentrate quality by geometallurgical data analysis at Fortescue Metals Group’s Iron Bridge Magnetite Mine. In Proceedings of the Iron Ore Conference 2015, Perth, WA, Australia, 13–15 July 2015; pp. 567–578. [Google Scholar]
- Romary, T.; Rivoirard, J.; Deraisme, J.; Quinones, C.; Freulon, X. Domaining by Clustering Multivariate Geostatistical Data. In Geostatistics Oslo 2012. Quantitative Geology and Geostatistics; Abrahamsen, P., Hauge, R., Kolbjørnsen, O., Eds.; Springer: Dordrecht, The Netherlands, 2012; Volume 17. [Google Scholar] [CrossRef]
- Rolo, R.M.; Moreira, G.; Guimarães, O.R.A.; Fonseca, C.; Usero, G. Machine learning driven domain modeling for stratigraphic deposits. In Proceedings of the APCOM 2023, Rapid City, SD, USA, 25–28 June 2023. [Google Scholar]
- Moreira, G.C.; Costa, J.F.C.L.; Marques, D.M. Defining geologic domains using cluster analysis and indicator correlograms: A phosphate-titanium case study. Appl. Earth Sci. 2020, 129, 176–190. [Google Scholar] [CrossRef]
- Koruk, K.; Ortiz, J.M. Geological Domaining with Unsupervised Clustering and Ensemble Support Vector Classification. Min. Metall. Explor. 2023, 40, 2537–2549. [Google Scholar] [CrossRef]
- Madani, N.; Maleki, M.; Sepidbar, F. Application of geostatistical hierarchical clustering for geochemical population identification in Bondar Hanza copper porphyry deposit. Geochemistry 2021, 81, 125794. [Google Scholar] [CrossRef]
- Hong, J.; Oh, S. Model Selection for Mineral Resource Assessment Considering Geological and Grade Uncertainties: Application of Multiple-Point Geostatistics and a Cluster Analysis to an Iron Deposit. Nat. Resour. Res. 2021, 30, 2047–2065. [Google Scholar] [CrossRef]
- Scheidt, C.; Caers, J. Representing Spatial Uncertainty Using Distances and Kernels. Math. Geosci. 2009, 41, 397–419. [Google Scholar] [CrossRef]
- Okada, R.; Costa, J.F.C.L.; Rodrigues, Á.L.; Kuckartz, B.T.; Marques, D.M. Scenario reduction using machine learning techniques applied to conditional geostatistical simulation. REM—Int. Eng. J. 2019, 72, 63–68. [Google Scholar] [CrossRef]
- Bye, A.R. Case studies demonstrating value from geometallurgy initiatives. In Proceedings of the GeoMet 2011: The First AusIMM International Geometallurgy Conference 2011, Brisbane, QLD, Australia, 5–11 September 2011; AusIMM Australasian Institute of Mining and Metallurgy: Carlton, VIC, Australia, 2011. [Google Scholar]
- Leal, R.S.; Peroni, R.L.; Costa, J.F.C.L.; Pereira, S.G.; Martins, R.M.; Capponi, L.N. Geostatistics applied to geometallurgical modeling. In Proceedings of the 24th World Mining Congress PROCEEDINGS, Rio de Janeiro, Brazil, 18–21 October 2016; IBRAM: Rio de Janeiro, Brazil, 2016. [Google Scholar]
- Vieira, M.; Costa, J.F.C.L. Geometallurgical modelling to help in predicting zinc metallurgical recovery. In Proceedings of the 24th World Mining Congress PROCEEDINGS, Rio de Janeiro, Brazil, 18–21 October 2016; IBRAM: Rio de Janeiro, Brazil, 2016. [Google Scholar]
- Sokal, R.R.; Sneath, P.H.A. Principles of Numerical Taxonomy; W. H. Freeman: New York, NY, USA, 1963. [Google Scholar]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA, 21 June–18 July 1965; Volume 1, pp. 281–297. [Google Scholar]
- Martin, R.; Boisvert, J. Towards justifying unsupervised stationary decisions for geostatistical modeling: Ensemble spatial and multivariate clustering with geomodeling-specific clustering metrics. Comput. Geosci. 2018, 120, 82–96. [Google Scholar] [CrossRef]
- Scrucca, L. Clustering multivariate spatial data based on local measures of spatial autocorrelation. Quad. Dip. Econ. Finanz. Stat. Univ. Perugia 2005, 20, 11. [Google Scholar]
- Calinski, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat.—Theory Methods 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Journel, A.G. The indicator approach to estimation of spatial data. In Proceedings of the 17th APCOM, New York, NY, USA, 9–22 April 1982; Port City Press: New York, NY, USA, 1982; pp. 793–806. [Google Scholar]
- Journel, A.G.; Huijbregts, C.J. Mining Geostatistics; Academic Press: London, UK, 1978; 600p. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997; 483p. [Google Scholar]
- Matheron, G. The Theory of Regionalized Variables and Its Applications; École des Mines de Paris: Paris, France, 1971; 211p. [Google Scholar]
- Armstrong, M.; Galli, A.; Beucher, H.; Le Loc’h, G.; Renard, D.; Doligez, B.; Eschard, R.; Geffroy, F. Plurigaussian Simulation in Geosciences, 2nd ed.; Springer: Berlin, Germany, 2011; 182p. [Google Scholar]
- Sektnan, A.; Vázquez, A.A.; Hauge, R.; Aarnes, I.; Skauvold, J.; Vevle, M.L. A Tree Representation of Pluri-Gaussian Truncation Rules. Math. Geosci. 2025, 57, 445–470. [Google Scholar] [CrossRef]
- Ortiz, R.B. Advances in Geostatistical Modeling of Categorical Variables. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2024. [Google Scholar]
- Amarante, F.A.N.; Rolo, R.M. Boundary simulation–a hierarchical approach for multiple categories. Appl. Earth Sci. 2021, 130, 123–135. [Google Scholar] [CrossRef]
- Sanchez, H.V. Truncation Trees in Hierarchical Truncated PluriGaussian Simulation. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2023. [Google Scholar]
- Rossi, M.E.; Deutsch, C.V. Mineral Resource Estimation; Springer Science & Business Media: Berlin, Germany, 2013; 332p. [Google Scholar]
- Porskamp, P.; Rattray, A.; Young, M.; Ierodiaconou, D. Multiscale and hierarchical classification for benthic habitat mapping. Geosciences 2018, 8, 119. [Google Scholar] [CrossRef]
- Volpi, B.; Galli, A.; Ravenne, C. Vertical proportion curves: A qualitative and quantitative tool for reservoir characterization. In Proceedings of the First Latin American Congress of Sedimentology, Isla de Margarita, Venezuela, 16–19 November 1997. [Google Scholar]
- Carrizo Vergara, R.; Allard, D.; Desassis, N. A general framework for SPDE-based stationary random fields. Bernoulli 2022, 28, 1–32. [Google Scholar] [CrossRef]
- Lindgren, F.; Rue, H.; Lindström, J. An Explicit Link between Gaussian Fields and Gaussian Markov Random Fields: The Stochastic Partial Differential Equation Approach. J. R. Stat. Soc. Ser. B Stat. Methodol. 2011, 73, 423–498. [Google Scholar] [CrossRef]
- Deutsch, C.V. Cleaning categorical variable (lithofacies) realizations with maximum a-posteriori selection. Comput. Geosci. 1998, 24, 551–562. [Google Scholar] [CrossRef]

| Variable | Anisotropy Rotation | Nugget Effect | 1st Structure | Range 1st Structure | Sill 1st Structure | 2nd Structure | Range 2nd Structure | Sill 2nd Structure |
|---|---|---|---|---|---|---|---|---|
| Residual - Cluster 0 | D0° N90° p90° | 0 | Spherical | 10/10/7.5 m | 0.05 | Spherical | 100/80/70 m | 0.04 |
| Residual - Cluster 1 | D0° N90° p90° | 0 | Spherical | 25/25/15 m | 0.05 | Spherical | 180/140/40 m | 0.03 |
| Residual - Cluster 2 | D0° N90° p90° | 0 | Spherical | 10/10/10 m | 0.08 | Spherical | 140/90/70 m | 0.05 |
| Residual - Cluster 3 NW-SE | D0° N60° p90° | 0 | Spherical | 30/30/10 m | 0.02 | Spherical | 150/170/60 m | 0.03 |
| Residual - Cluster 3 NE-SW | D0° N60° p90° | 0 | Spherical | 30/30/7.5 m | 0.02 | Spherical | 140/150/35 m | 0.04 |
| Mineral | Cluster 0 | Cluster 1 | Cluster 2 | Cluster 3 |
|---|---|---|---|---|
| Pyrochlore | 3.13 | 4.08 | 4.85 | 1.47 |
| Barite | 16.52 | 6.42 | 25.14 | 3.21 |
| Goethite | 28.54 | 39.86 | 30.88 | 38.71 |
| Hematite | 20.53 | 9.90 | 12.99 | 16.54 |
| Magnetite | 12.67 | 3.51 | 8.53 | 18.64 |
| Aluminophosphates | 3.36 | 7.54 | 2.29 | 8.94 |
| Clay minerals | 2.07 | 4.08 | 2.84 | 2.36 |
| Titanium oxide | 2.21 | 2.63 | 2.29 | 1.33 |
| Monazite | 3.51 | 4.11 | 3.59 | 2.48 |
| Quartz | 4.74 | 15.60 | 4.60 | 2.91 |
| Hollandite | 1.31 | 1.98 | 1.50 | 0.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, J.F.C.L.; Niquini, F.G.F.; Schneider, C.L.; Alcântara, R.M.; Capponi, L.N.; Rodrigues, R.S. Geometallurgical Cluster Creation in a Niobium Deposit Using Dual-Space Clustering and Hierarchical Indicator Kriging with Trends. Minerals 2025, 15, 755. https://doi.org/10.3390/min15070755
Costa JFCL, Niquini FGF, Schneider CL, Alcântara RM, Capponi LN, Rodrigues RS. Geometallurgical Cluster Creation in a Niobium Deposit Using Dual-Space Clustering and Hierarchical Indicator Kriging with Trends. Minerals. 2025; 15(7):755. https://doi.org/10.3390/min15070755
Chicago/Turabian StyleCosta, João Felipe C. L., Fernanda G. F. Niquini, Claudio L. Schneider, Rodrigo M. Alcântara, Luciano N. Capponi, and Rafael S. Rodrigues. 2025. "Geometallurgical Cluster Creation in a Niobium Deposit Using Dual-Space Clustering and Hierarchical Indicator Kriging with Trends" Minerals 15, no. 7: 755. https://doi.org/10.3390/min15070755
APA StyleCosta, J. F. C. L., Niquini, F. G. F., Schneider, C. L., Alcântara, R. M., Capponi, L. N., & Rodrigues, R. S. (2025). Geometallurgical Cluster Creation in a Niobium Deposit Using Dual-Space Clustering and Hierarchical Indicator Kriging with Trends. Minerals, 15(7), 755. https://doi.org/10.3390/min15070755






