Adaptive Differential Evolution Algorithm for Induced Polarization Parameters in Frequency-Domain Controlled-Source Electromagnetic Data
Abstract
1. Introduction
2. Methodology
2.1. One-Dimensional Forward-Modeling Theory of the Controlled-Source Frequency-Domain Electromagnetic Method Considering the Induced Polarization Effect
2.1.1. The Cole–Cole Model
2.1.2. One-Dimensional Forward-Modeling of the Controlled-Source Frequency-Domain Electromagnetic Method with a Finite-Length Source
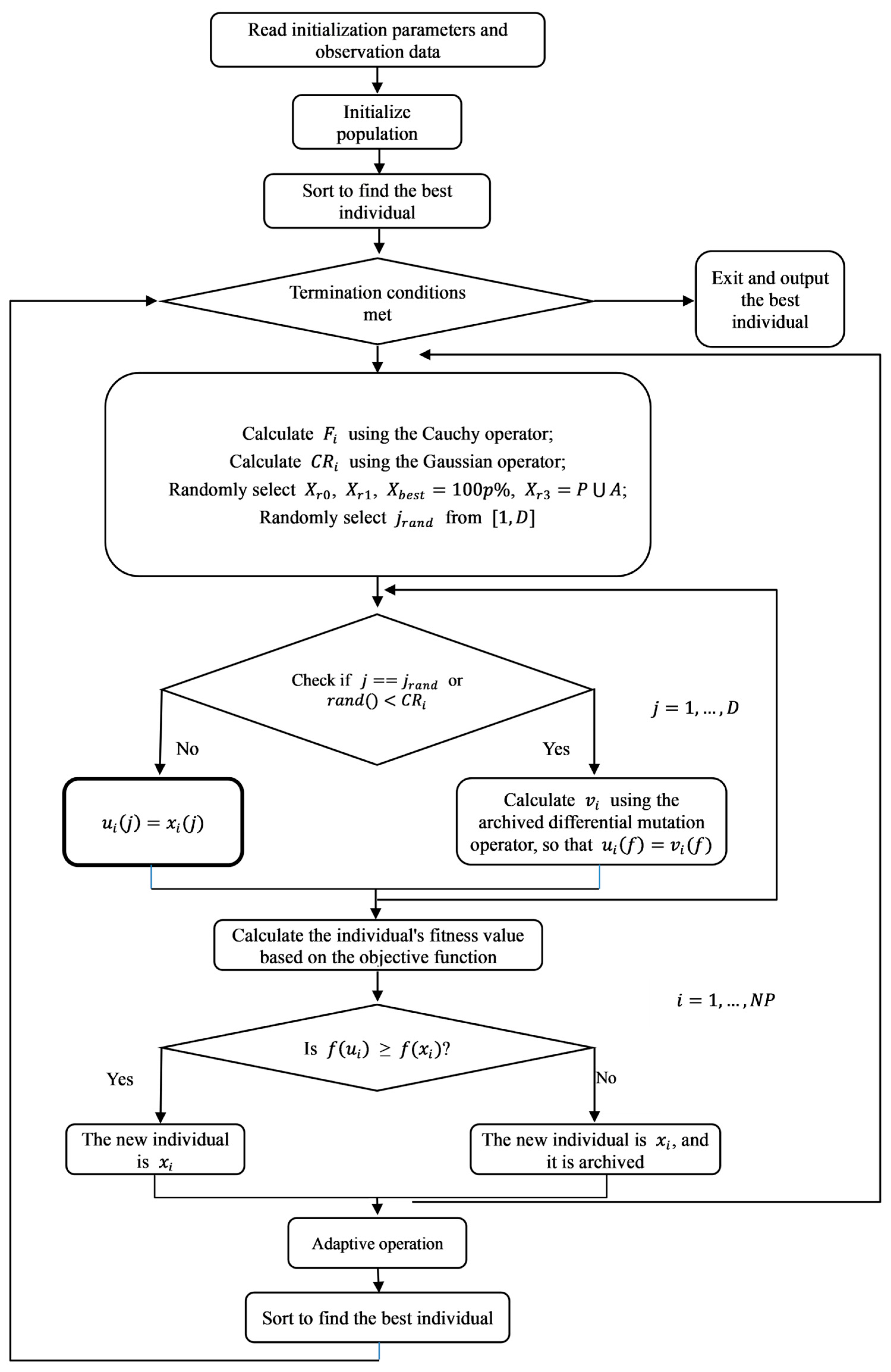
2.2. Adaptive Differential Evolution Algorithm
3. Inversion of the Controlled-Source Electromagnetic Method Considering the Induced Polarization Effect
3.1. Objective Function Construction
3.2. Introduction of Minimum Structure
4. Theoretical Model Validation
4.1. Representative Three-Layer Geoelectric Model
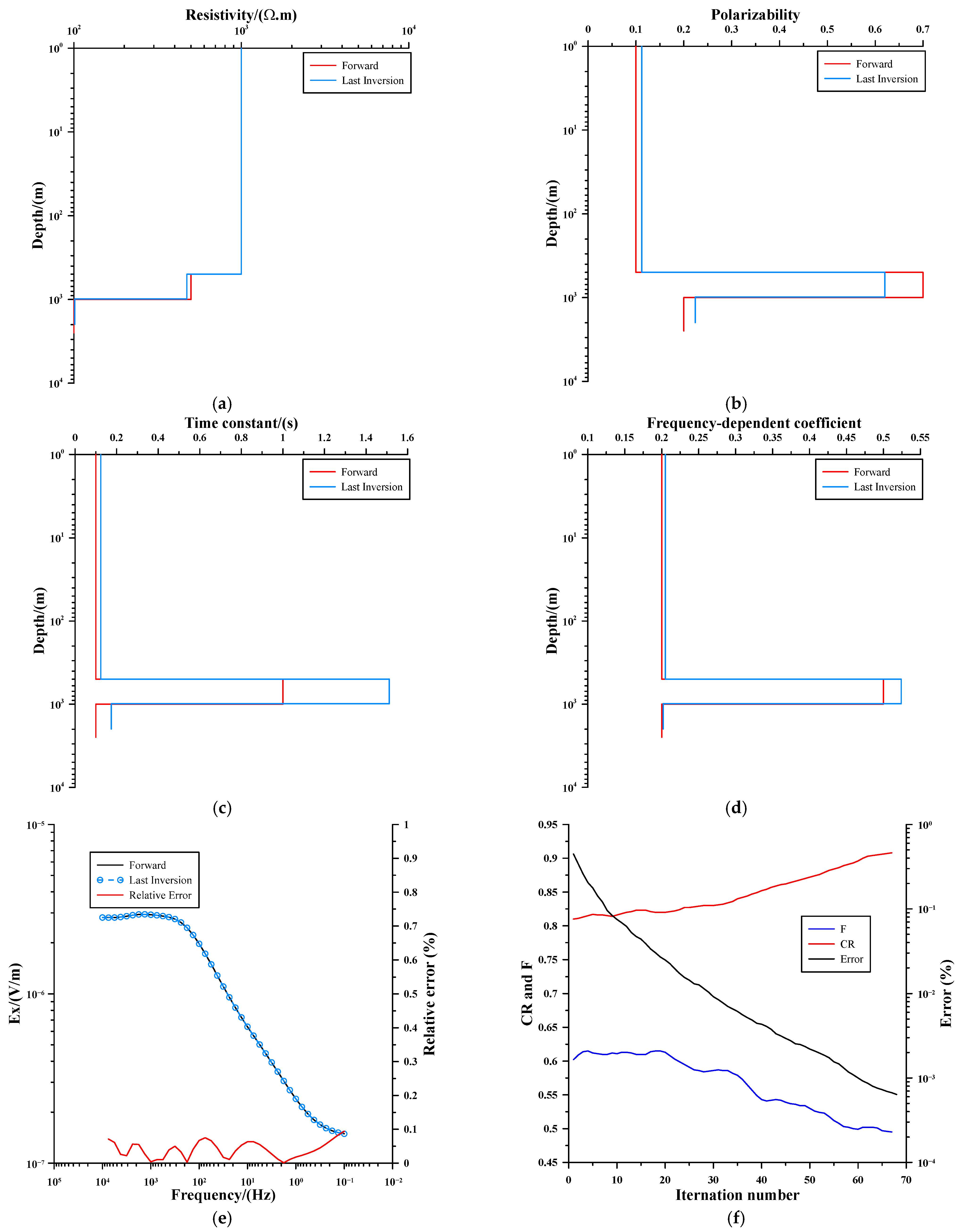
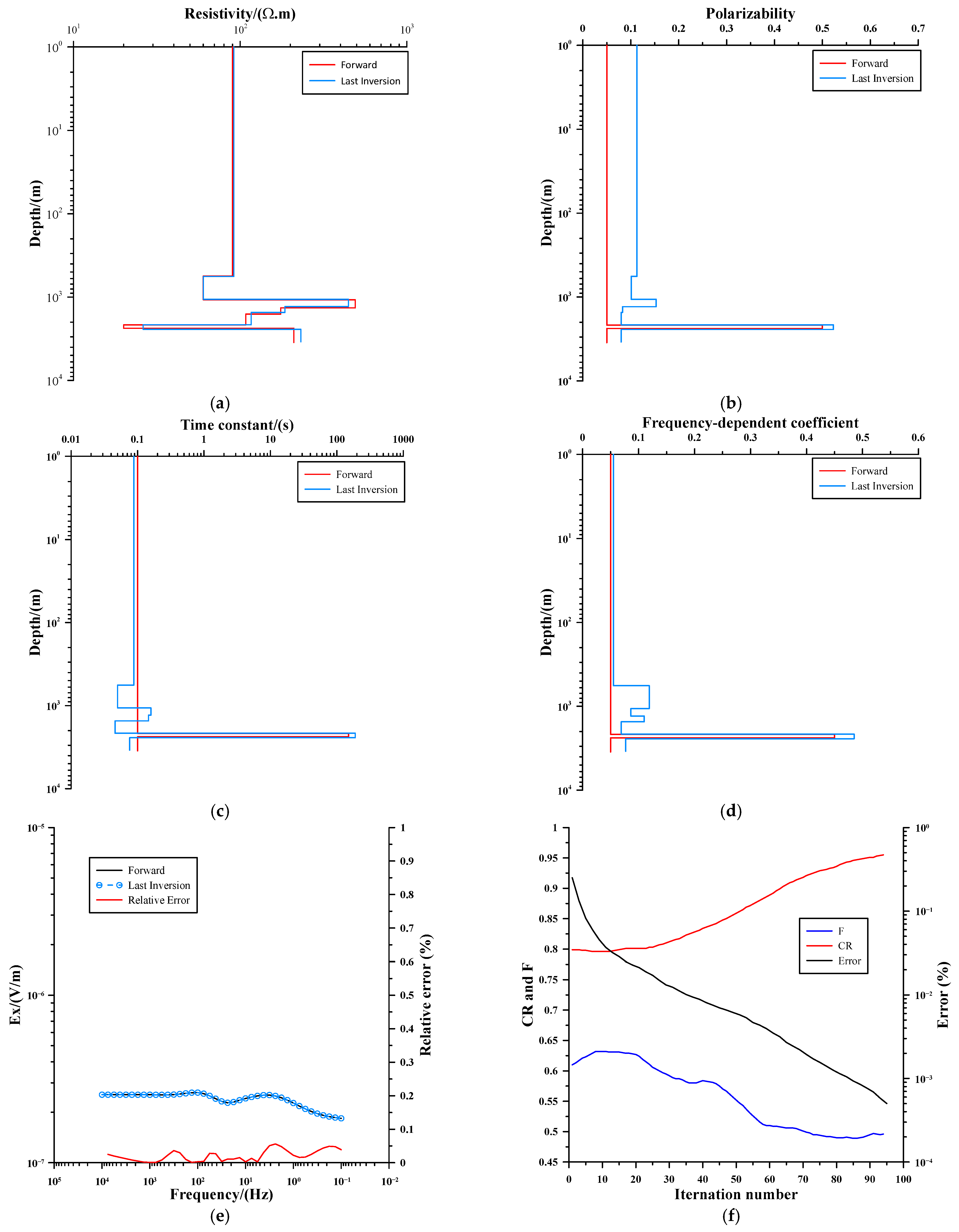
4.2. Real-World Geoelectric Model
4.2.1. Inversion of Theoretical Model Data
4.2.2. Inversion of Noisy Data
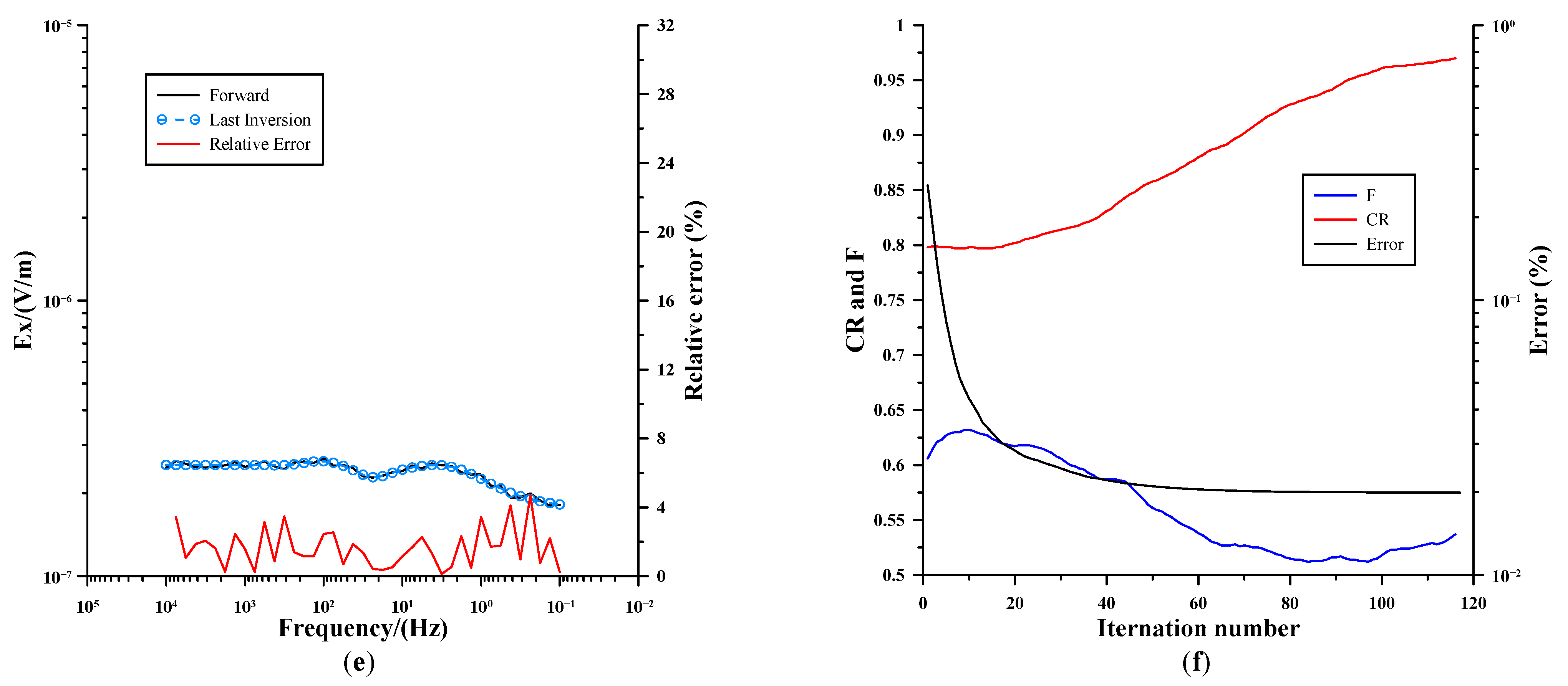
4.3. Practical Application
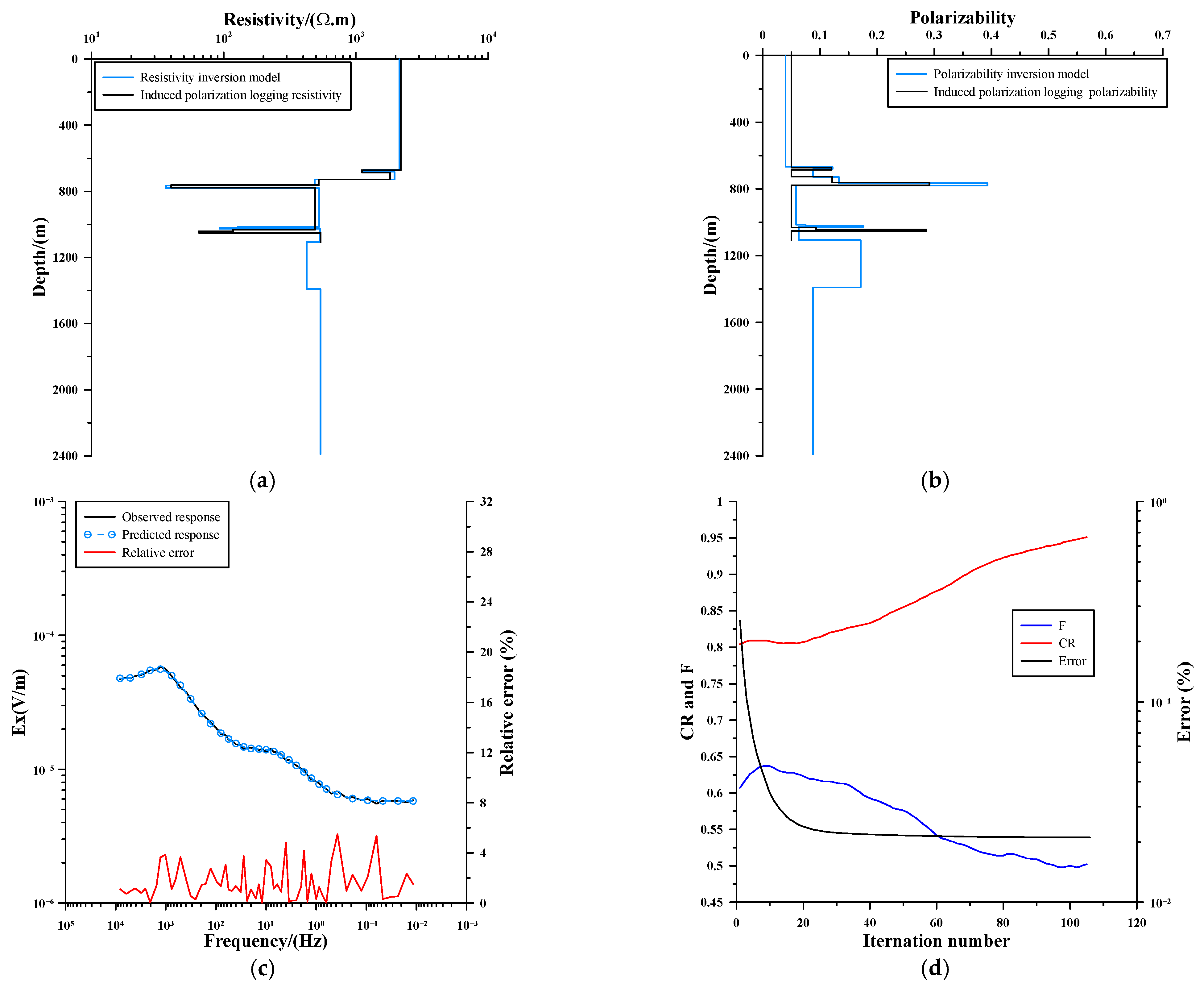
4.3.1. Induced Polarization Logging Results of Borehole ZK
4.3.2. Inversion of Survey Points Adjacent to Borehole ZK
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bertin, J.; Loeb, J.; Chen, L. Experiments and Theory of Induced Polarization; Geological Press: Beijing, China, 1980. [Google Scholar]
- Xu, W.D.; Che, Y.J. On IP Effect of Multi-polarization Layers from CSAMT. J. Eng. Geophys. 2012, 9, 511–515. [Google Scholar]
- Tang, J.T.; Huang, L.; Yu, C.L. The responsibility of apparent resistivity curves on CSAMT for polarized layer. Chin. J. Eng. Geophys. 2008, 5, 648–651. [Google Scholar]
- Yue, A.P.; Di, Q.Y.; Wang, M.Y.; Shi, K.F. 1D forward simulation of MT induced polarization (IP) effect of reservoir. Oil Geophys. Prospect. 2009, 44, 364–370. [Google Scholar]
- Yue, A.P.; Di, Q.Y.; Wang, M.Y.; Shi, K.F. 1-D forward modeling of the CSAMT signal incorporating IP effect. Chin. J. Geophys. 2009, 52, 1937–1946. (In Chinese) [Google Scholar] [CrossRef]
- Yu, C.T. 2D Forward Modeling and Joint Inversion of the CSAMT Signal Incorporation IP Effect. Ph.D. Thesis, Taiyuan University of Technology, Taiyuan, China, 2012. [Google Scholar]
- Wang, J.L.; Liu, M.W.; Li, D.; Li, J.H.; Lin, P.R.; Wang, M. Finite element numerical simulation on line controlled source based on Cole-Cole model. Comput. Tech. Geophys. Chem. Explor. 2015, 37, 32–39. [Google Scholar]
- Huang, Y.W. 3D Forward Modeling and Response Analysis of the Controlled Source Electromagnetic Signal with IP Effect. Master’s Thesis, East China University of Technology, Nanchang, China, 2017. [Google Scholar]
- Cheng, J.Z. Study and Application of Full-Parameter Inversion Method in Time-Frequency Electromagnetic Method. Master’s Thesis, Yangtze University, Wuhan, China, 2018. [Google Scholar]
- Joost, H.; Grigory, G.; Konstantin, T.; Andreas, K. Conversion of induced polarization data and their uncertainty from time domain to frequency domain using Debye decomposition. Minerals 2023, 13, 955. [Google Scholar] [CrossRef]
- He, H.Y.; Wang, J.R.; Wen, W.; Tian, R.C.; Lin, J.S.; Huang, W.Q.; Li, Y.B. Deep structure of epithermal deposits in Youxi area: Insights from CSAMT and Dual—Frequnency IP data. Minerals 2024, 14, 27. [Google Scholar] [CrossRef]
- Dong, L.; Jiang, F.B.; Li, D.Q. IP extraction from magnetotelluric sounding data based on adaptive differential evolution inversion. Oil Geophys. Prospect. 2016, 51, 613–624. [Google Scholar] [CrossRef]
- Yoshioka, K.; Zhdanov, M.S. Three-dimensional nonlinear regularized inversion of the induced polarization data based on the Cole-Cole model. Phys. Earth Planet. Inter. 2005, 150, 29–43. [Google Scholar] [CrossRef]
- Liu, L.; Chang, Y.J.; Cao, Z.L. Research on induced polarization effect of CSAMT on polarizable horizontal layer. Chin. J. Eng. Geophys. 2008, 5, 686–690. [Google Scholar]
- Huang, L. Extract IP Effect from CSAMT. Master’s Thesis, Central South University, Changsha, China, 2009. [Google Scholar]
- Xu, W.D. Study on Effection and Application of IP from CSAMT. Ph.D. Thesis, Jilin University, Changchun, China, 2011. [Google Scholar]
- Feng, B.; Wang, J.L.; Zhang, J.F.; Duan, M.J. The preliminary exploration to extract the IP effect which using CSAMT electromagnetic field response method. Prog. Geophys. 2013, 28, 2116–2122. [Google Scholar] [CrossRef]
- Xu, Y.C. 1D Forward Modeling and Inversion of the CSAMT Signal Incorporation IP Effect. Master’s Thesis, Chengdu University of Technology, Chengdu, China, 2016. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Pan, K.J.; Wang, W.J.; Tan, Y.J.; Cao, J.X. Geophysical linear inversion based on hybrid differential evolution algorithm. Chin. J. Geophys. 2009, 52, 3083–3090. (In Chinese) [Google Scholar] [CrossRef]
- Xiong, J.; Meng, X.H.; Liu, C.Y.; Peng, M. Magnetotelluric inversion based on differential evolution. Geophys. Geochem. Explor. 2012, 36, 448–451. [Google Scholar]
- Zeng, Z.W.; Chen, X.; Yang, H.Y.; Zhang, Z.Y.; Guo, Y.H.; Liu, X.; Ye, Y.X. Joint inversion of magnetotelluric and gravity based on improved differential evolution algorithm and wide-range petrophysical constraints. Chin. J. Geophys. 2020, 63, 4565–4577. (In Chinese) [Google Scholar] [CrossRef]
- Wang, T.Y.; Hou, Z.; He, Y.X.; Yang, J.; Chao, M.N.; Liu, G.H. Magnetotelluric inversion based on the improved differential evolution algorithm. Prog. Geophys. 2022, 37, 1605–1612. [Google Scholar] [CrossRef]
- Kenneth, S.C.; Robert, H.C. Dispersion and absorption in dielectrics I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Pelton, W.H.; Ward, P.G.; Half, P.G.; Sill, W.R.; Nelson, P.H. Mineral discrimination and removal of inductive coupling with multifrequency IP. Geophysics 1978, 43, 588–609. [Google Scholar] [CrossRef]
- Liu, Y. 2D Finite Element Modeling and Inversion for Marine Controlled-Source Electromagnetic Fields. Ph.D. Thesis, Ocean University of China, Qingdao, China, 2014. [Google Scholar]
- Zhang, J.Q.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Chen, X.B.; Zhao, G.Z.; Tang, J.; Zhan, Y.; Wang, J.J. An adaptive regularized inversion algorithm for magnetolluric data. Chin. J. Geophys. 2005, 48, 937–946. (In Chinese) [Google Scholar] [CrossRef]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
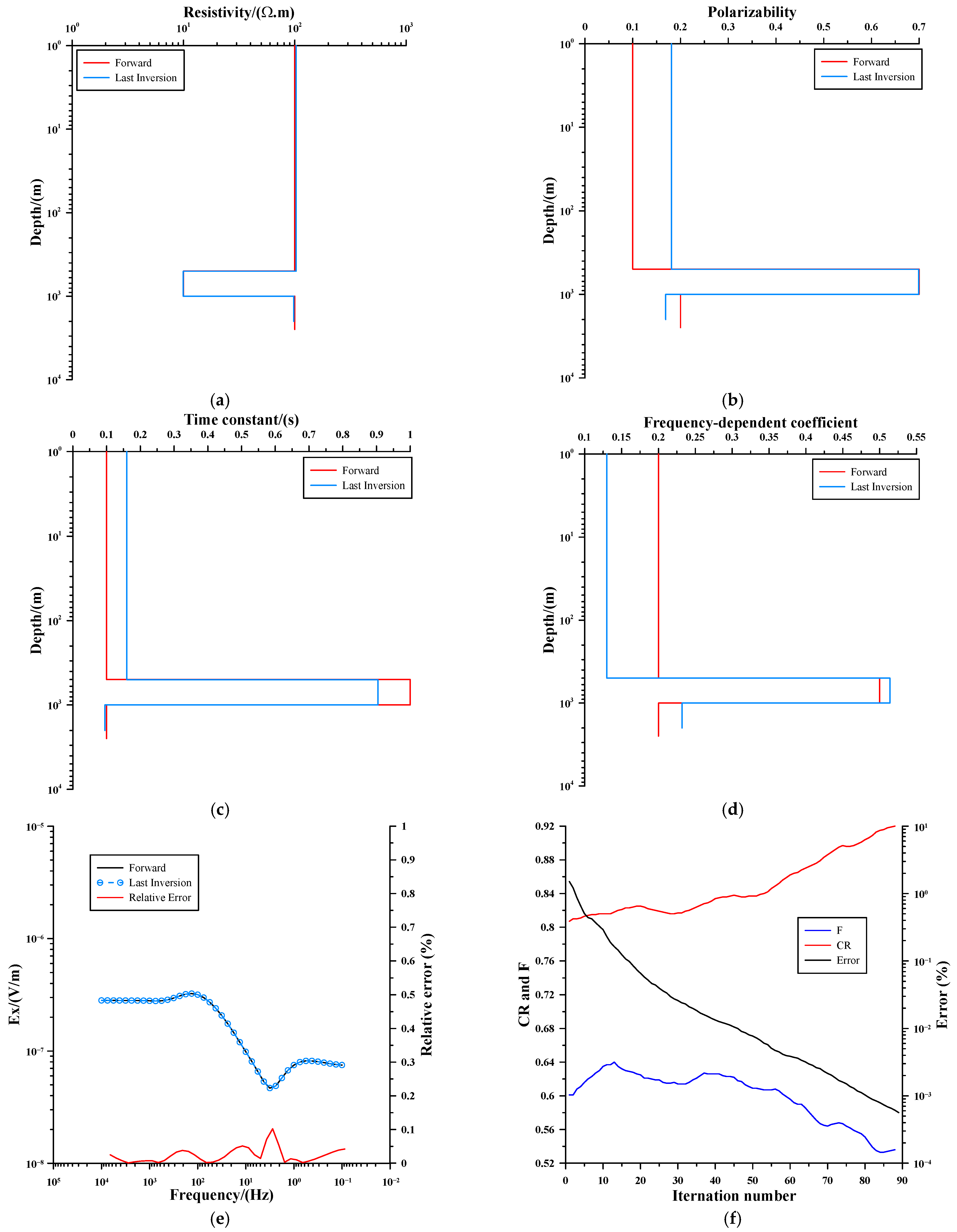
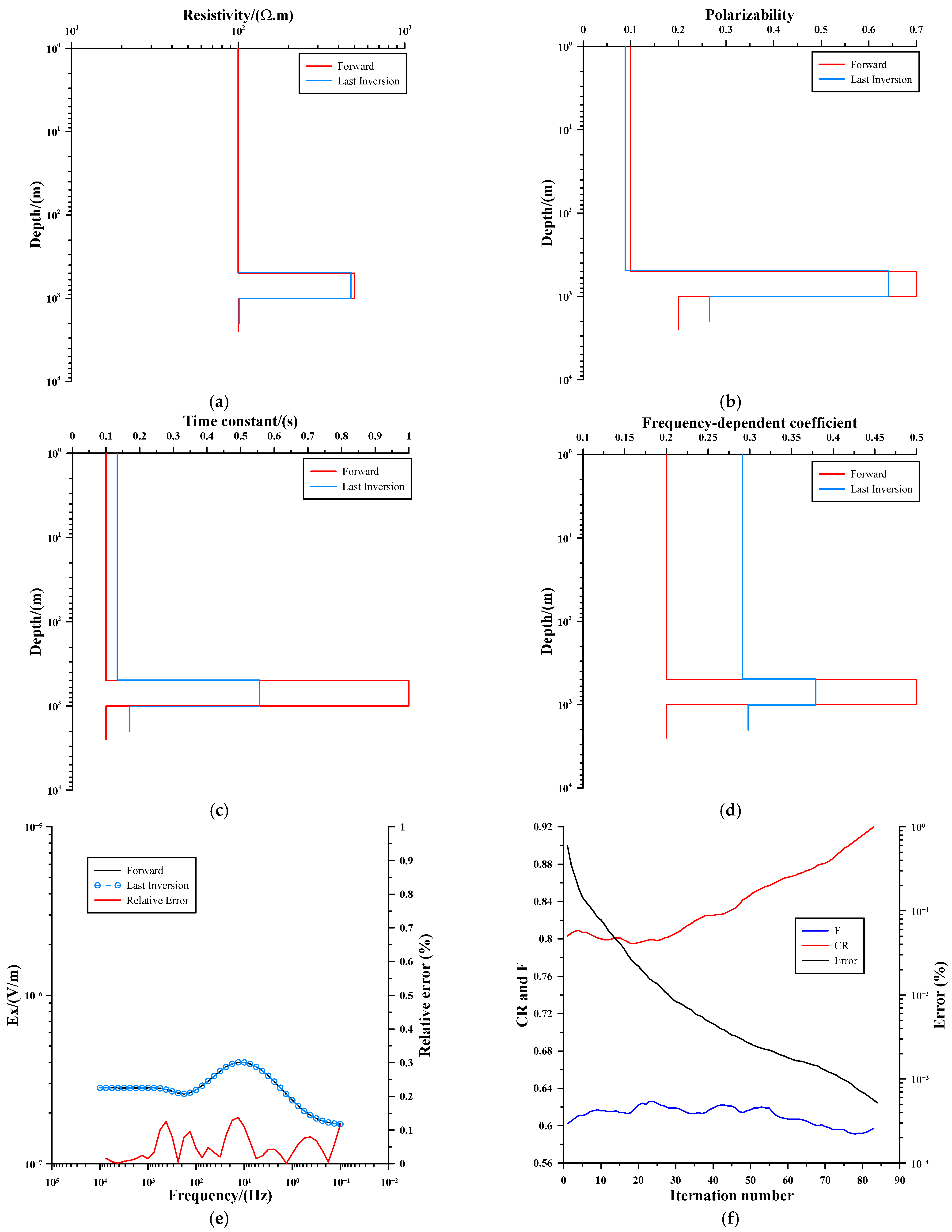
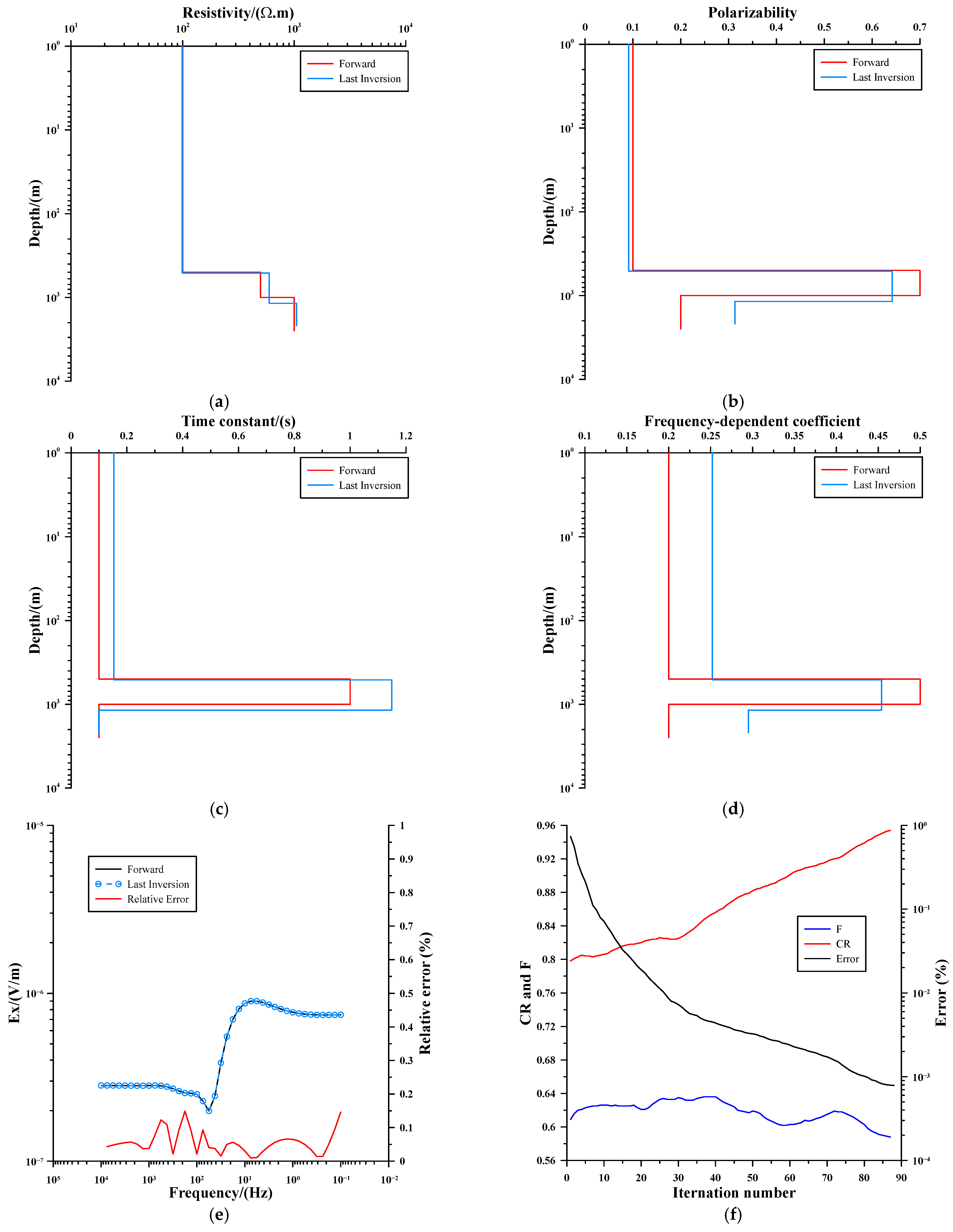

| Type | Resistivity (Ω·m) | Polarizability | Frequency-Dependent Coefficient | Time Constant (s) | Layer Thickness (m) |
|---|---|---|---|---|---|
| H | 100/10/100 | 0.1/0.7/0.2 | 0.2/0.5/0.2 | 0.1/1/0.1 | 500/500/∞ |
| K | 100/500/100 | 0.1/0.7/0.2 | 0.2/0.5/0.2 | 0.1/1/0.1 | 500/500/∞ |
| A | 100/500/1000 | 0.1/0.7/0.2 | 0.2/0.5/0.2 | 0.1/1/0.1 | 500/500/∞ |
| Q | 1000/500/100 | 0.1/0.7/0.2 | 0.2/0.5/0.2 | 0.1/1/0.1 | 500/500/∞ |
| Layer No. | Resistivity (Ω·m) | Polarizability | Frequency-Dependent Coefficient | Time Constant (s) | Layer Thickness (m) |
|---|---|---|---|---|---|
| 1 | 90 | 0.05 | 0.05 | 0.1 | 560 |
| 2 | 60 | 0.05 | 0.05 | 0.1 | 520 |
| 3 | 490 | 0.05 | 0.05 | 0.1 | 270 |
| 4 | 175 | 0.05 | 0.05 | 0.1 | 250 |
| 5 | 108 | 0.05 | 0.05 | 0.1 | 560 |
| 6 | 20 | 0.5 | 0.45 | 150 | 210 |
| 7 | 210 | 0.05 | 0.05 | 0.1 | ---- |
| Depth (m) | Lithology | Resistivity (Ω·m) | Polarizability |
|---|---|---|---|
| 20.00–671.92 | Quartz Monzodiorite Porphyry | 2184.00 | 5.00% |
| –686.32 | Chalcopyrite-mineralized Quartz Monzodiorite Porphyry | 1108.8 | 12.3% |
| –727.16 | Quartz Monzodiorite Porphyry | 1808 | 5.00% |
| –762.76 | Chalcopyrite-mineralized Dolomitic Marble | 524.59 | 12.15% |
| –777.96 | Copper–Iron Ore Body | 40.03 | 29.15% |
| –1031.80 | Marble | 491.82 | 5.00% |
| –1040.40 | Quartz Monzodiorite Porphyry | 118.03 | 9.28% |
| –1049.00 | Copper–Iron Ore Body | 65.35 | 28.56% |
| –1104.50 | Quartz Monzodiorite Porphyry | 573.65 | 8.19% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Cheng, T.; Yao, M.; Cheng, J.; Xie, X.; Mao, Y.; Yan, L. Adaptive Differential Evolution Algorithm for Induced Polarization Parameters in Frequency-Domain Controlled-Source Electromagnetic Data. Minerals 2025, 15, 754. https://doi.org/10.3390/min15070754
Zhou L, Cheng T, Yao M, Cheng J, Xie X, Mao Y, Yan L. Adaptive Differential Evolution Algorithm for Induced Polarization Parameters in Frequency-Domain Controlled-Source Electromagnetic Data. Minerals. 2025; 15(7):754. https://doi.org/10.3390/min15070754
Chicago/Turabian StyleZhou, Lei, Tianjun Cheng, Min Yao, Jianzhong Cheng, Xingbing Xie, Yurong Mao, and Liangjun Yan. 2025. "Adaptive Differential Evolution Algorithm for Induced Polarization Parameters in Frequency-Domain Controlled-Source Electromagnetic Data" Minerals 15, no. 7: 754. https://doi.org/10.3390/min15070754
APA StyleZhou, L., Cheng, T., Yao, M., Cheng, J., Xie, X., Mao, Y., & Yan, L. (2025). Adaptive Differential Evolution Algorithm for Induced Polarization Parameters in Frequency-Domain Controlled-Source Electromagnetic Data. Minerals, 15(7), 754. https://doi.org/10.3390/min15070754







