Shear Wave Velocity Estimation for Shale with Preferred Orientation Clay Minerals
Abstract
1. Introduction
2. Theory and Methodology
2.1. The Xu–White Model Used for Velocity Modeling of Rock
2.2. The Effect of Preferred Orientation Clay Minerals on Velocities of Shale
2.3. The Compaction Model for Shale Velocity Modeling
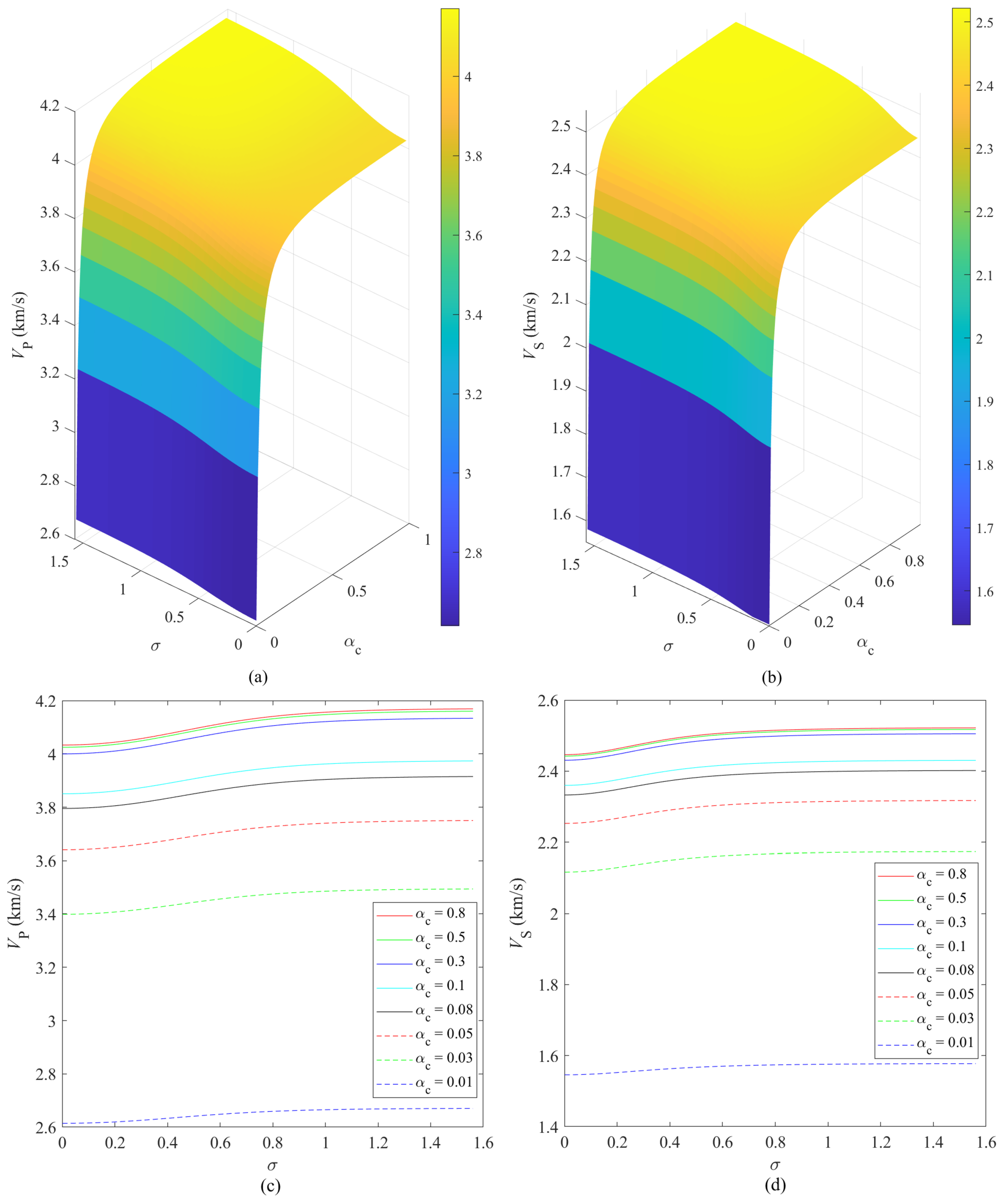
2.4. S-Wave Velocity Estimation for Shale Based on the Compaction Model
3. Result and Discussion
3.1. Model Test Using Laboratory Data
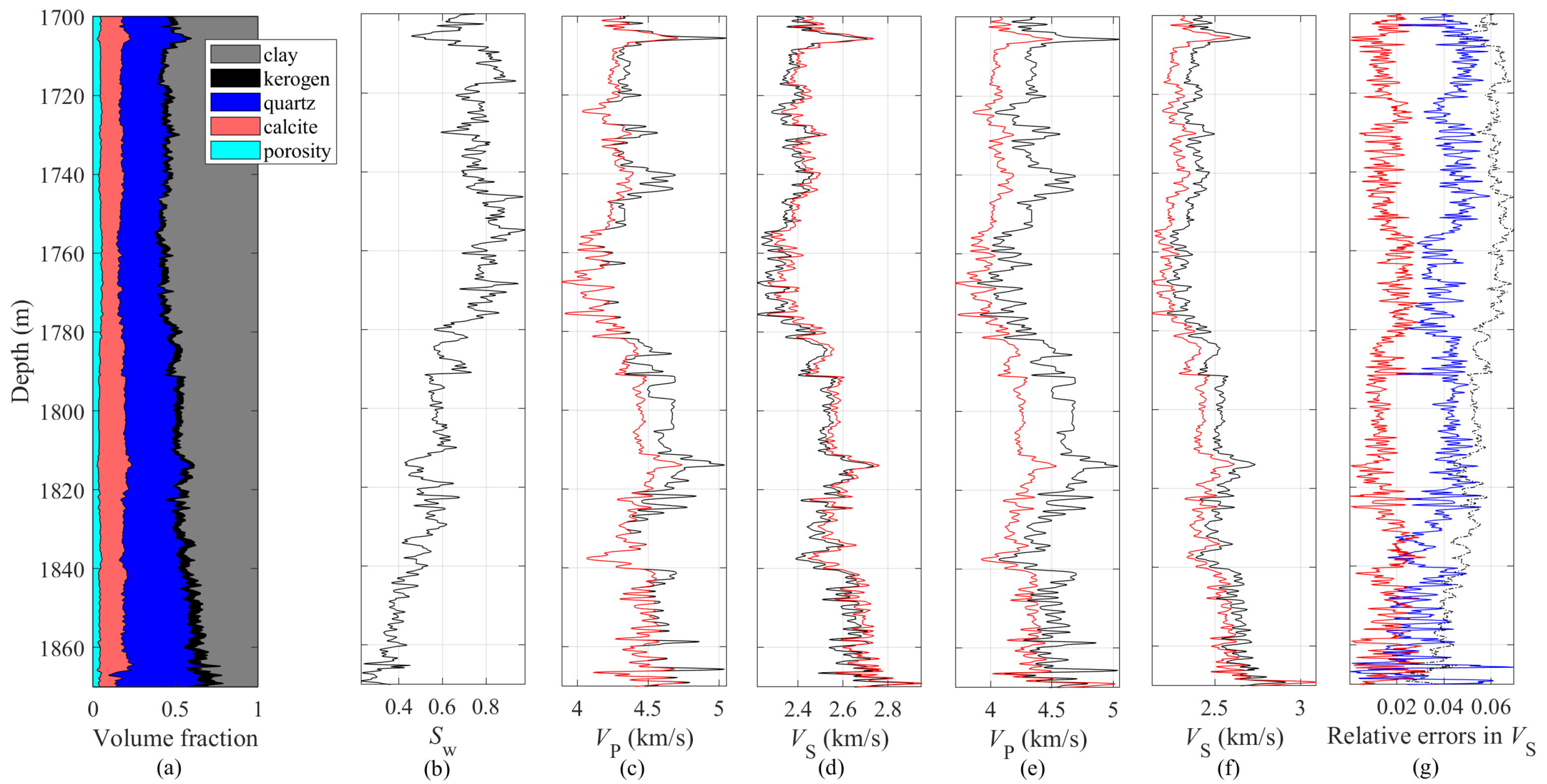
3.2. Application in a Shale Gas Reservoir
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, H.; He, C.; Xiao, S.; Chen, J.; Kalmykov, A.; Wu, W.; Wang, Y.; Wang, J. The Formation of Organic Matter Pores in Shales: Implications from Combined Thermal Heating and Scanning Electron Microscopy Imaging. Minerals 2025, 15, 336. [Google Scholar] [CrossRef]
- Peng, S.; Feng, C.; Qiu, Z.; Zhang, Q.; Liu, W.; Feng, J.; Hu, Z. Prediction of Lithofacies in Heterogeneous Shale Reservoirs Based on a Robust Stacking Machine Learning Model. Minerals 2025, 15, 240. [Google Scholar] [CrossRef]
- Schuster, G.T.; Li, J.; Lu, K.; Metwally, A.; AlTheyab, A.; Hanafy, S. Opportunities and pitfalls in surface-wave interpretation. Interpretation 2017, 5, T131–T141. [Google Scholar] [CrossRef]
- Guo, Z.; Lv, X.; Liu, C.; Liu, X.; Liu, Y. Prediction of organic richness in shale gas reservoirs using a novel organic-inorganic decoupling seismic inversion method. Gas Sci. Eng. 2023, 110, 204864. [Google Scholar] [CrossRef]
- Tan, M.; Peng, X.; Cao, H.; Wang, S.; Yuan, Y. Estimation of shear wave velocity from wireline logs in gas-bearing shale. J. Pet. Sci. Eng. 2015, 133, 352–366. [Google Scholar] [CrossRef]
- Sethi, C.; Motra, H.B.; Hazra, B.; Ostadhassan, M. Influence of lithological contrast on elastic anisotropy of shales under true-triaxial stress and thermal conditions. Int. J. Rock Mech. Min. Sci. 2025, 190, 106100. [Google Scholar] [CrossRef]
- Vernik, L.; Anantharamu, V. Estimating the elastic properties of mica and clay minerals. Geophysics 2020, 85, MR83–MR95. [Google Scholar] [CrossRef]
- Sayers, C.M. The effect of kerogen on the elastic anisotropy of organic-rich shales. Geophysics 2013, 78, D65–D74. [Google Scholar] [CrossRef]
- Ding, J.; Clark, A.C.; Vanorio, T.; Jew, A.D.; Bargar, J.R. Elastic anisotropy of shales: The roles of crack alignment and compliance ratio. Geophysics 2022, 87, A13–A17. [Google Scholar] [CrossRef]
- Xu, S.; White, R.E. A new velocity model for clay-sand mixtures. Geophys. Prospect. 1995, 43, 91–118. [Google Scholar] [CrossRef]
- Xu, S.; White, R.E. A physical model for shear-wave velocity prediction. Geophys. Prospect. 1996, 44, 687–717. [Google Scholar] [CrossRef]
- Xu, S.; Payne, M.A. Modeling elastic properties in carbonate rocks. Lead. Edge 2009, 28, 66–74. [Google Scholar] [CrossRef]
- Berryman, J.G. Long-wavelength propagation in composite elastic media II. Ellipsoidal inclusions. J. Acoust. Soc. Am. 1980, 68, 1820–1831. [Google Scholar] [CrossRef]
- Norris, A. A differential scheme for the effective moduli of composites. Mech. Mater. 1985, 4, 1–16. [Google Scholar] [CrossRef]
- Ruiz, F.; Dvorkin, J. Predicting elasticity in nonclastic rocks with a differential effective medium model. Geophysics 2010, 75, E41–E53. [Google Scholar] [CrossRef]
- Vernik, L.; Castagna, J.; Omovie, S.J. S-wave velocity prediction in unconventional shale reservoirs. Geophysics 2018, 83, MR35–MR45. [Google Scholar] [CrossRef]
- Zhang, B.; Jin, S.; Liu, C.; Guo, Z.; Liu, X. Prediction of shear wave velocity based on a statistical rock-physics model and Bayesian theory. J. Pet. Sci. Eng. 2020, 195, 107710. [Google Scholar] [CrossRef]
- Qiao, H.; Zhang, B.; Liu, C. Research on Prediction Method of Volcanic Rock Shear Wave Velocity Based on Improved Xu-White Model. Energies 2022, 15, 3611. [Google Scholar] [CrossRef]
- Liu, Z.S.; Lu, H.; Liu, J.Z.; Bao, Q.Z.; Shi, L.; Wang, Z.Y. Estimation of S-wave velocity from wire-line logs for organic-rich rocks. J. Pet. Sci. Eng. 2021, 205, 108928. [Google Scholar] [CrossRef]
- Miah, M.I.; Ahmed, S.; Zendehboudi, S. Model development for shear sonic velocity using geophysical log data: Sensitivity analysis and statistical assessment. J. Nat. Gas Sci. Eng. 2021, 88, 103778. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Z.; Zhou, Y.; Ai, H.; Han, H. Joint Inversion Method of Rock Physics Based on Hunger Games Search Correction and Bidirectional Long-Short-Term Memory Network. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5914310. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, J.; Xu, M.; Zhu, Z.; Chen, Y.; Geng, J. Rock-physics-guided machine learning for shear sonic log prediction. Geophysics 2024, 89, D75–D87. [Google Scholar] [CrossRef]
- Dang, Y.; Zhang, Y.; Wu, B.; Li, H.; Gao, J. An efficient method of predicting S-wave velocity using sparse Gaussian process regression for a tight sandstone reservoir. J. Appl. Geophys. 2024, 229, 105480. [Google Scholar] [CrossRef]
- Fang, Z.; Ba, J.; Guo, Q.; Xiong, F. Shear-wave velocity prediction of tight reservoirs based on poroelasticity theory: A comparative study of deep neural network and rock physics model. Geoenergy Sci. Eng. 2024, 240, 213028. [Google Scholar] [CrossRef]
- Wang, Z. Seismic anisotropy in sedimentary rocks, part 2: Laboratory data. Geophysics 2002, 67, 1423–1440. [Google Scholar] [CrossRef]
- Hornby, B.E.; Schwartz, L.M.; Hudson, J.A. Anisotropic effective-medium modeling of the elastic properties of shales. Geophysics 1994, 59, 1570–1583. [Google Scholar] [CrossRef]
- Sayers, C. Anisotropic velocity analysis1. Geophys. Prospect. 1995, 43, 541–568. [Google Scholar] [CrossRef]
- Johansen, T.A.; Ruud, B.O.; Jakobsen, M. Effect of grain scale alignment on seismic anisotropy and reflectivity of shales. Geophys. Prospect. 2004, 52, 133–149. [Google Scholar] [CrossRef]
- Bachrach, R. Elastic and resistivity anisotropy of shale during compaction and diagenesis: Joint effective medium modeling and field observations. Geophysics 2011, 76, E175–E186. [Google Scholar] [CrossRef]
- Pan, X.P.; Zhang, G.Z.; Chen, J.J. The construction of shale rock physics model and brittleness prediction for high-porosity shale gas-bearing reservoir. Pet. Sci. 2020, 17, 658–670. [Google Scholar] [CrossRef]
- Bandyopadhyay, K. Seismic Anisotropy: Geological Causes and Its Implications to Reservoir Geophysics. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2009. [Google Scholar]
- Qian, K.; Zhang, F.; Chen, S.; Li, X.; Zhang, H. A rock physics model for analysis of anisotropic parameters in a shale reservoir in Southwest China. J. Geophys. Eng. 2016, 13, 19–34. [Google Scholar] [CrossRef]
- Hudson, J.A. Overall properties of a cracked solid. Math. Proc. Camb. Philos. Soc. 1980, 88, 371–384. [Google Scholar] [CrossRef]
- Cheng, C.H. Crack models for a transversely isotropic medium. J. Geophys. Res. Solid Earth 1993, 98, 675–684. [Google Scholar] [CrossRef]
- Qian, K.R.; He, Z.L.; Chen, Y.Q.; Liu, X.W.; Li, X.Y. Prediction of brittleness based on anisotropic rock physics model for kerogen-rich shale. Appl. Geophys. 2017, 14, 463–479. [Google Scholar] [CrossRef]
- Zhang, F.; Li, X.y.; Qian, K. Estimation of anisotropy parameters for shale based on an improved rock physics model, part 1: Theory. J. Geophys. Eng. 2017, 14, 143–158. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T.; Dovorkin, J. The Rock Physics Handbook-Tools for Seismic Analysis of Porous Media, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Keys, R.G.; Xu, S. An approximation for the Xu-White velocity model. Geophysics 2002, 67, 1406–1414. [Google Scholar] [CrossRef]
- de Figueiredo, J.J.S.; do Nascimento, M.J.S.; Hartmann, E.; Chiba, B.F.; da Silva, C.B.; de Sousa, M.C.; Silva, C.; Santos, L.K. On the application of the Eshelby-Cheng effective model in a porous cracked medium with background anisotropy: An experimental approach. Geophysics 2018, 83, C209–C220. [Google Scholar] [CrossRef]
- de Figueiredo, J.; Chiba, B.F.; do Nascimento, M.J.; da Silva, C.B.; Santos, L.K. Can Hudson-Crampin effective model be applied in cracked medium in which the background is weakly anisotropic (VTI)? J. Appl. Geophys. 2019, 161, 255–260. [Google Scholar] [CrossRef]
- Sohail, G.M.; Hawkes, C.D. An evaluation of empirical and rock physics models to estimate shear wave velocity in a potential shale gas reservoir using wireline logs. J. Pet. Sci. Eng. 2020, 185, 106666. [Google Scholar] [CrossRef]
- Bai, J.Y.; Yue, C.Q.; Liang, Y.Q.; Song, Z.X.; Ling, S.; Zhang, Y.; Wu, W. Variable aspect ratio method in the Xu-White model for shear-wave velocity estimation. J. Geophys. Eng. 2013, 10, 035008. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Gassmann, F. Uber die elastizität poröser medien. Viertel. Naturforsch. Ges. Zürich 1951, 96, 1–23. [Google Scholar]
- Wyllie, M.R.J.; Gregory, A.R.; Gardner, G.H.F. An experimental investigation of factors affecting elastic wave velocities in porous media. Geophysics 1958, 23, 459–493. [Google Scholar] [CrossRef]
- Pillar, N.; Yan, J.; Lubbe, R. Variable Aspect Ratio Method in the Xu-White Model for AVO. In Proceedings of the 69th EAGE Conference and Exhibition Incorporating SPE EUROPEC 2007, London, UK, 11–14 June 2007; European Association of Geoscientists and Engineers: Bunnik, The Netherlands, 2007. [Google Scholar] [CrossRef]





| Bulk Modulus (Gpa) | Shear Modulus (Gpa) | Density () | |
|---|---|---|---|
| Quartz | 37.9 | 44.3 | 2.65 |
| Feldspar | 37.5 | 15 | 2.62 |
| Calcite | 76.8 | 32 | 2.71 |
| Dolomite | 94.9 | 45 | 2.87 |
| Pyrite | 147.4 | 132.5 | 4.93 |
| Clay | 25 | 9 | 2.55 |
| Kerogen | 5.53 | 3.2 | 1.25 |
| Gas | 0.18 | - | 0.26 |
| Brine | 2.65 | - | 0.99 |
| Model | RMSE | RMSE | r | r | |
|---|---|---|---|---|---|
| of | of | of | of | ||
| well 1 | Xu–White model (variable ) | 0.2443 | 0.0855 | 0.9295 | 0.9879 |
| Compaction model | 0.1006 | 0.0455 | 0.9570 | 0.9962 | |
| well 2 | Xu–White model (variable ) | 0.2855 | 0.0999 | 0.8494 | 0.9724 |
| Compaction model | 0.1150 | 0.0424 | 0.9322 | 0.9932 | |
| well 3 | Xu–White model (variable ) | 0.0647 | 0.0827 | 0.9879 | 0.9391 |
| Compaction model | 0.0009 | 0.0380 | 0.9999 | 0.9715 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Liu, C.; Yang, Z.; Qin, Y.; Li, M. Shear Wave Velocity Estimation for Shale with Preferred Orientation Clay Minerals. Minerals 2025, 15, 738. https://doi.org/10.3390/min15070738
Zhang B, Liu C, Yang Z, Qin Y, Li M. Shear Wave Velocity Estimation for Shale with Preferred Orientation Clay Minerals. Minerals. 2025; 15(7):738. https://doi.org/10.3390/min15070738
Chicago/Turabian StyleZhang, Bing, Cai Liu, Zhiqing Yang, Yao Qin, and Mingxing Li. 2025. "Shear Wave Velocity Estimation for Shale with Preferred Orientation Clay Minerals" Minerals 15, no. 7: 738. https://doi.org/10.3390/min15070738
APA StyleZhang, B., Liu, C., Yang, Z., Qin, Y., & Li, M. (2025). Shear Wave Velocity Estimation for Shale with Preferred Orientation Clay Minerals. Minerals, 15(7), 738. https://doi.org/10.3390/min15070738






