Investigation of Strength Diversity Characterization in Mineral Materials Using Discrete Element Method
Abstract
1. Introduction
2. DEM-Based Theory of Ore Fragmentation Model
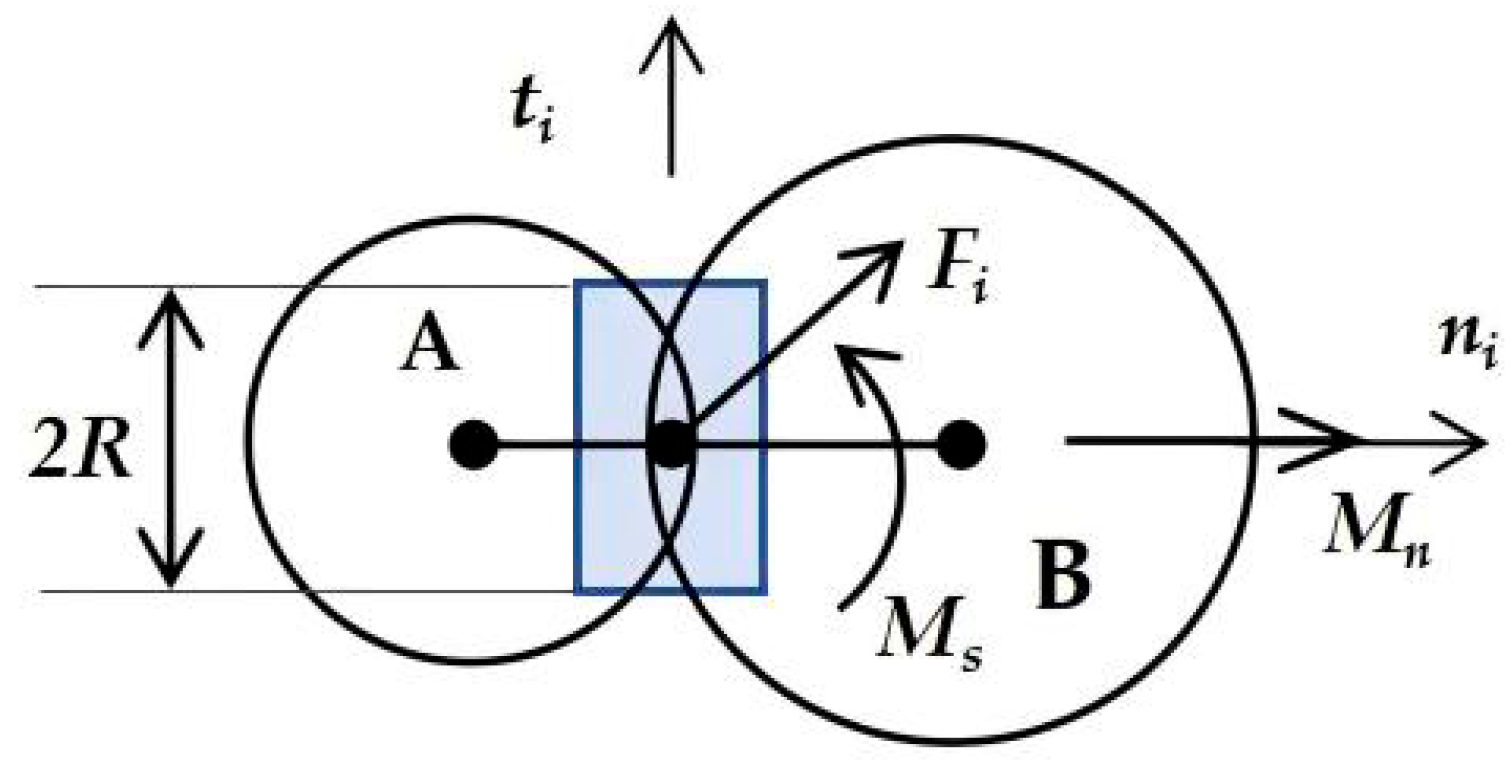
2.1. Mechanical Behavior of Bonds
2.2. Failure Criteria
- Maximum Stress Criterion
- Energy Criterion
3. Ore Strength Heterogeneity Modeling
3.1. Simulation of Ore Heterogeneity
3.2. Simulation of Ore Anisotropy in Different Strengths
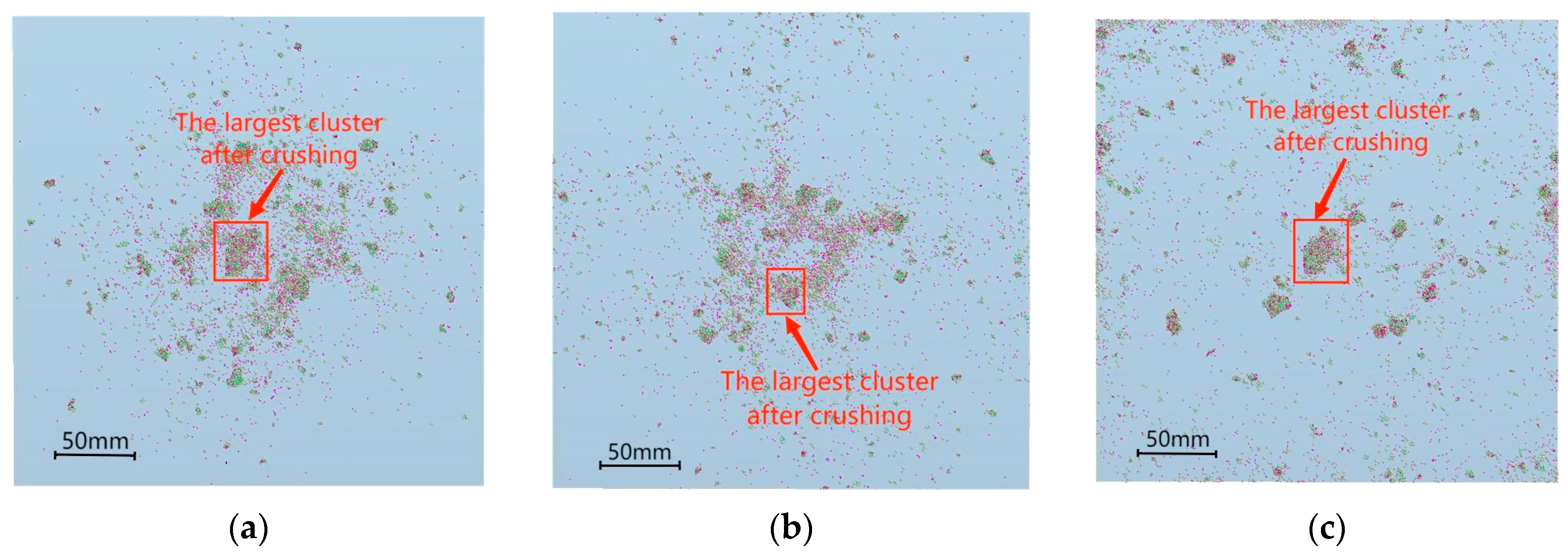
3.3. Modeling and Simulation of Ore Crushing and Result Analysis
4. Experimental Validation with Drop Weight Tests
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Z.X.; Sanchidrián, J.A.; Ouchterlony, F.; Luukkanen, S. Reduction of Fragment Size from Mining to Mineral Processing: A Review. Rock Mech. Rock Eng. 2023, 56, 747–778. [Google Scholar] [CrossRef]
- Vasilyeva, N.; Golyshevskaia, U.; Sniatkova, A. Modeling and Improving the Efficiency of Crushing Equipment. Symmetry 2023, 15, 1343. [Google Scholar] [CrossRef]
- Bersenev, I.S.; Pokolenko, S.I.; Sabirov, E.R.; Spirin, N.A.; Borisenko, A.V.; Kurochkin, A.R. Influence of the Iron Ore Pellets Macrostructure on Their Strength. Steel Transl. 2023, 53, 1018–1022. [Google Scholar] [CrossRef]
- Niu, L.; Liu, Z.; Zhang, J.; Lan, D.; Li, S.; Li, Z.; Wang, Y. Mineralogical characteristics, metallurgical properties and phase structure evolution of Ca-rich hematite sintering. Int. J. Miner. Metall. Mater. 2023, 30, 303–313. [Google Scholar] [CrossRef]
- Yin, Z.; Wang, N.; Li, T. Study on single particle compression crushing characteristics of iron ore with five different particle sizes. AIP Adv. 2024, 14, 105–222. [Google Scholar] [CrossRef]
- Gu, R.; Qin, Z.; Zhao, S.; Xing, H.; Chen, L.; Yang, F. Mechanical characteristics of roll crushing of ore materials based on discrete element method. Sci. Rep. 2025, 15, 771. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Tang, Y.; Chen, S.; Gao, L.; Wang, Y. Experimental study on the sandstone abrasiveness via mineral composition and microstructure analysis. Petroleum 2024, 10, 440–445. [Google Scholar] [CrossRef]
- Belhadj, B.; Houessou, J.; Montrelay, N.; Quéneudec, M. Effect of Substitution of Cement by Mineral Powders on the Physicomechanical Properties and Microstructure of Sand Concretes. J. Archit. Environ. Struct. Eng. Res. 2024, 5, 18–29. [Google Scholar] [CrossRef]
- Georgieva, S.; Vassileva, R.D.; Grozdev, V.; Milenkov, G.; Cempírek, J.; Škoda, R. Mineral composition and trace element characteristics of pegmatites from Smilovene, Sredna Gora Mountain, Bulgaria. Rev. Bulg. Geol. Soc. 2024, 85, 96–99. [Google Scholar] [CrossRef]
- Baraboshkin, E.Y.; Petrochenkov, D.A. Mineral Composition and Stratigraphic Position of Interior Jewelry Ammonites from the Middle Aptian of the Republic of North Ossetia-Alania. Mosc. Univ. Geol. Bull. 2024, 79, 186–195. [Google Scholar] [CrossRef]
- Hou, H.; Yang, W.; Yang, R.; Jiang, Z.; Miao, K.; Sun, W.; Xiao, Y. Formation and Evolution of Complex Pore-Fracture Systems in Shale Gas Reservoirs: Insights into Controlling Mechanisms. Energy Fuels 2025, 39, 3008–3038. [Google Scholar] [CrossRef]
- Wang, H.; Chen, S.; Zhang, S.; Zhang, C.; Wang, Y.; Yi, G.; Peng, Y. Study on fracture characteristics in coal and shale for coal-measure gas reservoir based on 3D CT reconstruction and fractal features. Front. Earth Sci. 2023, 17, 514–526. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, Z.; Zhao, J.; Chen, B.; Li, X.; Zhong, J. In-situ observation and modeling approach to evolution of pore-fracture structure in coal. J. Min. Sci. Technol. 2023, 33, 265–274. [Google Scholar] [CrossRef]
- Kovalev, K.P.; Kalinin, Y.A.; Lobanov, K.V.; Naumov, E.A.; Borovikov, A.A.; Sukhorukov, V.P. The Gorevskoe Pb–Zn Deposit (Siberia, Russia): Mineral Composition and Features of Ore Mineralization. Geol. Ore Depos. 2023, 65, 283–314. [Google Scholar] [CrossRef]
- Mohapatra, S.; Pradhan, S.K.; Oh, M.S. The impact of annealing temperature and time on the grain distribution and texture evolution of cold-rolled electric-furnace annealed low-carbon steel. Mater. Lett. 2024, 371, 136955. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, W.; Pang, Z.; Zhao, Z.; Liu, Z.; Liu, C.; Gao, F.; Li, W. Improvement in Grain Size Distribution Uniformity for Nuclear-Grade Austenitic Stainless Steel through Thermomechanical Treatment. Materials 2024, 17, 2313. [Google Scholar] [CrossRef]
- Zhao, C.; Xu, S.; Pan, L.Y. Effect of WC particle size on the microstructure and mechanical properties of Ni–Co coarse grain cemented carbide. Int. J. Appl. Ceram. Technol. 2023, 20, 3701–3713. [Google Scholar] [CrossRef]
- Roy, N.; Kuna, K.K. Influence of Aggregate Mineral Grain Size and Size Distribution on Pavement Surface Microtexture Deterioration. J. Transp. Eng. Part B Pavements 2024, 150, 04024014. [Google Scholar] [CrossRef]
- Du, X.; Chen, Y.; Xu, L.; Shen, A.; Lu, B.; Wu, J.; Fernandez-Steeger, T.M.; Azzam, R. Investigating the Causes of Substandard Concrete Strength: A Macro- and Microanalysis. Materials 2025, 18, 953. [Google Scholar] [CrossRef]
- Kohno, M.; Yoshida, T.; Nishimura, T. Impact of Clay Mineral Type on Rock Properties under Drying and Wetting Cycles. Mater. Trans. 2024, 65, 1390–1396. [Google Scholar] [CrossRef]
- Duan, P.; Li, Y.; Ji, N.; Zhang, S.; Zhang, F. Study on the Effect of Low Temperature on the Tensile Strength of Granite with Different Grain Size. In Proceedings of the International Conference on Mineral Resources, Geotechnology and Geological Exploration, Qingdao, China, 13–15 June 2025; Springer: Cham, Switzerland, 2025. [Google Scholar]
- Zhang, T.; Yu, L.; Peng, Y.; Jing, H.; Su, H.; Wei, J. Effect of the mineral spatial distribution heterogeneity on the tensile strength of granite: Insights from PFC3D-GBM numerical analysis. J. Rock Mech. Geotech. Eng. 2023, 15, 1144–1160. [Google Scholar] [CrossRef]
- Hou, L.; Liang, Y.; Wang, C.; Zhou, Z. Mineral protection explains the elevational variation of temperature sensitivity of soil carbon decomposition in the Eastern Himalaya. Appl. Soil Ecol. 2024, 197, 105346. [Google Scholar] [CrossRef]
- Matsuyama, K.; Michibayashi, K. Effects of mineral mode and textural variation on the seismic anisotropy in lithospheric mantle: An example from Horoman peridotites. Earth Planets Space 2024, 76, 154. [Google Scholar] [CrossRef]
- Zhou, S.Y.; Liu, X.Y. A simple image-based method for online moisture content estimation of iron ore green pellets. J. Iron Steel Res. Int. 2023, 30, 851–863. [Google Scholar] [CrossRef]
- Zhang, Q.; Yao, B.; Fan, X.; Li, Y.; Fantuzzi, N.; Ma, T.; Chen, Y.; Zeng, F.; Li, X.; Wang, L. A failure criterion for shale considering the anisotropy and hydration based on the shear slide failure model. J. Min. Sci. Technol. 2023, 33, 447–462. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, P.; Li, H.; Li, Z.; Huo, X.; Ma, S. Impact Crushing Characteristics and Relationship between Multicomponent Complex Ore and Its Component Minerals. Minerals 2023, 13, 676. [Google Scholar] [CrossRef]
- Liu, X.Y.; Xu, D.P.; Duan, S.Q.; Xu, H.S.; Feng, G.L.; Qiu, S.L.; Jiang, Q. Study on the micromechanical and crack characteristics of granite based on nanoindentation test and discrete element method. Comput. Part. Mech. 2024, 11, 1547–1563. [Google Scholar] [CrossRef]
- Yang, M.; He, Z.; Li, C.; Yang, B.; Liu, G.; Fu, C.; Wang, T.; Wei, Z. Experimental Study on Physical Characteristics of Deep Rocks at Different Depths in Songliao Basin. Geofluids 2022, 2022, 6070683. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Cundall, P.A.; Potyondy, D.O. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar]
- Potyondy, D.O. A Flat-Jointed Bonded-Particle Material for Hard Rock. In Proceedings of the 46th U.S. Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012; American Rock Mechanics Association (ARMA): Alexandria, VA, USA, 2012. [Google Scholar]
- Potyondy, D.O. The bonded-particle model as a tool for rock mechanics research and application: Current trends and future directions. Geosystem Eng. 2015, 18, 1–28. [Google Scholar] [CrossRef]
- Laptev, V.V.; Lukichev, S.V. DEM-Based Analysis of Ore Losses in Sublevel Stoping. J. Min. Scinece 2023, 59, 572–578. [Google Scholar] [CrossRef]
- Potyondy, D.O. A Flat-Jointed Bonded-Particle Model for Rock. In Proceedings of the 52nd U.S. Rock Mechanics/Geomechanics Symposium, Seattle, WA, USA, 17–20 June 2018; American Rock Mechanics Association (ARMA): Alexandria, VA, USA, 2018. [Google Scholar]
- Tavares, L.M.; King, R.P. Modeling of particle fracture by repeated impacts using continuum damage mechanics. Powder Technol. 2002, 123, 138–146. [Google Scholar] [CrossRef]
- Asadi, R.; Disfani, M.M.; Ghahreman-Nejad, B. A New Modified Replacement Method for Discrete Element Modelling of Rockfill Material. Comput. Geotech. 2024, 168, 106168. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Y.; Wang, Y.; Bai, Q. Discrete element method simulation of granular materials considering particle breakage in geotechnical and mining engineering: A short review. Green Smart Min. Eng. 2024, 1, 190–207. [Google Scholar] [CrossRef]
- Chang, W.; Xing, A.; Jin, K. Investigation of Dynamic Fragmentation Mechanism of Granular Column Collapse Via Discrete Element Analyses. In Proceedings of the Engineering Geology for a Habitable Earth: IAEG XIV Congress 2023 Proceedings, Chengdu, China, 21–27 September 2023; Springer: Singapore, 2024. [Google Scholar]
- Shang, C.; Li, L.; Chu, K.; Zhou, Z.; Casas, G.; Tu, W.; Chen, Y.; Sun, S. A coarse-grained bonded particle model for large-scale rock simulation. Microelectron. J. 2024, 3, 100133. [Google Scholar] [CrossRef]
- Liu, M.; Xu, Y.; Gao, X.; Fu, J.; Liu, X.; Liu, E. A Numerical Study of the Mechanical Behavior of Jointed Soft Rocks under Triaxial Loading Using a Bonded Particle Model. Materials 2024, 17, 4842. [Google Scholar] [CrossRef]
- Hertz, H. On the contact of elastic solids. J. Reine. Angew. Math. 1881, 92, 156–171. [Google Scholar]
- Mindlin, R.D. Compliance of elastic bodies in contact. J. Appl. Mech. 1949, 16, 259–268. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Deresiewicz, H. Elastic Spheres in Contact under Varying Oblique Force. ASME J. Appl. Mech. 1953, 20, 327–344. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Ozaki, E.; Igarashi, T. Plugging of the Flow of Granular Materials during the Discharge from a Silo. Int. J. Mod. Phys. B 1993, 7, 1949–1963. [Google Scholar] [CrossRef]
- Wang, X.; Xue, Y.J.; Cheng, B.; Liu, J.; Guan, Z.-Q.; Li, J.-S. Influence of basic particle diameter on accuracy of bonded-particle model. Chin. J. Nonferrous Met. 2022, 32, 1491–1503. [Google Scholar]
- Wang, X.; Xue, Y.J.; Cheng, B.; Liu, J.; Guan, Z.; Li, J. The influence of the number combination of basic particles on the accuracy of bonded-particle model. J. Henan Univ. Sci. Technol. Nat. Sci. 2022, 43, 27–33+5. [Google Scholar]
- Wang, X.; Xue, Y.J.; Cheng, B.; Liu, J.; Li, J. The characteristics and representation of bond key in bonded particle model for ore crushing. J. Henan Polytech. Univ. Nat. Sci. 2024, 43, 41–48. [Google Scholar]
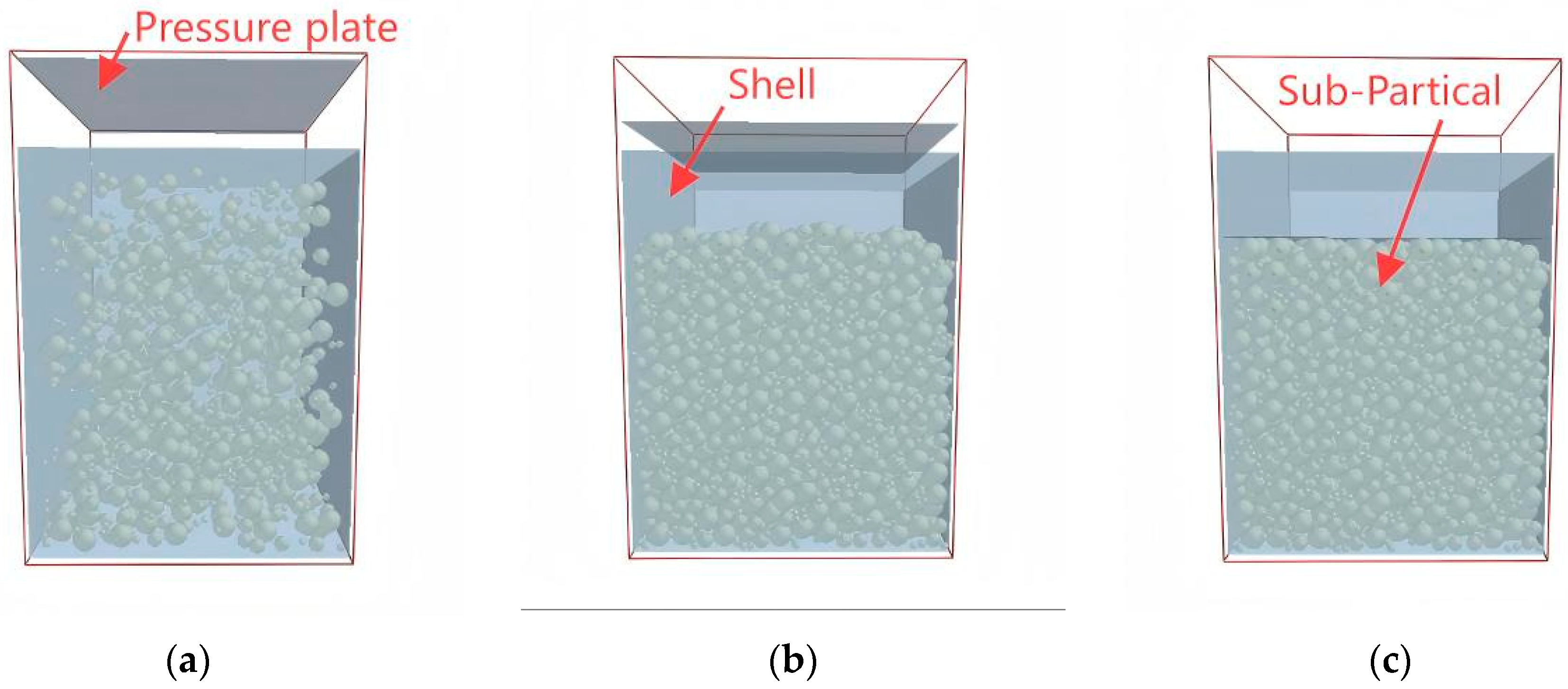



| Type | Diameter/mm | Number |
|---|---|---|
| P1 | 1 | 2900 |
| P2 | 1.5 | 2400 |
| P3 | 2 | 2500 |
| Bond | kn/GPa/m | σc/MPa | kt GPa/m | τc/MPa |
|---|---|---|---|---|
| K11 | 25.84 | 0.46 | 24.34 | 0.46 |
| K22 | 25.00 | 0.46 | 23.59 | 0.46 |
| K33 | 24.34 | 0.46 | 22.77 | 0.46 |
| K12 | 32.17 | 0.46 | 30.07 | 0.46 |
| K23 | 31.51 | 0.46 | 29.49 | 0.46 |
| K13 | 30.87 | 0.46 | 28.75 | 0.46 |
| Bond | kn/GPa/m | σc/MPa | kt GPa/m | τc/MPa |
|---|---|---|---|---|
| K11 | 26.43 | 0.42 | 24.48 | 0.42 |
| K22 | 25.37 | 0.42 | 23.50 | 0.42 |
| K33 | 24.39 | 0.42 | 22.59 | 0.42 |
| K12 | 32.67 | 0.42 | 30.68 | 0.42 |
| K23 | 31.59 | 0.42 | 29.66 | 0.42 |
| K13 | 30.58 | 0.42 | 28.71 | 0.42 |
| Bond | kn/GPa/m | σc/MPa | kt/GPa/m | τc/MPa |
|---|---|---|---|---|
| K11 | 25.60 | 0.48 | 23.90 | 0.48 |
| K22 | 24.40 | 0.48 | 22.80 | 0.48 |
| K33 | 23.40 | 0.48 | 21.90 | 0.48 |
| K12 | 31.40 | 0.48 | 29.20 | 0.48 |
| K23 | 30.30 | 0.48 | 28.20 | 0.48 |
| K13 | 29.30 | 0.48 | 27.20 | 0.48 |
| Type of Ore | Size Fraction/mm | |||||||
|---|---|---|---|---|---|---|---|---|
| <3.35 | 3.35 | 4.75 | 6.70 | 9.50 | 13.20 | 19.00 | 26.50 | |
| Gold ore | 39.98 | 11.90 | 14.07 | 19.14 | 12.25 | 2.66 | 0.00 | 0.00 |
| Iron ore | 43.33 | 7.03 | 12.76 | 24.08 | 10.37 | 2.44 | 0.00 | 0.00 |
| Copper ore | 38.31 | 7.20 | 10.78 | 17.48 | 14.56 | 6.96 | 4.71 | 0.00 |
| Type of Ore | Size Fraction/mm | |||||||
|---|---|---|---|---|---|---|---|---|
| <3.35 | 3.35 | 4.75 | 6.70 | 9.50 | 13.20 | 19.00 | 26.50 | |
| Gold ore | 37.76 | 12.42 | 15.26 | 20.88 | 11.20 | 2.49 | 0.00 | 0.00 |
| Iron ore | 41.47 | 11.63 | 13.67 | 22.55 | 9.65 | 1.03 | 0.00 | 0.00 |
| Copper ore | 33.29 | 10.93 | 12.38 | 20.95 | 15.39 | 6.13 | 0.93 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Liu, J.; Yang, F.; Zheng, G.; Xue, Y.; Guo, N. Investigation of Strength Diversity Characterization in Mineral Materials Using Discrete Element Method. Minerals 2025, 15, 665. https://doi.org/10.3390/min15070665
Wang X, Liu J, Yang F, Zheng G, Xue Y, Guo N. Investigation of Strength Diversity Characterization in Mineral Materials Using Discrete Element Method. Minerals. 2025; 15(7):665. https://doi.org/10.3390/min15070665
Chicago/Turabian StyleWang, Xiao, Jun Liu, Fang Yang, Guoqiang Zheng, Yujun Xue, and Nan Guo. 2025. "Investigation of Strength Diversity Characterization in Mineral Materials Using Discrete Element Method" Minerals 15, no. 7: 665. https://doi.org/10.3390/min15070665
APA StyleWang, X., Liu, J., Yang, F., Zheng, G., Xue, Y., & Guo, N. (2025). Investigation of Strength Diversity Characterization in Mineral Materials Using Discrete Element Method. Minerals, 15(7), 665. https://doi.org/10.3390/min15070665







