Next Article in Journal
Reprocessing of Sulphide Flotation Tailings for Copper Recovery: Characterisation
Previous Article in Journal
Reservoir Characteristics and Hydrocarbon Potential of Cretaceous Volcanic Rocks in the Shimentan Formation, Xihu Sag, East China Sea Shelf Basin
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Minerals
Volume 15
Issue 6
10.3390/min15060648
minerals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Theoretical Study on Impact of Chemical Composition and Water Content on Mechanical Properties of Stratlingite Mineral

by
Daniel Tunega
1,* and
Ali Zaoui
2,*
1
Institute for Soil Research, Department of Ecosystem Management, Climate and Biodiversity, BOKU University, Peter-Jordan-Strasse 82, A-1190 Wien, Austria
2
University Lille, IMT Nord Europe, JUNIA, University Artois, ULR 4515—LGCgE, Laboratoire de Génie Civil et Géo-Environnement, F-59000 Lille, France
*
Authors to whom correspondence should be addressed.
Minerals 2025, 15(6), 648; https://doi.org/10.3390/min15060648
Submission received: 9 April 2025 / Revised: 2 June 2025 / Accepted: 10 June 2025 / Published: 16 June 2025
(This article belongs to the Section Clays and Engineered Mineral Materials)
Browse Figures
Versions Notes

Abstract

Stratlingite is known as one of the hydration products of aluminum-rich cements. Its microstructure and, consequently, mechanical properties, depend on the Al/Si ratio and hydration conditions. The layered structure of stratlingite is characterized as defected, with vacancies in the aluminosilicate layer. This study uses density functional theory calculations on different stratlingite models to show how chemical composition, water content, and structural defects affect its mechanical properties. The developed models represent structures with full occupancy, with little or no content of structural water, and with vacancies in the aluminosilicate layer. It was shown that the full occupancy models have the highest toughness and are strongly anisotropic. The calculated bulk modulus (BH) of the models with full occupancy was about 40 GPa, being in the typical range for calcium aluminosilicate minerals. The water loss led to an increase in BH by approximately 40% compared to the models with full occupancy. In contrast, the models with vacancies exhibited a decrease in BH of about 30%. In models with the high silicon content (Al/Si ratio of 1/4), BH, Young’s (EH), and shear (GH) moduli decreased in a range 15%–30% compared to the models with an Al/Si ratio of 2/3 of Al/Si. Finally, according to Pugh’s ratio (BH/GH), which serves as a criterion for brittle–ductile transition (1.8), the models with full occupancy exhibit a brittle behavior, whereas the defected structures are closer to ductile. This could explain the elastic behavior of stratlingite binder in concretes. Generally, the calculations showed that all investigated parameters (chemical composition, water content, and structural defects) have a significant impact on the mechanical properties of stratlingite minerals.

Graphical Abstract

1. Introduction

Calcium aluminate silicate hydrate (CASH) phases are products of the hydration of cementitious materials in the preparation of concrete materials. In the CASH phases, numerous crystalline products have been detected, such as thaumasite, tobermorite, jennite, and others [1]. Which crystalline phases dominate depends on the parent material composition (e.g., important parameter is Ca/Al/Si ratio) [2] and/or thermodynamic conditions [3]. Depending on those factors, the final product has different mechanical and chemical properties such as toughness or chemical resistance.
Stratlingite mineral (Ca4Al2(OH)12[AlSi(OH)8]2·2H2O) belongs to calcium aluminosilicate hydrate cement phases, often referred as gehlenite hydrate [4]. This mineral is relatively rare, found in nature in several deposits [4,5,6,7]. It is often accompanied by other calcium aluminate silicate minerals such as tobermorite or vertumnite [6]. Stratlingite appears naturally as small hexagonal platy crystals (in size of 0.1–0.5 mm), having perfect (001) cleavage [7].
Stratlingite phases were also detected in the cements during the hydration of Portland binders with high alumina content [8,9,10]. This mineral was also detected in very old concretes in monuments from the Imperial Rome era [11]. In concretes, stratlingite microcrystals play the role of a binder among interfacial zones, impeding the macroscale propagation of crack segments [12].
The mineral stratlingite was also prepared synthetically to better understand and refine its atomistic structure [13,14,15]. The detailed microstructure of stratlingite and its properties were determined by synchrotron X-ray powder diffraction, NMR, scanning electron microscopy, and thermogravimetry [15]. X-ray studies showed stratlingite to be trigonal with the R3m symmetry. The structure is layered, consisting of two types of layers: a calcium aluminate layer of a brucite type and a defected double tetrahedra aluminosilicate layer. Details on the structure of layers are given later in Section 2.2.
Important features of cementitious materials include their mechanical properties and their structural stability. There are numerous studies of various CASH phases to determine their mechanical parameters such as elastic moduli, hardness, brittleness, and many others. Indeed, for stratlingite, the literature offers only a few papers, in which the bulk modulus was experimentally determined. A value of 23 GPa was presented in the work by Moon et al. (2012) [16], while in another work a value of 27 GPa was published [17]. These values are slightly smaller than those measured for structurally similar synthetic CAHS phases with varying Al content (30–38 GPa) [12]. Furthermore, some work [17] has identified a discontinuity in the volume change in stratlingite at pressures exceeding 1.5 GPa, resulting in an increased bulk modulus of 58 GPa within the pressure range of 1.5 to 5.3 GPa. This change was attributed to the loss of structural water. This water loss along with the shrinking of the volume was also observed in the hydration/dehydration study on several AFm phases [18]. However, there are no experimental studies that provide additional mechanical parameters, such as elastic constants, or that focus more deeply on water removal from the stratlingite structure and/or the relationship between mechanical properties and chemical composition.
The determination of mechanical properties experimentally is often difficult due to various factors; an example of this is a lack of perfect macroscopic crystals. In this context, it is possible to predict mechanical properties theoretically by using methods of computational chemistry. Moreover, theoretical methods can predict a complete elastic tensor, which is very difficult to achieve experimentally. For example, the bulk modulus of the hydrous calcium aluminum sulfate mineral ettringite was calculated by the density functional method (DFT), providing a value of 29.4 GPa [19]. This value was in a very good agreement with the measured bulk modulus (27.3 GPa) obtained through Brillouin spectroscopy for the ettringite monocrystal, as reported in the same paper. A similar good agreement was also found for the monocrystal of the mineral thaumasite, with 40.6 GPa (DFT) versus 38.5 GPa (Brillouin spectroscopy) [19]. To our best knowledge, no detailed theoretical DFT study of mechanical properties of stratlingite has been performed so far. This work aims to describe the complete mechanical properties of the stratlingite by using methods of quantum chemistry at the DFT level. These properties are studied with respect to chemical composition (varying Al/Si content), water content, and defected structures. For this purpose, several structural models were developed to show how mechanical properties are affected by those factors.

2. Computational and Structural Details

2.1. Computational Details

All calculations were carried out at the density functional theory (DFT) level by using the VASP code [20,21,22,23] developed to perform simulations on periodic structural models. The Perdew–Burke–Ernzerhof (PBE) functional [24] was taken to describe the exchange-correlation energy term within the frame of the generalized gradient approximation (GGA) theory. As stratlingite has a layered structure with hydrogen bonding between layers and water, and it is known that the PBE functional is not very reliable in the prediction of structures with non-bonding interactions (dispersions or hydrogen bonds), dispersion corrections of the D3 type [25] were included in the calculations. The PBE-D3 combination showed a good performance in the correct prediction of structural parameters of layered clay minerals, in which the dominant interlayer interactions are of dispersion or hydrogen bond nature [26]. The Kohn–Sham equations were solved variationally in a plane wave (PW) basis set and through using the projector-augmented wave (PAW) method [27,28]. For computational cells with a large size of (cell vectors > 10 Å), Brillouin-zone sampling was restricted to the Γ-point only; otherwise, the k-point sampling was performed automatically according to the Monkhorst–Pack mesh scheme [29] of 2 × 2 × 1. We also tested denser k-point schemes (4 × 4 × 1 and 6 × 6 × 1) on the Str_1 model, but no significant change in the optimized cell parameters was achieved. The change in the lattice vectors was at the level of 0.05% or less. Therefore, in the following calculations, we continued with the 2 × 2 × 1 k-point scheme.
The atomic positions and unit cell parameters of all models were fully relaxed without any symmetry restrictions (P1 symmetry). The calculations of elastic properties require very precisely relaxed atomic positions and cell vectors, together with a highly converged absolute energy and stress tensor. Therefore, all relaxations were performed with the strict criteria for convergence. The plane wave basis set was used with the kinetic energy cut-off of 600 eV. The relaxation criteria were 10−5 eV/atom for the total energy change and 0.015 eV/Å for the maximum allowed forces acting on each atom. The elastic constants, Cij, were calculated according to the energy-strain approach [30]. Mechanical properties were calculated by using Vaspkit suite [31]. This toolkit was developed to provide pre- and post-processing analysis of VASP inputs/outputs to derive various material properties. For example, it provides rich information on numerous mechanical features such as bulk (K), shear (G), or Young’s (E) moduli. In a prediction of mechanical properties, Vaspkit follows earlier works focused on the analysis of the second-order elastic tensor and the visualization of elastic properties (codes ElAM [32] and ELATE [33]).

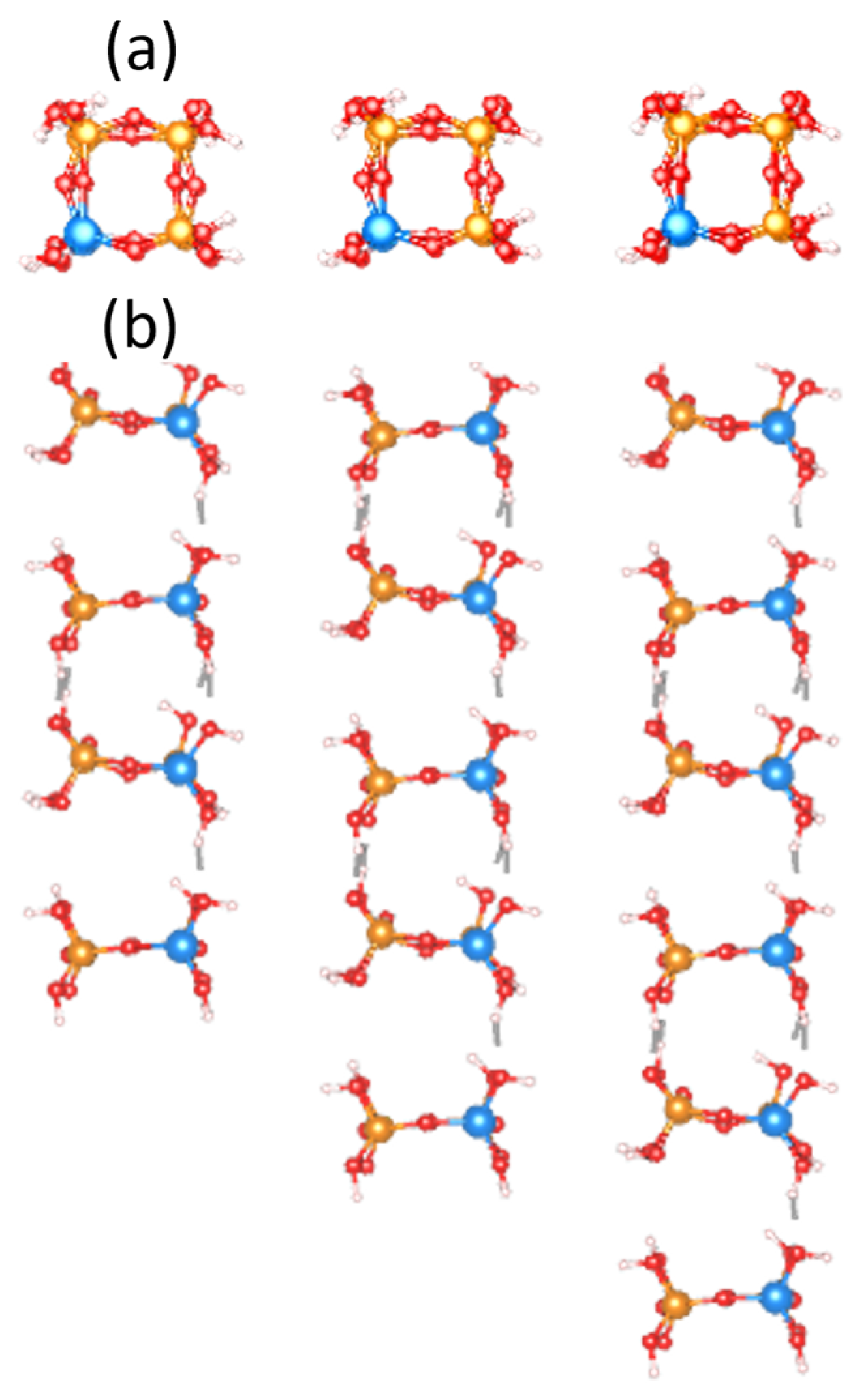
2.2. Structural Models

The models constructed for the calculations (Table 1) were based on the experimental structural data provided by Rinaldi et al. (1990) [7]. They determined the structure of stratlingite as trigonal with the R3m symmetry (unit cell parameters are in Table 2). As it was already mentioned, the structure of stratlingite is layered with two types of layers. Rinaldi et al. (1990) [7] proposed the structure of (a) calcium aluminate (CA) octahedral layer with a full occupancy, chemical composition [Ca2Al(OH)6·2H2O], and overall positive layer charge, and a (b) defected tetrahedral aluminosilicate (AS) layer with ~50% of vacancies and overall negative charge.
In the CA layer, edge-sharing polyhedra contain OH-/H2O ligands coordinating Al3+ cations in the six-fold configuration and Ca2+ cations in the seven-fold configuration (Figure 1a,b). The distribution of cations in the CA layer is relatively regular. On the other hand, the AS layer has more variable structure and composition where the Al:Si ratio can vary, and the number of vacancies can be variable as well.
In the AS layer, Al3+ and Si4+ are four-coordinated by O/OH species; this layer also contains a certain amount of H2O molecules, localized inside of a double layer. The complete AS model without vacancies is shown in Figure 1c,d (see also the chemical composition of the Str1 structure in Table 1).
CA and AS layers are held together mainly by the electrostatic interactions between charged layers. As the cations in the layers are coordinated by OH- and H2O species, the structure contains a lot of hydrogen bonds, which also contribute to the stabilization of the structure, especially hydrogen bonds formed between layers.
Based on the variability of the AS layer, we constructed several structural models. Their composition and overall chemical formula are collected in Table 1. Str1 is the structure with full occupancy of central positions in both layers with Ca:Al:Si ratio 2:2:3. From this structure, two models with the lower water content were developed—Str1-w, a model without structural water in the AS layer, and Str1-a, a completely anhydrous model (all water molecules removed). Further, a model with higher Si content was developed (Str2, Ca:Al:Si, ratio 2:1:4). In this model, the AS layer is fully silicious. Finally, we also created two models with defective AS layers, Str1_d and Str2_d. They were built from the original Str1 and Str2 models and both contain 50% vacancies in the double tetrahedral AS layer. The model of the AS layer of the defected structure Str1_d is shown in Figure 2. The Str1_d and Str2_d models correspond to the structure with the vacancies derived by Rinaldi et al. (1990) [7], with Str2_d having the higher Si content. Str1-w and Str1-a models could represent structures achieved after the dehydration steps of stratlingite, and Str1 and Str2 models represent more hypothetical structures with full occupancy.

3. Results and Discussion

3.1. Structural and Bonding Properties

Figure 3 shows completely optimized structures (all atomic positions and unit cell vectors) of the Str1 and Str2 models from Table 1. Optimized unit cell parameters are collected in Table 2 and compared to the experimental data [7]. Evidently, all optimized structural models deviate slightly from the perfect trigonal structure (see a and b cell vectors, and the three cell angles in Table 2). The differences between optimized models and the experimental structure are small. The parameters of defected models (Str1_d and Str2_d) are closest to the experimental data [7], showing less than a 5% difference between optimized unit cell volumes and the experimental volume. The optimized cell volumes of the remaining models vary more (Table 2). These models structurally differ from the structure by Rinaldi et al. [7], mainly in the AS layer, which is complete without vacancies, so there are no interrupted Si/Al–O covalent bonds as in the experimental and/or Str1_d/Str2_d models. As expected, the largest difference is observed for the anhydrous model Str1-a. This structure significantly shrinks when water is removed from the structure (~15% compared to the experimental cell volume). Similar volume reduction after the water loss was also observed experimentally [17,18]. Removing water from the interlayer space breaks the hydrogen bonds formed by this water with CA and AS layers, resulting in a 5% shortening of the c vector in the anhydrous model Str1-a compared to the parent Str1 model. The calculated cell vectors a and b are always shorter than experimental ones, while the calculated c vector values are slightly larger for the models with a complete AS layer and shorter for the models with a defected AS layer (Str1_d and Str2_d). Note that the c vector is much longer than the a and b vectors due to the form of stacking of the CA and AS layers (Figure 3).
Calculated bond lengths in the structures are typical for calcium aluminosilicates. Table 3 collects intervals and mean ± std values for the bond lengths for the structural model Str1 in the AS layer with the tetrahedral units (Si–O and AlIV–O), for the CA layer (AlVI–O and Ca–O), for O–H bonds (–OH and H2O species), and hydrogen bond lengths (H···O). The most interesting are hydrogen bonds formed between CA and AS layers being in a range 2.0–2.2 Å. According to the classification of hydrogen bonds, they are of moderate strength [34]. H2O molecules within the double tetrahedral AS layer form hydrogen bonds shorter than 1.8 Å or longer than 2.3 Å. The width of the bond intervals and standard deviation reflect the regularity of coordination of Ca, Al, and Si atoms. The data analysis indicates that the coordination of Al atoms (both six-fold and four-fold coordinated) is more consistent compared to the coordination of Ca and Si atoms. An analysis of the bonds in the rest of the models from Table 1 showed similar ranges and is not included in Table 3.

3.2. Mechanical Properties: Silicon and Water Content Effects

Elastic constants, Cij, were calculated by the stress–strain approach for all models. They are presented in Table 4. The original trigonal system has six or seven independent elastic constants (depending on site symmetry). As all optimized models have a perturbed trigonal structure, they were considered in the calculations in P1 symmetry (Table 2); therefore, Table 4 collects the complete set of all 21 elastic constants. Indeed, the main elastic constants typical for the trigonal system are emphasized in Table 3 in a bold style.
Comparing three C11–33 values showed that models with a full occupation are strongly anisotropic where the C33 constant (direction perpendicular to layered structure) is significantly smaller than two others (C11 ≈ C22); this is mainly evident for the structures Str1 and Str2. A partial loss of water in (Str1-w) structure resulted in small changes in the C11,22 constants and an increase in the C33 constant compared to the Str1 model. Thus, this structure still shows high anisotropy. For the fully anhydrous model, Str2-a, the difference between C33 and C11/22 is significantly less. This anisotropy reduction can be a consequence of the water removal from the space between CA and AS layers and the formation of numerous, relatively strong hydrogen bonds (~1.8–1.9 Å) directly between these layers. This is also reflected in the Bulk (BH) and Young’s (EH) moduli (Table 5) calculated according to Voigt–Reuss–Hill average scheme (VRH) [35,36,37]. The more silicious structure, Str2, showed the largest C11/22 constants from all models and a low C33 constant as observed for the corresponding Str1 structure (Table 4). Thus, this model also shows high anisotropy. The difference between Str1 and Str2 models could be a consequence of weaker bonding between CA and AS layers and a higher rigidity of the fully silicious AS layer in the Str2 model. The high anisotropy of the Str1, Str1-w, and Str2 models is also evidenced by the universal elastic anisotropy constant shown in Table 5. Thus, bonding within the AS and CA layers is stronger (typical polar covalent bonding) than bonding between layers (hydrogen bonding and electrostatic interactions).
Comparing elastic constants of defected structures (Str1_d and Str2_d) with the models with the full occupation (Str1 and Str2), it is evident that anisotropy almost disappears (see also universal elastic anisotropy factors in Table 5). Two C11/22 constants significantly decreased for the defected structures compared to non-defected ones. In contrast, the C33 constant increases to a value like that of C11/22 constants and is also significantly larger than C33 for the Str1 and Str2 models. The observed high anisotropy of models with full occupancy indicates that they are much less resistant to the uniaxial stress along the c-axis than along the a/b directions. The large drop of the C11/22 constants in the models with defects means that there is a significant decrease in resistance to uniaxial stress in the a/b directions. These changes can be explained by the interruption of the strong covalent bonds in the AS layer.
All calculated moduli (bulk, Young’s, and shear) for both defected models are lower than that for the corresponding models with the full occupancy (Table 5). It means an evident decrease in the hardness of the defected structures, which are structurally closest to the real stratlingite structure [7]. The calculated BH values of 32.0 GPa (Str1_d) and 26.3 GPa (Str2_d) are in good agreement with the experimentally determined bulk modulus of stratlingite (27 GPa) [15]. Lower values of Young’s modulus also reflect the decrease in the ability of the models with the defects to resist volume compression and uniaxial deformations as discussed above. Shear modulus, GH, reflects a resistance to the shear stress (“rigidity” of the material). Calculated GH values showed that the defected structures are less rigid than the structures with the full occupation. On the other hand, the water loss from the structure resulted in an increase in the values of all three moduli, meaning that the hardness of the models with complete AS layer and with removed water (Str1-w and Str1-a) is even higher than that of the corresponding Str1 model (Table 5).
The values of parameters such as Poisson’s ratio (νH, ratio between longitudinal and lateral stress) [38], Pugh’s ratio (BH/GH) [39], Vickers hardness [40], Cauchy pressure [41], and the Kleinman parameter (ξ) [42] also reflect differences in the material properties of the studied models discussed above. Poisson’s ratios are larger for the defected structures in comparison to non-defected structures (Table 5) but still have values typical for aluminosilicate materials (0.2–0.3). This difference corresponds to the Vickers hardness parameter that is significantly higher for the non-defected models.
Pugh’s ratio reflects the ductility/brittleness of material. Values below 1.8 indicate that the material is more brittle whereas values above are more ductile [43]. The values collected in Table 5 are around the limiting value, showing that defected models are slightly ductile. Similar features of the material can be indicated also from the Cauchy pressure. Values below 0 show that the material is more brittle, is resistant to the bond bending and, in the structure, covalent bonding prevails. The calculated values in Table 5 show the significant difference between the defected and non-defected models. The values for the defected models are small but still negative, showing that these modes are on a ductility/brittleness edge.
The domination of the covalent stretching bonding in the structure is confirmed by the Kleinman parameter ξ (this shows a tendency of bond bending versus bond stretching; if the value is >0.5, bond stretching dominates). Smaller values for the defected structures confirm that in the defected structures the Al–O/Si–O bonds are interrupted in the AS layer.
Overall, mechanical parameters derived from the DFT-calculated elastic constants showed that all studied structures are typical calcium aluminosilicate materials with relatively high hardness and are more brittle than ductile. The calculated Cij values of all models also fulfilled the elastic stability conditions required for the mechanical stability of the materials [44].

4. Conclusions

In this paper, we predicted the mechanical properties of several model structures based on the structure of stratlingite, a layered calcium aluminosilicate mineral, to study the impact of water content, chemical composition (Al/Si ratio), and structural vacancies (50% in the aluminosilicate layer) on the mechanical properties. The performed DFT calculations based on the PBE-D3 functional showed that mechanical properties are dependent on all studied factors. The models with the full occupancy (complete aluminosilicate layer) showed higher toughness than those with defects. The hardness and uniaxial resistance of the models with full occupancy and water loss were found to increase in comparison to the reference model (Str1). Conversely, these properties exhibited a slight decrease in the models with higher silicon content. All models with full occupancy showed high anisotropy. The models with the vacancies in the structure, which are the closest to the experimental structure of stratlingite, almost lost their anisotropy. Their toughness and rigidity were significantly reduced compared to the reference models with full occupancy (e.g., the drop of bulk modulus was about 25%–30%). The main factor responsible for the changes in the mechanical properties of the defected models is the breaking of the strong covalent Al/Si-O bonds in the aluminosilicate layer. According to the parameters determining ductile/brittle behavior, the models with full occupancy are more brittle, whereas the behavior of the defected structures is more ductile. This may explain the elastic behavior of stratlingite binder in concretes, which can play a role in impeding the propagation of microcracks in the material.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/min15060648/s1; Complete list of the PBE-D3 optimized structural data of all stratlingite models discussed in the main text (Table 1), in the POSCAR format of the program VASP (cell vectors are in Å, atomic positions in fractional coordinates). The details on the VASP calculations are in the main text.

Author Contributions

D.T.: conceptualization, data curation and analysis, writing—original draft; A.Z.: conceptualization, draft writing and editing. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data is contained within the article and Supplementary Materials.

Acknowledgments

The Vienna Scientific Cluster (Project No. 70544) is gratefully acknowledged for providing computational resources.

Conflicts of Interest

The authors declare no competing financial interests.

References

  1. Taylor, H.F.W. Cement Chemistry, 2nd ed.; Thomas Telford: London, UK, 1997. [Google Scholar]
  2. L’Hôpital, E.; Lothenbach, B.; Le Saout, G.; Kulik, D.; Scrivener, K. Incorporation of aluminium in calcium-silicate-hydrates. Cem. Concr. Res. 2015, 75, 91–103. [Google Scholar] [CrossRef]
  3. Matschei, T.; Lothenbach, B.; Glasser, F.P. Thermodynamic properties of Portland cement hydrates in the system CaO–Al2O3–SiO2–CaSO4–CaCO3–H2O. Cem. Concr. Res. 2007, 37, 1379–1410. [Google Scholar] [CrossRef]
  4. Hentschel, G.; Kuzel, H. Stratlingite, 2CaO.AI2O3-SiO2-8H2O, A new mineral. Neues Jahrb. Mineral. Monat. 1976, 326–331. [Google Scholar]
  5. Jambor, J. New mineral names. Am. Min. 1992, 77, 670–675. [Google Scholar]
  6. Passaglia, E.; Turconi, B. Silicati e altri minerali di Montalto di Castro (Viterbo). Riv. Miner. Ital. 1982, 4, 97–110. [Google Scholar]
  7. Rinaldi, R.; Sacerdoti, M.; Passaglia, E. Stratlingite: Crystal structure, chemistry, and a reexamination of its polytype vertumnite. Eur. J. Min. 1990, 2, 841–849. [Google Scholar] [CrossRef]
  8. Midgley, H.G.; Rao, P.B. Formation of Strätlingite, 2CaO·SiO2 Al2O3 8H2O, in relation to the hydration of high alumina cement. Cem. Concr. Res. 1978, 8, 169–172. [Google Scholar] [CrossRef]
  9. Kwan, S.; LaRosa, J.; Grutzeck, M.W. 29Si and 27Al MASNMR study of strätlingite. J. Am. Ceram. Soc. 1995, 78, 1921–1926. [Google Scholar] [CrossRef]
  10. Aranda, M.A.G.; De la Torre, Á.G.; León-Reina, L. Rietveld quantitative phase analysis of OPC clinkers, cement and hydration products. Rev. Miner. Geochem. 2012, 74, 169–209. [Google Scholar] [CrossRef]
  11. Jackson, M.D.; Landis, E.N.; Brune, P.F.; Vitti, M.; Chena, H.; Lia, Q.; Kunz, M.; Wenk, H.-R.; Monteiro, P.J.M.; Ingraffea, A.R. Mechanical resilience and cementitious processes in Imperial Roman architectural mortar. Proc. Natl. Acad. Sci. USA 2014, 11, 18484–18489. [Google Scholar] [CrossRef]
  12. Oh, J.E.; Clark, S.M.; Monteiro, P.J.M. Does the Al substitution in C-S-H(I) change its mechanical property? Cem. Concr. Res. 2011, 41, 102–106. [Google Scholar] [CrossRef]
  13. Matschei, T.; Lothenbach, B.; Glasser, F.P. The AFm phase in Portland cement. Cem. Concr. Res. 2007, 37, 118–130. [Google Scholar] [CrossRef]
  14. Balonis, M.; Glasser, F.P. The density of cement phases. Cem. Concr. Res. 2009, 39, 733–739. [Google Scholar] [CrossRef]
  15. Santacruz, I.; De la Torre, Á.G.; Sanz, J.; Alvarez-Pinazo, G.; Aranda, M.A.G.; Cabeza, A. Structure of stratlingite and effect of hydration methodology on microstructure. Adv. Cem. Res. 2016, 28, 13–22. [Google Scholar] [CrossRef]
  16. Moon, J.; Oh, J.E.; Balonis, M.; Glasser, F.P.; Clark, S.M.; Monteiro, P.J.M. Pressure induced reactions amongst calcium aluminate phases. Cem. Concr. Res. 2012, 41, 571–578. [Google Scholar] [CrossRef]
  17. Cuesta, A.; Rejmak, P.; Ayuela, A.; De la Torre, A.G.; Santacruz, I.; Carrasco, L.F.; Popescu, C.; Aranda, M.A.G. Experimental and theoretical high pressure study of calcium hydroxyaluminate phases. Cem. Concr. Res. 2017, 97, 1–10. [Google Scholar] [CrossRef]
  18. Baquerizo, L.G.; Matschei, T.; Scrivener, K.L.; Saeidpour, M.; Wadsö, L. Hydration states of AFm cement phases. Cem. Concr. Res. 2015, 73, 143–157. [Google Scholar] [CrossRef]
  19. Scholtzová, E.; Tunega, D.; Speziale, S. Mechanical properties of ettringite and thaumasite—DFT and experimental study. Cem. Concr. Res. 2015, 77, 9–15. [Google Scholar] [CrossRef]
  20. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  21. Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
  22. Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
  23. Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
  24. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  25. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
  26. Tunega, D.; Bučko, T.; Zaoui, A. Assessment of ten DFT methods in predicting structures of sheet silicates: Importance of dispersion corrections. J. Chem. Phys. 2012, 137, 114105. [Google Scholar] [CrossRef] [PubMed]
  27. Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
  28. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  29. Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  30. Le Page, Y.; Saxe, P. Symmetry-general least-squares extraction of elastic coefficients from ab initio total energy calculations. Phys. Rev. B 2001, 63, 174103. [Google Scholar] [CrossRef]
  31. Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A User-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
  32. Marmier, A.; Lethbridge, Z.A.D.; Walton, R.I.; Smith, C.W.; Parker, S.C.; Evans, K.E. ElAM: A computer program for the analysis and representation of anisotropic elastic properties. Comput. Phys. Commun. 2010, 181, 2102–2115. [Google Scholar] [CrossRef]
  33. Gaillac, R.; Pullumbi, P.; Coudert, F.-X. ELATE: An open-source online application for analysis and visualization of elastic tensors. J. Phys. Condens. Matter 2016, 28, 275201. [Google Scholar] [CrossRef]
  34. Scheiner, S. Hydrogen Bonding. A Theoretical Perspective; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
  35. Voigt, W. Lehrbuch der Kristallphysik; Teubner: Berlin, Germany, 1928. [Google Scholar]
  36. Reuss, A. Berechnung der Fliessgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
  37. Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A 1952, 65, 349. [Google Scholar] [CrossRef]
  38. Greaves, G.N.; Greer, A.L.; Lakes, R.S.; Rouxel, T. Poisson’s ratio and modern materials. Nat. Mater. 2011, 10, 823–837. [Google Scholar] [CrossRef] [PubMed]
  39. Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 2009, 45, 823–843. [Google Scholar] [CrossRef]
  40. Tian, Y.; Xu, B.; Zhao, Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Hard Mater. 2012, 33, 93–106. [Google Scholar] [CrossRef]
  41. Pettifor, D.G. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 2013, 8, 345–349. [Google Scholar] [CrossRef]
  42. Kleinman, L. Deformation potentials in silicon. I. Uniaxial strain. Phys. Rev. 1962, 128, 2614. [Google Scholar] [CrossRef]
  43. Thompson, R.P.; Clegg, W.J. Predicting whether a material is ductile or brittle. Curr. Opin. Solid State Mater. Sci. 2018, 22, 100–108. [Google Scholar] [CrossRef]
  44. Mouhat, F.; Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
Minerals 15 00648 g001
Figure 1. Two views on structures of CA (a,b) and AS layers (c,d) of the stratlingite model with the complete AS layer (Str1 in Table 1). Water molecules are not displayed. Color scheme: blue (Al), yellow (Si), green (Ca), red (O), white (H).
Figure 1. Two views on structures of CA (a,b) and AS layers (c,d) of the stratlingite model with the complete AS layer (Str1 in Table 1). Water molecules are not displayed. Color scheme: blue (Al), yellow (Si), green (Ca), red (O), white (H).
Minerals 15 00648 g001
Minerals 15 00648 g002
Figure 2. Two views (a,b) on the structure of defected AS layer of the stratlingite model Str1_d from Table 1. Water molecules are not displayed. Color scheme: blue (Al), yellow (Si), red (O), white (H).
Figure 2. Two views (a,b) on the structure of defected AS layer of the stratlingite model Str1_d from Table 1. Water molecules are not displayed. Color scheme: blue (Al), yellow (Si), red (O), white (H).
Minerals 15 00648 g002
Minerals 15 00648 g003
Figure 3. Optimized structures of two stratlingite models with complete AS layer—(a) Str1 and (b) Str2 from Table 1. Color scheme: blue (Al), yellow (Si), green (Ca), red (O), white (H). Hydrogen bonds are shown as blue dashed lines.
Figure 3. Optimized structures of two stratlingite models with complete AS layer—(a) Str1 and (b) Str2 from Table 1. Color scheme: blue (Al), yellow (Si), green (Ca), red (O), white (H). Hydrogen bonds are shown as blue dashed lines.
Minerals 15 00648 g003
Table 1. Composition of all structural models of stratlingite used in this work (UC = unit cell). Complete structural data in the VASP format are collected in the Supplementary Materials (SM).
Table 1. Composition of all structural models of stratlingite used in this work (UC = unit cell). Complete structural data in the VASP format are collected in the Supplementary Materials (SM).
ModelCA Layer Formula AS Layer FormulaSum Chem.
Formula/UC		Ca:Al:Si
Ratio
Str1 [Ca2Al(OH)6·2H2O] [(Si3AlO8)·H2O]Ca6Al6Si9O51H362:2:3
Str2[Ca2Al(OH)7·H2O][(Si4O8)·H2O]Ca6Al3Si12O51H332:1:4
Str1-w [Ca2Al(OH)6·2H2O][(Si3AlO8)]Ca6Al6Si9O48H302:2:3
Str1-a[Ca2Al(OH)6] [(Si3AlO8)]Ca6Al6Si9O42H182:2:3
Str1_d[Ca8Al4(OH)24·8H2O][(Si6Al2O10(OH)12)·4H2O]Ca24Al18Si18O174H1742:1.5:1.5
Str2_d[Ca8Al4(OH)24·8H2O][(Si8O12(OH)10)·4H2O]Ca24Al12Si24O174H1682:1:2
Table 2. Optimized unit cell parameters calculated for stratlingite models from Table 1 and their comparison with experimental data [7].
Table 2. Optimized unit cell parameters calculated for stratlingite models from Table 1 and their comparison with experimental data [7].
a/Åb/Åc/Åα/°β/°γ/°V/Å3dev/% b
Exp.5.7455.74537.77090.0090.00120.001079.5870.0
Str15.5095.50338.06489.6790.09119.941000.031−7.4
Str1-w5.5095.48738.17189.7098.99119.811000.973−7.3
Str1-a5.4645.46336.07290.2389.93120.01932.431−13.6
Str25.3775.43640.09692.2885.60120.081011.098−6.3
Str1_d a5.6865.67237.05289.7290.28120.291031.622−4.4
Str2_d a5.7275.67437.19492.0189.10120.611039.553−3.7
a Str1_d and Str2_d had computational cells of 2a and 2b dimensions. b Deviation from the experimental volume.
Table 3. Range of bond lengths (in Å) in the stratlingite structural model Str1. Subscripts “IV” and “VI” mean four- and six-fold coordinated Al atoms in AS and CA layers, respectively.
Table 3. Range of bond lengths (in Å) in the stratlingite structural model Str1. Subscripts “IV” and “VI” mean four- and six-fold coordinated Al atoms in AS and CA layers, respectively.
Str1IntervalMean ± Std
AlIV–O1.718–1.7631.743 ± 0.014
AlVI–O1.885–1.9031.894 ± 0.005
Si–O1.576–1.7231.653 ± 0.046
Ca–O2.313–2.4192.369 ± 0.037
O–H0.969–0.9850.975 ± 0.005
H···O1.771–2.6102.237 ± 0.230
Table 4. All 21 calculated elastic constants. The most relevant values typical for the trigonal system are shown in bold.
Table 4. All 21 calculated elastic constants. The most relevant values typical for the trigonal system are shown in bold.
Elastic ConstantsStr1Str1-wStr1-aStr2Str1_dStr2_d
C11154.1153.8146.3160.160.454.6
C22 ≈ C11148.4165.1145.8176.270.964.3
C3332.444.3135.320.360.648.9
C4420.222.815.25.012.08.8
C55 ≈ C4421.524.114.313.08.68.1
C66 ≈ 1/2 (C11–C12)47.847.247.349.118.415.4
C1266.071.448.975.219.315.3
C139.614.64.90.713.412.6
C140.53.10.72.1−0.00.0
C15 ≈ 03.1−0.50.94.61.93.2
C168.64.5−0.70.30.60.1
C23 ≈ C1313.219.67.35.616.69.9
C24 ≈ C140.63.10.0−0.62.00.6
C25−4.2−5.7−1.3−1.4−1.31.4
C263.5−0.40.4−2.8−0.8−2.0
C34−2.42.10.60.40.60.2
C350.8−2.81.2−2.51.33.6
C362.4−0.9−1.50.80.40.3
C451.82.71.14.6−0.5−0.8
C46−4.1−4.2−0.61.2−2.0−1.3
C56 ≈ C140.20.01.4−0.80.1−1.0
Table 5. Average mechanical properties of bulk polycrystalline structure: Subscript “H” means Hill’s averages of Voigt and Reuss values.
Table 5. Average mechanical properties of bulk polycrystalline structure: Subscript “H” means Hill’s averages of Voigt and Reuss values.
PropertyStr1Str1-wStr1-aStr2Str1-dStr2-d
BH/GPa42.650.860.337.532.026.3
EH/GPa72.780.383.452.040.934.9
GH/GPa29.932.532.920.515.913.6
Poisson’s Ratio νH0.2150.2360.2690.2690.2870.279
Pugh’s Ratio BH/GH1.421.561.841.832.021.93
Vickers Hardness/GPa 6.86.55.53.912.932.77
Universal Elast. Anisotropy2.731.922.6914.60.991.26
Cauchy Pressure pC/GPa −45.7−48.6−33.6−70.2−7.4−6.5
Kleinman parameter ξ0.720.780.580.790.560.50
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Tunega, D.; Zaoui, A. Theoretical Study on Impact of Chemical Composition and Water Content on Mechanical Properties of Stratlingite Mineral. Minerals 2025, 15, 648. https://doi.org/10.3390/min15060648

AMA Style

Tunega D, Zaoui A. Theoretical Study on Impact of Chemical Composition and Water Content on Mechanical Properties of Stratlingite Mineral. Minerals. 2025; 15(6):648. https://doi.org/10.3390/min15060648

Chicago/Turabian Style

Tunega, Daniel, and Ali Zaoui. 2025. "Theoretical Study on Impact of Chemical Composition and Water Content on Mechanical Properties of Stratlingite Mineral" Minerals 15, no. 6: 648. https://doi.org/10.3390/min15060648

APA Style

Tunega, D., & Zaoui, A. (2025). Theoretical Study on Impact of Chemical Composition and Water Content on Mechanical Properties of Stratlingite Mineral. Minerals, 15(6), 648. https://doi.org/10.3390/min15060648

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop