Abstract
A thorough understanding of the chemistry involved in reinjecting heat-depleted geothermal water into poorly consolidated sandstone is vital for the effective design of treatments targeting subsurface rock formations. The intricate chemical interactions occurring within sandstone systems can result in the dissolution of certain minerals and the subsequent precipitation of others, which may significantly contribute to damage within the formation. This process can alter the physical properties of the rock, potentially leading to reduced permeability and other challenges in resource extraction. Thus, it is imperative to monitor not only the concentration of various chemical species present in the geothermal water and sandstone, but also the spatial distribution of these geochemical reactions. By doing so, we can better predict and mitigate their potential adverse effects on rock formations, ensuring the long-term success and efficiency of geothermal energy extraction and other subsurface activities. In this study, we conducted laboratory experiments using both model and natural formation waters, as well as rock samples, to investigate water–rock interactions in a sandstone reservoir in the Szentes area of Hungary. Geochemical models were run with two different thermodynamic databases to simulate laboratory experiments, predict the effects of heat-depleted geothermal water reinjection into the reservoir, and assess predictions of different geochemical databases. Our study shows that calcite dissolves while quartz, kaolinite, and dolomite form. Other mineral reactions, however, remain less certain. The PHREEQC database indicates chlorite dissolution along with the formation of small amounts of feldspars and hematite, whereas the Thermoddem database predicts montmorillonite dissolution and chlorite precipitation. The reservoir porosity and permeability are expected to change over time as a result of mineral reactions. Modeling results, however, indicate negligible porosity changes as the reservoir reaches equilibrium state. The general concept proposed here, which focuses on the geochemical properties of the reinjected water and reservoir, provides a framework for detailed analysis of the geothermal system—a critical step for ensuring sustainable geothermal operations.
1. Introduction
Reinjection is crucial for all types of geothermal reservoirs in production and can be the key factor in the success or failure of geothermal power development [1]. The injection of heat-depleted brines into clastic sedimentary reservoirs with alternating clay, sand, and sandstone sequences has long been considered a delicate subject among petroleum and geothermal operators. Without thorough and careful planning, the injection can turn into a disaster, with scenarios including the reinjection of incompatible waters into the formation, particle entrainment, capture, and release, or unsuccessful well completion, which often leads to irreparable damage to the well and formation [1,2,3,4,5,6,7,8,9,10,11].
Sandstones often have poor reservoir quality [12,13]. This is due to the early development of secondary mineral phases and mechanical compaction, which reduce permeability and porosity [14,15,16]. The two most important cementing mineral phases for sandstones are carbonate minerals (calcite, dolomite, ankerite) and quartz. The factors determining the solubility of these mineral phases (e.g., temperature, pressure, solute content, and pH) often have opposite effects on the solubility of the two phases. The solubility of CaCO3 (e.g., calcite) is primarily controlled by the amount of dissolved CO2 and pH and increases with decreasing temperature. On the other hand, the solubility of SiO2 (e.g., quartz, amorphous SiO2) decreases with decreasing temperature. Similarly, a change in pH has the opposite effect on solubility, with the solubility of CaCO3 being highest at low pH (pH < 7, acidic medium) and that of SiO2 being highest at high pH (pH > 9–10, alkaline medium). In natural systems, the precipitation of carbonate minerals is typically promoted by the exsolution of dissolved CO2—driven by a decline in pore pressure or an increase in temperature or salinity (i.e., “salting out”)—which can lead to a significant increase in pH. The solubility of both SiO2 and CaCO3 increases with pressure and, to a certain extent, with an increase in dissolved ion concentrations [17,18,19].
This investigation focuses on water–rock interactions in a sandstone geothermal reservoir during recharge conditions, specifically in the Szentes area of Hungary. Previous studies, such as Markó et al. [6], describe injection-related issues in a Hungarian sandstone doublet system, emphasizing formation damage and pressure drawdown. Their research addresses similar reservoir conditions in the Pannonian Basin and highlights the risk of fines migration. Ungemach [3] provides a comprehensive operational perspective on reinjecting cooled geothermal brines into clastic formations and emphasizes potential plugging hazards. Sætre et al. [12] employed reactive transport modeling for intra-basaltic sandstones in the North Atlantic. Although they conducted 1D simulations to examine diagenetic alteration, the geological context—basalt–sandstone interfaces—differs from the unconsolidated sandstones of the Pannonian Basin. Koroncz et al. [13] investigated the Upper Miocene–Pliocene (Upper Pannonian) reservoir from a petrophysical standpoint, focusing on permeability and lithology. While this study considers scaling and diagenesis, it does not model short-term versus long-term geochemical reactions at the same experimental depth, meaning that it does not provide actual lab-measured reaction rates under controlled temperature and pressure conditions.
In this study, we design a series of laboratory experiments to evaluate geochemical interactions under specific conditions. Geochemical simulations of these laboratory experiments with two different thermodynamic databases align with the kinetic data obtained. Thermodynamic and kinetic models were developed to estimate water–rock interactions induced by the reinjection of heat-depleted water at the Szentes Geothermal Area. The findings of this research underline the importance of laboratory testing and site-specific analysis of geochemical reactions based on local conditions and provide a solid theoretical foundation and valuable technical guidance for understanding water–rock interactions, as well as addressing potential chemical plugging issues that may arise during geothermal development in sandstone reservoirs in Hungary.
2. Geological Setting
This study was conducted as part of a research and development project in the Szentes area (see Figure 1). During the project, two wells, SZT-1 and SZSZT-IX, were drilled and sampled continuously, but using different methods (rock chips, drill core) at various depth intervals, with a focus on sandy formations, in line with the project’s objectives. The Szentes area is located in the northeastern section of the Makó–Hódmezővásárhely Trough, where the pre-Neogene basement lies at depths of 4500–5000 m [20,21,22]. During the Miocene, the trough was filled with gravel and conglomerate as a result of erosion from the Algyő and Pusztaföldvár Highs, leading to the deposition of porous Pannonian sediments [23,24]. In this study area, the pre-Neogene basement has been reached by only two boreholes, FÁB-4 and Szentes ÉK-1, which have exposed Upper Cretaceous sandstone and siltstone, as well as Lower Triassic sandstone and clay layers [25]. During the Pannonian period, the sedimentary environments transitioned vertically from a deep basin to a delta slope, then to a delta front, and ultimately to a delta plain [26]. The total thickness of the Pannonian sediments can exceed 3000 m [26]. The thermal wells in Szentes revealed the Upper Pannonian (Upper Miocene–Pliocene) Újfalu Formation, characterized by delta front and delta plain facies, overlain by a delta top and alluvial plain facies known as the Zagyva Formation [26,27]. The Újfalu Formation consists of sandstone, siltstone, and clay marl, with sandstone layers being predominant. It is primarily composed of channel and mouth bar sediments, which possess good reservoir properties, but have limited lateral extension [27]. However, due to multiple erosion and superposition events, these layers are hydrodynamically interconnected. The overlying Zagyva Formation represents a depositional environment characterized by an alluvial plain with a highly heterogeneous composition. In this formation, the alternating layers of sandstone, silty sand, silty clay, and clay are quite common. In the alluvial plain, sedimentary cycles are dominated by channel and point-bar patterns [26,27]. The upper boundary of the Zagyva Formation is indicated by a decrease in the sandstone content, which is typically easy to identify. The Quaternary layers deposited over the Upper Pliocene sediments have an average thickness of 600–700 m and contribute to the water supply of Szentes.
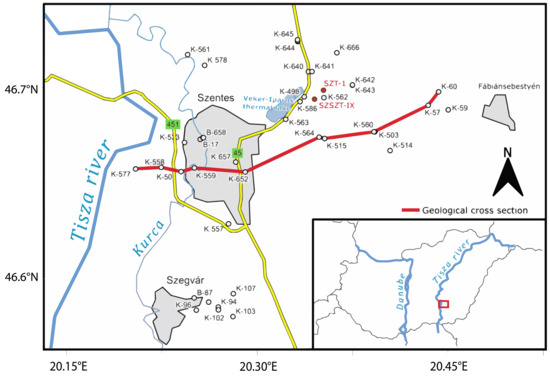
Figure 1.
The Szentes Geothermal Area, as depicted in [13].
Geothermal Reservoir Characterization
Based on the production history and well-test analysis of the 40 active wells in the Szentes Geothermal Field, three groups of aquifer layers can be identified. Most of the wells have production intervals completed in the Újfalu Formation. A stratigraphic cross-section of the study area, illustrating the wells and their production intervals, is presented in Figure 2. The upper aquifer layer group, referred to as Level A, consists of wells with production intervals located in the Újfalu and Zagyva Formations, at depths ranging from 1500 to 1800 m, with an average permeability of 1500 millidarcy (mD) [13,27]. The middle aquifer layer group, Level B, comprises wells with production intervals between depths of 1800 and 2000 m, primarily in the Újfalu Formation and partially in the Zagyva Formation, exhibiting an average permeability of 500 mD [13]. The lower aquifer layer group, Level C, comprises wells drilled below 2000 m, all of which are entirely within the Újfalu Formation, with an average permeability ranging from 1000 to 2000 mD. Thermal water production is primarily dominated by wells screened in Level B.
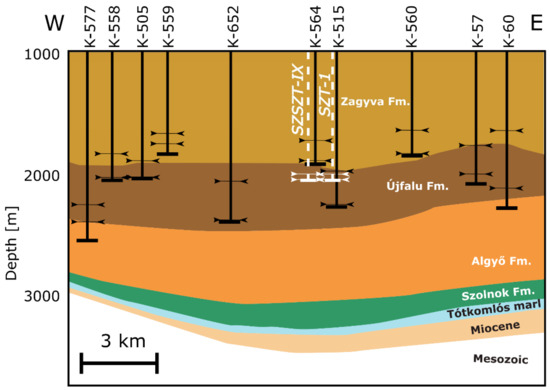
Figure 2.
Stratigraphic cross-section across the study area, showing wells and their corresponding production (screen) intervals (modified after [13,20,26]). The section path illustrated is shown in Figure 1. The wells “SZT-1” and “SZSZT-IX” were drilled as part of this study.
3. Methods
3.1. Characterization of Fluid and Rock Samples
Fluid samples from a geothermal well in the Szentes area were analyzed using inductively coupled plasma-mass spectrometry (SCIEX ELAN DRC-e ICP-MS, PerkinElmer, Waltham, MA, USA) for major dissolved cations and ion chromatography (Dionex ICS-1100, Thermo Scientific, Sunnyvale, CA, USA) for anions. The mineral abundances of a powdered sample of the poorly consolidated sandstone taken adjacent to the experimental core were determined using X-ray diffraction (XRD). All analyses were performed in the laboratories of the Environmental Analytical and Geoanalytical Research Group at the Szentágothai Research Centre, University of Pécs, and the laboratories of Mecsekérc Ltd., Pécs, Hungary.
Thin sections from 15 samples collected from boreholes SZT-1 and SZSZT-IX were analyzed. These thin sections were examined using a Nikon Eclipse E600POL (Nikon, Tokyo, Japan) polarized light microscope with both plane-polarized and cross-polarized light. The evaluation focused on grain size, sorting, roundness, and mineral composition. X-ray diffraction (XRD) patterns of the sandstone samples were obtained using Cu-Kα radiation (40 kV, 15 mA) with a Rigaku MiniFlex 600 (Rigaku, Tokyo, Japan). Scans were conducted at room temperature over a range of 5–70° 2θ, with a step size of 0.02/s. The XRD scans were analyzed for quantitative phase composition using a full profile fitting procedure. The total amount of identified crystalline phases is expressed as 100%. However, the actual percentages only reflect the relative abundances, as the proportion of amorphous components is unknown. The measurement uncertainties are ±1%, ensuring precise sample preparation and measurement.
3.2. Calorimetry and Geochemical Modeling of Laboratory Experiments
Calorimetry experiments were conducted using a Setaram C80 (KEP Technologies, Caluire, France) Calvet-type calorimeter equipped with a stainless steel cell rated for up to 220 °C and 100 bars to investigate and predict water–rock interactions. In a laboratory setting, the time available for these experiments is limited. Therefore, we increased the reaction rates compared to those in natural reservoirs. In our case, this was facilitated in several ways: (1) by increased temperature (120 °C) compared to natural repositories (~90 °C), and (2) by using the smallest grain size fraction (fraction below 63 µm), which significantly increases the specific surface area available for water–rock interactions. Additional experiments have been conducted with the biggest grain size fraction of the studied aquifer (>250 µm) in order to assess the effect of grain size on the reaction rate. Because pressure monitoring equipment was unavailable, pCO2 in the experiments was estimated using the carbonate–water equilibrium (~0.7 bar), and the total pressure in the cell was estimated to be ~3.8 bars at 120 °C. After cooling the reactor to 25 °C, fluid samples were collected for chemical analysis, filtered through a 0.2 µm Nylon Acrodisc syringe filter, and stabilized with nitric acid. The laboratory experiments were modeled using PHREEQC-3 [28], with mineral compositions as shown in Table 1 and the initial model and natural water compositions presented in Table 2, which were equilibrated with the atmosphere at 25 °C. Kinetic batch models simulating 3.5 days were run at 120 °C and 3.8 bars of pressure (estimated pressure at 120 °C in the calorimeter cells) using two databases: PHREEQC and Thermoddem [28,29]. The results of the models simulating the NaHCO3 solution experiment are shown in Section 4.2, while the results of the models simulating the experiment using the natural water sample are illustrated in Section 4.3.

Table 1.
Water composition used in modeling the Szentes geothermal area (data from Árpád-V/2 well, based on [30]) and mineral composition measured using X-ray diffraction (XRD) and recalculated to a unit used with the PHREEQC modeling program (mol/kg water, based on [31]).

Table 2.
Composition of the water phase from laboratory calorimetry experiments conducted at 120 °C, shown both before the experiment (in italics) and at the end of each run. Water sample compositions were analyzed at 25 °C.
3.3. Modeling Water–Rock Interactions at the Szentes Geothermal Area
Thermodynamic and kinetic batch models, as well as kinetic 1D reactive transport models, were developed for the Szentes area to investigate the potential effects of using heat-depleted thermal water for reinjection. All models were run using two different thermodynamic databases (PHREEQC and Thermoddem databases). The input data on water chemistry and rock mineral composition used in the models are summarized in Table 2. Other parameters estimated for water composition were pe (4), Al (0.05 mg/dm3), and Si (10 mg/dm3) concentrations, and pCO2 was estimated using the carbonate–water equilibrium. The rock composition was converted to the unit of measurement used by PHREEQC (mol/kgW) based on the equation published by Szabó et al. [31], with an estimated porosity of 20%. Siderite, goethite, hematite, and pyrite were considered as potentially forming secondary mineral phases. The kinetic data (Ea, k25) were determined for the kinetic models as reported by Palandri and Kharaka [32]. The specific surface areas of the minerals were taken as m2/g: calcite/siderite (22), quartz (58), K-feldspar (12), albite (21.6), kaolinite (200), dolomite (2.8), montmorillonite (725), chlorite (2.9), and goethite/hematite/pyrite (274). The reactive specific surface areas were taken as one-tenth of these, and mineral precipitation was defined as a reaction 100 times slower than dissolution. For the kinetic 1D reactive transport models, the diffusion flow rate at a depth of approximately 1500 m was assumed (6.01 × 10−9 m2/s, following [33,34]). The number of cells was defined as 30, the number of steps as 190, and the time interval between steps as 16,650 s. The total length of the model is 3 mm under diffusion and 3 cm, assuming a flow rate 10 times higher than that of diffusion.
4. Results and Discussion
The geothermal area of Szentes is one of Hungary’s oldest and most intensively produced areas, where long-term thermal water extraction has resulted in a significant pressure drop [30]. For this reason, it is essential to investigate the possibilities and impacts of reinjecting used thermal water. The mineral composition of the sandstones in the area includes calcite, dolomite, quartz, feldspar (albite and microcline), kaolinite, Ca-montmorillonite, and chlorite. If the cement phase of the sandstone is composed mostly of carbonate minerals (as in the Szolnok Sandstone Formation), an incorrectly chosen acid well treatment or dissolution due to the inflow of heat-depleted water can cause irreversible damage to the unconsolidated sandstone, leading to sand inflow into the well.
4.1. Mineralogical Characterization of the Geothermal Reservoir
The thin section analysis shows that the gray to light gray sandstones are characterized by well- to very-well-sorted grains (Figure 3). The grain size ranges from very fine to medium, with a predominantly fine distribution, and the grains are subangular to very angular, exhibiting low sphericity in their shape. The main composition includes quartz, feldspar (both K-feldspar and plagioclase), and mica (muscovite and chloritized biotite), along with carbonates, and minor components like granules, opaque minerals (coalified plant fragments, hematite), as well as accessory minerals such as zircon, apatite, staurolite, and tourmaline (see Figure 3). The sandstones are primarily poorly cemented. Cement phases are composed of calcite and dolomite carbonates, as well as clay minerals such as sericite, montmorillonite, kaolinite, and illite. Micritic calcite cement is found only in patches and narrow bands.

Figure 3.
Photomicrographs of SZT-1 (A) and SZSZT-IX (B) sandstone samples through cross-polarized light. Chl—chlorite, Qz—quartz, Cal—calcite, Pl—plagioclase, Bt—biotite, Ms—muscovite, Kfs—K-feldspar, CRF—carbonate rock fragments, VRF—volcanic rock fragments.
A weak textural orientation is indicated by the presence of oriented mica plates. The dark gray argillaceous marl and siltstone appear as massive units or as alternating layers of marl and siltstone laminae. The fine-grained marls and siltstones contain a significant amount of mica. The dark coloration is attributed to an increased presence of coaly plant fragments and clay minerals.
4.2. Calorimetry Experiments and Models
The experiments showed the dissolution of the mineral phases present under the experimental conditions, as indicated by elevated Na+, Si4+, Ca2+, K+, Mg2+, Fe2+, Al3+, and Mn2+ ions in solutions in the experiment using a model NaHCO3 solution and elevated Na+, Cl, and SO42− ions in the experiments using natural formation water (Table 2). As expected, the experiment using natural formation water and the bigger grain size fraction (>250 µm) showed more limited reactions than experiments with the <63 µm grain size fraction within the same timeframe, emphasizing the influence of surface area on the reaction rate. Moreover, the calorimetry experiments were conducted at an elevated temperature (120 °C) compared to the formation temperature (~90 °C). Hence, the experimental reaction rates are expected to overestimate reaction rates in the field scale.
The results of the PHREEQC-3 geochemical models (Figure 4) are consistent with the results of laboratory experiments and are similar in that they show increased ion concentrations in the solution after 3.5 days in the following order, HCO3− > Na+ > Si4+ > K+ > (Cl−) > Al3+ > (SO42−) > Ca2+ > Mg2+ > (Fe2+), with the ions in parentheses appearing only in the models using natural water. The main difference between the two models using the two databases is that the model using the Thermoddem database indicates a higher dissolved HCO3− concentration than the models run with the PHREEQC database, while for other ions such as Na+, Ca2+, and Mg2+, the PHREEQC database predicts higher concentrations. The Na+ ion concentrations predicted by the PHREEQC database match better with the experimental data, while concentrations of Ca2+ and Mg2+ are predicted better by the Thermoddem database. The two models are consistent in predicting the dissolution of K-feldspar, albite, dolomite, and montmorillonite, as well as the precipitation of calcite and chlorite, and the initial dissolution and subsequent precipitation of quartz in both the model NaHCO3 solution and natural water experiments. The precipitation of secondary silicate minerals, such as chlorite, can be quite sluggish; therefore, the modeling results should be interpreted with caution, particularly given the short time frame considered in this study. Kaolinite only shows dissolution in models run with the Thermoddem database, but later, precipitation was observed in models run with the PHREEQC database. The dissolution of feldspars and the precipitation of secondary minerals, including kaolinite, illite, and quartz, are significant diagenetic processes in arkosic sandstones [35]. Yuan et al. [35] conducted laboratory dissolution experiments, analyzed petrologic data, and measured in situ fluid chemistry to investigate feldspar dissolution and the precipitation of secondary minerals in sandstone. By iteratively adjusting their models and comparing the simulated outputs to observed fluid compositions, they demonstrated that effective calibration significantly enhances the reliability of predictive simulations.
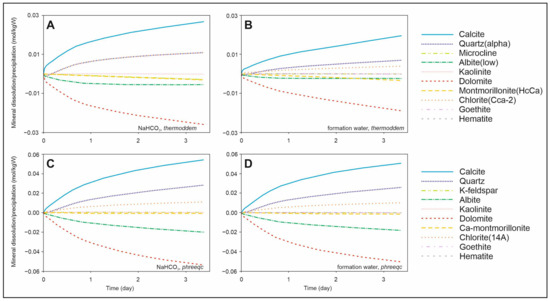
Figure 4.
Results of geochemical modeling using the Thermoddem (A,B) and PHREEQC (C,D) databases for calorimetry experiments with <63 µm grain size fraction and NaHCO3 solution (A,C) and natural formation water (B,D) at 120 °C and 3.8 bar.
Additionally, in models run using natural water composition, the precipitation of goethite and hematite was observed for both datasets. The latter reaction suggests that redox processes, such as oxidation, can also contribute to mineral precipitation in the system. Therefore, it is important to consider the contact of the recycled water with the atmosphere at the surface.
4.3. Modeling Water–Rock Interactions Induced by the Reinjection of Heat-Depleted Water at the Szentes Geothermal Area
The reinjected thermal water is at a lower temperature than the reservoir. The chemical effect of this temperature difference was investigated using an equilibrium and kinetic batch, as well as kinetic 1D reactive transport models at 180 bar pressure and 90 °C and 40 °C. The effect of temperature decrease is estimated by comparing the results obtained at the two different temperatures.
Equilibrium models show a minimal increase in pH (by 1.3–1.4 units) and a decrease in the concentration of several dissolved ions (HCO3− > Na+ > Si4+ > Al3+ > K+ > Cl− > SO42− > Fe2+) in both models due to the injection of the lower temperature solution into the reservoir that has been equilibrated with the atmosphere. In the case of Ca2+ and Mg2+ ions, the models estimate different directions of change: decreasing concentrations when using the PHREEQC database and increasing concentrations when using Thermoddem. The two models are consistent in predicting the dissolution of calcite and precipitation of quartz, kaolinite, and dolomite, but for some mineral phases, the predictions are less clear, e.g., using the PHREEQC database, in addition to the above-mentioned minerals, chlorite dissolution and minor precipitation of feldspars (albite and K feldspar) and hematite are observed, while using the Thermoddem database, montmorillonite dissolution and chlorite precipitation are observed. Differences between the models may stem from variations in how mineral chemistry and dissolution reactions are represented across different databases, especially for more complex minerals, even when reaction kinetics are defined separately. For example, the dissolution of montmorillonite is defined as Ca0.165Al2.33Si3.67O10(OH)2 + 12H2O = 0.165Ca2+ + 2.33Al(OH)4− + 3.67H4SiO4 + 2H+ in the PHREEQC database [Ca-montmorillonite] and as Ca0.17Mg0.34Al1.66Si4O10(OH)2 + 6H+ + 4H2O = 1.66Al3+ + 0.170Ca2+ + 0.340Mg2+ + 4H4SiO4 in the Thermoddem database [Montmorillonite (MgCa)]. Such slight differences may cause the model to favor certain mineral reactions over others when simulating complex systems. In our case, these mineral reactions, however, occur at rates six to eight orders of magnitude lower than the dissolution of calcite and precipitation of quartz, kaolinite, and dolomite. Thus, we conclude that both databases are in general agreement regarding the direction of the dominant long-term geochemical reactions expected in the reservoir. Minor differences in the extent of quartz and carbonate mineral reactions between the two models lead to opposing predictions of porosity change. The PHREEQC-based model predicts a porosity decrease of 0.014%, whereas the Thermoddem-based model predicts a porosity increase of 0.011%. These changes, however, are negligible in comparison to the estimated initial porosity of 20%. It should be noted that equilibrium models for the reinjection of cooled geothermal water in the Szentes Area deviate from those of the laboratory experiments. For example, while calcite precipitation was modeled in the laboratory experiments, the models predict calcite dissolution under real-life conditions. This discrepancy can be attributed to temperature differences between the two scenarios: the laboratory experiments were conducted at higher temperatures (120 °C), promoting calcite precipitation, whereas in the reservoir, cooling from the reinjection of colder water—capable of holding more dissolved CO2—increases calcite solubility [36]. Dissolution of even small amounts of calcite cement can positively impact reservoir performance by enhancing permeability, enlarging pore spaces, and improving fluid flow and injectivity. However, it may also pose risks by triggering rock matrix instability and fines migration, which can be particularly significant in poorly consolidated sandstone reservoirs, leading to pore throat blockage and reduced flow capacity.
Equilibrium models provide insights into the long-term behavior of the reservoir; however, geochemical reactions in a reinjection scenario exhibit both spatial and temporal variability. Consequently, it is essential to understand how these reactions may occur in the vicinity of the reinjection well, as they can influence injectivity and reservoir stability. Kinetic models can complement this understanding by capturing localized and short-term reaction dynamics.
Figure 5 presents the results of kinetic batch models, revealing significant discrepancies between the databases, as detailed below. According to the results obtained using the Thermoddem database, a decrease in temperature leads to a slight increase in pH, variations in dissolved ion concentrations, and the dissolution of calcite and montmorillonite, while quartz, kaolinite, and dolomite precipitate. These findings are in good agreement with the results of thermodynamic batch models. In contrast, simulations using the PHREEQC database indicate a continued increase in pH, a predominant decrease in dissolved ion concentrations, and the dissolution of quartz, kaolinite, calcite, and chlorite, accompanied by the simultaneous precipitation of dolomite and montmorillonite.
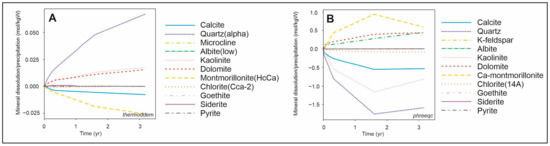
Figure 5.
Results of kinetic batch models run with the Thermoddem (A) and PHREEQC (B) databases and the original (non-equilibrium) solution composition: the graphs show the differences between the results obtained at 40 °C and those at 90 °C, thereby simulating the effect of cooled and reinjected thermal water and the resulting temperature decrease.
The kinetic 1D reactive transport models (Figure 6) indicate that montmorillonite and calcite will dissolve in the rock as the temperature decreases, with parallel precipitation of quartz and dolomite using the Thermoddem database. Models from the PHREEQC database suggest that the lower temperature in the rock will significantly reduce the intensity of reactions compared to the reference case.
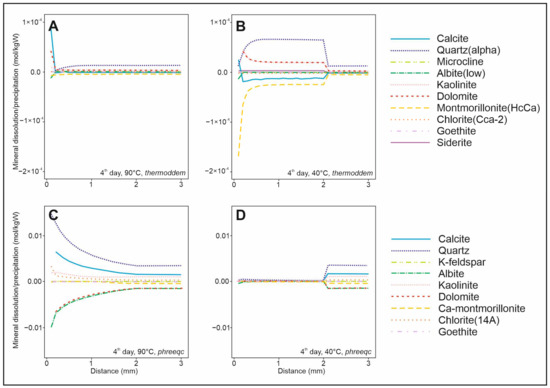
Figure 6.
Results of the 1D kinetic reactive transport models run with the Thermoddem (A,B) and PHREEQC (C,D) databases, simulating the inflow of a 90 °C (A,C) and a 40 °C (B,D) solution to the reservoir on day 4.
The significant discrepancies between the outcomes of kinetic models employing different thermodynamic databases underscore the need for further investigation. The recent study of Gelencsér et al. [37] demonstrated that some reactions predicted by geochemical models using unmodified thermodynamic databases may yield unreliable results when compared to laboratory experiments, emphasizing the importance of validating modeling outcomes through experimental work. Strategies to determine which model predictions more closely reflect reality may include the design of additional laboratory experiments featuring the continuous monitoring of ion concentration changes, extended experimental durations, and the simulation of temperature variations. A flow-through reactor setup may be particularly well-suited for such experiments. Furthermore, short-term field injection tests could provide valuable insights into changes in injectivity and permeability. Multidimensional reactive transport models (e.g., with TOUGHREACT) may further refine our understanding of the spatial distribution of mineral–water reactions and changes in porosity and permeability.
4.4. Comparison with Other Sandstone Reservoirs
A detailed analysis conducted by Markó et al. [6], utilizing hydrogeochemical modeling and laboratory analysis, examined the types of precipitating minerals at the Mezőberény study site in the South-Eastern Great Plain of Hungary. The model predicted the precipitation of goethite and calcite, which was subsequently confirmed using a sample analysis. This confirms the potential for the precipitation of carbonates, iron, and manganese minerals in the area. The primary reason for this precipitation is linked to the fluid composition (higher HCO3−, Na+, Ca2+, and Fe2+ concentrations), higher reservoir temperature (112 °C), and slight differences in mineralogy (e.g., barite, gypsum) in the case of the Mezőberény wells compared to our data. The formation of predominantly carbonate scaling has been observed at several geothermal sites in the Great Hungarian Plain [17]. This increased potential for scaling is likely due to fluid–rock interactions in the shallow-water Pannonian aquifers, which contain a significant amount of carbonate grains [18]. The presence of dissolved calcium and bicarbonate ions contributes to precipitation, particularly during pressure drops that occur during production in the area of Mezőberény. In contrast, at Szentes, calcite dissolution is predicted during the reinjection of cooled thermal water, accompanied by the precipitation of quartz, kaolinite, and dolomite.
Sætre et al. [12] investigated reactive transport processes in intra-basaltic sandstone reservoirs located on the North Atlantic Margin. They utilized laboratory-derived data and numerical modeling to analyze dissolution–precipitation reactions during fluid injection. They discovered that the evolution of primary minerals and the initial formation water supplied the essential elements needed for the precipitation of secondary minerals. Additionally, changes in aqueous silica concentration indicated that the silica released from the dissolution of plagioclase exceeded the silica consumed by the precipitation of quartz, K-feldspar, and illite. Modeled mineral precipitates (quartz and clay minerals) in the reservoir at Szentes may form through such a process.
5. Conclusions
Geochemical and reactive transport models can provide insight into the potential chemical effects of reinjecting cooled thermal water. However, the primary challenge at present is the significant discrepancy in the results provided by thermodynamic databases, which cannot yet be resolved based on the available information. It is, therefore, important to compare the models with laboratory experiments and field tests. The periodic extraction of recovery wells and long-term monitoring of the chemical composition of the water brought to the surface can help to better understand site-specific responses. It is also important to note that the reaction, largely dissolution, of carbonate minerals may affect the area around the injection wells in the short term. On the one hand, this is advantageous, as it can increase the porosity/permeability of the country rocks near the well. On the other hand, it also poses a risk in case these minerals are present as a cementing phase, as the reaction can significantly weaken the physical properties of the rock and cause fines migration (e.g., clay minerals) in the reservoir, potentially leading to formation damage.
Contrary to popular belief, geochemical models that predict the distribution of species in aqueous fluids do not always yield unique results [38]. In such scenarios, there can be multiple geochemical systems that adequately meet the conditions established by the modeler. The modeling software may identify any of the potential solutions to the governing equations, depending on the starting point of the iteration process [39].
In this study, we emphasize the significance of laboratory testing and the interaction between various potential problem sources. In conclusion, this concept enhances risk analysis during the exploration and site-development phases, helping to predict and prevent injectivity issues. We recommend using this approach as part of a checklist for reinjection sites that are experiencing challenges with reinserting water into a sandstone aquifer. A site-specific analysis can further enhance understanding based on local conditions. The most important takeaway is that damage prognosis and the optimal design of water injection strategies are typically empirical and tailored to specific sites. Therefore, it is crucial to conduct carefully designed and implemented field tests and laboratory experiments on formation cores to ensure reliable water injection programs.
Our reactive transport study results indicate that calcite dissolution occurs alongside the precipitation of quartz, kaolinite, and dolomite. However, predictions for some mineral phases are less clear. For instance, using the PHREEQC database, we observe chlorite dissolution and minor precipitation of feldspars (such as albite and K-feldspar) and hematite. In contrast, the Thermoddem database reveals the dissolution of montmorillonite and the precipitation of chlorite. In subsurface environments, silicate mineral reaction rates may be inhibited by the slow formation of secondary silicate phases; therefore, the modeling results should be interpreted with caution, as they may not fully capture these kinetic limitations.
Our models predict and quantify changes in porosity, which affects permeability and injection efficiency. Here are the short- and long-term problems and solutions.
Short term: The dissolution of calcite can enhance permeability, particularly in zones with high calcite content and favorable reservoir conditions. This process enlarges pore spaces and improves fluid flow, leading to better near-wellbore performance and increased productivity or injectivity.
Long term: However, the risk of permeability impairment grows over time if the reservoir water chemistry promotes the re-precipitation of dissolved minerals or if rock matrix instability triggers the migration of fine particles, which can block pore throats and reduce flow capacity.
Solution: To optimize the benefits while minimizing the risks, it is crucial to integrate key reservoir parameters—including porosity, permeability, mineralogical composition, formation water chemistry, and mechanical stability—into a comprehensive, balanced risk–benefit framework that supports effective decision-making and long-term reservoir management.
The PHREEQC geochemical and reactive transport modeling method described in this study offers a multi-step approach to understanding and predicting the chemical effects of reinjecting cooled thermal water. However, a significant challenge currently lies in the discrepancies in results from thermodynamic databases, which cannot be resolved with the available information. Therefore, additional work is necessary to clarify the expected reactions by implementing the following measures:
- Conducting further long-term laboratory experiments and sensitivity analyses on thermodynamic databases.
- Gathering more information on the pore solution present at depth, including the concentrations of dissolved ions and gases, as well as the chemistry of the cooled thermal water intended for reinjection.
- Refining the reactive mineral composition based on petrographic studies, with particular focus on the mineral phases in contact with the pore space.
Future investigations should also include the following:
- Assessing dissolved oxygen content and its chemical effects, since cooled thermal water may equilibrate with the atmosphere prior to reinjection.
- Estimating porosity and permeability and their spatial inhomogeneity in the reservoir.
- Employing multiphase, multidimensional models (e.g., with TOUGHREACT).
- Comparing models with experimental data and field tests.
Author Contributions
Conceptualization, E.S., R.A., and J.K.; methodology, E.S., R.A., Z.S.-K., and J.K.; validation, E.S., R.A., and Z.S.-K.; formal analysis, E.S., E.K.-B., and C.C.d.C.; investigation E.K.-B. and C.C.d.C.; data curation, E.S and Z.S.-K.; writing—original draft preparation, E.S., R.A., and J.K.; writing—review and editing, all authors; supervision, J.K.; project administration, J.K.; funding acquisition, J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Hungarian National Research, Development, and Innovation Office (NKFIH), grant number: GINOP-2.2.1-15-2017-00102.
Data Availability Statement
The data are unavailable due to privacy concerns.
Acknowledgments
The authors would like to thank T. Pernyeszi for her technical support during the calorimetry experiments and P. Koroncz and F. Fedor for their constructive advice on the research work. Lastly, we thank two anonymous reviewers and the academic editor for their constructive comments that improved this manuscript.
Conflicts of Interest
Author R.A. was jointly employed by the company Mecsekérc Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The funders had no role in the design of the study, in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
References
- Rivera Diaz, A.; Kaya, E.; Zarrouk, S.J. Reinjection in geothermal fields—A worldwide review update. Renew. Sust. Energy Rev. 2016, 53, 105–162. [Google Scholar] [CrossRef]
- Szanyi, J.; Medgyes, T.; Kóbor, B.; Tari, C.; Bálint, A. Experiences with geothermal water injection into porous aquifers. Tech. Poszuk. Geol. 2014, 2, 3–18. [Google Scholar]
- Ungemach, P. Reinjection of cooled geothermal brines into sandstone reservoirs. Geothermics 2003, 32, 743–761. [Google Scholar] [CrossRef]
- Akin, S. Geothermal re-injection performance evaluation using surveillance analysis methods. Renew. Energy 2019, 139, 635–642. [Google Scholar] [CrossRef]
- Suzuki, A.; Niibori, Y.; Fomin, S.; Chugunov, V.; Hashida, T. Prediction of reinjection effects in fault-related subsidiary structures by using fractional derivative-based mathematical models for sustainable design of geothermal reservoirs. Geothermics 2015, 57, 196–204. [Google Scholar] [CrossRef]
- Markó, Á.; Mádl-Szőnyi, J.; Brehme, M. Injection related issues of a doublet system in a sandstone aquifer—A generalized concept to understand and avoid problem sources in geothermal systems. Geothermics 2021, 97, 102234. [Google Scholar] [CrossRef]
- Zhang, L.; Geng, S.; Yang, L.; Wen, R.; He, C.; Zhao, Z.; Qin, G. Formation blockage risk analysis of geothermal water reinjection: Rock property analysis, pumping and reinjection tests, and long-term reinjection prediction. Geosci. Front. 2022, 13, 101299. [Google Scholar] [CrossRef]
- Roded, R.; Aharonov, E.; Szymczak, P.; Veveakis, M.; Lazar, B.; Dalton, L.E. Solutions and case studies for thermally driven reactive transport and porosity evolution in geothermal systems (reactive Lauwerier problem). Hydrol. Earth Syst. Sci. 2024, 28, 4559–4576. [Google Scholar] [CrossRef]
- Farina, A.; Fasano, A.; Primicerio, M.; Rosso, F. Evolution of a Geothermal System with Fluid Re-Injection. Appl. Sci. 2020, 10, 7561. [Google Scholar] [CrossRef]
- Huang, G.; Liu, L.; Mu, M.; Yang, J.; Ding, H. Prediction of Dynamic Temperature and Thermal Front in a Multi-Aquifer Thermal Energy Storage System with Reinjection. Energies 2023, 16, 7358. [Google Scholar] [CrossRef]
- Huang, Y.; Lei, H.; Na, J.; Yuan, Y.; Tian, H. Investigations of the impact of geothermal water reinjection on water-rock interaction through laboratory experiments and numerical simulations. Appl. Geochem. 2024, 175, 106180. [Google Scholar] [CrossRef]
- Sætre, C.; Hellevang, H.; Dennehy, C.; Dypvik, H. Reactive transport modelling of an intra-basalt sandstone reservoir, Rosebank, UK. Sci. Rep. 2021, 11, 6907. [Google Scholar] [CrossRef] [PubMed]
- Koroncz, P.; Vizhányó, Z.; Farkas, M.P.; Kuncz, M.; Ács, P.; Kocsis, G.; Mucsi, P.; Fedorné Szász, A.; Fedor, F.; Kovács, J. Experimental Rock Characterisation of Upper Pannonian Sandstones from Szentes Geothermal Field, Hungary. Energies 2022, 15, 9136. [Google Scholar] [CrossRef]
- Galloway, E.W. Diagenetic control of reservoir quality in arc-derived sandstones: Implications for petroleum exploration. SEPM Spec. Publ. 1979, 26, 251–262. [Google Scholar] [CrossRef]
- Larsen, M.; Bell, B.; Guarnieri, P.; Vosgerau, H.; Weibel, R. Exploration challenges along the North Atlantic volcanic margins: The intra-volcanic sandstone play in subsurface and outcrop. Pet. Geol. Conf. Proc. 2018, 8, 231–245. [Google Scholar] [CrossRef]
- Njeru, R.M.; Halisch, M.; Szanyi, J. Micro-scale investigation of the pore network of sandstone in the Pannonian Basin to improve geothermal energy development. Geothermics 2024, 122, 103071. [Google Scholar] [CrossRef]
- Boch, R.; Szanyi, J.; Leis, A.; Mindszenty, A.; Deák, J.; Kluge, T.; Hippler, D.; Demény, A.; Dietzel, M. Geothermal Carbonate Scaling: Forensic Studies Applying High-Resolution Geochemical Methods. In Proceedings of the European Geothermal Congress 2016, Strasbourg, France, 19–24 September 2016. [Google Scholar]
- Varga, A.; Bozsó, G.; Garaguly, I.; Raucsik, B.; Bencsik, A.; Kóbor, B. Cements, Waters, and Scales: An Integrated Study of the Szeged Geothermal Systems (SE Hungary) to Characterize Natural Environmental Conditions of the Thermal Aquifer. Geofluids 2019, 2019, 4863814. [Google Scholar] [CrossRef]
- Boch, R.; Kluge, T.; Leis, A.; Dietzel, M.; Szanyi, J. Mineral deposits affecting geothermal energy production—Insights, analytical approaches and implementation strategies. Geomech. Tunn. 2024, 17, 453–464. [Google Scholar] [CrossRef]
- Bálint, A.; Szanyi, J. A half century of reservoir property changes in the Szentes geothermal field, Hungary. Cent. Eur. Geol. 2015, 58, 28–49. [Google Scholar] [CrossRef]
- Békési, E.; Fokker, P.A.; Candela, T.; Szanyi, J.; van Wees, J.-D. Ground motions induced by pore pressure changes at the Szentes geothermal area, SE Hungary. Geotherm. Energy 2022, 10, 3. [Google Scholar] [CrossRef]
- Njeru, R.M.; Sofyan, A.; Halisch, M.; Kóbor, B.; Szanyi, J. Optimizing Micro-CT Resolution for Geothermal Reservoir Characterization in the Pannonian Basin. Energies 2024, 17, 3081. [Google Scholar] [CrossRef]
- Babinszki, E.; Piros, O.; Csillag, G.; Fodor, F.; Gyalog, L.; Kercsmár, Z.; Less, G.; Lukács, R.; Sebe, K.; Selmeczi, I.; et al. Description of the lithostratigraphic units of Hungary II. Cenozoic formations. In Hungarian: Magyarország Litosztratigráfiai Egységeinek Leírása II; Kainozoos Képződmények, SZTFH: Budapest, Hungary, 2023; pp. 1–181. [Google Scholar]
- Magyar, I.; Radivojević, D.; Sztanó, O.; Synak, R.; Ujszászi, K.; Pócsik, M. Progradation of the paleo-Danube shelf margin across the Pannonian Basin during the Late Miocene and Early Pliocene. Glob. Planet. Change 2013, 103, 168–173. [Google Scholar] [CrossRef]
- Korim, K. A szentesi hévízmező feltárásának és termelésének három évtizedes története (Three decades of research and utilization in the Szentes Geothermal Field). Bányászati Kohászati Lapok 1991, 124, 179–184. (In Hungarian) [Google Scholar]
- Juhász, G. Lithostratigraphical and sedimentological framework of the Pannonian (s.l.) sedimentary sequence in the Hungarian Plain (Alföld), eastern Hungary. Acta Geol. Hung. 1991, 34, 53–72. [Google Scholar]
- Willems, C.J.L.; Cheng, C.; Watson, S.M.; Minto, J.; Williams, A.; Walls, D.; Milsch, H.; Burnside, N.M.; Westaway, R. Permeability and Mineralogy of the Újfalu Formation, Hungary, from Production Tests and Experimental Rock Characterization: Implications for Geothermal Heat Projects. Energies 2021, 14, 4332. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; U.S. Geological Survey Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2013; Volume 6-A43, p. 497. [Google Scholar] [CrossRef]
- Blanc, P.; Lassin, A.; Piantone, P.; Azaroual, M.; Jacquemet, N.; Fabbri, A.; Gaucher, E.C. Thermoddem: A geochemical database focused on low temperature water/rock interactions and waste materials. Appl. Geochem. 2012, 27, 2107–2116. [Google Scholar] [CrossRef]
- Bálint, A. A Szentesi Geotermikus Terület Vízföldtani és Vízkémiai Adatainak Értékelése (in Hungarian) Evaluation of the Hydrogeological and Hydrochemical Data of the Geothermal Area of Szentes—GINOP-2.2.1-15-2017-00102 Project Report; Mecsekérc Ltd.: Pécs, Hungary, 2020. [Google Scholar]
- Szabó, Z.; Gál, N.E.; Kun, É.; Szőcs, T.; Falus, G. Accessing effects and signals of leakage from a CO2 reservoir to a shallow freshwater aquifer by reactive transport modelling. Environ. Earth Sci. 2018, 77, 460. [Google Scholar] [CrossRef]
- Palandri. J., L.; Kharaka, Y.K. A Compilation of Rate Parameters of Water-Mineral Interaction Kinetics for Application to Geochemical Modeling; U.S. Geological Survey Open File Report 2004–1068; U.S. Geological Survey: Reston, VA, USA, 2004; p. 64. [Google Scholar] [CrossRef]
- Diffusion Coefficients of Water. Available online: https://dtrx.de/od/diff/ (accessed on 10 January 2025).
- Szabó-Krausz, Z.; Gál, N.E.; Gável, V.; Falus, G. Wellbore cement alteration during decades of abandonment and following CO2 attack—A geochemical modelling study in the area of potential CO2 reservoirs in the Pannonian Basin. Appl. Geochem. 2020, 113, 104516. [Google Scholar] [CrossRef]
- Yuan, G.; Cao, Y.; Gluyas, J.; Jia, Z. Reactive transport modeling of coupled feldspar dissolution and secondary mineral precipitation and its implication for diagenetic interaction in sandstones. Geochim. Cosmochim. Acta 2017, 207, 232–255. [Google Scholar] [CrossRef]
- Arvidson, R.S.; Ertan, I.E.; Amonette, J.E.; Luttge, A. Variation in calcite dissolution rates: A fundamental problem? Geochim. Cosmochim. Acta 2003, 67, 1623–1634. [Google Scholar] [CrossRef]
- Gelencsér, O.; Árvai, C.; Mika, L.T.; Breitner, D.; LeClair, D.; Szabó, C.; Falus, G.; Szabó-Krausz, Z. Effect of hydrogen on calcite reactivity in sandstone reservoirs: Experimental results compared to geochemical modeling predictions. J. Energy Storage 2023, 61, 106737. [Google Scholar] [CrossRef]
- Bethke, C.M. The question of uniqueness in geochemical modeling. Geochim. Cosmochim. Acta 1992, 56, 4315–4320. [Google Scholar] [CrossRef]
- Kirk Nordstrom, D. Models, validation, and applied geochemistry: Issues in science, communication, and philosophy. Appl. Geochem. 2012, 27, 1899–1919. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).