Research and Application of 3D Magnetic Inversion Method Based on Residual Convolutional Neural Network
Abstract
1. Introduction
2. Methodological Framework
2.1. Training Sample Generation Protocol
2.1.1. Memory-Efficient Sensitivity Handling
- Row-parallel mode: Computes magnetic contributions from all model units to individual measurement points.
- Column-parallel mode: Calculates the influence of single model units across all measurement points.
2.1.2. Sparse Matrix Optimization
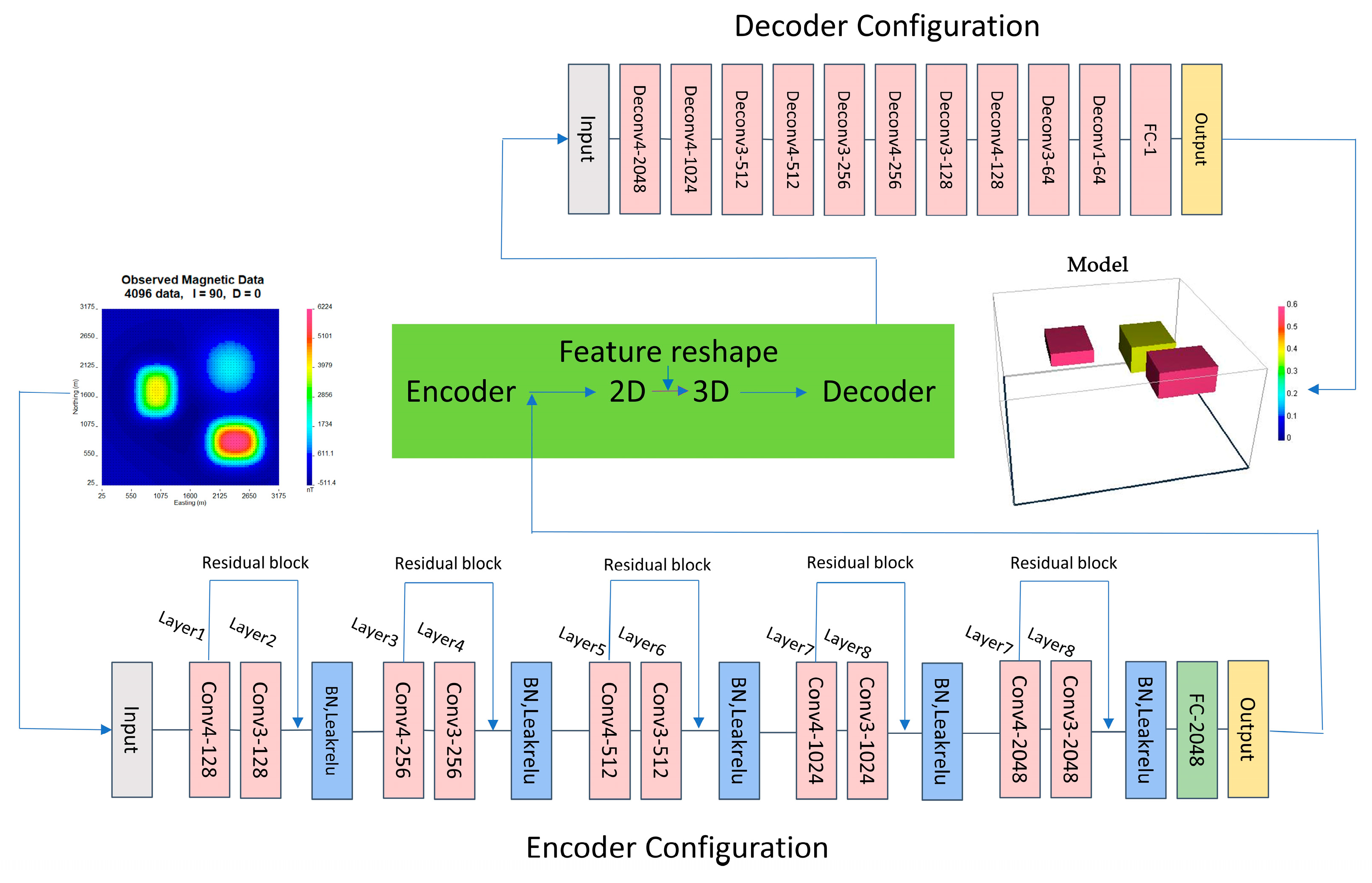
2.2. Based on Convolutional Neural Networks
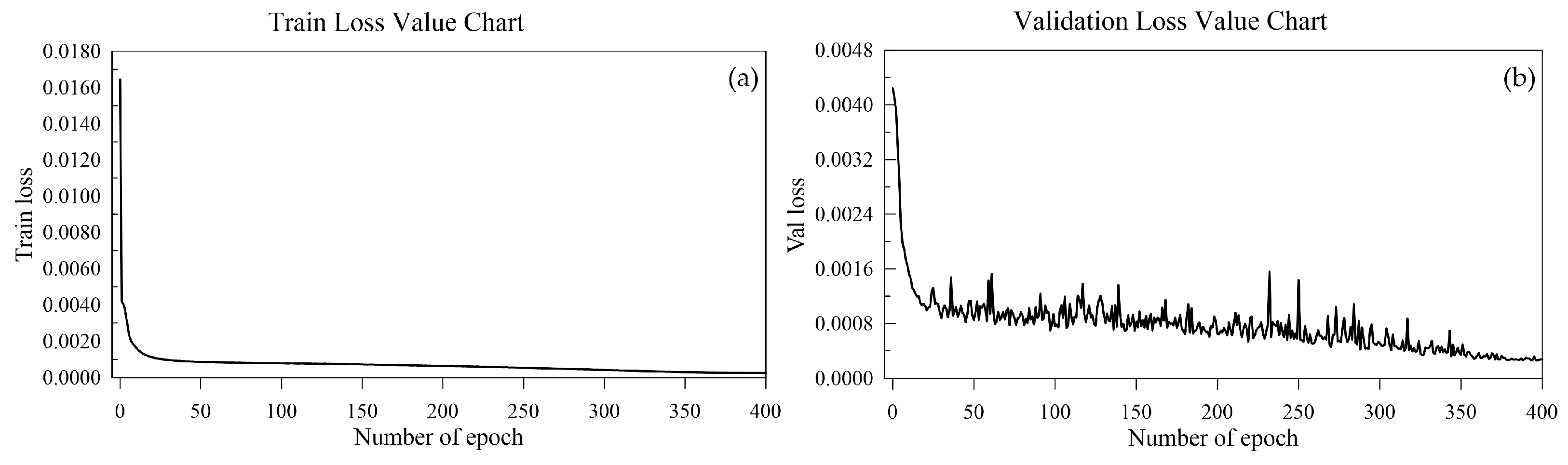
2.3. Training and Evaluation Metrics for Neural Networks
2.4. Building a Dataset
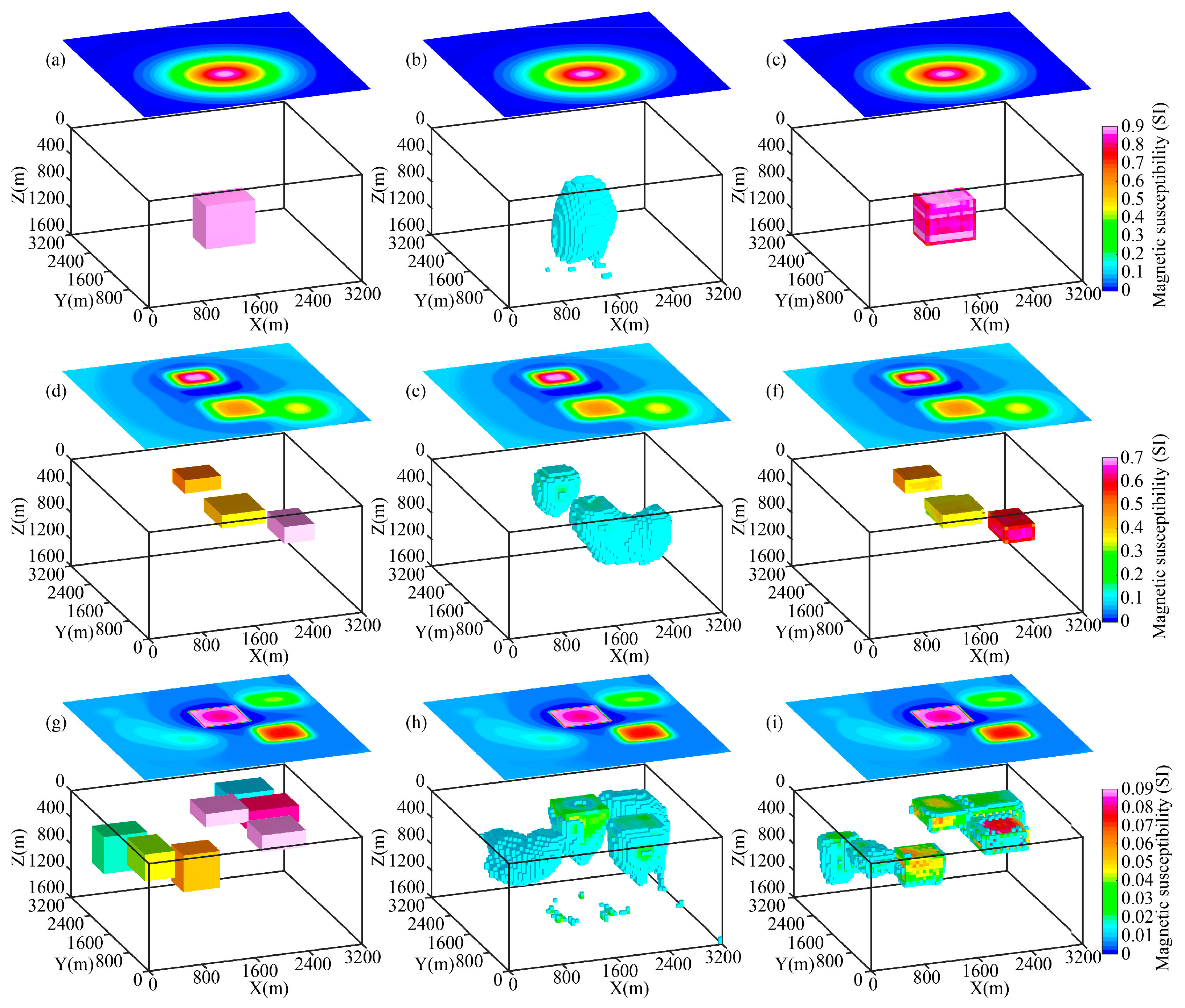
3. Theoretical Model Experiment
4. Application Examples
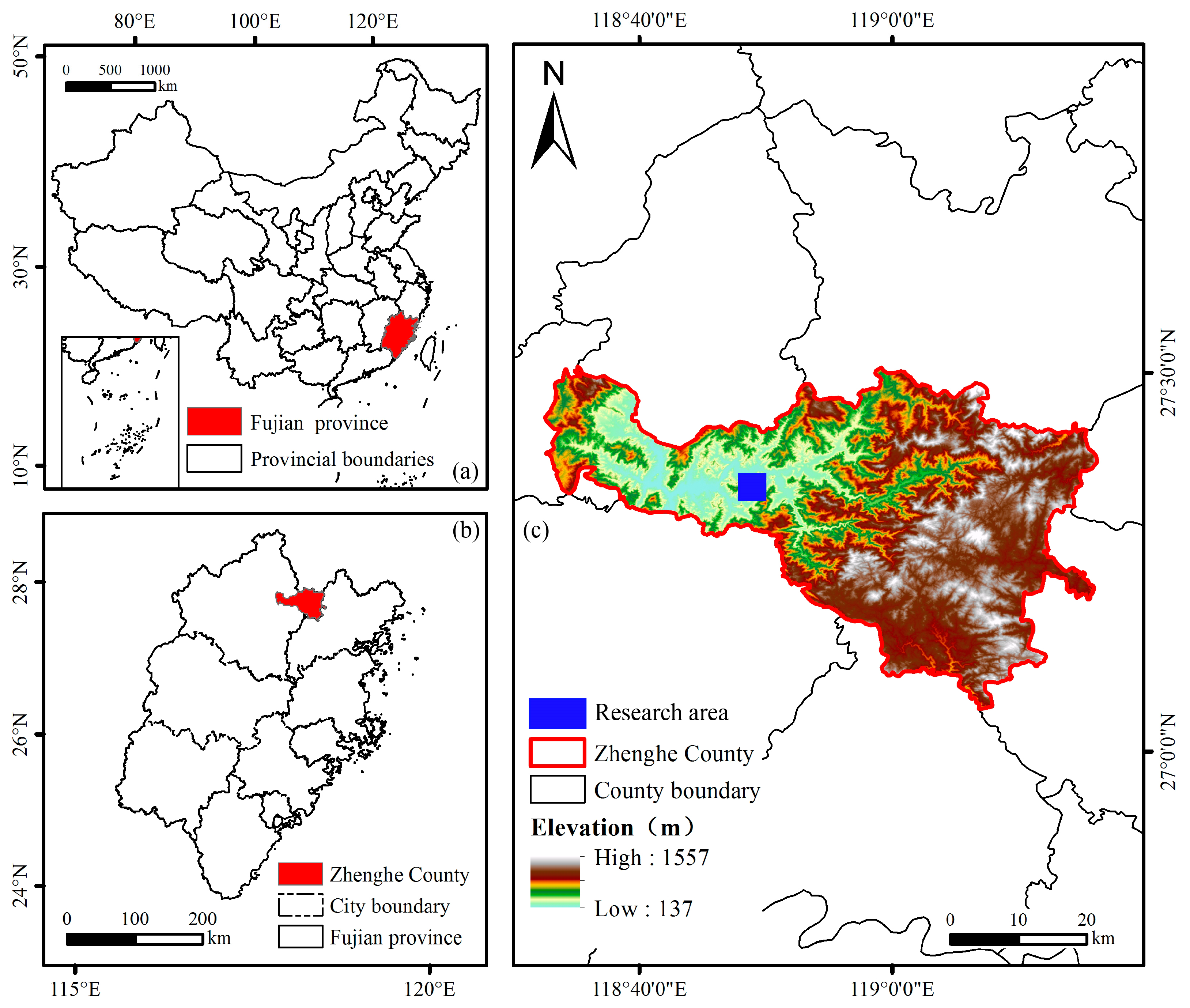
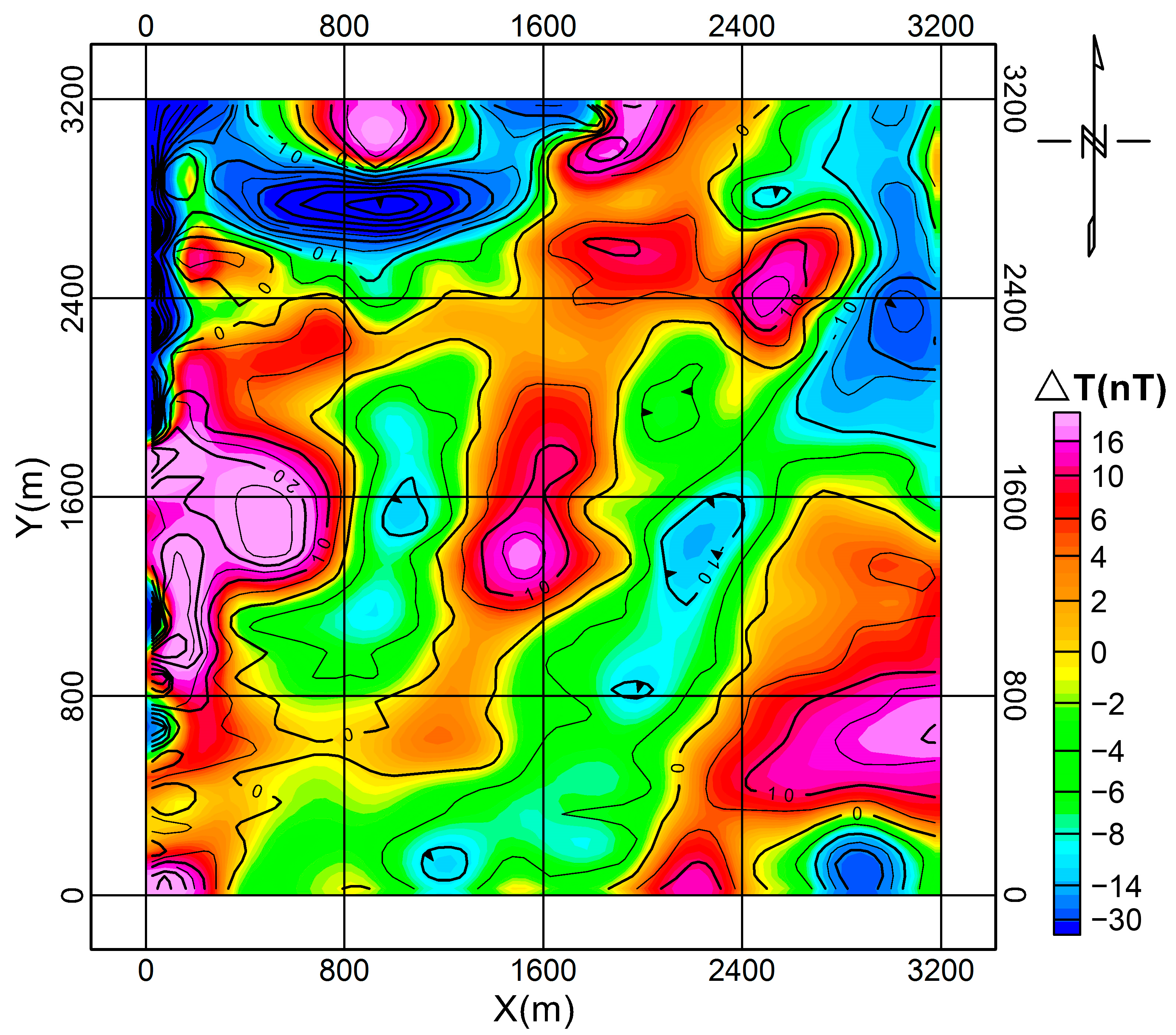
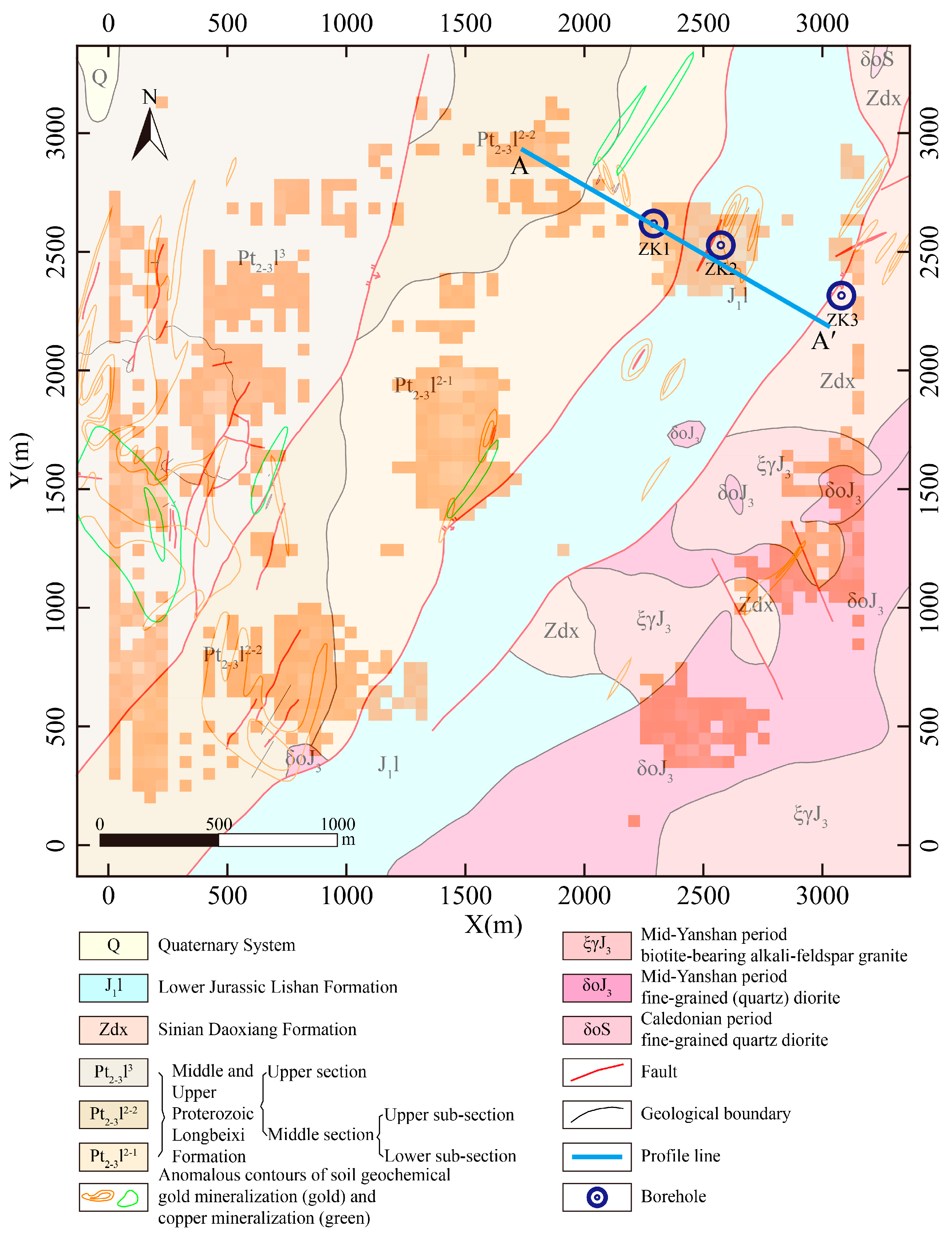
4.1. Geological Background
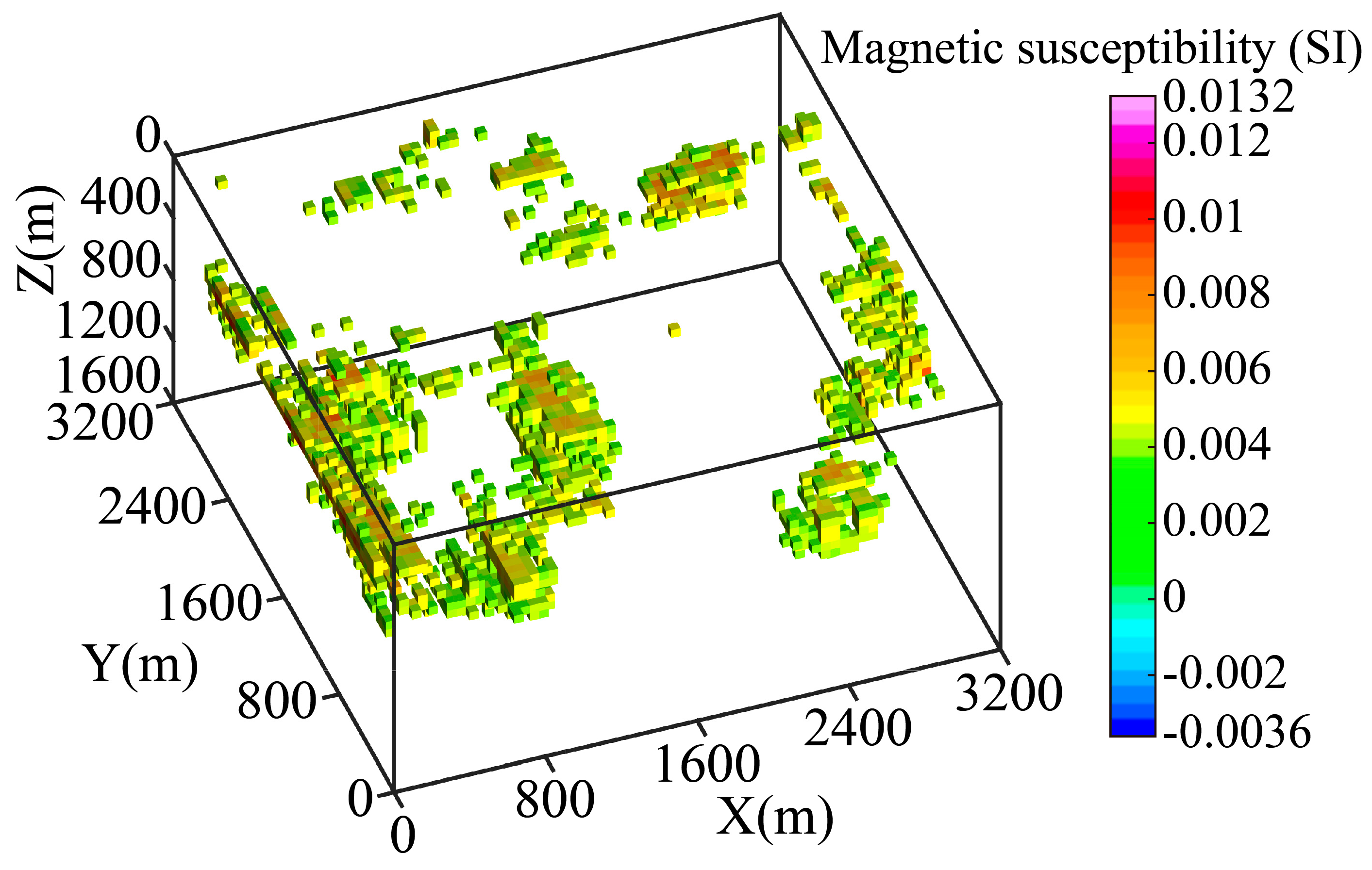
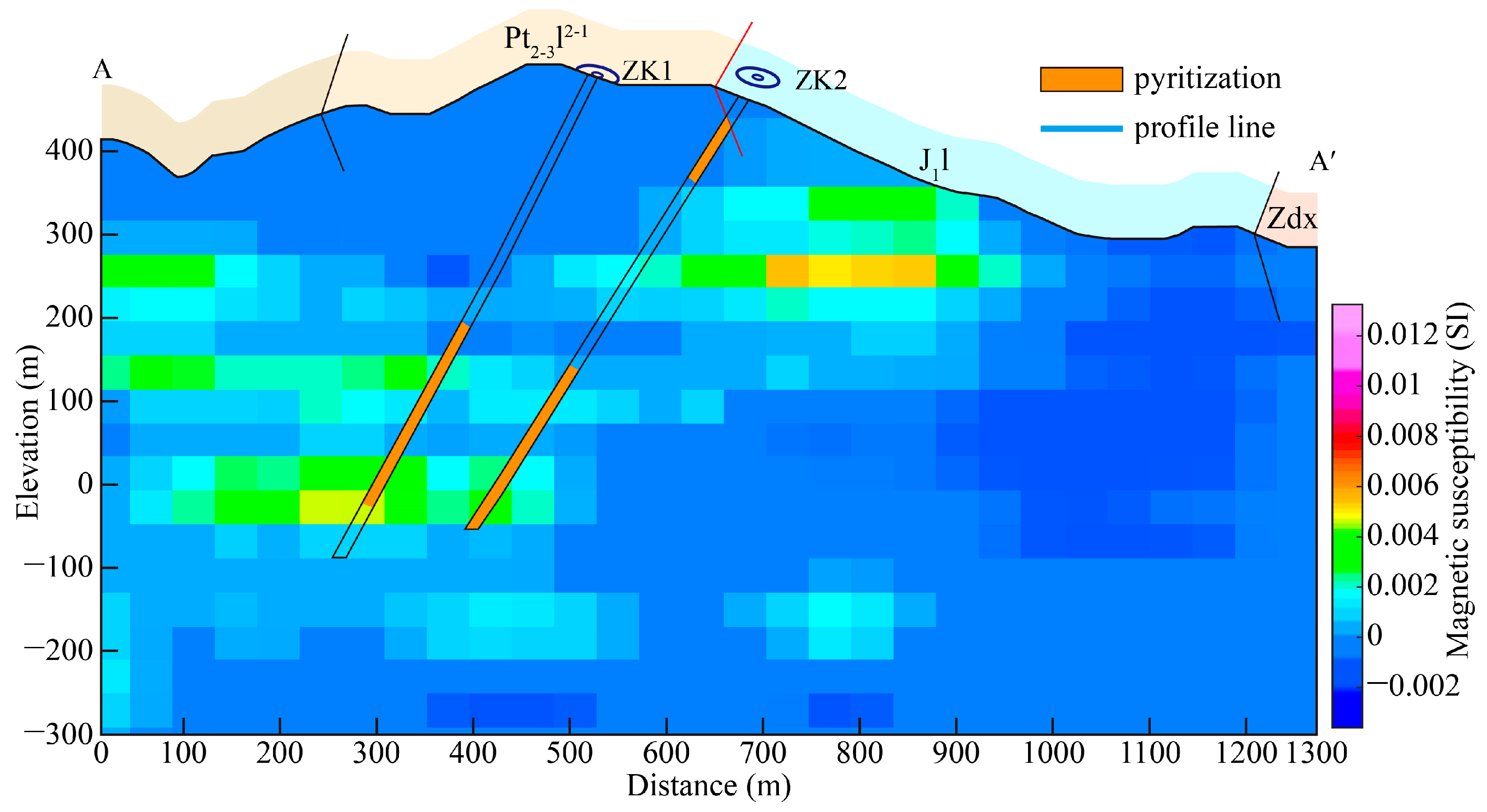
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shamsipour, P.; Marcotte, D.; Chouteau, M. 3D stochastic joint inversion of gravity and magnetic data. J. Appl. Geophys. 2012, 79, 27–37. [Google Scholar] [CrossRef]
- Oldenburg, D.W.; Li, Y. Inversion for applied geophysics: A tutorial. In Near-Surface Geophysics; Society of Exploration Geophysicists: Houston, TX, USA, 2005; pp. 89–150. [Google Scholar]
- Pilkington, M. 3D magnetic data-space inversion with sparseness constraints. Geophysics 2009, 74, L7–L15. [Google Scholar] [CrossRef]
- Chenot, D.; Debeglia, N. Three-dimensional gravity or magnetic constrained depth inversion with lateral and vertical variation of contrast. Geophysics 1990, 55, 327–335. [Google Scholar] [CrossRef]
- Vitale, A.; Fedi, M. Inversion of potential fields with an inhomogeneous depth weighting function. In SEG Technical Program Expanded Abstracts 2019; Society of Exploration Geophysicists: Houston, TX, USA, 2019; pp. 1749–1753. [Google Scholar]
- Shearer, S.; Li, Y. 3D inversion of magnetic total gradient data in the presence of remanent magnetization. In Proceedings of the SEG International Exposition and Annual Meeting, Denver, CO, USA, 10–15 October 2004; p. SEG-2004. [Google Scholar]
- Wang, Y.; Rong, L.; Qiu, L.; Lukyanenko, D.V.; Yagola, A.G. Magnetic susceptibility inversion method with full tensor gradient data using low-temperature SQUIDs. Pet. Sci. 2019, 16, 794–807. [Google Scholar] [CrossRef]
- Sanchez, V.; Sinex, D.; Li, Y.; Nabighian, M.; Wright, D.; vonG Smith, D. Processing and Inversion of Magnetic Gradient Tensor Data for Uxo Applications. In Proceedings of the 18th EEGS Symposium on the Application of Geophysics to Engineering and Environmental Problems, Atlanta, GA, USA, 3–7 April 2005; p. cp-183. [Google Scholar]
- Nakagawa, I.; Yukutake, T.; Fukushima, N. Extraction of magnetic anomalies of crustal origin from Magsat data over the area of the Japanese Islands. J. Geophys. Res. Solid Earth 1985, 90, 2609–2615. [Google Scholar] [CrossRef]
- Billings, S.D. Discrimination and classification of buried unexploded ordnance using magnetometry. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1241–1251. [Google Scholar] [CrossRef]
- Ma, G.; Wang, J.; Meng, Q.; Meng, Z.; Qin, P.; Wang, T.; Li, L. Research Develpment of Airborne Gravity (Magnetic) Multi-Components Gradient Detection and Inversion Technology. J. Jilin Univ. (Earth Sci. Ed.) 2023, 53, 1928–1949. [Google Scholar]
- Ma, G.; Ma, S.; Li, L.; Cai, J. Method of self-structure-constrained inversion of magnetic anomalies and their magnetic gradients and its application in the exploration of coal burning area. Prog. Geophys. 2024, 39, 1026–1037. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, R.; Liao, X.; Xu, Z.; Qiao, Z.; Fan, X.; Yao, Y.; Shi, Z.; Liu, P.; Lu, S. Inversion of magnetic anomaly and magnetic gradient anomaly based on fully convolution network. Prog. Geophys. 2021, 36, 325–337. (In Chinese) [Google Scholar]
- Mukherjee, S.; Lelièvre, P.; Farquharson, C.; Adavani, S. Three-dimensional inversion of geophysical field data on an unstructured mesh using deep learning neural networks, applied to magnetic data. In Proceedings of the First International Meeting for Applied Geoscience & Energy, Denver, CO, USA, 26 September–1 October 2021; Society of Exploration Geophysicists: Houston, TX, USA, 2021; pp. 1465–1469. [Google Scholar]
- Deng, H.; Hu, X.; Cai, H.; Liu, S.; Peng, R.; Liu, Y.; Han, B. 3D Inversion of Magnetic Gradient Tensor Data Based on Convolutional Neural Networks. Minerals 2022, 12, 566. [Google Scholar] [CrossRef]
- Yao, L. Theoretical study on cuboid magnetic field and gradient expression without singular point. Oil Geophys. Prospect. 2007, 42, 714. (In Chinese) [Google Scholar]
- Jia, Z.; Li, Y.; Wang, Y.; Li, Y.; Jin, S.; Li, Y.; Lu, W. Deep Learning for 3-D Magnetic Inversion. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5905410. [Google Scholar] [CrossRef]
- Chen, Z.; Meng, X.; Guo, L.; Liu, G. GICUDA: A parallel program for 3D correlation imaging of large scale gravity and gravity gradiometry data on graphics processing units with CUDA. Comput. Geosci. 2012, 46, 119–128. [Google Scholar] [CrossRef]
- Tondi, R.; Cavazzoni, C.; Danecek, P.; Morelli, A. Parallel, ‘large’, dense matrix problems: Application to 3D sequential integrated inversion of seismological and gravity data. Comput. Geosci. 2012, 48, 143–156. [Google Scholar] [CrossRef]
- Moorkamp, M.; Jegen, M.; Roberts, A.; Hobbs, R. Massively parallel forward modeling of scalar and tensor gravimetry data. Comput. Geosci. 2010, 36, 680–686. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, G. Forward modeling of gravity anomalies based on cell mergence and parallel computing. Comput. Geosci. 2018, 120, 1–9. [Google Scholar] [CrossRef]
- Lin, Y.; Wu, Y. InversionNet: A real-time and accurate full waveform inversion with convolutional neural network. J. Acoust. Soc. Am. 2018, 144, 1683. [Google Scholar] [CrossRef]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. Adv. Neural Inf. Process Syst. 2014, 27, 2366–2374. [Google Scholar]
- Eigen, D.; Fergus, R. Predicting depth, surface normals and semantic labels with a common multi-scale convolutional architecture. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2650–2658. [Google Scholar]
- Zhang, L.; Zhang, G.; Liu, Y.; Fan, Z. Deep learning for 3-D inversion of gravity data. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5905918. [Google Scholar] [CrossRef]
| Model Type | Design Parameters | Magnetic Susceptibility Settings |
|---|---|---|
| Single Block | Horizontal coordinates of SW corner: Select one of the 48 meshes from the center randomly Horizontal mesh length: 8–24 Depth of top interface: 2–16 Vertical mesh length: 2–16 | 0.01~1 SI, with an interval of 0.01 |
| Combined Block | Number of blocks: 3–7 Horizontal coordinates of SW corner: Select one of the 48 meshes from the center randomly Horizontal mesh length: 8–24 Depth of top interface: 2–10 Vertical mesh length: 2 + (random number between 1 and top burial depth) | 0.01~1 SI, with an interval of 0.01 |
| Single Step | Horizontal coordinates of SW corner: Select one of the 60 meshes from the center randomly Horizontal mesh length: 3–16 Depth of top interface: 1–10 Vertical mesh length: 5–54 Thickness of each step: 1–3 Horizontal dislocation distance for each step: 1–3 | 0.01~1 SI, with an interval of 0.01 |
| Combined Step | The same as the single step. | 0.01~1 SI, with an interval of 0.01 |
| Combination of Single Block and Step | The same as the single block and the single step. | 0.01~1 SI, with an interval of 0.01 |
| Combination of Complex Block and Step | The same as the single block and the single step. | 0.01~1 SI, with an interval of 0.01 |
| Combination of Step with Heterogeneous Block | Add multiple small blocks or steps around the block or step model of a certain scale. | 0.01~1 SI, with an interval of 0.01 |
| Evaluation Area | Evaluation Metric | 4000 | 8000 | 16,000 | 24,000 | 32,000 | 40,000 | 48,000 |
|---|---|---|---|---|---|---|---|---|
| Full Grid Region | MAE (10−3) | 11.03 | 3.76 | 2.82 | 2.42 | 2.35 | 2.30 | 2.26 |
| Eacc (r = 0.01) | 92.35 | 95.08 | 96.50 | 96.52 | 96.55 | 96.56 | 96.53 | |
| Anomalous Grid Area | MAE (10−2) | 23.34 | 9.57 | 8.52 | 7.93 | 7.30 | 6.88 | 6.16 |
| Nacc (t = 1.2) | 26.09 | 67.31 | 72.97 | 76.01 | 78.97 | 79.51 | 79.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Jia, Z.; Zhang, G.; Xiong, L.; Zheng, G.; Niu, T.; Zhang, G. Research and Application of 3D Magnetic Inversion Method Based on Residual Convolutional Neural Network. Minerals 2025, 15, 507. https://doi.org/10.3390/min15050507
Xu S, Jia Z, Zhang G, Xiong L, Zheng G, Niu T, Zhang G. Research and Application of 3D Magnetic Inversion Method Based on Residual Convolutional Neural Network. Minerals. 2025; 15(5):507. https://doi.org/10.3390/min15050507
Chicago/Turabian StyleXu, Supeng, Zhengyuan Jia, Gang Zhang, Luofan Xiong, Guangshi Zheng, Tingting Niu, and Guibin Zhang. 2025. "Research and Application of 3D Magnetic Inversion Method Based on Residual Convolutional Neural Network" Minerals 15, no. 5: 507. https://doi.org/10.3390/min15050507
APA StyleXu, S., Jia, Z., Zhang, G., Xiong, L., Zheng, G., Niu, T., & Zhang, G. (2025). Research and Application of 3D Magnetic Inversion Method Based on Residual Convolutional Neural Network. Minerals, 15(5), 507. https://doi.org/10.3390/min15050507







