Antimony Ore Identification Method for Small Sample X-Ray Images with Random Distribution
Abstract
1. Introduction
2. Materials and Methods
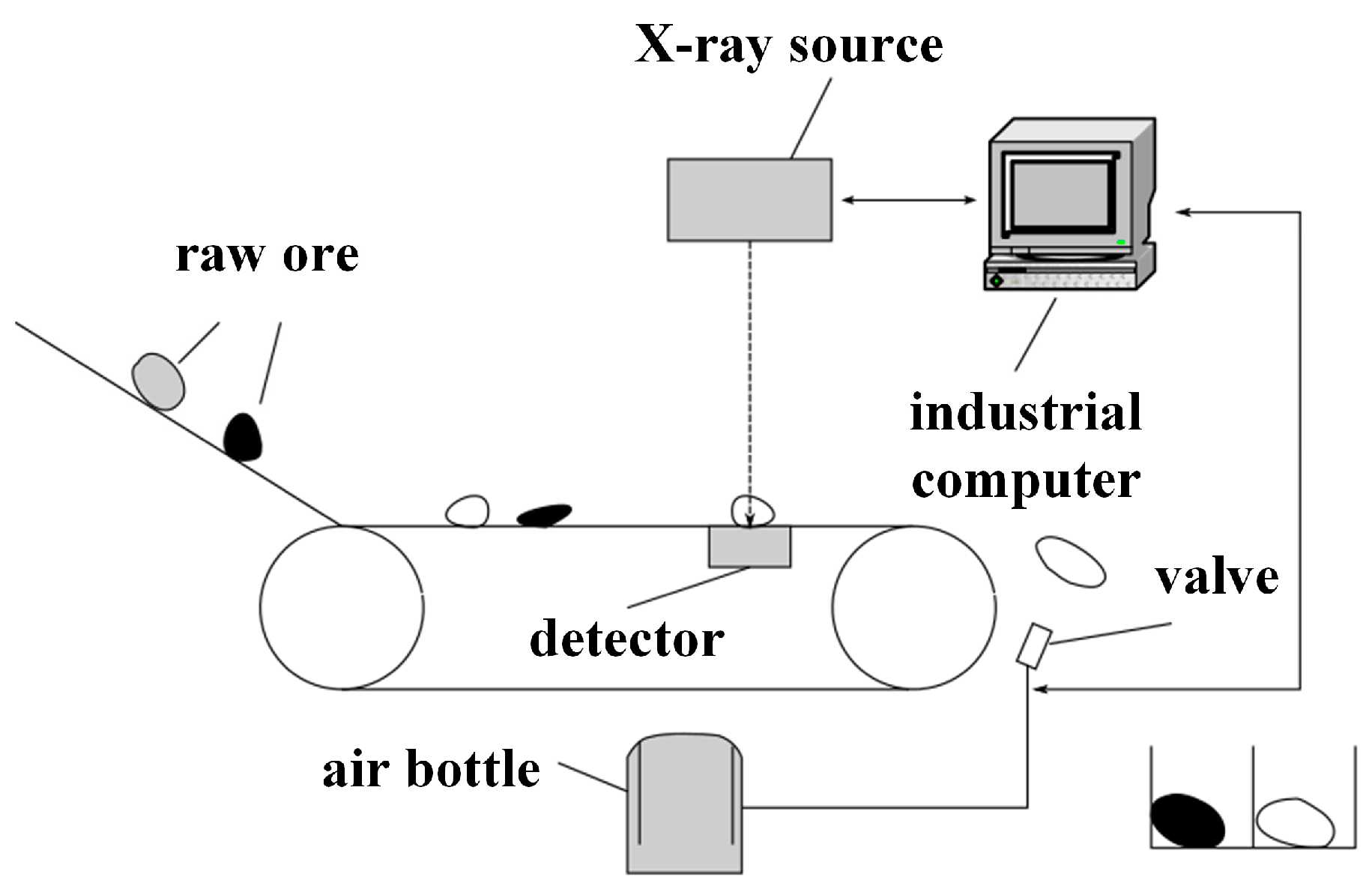
2.1. Materials
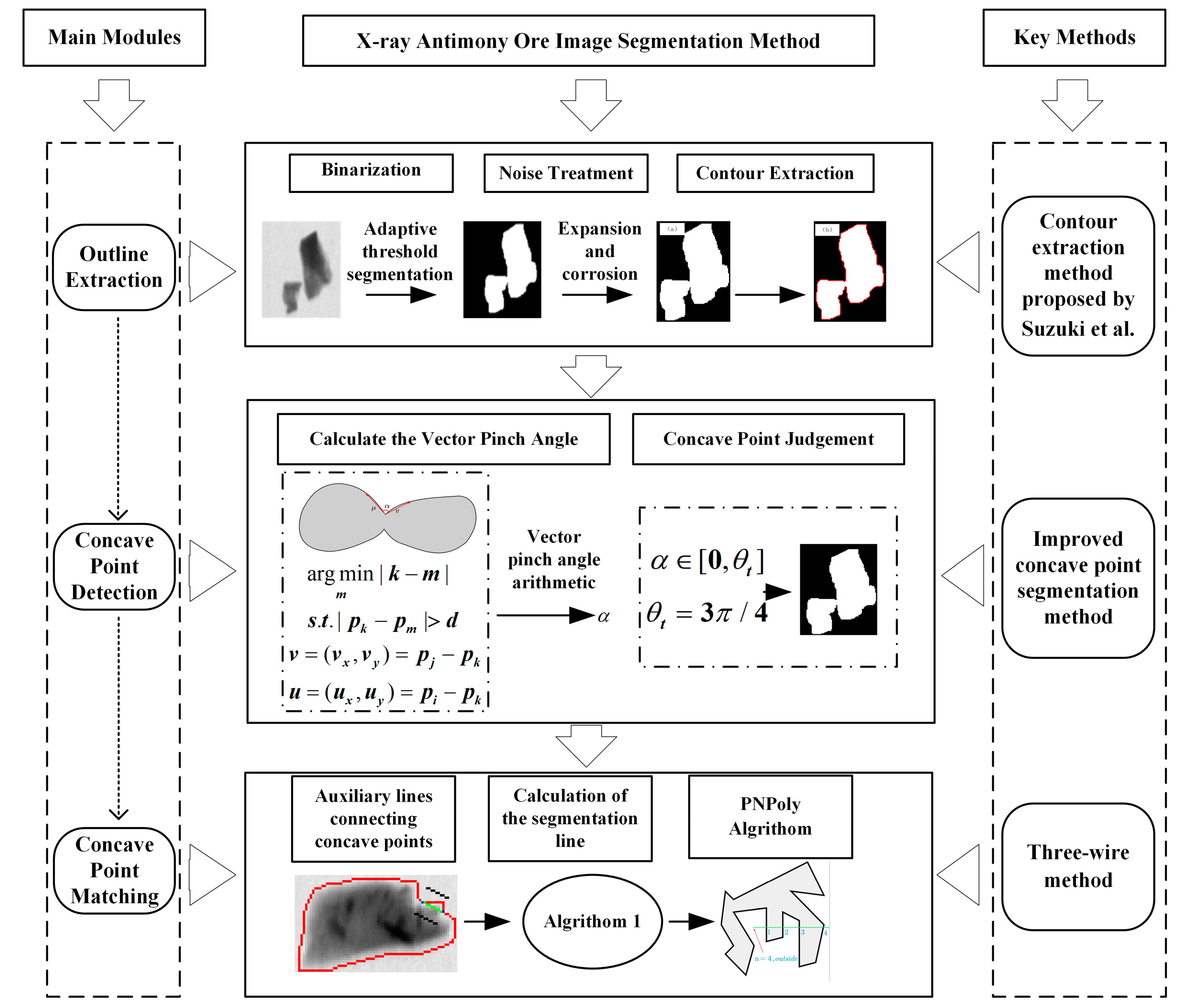
2.2. Design of X-Ray Antimony Ore Image Segmentation Method
| Algorithm 1: Calculate candidate segmentation lines. |
| Input: The set of concave points on the contour C, the contour. Output: Collection of segmentation lines . |
| Step 1. For the set of concave points get the permutations , , , …, Step 2. Calculate the distance between elements ,,,…,,where Step 3. Find the smallest value in the set D Step 4. Remove in set D where Step 5. Repeat steps 3–4, until there are fewer than 2 elements in C Step 6. For all line of the do Plot its auxiliary line at distance d ; If are all in contours then Addition to . End if End for |
2.3. A Method for Ore Classification Incorporating Transfer Learning and Model Shallow Part Initialization
2.3.1. Model Pre-Training
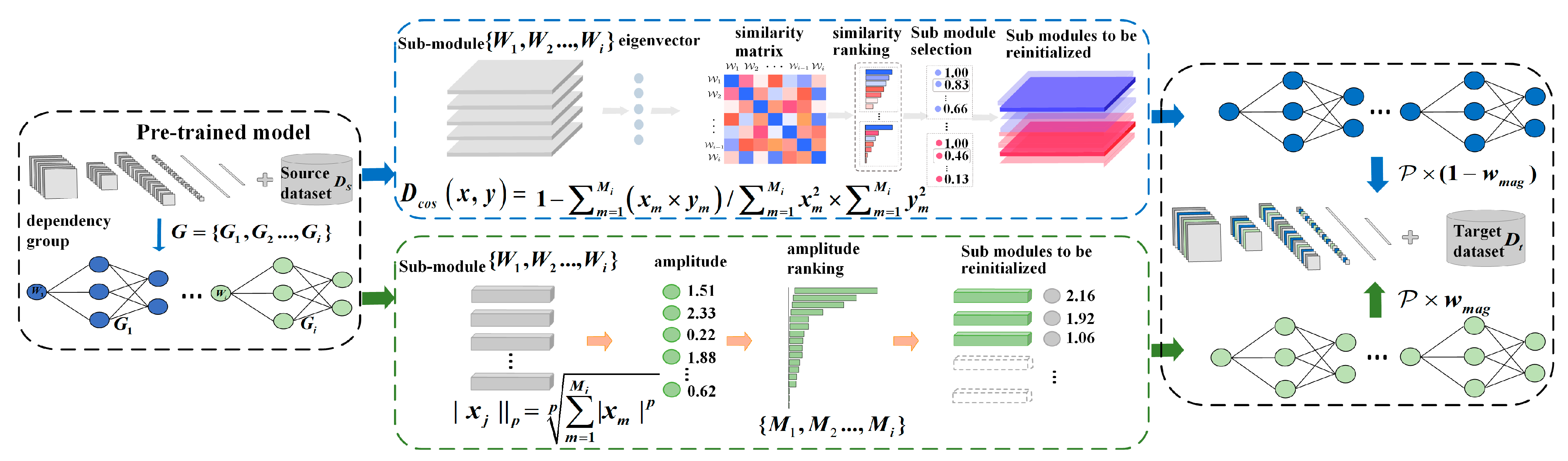
2.3.2. Partial Reinitialization of the Pre-Trained Model
| Algorithm 2: Pre-trained model reinitialization |
| Input: Dataset , pre-trained model , given initialization rate , magnitude pruning ratio . Output: Models after reinitialization . |
| Step 1. Initialization: , , List of trimmed parameters: Step 2. Find all submodules and their corresponding dependency groups in the shallow module Step 3. While do If then For in do Calculate the magnitude of the convolutional kernel amplitude for each sub-module in the model according to Equation (10) and get the smallest amplitude End for Else For in do Calculate the similarity matrix between the sub-modules according to Equation (11), where denotes the similarity between the th matrix and the th matrix. Sort the items in the similarity matrix in descending order: .If is the maximum of these, then crop out and remove the term in the similarity matrix from the module to be cropped, where and where . Avoid that -related terms are also cropped out.Add and the corresponding parameter corresponding to it in the dependency group to . End for End if End while |
2.3.3. Reinitialize Model Training
3. Results and Discussion
3.1. Experiments on an Improved Antimony Ore Segmentation Method Based on Concave Point Detection
3.2. Experimental Validation of Transfer Learning with Shallow Partial Initialization
3.2.1. Experimental Dataset
3.2.2. Deep Learning Model
3.2.3. Analysis of the Effectiveness of the Classification Algorithm
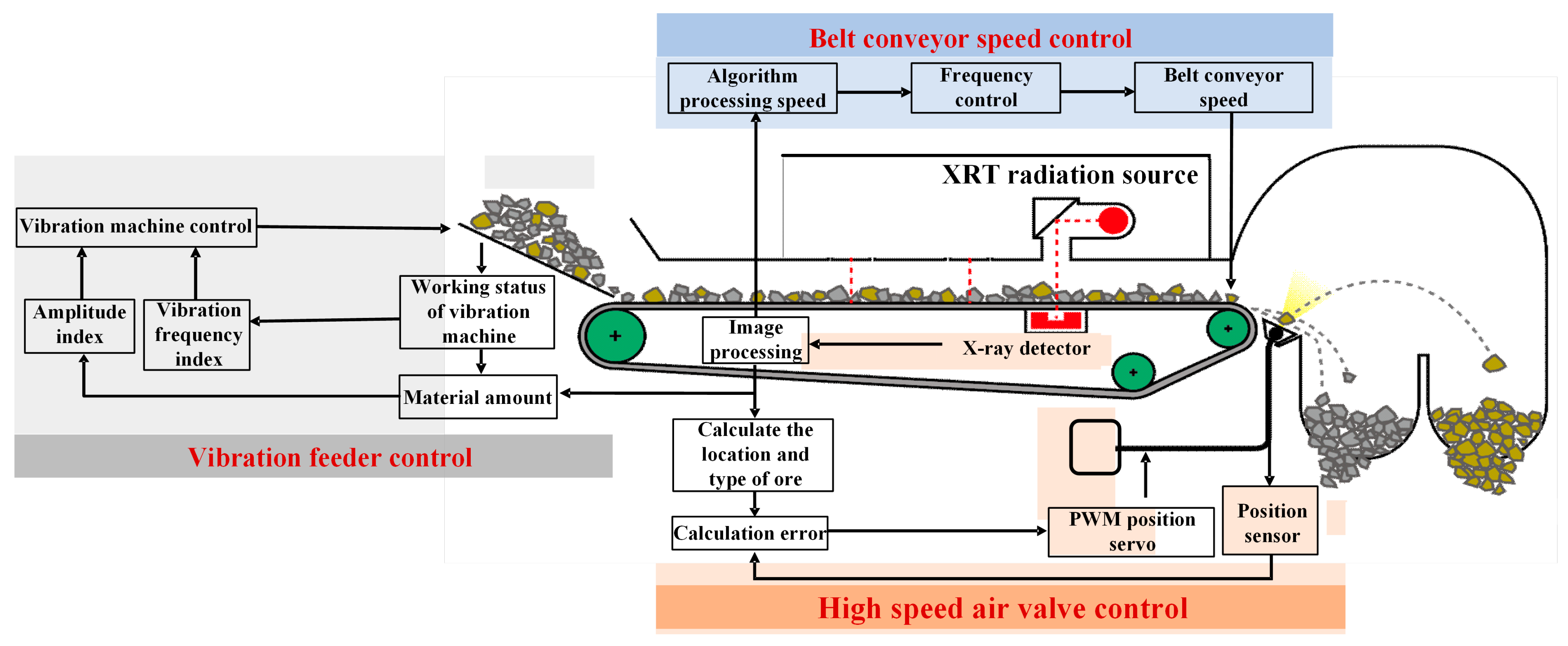
3.3. Industrial Application Analysis
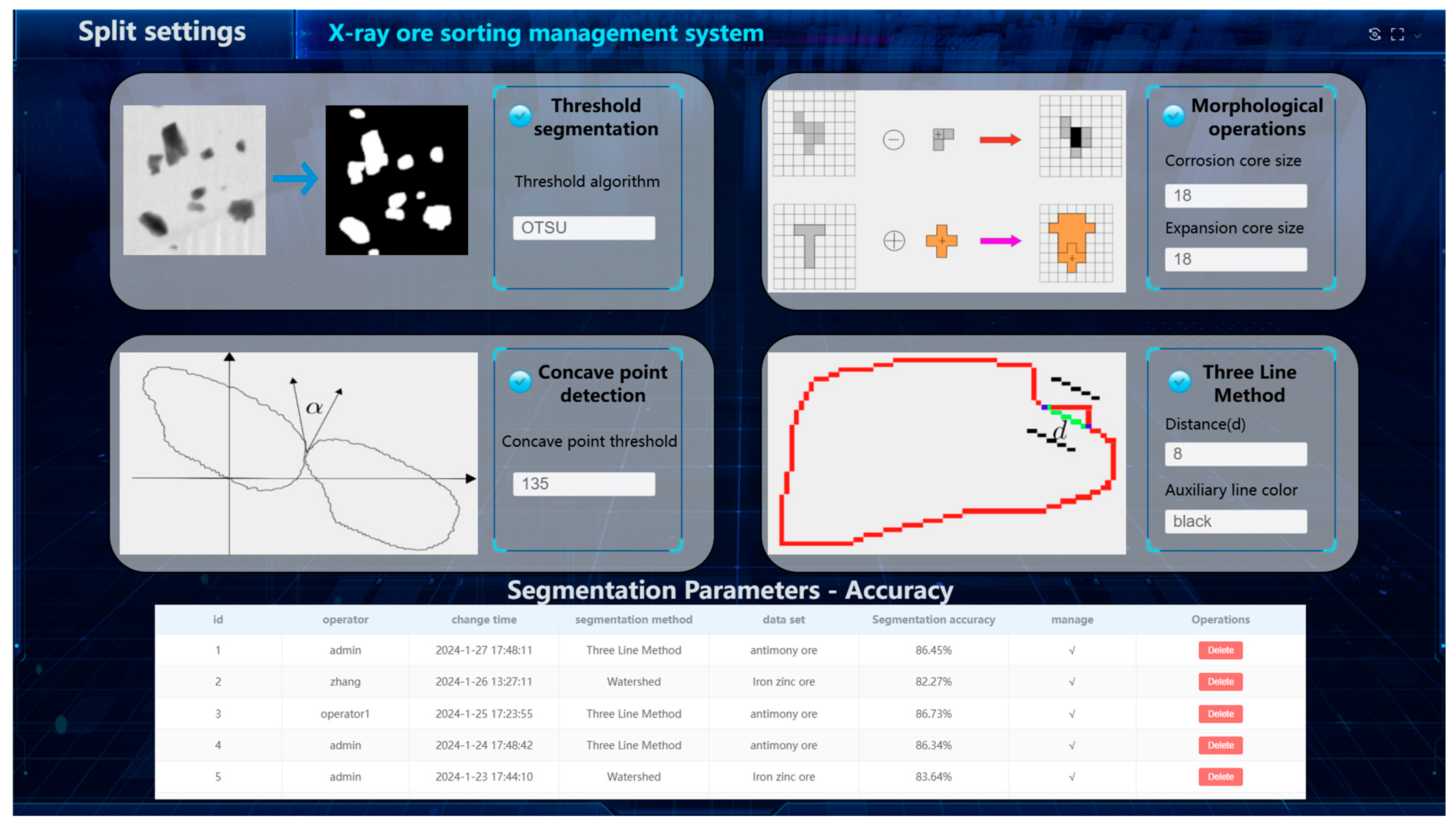
3.3.1. Split Parameter Settings
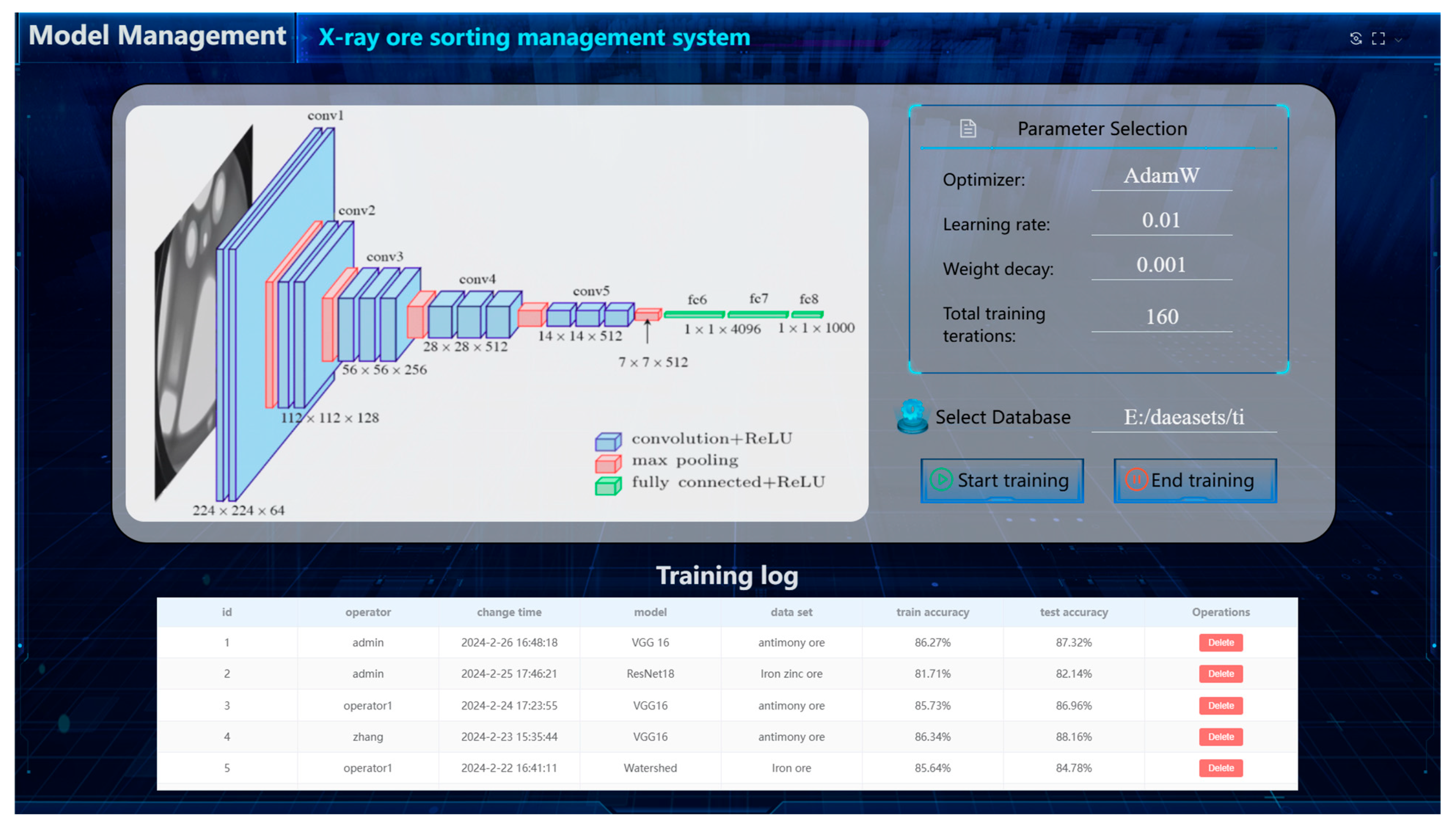
3.3.2. Classification Model Management
3.3.3. Real-Time Monitoring
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qin, X.; Deng, J.; Lai, H.; Zhang, X. Beneficiation of Antimony Oxide Ore: A Review. Russ. J. Non-Ferr. Met. 2017, 58, 321–329. [Google Scholar] [CrossRef]
- Jung, D.; Choi, Y. Systematic Review of Machine Learning Applications in Mining: Exploration, Exploitation, and Reclamation. Minerals 2021, 11, 148. [Google Scholar] [CrossRef]
- Bhuiyan, I.U.; Mouzon, J.; Hedlund, J.; Forsberg, F.; Sjödahl, M.; Forsmo, S.P.E. Consideration of X-Ray Microtomography to Quantitatively Determine the Size Distribution of Bubble Cavities in Iron Ore Pellets. Powder Technol. 2013, 233, 312–318. [Google Scholar] [CrossRef]
- Von Ketelhodt, L.; Bergmann, C. Dual Energy X-Ray Transmission Sorting of Coal. J. South. Afr. Inst. Min. Metall. 2010, 110, 371–378. [Google Scholar]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Wang, Y. Overview of Image Segmentation Methods Based on Deep Learning; SPIE: Bellingham, WA, USA, 2024; p. 13184. [Google Scholar]
- Rosenfeld, A. The Max Roberts Operator Is a Hueckel-Type Edge Detector. IEEE Trans. Pattern Anal. Mach. Intell. 1981, PAMI-3, 101–103. [Google Scholar] [CrossRef]
- Khan, J.F.; Bhuiyan, S.M.A.; Adhami, R.R. Image Segmentation and Shape Analysis for Road-Sign Detection. IEEE Trans. Intell. Transport. Syst. 2011, 12, 83–96. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, X.; Yang, L.; Liu, H. An Improved Sobel Edge Detection. In Proceedings of the 2010 3rd International Conference on Computer Science and Information Technology, Chengdu, China, 9–11 July 2010; Volume 5, pp. 67–71. [Google Scholar] [CrossRef]
- Er-sen, L.; Shu-long, Z.; Bao-shan, Z.; Yong, Z.; Chao-gui, X.; Li-hua, S. An Adaptive Edge-Detection Method Based on the Canny Operator. In Proceedings of the 2009 International Conference on Environmental Science and Information Application Technology, Wuhan, China, 4–5 July 2009; Volume 1, pp. 465–469. [Google Scholar] [CrossRef]
- Pham, D.L.; Xu, C.; Prince, J.L. Current methods in medical image segmentation. Annu. Rev. Biomed. Eng. 2000, 2, 315. [Google Scholar] [CrossRef]
- Tremeau, A.; Borel, N. A Region Growing and Merging Algorithm to Color Segmentation. Pattern Recognit. 1997, 30, 1191–1203. [Google Scholar] [CrossRef]
- Chandra, J.N.; Supraja, B.S.; Bhavana, V. A Survey on Advanced Segmentation Techniques in Image Processing Applications. In Proceedings of the 2017 IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), Computational Intelligence and Computing Research (ICCIC), Coimbatore, India, 14–16 December 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Chien, S.Y.; Huang, Y.W.; Chen, L.G. Predictive Watershed: A Fast Watershed Algorithm for Video Segmentation. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 453–461. [Google Scholar] [CrossRef]
- Yao, Y.; Wu, W.; Yang, T.; Liu, T.; Chen, W.; Chen, C.; Li, R.; Zhou, T.; Sun, C.; Zhou, Y.; et al. Head Rice Rate Measurement Based on Concave Point Matching. Sci. Rep. 2017, 7, 41353. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Zhao, Q.; Liu, Y. Splitting Touching Cells Based on Concave-Point and Improved Watershed Algorithms. Front. Comput. Sci. Sel. Publ. Chin. Univ. 2014, 8, 156–162. [Google Scholar] [CrossRef]
- Jin, C.; Wang, K.; Han, T.; Lu, Y.; Liu, A.; Liu, D. Segmentation of Ore and Waste Rocks in Borehole Images Using the Multi-Module Densely Connected U-Net. Comput. Geosci. 2022, 159, 105018. [Google Scholar] [CrossRef]
- Cai, Y.; Xu, D.; Shi, H. Rapid Identification of Ore Minerals Using Multi-Scale Dilated Convolutional Attention Network Associated with Portable Raman Spectroscopy. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 267, 120607. [Google Scholar] [CrossRef]
- Qiu, J.; Zhang, Y.; Fu, C.; Yang, Y.; Ye, Y.; Wang, R.; Tang, B. Study on Photofluorescent Uranium Ore Sorting Based on Deep Learning. Miner. Eng. 2024, 206, 108523. [Google Scholar] [CrossRef]
- Huang, J.-T.; Li, J.; Yu, D.; Deng, L.; Gong, Y. Cross-Language Knowledge Transfer Using Multilingual Deep Neural Network with Shared Hidden Layers. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 7304–7308. [Google Scholar] [CrossRef]
- Garg, S.; Singh, P. Transfer Learning Based Lightweight Ensemble Model for Imbalanced Breast Cancer Classification. IEEE/ACM Trans. Comput. Biol. Bioinf. 2023, 20, 1529–1539. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, H.; Wan, Z. Ore Image Classification Based on Improved CNN. Comput. Electr. Eng. 2022, 99, 107819. [Google Scholar] [CrossRef]
- Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning Filters for Efficient ConvNets. arXiv 2016, arXiv:1608.08710. [Google Scholar]
- Liu, Z.; Li, J.; Shen, Z.; Huang, G.; Yan, S.; Zhang, C. Learning Efficient Convolutional Networks through Network Slimming. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2755–2763. [Google Scholar] [CrossRef]
- Lin, M.; Ji, R.; Wang, Y.; Zhang, Y.; Zhang, B.; Tian, Y.; Shao, L. HRank: Filter Pruning Using High-Rank Feature Map. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1526–1535. [Google Scholar] [CrossRef]
- He, Y.; Liu, P.; Wang, Z.; Hu, Z.; Yang, Y. Filter Pruning via Geometric Median for Deep Convolutional Neural Networks Acceleration. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4335–4344. [Google Scholar] [CrossRef]
- Suzuki, S.; Be, K. Topological Structural Analysis of Digitized Binary Images by Border Following. Comput. Vis. Graph. Image Process. 1985, 30, 32–46. [Google Scholar] [CrossRef]
- Skala, V. Point-in-Convex Polygon and Point-in-Convex Polyhedron Algorithms with O(1) Complexity Using Space Subdivision. AIP Conf. Proc. 2016, 1738, 480034. [Google Scholar] [CrossRef]
- Fang, G.; Ma, X.; Song, M.; Bi Mi, M.; Wang, X. DepGraph: Towards Any Structural Pruning. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 16091–16101. [Google Scholar] [CrossRef]
- He, Y.; Liu, P.; Zhu, L.; Yang, Y. Filter Pruning by Switching to Neighboring CNNs With Good Attributes. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 8044–8056. [Google Scholar] [CrossRef] [PubMed]
- Nesteruk, S.; Agafonova, J.; Pavlov, I.; Gerasimov, M.; Dimitrov, D.; Kuznetsov, A.; Kadurin, A.; Latyshev, N.; Plechov, P. MineralImage5k: A Benchmark for Zero-Shot Raw Mineral Visual Recognition and Description. Comput. Geosci. 2023, 178, 105414. [Google Scholar] [CrossRef]
- Kermany, D.S.; Liang, H.; Dong, J.; Pei, J.; Zhu, J.; Hewett, S.; Dong, J.; Fu, X.; Huu, V.A.N.; Zhang, E.D.; et al. Identifying Medical Diagnoses and Treatable Diseases by Image-Based Deep Learning. Cell 2018, 172, 1122–1131.e9. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar] [CrossRef]
- Pu, Y.; Apel, D.B.; Szmigiel, A.; Chen, J. Image Recognition of Coal and Coal Gangue Using a Convolutional Neural Network and Transfer Learning. Energies 2019, 12, 1735. [Google Scholar] [CrossRef]
- Ma, L.; Hu, Y.; Meng, Y.; Li, Z.; Chen, G. Multi-Plant Disease Identification Based on Lightweight ResNet18 Model. Agronomy 2023, 13, 2702. [Google Scholar] [CrossRef]



| Types of Antimony Ore | Weight | Grade |
|---|---|---|
| High-grade ore | 1.91 kg | 26.83% |
| Medium-grade ore 1 | 1.7 kg | 4.74% |
| Medium-grade ore 2 | 4.8 kg | 0.556% |
| Tailings | 17.9 kg | 0.024% |
| Method | Under-Segmentation (%) | Over-Segmentation (%) | Right Segmentation (%) |
|---|---|---|---|
| Simple concave point matching | 3.73 | 7.46 | 88.81 |
| Watershed algorithm | 5.22 | 2.24 | 92.54 |
| Algorithm of this article | 3.73 | 0 | 96.27 |
| Dataset | Accuracy | Transfer Effect |
|---|---|---|
| - | 85.762 | - |
| Mineral | 85.456 | Negative |
| Chest X-Ray | 85.672 | Negative |
| Cifar10 | 85.852 | Positive |
| ImageNet | 86.43 | Positive |
| Classes | Training Image Number | Test Image Number |
|---|---|---|
| Concentrate | 952 | 239 |
| Tailings | 3464 | 867 |
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | |
| 0 | 0.20 | 0.36 | 0.52 | 0.64 | 0.74 | 0.84 | 0.90 | |
| 86.43 ± 0.57 | 86.61 ± 0.53 | 86.38 ± 0.39 | 86.76 ± 0.21 | 86.70 ± 0.31 | 86.63 ± 0.23 | 86.68 ± 0.42 | 86.50 ± 0.52 | |
| 85.37 ± 0.39 | 85.44 ± 0.67 | 85.58 ± 0.37 | 85.37 ± 0.28 | 85.09 ± 0.46 | 85.35 ± 0.52 | 85.33 ± 0.47 | 85.12 ± 0.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Ding, C.; Hu, H.; Wang, H.; Dai, W. Antimony Ore Identification Method for Small Sample X-Ray Images with Random Distribution. Minerals 2025, 15, 483. https://doi.org/10.3390/min15050483
Wang L, Ding C, Hu H, Wang H, Dai W. Antimony Ore Identification Method for Small Sample X-Ray Images with Random Distribution. Minerals. 2025; 15(5):483. https://doi.org/10.3390/min15050483
Chicago/Turabian StyleWang, Lanhao, Chen Ding, Hongdong Hu, Hongyan Wang, and Wei Dai. 2025. "Antimony Ore Identification Method for Small Sample X-Ray Images with Random Distribution" Minerals 15, no. 5: 483. https://doi.org/10.3390/min15050483
APA StyleWang, L., Ding, C., Hu, H., Wang, H., & Dai, W. (2025). Antimony Ore Identification Method for Small Sample X-Ray Images with Random Distribution. Minerals, 15(5), 483. https://doi.org/10.3390/min15050483






