The Sedimentation Mechanical Properties of Coal and Gangue Particles at Different Granularity Levels

Abstract

Coal gangue, the primary bulk solid waste generated during coal utilization, requires decarbonization and the enrichment of valuable components such as calcium and magnesium through methods like hydrocyclone separation for comprehensive utilization. This study observed the free-settling behavior of coal gangue particles using a high-speed dynamic image analysis system and analyzed their kinematic characteristics to guide the hydrocyclone separation process. The results indicate that particle size and density significantly influence settling behavior. Fine-grained, low-density particles exhibited more pronounced directional deflection and velocity fluctuations, while high-density coarse particles demonstrated higher settling velocities. Based on terminal velocity, the drag coefficient of fluid resistance acting on particles was calculated. The findings show that high-density coarse particles have larger drag coefficients, likely due to fluid disturbances and the hydrophobic nature of particle surfaces. Additionally, the mechanical properties of settling motion were analyzed, indicating that gravity dominates the settling process of coarse particles, while fine particles are subjected to relatively balanced forces. Furthermore, density variations primarily affect hydrodynamic drag, which is related to the surface properties of particles. Therefore, enhancing the centrifugal force field through cyclone structural optimization is necessary to improve separation precision for fine coal and gangue particles.

1. Introduction

Coal, as a major energy mineral resource, generates significant solid waste during its beneficiation process, among which coal gangue is predominant. Coal gangue typically accounts for over 10% of the raw coal output [1,2]. Due to its low calorific value and limited utility, a substantial amount of coal gangue is stored in open fields, causing severe land wastage and atmospheric dust pollution [3]. Additionally, coal gangue contains various heavy metals, such as Cr, Mn, Zn, and Pb [4], posing risks of soil and groundwater contamination, geological hazards, and self-ignition, thereby severely harming the ecological environment and restricting the clean and efficient utilization of coal. It is imperative to implement proper treatment strategies. Current utilization approaches for coal gangue include building materials production, soil improvement [5], the development of coal gangue based adsorbent materials [6], etc. These methods require separating and enriching specific components within coal gangue to meet the necessary property requirements. Among them, it is of great necessity to enrich the calcium and magnesium components in coal gangue. Calcium and magnesium are key raw materials for industries such as cement and ceramics. After enrichment, they can replace natural minerals such as limestone and be used to prepare high value-added products such as light calcium carbonate and soil conditioners. Techniques for separating coal gangue components primarily include jigging, hydrocyclone separation, and intelligent sorting based on machine learning [7]. Among these methods, jigging has low separation accuracy and a high lower limit of separation particle size, and both it and the hydrocyclone separation require water consumption. In addition, intelligent separation technology is still in the development stage [8]. Hydrocyclone separation exploits centrifugal forces generated by rotating fluids within a hydrocyclone to separate minerals based on size or density differences. It features advantages such as simplicity, high throughput, precision, and a low processing limit [9], making it especially suitable for the precise separation of fine-grained coal gangue particles.

During hydrocyclone separation, the trajectory of particle motion determines separation efficiency. Thus, analyzing particle motion behavior, resolving force characteristics, and understanding the mechanics driving particle movement are crucial for optimizing hydrocyclone design and enhancing separation efficiency. Particles in the hydrocyclone are subjected to radial and axial forces. Radial forces primarily influence separation effectiveness and include inertial centrifugal force, centripetal buoyancy, and hydrodynamic drag. Other stochastic forces, such as the Magnus force [10,11] and Saffman lift force induced by velocity gradients [12,13], also contribute. Moreover, the internal flow field of a hydrocyclone exhibits turbulence randomness, significantly affecting particle motion, especially radially. Direct observation of particle motion within hydrocyclones is challenging due to the complex flow field and random forces involved. Most existing studies rely on Computational Fluid Dynamics (CFD) simulation, and effective numerical models have been developed. Chu et al. [14] developed a numerical model for hydrocyclone separation based on the combination of CFD and the Discrete Element Method (DEM), successfully simulating the overall flow characteristics of particles inside the hydrocyclone. Zhang et al. [15] used the Lagrangian Particle Random Tracking Model (LPT) to analyze the fluid forces acting on particles within the hydrocyclone and their spatial distribution without considering particle–particle interactions, and the cyclonic separation mechanism was analyzed accordingly.

In hydrocyclones, particles are separated based on the principle of centrifugal settling [16]. Both centrifugal settling and gravitational settling rely on the relative motion induced by external forces due to the density differences between the dispersed and continuous phases [17]. Therefore, understanding the settling behavior of particles in a gravitational field and analyzing the forces acting on them can help predict the force characteristics and motion behavior of particles in a centrifugal force field, and providing guidance for optimizing hydrocyclone separation processes. The free settling of solid particles in the fluid has been extensively studied, with hydrodynamic drag identified as a critical factor affecting particle motion during settling. For fine mineral particles, Kynch was the first to propose a sedimentation theory [18]. Building on this, various empirical models for fluid resistance under different Reynolds number ranges have been developed [19]. Terfous et al. [20] established a sedimentation velocity prediction model based on fluid and particle characteristics, which demonstrated good accuracy for spherical particles. Wang et al. [21] experimentally investigated the settling process of spherical glass beads with varying hydrophobicity, developing a model that accounts for the effects of surface hydrophobicity on the terminal settling velocity and drag coefficient. For non-spherical particles, Song et al. [22] proposed a resistance coefficient model and sedimentation equation incorporating particle sphericity and settling orientation based on extensive experiments, significantly improving the prediction accuracy of sedimentation behavior for commonly non-spherical particles. Sun et al. [23] used a triaxial method to describe the equivalent diameter of particles and studied the drag coefficient and settling velocity of non-spherical particles. Additionally, numerical simulation methods have been widely applied in particle settling research. Rosa et al. [24] used direct numerical simulations (DNS) to investigate the gravitational settling process of small heavy particles in a three-dimensional turbulent flow, analyzing the settling mechanisms under a broad range of Taylor microscale Reynolds numbers. For real mineral particles, Lv et al. [25] analyzed the sedimentation dynamics of kaolinite particles with different sizes and sphericities using experiments and CFD-DEM methods. Liu et al. [26] used similar methods to revise the sedimentation resistance model for fine quartz particles, achieving accurate predictions of settling equilibrium for particles with different long-to-middle axis ratios.

However, coal gangue and its associated coal particles are characterized by high density, high hydrophilicity, and irregular shape distribution. These factors make it challenging to accurately describe their settling process using empirical models, rendering them less effective in guiding and predicting hydrocyclone separation performance. Consequently, this study utilized a high-speed dynamic image analysis system to observe and analyze the settling behavior of coal and gangue particles with different sizes and densities in water. The forces acting on particles during settling and their motion characteristics were investigated. The study also examined the feasibility of enriching valuable calcium and magnesium components through hydrocyclone separation for the preparation of high-value materials, such as those used in CO₂ capture, thereby providing insights into the comprehensive utilization of coal gangue.

2. Experiments

2.1. Sample Preparation

The gangue samples for this experiment were obtained from the Wangjialing coal washing plant in Shanxi, China, which are waste products resulting from the coal separation process, with an ash content of 80.55%. The samples have a high carbon content, and the coal and gangue are intimately mixed. They need to be crushed and liberated by dissociation, then the carbon component removed and the calcium and magnesium components enriched by hydrocyclone separation before they can be effectively recycled. The samples were homogenized and crushed to −1 mm using a jaw crusher and a double-roller crusher. This method is commonly used in coal separation and can make the properties of the product particles closer to the actual cyclone separation. Subsequently, various particle sizes and densities of coal and gangue were obtained by sieving and heavy liquid separation, and these samples were used for settling motion analysis. The heavy liquid was prepared by mixing miscible benzene, carbon tetrachloride, and bromoform in different proportions to obtain heavy liquids of different densities for density analysis.

The elemental analysis of the prepared samples with different particle sizes and densities was performed using XRF, (Panalytical Axi-os, Almelo, The Netherlands) (

Table 1. Chemical composition analysis of coal gangue particles.

Size Grades (mm)	Average Density (g/cm3)	Element Contents (%)
		C	Mg	Al	Si	Ca	Fe	Others
–0.074	1.89	53.89	0.33	18.55	22.16	0.65	1.58	2.83
	2.30	18.44	0.59	26.02	41.77	1.43	5.21	6.53
	2.65	11.84	0.60	26.89	45.27	1.61	6.31	7.49
0.125–0.074	1.89	60.00	0.14	18.98	17.51	0.77	0.61	2.00
	2.30	18.37	0.27	32.85	37.70	3.08	2.07	5.67
	2.65	11.16	0.41	23.90	46.11	3.20	7.31	7.91
0.25–0.125	1.89	54.13	0.14	21.75	20.16	1.01	0.61	2.20
	2.30	19.25	0.21	33.45	37.42	3.53	1.60	4.53
	2.65	11.93	0.42	23.88	44.28	2.96	8.04	8.49
0.5–0.25	1.89	54.19	0.14	21.44	20.07	1.28	0.64	2.24
	2.30	18.85	0.22	31.98	35.58	5.71	2.20	5.46
	2.65	11.67	0.52	24.56	46.07	2.38	6.82	7.98
1–0.5	1.89	53.50	0.09	21.68	20.24	1.40	0.65	2.43
	2.30	18.93	0.20	33.60	36.97	4.71	1.52	4.07
	2.65	11.37	0.47	24.92	45.65	2.22	7.57	7.80

). The results showed that the carbon content of the gangue particles did not change significantly with the particle size. The carbon content of the particles with an average density of 1.89 g/cm³ was significantly higher. The high-density particles with an average density higher than 2.0 g/cm³ were mainly gangue. Decarbonized gangue requires the separation of low-density coal particles. Analysis of the calcium and magnesium content showed that the average calcium content was 2.40% and the magnesium content was 0.32%, both of which had recovery value. Under different particle sizes and densities, the calcium and magnesium content of the –0.074 mm particle size grade was significantly different from that of other grades. The calcium and magnesium content in the particles with a density of +2.0 g/cm³ was higher. Therefore, calcium and magnesium can be enriched by particle size or density separation. The feasibility of studying the sedimentation movement of gangue particles can be further analyzed.

To characterize the surface hydrophobicity of particles with different densities and sizes, the contact angle of the particles was measured using the tableting method, as shown in Figure 1. It can be seen that the surface hydrophobicity of the particles shows an overall fluctuating downward trend with decreasing particle size; the hydrophilicity of the fine particles is higher. At the same time, the surface hydrophobicity decreases substantially with increasing particle density, which is related to the increase in particle ash content. The variation of surface hydrophobicity of particles may affect the cyclonic separation process.

Furthermore, the composition and distribution characteristics of minerals in coal gangue particles were analyzed using the Automatic Mineral Characterization System (AMICS), as shown in Figure 2. Figure 2a presents an overall image of the particles and the mineral categories identified through an energy spectrum analyzer. Figure 2b–d illustrate the distribution characteristics of major minerals in coal gangue particles. It can be observed that the primary minerals in coal gangue include quartz, illite, calcite, dolomite, hematite, pyrite, biotite, and anorthite. Among these, calcite, dolomite, and anorthite contain calcium components, while dolomite and biotite contain magnesium components. Enriching these minerals through hydrocyclone separation can achieve the goal of calcium and magnesium enrichment. From the particle’s images, it is evident that calcite exhibits relatively coarse grain sizes and is highly liberated, making it easier to separate. In contrast, other minerals containing calcium and magnesium components, such as biotite, have finer grain sizes and more intergrowths. Therefore, enhancing the efficiency of fine-grained hydrocyclone separation is essential to improve the recovery of these minerals.

2.2. Experimental System and Testing Method

As shown in Figure 3, a self-built visualization platform was used to observe the settling process of coal and gangue particles. The observation tank, filled with ultrapure water, had dimensions of 5 cm × 5 cm × 50 cm (length × width × height) for particle settling. The tank is wide enough to avoid the impact of the container side walls. Coal and gangue particles were dispersed in a beaker using a magnetic stirrer for 5 min, forming a homogeneous suspension, then transferred into a syringe, and injected into the observation tank from the top center for vertical release. After releasing the particles, they achieved a settling equilibrium within a distance of 250 mm [25,26]. Therefore, the experiment captured particle settling behavior at a distance of 350 mm from the release point. The image acquisition system consisted of an i-SPEED 230 high-speed camera (iX Cameras Inc., Rochford, UK) and a flat LED light source, allowing for capturing particle settling images 8 mm in height at 1280 × 864 pixels resolution with a frame rate of 1000 fps. For fine particles of –0.074 mm, to capture clear images, the field of view was reduced to a height of 3 mm. The experiment was conducted using ultrapure water with a resistivity of 18.2 MΩ/cm at room temperature, and measurements were repeated at least three times to minimize measurement errors.

2.3. Image Analysis and Data Processing Method

The images obtained from the high-speed camera were used to analyze the settling behavior characteristics of coal and gangue particles. First, the video was converted into a sequence of single-frame images using the i-SPEED Viewer 2.0, and then imported into Image-Pro Plus 6.0 for further image processing. The original RGB images were converted into 8-bit grayscale images to identify particle boundaries based on the grayscale difference between the coal and gangue particles and the background. The software then automatically extracted the particle center coordinates (x, y) at different times, and the particle’s average diameter d_p was measured at 2° intervals through the center of the particles. According to the particle position information, the instantaneous settling velocity can be calculated by Equation (1).

$$v={\displaystyle \frac{\sqrt{{(x_{i+\mathrm{n}}-x_i)}^2+{(y_{i+\mathrm{n}}-y_i)}^2}}{\Delta t}}$$

(1)

where Δt represents the time interval between n frames, with the downward velocity direction of the particle defined as positive.

In this study, the resolution of the captured images was 1280 × 864 pixels. For particles with sizes of +74 μm and −74 μm, the visible area was controlled to 8.00 mm × 5.40 mm and 3.00 mm × 2.03 mm, respectively. Therefore, the spatial resolution (S) of the images was 6.25 μm per pixel and 2.34 μm per pixel, respectively. Given a maximum edge detection error of ±0.5 pixels, the maximum error in particle size recognition was ±1 pixel, corresponding to ±6.25 μm for +74 μm particles and ±2.34 μm for −74 μm particles. The relative error for both cases was less than 8.45%. Furthermore, during the calculation of particle settling velocity, errors include particle centroid identification errors, spatial resolution errors, and shooting frequency errors, which can be determined using Equation (2) [27,28].

$$\Delta u=\sqrt{{\left({\displaystyle \frac{\partial u}{\partial P_1}}\mathrm{d}{P}_1\right)}^2+{\left({\displaystyle \frac{\partial u}{\partial P_2}}\mathrm{d}{P}_2\right)}^2+{\left({\displaystyle \frac{\partial u}{\partial \mathsf{\Delta }t}}\mathrm{d}\mathsf{\Delta }t\right)}^2+{\left({\displaystyle \frac{\partial u}{\partial S}}\mathrm{d}S\right)}^2}$$

(2)

where P₁ and P₂ are the centroid positions of the particle, and u is the instantaneous velocity of the particle. Using this method, the calculated error for particle settling velocity ranged from 0.45% to 7.70%. Among them, the velocity error for fine-grained particles is relatively high, which is mainly caused by the large image recognition error, but its absolute error is small and within the controllable range.

3. Results and Discussions

3.1. Analysis of Particle Settling Behavior

In this study, the settling behavior of coal and gangue particles with three different densities and five different sizes was observed, as shown in Figure 4. For coarse particles of +0.074 mm size, as shown in Figure 4a–l, images were recorded at 30 ms intervals, while for fine particles of –0.074 mm size, as shown in Figure 4m–o, images were recorded at 60 ms intervals. It can be observed that in all images, the displacement of particles during settling remained stable over the same time intervals, indicating a stable settling velocity. Additionally, the angle of the particles did not change significantly, and the self-spin phenomenon was not evident, suggesting that the particles had reached a stable settling state. At the same time, particles with similar shapes were selected in the experiment to avoid the influence of shape parameters and spin on subsequent sedimentation behavior and mechanical analysis. Analysis of the particle images shows that particles of different sizes and densities have irregular polygonal shapes, making it difficult to directly use traditional settling models to predict the settling process. Furthermore, the settling process of the particles forms a straight line in the images, which is distinctly different from the rising process of bubbles. Bubbles, being small and highly deformable, are easily tilted due to slight unconstrained motions, causing them to rise in a spiral motion due to minor fluid disturbances [29]. However, for the high-density and high-mass coal and gangue particles, gravity dominates, making them less susceptible to fluid disturbance and causing them to settle nearly vertically. However, for fine-grained and low-density particles, slight lateral deflection during settling can be observed. This is likely caused by the disordered fluid flow resulting from the settling process. Moreover, comparing the settling velocities of different particles reveals that for the same density, as particle size decreases, the displacement in the same time interval significantly decreases, and the settling velocity is reduced. For the same particle size, as particle density increases, the settling velocity slightly increases, though the effect of density on velocity is less significant compared to the effect of particle size.

3.2. Analysis of Particle Settling Velocity Characteristics

The instantaneous settling velocities of coal and gangue particles are shown in Figure 5. It can be seen that the particles’ settling velocity has stabilized, indicating that the particles have reached settling equilibrium. Furthermore, as the particle size decreases, the fluctuation in settling velocity gradually increases. For particles of –0.074 mm, the fluctuation can be as much as 15% above the average value. This is likely because finer particles are lighter and more hydrophilic, making them more susceptible to small fluid disturbances caused by tail vortices during settling.

Comparing the settling velocities of different particles, it is clear that particle size has a significant effect on settling velocity. As the particle size decreases, the settling velocity decreases significantly, from an approximately 100 mm/s size range to about 1 mm/s, representing a two-order magnitude decrease. In addition, for particles of the same size, there is a noticeable difference in the settling velocity between different densities. For all size grades, low-density particles (1.89 g/cm³) have a settling velocity approximately 30% lower than high-density particles (2.65 g/cm³), though the impact of particle size is more pronounced than that of density. Therefore, during hydrocyclone separation, both size-based and density-based separation are feasible. Separation based on the 0.074 mm particle size and 2.0 g/cm³ density could achieve effective enrichment of calcium and magnesium. However, as the density has less impact on settling velocity, density-based separation might be less effective. Therefore, to improve separation precision, it may be necessary to limit the particle size range to amplify the settling characteristic differences between different density particles.

At the same time, it was observed that as particle size decreases, the absolute differences in terminal velocities among particles of different sizes and densities significantly decrease. For particles in the –0.074 mm size range, the velocity differences are less than 1 mm/s. This presents considerable challenges for size-based classification at the 0.074 mm threshold. To resolve this, measures such as reducing the hydrocyclone diameter are needed to further enhance the centrifugal force field, thereby improving the effectiveness of separation and classification.

3.3. Analysis of Drag Coefficients in Settling Process

Based on the instantaneous settling velocities obtained after particle settling stabilization, the terminal velocities of coal and gangue particles with different sizes and densities were calculated, as shown in Figure 6a. It can be seen that terminal velocity is closely related to both particle size and density. As the density and size of particles increase, their terminal velocities also increase significantly. However, the effect of particle size changes is more pronounced. Reducing the particle size by one grade results in a more than 50% decrease in terminal velocity. Furthermore, density has a larger effect on the settling velocity of coarse particles, while the terminal velocity for –0.074 mm fine particles is relatively close across different densities.

The terminal velocity variation for particles of different sizes and densities reflects changes in the forces acting during the settling process. During the settling of coal and gangue particles, they are mainly affected by gravity (F_grav), buoyancy (F_bou), and hydrodynamic drag force (F_hd). The direction of particle settling is considered to be positive.

Gravity is the primary driving force for particle settling and always acts vertically downward, as shown in Equation (3). Among them, d_p was measured at 2° intervals through the center of the particle.

$$F_{grav}={\displaystyle \frac{1}{6}}\pi d_p^3{\rho }_{p}g$$

(3)

Buoyancy and hydrodynamic drag are the main resistive forces during the settling process. Buoyancy acts vertically upward and is related to the particle volume and fluid density (ρ_l), as shown in Equation (4).

$$F_{buo}=-{\displaystyle \frac{1}{6}}\pi d_p^3{\rho }_{l}g$$

(4)

When solid particles experience relative motion in a viscous fluid, due to momentum transfer, the fluid generates a resisting force, including frictional resistance and pressure resistance. This can be defined by Stokes’ drag law [30], as shown in Equation (5). The drag coefficient k_f is related to the particle and fluid properties, as well as the flow field environment.

$$F_{hd}=-3\pi k_f\mu d_{p}v$$

(5)

where μ is the dynamic viscosity of the fluid, and v is the relative velocity between the particle and the fluid.

When particles begin to settle from a stationary state, they are primarily affected by gravity and buoyancy. Because the particle density (ρ_p) is significantly higher than the fluid density (ρ_l), the gravitational force is larger, causing the particle to accelerate downward. According to Equation (5), hydrodynamic drag is positively correlated with relative velocity. As the particle accelerates, the drag force increases until it balances the gravitational force and buoyancy, at which point the particle achieves terminal velocity, as shown in Equation (6).

$$F_{grav}+F_{buo}+F_{hd}=0$$

(6)

When particles settle in a static aqueous environment, the drag coefficient primarily depends on the particle’s mass, shape, surface hydrophobicity, etc. This makes it an effective indicator of the resistance characteristics encountered during settling. According to the analyzed particle terminal velocity (v_ter) and the force balance, the drag coefficient of different-sized and different-density particles can be calculated by Equation (7).

$$k_f={\displaystyle \frac{d_p^2({\rho }_p-{\rho }_l)g}{18v_{ter}\mu }}$$

(7)

The calculated drag coefficients for coal and gangue particles of different sizes and densities are shown in Figure 6b. The analysis reveals that coarser particles exhibit larger drag coefficients, indicating that fluid resistance has a more significant effect on larger particles with the same other characteristics. This is likely due to the higher settling velocities of coarse particles, which generate stronger fluid turbulence and more pronounced wake effects and cause larger pressure differences on the upper and lower surfaces of the particles, thus creating additional fluid resistance. It can be observed that the variation in particle size leads to significant variations in drag coefficients only for coarse particles of +0.25 mm. As particle size decreases further, although the terminal velocity continues to decrease significantly (as shown in Figure 6a), the variation in the drag coefficient becomes less significant. This is likely because finer particles have lower terminal velocities and Reynolds numbers. In such cases, the hydrodynamic drag coefficient is primarily influenced by the particle’s shape, surface properties, and other intrinsic characteristics, while the additional fluid resistance caused by wake effects and pressure differences induced by particle settling motion is not significant. Additionally, when comparing the drag coefficients of coal and gangue particles of the same size range, it is evident that an increase in particle density leads to a corresponding rise in the drag coefficient, with this effect being more pronounced for coarse particles. This can be attributed to two main reasons: First, high-density particles experience greater gravitational force, resulting in higher terminal velocities and stronger additional fluid resistance. For fine particles, as previously mentioned, this effect is less significant. Second, the surface hydrophilicity of coal and gangue particles generally increases with particle density, leading to stronger interactions between hydrophilic particles and the fluid, thereby contributing to a higher drag coefficient. This effect is consistent across all size ranges.

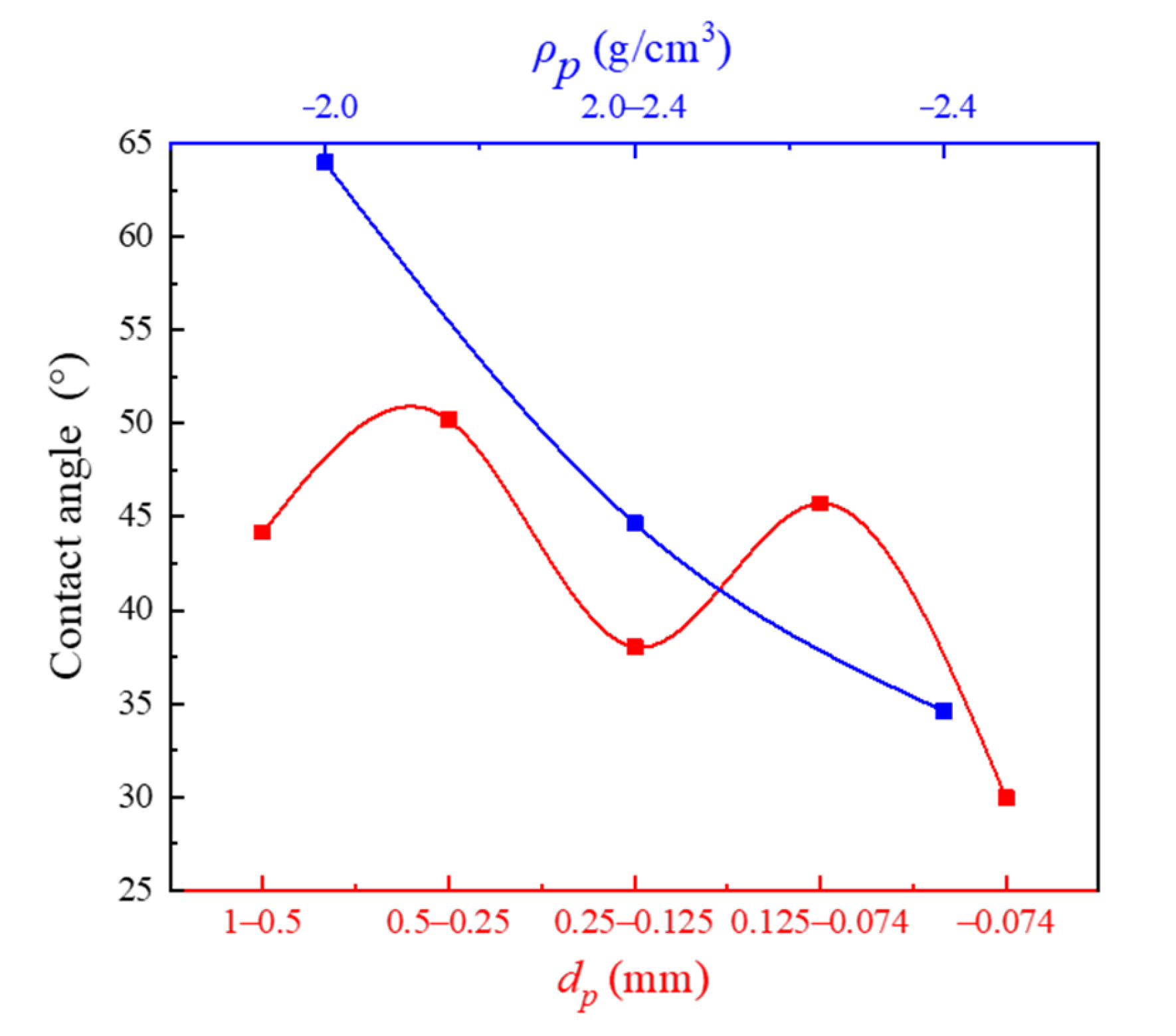
Based on the differences in hydrodynamic drag coefficients observed during the free-settling process of particles with various sizes and densities, it is possible to predict the magnitude of fluid resistance, estimate the forces acting on particles within a centrifugal force field, and thereby forecast the effectiveness of hydrocyclone separation. Both the density and size of coal and gangue particles influence their drag coefficients. Thus, hydrocyclone separation can be achieved based on differences in size and density. However, for fine particles, the impact of changes in size and density is less significant. Consequently, the separation precision for fine-grained coal and gangue particles may be lower, consistent with conclusions derived from the analysis of settling velocity characteristics.

3.4. Force Characteristics of Particle Sedimentation Motion

Based on Equations (3)–(5), the force characteristics during the settling process can be calculated, as shown in Figure 7. Gravity is the sole driving force for particle settling, while resistance consists of buoyancy and hydrodynamic drag force. The magnitude of the forces acting on particles is closely related to their size. For coarse particles, gravity is significantly larger and dominates the settling process. For high-density coarse particles, the maximum gravity can reach 5.58 μN. However, as particle size decreases, the differences between the forces reduce rapidly. For fine particles, the differences between buoyancy, hydrodynamic drag, and gravity are substantially reduced; the minimum difference can be reduced to about 0.001 μN, and all forces significantly affect the settling process.

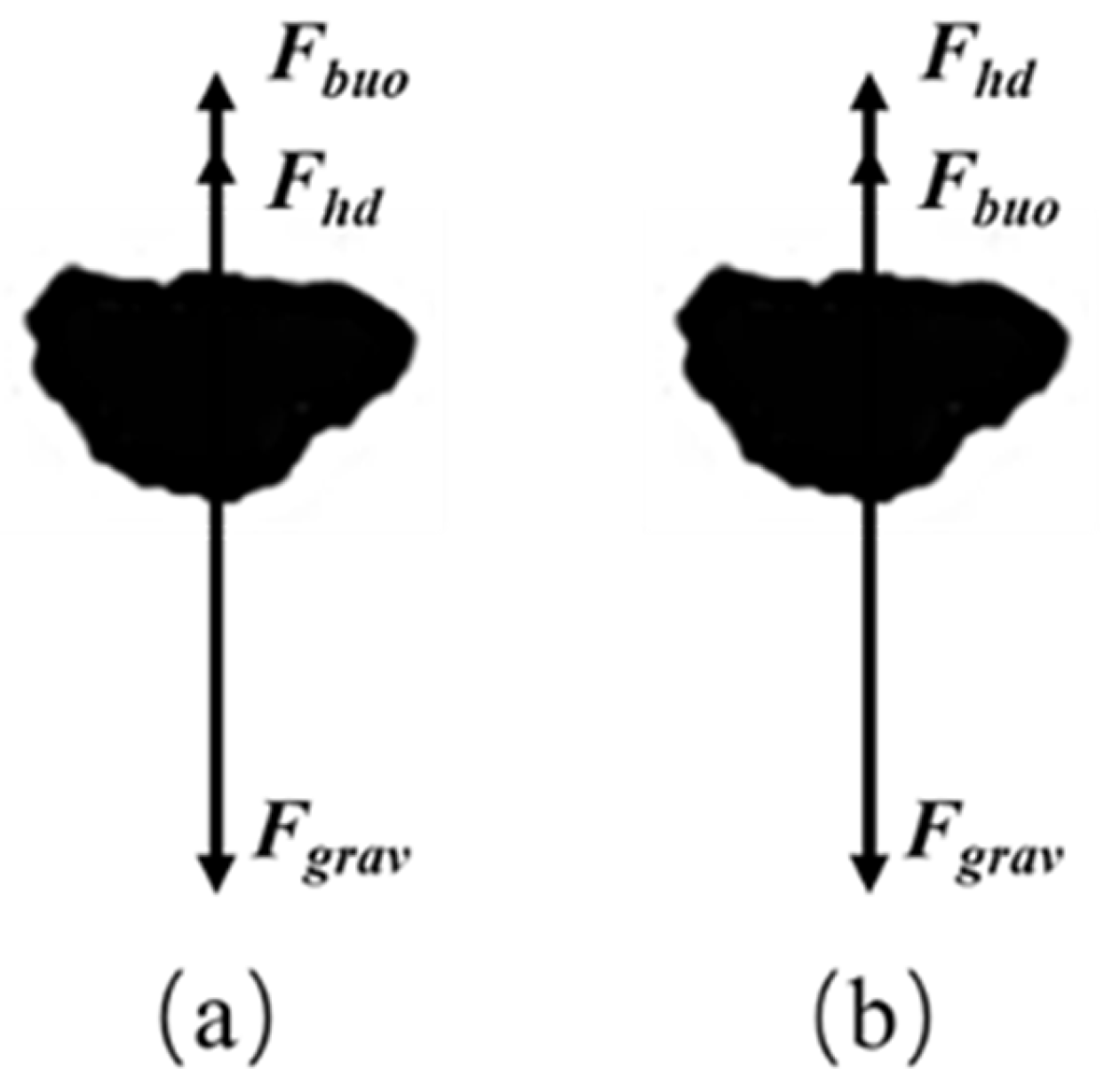
Among the resistance forces acting on particles, the relationship between hydrodynamic drag and buoyancy varies with particle size and density. For low-density particles, the two forces are relatively similar, with buoyancy slightly exceeding drag by 11%, as shown in Figure 8a. However, as particle density increases, hydrodynamic drag becomes significantly larger, while buoyancy remains nearly stable. For high-density particles, hydrodynamic drag becomes the dominant resistance force during settling, the drag force can exceed the buoyancy by more than 50%, as shown in Figure 8b. This is primarily due to the higher settling velocity of high-density particles and their stronger hydrophilicity, which enhances interactions with the fluid. Additionally, while the magnitudes of hydrodynamic drag and buoyancy decrease with smaller particle sizes, their relative relationship remains unchanged, indicating that the mechanisms of resistance for particles of different sizes are similar.

Based on the force characteristics during the settling motion, it is evident that hydrodynamic drag plays a crucial role in particle motion. In hydrocyclone separation processes, regulating the hydrodynamic drag can effectively improve separation efficiency and precision. Furthermore, for fine particles of −0.25 mm, the differences in forces are relatively small. From the perspective of force differentiation, strengthening the centrifugal force field in the hydrocyclone is necessary to amplify the force differences.

4. Conclusions

In this study, the free-settling process of coal and gangue particles with different sizes and densities in static water was observed. The kinematic and mechanical properties of the particles were analyzed to guide the separation and enrichment of calcium and magnesium components through hydrocyclone methods. The principal findings of this study are summarized below:

(1)

The study revealed that particle size and density significantly influence settling characteristics. Fine-grained particles exhibited more pronounced velocity fluctuations, and terminal settling velocity increased significantly with both particle size and density, with size having a stronger effect.

(2)

The drag coefficient of the hydrodynamic fluid resistance was calculated. It was found that high-density and coarse-grained particles had larger drag coefficients, likely due to fluid disturbances generated during settling and the hydrophilic nature of the particle surfaces.

(3)

The mechanical behavior of particle motion was analyzed. The settling process of coarse particles was primarily dominated by gravity, while fine-grained particles were influenced more equally by various forces. The impact of density on the hydrodynamic drag acting on particles was also significant, with high-density particles experiencing substantially higher drag.

(4)

Since particle size has a more pronounced effect than density on terminal settling velocity, drag coefficient, and force characteristics, size-based separation of coal and gangue particles is likely to be more efficient. Moreover, fine-grained particles exhibited smaller differences in both terminal velocity and force magnitude; thus, optimizing the structure of the hydrocyclone and enhancing the centrifugal force field are necessary to improve separation precision.