Machine Learning Approaches for Predicting the Elastic Modulus of Basalt Fibers Combined with SHapley Additive exPlanations Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Pre-Processing
2.2. Machine Learning Models
2.3. Hyper-Parameter Optimization
2.4. Model Performance Evaluation
2.5. Interpretability Analysis
3. Results
3.1. Description of Variables and Correlation Analysis
3.2. Model Performance
3.3. SHAP Interpretation
4. Conclusions
- (1)
- The correlation among the oxide variables is weak, and there is no significant linear correlation with the elastic modulus.
- (2)
- The CatBoost model performed best for elastic modulus prediction, scoring 0.9554, 4.7556, and 2.0323 of R2, RMSE, and MAE, respectively.
- (3)
- The SHAP results revealed a ranking of the input variable importance for the XGBR model of, in descending order, CaO > SiO2 > Al2O3 > MgO > K2O > Na2O > Fe2O3 > FeO > TiO2.
- (4)
- The calcium oxide content has a significant impact on the elastic modulus of basalt fibers, indicating that adjusting the calcium oxide content is an important approach to improving the elastic modulus of basalt fibers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. An Overview of the Employed Machine Learning Models
Appendix A.1. Multiple Linear Regression
Appendix A.2. K-Nearest Neighbors Regression (KNN)
Appendix A.3. Decision Tree (DT)
Appendix A.4. Support Vector Regression (SVR)
Appendix A.5. Artificial Neural Networks (ANNs)
Appendix A.6. Random Forest (RF)
Appendix A.7. Extreme Gradient Boosting (XGBoost)
Appendix A.8. Categorical Boosting (CatBoost))
Appendix B
| Analytical Methods for Chemical Composition | Analytical Methods for Elastic Modulus | Fiber or Roving | References |
|---|---|---|---|
| Chemical analysis (ASTMC169-92) | ISO 9163:2005(E) | roving | [16] |
| ICP-OES | EN ISO 5079:1999 | fiber | [17] |
| ICP-OES | German standard DIN 65382 | fiber | [23] |
| EDS | GB/T 7690.1-7690.6-2001 | fiber | [24] |
| XRF | ISO 5079 | fiber | [25] |
| GB/T 1549-2008 | GB/T 38897-2020 | fiber | [26] |
| XRF | ISO 5079 | fiber | [27] |
| Not mentioned | Not mentioned | fiber | [28] |
| XRF | ISO 5079 | fiber | [29] |
| Not mentioned | Not mentioned | fiber | [30] |
| ICP | GB/T3362-82 | roving | [31] |
| Not mentioned | Not mentioned | fiber | [32] |
| Not mentioned | Not mentioned | fiber | [33] |
| Not mentioned | Not mentioned | fiber | [34] |
| ICP | ASTM C1557–14 | fiber | [35] |
| XRF | ASTM D 3379-75 | fiber | [36] |
| Not mentioned | Not mentioned | fiber | [37] |
| Not mentioned | Not mentioned | fiber | [38] |
| Not mentioned | Not mentioned | fiber | [39] |
| Not mentioned | Not mentioned | fiber | [40] |
| XRF | Not mentioned | fiber | [41] |
| Not mentioned | Not mentioned | fiber | [42] |
| Model | Hyper-Parameter | Range | Optimum |
|---|---|---|---|
| MLR | - | - | - |
| KNN | n_neighbors | [1, 50] | 22 |
| weights | [’uniform’, ’distance’] | uniform | |
| metric | [’euclidean’, ’manhattan’, ’minkowski’] | minkowski | |
| DT | criterion | [’squared_error’, ’friedman_mse’, ’absolute_error’, ’poisson’] | squared_error |
| max_depth | [1, 100] | 4 | |
| min_samples_split | [2, 20] | 2 | |
| min_samples_leaf | [1, 20] | 1 | |
| max_features | [None, ’sqrt’, ’log2’] | None | |
| SVR | C | [0.1, 1, 10, 100, 1000] | 1.0 |
| kernel | [’linear’, ’poly’, ’rbf’, ’sigmoid’] | rbf | |
| gamma | [’scale’, ’auto’] | scale | |
| ANN | hidden_layer_sizes | [(50,50), (100, 100), (100, 50)] | (100, 100) |
| activation | [’identity’, ’logistic’, ’tanh’, ’relu’] | relu | |
| solver | [’lbfgs’, ’sgd’, ’adam’] | adam | |
| learning_rate | [’constant’, ’invscaling’, ’adaptive’] | constant | |
| alpha | [0.0001, 0.02, 0.05] | 0.02 | |
| RF | n_estimators | [10, 300] | 141 |
| max_depth | [1, 100] | 12 | |
| min_samples_split | [2, 10] | 2 | |
| min_samples_leaf | [1, 10] | 1 | |
| XGBoost | n_estimators | [50, 500] | 86 |
| learning_rate | [0.01, 0.1, 0.2, 0.3] | 0.1 | |
| max_depth | [3, 10] | 6 | |
| subsample | [0.5, 1.0] | 0.9 | |
| gamma | [0, 10] | 0 | |
| CatBoost | iterations | [50, 1000] | 1000 |
| learning_rate | [0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.1, 0.2, 0.3] | 0.03 | |
| depth | [3, 10] | 7 | |
| l2_leaf_reg | [1, 10] | 3 | |
| bagging_temperature | [0, 1] | 1 | |
| random_strength | [1, 10] | 1 |
References
- Dhand, V.; Mittal, G.; Rhee, K.Y.; Park, S.J.; Hui, D. A short review on basalt fiber reinforced polymer composites. Compos. B Eng. 2015, 73, 166–180. [Google Scholar] [CrossRef]
- Ivanitskii, S.G.; Gorbachev, G.F. Continuous basalt fibers: Production aspects and simulation of forming processes. I. State of the art in continuous basalt fiber technologies. Powder Metall. Met. Ceram. 2011, 50, 125. [Google Scholar] [CrossRef]
- Shi, F.J. A study on structure and properties of basalt fiber. Appl. Mech. Mater. 2012, 238, 17–21. [Google Scholar]
- Antunes, P.; Domingues, F.; Granada, M.; André, P. Mechanical Properties of Optical Fibers; INTECH Open Access Publisher: London, UK, 2012. [Google Scholar]
- Li, G.; Chen, Y.; Wei, G. Continuous fiber reinforced meta-composites with tailorable Poisson’s ratio and effective elastic modulus: Design and experiment. Compos. Struct. 2024, 329, 117768. [Google Scholar]
- Bi, C.; Tang, G.H.; He, C.B.; Yang, X.; Lu, Y. Elastic modulus prediction based on thermal conductivity for silica aerogels and fiber reinforced composites. Ceram. Int. 2022, 48, 6691–6697. [Google Scholar]
- Alshahrani, A.; Kulasegaram, S.; Kundu, A. Elastic modulus of self-compacting fibre reinforced concrete: Experimental approach and multi-scale simulation. Case Stud. Constr. Mater. 2023, 18, e01723. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, S.; Sun, X. Experimental investigation on the elastic modulus and fracture properties of basalt fiber-reinforced fly ash geopolymer concrete. Constr. Build. Mater. 2022, 338, 127570. [Google Scholar] [CrossRef]
- Asadi, A.; Baaij, F.; Mainka, H.; Rademacher, M.; Thompson, J.; Kalaitzidou, K. Basalt fibers as a sustainable and cost-effective alternative to glass fibers in sheet molding compound (SMC). Compos. B Eng. 2017, 123, 210–218. [Google Scholar]
- Jagadeesh, P.; Rangappa, S.M.; Siengchin, S. Basalt fibers: An environmentally acceptable and sustainable green material for polymer composites. Constr. Build. Mater. 2024, 436, 136834. [Google Scholar]
- Khandelwal, S.; Rhee, K.Y. Recent advances in basalt-fiber-reinforced composites: Tailoring the fiber-matrix interface. Compos. B Eng. 2020, 192, 108011. [Google Scholar]
- Guo, Z.S.; Hao, N.; Wang, L.M.; Chen, J.X. Review of Basalt-Fiber-Reinforced Cement-based Composites in China: Their Dynamic Mechanical Properties and Durability. Mech. Compos. Mater. 2019, 55, 107–120. [Google Scholar] [CrossRef]
- Tumadhir, M. Borhan Thermal and mechanical properties of basalt fibre reinforced concrete. Int. J. Civ. Environ. Eng. 2013, 7, 334–337. [Google Scholar]
- Wang, D.; Ju, Y.; Shen, H.; Xu, L. Mechanical properties of high performance concrete reinforced with basalt fiber and polypropylene fiber. Constr. Build. Mater. 2019, 197, 464–473. [Google Scholar]
- Lopresto, V.; Leone, C.; De Iorio, I. Mechanical characterisation of basalt fibre reinforced plastic. Compos. B Eng. 2011, 42, 717–723. [Google Scholar]
- Ding, L.; Liu, Y.; Liu, J.; Wang, X. Correlation analysis of tensile strength and chemical composition of basalt fiber roving. Polym. Compos. 2019, 40, 2959–2966. [Google Scholar] [CrossRef]
- Deák, T.; Czigány, T. Chemical Composition and Mechanical Properties of Basalt and Glass Fibers: A Comparison. Text. Res. J. 2009, 79, 645–651. [Google Scholar]
- Wu, Z.; Liu, J.; Chen, X. Continuous Basalt Fiber Technology; Chemical Industry Press Co., Ltd.: Beijing, China, 2020; p. 238. [Google Scholar]
- Wei, C.; Zhou, Q.; Deng, K.; Lin, Y.; Wang, L.; Luo, Y.; Zhang, Y.; Zhou, H. Alkali resistance prediction and degradation mechanism of basalt fiber: Integrated with artificial neural network machine learning model. J. Build. Eng. 2024, 86, 108850. [Google Scholar]
- Sun, Z.; Li, Y.; Yang, Y.; Su, L.; Xie, S. Splitting tensile strength of basalt fiber reinforced coral aggregate concrete: Optimized XGBoost models and experimental validation. Constr. Build. Mater. 2024, 416, 135133. [Google Scholar]
- Alarfaj, M.; Qureshi, H.J.; Shahab, M.Z.; Javed, M.F.; Arifuzzaman, M.; Gamil, Y. Machine learning based prediction models for spilt tensile strength of fiber reinforced recycled aggregate concrete. Case Stud. Constr. Mater. 2024, 20, e02836. [Google Scholar]
- Machello, C.; Bazli, M.; Rajabipour, A.; Rad, H.M.; Arashpour, M.; Hadigheh, A. Using machine learning to predict the long-term performance of fibre-reinforced polymer structures: A state-of-the-art review. Constr. Build. Mater. 2023, 408, 133692. [Google Scholar] [CrossRef]
- Eduard, K.; Rainer, G.; Jona, S. Basalt, glass and carbon fibers and their fiber reinforced polymer composites under thermal and mechanical load. AIMS Mater. Sci. 2016, 3, 1561–1576. [Google Scholar]
- Wei, B.; Cao, H.; Song, S. Tensile behavior contrast of basalt and glass fibers after chemical treatment. Mater. Des. 2010, 31, 4244–4250. [Google Scholar] [CrossRef]
- Sergey, I.G.; Evgeniya, S.Z.; Sergey, S.P.; Bogdan, I.L. Correlation of the chemical composition, structure and mechanical properties of basalt continuous fibers. AIMS Mater. Sci. 2019, 6, 806–820. [Google Scholar]
- Wang, L. Study on Effect of Basalt Fiber Component on Elastic Modulus. Master of Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Kuzmin, K.L.; Gutnikov, S.I.; Zhukovskaya, E.S.; Lazoryak, B.I. Basaltic glass fibers with advanced mechanical properties. J. Non-Cryst. Solids 2017, 476, 144–150. [Google Scholar] [CrossRef]
- Manylov, M.S.; Gutnikov, S.I.; Lipatov, Y.V.; Malakho, A.P.; Lazoryak, B.I. Effect of deferrization on continuous basalt fiber properties. Mendeleev Commun. 2015, 25, 386–388. [Google Scholar] [CrossRef]
- Kuzmin, K.L.; Zhukovskaya, E.S.; Gutnikov, S.I.; Pavlov, Y.V.; Lazoryak, B.I. Effects of Ion Exchange on the Mechanical Properties of Basaltic Glass Fibers. Int. J. Appl. Glass Sci. 2016, 7, 118–127. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, J.; Jiang, M.; Wang, Y.; Lei, L. A High-Temperature Resistant Basalt Fiber Composition. China Patent CN 201410139342.1, 6 January 2016. [Google Scholar]
- Wei, B. Evaluation of Basalt Fiber and Its Hybrid Reinforced Composite Performance. Master’ Thesis, Harbin Institute of Technology, Harbin, China, 2008. [Google Scholar]
- Wang, X.; Sun, K.; Shao, J.; Ma, J. Fracture properties of graded basalt fiber reinforced concrete: Experimental study and Mori-Tanaka method application. Constr. Build. Mater. 2023, 398, 132510. [Google Scholar] [CrossRef]
- Ramachandran, B.E.; Velpari, V.; Balasubramanian, N. Chemical durability studies on basalt fibres. J. Mater. Sci. 1981, 16, 3393–3397. [Google Scholar] [CrossRef]
- Dong, J.F.; Wang, Q.Y.; Guan, Z.W.; Chai, H.K. High-temperature behaviour of basalt fibre reinforced concrete made with recycled aggregates from earthquake waste. J. Build. Eng. 2022, 48, 103895. [Google Scholar] [CrossRef]
- Xing, D.; Chang, C.; Xi, X.Y.; Hao, B.; Zheng, Q.; Gutnikov, S.I.; Lazoryak, B.I.; Ma, P.C. Morphologies and mechanical properties of basalt fibre processed at elevated temperature. J. Non-Cryst. Solids 2022, 582, 121439. [Google Scholar] [CrossRef]
- Nasir, V.; Karimipour, H.; Taheri-Behrooz, F.; Shokrieh, M.M. Corrosion behaviour and crack formation mechanism of basalt fibre in sulphuric acid. Corros. Sci. 2012, 64, 1–7. [Google Scholar]
- Li, R.; Gu, Y.; Zhang, G.; Yang, Z.; Li, M.; Zhang, Z. Radiation shielding property of structural polymer composite: Continuous basalt fiber reinforced epoxy matrix composite containing erbium oxide. Compos. Sci. Technol. 2017, 143, 67–74. [Google Scholar]
- Ahmad, M.R.; Chen, B. Effect of silica fume and basalt fiber on the mechanical properties and microstructure of magnesium phosphate cement (MPC) mortar. Constr. Build. Mater. 2018, 190, 466–478. [Google Scholar]
- Vejmelková, E.; Koňáková, D.; Scheinherrová, L.; Doleželová, M.; Keppert, M.; Černý, R. High temperature durability of fiber reinforced high alumina cement composites. Constr. Build. Mater. 2018, 162, 881–891. [Google Scholar] [CrossRef]
- Qin, J.; Qian, J.; Li, Z.; You, C.; Dai, X.; Yue, Y.; Fan, Y. Mechanical properties of basalt fiber reinforced magnesium phosphate cement composites. Constr. Build. Mater. 2018, 188, 946–955. [Google Scholar] [CrossRef]
- Tang, C.; Jiang, H.; Zhang, X.; Li, G.; Cui, J. Corrosion Behavior and Mechanism of Basalt Fibers in Sodium Hydroxide Solution. Materials 2018, 11, 1381. [Google Scholar] [CrossRef]
- Li, M.; Gong, F.; Wu, Z. Study on mechanical properties of alkali-resistant basalt fiber reinforced concrete. Constr. Build. Mater. 2020, 245, 118424. [Google Scholar] [CrossRef]
- ISO 9163:2005(E); Textile Glass—Rovings—Manufacture of Test Specimens and Determination of Tensile Strength of Impregnated Rovings. International Organization Standardization: Brussels, Belgium, 2005.
- ISO/DIS 5079(en); Textile Fibres—Determination of Breaking Force and Elongation at Break of Individual Fibres. International Organization Standardization: Brussels, Belgium, 1999.
- DIN 65382; Aerospace; Reinforcement Fibres for Plastics; Tensile Test of Impregnated Yarn Test Specimens. German Institute for Standardisation: Berlin, Germany, 1988.
- GB/T 7690.1−2001; Reinforcements—Test Method for Yarns—Part 1: Determination of Linear Density. Standardization Administration of China: Beijing, China, 2001.
- GB/T 38897−2020; Non-Destructive Testing—Measurement Method for Material Elastic Modulus and Poisson’s Ratio Using Ultrasoinc Velocity. Standardization Administration of China: Beijing, China, 2020.
- GB/T 3362−2017; Test Methods for Tensile Properties of Carbon Fiber Multifilament. Standardization Administration of China: Beijing, China, 2017.
- ASTM, C1557−14; Standard Test Method for Tensile Strength and Young’s Modulus of Fibers. American Society Testing and Materials: West Conshohocken, PA, USA, 2014.
- ASTM, D3379-75; Standard Test Method for Tensile Strength and Young’s Modulus for High-Modulus Single-Filament Materials. American Society Testing and Materials: West Conshohocken, PA, USA, 1989.
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 4768–4777. [Google Scholar]
- Cao, H.; Yan, Y.; Yue, L.; Zhao, J. Basalt Fiber; National Defense Industry Press: Beijing, China, 2017; p. 188. [Google Scholar]
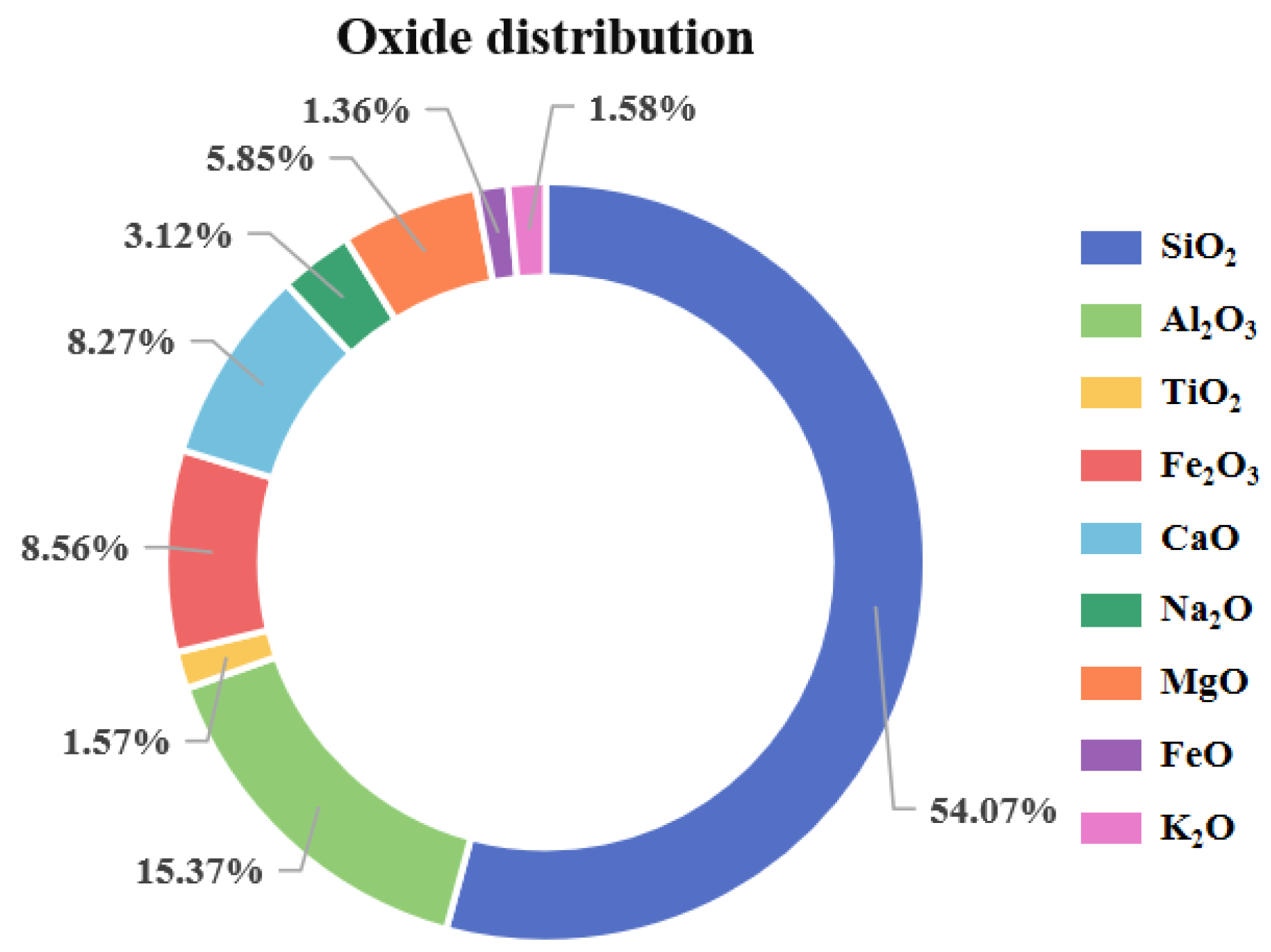


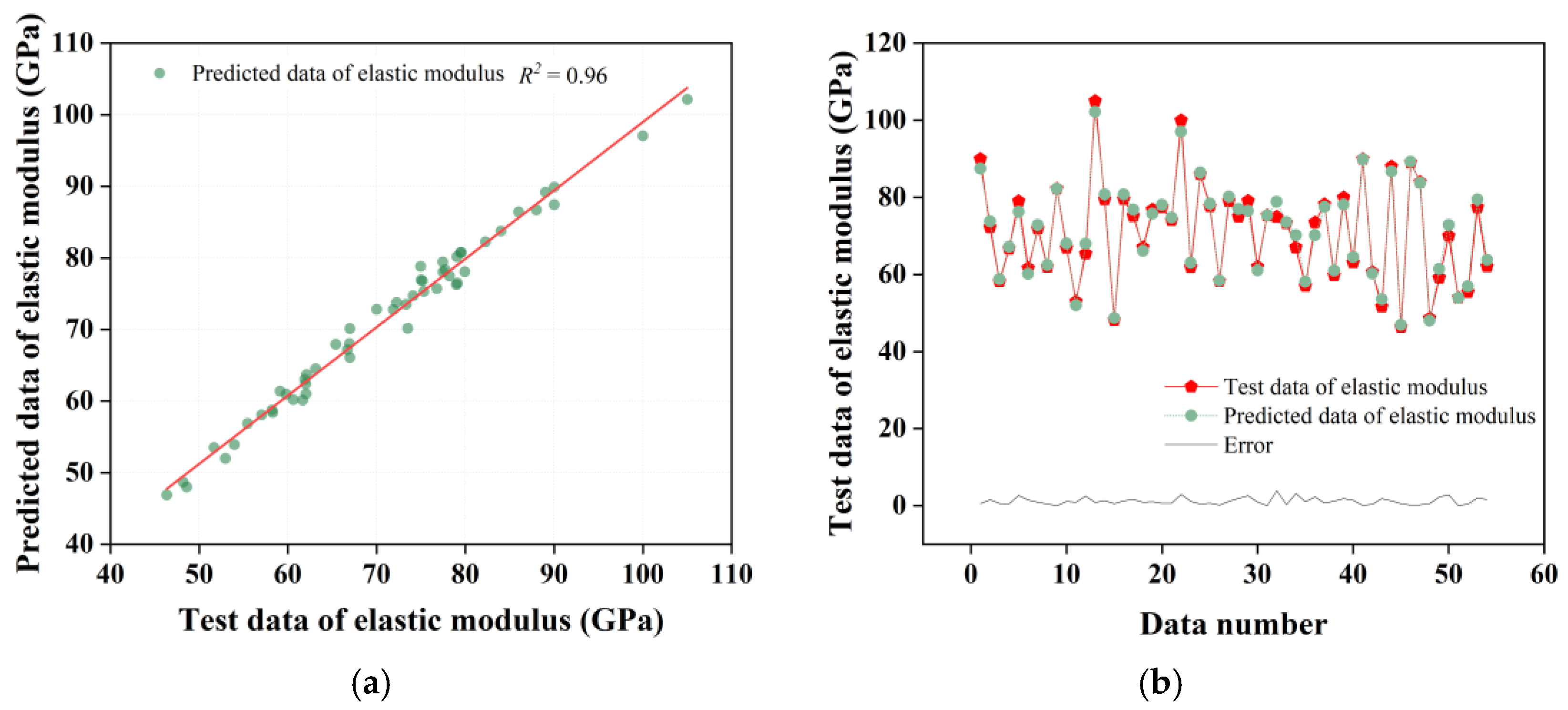
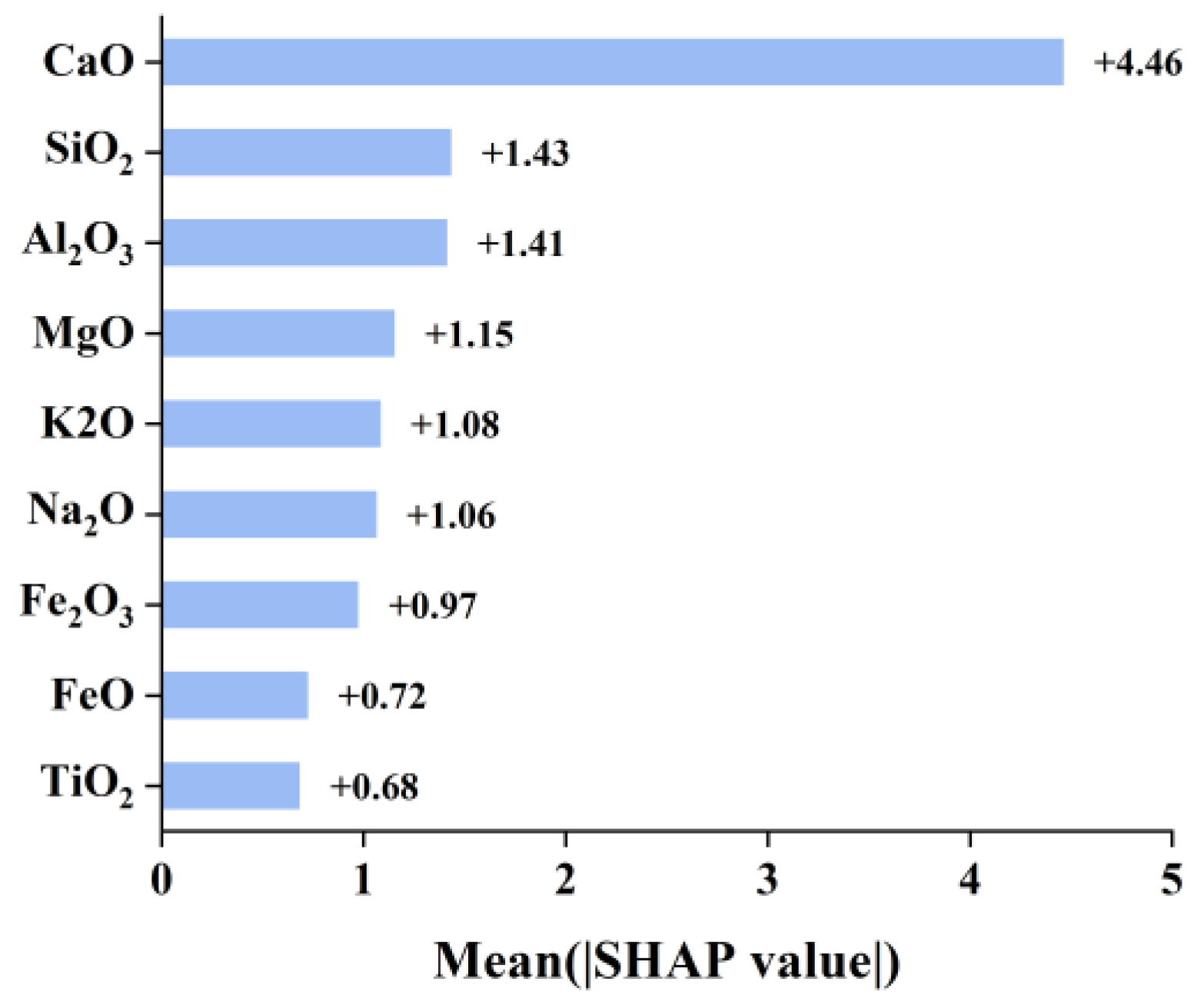

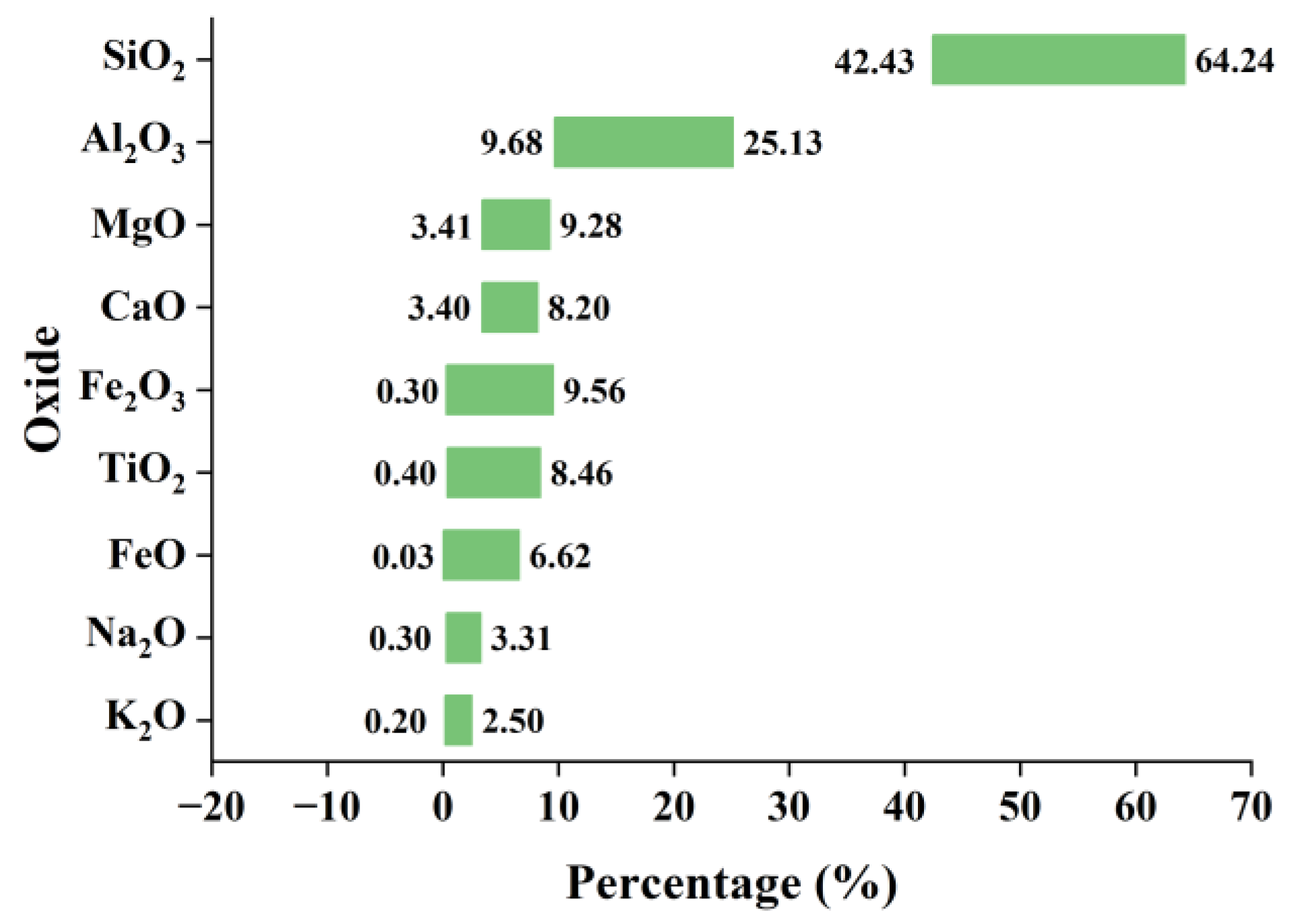
| Input Variable | Minimum–Maximum | Mean | Standard Deviation |
|---|---|---|---|
| SiO2/wt% | 42.43–66.90 | 54.07 | 4.54 |
| Al2O3/wt% | 8.70–25.60 | 15.37 | 3.75 |
| TiO2/wt% | 0.00–8.46 | 1.57 | 1.31 |
| Fe2O3/wt% | 0.30–19.34 | 8.56 | 3.65 |
| CaO/wt% | 3.20–18.91 | 8.27 | 2.26 |
| Na2O/wt% | 0.20–14.00 | 3.12 | 1.75 |
| MgO/wt% | 1.70–19.44 | 5.85 | 2.69 |
| FeO/wt% | 0.00–6.62 | 1.36 | 1.86 |
| K2O/wt% | 0.00–9.35 | 1.58 | 1.18 |
| Model | Training Data | Test Data | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | |
| MLR | 0.2951 | 10.3082 | 8.0533 | 0.1703 | 11.6958 | 8.7801 |
| KNN | 0.5318 | 8.4015 | 5.4992 | 0.4270 | 9.7199 | 6.8333 |
| DT | 1.0000 | 0.0407 | 0.0052 | 0.0516 | 12.5045 | 8.1983 |
| SVR | 0.1854 | 11.0816 | 8.6477 | 0.1099 | 12.1137 | 9.1008 |
| ANN | 0.9856 | 1.2547 | 0.3789 | 0.9209 | 5.3056 | 2.5518 |
| RF | 0.9184 | 3.5075 | 2.3776 | 0.3916 | 10.0152 | 6.4477 |
| XGBoost | 1.0000 | 0.0408 | 0.0058 | 0.9390 | 4.9997 | 2.2462 |
| CatBoost | 0.9993 | 0.3207 | 0.2613 | 0.9554 | 4.7556 | 2.0323 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Lin, N.; Yang, L. Machine Learning Approaches for Predicting the Elastic Modulus of Basalt Fibers Combined with SHapley Additive exPlanations Analysis. Minerals 2025, 15, 387. https://doi.org/10.3390/min15040387
Zhang L, Lin N, Yang L. Machine Learning Approaches for Predicting the Elastic Modulus of Basalt Fibers Combined with SHapley Additive exPlanations Analysis. Minerals. 2025; 15(4):387. https://doi.org/10.3390/min15040387
Chicago/Turabian StyleZhang, Ling, Ning Lin, and Lu Yang. 2025. "Machine Learning Approaches for Predicting the Elastic Modulus of Basalt Fibers Combined with SHapley Additive exPlanations Analysis" Minerals 15, no. 4: 387. https://doi.org/10.3390/min15040387
APA StyleZhang, L., Lin, N., & Yang, L. (2025). Machine Learning Approaches for Predicting the Elastic Modulus of Basalt Fibers Combined with SHapley Additive exPlanations Analysis. Minerals, 15(4), 387. https://doi.org/10.3390/min15040387






