Machine Learning Classification of Fertile and Barren Adakites for Refining Mineral Prospectivity Mapping: Geochemical Insights from the Northern Appalachians, New Brunswick, Canada

Abstract

This study applies machine learning (ML) techniques to classify fertile [for porphyry Cu and (or) Au systems] and barren adakites using geochemical data from New Brunswick, Canada. It emphasizes that not all intrusive units, including adakites, are inherently fertile and should not be directly used as the heat source evidence layer in mineral prospectivity mapping without prior analysis. Adakites play a crucial role in mineral exploration by helping distinguish between fertile and barren intrusive units, which significantly influence ore-forming processes. A dataset of 99 fertile and 66 barren adakites was analyzed using seven ML models: support vector machine (SVM), neural network, random forest (RF), decision tree, AdaBoost, gradient boosting, and logistic regression. These models were applied to classify 829 adakite samples from around the world into fertile and barren categories, with performance evaluated using area under the curve (AUC), classification accuracy, F1 score, precision, recall, and Matthews correlation coefficient (MCC). SVM achieved the highest performance (AUC = 0.91), followed by gradient boosting (0.90) and RF (0.89). For model validation, 160 globally recognized fertile adakites were selected from the dataset based on well-documented fertility characteristics. Among the tested models, SVM demonstrated the highest classification accuracy (93.75%), underscoring its effectiveness in distinguishing fertile from barren adakites for mineral prospectivity mapping. Statistical analysis and feature selection identified middle rare earth elements (REEs), including Gd and Dy, with Hf, as key indicators of fertility. A comprehensive analysis of 1596 scatter plots, generated from 57 geochemical variables, was conducted using linear discriminant analysis (LDA) to determine the most effective variable pairs for distinguishing fertile and barren adakites. The most informative scatter plots featured element vs. element combinations (e.g., Ga vs. Dy, Ga vs. Gd, and Pr vs. Gd), followed by element vs. major oxide (e.g., Fe₂O₃T vs. Gd and Al₂O₃ vs. Hf) and ratio vs. element (e.g., La/Sm vs. Gd, Rb/Sr vs. Hf) plots, whereas major oxide vs. major oxide, ratio vs. ratio, and major oxide vs. ratio plots had limited discriminatory power.

1. Introduction

The primary objective of mineral exploration is to differentiate prospective from non-prospective areas, ultimately facilitating the discovery of new sources of raw earth materials [1]. This is achieved by collecting diverse exploration datasets, translating them into spatial proxies using the mineral systems approach, and integrating these proxies through robust methodologies [1,2,3]. The outcome is a mineral prospectivity map that highlights potential areas in both greenfield (underexplored) and brownfield (previously explored) environments, a process referred to as mineral prospectivity mapping (MPM) [1,2,3]. The mineral systems approach focuses on the ore-forming processes described in deposit models, translating exploration layers into proxies [2]. The mineral systems approach encompasses key processes such as source, trigger, transport, trap, deposition, and preservation, providing a comprehensive, process-driven, and scale-independent framework for understanding deposit formation [2]. In this paper, we place a particular emphasis on the source as a critical component, highlighting its fundamental role in driving mineralizing systems. In the mineral systems approach, intrusive units are often regarded as key sources driving magmatism, hydrothermal fluid circulation, and the mobilization of metals necessary for mineral deposit formation. However, not all intrusive units are fertile; many are barren, with their fertility varying depending on various factors, such as magma source composition, the degree of crustal contamination, oxidation state, and magmatic differentiation processes [4]. While intrusive units are commonly incorporated as heat sources in MPM, it is essential to recognize that their fertility and mineralizing potential differ significantly. Assigning varying weights to these units, based on their fertility to form porphyry Cu, Cu-Au, and Au systems, could enhance the accuracy and reliability of mineral prospectivity models by better reflecting the mineralization potential of each unit.

Adakites are particularly significant due to the ability to distinguish between fertile and barren units, with implications for understanding mineral deposits and critical mineral exploration. Defined by geochemical characteristics, adakites are classified into high-silica adakites (HSA) and low-silica adakites (LSA), based on SiO₂ content [5,6,7]. HSAs, with SiO₂ > 67 wt.%, Al₂O₃ > 15 wt.%, Sr > 300 ppm, Y < 20 ppm, and specific elemental ratios like Sr/Y (>50) and La/Yb (>10), are indicative of formation through the partial melting of hydrothermally altered oceanic crust. Their genesis, particularly in late to post-collisional settings, contrasts with calc-alkaline andesite–dacite–rhyolite (ADR) series typically formed during subduction stages [8,9]. Numerous studies [10,11,12] highlight the association of oxidized I-type granitoids with Cu-Au mineralization, emphasizing the exploration relevance of adakites.

Recent advances in ML have introduced powerful tools for enhancing data analysis, pattern recognition, and predictive modeling in petrology and economic geology. By using computational algorithms to detect patterns and relationships in data, ML allows for more accurate predictions and classifications compared to traditional geological methods. ML techniques, such as supervised classification and regression models, have been effectively applied to analyze various types of data, including geochemical data [13]. For instance, Zou et al. [14] applied random forest (RF) and deep neural networks to assess magma fertility for porphyry Cu systems, showing that ML improves the accuracy of distinguishing fertile from barren rocks and identifying deeply buried deposits. Nathwani et al. [15] used four ML algorithms (logistic regression, neural networks, support vector machine (SVM), and RF) to classify rock metallogenic fertility, compare classifier performance, and identify key parameters for porphyry Cu exploration. Zhang et al. [16] utilized RF and a Monte Carlo-based ranking framework to identify elements crucial for ore formation and assess ore potential, while also explaining the scarcity of porphyry Cu deposits in the Paleo-Tethyan Ocean basin. Additionally, Zhang et al. [17] applied RF, SVM, and multilayer perception classifiers to classify ore deposit genetic types, distinguishing iron oxide–copper–gold (IOCG) and iron oxide–apatite deposits from other types.

In this paper, we focus on adakites as a key source in the mineral systems approach and aim to apply ML techniques to predict their fertility. We highlight that not all intrusive units, including adakites, are inherently fertile and should not be directly used as the heat source evidence layer in mineral prospectivity mapping without prior analysis. ML models, including SVM, neural network, RF, decision tree, AdaBoost, gradient boosting, and logistic regression were applied to classify fertile and barren adakites using geochemical data from New Brunswick, Canada. This study focused on evaluating the performance of these models to distinguish between fertile and barren adakites, leveraging a wide range of geochemical variables and ratios. This research also explored the significance of various geochemical features, such as elements, major oxides, and ratios, in determining adakite fertility.

2. Geology of Adakitic Intrusions in New Brunswick

New Brunswick, located within the Canadian Appalachians (Figure 1), features diverse tectonic zones including the Humber, Dunnage, Gander, and Avalon zones. These zones record complex geological histories shaped by multiple orogenic events, including the Taconic, Salinic, and Acadian orogenies. The Acadian Orogeny (~420–350 Ma) was particularly influential, leading to the emplacement of numerous Devonian plutonic and subvolcanic rocks during and after this mountain-building phase. The potential for mineralization in New Brunswick (e.g., [18,19,20]) associated with these igneous rocks depends on several factors, including the depth of emplacement, the chemical composition of the intrusions, and the nature of the host rock sequences [21]. Several adakitic intrusions in New Brunswick are associated with Cu-Au (±Mo) occurrences, including the Blue Mountain Granodiorite Suite (400.7 ± 0.4 Ma, U-Pb zircon; [22]), Nicholas Denys Granodiorite (381 ± 4 Ma, U-Pb zircon; [23]), Sugarloaf Porphyry, Meto’mqwijuig Mountain Felsite (415 ± 0.5 Ma, U-Pb zircon; [24]), North Dungarvan River Granite (382 ± 16 Ma, K-Ar muscovite; [25]), Magaguadavic Granite (403 ± 2 Ma, U-Pb zircon [26]), Tower Hill Granite (422 ± 15 Ma, Rb-Sr whole rock age [27]; 401 ± 4 Ma, Rb-Sr muscovite [24]), Watson Brook Granodiorite (382.1 ± 2.8 Ma, Rb-Sr biotite), Rivière-Verte Porphyry (368 ± 2 Ma, U-Pb zircon; [28]) (Figure 2a), Eagle Lake Granite (360 ± 5 Ma, U-Pb zircon; [29]), Evandale Granodiorite (391.2 ± 3.2 Ma, U-Pb zircon; [30]) (Figure 2b), North Pole Stream Suite (417 ± 1 Ma, U-Pb monazite; [31]), Beech Hill (343 ± 33 Ma, Rb-Sr whole rock age [27]), Pabineau Falls Granite (397 ± 2 Ma, U-Pb zircon [32]), and McKenzie Gulch Porphyry dykes (386.2 ± 3.1 and 386.4 ± 3.3 Ma, U-Pb zircon; [33]) (Figure 1).

These intrusions are similar to the Cu porphyry intrusions at Mines Gaspé [36], Québec, which host the largest copper–molybdenum deposit in Eastern North America. The Porphyry Mountain and Copper Mountain intrusions at Mines Gaspé were initially dated to 384.8 ± 2.8 Ma and 384.9 ± 2.5 Ma (Middle Devonian), respectively [37]. However, these ages were later refined using U-Pb zircon geochronology to 378.80 ± 0.37 Ma and 377.60 ± 0.45 Ma, respectively [38]; these ages [37,38], while differing, are similar to those of the adakitic intrusions in New Brunswick. These fertile adakitic intrusions, though they do not host any major deposits at the time of writing, contain occurrences exhibiting characteristics of porphyry Cu-Au-Mo mineralization, as reported in [39,40]. Two of the most significant examples are the Evandale porphyry Cu-Mo (Au) occurrence [30] and the Cu-Mo-Au porphyry system of the Eagle Lake Granite [12]. The Evandale Granodiorite is associated with porphyry-style Cu-Mo-Au mineralization, linked to porphyritic to aplitic dykes and a white granitoid phase, rather than the earlier coarse-grained pink granodiorite. Ore minerals include chalcopyrite, molybdenite, gold, silver, and locally tungsten, with minor sphalerite and galena [30]. Potassic alteration is evident in the pink granodiorite along northwesterly trending fractures, veins, and dykes, with these dykes sourced from deeper intrusive stocks, suggesting a genetic connection to the Late Silurian–Devonian Saint George Plutonic Suite [30,41]. The Eagle Lake Granite is recognized as a fertile Cu-Mo-Au porphyry system, exhibiting potassic alteration, locally overprinted by phyllic and propylitic assemblages [12]. Mineralization is characterized by quartz–sulfide stockworks and replacement zones containing disseminated pyrite, molybdenite, and chalcopyrite [12]. Extensive pyrite and quartz–pyrite–chalcopyrite veins are typical of the potassic stage, while gold-bearing quartz-sulfide veins dominate the phyllic stage [12].

One of the recent hypotheses proposed for the adakite rocks in New Brunswick, alongside other theories, is the late tectonic slab break-off hypothesis for adakite generation [9]. An important aspect is that the emplacement of this substantial volume of fertile intermediate-to-acidic magmas into the crust, occurring during a slab break-off event, is associated with transpressional-to-transtensional extension during the post-collisional orogenic phase. This process enables fertile magmas to ascend (rapidly) through the subduction-altered lithosphere, eventually rising into hypabyssal parts of the upper crust [9]. The studied intrusions, along with previously published and newly obtained geochronological data for oxidized porphyry-related intrusive rocks in southern to northern New Brunswick and their associated mineral occurrences, are summarized in

Table 1. Geochronological data and mineral occurrences of Devonian intrusions in New Brunswick [42]. Those intrusions with a dash in the mineral occurrence column indicate that they do not have significant mineral occurrences.

Intrusion	Age	Mineral Occurrence
Nashwaak	420.7 ± 1.8 Ma, U-Pb zircon, Late Silurian-Early Devonian [43]	—
Mulligan Gulch	419 ± 1 Ma, U-Pb zircon, Early Devonian [44]	Au
Meto’mqwijuig Mountain	415 ± 0.5 Ma, U-Pb zircon, Early Devonian [24]	—
Hartfield	415 ± 2 Ma, U-Pb titanite, Early Devonian [31]	Cu-Au-Mo
Hawkshaw	411 ± 1 Ma, U-Pb on titanite, Early Devonian [45]	W-Mo-Au
Skiff Lake	409 ± 2 Ma, U-Pb zircon, Early Devonian [31]	Mo
Magaguadavic	403 ± 2 Ma, U-Pb zircon, Early Devonian [26]	Cu-Mo-Au
Allandale	402 ± 1 Ma, U-Pb monazite, Early Devonian [31]	Be-W-Au
Blue Mountain Granodiorite Suite	400.7 ± 0.4 Ma, U-Pb zircon, Early Devonian [22]	Cu, Au, Mo
Falls Creek	394 ± 2 Ma, U-Pb zircon, Early Devonian (more details in [46])	Mo, W
Evandale	391.2 ± 3.2 Ma, U-Pb zircon, Middle Devonian [29]	Cu-Mo
McKenzie Gulch dykes	386.2 ± 3.1 and 386.4 ± 3.3 Ma, U-Pb zircon, Late Devonian [32]	Cu-Ag-Au
Popelogan (Cu-Mo), which is related to the Red Brook Granodiorite	383 + 1/−3 Ma, U-Pb zircon, Late Devonian [DL]	Cu-Mo
Nicholas Denys	381 ± 4 Ma, U-Pb zircon, Late Devonian [23]	Mo-Cu-Fe
Sorrel Ridge	378.5 ± 3.0 Ma, U-Pb zircon, Late Devonian [47]	Cu-Mo, Sn, W
Rivière Verte	368 ± 2 Ma, U-Pb zircon, Late Devonian [28]	Cu-Mo
Patapedia	364.4 ± 0.4 Ma, U-Pb zircon, Late Devonian (V. McNicoll, in [48])	Cu-Zn-Pb
Eagle Lake	360 ± 5 Ma, U-Pb zircon, Late Devonian [28]	Cu-Mo-Au
Quisibis porphyry	undated	Cu-Mo
Sugarloaf	undated	—

[42].

3. Methodology

The methodology of this study involved leveraging geochemical analyses of adakites to train and apply ML models for fertility prediction. Figure 3 shows a schematic diagram illustrating the methodology utilized in this study. A dataset consisting of 99 geochemical analyses of fertile adakites and 66 analyses of barren adakites from New Brunswick was used [22,32,36,42,49]. This dataset was used to train seven ML models: decision tree, SVM, neural network, AdaBoost, gradient boosting, logistic regression, and random forest. The ML analyses in this study were conducted using Scikit-Learn (version 1.3.0) and Orange (version 3.36). Scikit-Learn, a Python-based machine learning library (Python version 3.13), was used for hyperparameter tuning and model robustness enhancement, while Orange, a visual programming platform for machine learning and data mining, facilitated data analysis and model evaluation in a user-friendly environment. Prior to model implementation, data preprocessing was performed to ensure consistency and mitigate potential biases. Geochemical datasets were examined for outliers using statistical summaries and visual inspection methods, such as boxplots and histograms. As no significant missing values were identified, imputation was not required. To address variations in magnitude among geochemical parameters and improve model stability, all continuous variables were log-transformed (e.g., [50]) and standardized using z-score normalization (e.g., [51]) for SVM, neural networks, and logistic regression. This transformation was particularly beneficial for the SVM, neural network, and logistic regression models, which are sensitive to feature scaling, as it improved numerical stability and ensured optimal convergence during training [52,53,54]. However, for tree-based models, such as RF, decision tree, AdaBoost, and gradient boosting, feature scaling was unnecessary and therefore not applied [55]. All the models were rigorously evaluated and optimized to ensure their robustness and accuracy. Subsequently, the optimized models were applied to a global dataset of 829 geochemical analyses of adakites [56] to predict their fertility, enabling insights into their mineralization potential on a worldwide scale.

3.1. Dataset and Geochemical Characteristics

This study analyzed 99 geochemical datasets of fertile adakites and 66 geochemical datasets of barren adakites from New Brunswick to train ML models. The analysis results were sourced from [22,32,36,42,49], with the fertility or barren nature of the adakites discussed [42,46]. To distinguish fertile adakites from barren ones, specific criteria are considered in this paper. As discussed in Section 2, fertile adakitic intrusions are associated with Cu-Au (±Mo) mineralization, as indicated by the mineral occurrence database of the Government of New Brunswick [39]. These mineral occurrences are primarily documented through visible mineralization and/or polished sections in outcrops. Additionally, the identification of fertile intrusions for porphyry Cu and (or) Au systems can be achieved using porphyry indicator minerals (PIMs), such as zircon, plagioclase, titanite, apatite, magnetite, and tourmaline [57]. Yousefi [42] and Yousefi et al. [58] employed zircon trace element ratios and calculated logƒO₂ values to differentiate fertile from barren adakites. Specifically, Eu/Eu* ratios greater than 0.3, (Ce/Nd)/Y ratios ranging between 0.001 and 1.0, and log ƒO₂ values exceeding FMQ+2 (where FMQ represents the fayalite–magnetite–quartz oxygen fugacity buffer) were used as distinguishing criteria. Fertile porphyry systems are typically associated with high ƒO₂ conditions, while ƒO₂ values lower than FMQ+2 suggest an infertile system [59].

Geochemical data from 99 adakitic rock samples in New Brunswick, including archived and newly acquired data, are presented in the Supplementary Materials, Table S1, of [9]. On the SiO₂ vs. Na₂O + K₂O diagram [60], the samples are classified as granite, granodiorite, quartz diorite, and diorite. Their calc-alkaline to shoshonitic affinity is confirmed by selected major element compositions. The molar Al₂O₃/(CaO + Na₂O + K₂O) (A/CNK) ratios range from 0.8 to 1.2, indicating compositions that span peraluminous to metaluminous, with elevated A/CNK values attributed to cryptic alteration or biotite influence. These rocks are oxidized I-type granitoids, predominantly magnesian but extending into the ferroan field [9,42]. Geochemical analyses confirm their adakitic characteristics, with most samples plotting in the high-silica adakite field and showing low MgO content. The primitive mantle-normalized trace-element spider diagram reveals enrichment in large-ion lithophile elements (LILE) and notable depletion in high-field strength elements (HFSE). In our studied adakitic rocks, the enrichment of Cs, Rb, U, Th, and K, coupled with the depletion of Ti, Nb, P, Ba, and Sr, highlights their distinct arc-like geochemical signature [42]. Several hypotheses have been proposed for the genesis of adakite rocks, including the (1) melting of the lower crust or overlying rocks induced by rising basaltic magmas; (2) high-pressure crystal fractionation of basaltic magma; and (3) low-pressure crystal fractionation of water-enriched basaltic magma, along with magma mixing processes occurring in both arc and non-arc tectonic settings [61]. Additional theories on the formation of adakite magma include oceanic crustal melting, the high-pressure crystal fractionation of garnet and amphibole from hydrous basaltic magma, lower continental crustal melting triggered by basaltic magma underplating, the melting of eclogite or garnet amphibolite rocks, and the crystal fractionation of mafic magma. Another suggestion is the melting of lower continental crust in proximity to the mantle [6,62]. A review on oxidized I-type adakitic rocks selected from the GEOROC database was recently presented [8], but no information regarding the association of these rocks with mineralization was available. Along with all the theories on the genesis of adakite rocks, the slab-failure hypothesis has also been discussed in the review by Whalen and Hildebrand [11] and Archibald and Murphy [63]. The relationship between adakitic rocks, mineralization, and slab failure has been further explored, and many of the Devonian adakite rocks in New Brunswick are associated with Cu-Au-Mo porphyry mineralization [42]. To support the slab break-off/slab failure hypothesis for the origin of the adakite rocks in New Brunswick, it is important to examine geochemical indicators. The rocks from New Brunswick show Sr/Y ≥ 33 to 50, Nb/Y > 0.4, Ta/Yb > 0.3, La/Yb > 10, Sm/Yb > 2.5, Gd/Yb > 2.0, Nb + Y < 60 ppm, and Ta + Yb < 6 ppm. These values for Nb/Y, Ta/Yb, La/Yb, and Sm/Yb are notably higher than those typically found in arc magmas [42]. Slab rollback to failure—break-off is considered a significant consequence of the terminal subduction process, associated with post-collisional uplift and often transpression. The connection between these late adakitic rocks and earlier volcanic arcs in convergent margin setting is supported by their elevated Th/Yb ratios and lower Nb/Yb values. The formation of adakitic magmas is thought to involve the formation of a thicker lithospheric zone and a rising of a hotter mantle than in typical subduction zones, leading to adakitic melt generation from the slab and (or) suprasubduction zone mantle affected in similar ways. A key question is why adakitic rocks associated with melting slabs exhibit higher concentrations of Nb and Ta compared to conventional arc-type rocks. This high-T melting hypothesis proposal suggests that the instability of rutile or other titanium (Ti)-bearing phases, which host Nb and Ta, within the magmatic system causes the release of these elements. This release leads to higher concentrations of Nb and Ta in adakitic magmas. The instability of titanium-rich phases (such as rutile and titanomagnetite) is driven by increased heat in environments that produce Nb-Ta enriched adakite magmas [8]. In adakitic rocks, the enrichment of S, Cu, Au, and Cl is associated with the high oxidation state and water-rich nature of melts derived from subducted slabs, which enhances metal transport and ore-forming potential. The fertility of slabs and supra-subduction zones controls the metal endowment of these magmas, influencing their ability to generate porphyry Cu-Au-Mo mineralization [42]. According to the available analytical results on fertile and barren adakites in New Brunswick, the geochemical dataset included major oxides such as SiO₂, Al₂O₃, Fe₂O₃, MgO, CaO, Na₂O, K₂O, TiO₂, P₂O₅, and MnO, and trace elements such as Ba, Cs, Ga, Hf, Nb, Rb, Sr, Ta, Th, U, V, Zr, Y, La, Ce, Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Er, Yb, and Lu. Additionally, it incorporated geochemical ratios such as Sr/Y [64], La/Yb [64], K₂O/Na₂O [65], Th/Ta [66], Zr/Sm [67], Nb/Ta [68,69], Sm/Yb [67], La/Sm [70], Cs/Th [71], Rb/Th [67], Nb/Y [72], Rb/Y [72,73], Th/La [74], Zr/Nb [75], Rb/Sr [7], Eu/Eu* [76], Eu/Eu*/Y [77], Ce/Nd [78], Ce/Ce* [79], Y/MgO [80], and Sr/MnO [81]. The geochemical ratios included in this study were carefully chosen to capture key petrogenetic processes and geochemical signatures indicative of adakite fertility. Ratios such as Sr/Y (>33 to 50) and La/Yb (>10) highlight the involvement of garnet and amphibole in magma genesis, reflecting high-pressure melting conditions typical of fertile adakitic magmas [63]. Indicators like K₂O/Na₂O [64], Th/Ta [59], and Zr/Sm [60] provide insights into magma source characteristics, crustal contamination, and fractional crystallization. Additionally, Nb/Ta [61,62], Sm/Yb [60], and La/Sm [63] reveal the degree of partial melting and the depth of magma generation. Ratios such as Cs/Th [64], Rb/Th [60], Nb/Y [65], and Rb/Y [65,66] are essential for tracing subduction-related enrichment and tectonic settings, while Th/La [67] and Zr/Nb [68] evaluate subduction processes and crustal assimilation. The Rb/Sr [7] ratio helps indicate the degree of fractional crystallization or crustal assimilation in magmatic systems. Anomalies in Eu/Eu* [76], Ce/Ce* [79], and Sr/MnO [80] detect plagioclase fractionation and redox conditions, while Ce/Nd [78] highlights redox sensitivity, with Ce affected by oxidation while Nd remains stable. Y/MgO [80] and Sr/MnO [82] highlight mineralogical controls during crystallization. Together, these ratios provide a comprehensive framework for distinguishing fertile adakites from barren ones, aiding ML models in predicting mineralization potential.

3.2. ML Models

In this study, we employed several ML algorithms, including support vector machine (SVM; [83]), neural network [84], random forest (RF; [85]), decision tree [86], AdaBoost [87], gradient boosting [88], and logistic regression [89], and compared their results in predicting the fertility of adakites. These methods were chosen for their widespread application and strong citation records in machine learning, particularly in economic geology, petrology, and geochemistry (e.g., [14,15,16,17,90]). Their effectiveness in handling complex classification tasks and high-dimensional datasets, along with their alignment with established practices in the field, made them ideal candidates for this study.

The SVM is known for its robustness in identifying the optimal hyperplane that separates classes, particularly in high-dimensional spaces. It has been extensively applied in geosciences, including petrology, to classify and analyze geochemical data (e.g., [91,92]). The neural network was selected for its ability to model non-linear relationships and detect intricate patterns, making it highly suitable for geological systems (e.g., [93,94]). Ensemble methods like RF, AdaBoost, and gradient boosting are particularly popular due to their robustness and versatility. Random forest, for instance, is highly cited in petrological studies for its capacity to manage noisy data and assess variable importance [95,96,97]. Boosting methods such as AdaBoost and gradient boosting are widely used for their iterative refinement of weak learners, improving classification performance with each step (e.g., [97,98,99,100]). Logistic regression (e.g., [101]) and decision tree (e.g., [102]) were included as foundational models to provide interpretability and serve as benchmarks for comparison. Both methods are classic approaches that are simple to implement and interpret, making them common choices in petrological and geochemical studies.

4. Results

4.1. Key Geochemical Variables for Adakite Fertility

The importance of input geochemical variables in predicting the fertility of adakites is evaluated using various scoring metrics, each designed to assess the relevance of a feature from different statistical and informational perspectives. The statistical analysis and scoring metrics, including ANOVA, information gain, gain ratio, Gini index, chi-square, and ReliefF, aim to distinguish fertile from barren adakites based on geochemical variables such as major oxides, elements, and ratios, as discussed in Section 3.1.

Table 2. Results of the statistical analysis conducted to distinguish fertile and barren adakites based on geochemical variables.

Ranks	Variables	ANOVA	Info. Gain	Gain Ratio	Gini	χ2	ReliefF	Scores
1	Gd	233.715	0.618	0.309	0.324	76.469	0.186	0.982
2	Dy	135.944	0.567	0.283	0.306	74.223	0.110	0.803
3	Hf	116.380	0.594	0.297	0.314	85.731	0.073	0.797
4	La	123.147	0.543	0.272	0.294	78.748	0.071	0.749
5	Ho	126.758	0.524	0.262	0.287	67.687	0.105	0.746
6	Ce	118.828	0.514	0.257	0.281	74.223	0.080	0.723
7	Th	104.741	0.503	0.252	0.271	74.678	0.086	0.708
8	Ga	13.501	0.486	0.244	0.268	61.920	0.154	0.669
9	Pr	107.823	0.444	0.222	0.245	65.575	0.072	0.634
10	Zr	91.049	0.372	0.186	0.215	59.762	0.089	0.572
11	Nd	72.105	0.392	0.196	0.214	59.440	0.054	0.537
12	U	51.010	0.396	0.198	0.215	60.000	0.031	0.505
13	Sm	67.836	0.325	0.163	0.175	40.669	0.075	0.460
14	Eu/Eu*	47.822	0.289	0.145	0.172	39.199	0.057	0.406
15	Rb	55.789	0.252	0.126	0.125	30.367	0.091	0.381
16	(Eu/Eu*)/Y	30.182	0.302	0.151	0.159	31.519	0.050	0.372
17	Ta	52.113	0.277	0.138	0.157	36.690	0.031	0.366
18	Rb/Sr	19.566	0.308	0.154	0.163	42.844	0.015	0.361
19	Sr	59.759	0.211	0.106	0.132	36.027	0.071	0.358
20	Ce/Nd	0.665	0.301	0.151	0.182	49.886	0.000	0.354
21	Rb/Th	42.107	0.281	0.141	0.175	27.312	0.030	0.352
22	Nb	68.889	0.214	0.107	0.129	35.623	0.053	0.348
23	Al2O3	45.813	0.188	0.094	0.116	32.232	0.097	0.343
24	Cs	41.100	0.219	0.110	0.118	27.040	0.078	0.331
25	K2O/Na2O	23.702	0.277	0.138	0.156	21.207	0.040	0.323
26	Th/La	35.438	0.233	0.117	0.136	33.286	0.035	0.317
27	La/Sm	45.109	0.213	0.107	0.133	36.338	0.026	0.310
28	CaO	18.511	0.228	0.114	0.133	22.171	0.066	0.307
29	K2O	22.367	0.198	0.099	0.105	15.669	0.109	0.305
30	MnO	44.093	0.184	0.092	0.113	29.356	0.064	0.303
31	Sr/Y	38.322	0.177	0.089	0.105	25.977	0.051	0.273
32	SiO2	27.911	0.173	0.087	0.109	21.207	0.055	0.260
33	Eu	32.005	0.182	0.091	0.098	25.021	0.044	0.259
34	Y/MgO	11.956	0.201	0.101	0.127	33.286	0.012	0.258
35	Fe2O3T	32.708	0.124	0.062	0.082	11.663	0.113	0.256
36	Y	28.925	0.188	0.094	0.098	14.661	0.047	0.243
37	MgO	22.192	0.147	0.073	0.094	16.499	0.061	0.230
38	Er	24.205	0.201	0.100	0.107	10.967	0.029	0.228
39	Yb	27.683	0.170	0.085	0.094	14.661	0.031	0.216
40	La/Yb	25.948	0.121	0.060	0.071	14.661	0.067	0.209
41	Lu	16.351	0.189	0.095	0.116	3.512	0.023	0.201
42	Nb/Y	0.086	0.118	0.059	0.077	4.128	0.087	0.189
43	Th/Ta	10.093	0.133	0.067	0.086	23.692	0.012	0.180
44	V	15.625	0.125	0.062	0.079	14.464	0.031	0.175
45	Nb/Ta	0.654	0.142	0.071	0.088	22.817	0.007	0.173
46	Ba	16.685	0.122	0.061	0.072	11.840	0.035	0.169
47	Zr/Nb	4.607	0.036	0.018	0.024	3.969	0.112	0.143
48	Na2O	14.982	0.057	0.029	0.036	9.963	0.057	0.131
49	P2O5	2.841	0.066	0.033	0.044	3.133	0.056	0.117
50	Ce/Ce*	11.482	0.085	0.042	0.052	13.497	0.010	0.116
51	Sm/Yb	1.550	0.096	0.048	0.064	1.542	0.021	0.108
52	TiO2	5.791	0.073	0.036	0.048	0.115	0.027	0.092
53	Cs/Th	0.050	0.078	0.039	0.048	4.072	0.017	0.090
54	Rb/Y	3.867	0.046	0.023	0.031	6.428	0.027	0.080
55	Zr/Sm	2.319	0.004	0.002	0.003	0.217	0.074	0.072
56	Ce/(Nd×Y)	0.665	0.077	0.039	0.049	1.479	0.000	0.070
57	Sr/MnO	0.436	0.009	0.004	0.006	0.488	0.009	0.017

presents the results of the statistical analysis conducted to differentiate fertile and barren adakites.

Multiple metrics were used to assess the relationship between geochemical variables and adakite fertility. The scores highlight the relative importance of each variable. One key metric is the ANOVA (analysis of variance) test [103], which evaluates the differences in the mean values of the target variable across groups defined by a geochemical variable. This method is particularly useful for assessing the significance of numerous geochemical variables in relation to the target variable (fertile adakites). A higher value indicates a stronger relationship between the geochemical variables and the fertility of adakites.

Another key metric is information gain [104], which quantifies the reduction in entropy (uncertainty) when a geochemical variable is used to partition the data. It reflects how much information a geochemical variable provides about the fertility of adakites. A higher information gain indicates that the geochemical variable contributes more valuable information for predicting fertility.

Another important metric is the gain ratio [105], which normalizes information gain to address its inherent bias toward geochemical variables with many distinct values. By dividing information gain by the intrinsic information (entropy) of the geochemical variable itself, the gain ratio provides a more balanced evaluation, ensuring that geochemical variables with many values are not unfairly favored.

The Gini index [106] measures the impurity or diversity of the dataset following a split. Features that lead to greater reduction in impurity are considered more relevant, with lower Gini values indicating more effective features for classification tasks.

The chi-square (χ²) test [107] evaluates the independence between a geochemical variable and the fertility of adakites. It is particularly effective for categorical geochemical variables and the categorical target variable (fertility of adakites), with larger chi-square values indicating a stronger association between the geochemical variable and fertility.

Finally, the ReliefF algorithm [108] evaluates feature relevance by iteratively sampling instances and examining the differences between the nearest neighbors of the same and different classes. This method is capable of identifying the most informative geochemical variables in distinguishing between fertile and barren adakites, particularly in the presence of noisy or redundant features.

The score for each geochemical variable is calculated by first normalizing the values of each feature selection metric (ANOVA, information gain, gain ratio, Gini, χ², ReliefF) to a common scale between 0 and 1. This normalization ensures comparability across different metrics, eliminating discrepancies due to differing units or scales. Equal weights are then assigned to each normalized metric, treating all metrics as equally important in the ranking process. The final score for each variable is determined by calculating the simple average of the normalized values across all criteria. This approach produces a composite score that reflects the combined performance of each variable across multiple feature selection metrics. According to Table 2, Gd ranks first with a score of 0.982, indicating its importance in recognizing fertile adakites. Following Gd, Dy ranks second with a score of 0.803, and Hf ranks third with a score of 0.797, both contributing significantly to the classification process. The variable Eu/Eu*, as the highest-ranked ratio, ranks 14th with a score of 0.406, and the major oxide Al₂O₃, as the highest-ranked major oxide, ranks 23rd with a score of 0.343. These results emphasize the varying degrees of influence that different elements and major oxides have on identifying fertile adakites, with Gd playing the most prominent role. Additionally, we classified geochemical variables by ranking them based on standard deviation classification. This approach categorized the variables into four distinct classes. Figure 4 presents the plot of scores versus ranks from Table 2, using standard deviation classification. Class 1 ($\overline{X}$ + 2σ to maximum score) comprises variables with the highest-ranking scores (≥0.775), including Gd, Dy, and Hf (red dots in Figure 4). These variables exhibit the strongest correlation with fertile adakites. Class 2 ($\overline{X}$ + 1σ to $\overline{X}$ + 2σ) includes elements with scores ranging from 0.556 to 0.775, such as La, Ho, Ce, Th, Ga, Pr, and Zr (orange dots in Figure 4). While these variables contribute significantly to fertility classification, they have lower discriminative power than those in Class 1. Class 3 ($\overline{X}$ to $\overline{X}$ + 1σ) consists of variables with scores between 0.338 and 0.556, including Nd, U, Sm, Eu/Eu*, Rb, Eu/Eu*/Y, Ta, Rb/Sr, Sr, Ce/Nd, Rb/Th, Nb, and Al₂O₃ (green dots in Figure 4). Finally, Class 4 (minimum score to $\overline{X}$) encompasses variables with scores below 0.338, such as Cs, K₂O/Na₂O, Th/La, La/Sm, CaO, K₂O, MnO, Sr/Y, SiO₂, Eu, Y/MgO, Fe₂O₃T, Y, MgO, Er, Yb, La/Yb, Lu, Nb/Y, Th/Ta, V, Nb/Ta, Ba, Zr/Nb, Na₂O, P₂O₅, Ce/Ce*, Sm/Yb, TiO₂, Cs/Th, Rb/Y, Zr/Sm, Ce/(Nd×Y), and Sr/MnO (blue dots in Figure 4). Although these variables may have geological significance, their predictive capability for fertility assessments is limited.

4.2. Scatter Plot Analysis for Classifying Fertile and Barren Adakites

A comprehensive analysis of 1596 scatter plots, derived from 57 geochemical variables, was conducted to identify the most effective plots for distinguishing fertile and barren adakites. The evaluation was performed using the linear discriminant analysis (LDA) algorithm [109], which maximizes class separability by finding linear projections with optimal discriminatory power. The number of comparisons was calculated using the formula ${\displaystyle \frac{n\times (n-1)}{2}}$, where n represents the 57 geochemical variables listed in Table 2. Each scatter plot represented a pair of geochemical variables plotted against each other to evaluate their ability to separate fertile and barren classes. The LDA algorithm assessed the discriminatory performance of each combination by maximizing the inter-class variance while minimizing the intra-class variance [109]. LDA is a supervised ML algorithm that aims to find a linear combination of variables that best separates two or more classes. Its primary objective is to maximize the distance between the means of different classes while minimizing the variability within each class. LDA works by computing two key measures: within-class variance, which captures the spread of data points within each class, and between-class variance, which quantifies the distance between the means of different classes. The algorithm then selects the scatter plot that optimizes the ratio of between-class variance to within-class variance, ensuring the classes are as distinct as possible in the resulting feature space. In the context of this study, LDA was applied to identify which pairs of geochemical variables could best separate fertile and barren adakites. By analyzing the performance of different variable combinations, the LDA highlighted the most informative scatter plots. The most informative scatter plots for classifying fertile and barren adakites were those that displayed elements vs. elements. Among the highest-ranking plots, Ga vs. Dy (Figure 5a), Ga vs. Gd (Figure 5b), and Pr vs. Gd (Figure 5c) were the most effective in distinguishing the two groups. In terms of elements vs. major oxides, Fe₂O₃ vs. Gd (Figure 5d), Al₂O₃ vs. Hf (Figure 5e), and K₂O vs. Hf (Figure 5f) proved to be informative, while ratios vs. elements such as La/Sm vs. Gd (Figure 5g), Rb/Sr vs. Hf (Figure 5h), and La/Sm vs. Dy (Figure 5i) further enhanced classification performance. Scatter plots involving major oxides vs. major oxides, ratios vs. ratios, and major oxides vs. ratios performed poorly, suggesting that these combinations had limited discriminatory power for distinguishing between fertile and barren adakites.

4.3. Modeling

4.3.1. Training Data

Most of the geochemical and petrological data in this study are sourced from [36], with additional data from [22,32]. Further data collected as part of [42] were analyzed at the Actlabs laboratory [110]. Whole-rock major and trace-element geochemical analyses were conducted using a combination of X-ray fluorescence spectrometry [111], lithium metaborate fusion inductively coupled plasma-mass spectrometry (ICP-MS; Thermo iCAP 6500 ICP (Thermo Fisher Scientific, Waltham, MA, USA)), and instrumental neutron activation analysis (INAA) using the 4 Lithoresearch + 4B-INAA packages at Actlabs (Ancaster, ON, Canada). The INAA technique is described [112]. To ensure data quality, analytical precision was assessed using certified reference materials SY4 (diorite gneiss powder), GSP2 (granodiorite powder), and RGM2 (rhyolite powder), with reference values obtained from the GeoReM database (Geological and Environmental Reference Materials). Reproducibility was evaluated by analyzing duplicate samples, with relative standard deviations (RSD) for major elements generally below 1–2% and trace elements below 2–5%. Detection limits for key trace elements ranged from 0.01 to 0.1 ppm. The measured values of reference materials were within ±3% of the certified values, indicating high analytical accuracy. Quality control also included blank samples and internal duplicates to monitor precision and potential contamination.

4.3.2. Applying ML Methods and Optimization

As mentioned in Section 3.2, decision tree, SVM, neural network, AdaBoost, gradient boosting, logistic regression, and RF were applied in this study. These models were rigorously evaluated and optimized to ensure their robustness and accuracy. The following section details the hyperparameter tuning process employed for each model.

This study uses 99 fertile and 66 barren adakite analyses, reflecting the availability of high-quality data that met the criteria for inclusion. While the dataset is imbalanced, we did not choose oversampling or class weighting [113], as these techniques can introduce challenges, including the risk of overfitting [114] or biasing the model towards the minority class [115]. Oversampling artificially inflates the minority class, while class weighting can cause the model to overemphasize the minority class, leading to skewed predictions [113,114,115]. Instead, the performance of the models was optimized as much as possible and evaluated using metrics such as the area under the curve (AUC) [116] and Matthews correlation coefficient (MCC) [117], which are less sensitive to class imbalance and provide a more balanced measure of model performance.

To optimize the decision tree model, key hyperparameters influencing its performance were systematically tuned. The maximum tree depth (max_depth) parameter was tested between 3 and 20, with 7 providing the best balance—achieving 95% training accuracy and 88% validation accuracy. Shallower depths resulted in underfitting, while deeper trees led to overfitting. The min_samples_split parameter, governing the minimum number of samples required to split an internal node, was varied between 2 and 10. The optimal value of 5 effectively mitigated overfitting while maintaining high accuracy. Similarly, the min_samples_leaf, specifying the minimum number of samples allowed in a leaf node, was tested with values between 1 and 10, with 3 ensuring stability and preventing the formation of excessively small leaf nodes. These optimizations enhanced the decision tree’s generalizability and classification robustness.

The SVM model was optimized by C, gamma, and kernel type. The C parameter, which controls the trade-off between margin width and classification accuracy, was tested over values from 0.1 to 100, with C = 10 providing the best trade-off and an AUC score of 0.89. Among kernel types (linear, RBF, and polynomial), RBF performed best, yielding an AUC score of 0.91. The gamma parameter, controlling the influence of individual data points, was tested between 0.001 and 1, with gamma = 0.01 proving optimal for the RBF kernel. The results confirmed that simpler kernels (like RBF) outperformed polynomial kernels for this dataset.

Neural network optimization involved selecting the architecture and key hyperparameters. Various hidden layer configurations were tested, ranging from a single layer with 10 neurons to multiple layers with (100, 50, and 25). The best-performing architecture featured two hidden layers (50, 25), achieving an 87% validation accuracy. Among activation functions, ReLU outperformed than in both training speed and predictive accuracy. The learning rate, tested between 0.001 and 0.1, was optimal at 0.01. Regularization strength (alpha) was tested from 0.0001 to 0.01, with alpha = 0.001 effectively reducing overfitting.

AdaBoost optimization focused on the number of estimators (n_estimators) and learning rate. Evaluating n_estimators between 50 and 500 showed that 200 estimators yielded optimal performance. The learning rate, tested from 0.01 to 1, was optimal at 0.1. The base estimator was a decision tree (max_depth = 3), effectively reducing overfitting while maintaining an AUC score of 0.88. These settings ensured a balance between interpretability and predictive strength.

Gradient boosting was optimized by tuning n_estimators, learning_rate, and tree depth. Evaluating n_estimators between 50 and 300 showed that 150 provided the best balance between accuracy and computational efficiency. The learning rate, tested from 0.01 to 0.2, was optimal at 0.05, yielding an AUC score of 0.90. The tree depth, tested from 3 to 10, showed that max_depth = 5 prevented overfitting while maintaining strong performance. Additional optimizations included min_samples_split = 4 and min_samples_leaf = 2, further enhancing model generalization.

The optimization of logistic regression involved testing different regularization techniques (L1, L2, and ElasticNet) and tuning the regularization strength (C). Among these, L2 regularization yielded the best results. The C parameter, tested between 0.01 and 100, was optimal at C = 1, achieving an AUC score of 0.88. Various solvers were tested, with liblinear proving most effective for handling regularized binary classification.

RF optimization focused on n_estimators, max_depth, and feature selection. Evaluating n_estimators between 50 and 300 showed that 200 trees maximized performance. The max_depth parameter, tested up to 20, was optimal at 10, achieving an 89% validation accuracy while minimizing overfitting. Feature selection was optimized using max_features, with the sqrt option yielding the highest accuracy. The additional tuning of min_samples_split = 4 and min_samples_leaf = 2 improved generalization, ensuring robust performance on the validation set.

4.3.3. Performance Results

The performance of the applied methods were evaluated using key metrics such as AUC, classification accuracy (CA), F1 score, precision, recall, and Matthews correlation coefficient (MCC). AUC measures a model’s ability to distinguish between classes, with higher values indicating better performance, especially in imbalanced datasets. Classification accuracy (CA) shows the proportion of correct predictions but may be misleading when one class dominates. The F1 Score balances precision and recall, making it useful for imbalanced data by emphasizing the trade-off between false positives and false negatives. Precision quantifies the reliability of positive predictions, while recall focuses on identifying as many positives as possible. MCC provides a comprehensive evaluation by considering all four categories in the confusion matrix, with values closer to +1 indicating better model performance, particularly in imbalanced datasets. The results, summarized in

Table 3. Performance results of ML methods applied to predict fertile adakites on 165 geochemical analyses of adakites in NB.

Model	AUC	CA	F1	Precision	Recall	MCC
SVM	0.91	0.88	0.89	0.88	0.89	0.87
Gradient boosting	0.90	0.89	0.89	0.87	0.90	0.88
Random forest	0.89	0.89	0.90	0.91	0.88	0.88
Neural network	0.87	0.87	0.88	0.86	0.89	0.85
Decision tree	0.88	0.88	0.87	0.86	0.89	0.86
AdaBoost	0.88	0.87	0.88	0.85	0.88	0.85
Logistic regression	0.88	0.85	0.86	0.84	0.87	0.82

, reveal small variations in model effectiveness, highlighting the strengths and weaknesses of each approach. The SVM is the top performer, achieving the highest AUC (0.91) and strong results in MCC (0.87) and F1 score (0.89). Gradient boosting follows closely with an AUC of 0.90, and RF ranks third with an AUC of 0.89 and an excellent F1 score of 0.90. The neural network ranks fourth with an AUC of 0.87, while decision tree and AdaBoost exhibit similar, lower performances. Logistic regression ranks last with an AUC of 0.88 and the weakest balance between precision and recall.

The classification of 829 adakite samples, based on geochemical data compiled by the [56] from the GEOROC dataset “JETOA_ADAKITE.csv”, a comprehensive collection of adakite geochemical information, into fertile and barren categories was performed using the seven optimized ML methods mentioned. Each algorithm’s predictive performance was assessed in terms of the number and percentage of samples classified as fertile and barren (

Table 4. Geochemical analyses of 829 adakite samples, showing the number and percentage of samples predicted as fertile and barren by each ML method.

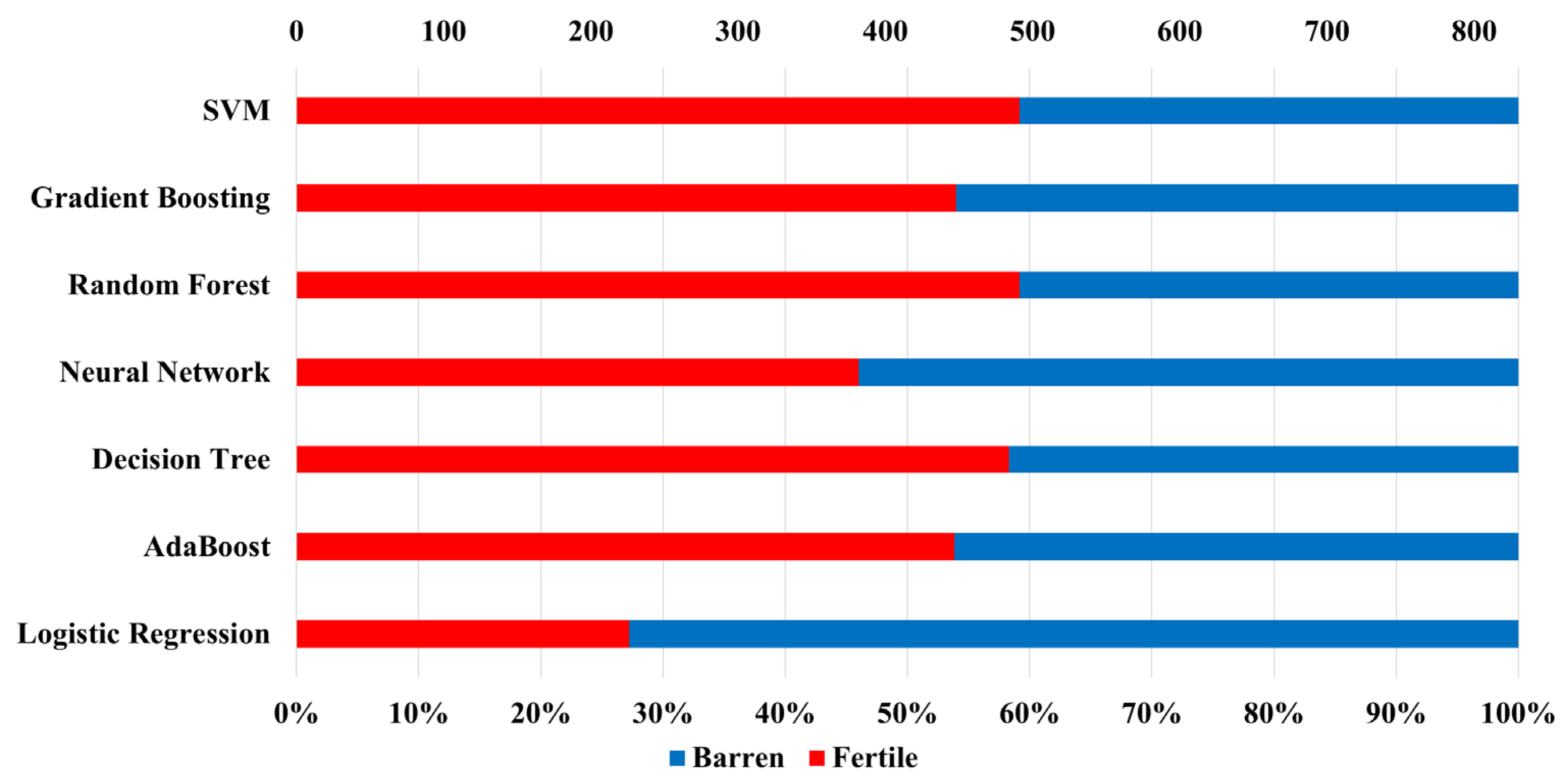
Methods		Fertile	Barren
SVM	Number	491	338
	%	59.2	40.8
Gradient boosting	Number	448	381
	%	54.0	46.0
Random forest	Number	491	338
	%	59.2	40.8
Neural network	Number	382	447
	%	46.1	53.9
Decision tree	Number	484	345
	%	58.4	41.6
AdaBoost	Number	447	382
	%	53.9	46.1
Logistic regression	Number	226	603
	%	27.3	72.7

). Among the methods, SVM and RF exhibited identical results, categorizing 59.2% of the samples as fertile and 40.8% as barren. Gradient boosting predicted 54% as fertile and 46% as barren, while the decision tree model performed similarly, with 58.4% fertile and 41.6% barren. The neural network and AdaBoost methods displayed a preference for barren classifications, with neural network predicting 53.9% as barren and 46.1% as fertile, and AdaBoost showing a slightly more balanced performance (53.9% fertile and 46.1% barren). Logistic regression demonstrated the most distinct classification pattern, predicting 72.7% of the samples as barren and only 27.3% as fertile. These results are visualized in Figure 6, which presents a stacked bar chart illustrating the distribution of fertile and barren predictions across the different ML methods. This chart highlights the variation in classification trends and provides a comparative perspective on the predictive behavior of each algorithm.

Among the 829 analyzed adakites [56], 160 samples were selected based on their clear and consistent fertility characteristics, identified through an extensive review of reputable references (

Table 5. Performance results of ML methods applied to predict 160 fertile adakite samples from around the world.

Place	Mineralization	Reference	Number of Fertile Samples	Total Number of Fertile Samples	Machine Learning Method	True Predicted as Fertile	Accuracy of Prediction (%)
South and Central Tibet	Cu-Au Porphyry and Epithermal deposits	[72,132,133]	82	160	SVM	150	93.75
Dharwar Greenstone Belts of India	Orogenic Au deposits	[126]	17		Random forest	136	85
Guerrero Terrane of Southwestern Mexico	Au-Fe skarn deposits	[127]	18		Gradient boosting	135	84.4
Superior Province in Canada (Ontario and Quebec)	Porphyry-Epithermal-Skarn-REE deposits	[128,129]	28		Neural network	135	84.4
The Pichincha Volcano in Ecuador	Cu-Au porphyry and epithermal deposits	[130]	2		Decision tree	132	82.5
Sulu Belt in Eastern China	Cu porphyry deposits	[130]	13		AdaBoost	131	81.88
-	-	-	-		Logistic regression	86	53.75

). Only samples with strong support from multiple studies were considered, while those with uncertainty or insufficient evidence were excluded. Of the 160 fertile adakites, 82 samples were from southern and central Tibet. The post-collisional adakites from southern Tibet, formed by the partial melting of subduction-modified lower crust [118], and the high-K calc-alkaline adakites from central Tibet, related to the melting of subducted continental crust [72], are associated with fertile mineral systems. These regions, known for their porphyry and epithermal deposits, are particularly recognized for their potential to host porphyry copper deposits (e.g., [119,120,121,122,123,124,125]). Seventeen samples were from the Dharwar Greenstone Belts of India [126], where studies on adakitic magmatism highlight their potential in gold environments. These Neoarchaean adakitic rocks, associated with subduction-related processes, are enriched in gold, underscoring their significance in mineral exploration. Eighteen samples were from the Guerrero Terrane of Southwestern Mexico, associated with Au-Fe skarn deposits [127]. The Paleocene adakites in this region are known to be Au-Fe bearing, suggesting a link between adakitic magmatism and gold mineralization, making them an example of fertile adakites in economic geology. Twenty-eight samples were from the Superior Province in Canada (Ontario and Quebec) [128,129], associated with porphyry, epithermal, skarn, and REE deposits. Studies on Archean adakite rocks from the Superior Province [128,129] have been crucial in exploring the links between ancient subduction processes and crustal growth. These regions are considered fertile due to their association with magnesian andesite and Nb-enriched basalt-andesite, both favorable for the formation of mineral deposits. Two samples are from Pichincha Volcano in Ecuador [130], which serves as an example where slab melting and melt metasomatism have produced adakites linked with fertile mineralization, particularly in the Northern Andean Volcanic Zone. These adakites are associated with copper–gold porphyry and epithermal systems (e.g., [131]). Thirteen samples were from the Sulu Belt in Eastern China, associated with Cu porphyry deposits [119].

Table 5 provides geochemical analyses of these fertile adakites, detailing the locations, associated mineralization types, and references. It also includes the number and percentage of samples predicted as fertile and barren by each ML method. The ML techniques mentioned were applied to these 160 fertile adakites, resulting in varying levels of accuracy. For instance, SVM achieved an impressive prediction accuracy of 93.75%, correctly identifying 150 out of the 160 fertile samples. Similarly, the RF method demonstrated an 85% accuracy, accurately classifying 136 fertile samples. Other methods, such as gradient boosting, neural networks, and decision trees, achieved prediction accuracies of 84.4, 84.4, and 82.5%, respectively. Logistic regression, while less accurate at 53.75%, still correctly predicted 86 fertile samples.

5. Discussion

This study analyzed a dataset of 99 fertile and 66 barren adakites from New Brunswick, including major oxides, elements, and geochemical ratios, to identify key signatures of fertility for ML models. Firstly, we aimed to identify the key geochemical variables for adakite fertility in New Brunswick, which can be generalized to all adakites globally. The results of the statistical analysis, as summarized in Table 2, highlight the varying degrees of influence that different geochemical variables exert on the classification of fertile and barren adakites. We used various feature selection metrics to evaluate the performance of each variable in identifying the fertility of adakites. For instance, ANOVA’s emphasis on mean differences between groups [103] aligns closely with the high importance assigned to variables like Gd and Dy, as these elements exhibit significant variability between fertile and barren adakites. Similarly, information gain and gain ratio highlight the capacity of variables to reduce uncertainty in predicting fertility, with REEs consistently performing well under these metrics. Interestingly, ReliefF, which evaluates variable importance by comparing instances within the dataset, also emphasizes REEs like Gd and Dy, but assigns relatively lower scores to major oxide variables, indicating their limited discriminative power in the presence of noisy or redundant features. The chi-square test, which assesses independence between variables, reinforces the importance of elements like Gd and Hf in differentiating fertile from barren adakites. The variables were ranked based on the statistical significance of these metrics (ANOVA, information gain, gain ratio, Gini, χ², ReliefF). The values were normalized to a 0–1 scale for comparability, with equal weights assigned to each metric. The final score for each variable was determined by averaging the normalized values, reflecting its combined performance across metrics. According to Table 2, Gd ranks first with a score of 0.982, underscoring its critical importance in identifying fertile adakites, followed by Dy and Hf with scores of 0.803 and 0.797, respectively. These trace elements, particularly the middle REEs Gd and Dy, demonstrate strong predictive power due to their geochemical stability and associations with mineral phases indicative of magmatic fertility. REEs, including Gd, Dy, and La, with Hf, consistently show strong scores across multiple metrics, such as ANOVA, information gain, and Gini index. These elements, critical for understanding magma chemistry and mineralization processes, significantly influence the model’s predictive capability. The enrichment of middle rare earth elements (MREEs), such as Gd and Dy, in fertile adakites is primarily controlled by magmatic differentiation, oxidation state, and source rock composition. Amphibole fractionation plays a crucial role, as it preferentially incorporates MREEs, leading to their relative enrichment in evolved, water-rich magmas associated with porphyry Cu systems. Additionally, the generation of adakitic magmas through partial melting of garnet-bearing lithologies results in depletion of heavy REEs while retaining MREEs, producing characteristic REE patterns linked to mineralized intrusions. The oxidation state and sulfur content of the magma further influence both REE distribution and the transport of Cu and Mo, as oxidized, sulfur-rich systems are more conducive to metal enrichment. Hydrothermal processes can also redistribute REEs in mineralized systems, with fluid chemistry playing a key role in selective element mobility. These geochemical processes collectively contribute to the correlation between MREE enrichment and the fertility of adakitic intrusions, supporting their application in mineral prospectivity assessments. Hf also plays a significant role in the geochemistry of fertile magmatic systems, especially in the context of adakitic intrusions. Hf is highly compatible in zircon, a common mineral in evolved, differentiated magmas. As such, the enrichment of Hf in these systems can indicate extensive fractional crystallization or high-temperature conditions during magma differentiation. Additionally, Hf’s behavior, along with MREEs like Gd and Dy, is influenced by the composition of the source rocks and the extent of partial melting, which contributes to the formation of fertile intrusions. Its correlation with Cu and Mo may therefore be related to the degree of magma evolution and the associated changes in the geochemical characteristics of the melt, which ultimately influence metal mobility and concentration in mineralized systems. Regarding the performance of ratios and major oxides, they rank lower than the elements. For example, Eu/Eu*, ranked 14th with a score of 0.406, offers information on plagioclase fractionation but is surpassed by individual REEs. Various ratios and normalized variables, like Eu/Eu*, Rb/Sr, and La/Sm, serve as important discriminators in the model, showcasing how combined element ratios can provide enhanced predictive power compared to individual elements alone.

The additional analysis of 1596 scatter plots derived from 57 geochemical variables further supports the dominance of specific trace elements in distinguishing fertile and barren adakites. Using the LDA algorithm, the most informative scatter plots were identified, with elements such as Ga, Dy, Gd, and Hf emerging as key variables. Among the highest-ranking scatter plots, combinations such as Ga vs. Dy, Ga vs. Gd, and Pr vs. Gd (Figure 5a–c) were found to be particularly effective in separating the two classes. These results align with the earlier statistical findings, highlighting the predictive power of REEs like Gd, Dy, and Ga. Interestingly, scatter plots involving elements versus major oxides, such as Fe₂O₃ vs. Gd (Figure 5d) and Al₂O₃ vs. Hf (Figure 5e), also proved to be valuable, though not as informative as the element–element combinations. This indicates that while major oxides may provide some insight into adakite fertility, they are not as powerful in classifying adakites compared to trace elements. Moreover, scatter plots involving ratios, such as La/Sm vs. Gd (Figure 5g) and Rb/Sr vs. Hf (Figure 5h), further enhanced the classification performance, though they still lagged behind the most discriminative element–element scatter plots. These results suggest that ratios may capture more nuanced geochemical variations, but their discriminatory power is less consistent and potentially more context-dependent. In contrast, scatter plots involving major oxides vs. major oxides, ratios vs. ratios, and major oxides vs. ratios performed poorly in terms of separating fertile and barren adakites, reinforcing the finding that elemental concentrations, particularly those of REEs, are more effective predictors of fertility.

The results of applying ML models to classify fertile and barren adakites based on geochemical data demonstrate the varying performance of different algorithms. Among the models tested, SVM emerged as the top performer, achieving the highest AUC of 0.91, followed closely by gradient boosting and RF with AUC values of 0.90 and 0.89, respectively. These findings align with existing literature that has highlighted the strength of SVM in handling complex datasets with imbalances, as it effectively maximizes the margin between classes [83]. RF and gradient boosting, known for their ensemble learning approach, also performed well, corroborating their effectiveness in dealing with high-dimensional and heterogeneous data [85,88]. In contrast, the decision tree and AdaBoost models, while providing reasonably strong results, were less robust in distinguishing between fertile and barren adakites, as evidenced by their relatively lower AUC values. This may be attributed to the tendency of decision trees to overfit or underfit based on hyperparameter settings, a challenge that was mitigated in the models with ensemble learning. Logistic regression, the least effective model in this study, struggled to balance precision and recall, resulting in a bias toward predicting barren samples. This underperformance may be due to the linear nature of logistic regression, which might not capture the complex non-linear relationships present in the geochemical dataset.

A crucial observation is the similarity in the model performance between training and test data, indicating that the models have learned to generalize well without overfitting to the training data. For example, SVM achieved an impressive 93.75% prediction accuracy on the test data, correctly identifying 150 out of 160 fertile samples. This consistency suggests that SVM is not overly tuned to the training dataset but has effectively captured the underlying patterns that differentiate fertile from barren adakites. Similarly, RF demonstrated an accuracy of 85% on test data, correctly identifying 136 fertile samples, aligning with its performance during training. The small discrepancies in prediction accuracy between training and test data, such as those observed for gradient boosting (84.4%) and neural networks (84.4%), further confirm that these models generalize well to new, unseen data. These models are robust and capable of providing reliable predictions even when tested on data not seen during the training phase. In contrast, logistic regression’s performance was noticeably weaker on both the training and test sets, with a prediction accuracy of only 53.75%. This suggests that logistic regression may not be suitable for this particular problem, possibly due to the complexity of the relationships [134] between the input features and the fertility of the adakites. The model’s lower precision and recall further reinforce the idea that it struggles to make accurate predictions in the context of imbalanced data. SVM achieved the highest classification performance in distinguishing fertile from barren adakites; however, its effectiveness may vary with geological setting, deposit type, and dataset characteristics. Further validation across diverse mineral systems is needed to assess its generalizability. Future research could explore transfer learning and region-specific model optimization to improve adaptability across deposit types.

While traditional methods will likely remain valuable for many scientific purposes [135], the rapid growth of ML in solid Earth geosciences, though still in its early stages, highlights the need for new strategies and techniques to assess larger geochemical datasets more cost-effectively and efficiently [136,137,138]. There is still much to be done with existing datasets from long-standing data sources, many of which remain largely unexplored [138]. By applying ML models to regional geochemical datasets, exploration can be better targeted, reducing both cost and time associated with traditional methods. Identifying fertile adakites as indicators of porphyry and epithermal mineralization holds particular promise, especially in underexplored regions where conventional techniques may have fallen short. The primary goal of mineral exploration is to distinguish between prospective and non-prospective areas, facilitating the discovery of new sources of raw earth materials. This process involves collecting diverse exploration datasets, transforming them into spatial proxies using the mineral systems approach, and integrating these proxies through robust methodologies. The result is a mineral prospectivity map that highlights potential areas in both greenfield (underexplored) and brownfield (previously explored) environments. In this context, the mineral systems approach is fundamental, focusing on the ore-forming processes outlined in deposit models. It provides a comprehensive, process-driven framework for understanding deposit formation by translating exploration layers into proxies that represent key processes such as source, trigger, transport, trap, deposition, and preservation. Among these, the source plays a pivotal role in driving mineralizing systems. Intrusive units, often seen as key sources of magmatism, hydrothermal fluid circulation, and metal mobilization, are central to mineral deposit formation. However, not all intrusive units are equally fertile. Their fertility can vary depending on factors such as magma source composition, degree of crustal contamination, oxidation state, and magmatic differentiation. By assigning varying weights to these units based on their fertility, it is possible to enhance the accuracy of mineral prospectivity models, reflecting the true mineralization potential of each unit. This paper emphasizes adakites as a critical source in the mineral systems approach and aims to leverage ML techniques to predict their fertility, offering a new approach to refining mineral prospectivity mapping.

6. Conclusions

The key findings of this study are as follows:

• This study demonstrates the efficacy of ML in classifying fertile and barren adakites, highlighting the importance of geochemical assessment prior to utilizing adakitic intrusions as evidence layers in mineral prospectivity mapping;
• Analyzing a dataset of 99 fertile and 66 barren adakites from New Brunswick, this research identifies REEs, including Gd, Dy, and La, with Hf, as the most reliable indicators of fertility, consistently ranking highest across multiple feature selection techniques, including ANOVA, information gain, and ReliefF;
• Among the seven ML models tested, SVM exhibited the best performance, achieving an AUC of 0.91 and a classification accuracy of 93.75%. This was followed by gradient boosting, with an AUC of 0.90, and random forest, which attained an AUC of 0.89;
• These models were subsequently applied to a global dataset comprising 829 adakite samples, predicting fertility patterns. Validation with 160 globally recognized fertile adakites further confirmed the superior predictive accuracy of the SVM model;
• The linear discriminant analysis (LDA) of 1596 scatter plots revealed that element–element relationships (e.g., Ga vs. Dy, Ga vs. Gd, and Pr vs. Gd) and element–major oxide relationships (e.g., Fe₂O₃ vs. Gd and Al₂O₃ vs. Hf) provided the highest discriminatory power, whereas major oxide–major oxide, ratio–ratio, and major oxide–ratio plots were less effective;
• These findings underscore the potential of machine learning-based classification to enhance mineral exploration strategies. It emphasizes that not all intrusive units, including adakites, are inherently fertile and should not be directly used as evidence layers in mineral prospectivity mapping without prior analysis.