Correlation and Knowledge-Based Joint Feature Selection for Copper Flotation Backbone Process Design
Abstract
1. Introduction
2. Preliminaries
2.1. Notations
2.2. Sublabels
2.3. Original Features
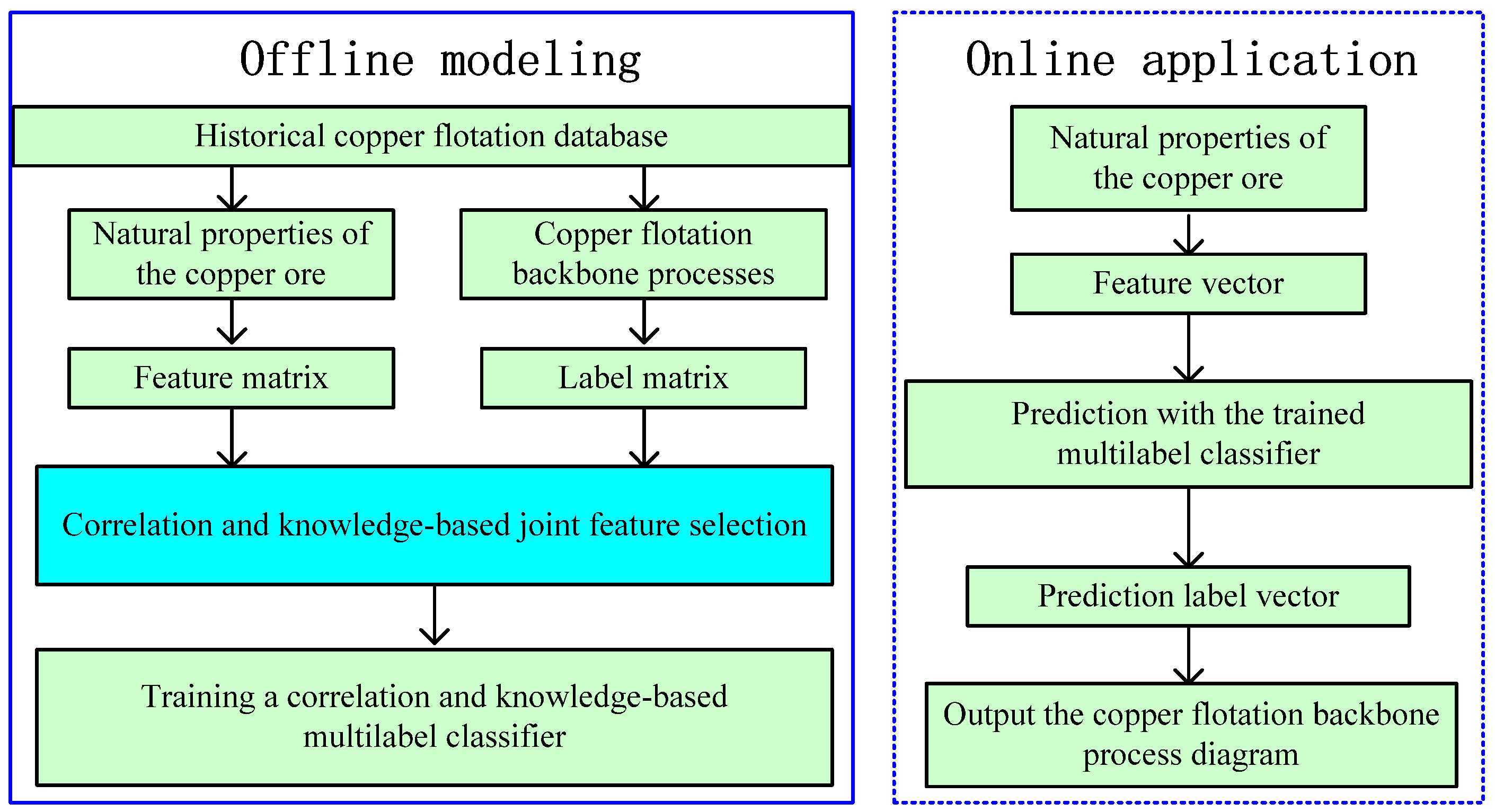
3. Proposed Approach
3.1. Objective Function
3.1.1. Non-Unique Terms
3.1.2. Unique Terms
3.2. Correlation-Based Function
3.3. Knowledge-Based Function
3.4. Optimization via Accelerated Proximal Gradient
| Algorithm 1 Optimization process of CK-JFS |
| Input: training set{X, Y}, hyperparameter λ1, λ2, λ3, λ4, θ, η. Initialization: calculate the matrix C as Equation (7) calculate the diagonal matrix A(1) as Equation (8) calculate the diagonal matrix A(2) as Equation (12) calculate the diagonal matrix D(A1) as Equation (14) calculate the matrix B(1) as Equation (19) calculate the matrix B(2) as Equation (21) calculate the matrix as Equation (35) repeat update Wt as Equation (39) until stop criterion reached Output: W |
4. Experiments
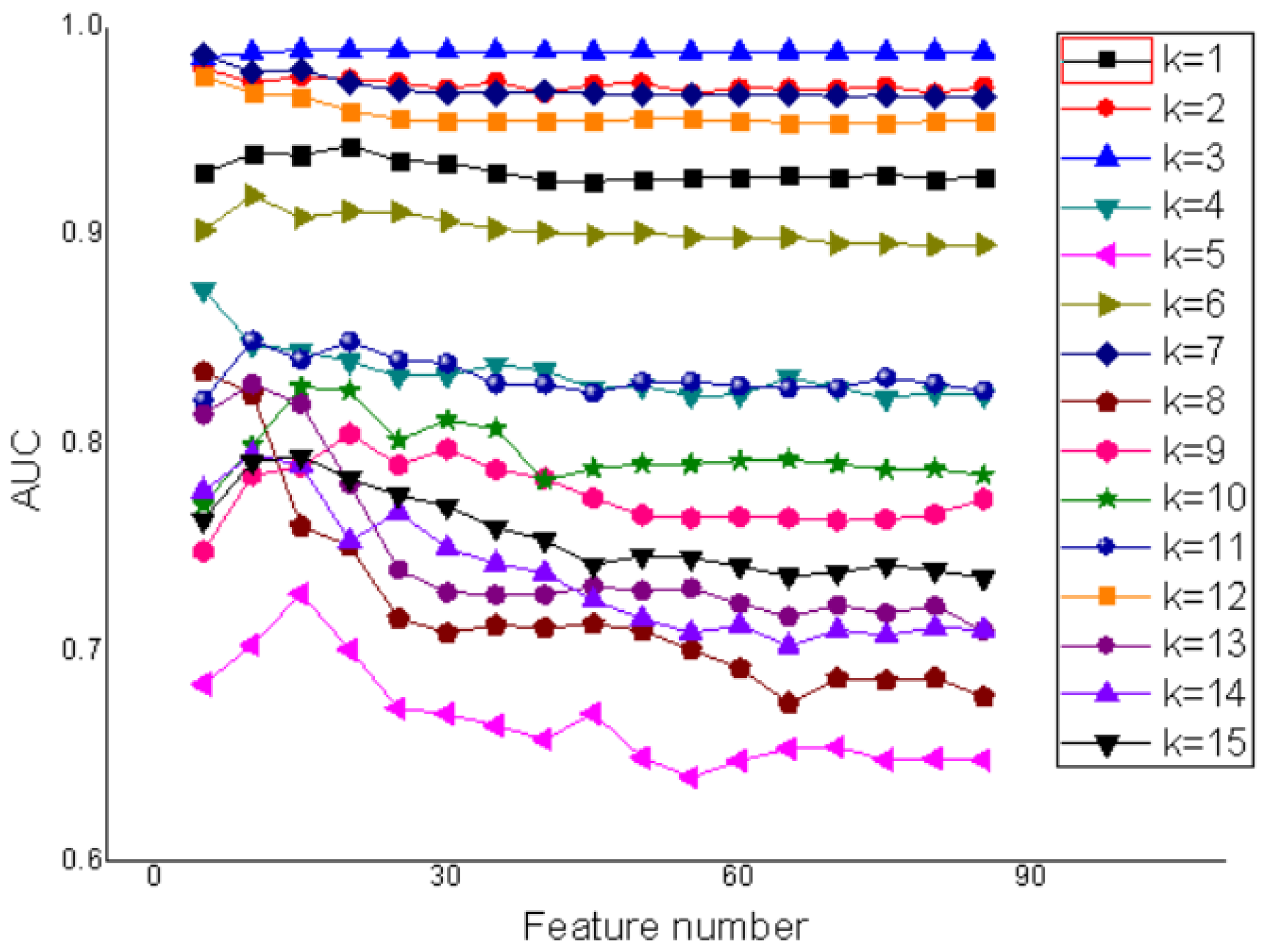
4.1. Label-Specific Feature Selection
4.2. Benchmark Multilabel Feature Selection Algorithm
4.3. Experimental Result
- (1)
- AllFea performs best in 1 case and worst in 51 cases. This is because dimension disasters reduce the performance of the classifier, indicating the necessity of feature selection.
- (2)
- F-score performs best in 1 case and worst in 12 cases. Although the F-score reduces the feature dimensions, it does not use the correlation between labels.
- (3)
- LLSF, JFSC, and C-JFS perform best in two, five, and eight cases, respectively, because they use label correlations; however, they do not use domain knowledge.
- (4)
- K-JFS performs best in 17 cases because it uses domain knowledge, but it does not use label correlation.
- (5)
- The proposed CK-JFS achieves the best performance in 41 cases and is ranked second in 20 cases. This is because the algorithm not only utilizes domain knowledge but also utilizes label correlation. The fusion of data and domain knowledge notably mitigates the reliance on label-specific feature selection on the quantity of training samples, enabling the proposed method to achieve superior performance under small-sample conditions.
- (6)
- Thus, the proposed CK-JFS outperforms the benchmark multilabel feature selection algorithms.
4.4. Hypothesis Test
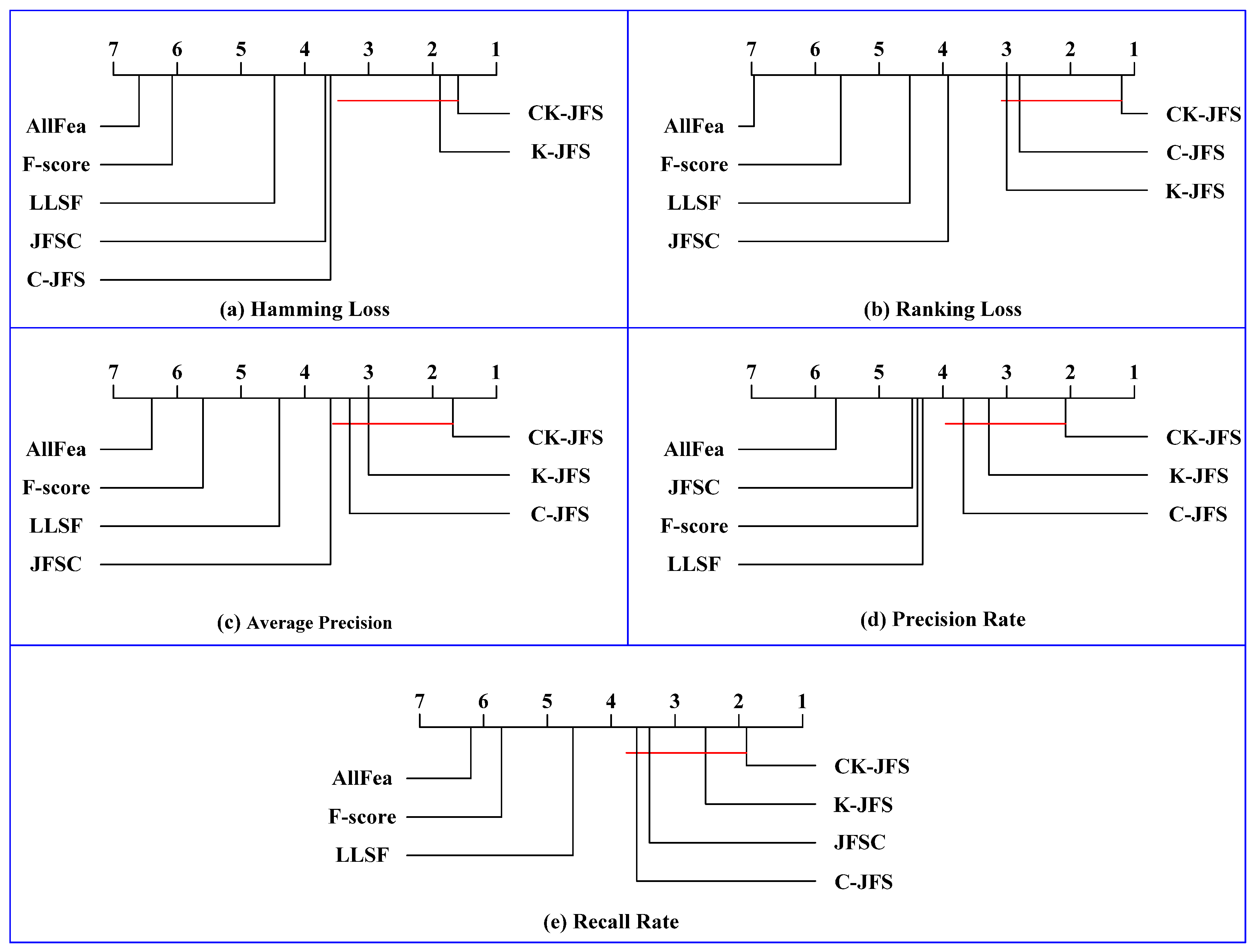
4.4.1. Bonferroni–Dunn Test
- (1)
- The average rankings of the proposed CK-JFS on all metrics are marked on the rightmost side of the axis, indicating that the proposed CK-JFS achieves superior performance over the entire metric to those of the benchmark algorithms.
- (2)
- CK-JFS achieves statistically superior performance to that of the benchmark algorithms AllFea, F-score, and LLSF.
- (3)
- CK-XGBoost does not achieve superior performance to that of JFSC in recall rates, but it achieves superior performance to that of JFSC in the other four metrics.
- (4)
- CK-JFS achieves a superior performance to that of C-JFS in terms of the Hamming loss, but it does not achieve superior performance to that of C-JFS in the other four metrics.
- (5)
- The statistical differences between CK-JFS and K-JFS cannot be proven for all metrics.
4.4.2. T-Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, Q.; Zhang, Y.; Zhang, G.; Han, G.; Zhao, W. A novel sulfidization system for enhancing hemimorphite flotation through Cu/Pb binary metal ions. Int. J. Min. Sci. Technol. 2024, 34, 1741–1752. [Google Scholar] [CrossRef]
- Shen, Q.; Wen, S.; Hao, J.; Feng, Q. Flotation separation of chalcopyrite from pyrite using mineral fulvic acid as selective depressant under weakly alkaline conditions. Trans. Nonferrous Met. Soc. China 2025, 35, 313–325. [Google Scholar] [CrossRef]
- Dong, H.; Wang, F.; He, D.; Liu, Y. The intelligent decision-making of copper flotation backbone process based on CK-XGBoost. Knowl.-Based Syst. 2022, 243, 108429. [Google Scholar] [CrossRef]
- Dong, H.; Wang, F.; He, D.; Liu, Y. Decision system for copper flotation backbone process. Eng. Appl. Artif. Intell. 2023, 123, 106410. [Google Scholar] [CrossRef]
- Siblini, W.; Kuntz, P.; Meyer, F. A Review on Dimensionality Reduction for Multi-label Classification. IEEE Trans. Knowl. Data Eng. 2019, 33, 839–857. [Google Scholar] [CrossRef]
- Dong, H.; Sun, J.; Sun, X.; Ding, R. A many-objective feature selection for multi-label classification. Knowl.-Based Syst. 2020, 208, 106456. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Weng, W.; Zhang, J.; Chen, B.; Wu, S. Feature selection for multi-label learning with streaming label. Neurocomputing 2020, 387, 268–278. [Google Scholar] [CrossRef]
- Liu, J.; Lin, Y.; Li, Y.; Weng, W.; Wu, S. Online multi-label streaming feature selection based on neighborhood rough set. Pattern Recognit. 2018, 84, 273–287. [Google Scholar] [CrossRef]
- Huang, J.; Li, G.; Huang, Q.; Wu, X. Learning label specific Features and Class-Dependent Labels for Multi-Label Classification. IEEE Trans. Knowl. Data Eng. 2016, 28, 3309–3323. [Google Scholar] [CrossRef]
- Zhao, Z.; Morstatter, F.; Sharma, S.; Alelyani, S.; Anand, A.; Liu, H. Advancing Feature Selection Research–ASU Feature Selection Repository; Technical Report; Arizona State University: Tempe, AZ, USA, 2011. [Google Scholar]
- Yu, K.; Yu, S.-P.; Tresp, V. Multi-label informed latent semantic indexing. In Proceedings of the 28th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Salvador, Brazil, 15–19 August 2005; pp. 258–265. [Google Scholar]
- Ji, S.-W.; Tang, L.; Yu, S.-P.; Ye, J.-P. Extracting shared subspace for multi-label classification. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 381–389. [Google Scholar]
- Zhang, M.-L.; Pe, J.M.; Robles, V. Feature selection for multilabel naive bayes classification. Inf. Sci. 2009, 179, 3218–3229. [Google Scholar] [CrossRef]
- Kong, X.-N.; Yu, P.S. Multi-label feature selection for graph classification. In Proceedings of the 2010 IEEE International Conference on Data Mining Workshops (ICDMW), Sydney, Australia, 13 December 2010; pp. 274–283. [Google Scholar]
- Zhang, Y.; Zhou, Z.-H. Multilabel dimensionality reduction via dependence maximization. Knowl. Discov. Data ACM 2010, 4, 14. [Google Scholar] [CrossRef]
- Nie, F.; Huang, H.; Ding, C. Efficient and Robust Feature Selection via Joint L2,1-Norms Minimization. In Advances in Neural Information Processing Systems 23: Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–9 December 2010; Lafferty, J., Williams, C.K.I., Shawe-Taylor, J., Zemel, R.S., Culotta, A., Eds.; Curran Associates, Inc.: San Francisco, CA, USA, 2010; pp. 1813–1821. [Google Scholar]
- Jalali, A.; Sanghavi, S.; Ruan, C.; Ravikumar, P.K. A Dirty Model for Multi-Task Learning. In Proceedings of the Neural Information Processing Systems, Vancouver, BC, Canada, 6–9 December 2010; pp. 964–972. [Google Scholar]
- Kim, S.; Sohn, K.A.; Xing, E.P. A multivariate regression approach to association analysis of a quantitative trait network. Bioinformatics 2009, 25, 204–212. [Google Scholar]
- Pan, S.; Wu, J.; Zhu, X.; Long, G.; Zhang, C. Task sensitive feature exploration and learning for multitask graph classification. IEEE Trans. Cybern 2016, 47, 744–758. [Google Scholar]
- Huang, J.; Li, G.-R.; Huang, Q.-M.; Wu, X.-D. Learning label specific features for multi-label classification. In Proceedings of the IEEE International Conference on Data Mining, Atlantic City, NJ, USA, 14–17 November 2015; pp. 181–190. [Google Scholar]
- Huang, J.; Li, G.-R.; Huang, Q.-M.; Wu, X.-D. Joint Feature Selection and Classification for Multilabel Learning. IEEE Trans. Cybern. 2018, 48, 876–889. [Google Scholar] [CrossRef]
- Zhang, J.; Luo, Z.; Li, C.; Zhou, C.; Li, S. Manifold regularized discriminative feature selection for multi-label learning. Pattern Recognit. 2019, 95, 136–150. [Google Scholar]
- Li, F.; Miao, D.; Pedrycz, W. Granular multi-label feature selection based on mutual information. Pattern Recognit. 2017, 67, 410–423. [Google Scholar]
- Lin, Z.-C.; Ganesh, A.; Wright, J.; Wu, L.-Q.; Chen, M.-M.; Ma, Y. Fast Convex Optimization Algorithms for Exact Recovery of a Corrupted Low-Rank Matrix; UIUC Technical Report UILU-ENG-09-2214; University of Illinois at Urbana-Champaign: Urbana, IL, USA, 2009. [Google Scholar]
- Duda, R.; Hart, P.; Stork, D. Pattern Classification, 2nd ed.; Wiley-Interscience: New York, NY, USA, 2001. [Google Scholar]
- Zhang, M.L.; Zhou, Z.H. ML-KNN: A lazy learning approach to multi label learning. Pattern Recognit. 2007, 40, 2038–2048. [Google Scholar] [CrossRef]
- Elisseeff, A.; Weston, J. A kernel method for multi labelled classification. Adv. Neural Inf. Process. Syst. 2002, 14, 681–687. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees (CART). Biometrics 1984, 40, 358. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Read, J.; Pfahringer, B.; Holmes, G.; Frank, E. Classifier chains for multi label classification. Mach. Learn. 2011, 85, 333–359. [Google Scholar] [CrossRef]
- Demšar, J. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Dunn, O.J. Multiple Comparisons among Means. J. Am. Stat. Assoc. 1961, 56, 52–64. [Google Scholar]
| Feature Grouping | m | Feature Meanings | m | Feature Meanings | m | Feature Meanings | |
|---|---|---|---|---|---|---|---|
| Chemical composition content | 1 | Mo | 2 | Cu | 3 | Pb | |
| 4 | Zn | 5 | S | 6 | Co | ||
| 7 | Fe | 8 | Au | 9 | Ag | ||
| 10 | Mn | 11 | SiO2 | 12 | Al2O3 | ||
| 13 | CaO | 14 | MgO | 15 | K2O | ||
| 16 | Na2O | 17 | C | -- | -- | ||
| Chemical phase analysis | 18 | Molybdenum oxide content | 19 | Molybdenum sulfide content | 20 | Free copper oxide content | |
| 21 | Bound copper oxide content | 22 | Total copper oxide content | 23 | Primary copper sulfide content | ||
| 24 | Secondary copper sulfide content | 25 | Total copper sulfide content | 26 | Lead oxide content | ||
| 27 | Lead sulfide content | 28 | Zinc oxide content | 29 | Zinc sulfide content | ||
| Ore content | 30 | Chalcopyrite | 31 | Bornite | 32 | Chalcocite | |
| 33 | Malachite | 34 | Cuprite | 35 | Tetrahedrite | ||
| 36 | Pyrite and marcasite | 37 | Hematite | 38 | Magnetite | ||
| 39 | Pyrrhotite | 40 | Phosphorite | 41 | Ilmenite | ||
| 42 | Galena | 43 | Sphalerite | 44 | Molybdenite | ||
| Gangue content | 45 | Quartz | 46 | Muscovite | 47 | Biotite | |
| 48 | Feldspar | 49 | Talc | 50 | Calcite | ||
| 51 | Chlorite | 52 | Apatite | 53 | Garnet | ||
| 54 | Kaolinite | 55 | All gangue contents | -- | -- | ||
| Symbiosis relationship | 56 | Molybdenum ore | 57 | Copper ore | 58 | Lead ore | |
| 59 | Zinc ore | 60 | Sulfur ore | 61 | Iron ore | ||
| Particle size | Upper limit | 62 | Molybdenum ore | 63 | Copper ore | 64 | Lead ore |
| 65 | Zinc ore | 66 | Sulfur ore | 67 | Iron ore | ||
| Lower limit | 68 | Molybdenum ore | 69 | Copper ore | 70 | Lead ore | |
| 71 | Zinc ore | 72 | Sulfur ore | 73 | Iron ore | ||
| Proportion of +0.074 mm | 74 | Molybdenum ore | 75 | Copper ore | 76 | Lead ore | |
| 77 | Zinc ore | 78 | Sulfur ore | 79 | Iron ore | ||
| Proportion of −0.074 mm | 80 | Molybdenum ore | 81 | Copper ore | 82 | Lead ore | |
| 83 | Zinc ore | 84 | Sulfur ore | 85 | Iron ore | ||
| k | Optimal Feature Number | Label-Specific Features |
|---|---|---|
| 1 | 17 | [2, 1, 56, 4, 3, 11, 21, 66, 55, 16, 25, 5, 57, 69, 8, 9, 17] |
| 2 | 5 | [3, 2, 26, 5, 22] |
| 3 | 18 | [4, 2, 60, 9, 8, 57, 28, 59, 69, 11, 22, 12, 5, 42, 29, 20, 36, 55] |
| 4 | 5 | [5, 3, 75, 22, 2] |
| 5 | 12 | [5, 3, 13, 25, 24, 78, 45, 8, 2, 75, 72, 1] |
| 6 | 8 | [2, 11, 5, 1, 56, 3, 21, 16] |
| 7 | 6 | [3, 4, 26, 25, 20, 77] |
| 8 | 9 | [5, 2, 77, 59, 29, 3, 20, 36, 69] |
| 9 | 16 | [5, 9, 12, 3, 24, 36, 2, 75, 81, 69, 22, 13, 37, 59, 46, 29] |
| 10 | 13 | [3, 12, 2, 14, 17, 5, 9, 43, 7, 22, 36, 13, 24] |
| 11 | 13 | [2, 74, 5, 16, 12, 25, 9, 14, 55, 1, 3, 72, 8] |
| 12 | 5 | [3, 27, 28, 29, 13] |
| 13 | 11 | [60, 5, 28, 2, 21, 13, 4, 8, 12, 55, 14] |
| 14 | 11 | [5, 12, 9, 4, 25, 3, 24, 2, 20, 75, 63] |
| 15 | 16 | [5, 1, 8, 4, 2, 23, 12, 22, 36, 11, 75, 3, 55, 21, 14, 7] |
| Classifier | DECISION TASK | AllFea | F-Score | LLSF | JFSC | C-JFS | K-JFS | CK-JFS |
|---|---|---|---|---|---|---|---|---|
| MLKNN | Product scheme | 0.1721 | 0.1250 | 0.1042 | 0.0932 | 0.1151 | 0.0877 | 0.0998 |
| Flotation scheme | 0.3648 | 0.3092 | 0.2719 | 0.2463 | 0.2215 | 0.2113 | 0.2251 | |
| Grinding scheme | 0.3675 | 0.3439 | 0.3298 | 0.2368 | 0.2237 | 0.2360 | 0.2123 | |
| MLSVM | Product scheme | 0.1228 | 0.1140 | 0.1162 | 0.1075 | 0.1096 | 0.1009 | 0.0921 |
| Flotation scheme | 0.3136 | 0.2734 | 0.2478 | 0.2332 | 0.2427 | 0.2251 | 0.2018 | |
| Grinding scheme | 0.3614 | 0.3404 | 0.2719 | 0.2342 | 0.2368 | 0.2219 | 0.2026 | |
| CK-JFS | Product scheme | 0.1151 | 0.1228 | 0.1020 | 0.1217 | 0.1031 | 0.0932 | 0.0899 |
| Flotation scheme | 0.2975 | 0.2610 | 0.2558 | 0.2434 | 0.2244 | 0.2135 | 0.1981 | |
| Grinding scheme | 0.3596 | 0.3447 | 0.2623 | 0.2360 | 0.2272 | 0.2272 | 0.1974 | |
| CC-CT | Product scheme | 0.1173 | 0.1184 | 0.0844 | 0.0943 | 0.0976 | 0.0746 | 0.0910 |
| Flotation scheme | 0.2617 | 0.2259 | 0.2222 | 0.2230 | 0.2003 | 0.2230 | 0.2010 | |
| Grinding scheme | 0.3114 | 0.2465 | 0.2333 | 0.2289 | 0.2061 | 0.1904 | 0.1781 | |
| CC-XGBoost | Product scheme | 0.1020 | 0.0987 | 0.1009 | 0.0910 | 0.0866 | 0.0822 | 0.0855 |
| Flotation scheme | 0.2018 | 0.2083 | 0.2003 | 0.1981 | 0.2105 | 0.1879 | 0.1601 | |
| Grinding scheme | 0.2132 | 0.2298 | 0.1956 | 0.1702 | 0.1772 | 0.1456 | 0.1649 | |
| Average ranking | 6.600 | 6.067 | 4.533 | 3.667 | 3.600 | 1.867 | 1.600 | |
| Classifier | Decision Task | AllFea | F-Score | LLSF | JFSC | C-JFS | K-JFS | CK-JFS |
|---|---|---|---|---|---|---|---|---|
| MLKNN | Product scheme | 0.1179 | 0.0736 | 0.0767 | 0.0712 | 0.0731 | 0.0677 | 0.0655 |
| Flotation scheme | 0.2682 | 0.2080 | 0.2013 | 0.2056 | 0.1973 | 0.2027 | 0.1770 | |
| Grinding scheme | 0.2523 | 0.2174 | 0.1966 | 0.2078 | 0.1998 | 0.1814 | 0.1720 | |
| MLSVM | Product scheme | 0.0769 | 0.0778 | 0.0732 | 0.0596 | 0.0667 | 0.0679 | 0.0627 |
| Flotation scheme | 0.2317 | 0.2037 | 0.2068 | 0.2007 | 0.1897 | 0.1921 | 0.1640 | |
| Grinding scheme | 0.2191 | 0.2012 | 0.2099 | 0.2094 | 0.1887 | 0.1787 | 0.1660 | |
| CK-JFS | Product scheme | 0.0756 | 0.0714 | 0.0749 | 0.0676 | 0.0691 | 0.0694 | 0.0637 |
| Flotation scheme | 0.2199 | 0.2085 | 0.2010 | 0.1965 | 0.1962 | 0.1836 | 0.1679 | |
| Grinding scheme | 0.2156 | 0.1959 | 0.1996 | 0.2009 | 0.1839 | 0.1739 | 0.1503 | |
| CC-CT | Product scheme | 0.0727 | 0.0716 | 0.0596 | 0.0641 | 0.0688 | 0.0694 | 0.0587 |
| Flotation scheme | 0.1989 | 0.1985 | 0.1956 | 0.1859 | 0.1757 | 0.1605 | 0.1539 | |
| Grinding scheme | 0.2061 | 0.1879 | 0.1860 | 0.1595 | 0.1550 | 0.1543 | 0.1501 | |
| CC-XGBoost | Product scheme | 0.0693 | 0.0656 | 0.0571 | 0.0592 | 0.0535 | 0.0654 | 0.0577 |
| Flotation scheme | 0.1929 | 0.1852 | 0.1578 | 0.1575 | 0.1471 | 0.1505 | 0.1420 | |
| Grinding scheme | 0.1717 | 0.1652 | 0.1593 | 0.1619 | 0.1474 | 0.1547 | 0.1449 | |
| Average ranking | 6.933 | 5.600 | 4.533 | 3.933 | 2.800 | 3.000 | 1.200 | |
| Classifier | Decision Task | AllFea | F-Score | LLSF | JFSC | C-JFS | K-JFS | CK-JFS |
|---|---|---|---|---|---|---|---|---|
| MLKNN | Product scheme | 0.7525 | 0.8079 | 0.8369 | 0.8180 | 0.8331 | 0.8486 | 0.8417 |
| Flotation scheme | 0.4244 | 0.4355 | 0.4667 | 0.4423 | 0.4422 | 0.4454 | 0.4915 | |
| Grinding scheme | 0.3476 | 0.4322 | 0.4595 | 0.4602 | 0.4582 | 0.4851 | 0.5064 | |
| MLSVM | Product scheme | 0.7994 | 0.7936 | 0.8282 | 0.8593 | 0.8413 | 0.8260 | 0.8480 |
| Flotation scheme | 0.4042 | 0.4354 | 0.4290 | 0.4400 | 0.4946 | 0.4625 | 0.4924 | |
| Grinding scheme | 0.4355 | 0.4490 | 0.4361 | 0.4615 | 0.4781 | 0.4888 | 0.4973 | |
| CK-JFS | Product scheme | 0.8036 | 0.8085 | 0.8376 | 0.8482 | 0.8234 | 0.8229 | 0.8460 |
| Flotation scheme | 0.4360 | 0.4288 | 0.4390 | 0.4453 | 0.4848 | 0.5005 | 0.4925 | |
| Grinding scheme | 0.4310 | 0.4698 | 0.4665 | 0.4733 | 0.4795 | 0.4922 | 0.5370 | |
| CC-CT | Product scheme | 0.8398 | 0.8354 | 0.8458 | 0.8345 | 0.8269 | 0.8332 | 0.8497 |
| Flotation scheme | 0.4438 | 0.4421 | 0.4436 | 0.4614 | 0.4843 | 0.5347 | 0.5499 | |
| Grinding scheme | 0.4410 | 0.4620 | 0.4922 | 0.5019 | 0.5342 | 0.5303 | 0.5329 | |
| CC-XGBoost | Product scheme | 0.8463 | 0.8525 | 0.8715 | 0.8626 | 0.8716 | 0.8373 | 0.8634 |
| Flotation scheme | 0.4653 | 0.5100 | 0.5098 | 0.5662 | 0.5291 | 0.5799 | 0.5522 | |
| Grinding scheme | 0.4952 | 0.5167 | 0.4962 | 0.5000 | 0.5453 | 0.5463 | 0.5712 | |
| Average ranking | 6.400 | 5.600 | 4.400 | 3.600 | 3.333 | 3.000 | 1.667 | |
| Classifier | Decision Task | AllFea | F-Score | LLSF | JFSC | C-JFS | K-JFS | CK-JFS |
|---|---|---|---|---|---|---|---|---|
| MLKNN | Product scheme | 0.9575 | 0.9546 | 0.9467 | 0.9420 | 0.9561 | 0.9406 | 0.9496 |
| Flotation scheme | 0.9317 | 0.9416 | 0.9375 | 0.9372 | 0.9311 | 0.9320 | 0.9442 | |
| Grinding scheme | 0.8907 | 0.9041 | 0.9127 | 0.9126 | 0.9096 | 0.9245 | 0.9213 | |
| MLSVM | Product scheme | 0.9467 | 0.9475 | 0.9523 | 0.9436 | 0.9530 | 0.9527 | 0.9500 |
| Flotation scheme | 0.9334 | 0.9320 | 0.9331 | 0.9316 | 0.9407 | 0.9443 | 0.9395 | |
| Grinding scheme | 0.9130 | 0.9094 | 0.9127 | 0.9133 | 0.9208 | 0.9177 | 0.9335 | |
| CK-JFS | Product scheme | 0.9462 | 0.9538 | 0.9440 | 0.9567 | 0.9524 | 0.9497 | 0.9516 |
| Flotation scheme | 0.9335 | 0.9312 | 0.9373 | 0.9386 | 0.9360 | 0.9373 | 0.9424 | |
| Grinding scheme | 0.9079 | 0.9161 | 0.9164 | 0.9134 | 0.9148 | 0.9356 | 0.9245 | |
| CC-CT | Product scheme | 0.9529 | 0.9585 | 0.9378 | 0.9495 | 0.9544 | 0.9466 | 0.9600 |
| Flotation scheme | 0.9331 | 0.9386 | 0.9411 | 0.9436 | 0.9361 | 0.9563 | 0.9530 | |
| Grinding scheme | 0.9188 | 0.9251 | 0.9227 | 0.9220 | 0.9227 | 0.9252 | 0.9313 | |
| CC-XGBoost | Product scheme | 0.9539 | 0.9530 | 0.9585 | 0.9557 | 0.9536 | 0.9568 | 0.9593 |
| Flotation scheme | 0.9310 | 0.9374 | 0.9439 | 0.9449 | 0.9557 | 0.9535 | 0.9543 | |
| Grinding scheme | 0.9121 | 0.9367 | 0.9293 | 0.9243 | 0.9293 | 0.9189 | 0.9338 | |
| Average ranking | 5.667 | 4.400 | 4.333 | 4.533 | 3.667 | 3.333 | 2.067 | |
| Classifier | Decision Task | AllFea | F-Score | LLSF | JFSC | C-JFS | K-JFS | CK-JFS |
|---|---|---|---|---|---|---|---|---|
| MLKNN | Product scheme | 0.7907 | 0.8688 | 0.9012 | 0.9290 | 0.8785 | 0.9398 | 0.9163 |
| Flotation scheme | 0.6236 | 0.6792 | 0.7240 | 0.7538 | 0.7922 | 0.8048 | 0.7749 | |
| Grinding scheme | 0.6770 | 0.6836 | 0.6937 | 0.7649 | 0.7957 | 0.7541 | 0.8034 | |
| MLSVM | Product scheme | 0.8902 | 0.8997 | 0.8832 | 0.9203 | 0.8918 | 0.8991 | 0.9172 |
| Flotation scheme | 0.6793 | 0.7330 | 0.7616 | 0.7812 | 0.7620 | 0.7657 | 0.8100 | |
| Grinding scheme | 0.6315 | 0.6860 | 0.7241 | 0.7655 | 0.7598 | 0.7875 | 0.7750 | |
| CK-JFS | Product scheme | 0.8997 | 0.8740 | 0.9188 | 0.8723 | 0.8961 | 0.9155 | 0.9185 |
| Flotation scheme | 0.6994 | 0.7473 | 0.7454 | 0.7562 | 0.7838 | 0.7968 | 0.8088 | |
| Grinding scheme | 0.6617 | 0.6735 | 0.7346 | 0.7703 | 0.7888 | 0.7395 | 0.8139 | |
| CC-CT | Product scheme | 0.8785 | 0.8700 | 0.9526 | 0.9138 | 0.9014 | 0.9512 | 0.9049 |
| Flotation scheme | 0.7476 | 0.7701 | 0.7734 | 0.7712 | 0.8156 | 0.7562 | 0.7880 | |
| Grinding scheme | 0.6765 | 0.7411 | 0.7647 | 0.7837 | 0.8092 | 0.8192 | 0.8271 | |
| CC-XGBoost | Product scheme | 0.8949 | 0.9022 | 0.8998 | 0.9126 | 0.9224 | 0.9238 | 0.9164 |
| Flotation scheme | 0.8182 | 0.8018 | 0.8040 | 0.8048 | 0.7729 | 0.8053 | 0.8342 | |
| Grinding scheme | 0.8167 | 0.7534 | 0.8010 | 0.8374 | 0.8249 | 0.8813 | 0.8386 | |
| Average ranking | 6.200 | 5.733 | 4.600 | 3.400 | 3.600 | 2.533 | 1.933 | |
| JFSC | C-JFS | K-JFS | ||
|---|---|---|---|---|
| Hamming loss | tt | 1.8156 | ||
| p-value | 0.0909 | |||
| Ranking loss | tt | 4.7252 | 5.6296 | |
| p-value | 0.0003 | 0.0001 | ||
| Average precision | tt | 3.9182 | 3.1113 | |
| p-value | 0.0015 | 0.0077 | ||
| Precision rate | tt | 3.0950 | 1.8145 | |
| p-value | 0.0079 | 0.0911 | ||
| Recall rate | tt | 3.7129 | 2.8005 | 0.7939 |
| p-value | 0.0023 | 0.0142 | 0.4405 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, H.; Wang, F.; He, D.; Liu, Y. Correlation and Knowledge-Based Joint Feature Selection for Copper Flotation Backbone Process Design. Minerals 2025, 15, 353. https://doi.org/10.3390/min15040353
Dong H, Wang F, He D, Liu Y. Correlation and Knowledge-Based Joint Feature Selection for Copper Flotation Backbone Process Design. Minerals. 2025; 15(4):353. https://doi.org/10.3390/min15040353
Chicago/Turabian StyleDong, Haipei, Fuli Wang, Dakuo He, and Yan Liu. 2025. "Correlation and Knowledge-Based Joint Feature Selection for Copper Flotation Backbone Process Design" Minerals 15, no. 4: 353. https://doi.org/10.3390/min15040353
APA StyleDong, H., Wang, F., He, D., & Liu, Y. (2025). Correlation and Knowledge-Based Joint Feature Selection for Copper Flotation Backbone Process Design. Minerals, 15(4), 353. https://doi.org/10.3390/min15040353






