Towards an Extended Concept of Tolerance Factors for Postspinel Phases

Abstract

It is shown that molar and ionic volumes are linearly related for compounds AB₂O₄ in the spinel-, calcium-ferrate, -titanate, and -manganate structure types at ambient and at high pressure. These relations quantify the concept of ‘chemical pressure’ by relating it to thermodynamic pressure.

1. Introduction

Ratios of ionic radii and tolerance factors [1] have proven useful in material science, solid state chemistry, and mineralogy. These ratios are simple, approximate tools for assessing which compounds potentially assumes what type of structure. Using pressure-dependent ionic radii, the concept can be extended to structures that form at non-ambient pressure and to ‘chemical pressure’, where phases that form under elevated thermodynamic pressure are related to isostructural phases of different compositions. This concept is widely employed in material science and applied physics; for instance, as part of the effort to bring the high-temperature ferromagnetic ordering or superconducting transitions observed at high pressure down to ambient pressure through chemical substitution.

Here, it is attempted to extend the concept of structure–composition tolerance ranges for the important class of compounds AB₂O₄ with an emphasis on those that assume the spinel structure at low and postspinel structures at high pressure. ostspinel structures of compounds AB₂O₄ are in particular, the calciumferrite (harmunite)-, calciumtitanate-, and calciummanganate (marokite)-type structures, which hereafter are abbreviated as CF, CT, and CM types, respectively. These three structures types are closely related: CF- and CT-type are mostly distinguished by the coordination of the A-cation by O²⁻ which is irregular eight-fold in the CF- but 6+2-fold in the CT-type, whereas the CM-type is the result of a Jahn-Teller distortion of the B-centred octahedra of the CT-type [2]. Although not all CF-, CT-, and CM-type AB₂O₄ compounds possess a spinel-type dimorph, the term ‘postspinel’ structures shall be used here as a general header for all three of these closely related structures. A recent review has summarized the current state of research on these phases [2], some of which have important industrial applications, such as in battery materials, exhibit remarkable properties such as metallic behaviour in oxides, or are geochemically important high-pressure minerals [2,3,4,5,6,7]. For instance, (Na,K)AlSiO₄ is a potential main host of alkaline elements in the Earth’s lower mantle [3]

The present paper attempts to find a more quantitative criterion for assessing whether an AB₂O₄ -compound will assume spinel–postspinel dimorphism and to make use of the pressure-dependent crystal ionic radii that have recently become available for a large set of elements [8], rather than using ambient-pressure ionic radii, to assess the structures of phases that form at pressures in the range of tens of GPa.

2. Materials and Methods

All the examined experimental data are for 300 K. Experimental pressures were between ambient and 55 GPa. Postspinel structures (as defined above) were very anisotropic unit cells with two long axes and one very short axis. This causes the ‘dominant zone sampling’ problem in indexation and structure analysis, in particular, for powder diffraction data [9].

Here it is attempted to minimize the risk of involving faulty volumes and structures by preferring (a) single crystal- over powder-diffraction analyses. (b) high-over low-resolution data with respect to both angular and real space resolution, which implies that (c) newer data are generally preferred over elder ones and data obtained by synchrotron or neutron diffraction over in-house diffraction (d) high-pressure data are used only if they were obtained under hydrostatic pressure or at least from samples compressed in neon as pressure-transmitting medium.

Although the AB₂O₄ -spinel structure is very simple, difficulties arise from the more or less pronounced degree of inversion, which affects both volume and any potential assessment that is based on ionic radii: the degree of inversion has to be taken into account because it changes the coordination of a fraction of A and B ions, and thereby, their radii. The present approach accommodates inversion. In addition, data where inversion remains unassessed are omitted.

Instead of ionic radii, crystal radii are used here as the spatial spherical averages of valence electron states [10,11]. Henceforth, the terms ‘radius’ and ‘radii’ are used in the sense of crystal radii, unless otherwise stated. Ambient-pressure radii were taken from [12]. Pressure-dependent radii were taken from [8]. Pressure-dependent radii that were not tabulated in that paper are computed here as r(P) = r_o(1 − (dr/dp)_T·P) where (dr/dP)_T = 0.00329r_o − 0.0010 [8] and P = pressure in GPa; r_o = radius in Å at ambient pressure.

Following the fourth Figure in the work of Akaogi et al. (2024) [2], the A²⁺- and B³⁺- cation radii or the arithmetic middle of the B³⁺ and B⁴⁺ radii, respectively, define the ranges of ratios that are compatible with the CF-, CT-, and CM-type structures. Thereby, the high-pressure postspinel phases of those types exhibit smaller A- and B-radii, while their formation is supported by the contraction of the four-fold-coordinated O-anion, which is stronger than that of the cations [2,8]. Here, the pressure-dependencies of the radii are taken into account and the ionic volume of each compound is calculated as

$${\mathrm{V}\left(\mathrm{P}\right)}_{\mathrm{i}\mathrm{o}\mathrm{n}}={\displaystyle \frac{4\mathsf{\pi }}{3}}[{\mathrm{r}\left(\mathrm{P}\right)}_{\mathrm{A}}^3+2·{\mathrm{r}\left(\mathrm{P}\right)}_{\mathrm{B}}^3+4·{\mathrm{r}\left(\mathrm{P}\right)}_{\mathrm{O}}^3]$$

(1)

where the radii r(P)_A,B,O are the pressure-dependent crystal radii for a given valence and coordination and spin state [8] in spinel- and postspinel-phases.

The coordination of O by a cation in a normal spinel is four-fold, while that of A by O is four-fold, and that of B is six-fold. In the postspinel phases, O is also four-fold-coordinated by the cations, A is eightfold-coordinated by O in CF types but 6 + 2-fold in CT and CM types, and B is sixfold-coordinated by O. However, for fully or partially inverse spinels and for solid solutions, the formula needs to be augmented, e.g., for a spinel (A_0.90B_0.10)(B_0.85A_0.05)₂O₄ in Equation (1), 2r_B³ is substituted by 1.9r_B³ + 0.1r_A³ in six-fold and r_A³ by 0.9r_A³ + 0.1r_B³ in four-fold coordinations (and all radii are functions of P). Furthermore, the spin-state of ions that occur in both high- and low-spin states requires further consideration as, in several cases, the spinel–postspinel transition appears to be driven by pressure-induced high-spin-to-low-spin transitions [13] and as spin state may change upon inversion in spinels. In addition to the pressure-dependent crystal radii, the pressure-dependent electronegativities of Rahm et al. [14] are used here.

3. Results

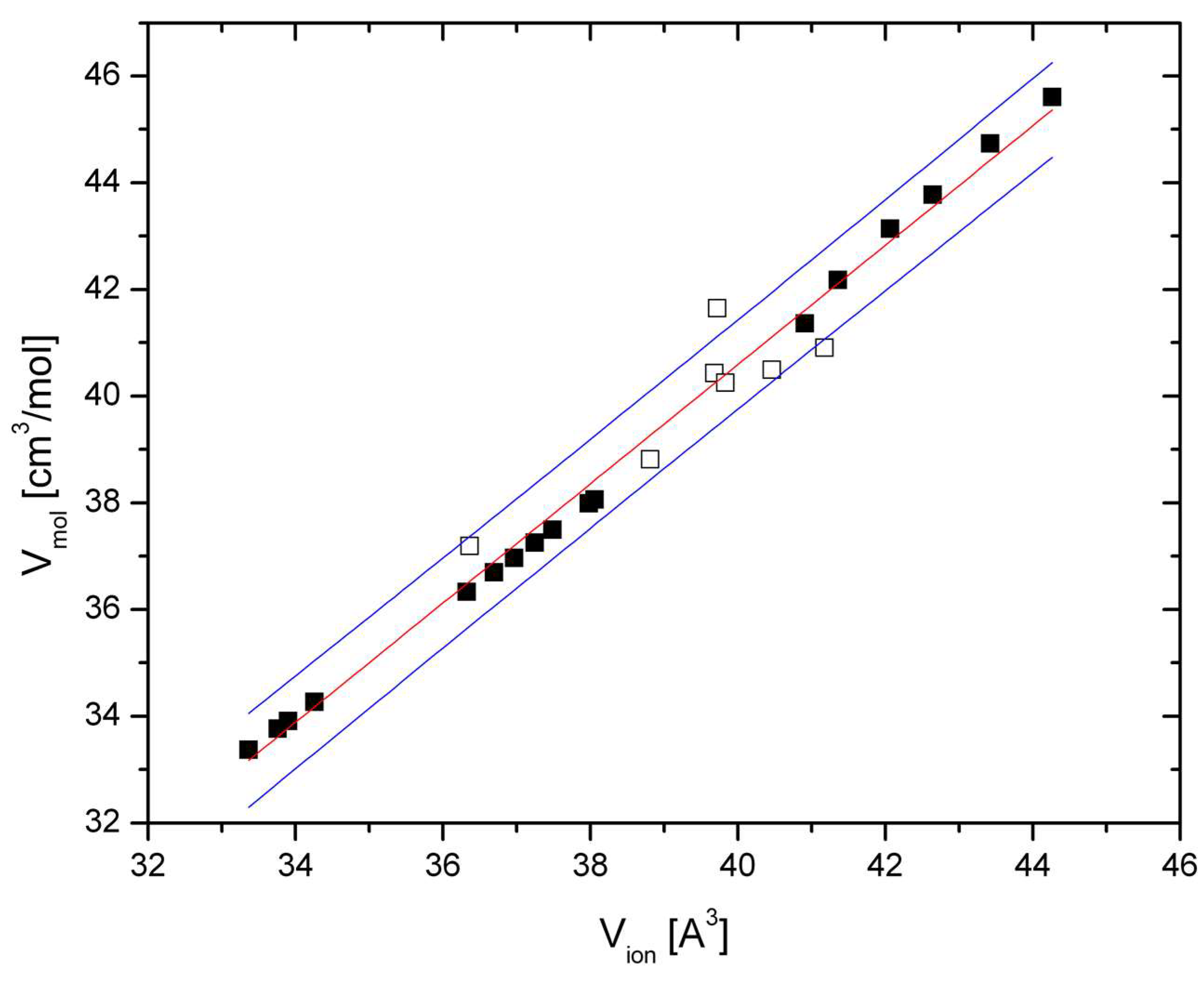
Figure 1 shows the relation between molar and ionic volumes of various spinels at ambient and elevated pressure at 300 K with filled and hollow squares, respectively. The plotted data are given in Table 1. The relation is linear within uncertainties and leads to the following equation:

$$V_{mol}{=2.54\left(13\right)V}_{ion}-50.8\left(4.7\right),$$

(2)

with a R² = 0.919. V_mol is the molar volume in cm³/mol; V_ion is the ionic volume in ų, as defined in Equation (1), but with partial inversion taken into consideration (Table 1).

Linear relations of the type V_mol = A⋅V_ion − V’, where V_mol and V_ion are functions of pressure P, have been reported for the compression of a large number of oxide compounds and also for halides in Tschauner 2024 [15]. In [15], it was observed that the values of A and V’ are very similar for isotopic oxides (e.g., MgO and CaO or corundum and eskolaite; see first figure in [15]) and for structurally related oxides such as bridgmanite and davemaoite [15].

V’ defines a contractive offset volume that results from bond overlap (because V’ would be zero if there were no penetration of the electron distributions of cat- and anions; in [15], V’ was simply described as a contractive ‘void space’). Furthermore, parameter A depends on (V’/V_mol)^3/2 [15] and can be eliminated through the following empirical relation:

$$V_{mol}(P)=N_A{V}_{ion}(P)·\left[0.61\left(2\right){\left({\displaystyle \frac{V^{\prime }}{V_0}}\right)}^{{\displaystyle \frac{3}{2}}}-1.06(9)\right]-V^{\prime }$$

(3)

The correlation given by Relation (2) and Figure 1 in the present paper show that the systematics of compressed oxides hold for spinel-type phases at both ambient and elevated pressure. Within uncertainties, the molar volumes of the compressed spinels chromite, magnesiochromite, and the mineral spinel itself obey the same correlation, with ionic volumes as the various spinel-type phases at 300 K, although chromite and magnesiochromite are slightly but systematically shifted toward lower V_ion (Figure 1). This point is discussed further below. In addition, a slight non-linearity of the ionic volume–molar volume relations is observed for these three spinels below 3 GPa. Non linear relations between ionic and molar volumes have been observed for a large set of oxide compounds [15] for compression data below 2–5 GPa and is discussed in [3,15]. Theoverall linear correlation for spinel-type materials holds for spinels of different compositions, as well as for the same spinel phase under compression to within ±20% of the spinel volumes as a function of crystal ionic radii. Thus, within this range of uncertainty, (2) reflects corresponding states of low- and high-pressure states and, within these limits, it quantifies the concept of chemical pressure. For instance, in this relation spinel (MgAl₂O₄) at 2 GPa corresponds to magnetite at 27 GPa, inverse ulvøspinel at ambient pressure to chromite at 3 GPa etc. (all data given in Table 1). Thus, using pressure-dependent crystal radii and Relation (2) for spinels, the ‘chemical pressure’ of chemical substitution can be related to thermodynamic pressure by means of corresponding states. The strong interaction of chemically bonded atoms in condensed matter implies that this relation comes with an intrinsic uncertainty, beyond the uncertainties of data, caused by the non-ideality of composition–volume relations. In particular, this holds for non-ideal mixing volumes, beyond effects that modify the crystal radii themselves (changes in bond coordination charge transfer, a change in valence electron spin-state or inversion). Based on relation (3), the variation in parameters A and V’ for different isotypic compounds follows its own systematics (see below; Figure 2). For instance, modelling a solid solution between the mineral spinel and magnesiochromite will reflect these changes and, therefore, at least a part of the excess molar volume.

Table 1. Molar and ionic volumes as depicted in Figure 1, Figure 3, Figure 4, and Figure 5. For each compound, the spinel phase is listed above its corresponding postspinel phase. This paper follows the general practice of avoiding ambiguities for polymorphic compounds by using mineral names as identifiers of both structure and composition. For purely synthetic phases, the chemical formula stands here for the spinel phase, unless labels CT or CF indicate the postspinel structure (no other structures are considered here). Prefixes i and n stand for inverse and normal spinel. Pressure is ambient, unless stated otherwise.

Name	Vmol [cm3/mol]	Vion [Å3]
Chromite, FeCr2O4 [16]	44.62	37.46
Xieite, FeCr2O4 [5]	40.32	40.54
Chromite 1 [6]	43.16	37.18
Chenmingite 1 [6]	39.83	40.25
Chenmingite, Endmember [5]	41.64	38.13
Ulvøspinel 2 [7]	44.41	37.67
Tschaunerite 2 [7]	39.69	40.43
Magnetite, 27.4 GPa [13]	40.20	36.0 (mixed spin: 35.58)
Fe3O4-CT, 27.4 GPa [13]	36.88	38.0
Magnesioferrite, 35 GPa [13]	38.39	35.5
MgFe2O4-CF, 35 GPa [13]	35.78	37.84 (mixed spin: 36.71)
Magnesioferrite 3 [4]	45.47	38.3
Maohokite 3 [4]	39.72	41.65
ZnGa2O4, 55 GPa [17]	38.0	34.09
ZnGa2O4-CT [17]	35.53	34.67
CdRh2O4 [18]	49.94	39.57
CdRh2O4-CF [18]	45.26	44.29
CdCr2O4 [19]	47.80	38.8
CdCr2O4-CF [19]	42.81	40.97 4
CuRh2O4 [20]	45.45	38.01
CuRh2O4-CF [20]	44.56	39.07
Manganochromite [21]	45.23	37.69 (inv: 40.31)
MnCr2O4-CF [21]	40.82	41.12 (CT: 37.77)
Coulsonite [21]	45.54	37.82
FeV2O4-CT [21]	41.18	40.9
Magnesiocoulsonite [21]	44.92	38.21 (i, n: 37.42)
MgV2O4-CT [21]	40.46	40.49
LiTiRhO4 [22]	44.935	37.48
LiTiRhO4-CF [22]	42.58	40.84
n-Spinel [23]	39.77	36.52
MgAl2O4-CF [24,25,26]	36.83	38.14
i/n-Spinel, 4 GPa [27]	39.037	35.67
i/n-Spinel, 18.2 GPa [27]	36.891	34.69
ZnFe2O4, 25 GPa [13]	40.50	36.33
ZnFe2O4-CT, 25 GPa [13]	37.12	38.38
ZnFe2O4, 30 GPa [13]	39.83	36.06
ZnFe2O4-CT, 30 GPa [13]	36.44	38.02
MnMn2O4 [28]	42.59	39.67

¹ (Fe²⁺_0.75Mg_0.23Mn_0.02)(Cr_1.60Al_0.29Fe³⁺_0.06Fe²⁺_0.04Ti_0.02)_Σ2.01O₄ [6]. ² (Fe²⁺_0.91Mg_0.06Mn_0.02Ca_0.01) (Fe²⁺_0.83Ti⁴⁺_0.78Fe³⁺_0.22Al_0.09Si_0.05Cr_0.02)O₄ [7]. ³ (Mg_0.62Fe_0.35Mn_0.03)²⁺Fe³⁺₂O₄ [4]. ⁴ for [A] = 6, with [A] = 8 one obtains 43.54 ų. However, the distinction between CT and CF is also one of space group. Present data indicate that the effective bond coordination is rather 6- than 8-fold.

Table 1. Molar and ionic volumes as depicted in Figure 1, Figure 3, Figure 4, and Figure 5. For each compound, the spinel phase is listed above its corresponding postspinel phase. This paper follows the general practice of avoiding ambiguities for polymorphic compounds by using mineral names as identifiers of both structure and composition. For purely synthetic phases, the chemical formula stands here for the spinel phase, unless labels CT or CF indicate the postspinel structure (no other structures are considered here). Prefixes i and n stand for inverse and normal spinel. Pressure is ambient, unless stated otherwise.

Name	Vmol [cm3/mol]	Vion [Å3]
Chromite, FeCr2O4 [16]	44.62	37.46
Xieite, FeCr2O4 [5]	40.32	40.54
Chromite 1 [6]	43.16	37.18
Chenmingite 1 [6]	39.83	40.25
Chenmingite, Endmember [5]	41.64	38.13
Ulvøspinel 2 [7]	44.41	37.67
Tschaunerite 2 [7]	39.69	40.43
Magnetite, 27.4 GPa [13]	40.20	36.0 (mixed spin: 35.58)
Fe3O4-CT, 27.4 GPa [13]	36.88	38.0
Magnesioferrite, 35 GPa [13]	38.39	35.5
MgFe2O4-CF, 35 GPa [13]	35.78	37.84 (mixed spin: 36.71)
Magnesioferrite 3 [4]	45.47	38.3
Maohokite 3 [4]	39.72	41.65
ZnGa2O4, 55 GPa [17]	38.0	34.09
ZnGa2O4-CT [17]	35.53	34.67
CdRh2O4 [18]	49.94	39.57
CdRh2O4-CF [18]	45.26	44.29
CdCr2O4 [19]	47.80	38.8
CdCr2O4-CF [19]	42.81	40.97 4
CuRh2O4 [20]	45.45	38.01
CuRh2O4-CF [20]	44.56	39.07
Manganochromite [21]	45.23	37.69 (inv: 40.31)
MnCr2O4-CF [21]	40.82	41.12 (CT: 37.77)
Coulsonite [21]	45.54	37.82
FeV2O4-CT [21]	41.18	40.9
Magnesiocoulsonite [21]	44.92	38.21 (i, n: 37.42)
MgV2O4-CT [21]	40.46	40.49
LiTiRhO4 [22]	44.935	37.48
LiTiRhO4-CF [22]	42.58	40.84
n-Spinel [23]	39.77	36.52
MgAl2O4-CF [24,25,26]	36.83	38.14
i/n-Spinel, 4 GPa [27]	39.037	35.67
i/n-Spinel, 18.2 GPa [27]	36.891	34.69
ZnFe2O4, 25 GPa [13]	40.50	36.33
ZnFe2O4-CT, 25 GPa [13]	37.12	38.38
ZnFe2O4, 30 GPa [13]	39.83	36.06
ZnFe2O4-CT, 30 GPa [13]	36.44	38.02
MnMn2O4 [28]	42.59	39.67

¹ (Fe²⁺_0.75Mg_0.23Mn_0.02)(Cr_1.60Al_0.29Fe³⁺_0.06Fe²⁺_0.04Ti_0.02)_Σ2.01O₄ [6]. ² (Fe²⁺_0.91Mg_0.06Mn_0.02Ca_0.01) (Fe²⁺_0.83Ti⁴⁺_0.78Fe³⁺_0.22Al_0.09Si_0.05Cr_0.02)O₄ [7]. ³ (Mg_0.62Fe_0.35Mn_0.03)²⁺Fe³⁺₂O₄ [4]. ⁴ for [A] = 6, with [A] = 8 one obtains 43.54 ų. However, the distinction between CT and CF is also one of space group. Present data indicate that the effective bond coordination is rather 6- than 8-fold.

The correlation between parameter A on (V’/V_mol)^3/2 [15] accounts for much of the ±20% deviations from the general relation (2) for spinels that is shown in Figure 1. Thus, Relation (2) provides a measure of the structure-type-specific values of A and V’, while these parameters vary for various compounds with spinel structure. This is shown here for ambient-pressure volume and for compression data of spinel- and postspinel-type phases (filled symbols) in comparison to other oxide compounds (hollow symbols; data from [15]). Figure 2 shows that the correlation between A and (V’/V_mol)^3/2 for spinels and postspinels follows the general trend of oxides [15].

Figure 2. Dependence of parameter A on V’ and molar volume based on a relation provided in [15]. Filled diamonds: Spinels and postspinel phases (Table 2), hollow squares: Data from [15]. A and V’ were obtained through the relation V_mol = A V_ion − V’ [15].

Figure 2. Dependence of parameter A on V’ and molar volume based on a relation provided in [15]. Filled diamonds: Spinels and postspinel phases (Table 2), hollow squares: Data from [15]. A and V’ were obtained through the relation V_mol = A V_ion − V’ [15].

Table 2. Relations V_mol = A·V_ion − V’ [15] between ionic and molar volumes in compressed spinels and postspinels.

Phase	A	V’ [Å3]
Spinel [27,29]	1.57 (1)	16.5 (2)
MgAl2O4-CF [25]	1.62 (3)	12.6 (1.0)
Chromite [16,30]	1.66 (10)	17.4 (3.6)
Magnesiochromite [16]	1.93 (9)	27.1 (3.3)
Harmunite [31,32]	3.13 (3)	58.05 (97)
Marokite [31]	1.14 (12)	5.6 (4.9)
Marokite-CT [31]	0.52 (6)	17.7 (2.3)
CaTi2O4 [31]	1.24 (5)	9.4 (2.2)

Table 2. Relations V_mol = A·V_ion − V’ [15] between ionic and molar volumes in compressed spinels and postspinels.

Phase	A	V’ [Å3]
Spinel [27,29]	1.57 (1)	16.5 (2)
MgAl2O4-CF [25]	1.62 (3)	12.6 (1.0)
Chromite [16,30]	1.66 (10)	17.4 (3.6)
Magnesiochromite [16]	1.93 (9)	27.1 (3.3)
Harmunite [31,32]	3.13 (3)	58.05 (97)
Marokite [31]	1.14 (12)	5.6 (4.9)
Marokite-CT [31]	0.52 (6)	17.7 (2.3)
CaTi2O4 [31]	1.24 (5)	9.4 (2.2)

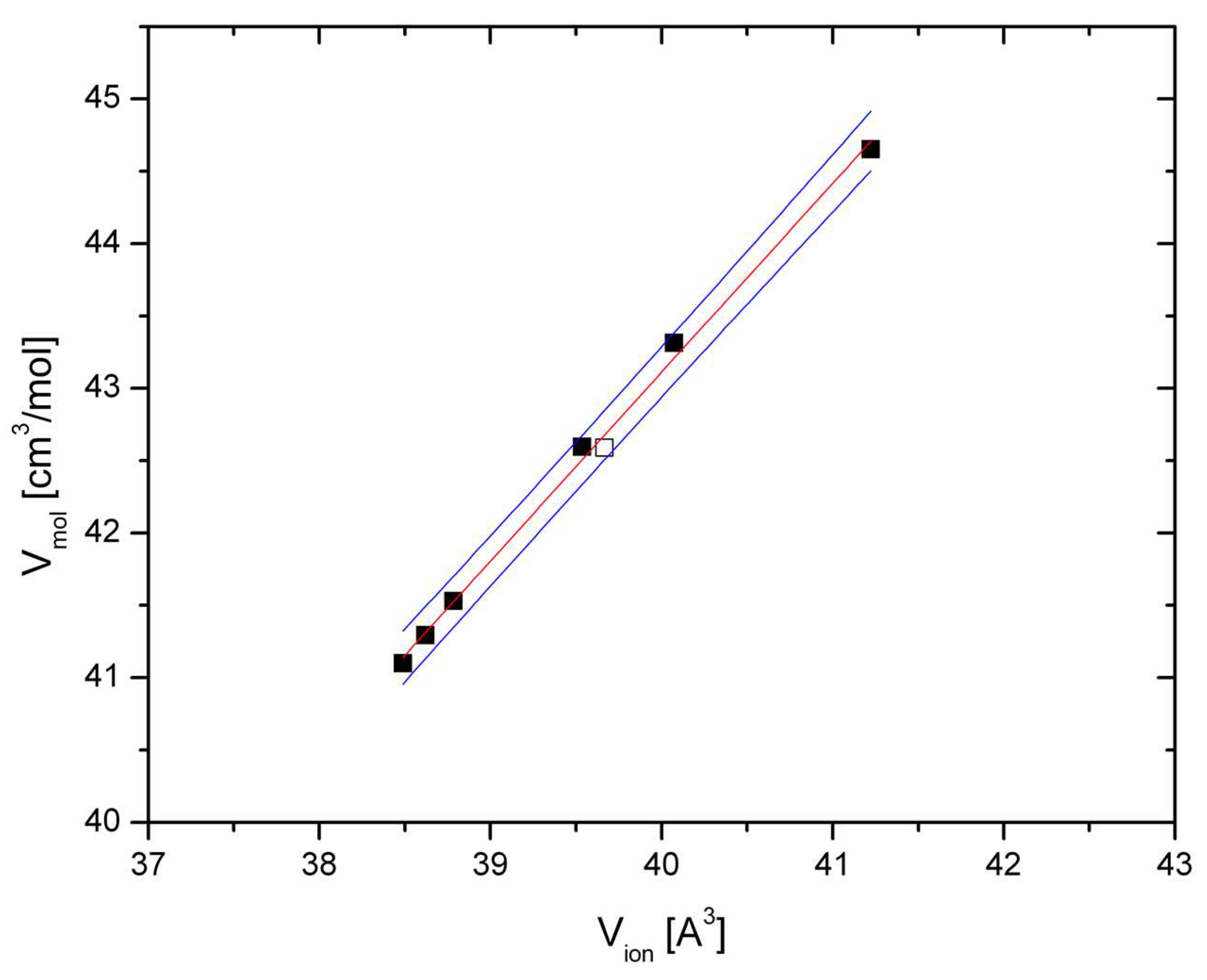
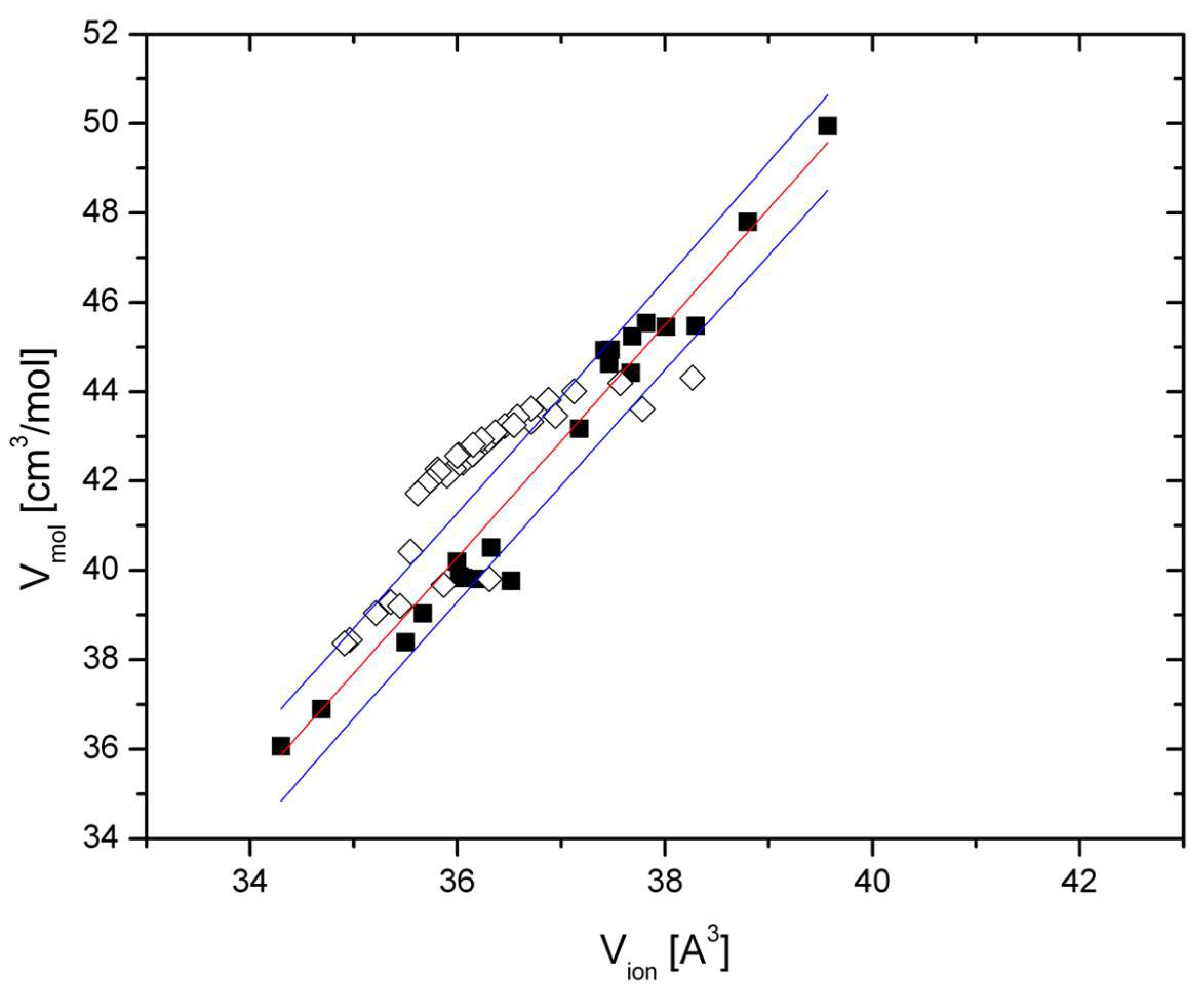
It was found that equivalent relations of the type V_mol = A·V_ion − V’ [15] also hold for the postspinel phases. Figure 3, Figure 4 and Figure 5 show the relation between ionic and molar volume for CT-, CM-, and CF-type phases, where ambient pressure volumes are indicated by hollow symbols and high-pressure volumes are indicated by filled symbols. The relations were fitted as follows:

$$V_{mol}{=1.136\left(17\right)V}_{ion}-4.85\left(65\right),$$

(4)

for CT-type, and

$$V_{mol}{=1.305\left(33\right)V}_{ion}-9.1\left(1.3\right),$$

(5)

for CM-type, and

$$V_{mol}{=1.710\left(77\right)V}_{ion}-30.2\left(3.2\right)$$

(6)

for CF-type postspinels, with R² = 0.996, 0.996, and 0.976, respectively. As in the case of spinels ‘chemical pressure’ is quantifiable through Relations (4)–(6): for instance the V_ion and V_mol for CF-type CdCr₂O₄ at ambient pressure and harmunite (CaFe₂O₄) at 8.7 GPa plot at about the same point in Figure 3, and so do the values for MnCr₂O₄ at ambient and harmunite at ~23 GPa pressure, further CT-type FeV₂O₄ and CaTi₂O₄ at ~30 GPa, CT-type MgAl₂O₄ recovered to ambient conditions [24,26] and the high-P CT-type phase of marokite (CaMn₂O₄) around 50 GPa, CM-type Mn₃O₄ [28] at ambient and marokite at 11 GPa pressure. It is noted that the small deviations of individual data from Relations (4) to (6) as compared to Relation (2) are in part owed to the statistical weight of compression data (Figure 3, Figure 4 and Figure 5). It is worth noting that the much smaller deviations in the individual data from Relations (4)–(6) as compared to (2) are in part due to the higher statistical weight of the compression data (Figure 3, Figure 4 and Figure 5).

The relation V_ion∝V_mol of the high-pressure phase of CaFe₂O₄ (Figure 4) obeys a somewhat different slope than that of the other CF-type phases while its highest-pressure–volume point for this phase falls quite onto the general V_ion∝V_mol relation. The formation of this phase is assigned toa high-spin-to-low-spin transition of Fe³⁺ [32] and it seems plausible that, up to that pressure Fe³⁺ assumes a mixed-spin state in this phase, such as it has been reported for other postspinel phases of ferrites [13]. Here, no correction for the mixed-spin state is applied. Accordingly, the compression data from [13] are not included in Figure 3 and Figure 4 because the ionic volume has to be adjusted for the gradual spin change, which makes it no independent support of the observed correlations. For each of these postspinel ferrites, one high-pressure data point is provided in Table 1 for reference.

Figure 3. Molar volume of CT-type postspinels (Table 1) at ambient and elevated pressures (hollow and filled squares, respectively). Data are taken from Table 1 and References [25,31]. All volumes were measured at 300 K. Red line: Fitted Relation (4); blue lines are 90% prediction bands.

Figure 3. Molar volume of CT-type postspinels (Table 1) at ambient and elevated pressures (hollow and filled squares, respectively). Data are taken from Table 1 and References [25,31]. All volumes were measured at 300 K. Red line: Fitted Relation (4); blue lines are 90% prediction bands.

Figure 4. Molar volume of CM-type postspinels: marokite between ambient pressure and 30 GPa (filled squares), and CM-type Mn₃O₄ at ambient pressure (hollow square). Data were taken from Table 1 and Reference [31]. All volumes were measured at 300 K. Red line: Fitted Relation (5); blue lines are 90% prediction bands.

Figure 4. Molar volume of CM-type postspinels: marokite between ambient pressure and 30 GPa (filled squares), and CM-type Mn₃O₄ at ambient pressure (hollow square). Data were taken from Table 1 and Reference [31]. All volumes were measured at 300 K. Red line: Fitted Relation (5); blue lines are 90% prediction bands.

Figure 5. Molar volume of CF-type postspinels at ambient and elevated pressure (hollow and filled squares, respectively). Data were taken from Table 1 and References [31,32]. All volumes were measured at 300 K. Red line: Fitted Relation (6); blue lines are 90% prediction bands.

Figure 5. Molar volume of CF-type postspinels at ambient and elevated pressure (hollow and filled squares, respectively). Data were taken from Table 1 and References [31,32]. All volumes were measured at 300 K. Red line: Fitted Relation (6); blue lines are 90% prediction bands.

4. Discussion

Overall, Figure 2, Figure 3 and Figure 4 and fit Equations (3)–(5) show that, for the relations V_mol = A·V_ion − V’ [15] (a) the slopes A and the V’ are different for all three postspinel structure types, with their parameters A being markedly smaller than that of spinel in the sequence A(CF) > A(CM) > A(CT) and A(CF) ~ 2/3 times A(Sp). (b) Their V’ relate\ to each other and to that of spinel, approximately as V’(CM):V’(CT):V’(CF):V’(Sp) ~ 1:2:6:8.5.

As mentioned above, V’ defines a contractive offset volume that results from bond overlap and above relation of the magnitudes of V’ for spinel and postspinel structures is a measure of ‘ionicity’ of the average bonds for each of these structure types. Higher values of V’ correspond to more overlap; that is, a lower ‘ionicity’ of all bonds on average. Once more, it is stressed that the uncertainty of V’ is not primarily a consequence of less than perfect data, but of the intrinsic limitations to the concept of corresponding states in strongly bonded condensed matter. Clearly, for a given structure type, ‘ionicity’ varies with composition and directional differences result in deviations from the average V’ even in terms of the spatial average.

The relation of A to (V’/V_mol)^3/2 for spinels and postspinels shows these types of oxide structures to have pronounced ionic bonding compared to borates, silicates, alumo-, and beryllosilicates, which is not a new finding but finds an approximate quantification through Figure 2 and Equation (3). Taking a closer look at spinel and postspinel oxides, their values of A and V’ indicate that the postspinel phases exhibit less bond–electron overlap than spinels with an approximate sequence from stronger to lesser overlap: spinel > CF > CT > CM. It is noted here that the relation between V_ion∝V_mol appears to be linear for isotypic compounds with anions other than oxides, but with A and V’ following a different functional relation. This has been shown in [15], at least for B1- and B2-type oxides and halides, as the one class of solids where compression data over extensive pressure ranges are available for compounds with different anions.

Equations (2)–(5) and Figure 1, Figure 3, Figure 4 and Figure 5 define relations between thermodynamic and ionic volumes; thus, they allow thermodynamic volume to be computed for a given composition and pressure, although only within noticeable uncertainties, because individual phases deviate from the generic structure-related parameters A and V’ of those relations, as is evident from Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5.

However, the concept of assessing relative stability of structures through tolerance-factors and radii ratios stretches beyond such volume relations. Thus, in a next step, these relations are implemented into estimates of free energy. Here, the recently assessed pressure-dependent total ionization energies (‘electronegativities’ χ) of elements [14] are used to calculate ΔH(P) as Δχ = χ_i + χ_j +χ(O) [14], where χ_i,j are the electronegativities of the cations i,j, and χ(O) is the electronegativity of oxygen; all values are pressure-dependent and negative at ambient pressure [14], such that, for stable bonds, ΔH(P) = Δχ < 0. This concept of pressure-dependent electronegativity is consistent with that of pressure-dependent crystal radii. It is noted that the estimates of ΔH(P) thus obtained are strictly valid for low temperature only (T close to 0 K); furthermore, no high level of accuracy is expected when estimating F, for the same reasons as indicated above for the uncertainties of the relations V_ion ∝ V_mol.

The proposed relation is, therefore, between V_mol(P) = A V_ion(P) − V’ and Δχ(P), and a comparison of this relation for different isochemical structures, such as spinel and postspinel phases, gives a pressure at which one structure becomes favourable over the other at T close to 0 K. The salient point is that, within this approximation, V_mol(P) does not need to be measured, nor is it required as a constraint, such as in self-consistent electron density functional calculations. Instead, V_mol(P) is computed based on ionic volumes. This approach is a quantitative extension of the assessment of structure stability by means of ionic radii and as a potential tool for predicting structures of compounds at any pressure. As is shown here, this approach does not work well, mainly because of the variability of V’. Two examples are discussed here: Mg₂SiO₄ and MgAl₂O₄. The reason for this choice is the absence of charge-transfer or changes in spin state in these compounds, their importance in Earth science, and the availability of extensive experimental data for both of them.

Figure 6 shows the same relation for Mg₂SiO₄ for forsterite, ringwoodite, periclase + bridgmanite, and forsterite-III (CT- type Mg₂SiO₄). For each compound, the relations V_mol(P)∝Δχ(P) closely resemble Rydberg-potential curves (which is expected based on the underlying concepts of the radii and the computation of χ(P) [14]). The sequence of transitions with increasing pressure is predicted correctly as forsterite → ringwoodite → periclase + bridgmanite. Two values of A and V’ are used for ringwoodite: the values from Equation (2) and the values obtained directly from the relation V_ion∝V_mol for ringwoodite [15] (also plotted in Figure 2). Clearly the different sets of A and V’ shift the enthalpy–volume relation significantly. This results in markedly different transition pressures: 30 GPa based on the values from [15] but 48 GPa based on the average A and V’ for spinels (Equation (2)). These values correspond to low temperature close to 0K. In the actual phase diagram, wadsleyite is intermediate between forsterite and ringwoodite at 12–16 GPa, interpolated to 0 K. Thus, the material-specific values A and V’ predict the transition closer to observation. However, the decomposition ringwoodite → bridgmanite + periclase is predicted to occur at 86 GPa or 56 GPa respectively; which both values are notably higher than the interpolated measured boundary (~ 28 GPa). The intersection of the V_mol(P) ∝ Δχ(P) curves of forsterite and bridgmanite + periclase occurs at 25 GPa. The CT-type phase is predicted to become stable relative to forsterite at 27 GPa. Finkelstein et al. [33] observed a monoclinic modification of this structure (there labelled as ‘inverted CT-type’ because Mg assumes the B-site in this CT-type phase [33]) that occurs above 48 GPa 300 K, and vitrifies upon release to below 12 GPa, which, on average, gives a transition pressure of 30 GPa 300 K. This is not far from the predicted transition and suggests that the proposed relation between calculated V_mol(P) and Δχ(P) assesses low-temperature pressure-induced transitions better than the interpolated boundaries of transitions, which involve significant thermal energy. In any case, the variations in A, and particularly V’, cause significant variation in the predicted transformation pressures.

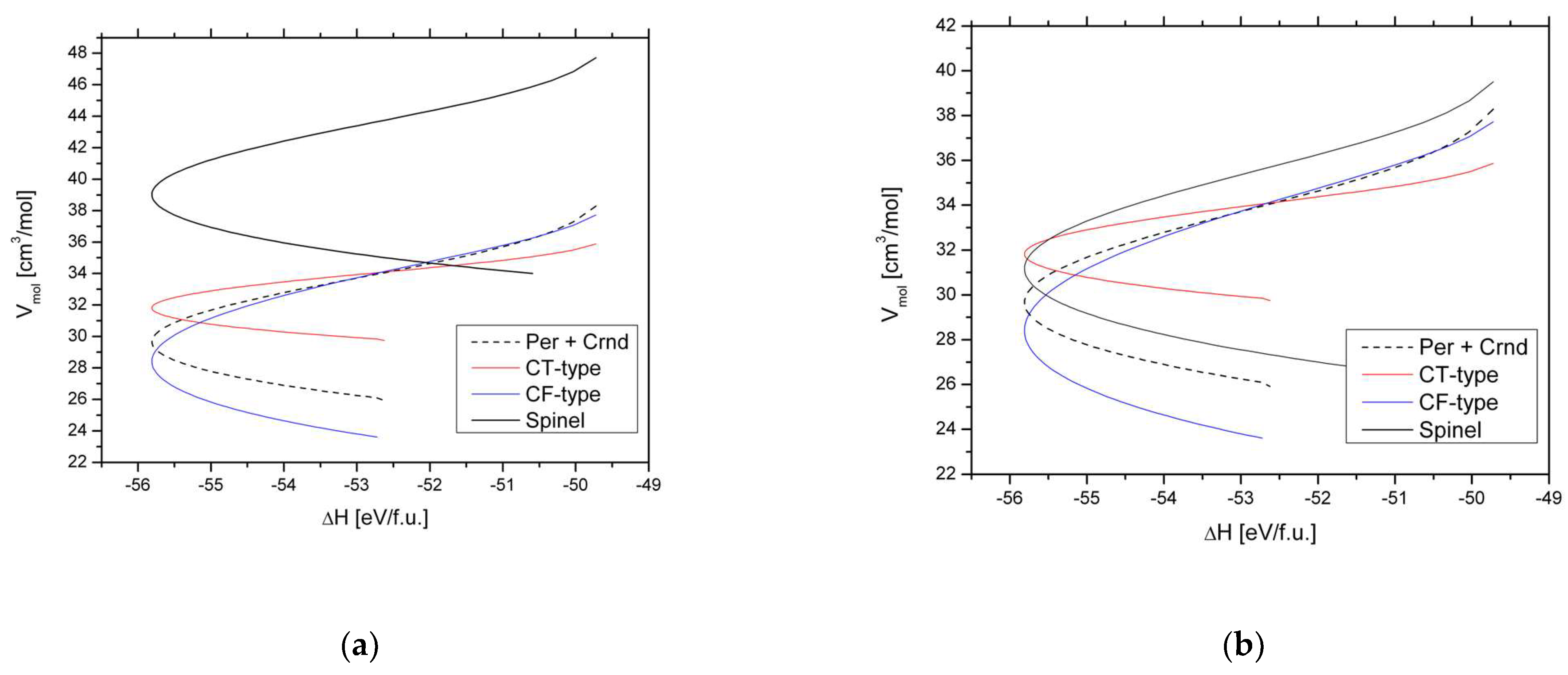
Figure 7a,b show the relation between V_mol(P), calculated as A V_ion(P) − V’ and Δχ(P) for spinel (MgAl₂O₄), CF- and CT-type MgAl₂O₄, and periclase + corundum (MgO + Al₂O₃). The relations indicate spinel to be stable at low pressure. Negative pressure (which can be treated as equivalent to high temperature) favours decomposition. CF- and CT-type MgAl₂O₄ are predicted to gain over spinel at high pressure, as observed in experiments. With A and V’ = 1.57 and 16.5 (Table 2) for the spinel-type phase, the sequence of the observed phase boundaries interpolated to 0 K is as follows: spinel → periclase + corundum (15 GPa) → CF-type (32 GPa) → CT-type (~65 GPa). However, with the average A and V’ from Equation (2), the predicted transition sequence is spinel → CT-type (46 GPa) → periclase + corundum (54 GPa), at the pressure where the latter function also intersects with that of the CF type, which becomes energetically unfavourable over the oxides at slightly higher pressure.

Hence, the correlation between A V_ion(P) − V’ and Δχ(P) does not provide a good prediction of the pressures of phase-transformations, at least not for spinels and with using A and V’ value averages for the structure types. The two cases, SiMg₂O₄ and MgAl₂O₄, suggest that the use of A and V’ values of specific compounds improves the assessment of transition pressures and that, eventually, a library of values can be obtained, as in [15]. However, this is not the generic tool of structure predictions that promises a more quantitative assessment of structure stability based only on ionic radii.

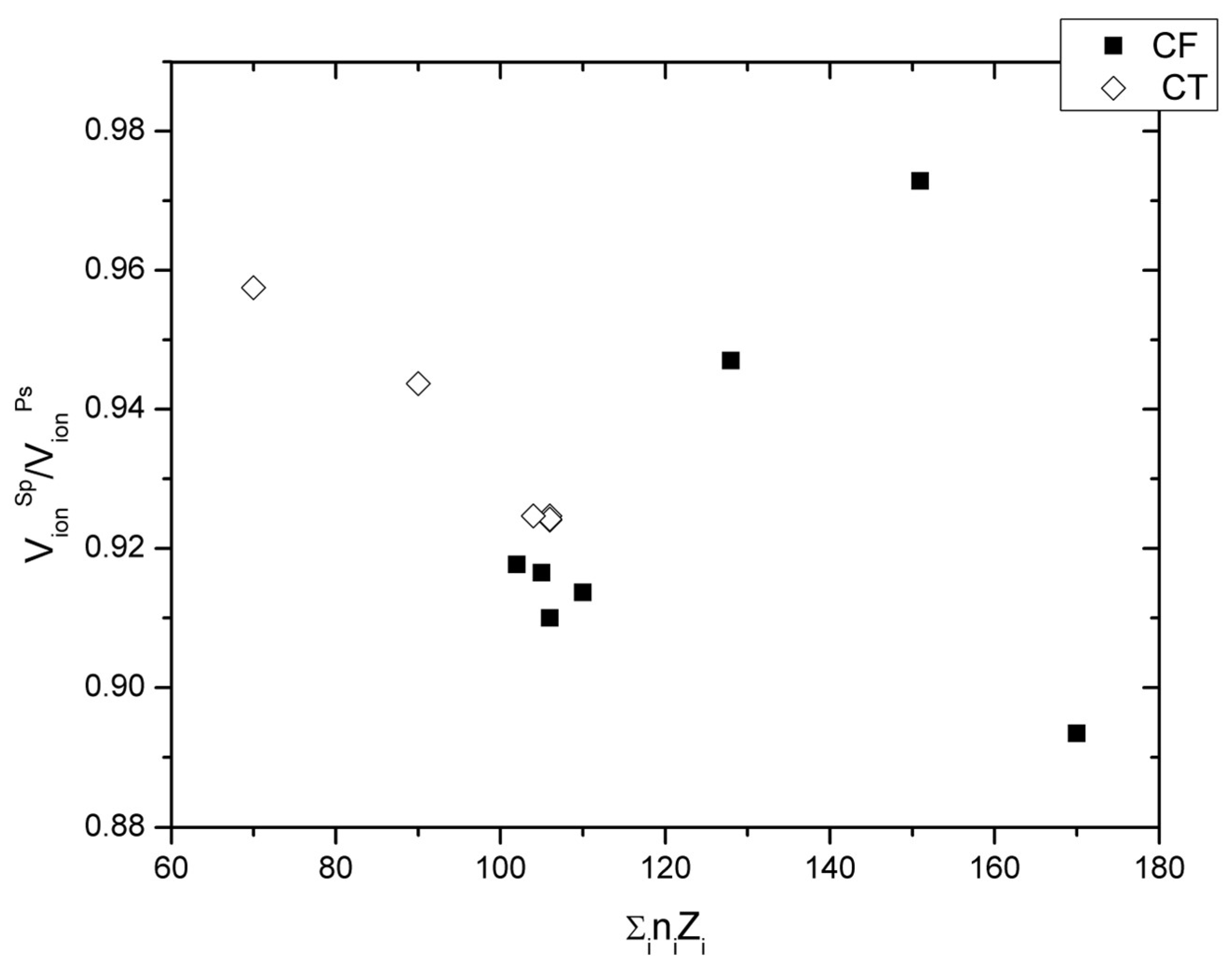
Finally, another extension of the concept of ionic radii ratios as a relative measure of structure type stability is noteworthy: instead of ratios of radii, the ratios of the total ionic volumes are considered. Based on what was said above in the context of the relations of molar and ionic volumes, it is expected that V_ion^Sp/V_ion^PS is smaller than unity. In fact, it was found to range between 0.89 and 0.99 for spinel and postspinel phases at ambient pressure (Figure 8). This range is not as small as by a total variation of ±5% may appear. For comparison, the ratio of V_ion^Sp over the sum of V_ion of the decomposition oxides AO + B₂O₃ covers a much narrower range of 0.94 to 0.97. In Figure 8, the ratio of spinel and postspinel ionic volumes is shown as function of the total nuclear charge number Σ_i n_iZ_i, which is the sum of the Z of each chemical species i multiplied by its stoichiometric factor n_i.

The correlation between Σ_i n_iZ_i and those ratios provides a relative measure of ground state energies based on coordination, valence, and stoichiometry, thereby abstracting from the actual structural configurations. V_ion^Sp/V_ion^PS follows a V-shaped relation with Σ_i n_iZ_i, where CT-type phases establish the left side of the V (=small Σ_i n_iZ_i) and the CF-type phases the right one (=large Σ_i n_iZ_i), both overlapping at values of Σ_i n_iZ_i between 100 and 110 and with an offset in ratios of V_ion^Sp/V_ion^PS of ~0.925 for CT- and between 0.91 and 0.92 for CF-type phases, in agreement with Equations (2)–(4). The heaviest of all compounds, CdRu₂O₄, gives a markedly lower V_ion^Sp/V_ion^PS, suggesting a second minimum in this functional relation. Based on this relation, compounds with 100 < Σ_i n_iZ_i < 120 and above ~160 are expected to favour postspinel- over spinel structures, because they represent minima in this functional relation; and this is the relative stability that has been observed, indeed [2]. Moreover, based on Figure 8, the CF type is favoured over the CT type for larger Σ_i n_iZ_i, reflecting the tendency of high-Z ions to assume higher coordination. Thus, in sum intermediate and high Σ_i n_iZ_i favours postspinels over spinels, with postspinel-phase formation pressures decreasing with increasing Σ_i n_iZ_i, consistent with observation [2]. It is suggested here that, for a given pressure, this ionic volume ratio varies only within certain bounds, beyond which either spinels or postspinel phases do not form. However, a sufficient set of volumes for testing this relation is available only at ambient pressure.

5. Conclusions

The present paper assesses types of AB₂O₄ structures in terms of their pressure-dependent crystal radii. The relation between molar and ionic volumes of spinel- and postspinel phases was found to be linear, of the type V_mol(P) = A V_ion(P)−V’, and to hold at ambient and elevated pressures. Thus, these relations establish corresponding states between isostructural phases of different compositions, and thereby quantify the concept of ‘chemical pressure’ by relating it to thermodynamic volume. This relation can be used as a constraint for more sophisticated calculations and for synthesis experiments of novel materials, such as in the class of AB₂O₄ compounds. However, these linear relations hold only to ±10% for postspinel-type phases and to ±20% for spinel-type phases. These deviations are further quantified by observing both spinels and postspinels to obey a more general dependence of A, by (V’/V_o)^3/2, which relation has been observed previously for a large number of compounds with O as the constituent anion. This relation shows both oxide spinels and postspinels as rather ionically bonded compounds (exhibiting low to modest bond electron overlap) than silicates, borates, and other typical covalent oxides. V’ is a measure of spatially averaged but structure-type-specific overlap of bond electrons in (‘ionicity’), where higher values correspond to more overlap, that is: lower ‘ionicity’ of all bonds in average. For spinels and postspinels, V’ relates approximately as V’(CM):V’(CT):V’(CF):V’(Sp) ~ 1:2:6:8.5. It is found that individual compounds deviate significantly from these purely structure-specific values A and V’; where part of the compound-specific deviations are accounted for by the general corelation between A and (V’/V_o)^3/2.

In a second step, the ~0 K formation enthalpies of AB₂O₄ compounds were estimated based on pressure-dependent total ionization energies and correlated with the thermodynamic volumes calculated from the relations between ionic and molar volumes. The functional relations provide phase transformation sequences at 0 K, which, however, largely overestimate the transformation pressures for most of the transitions based on interpolated empirical boundaries. While such extremely simple energy-calculations are not expected to provide accurate pressures or compete with more sophisticated computations, the present findings discourage hopes of finding a computationally cheap predictive tool that provides both volumes and plausible structures for any given oxide composition and pressure (density functional theory requires realistic volumes and structures as input, genetic algorithms require volumes).

The ratios of the ionic radii of spinels and their postspinel dimorphs relate to the total nuclear charge number Σ_i n_iZ_i in an interesting way, suggesting that those ratios are never beyond certain bounds for a given Σ_i n_iZ_i. It is proposed that this relation, as well as the molar–ionic volume relations for postspinels, serve as constraints for volume assessments of initial structure models in structure analyses, although specific instances that shift the volumes beyond those limits, such as the onset of disorder in weakly metastable phases, must be considered.

Thus, the present results show that, within uncertainties in the 10%–20% range, thermodynamic volumes can be constrained based on ionic volumes only and provide structure-related measures of spatially averaged bond ionicity. Hence, the ‘ionic volume’ concept can serve towards establishing a taxonomy of structures according to their bond character.