Unlocking Subsurface Geology: A Case Study with Measure-While-Drilling Data and Machine Learning
Abstract
1. Introduction
2. Methods
2.1. Mine Site
2.2. Geological Qualities from Geophysical Measurements
2.3. MWD Systems
MWD Data Pre-Processing
2.4. Feature-Importance-Based Methods
2.5. Regression-Based ML Methods
3. Results
3.1. Feature-Importance-Based Results
3.2. Regression-Based ML Analytical Prediction Results
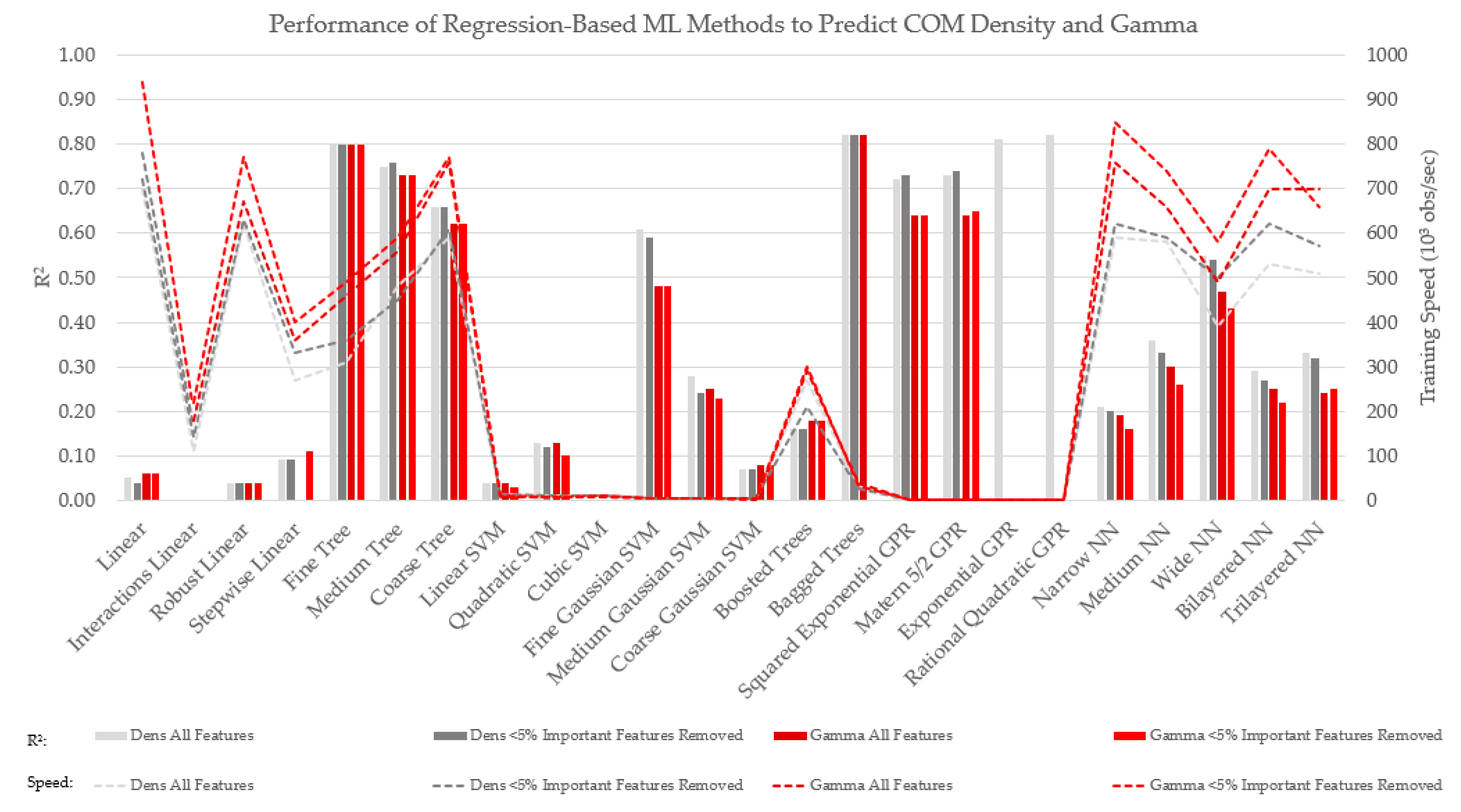
3.2.1. Density and Gamma Prediction
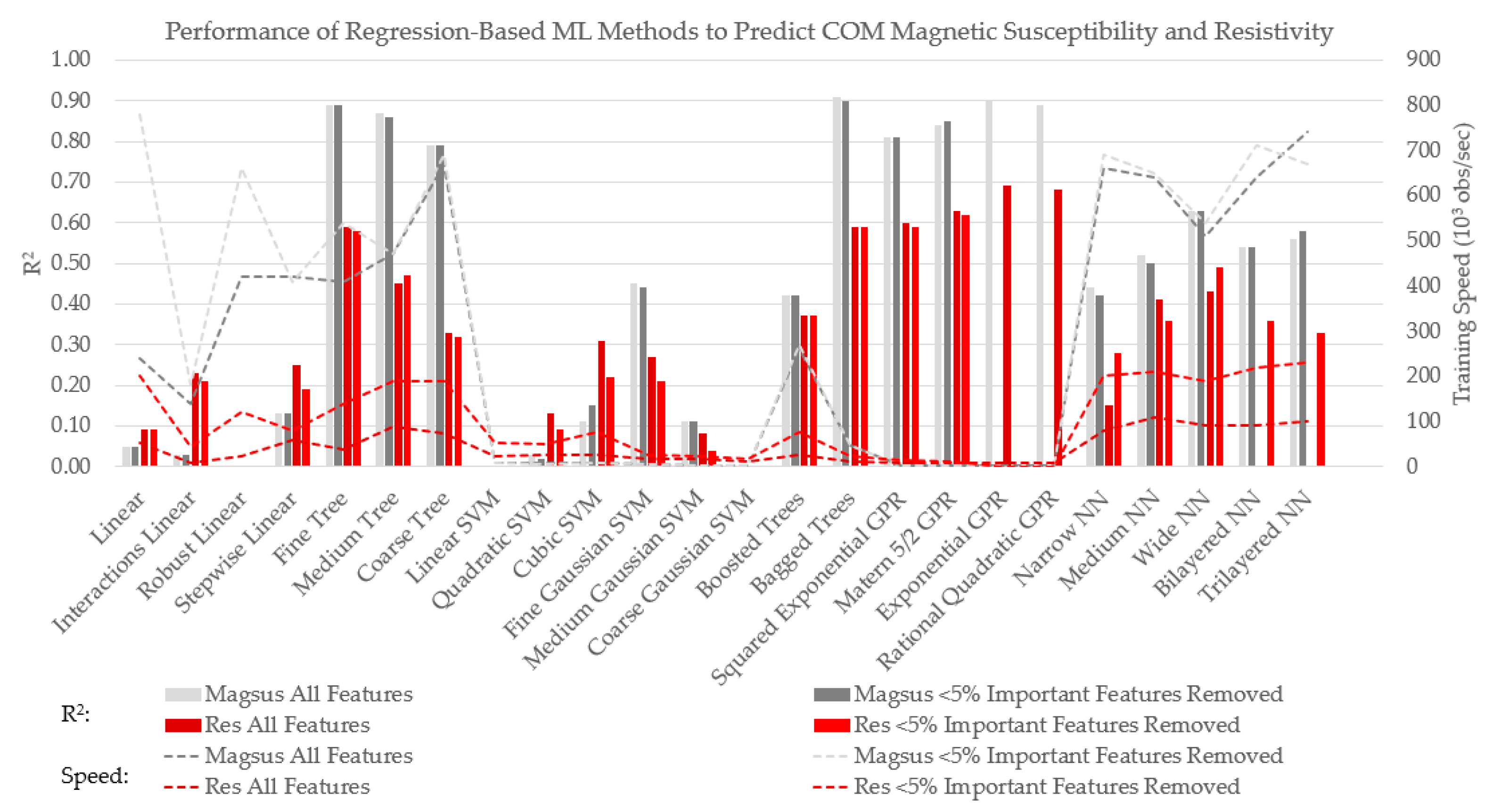
3.2.2. Magsus and Res Prediction
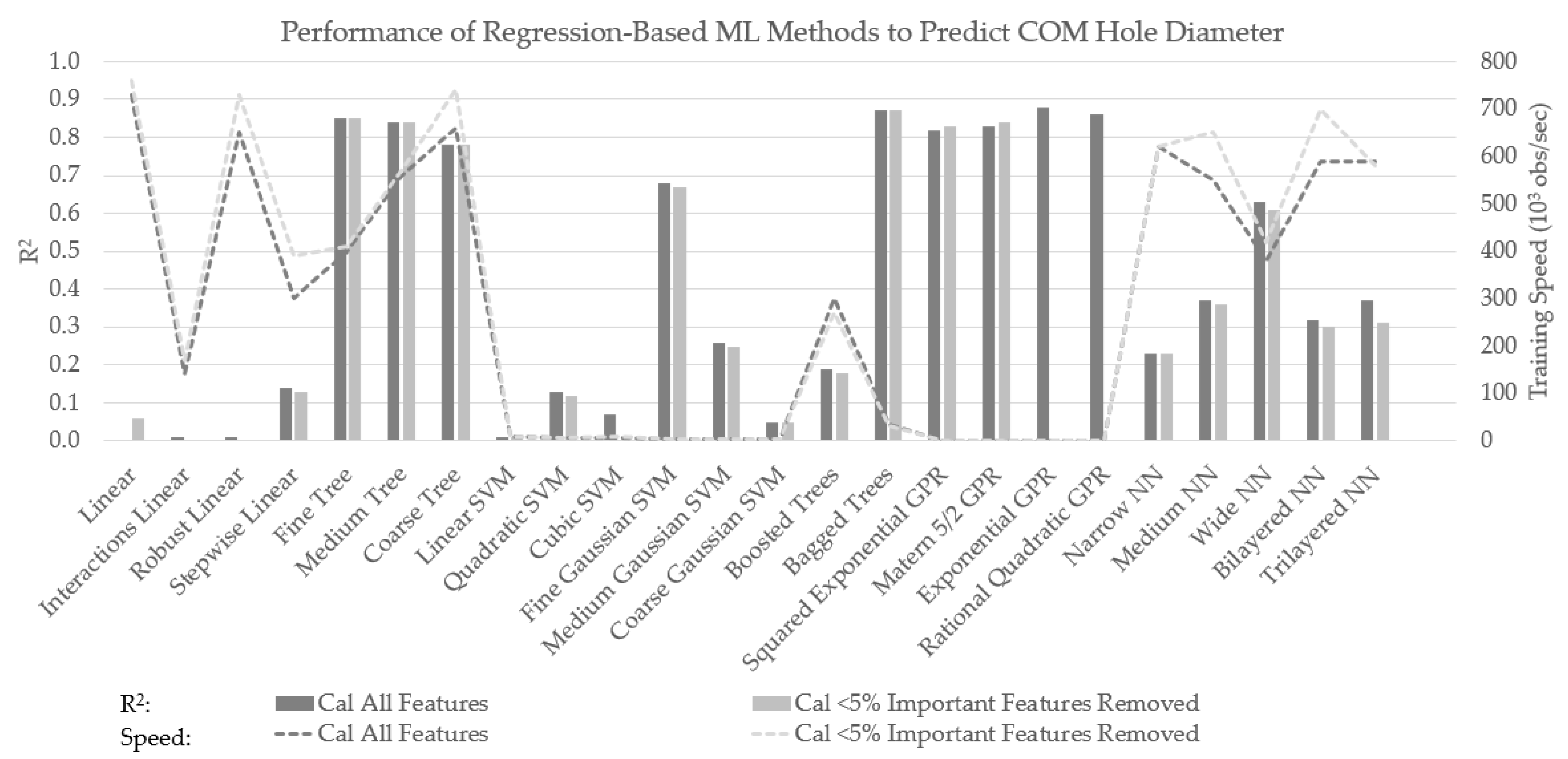
3.2.3. Caliper Predictions
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Silversides, K.; Melkumyan, A.; Wyman, D.; Hatherly, P. Automated Recognition of Stratigraphic Marker Shales from Geophysical Logs in Iron Ore Deposits. Comput. Geosci. 2015, 77, 118–125. [Google Scholar] [CrossRef]
- Wedge, D.; Hartley, O.; McMickan, A.; Green, T.; Holden, E.J. Machine Learning Assisted Geological Interpretation of Drillhole Data: Examples from the Pilbara Region, Western Australia. Ore Geol. Rev. 2019, 114, 103118. [Google Scholar] [CrossRef]
- Barr, M.V. Instrumented Horizontal Drilling for Tunnelling Site Investigation. Ph.D. Thesis, University of London, Imperial College of Science and Technology, London, UK, 1984. [Google Scholar]
- Hatherly, P.; Leung, R.; Scheding, S.; Robinson, D. Drill Monitoring Results Reveal Geological Conditions in Blasthole Drilling. Int. J. Rock Mech. Min. Sci. 2015, 78, 144–154. [Google Scholar] [CrossRef]
- Khorzoughi, M.B. Use of Measurement While Drilling Techniques for Improved Rock Mass Characterization in Open-Pit Mines. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 2011. [Google Scholar]
- Navarro, J.; Sanchidrian, J.A.; Segarra, P.; Castedo, R.; Paredes, C.; Lopez, L.M. On the Mutual Relations of Drill Monitoring Variables and the Drill Control System in Tunneling Operations. Tunn. Undergr. Space Technol. 2018, 72, 294–304. [Google Scholar] [CrossRef]
- van Eldert, J.; Schunnesson, H.; Johansson, D.; Saiang, D. Application of Measurement While Drilling Technology to Predict Rock Mass Quality and Rock Support for Tunnelling. Rock Mech. Rock Eng. 2020, 53, 1349–1358. [Google Scholar] [CrossRef]
- Kadkhodaie-Ilkhchi, A.; Monteiro, S.T.; Ramos, F.; Hatherly, P. Rock Recognition from MWD Data: A Comparative Study of Boosting, Neural Networks, and Fuzzy Logic. IEEE Geosci. Remote Sens. Lett. 2010, 7, 680–684. [Google Scholar] [CrossRef]
- Galende-Hernández, M.; Menéndez, M.; Fuente, M.J.; Sainz-Palmero, G.I. Monitor-While-Drilling-Based Estimation of Rock Mass Rating with Computational Intelligence: The Case of Tunnel Excavation Front. Autom. Constr. 2018, 93, 325–338. [Google Scholar] [CrossRef]
- Klyuchnikov, N.; Zaytsev, A.; Gruzdev, A.; Ovchinnikov, G.; Antipova, K.; Ismailova, L.; Muravleva, E.; Burnaev, E.; Semenikhin, A.; Cherepanov, A.; et al. Data-Driven Model for the Identification of the Rock Type at a Drilling Bit. J. Pet. Sci. Eng. 2019, 178, 506–516. [Google Scholar] [CrossRef]
- Peck, J.P. Performance Monitoring of Rotary Blasthole Drills. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 1989. [Google Scholar]
- Scoble, M.J.; Peck, J.; Hendricks, C. Correlation between Rotary Drill Performance Parameters and Borehole Geophysical Logging. Min. Sci. Technol. 1989, 8, 301–312. [Google Scholar] [CrossRef]
- Segui, J.B.; Higgins, M. Blast Design Using Measurement While Drilling Parameters; Fragblast: Hunter Valley, NSW, Australia, 2001; pp. 28–31. [Google Scholar]
- Navarro, J.; Seidl, T.; Hartlieb, P.; Sanchidrián, J.A.; Segarra, P.; Couceiro, P.; Schimek, P.; Godoy, C. Blastability and Ore Grade Assessment from Drill Monitoring for Open Pit Applications. Rock Mech. Rock Eng. 2021, 54, 3209–3228. [Google Scholar] [CrossRef]
- Akyildiz, O.; Basarir, H.; Vezhapparambu, V.S.; Ellefmo, S. MWD Data-Based Marble Quality Class Prediction Models Using ML Algorithms. Math. Geosci. 2023, 55, 1059–1074. [Google Scholar] [CrossRef]
- Basarir, H.; Wesseloo, J.; Karrech, A.; Pasternak, E.; Dyskin, A. The Use of Soft Computing Methods for the Prediction of Rock Properties Based on Measurement While Drilling Data. In Proceedings of the Eighth International Conference on Deep and High Stress Mining, Perth, WA, Canada, 16–18 November 2017; pp. 537–551. [Google Scholar] [CrossRef]
- Beattie, N. Monitoring-While-Drilling for Open-Pit Mining in a Hard Rock Environment. Master’s Thesis, Queen’s University, Kingston, ON, Canada, 2009. [Google Scholar]
- Khushaba, R.N.; Melkumyan, A.; Hill, A.J. A Machine Learning Approach for Material Type Logging and Chemical Assaying from Autonomous Measure-While-Drilling (MWD) Data. Math. Geosci. 2021, 54, 285–315. [Google Scholar] [CrossRef]
- Martin, J. Application of Pattern Recognition Techniques to Monitoring-While-Drilling on a Rotary Electric Blasthole Drill at an Open-Pit Coal Mine. Master’s Thesis, Queen’s University, Kingston, ON, Canada, 2007. [Google Scholar]
- Silversides, K.L.; Melkumyan, A. Multivariate Gaussian Process for Distinguishing Geological Units Using Measure While Drilling Data. In Minig Goes Digitial; Taylor & Francis Group: London, UK, 2019; pp. 94–100. [Google Scholar]
- Silversides, K.L.; Melkumyan, A. Boundary Identification and Surface Updates Using MWD. Math. Geosci. 2020, 53, 1047–1071. [Google Scholar] [CrossRef]
- Schunnesson, H. Drill Process Monitoring in Percussive Drilling: A Multivariate Approach for Data Analysis. Licentiate Thesis, Lulea University of Technology, Lulea, Sweden, 1990. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal Component Analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Goldstein, D.M.; Aldrich, C.; O’Connor, L. A Review of Orebody Knowledge Enhancement Using Machine Learning on Open-Pit Mine Measure-While-Drilling Data. Mach. Learn. Knowl. Extr. 2024, 6, 1343–1360. [Google Scholar] [CrossRef]
- Ker, P. Iron Ore Supply Slump as Rio Runs Late on New Mines. Available online: https://www.afr.com/companies/mining/rio-tinto-iron-ore-takes-300m-inflation-hit-20210716-p58a8l (accessed on 15 January 2025).
- De-Vitry, C.; Vann, J.; Arvidson, H. Multivariate Iron Ore Deposit Resource Estimation—A Practitioner’s Guide to Selecting Methods. Trans. Inst. Min. Metall. Sect. B 2010, 119, 154–165. [Google Scholar] [CrossRef]
- Jones, H.; Walraven, F.; Knott, G.G. Natural gamma logging as an aid to iron ore exploration in the Pilbara region of Western Australia. In Proceedings of the Australasian Institute of Mining and Metallurgy Annual Conference, Perth, Australia, 24–25 May 2023; pp. 53–60. [Google Scholar]
- Tittman, J.; Wahl, J.S. The Physical Foundations of Formation Density Logging (Gamma-Gamma). Geophysics 1965, 30, 284–294. [Google Scholar] [CrossRef]
- Yang, Q.; Tan, M.; Zhang, F.; Bai, Z. Wireline Logs Constraint Borehole-to-Surface Resistivity Inversion Method and Water Injection Monitoring Analysis. Pure Appl. Geophys. 2021, 178, 939–957. [Google Scholar] [CrossRef]
- Elsayed, M.; Isah, A.; Hiba, M.; Hassan, A.; Al-Garadi, K.; Mahmoud, M.; El-Husseiny, A.; Radwan, A.E. A Review on the Applications of Nuclear Magnetic Resonance (NMR) in the Oil and Gas Industry: Laboratory and Field-Scale Measurements. J. Pet. Explor. Prod. Technol. 2022, 12, 2747–2784. [Google Scholar] [CrossRef]
- Goldstein, D.; Aldrich, C.; O’Connor, L. Enhancing Orebody Knowledge Using Measure-While-Drilling Data: A Machine Learning Approach. IFAC-PapersOnLine 2024, 58, 72–76. [Google Scholar] [CrossRef]
- Khorzoughi, B.M.; Hall, R. Processing of Measurement While Drilling Data for Rock Mass Characterization. Int. J. Min. Sci. Technol. 2016, 26, 989–994. [Google Scholar] [CrossRef]
- van Eldert, J.; Schunnesson, H.; Saiang, D.; Funehag, J. Improved Filtering and Normalizing of Measurement-While-Drilling (MWD) Data in Tunnel Excavation. Tunn. Undergr. Space Technol. 2020, 103, 103467. [Google Scholar] [CrossRef]
- Ghosh, R.; Gustafson, A.; Schunnesson, H. Development of a Geological Model for Chargeability Assessment of Borehole Using Drill Monitoring Technique. Int. J. Rock Mech. Min. Sci. 2018, 109, 9–18. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Shao, Q.; Traylen, A.; Zhang, L. Nonparametric Method for Estimating the Effects of Climatic and Catchment Characteristics on Mean Annual Evapotranspiration: Nonparametric Method for Mean Annual Evapotranspiration. Water Resour. Res. 2012, 48, 1–13. [Google Scholar] [CrossRef]
- Kaveh, A.; Hamze-Ziabari, S.M.; Bakhshpoori, T. Estimating Drying Shrinkage of Concrete Using a Multivariate Adaptive Regression Spline Approach. Int. J. Optim. Civ. Eng. 2018, 8, 181–194. [Google Scholar]
- Menon, R.; Bhat, G.; Saade, G.R.; Spratt, H. Multivariate Adaptive Regression Splines Analysis to Predict Biomarkers of Spontaneous Preterm Birth. Acta Obstet. Gynecol. Scand. 2014, 93, 382–391. [Google Scholar] [CrossRef]
- Earth: Multivariate Adaptive Regression Splines, version 5.3.4; Stephen Milborrow: Cape Town, South Africa, 2023.
- Friedman, J.H.; Stuetzle, W. Projection Pursuit Regression. J. Am. Stat. Assoc. 1981, 76, 817–823. [Google Scholar] [CrossRef]
- Sepulveda, E.; Dowd, P.A.; Xu, C.; Addo, E. Multivariate Modelling of Geometallurgical Variables by Projection Pursuit. Math. Geosci. 2017, 49, 121–143. [Google Scholar] [CrossRef]
- Yu, X.; Liu, B.; Lai, Y. Monthly Pork Price Prediction Applying Projection Pursuit Regression: Modeling, Empirical Research, Comparison, and Sustainability Implications. Sustainability 2024, 16, 1466. [Google Scholar] [CrossRef]
- Du, H.; Wang, J.; Zhang, X.; Yao, X.; Hu, Z. Prediction of Retention Times of Peptides in RPLC by Using Radial Basis Function Neural Networks and Projection Pursuit Regression. Chemom. Intell. Lab. Syst. 2008, 92, 92–99. [Google Scholar] [CrossRef]
- R Core Team. R Stats Package; R Foundation for Statistical Computing: Indianapolis, IN, USA, 2022. [Google Scholar]
- Su, X.; Yan, X.; Tsai, C.-L. Linear Regression. WIREs Comput. Stat. 2012, 4, 275–294. [Google Scholar] [CrossRef]
- Kotsiantis, S.B. Decision Trees: A Recent Overview. Artif. Intell. Rev. 2013, 39, 261–283. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support Vector Machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A Tutorial on Gaussian Process Regression: Modelling, Exploring, and Exploiting Functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks and Their Applications. Rev. Sci. Instrum. 1993, 65, 1803–1832. [Google Scholar] [CrossRef]
- Regression Learner Toolbox; The MathWorks Inc.: Natick, MA, USA, 2024.
- Ghosh, R.; Schunnesson, H.; Kumar, U. Evaluation of Rock Mass Characteristics Using Measurement While Drilling in Boliden Minerals Aitik Copper Mine, Sweden. In Mine Planning and Equipment Selection; Drebenstedt, C., Singhal, R., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 81–91. ISBN 978-3-319-02677-0. [Google Scholar]
- Roe, K.D.; Jawa, V.; Zhang, X.; Chute, C.G.; Epstein, J.A.; Matelsky, J.; Shpitser, I.; Taylor, C.O. Feature Engineering with Clinical Expert Knowledge: A Case Study Assessment of Machine Learning Model Complexity and Performance. PLoS ONE 2020, 15, e0231300. [Google Scholar] [CrossRef]
- Aldrich, C. Process Variable Importance Analysis by Use of Random Forests in a Shapley Regression Framework. Minerals 2020, 10, 420. [Google Scholar] [CrossRef]
- Deng, S.; Aldrich, C.; Liu, X.; Zhang, F. Explainability in Reservoir Well-Logging Evaluation: Comparison of Variable Importance Analysis with Shapley Value Regression, SHAP and LIME. IFAC-PapersOnLine 2024, 58, 66–71. [Google Scholar] [CrossRef]

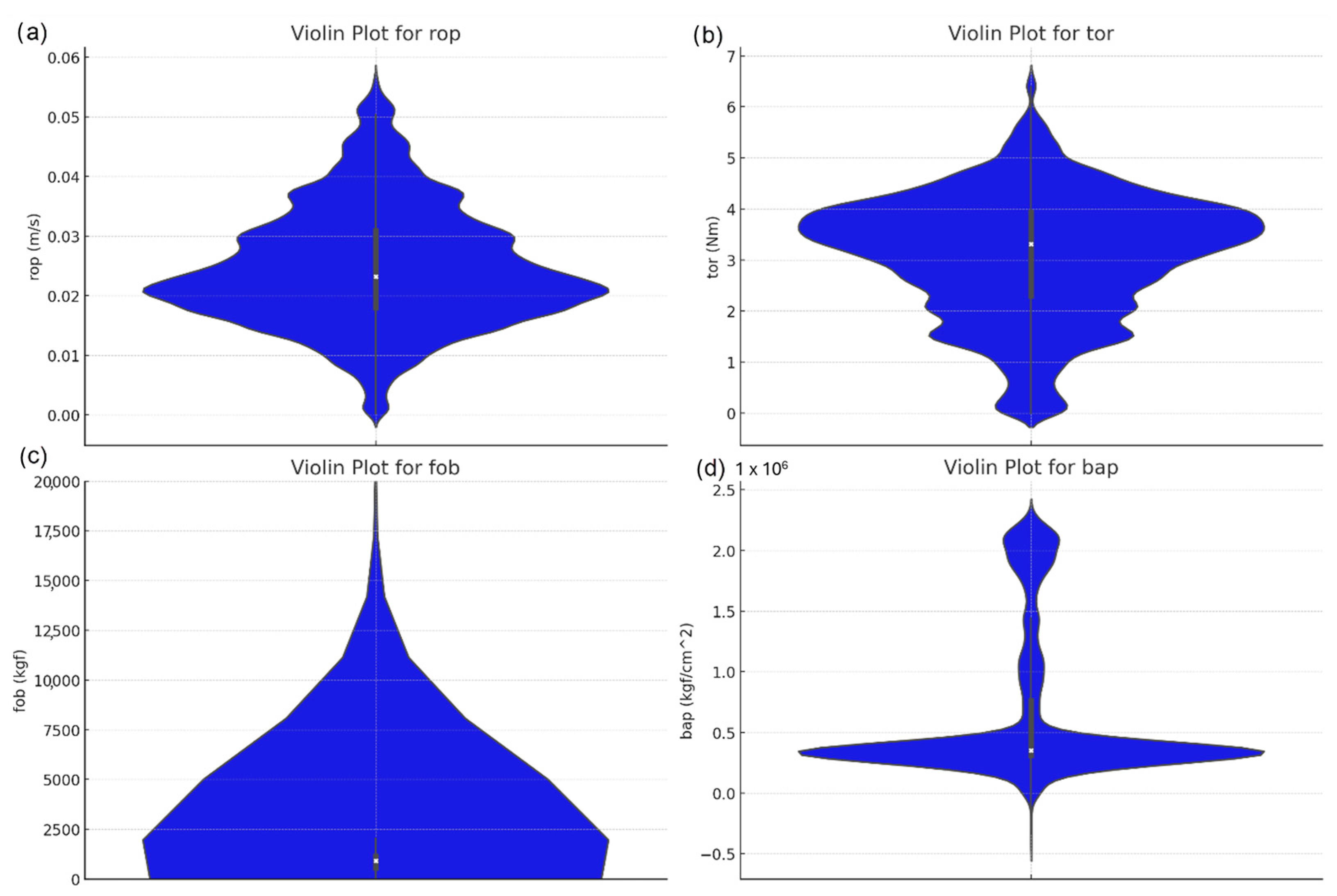
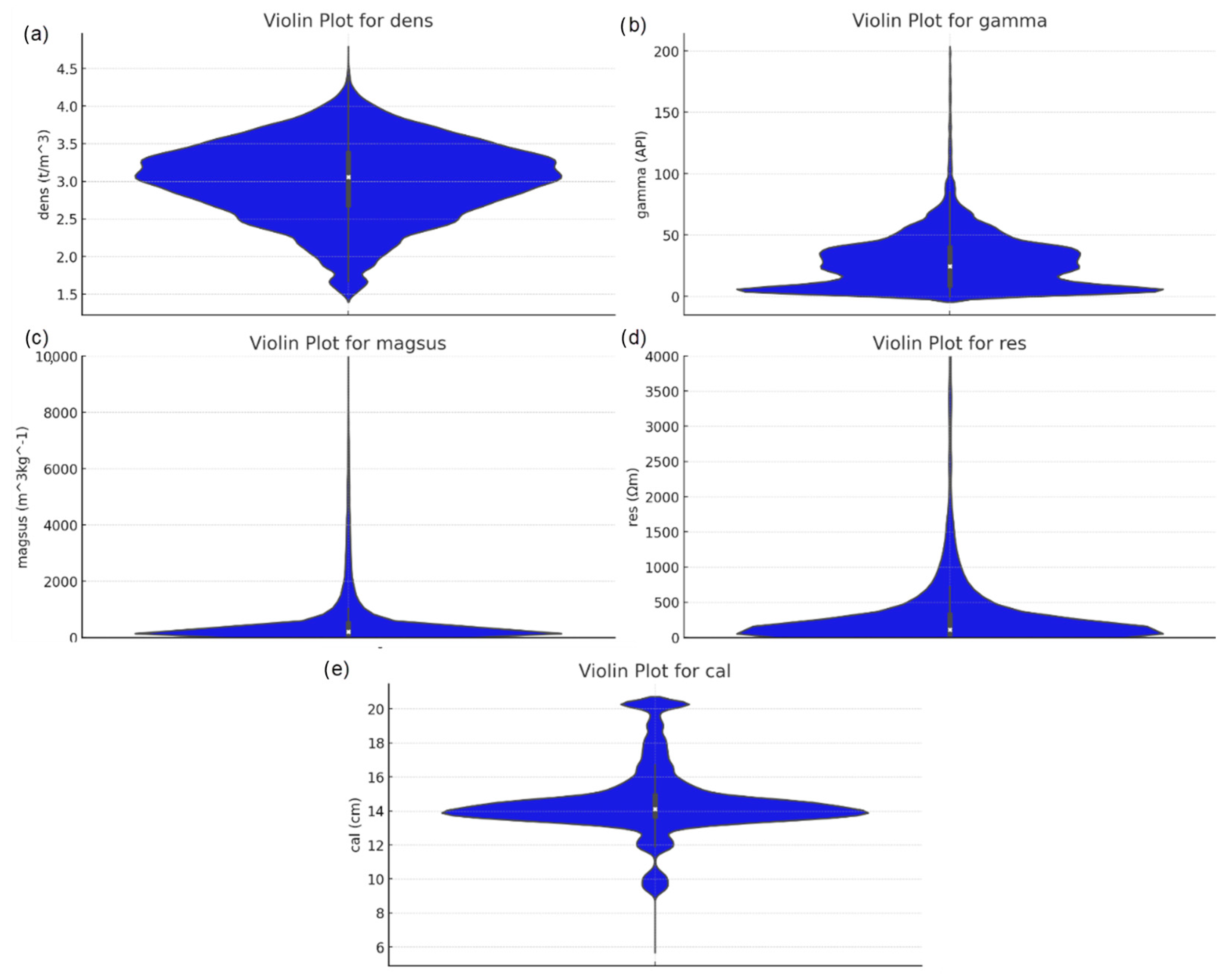
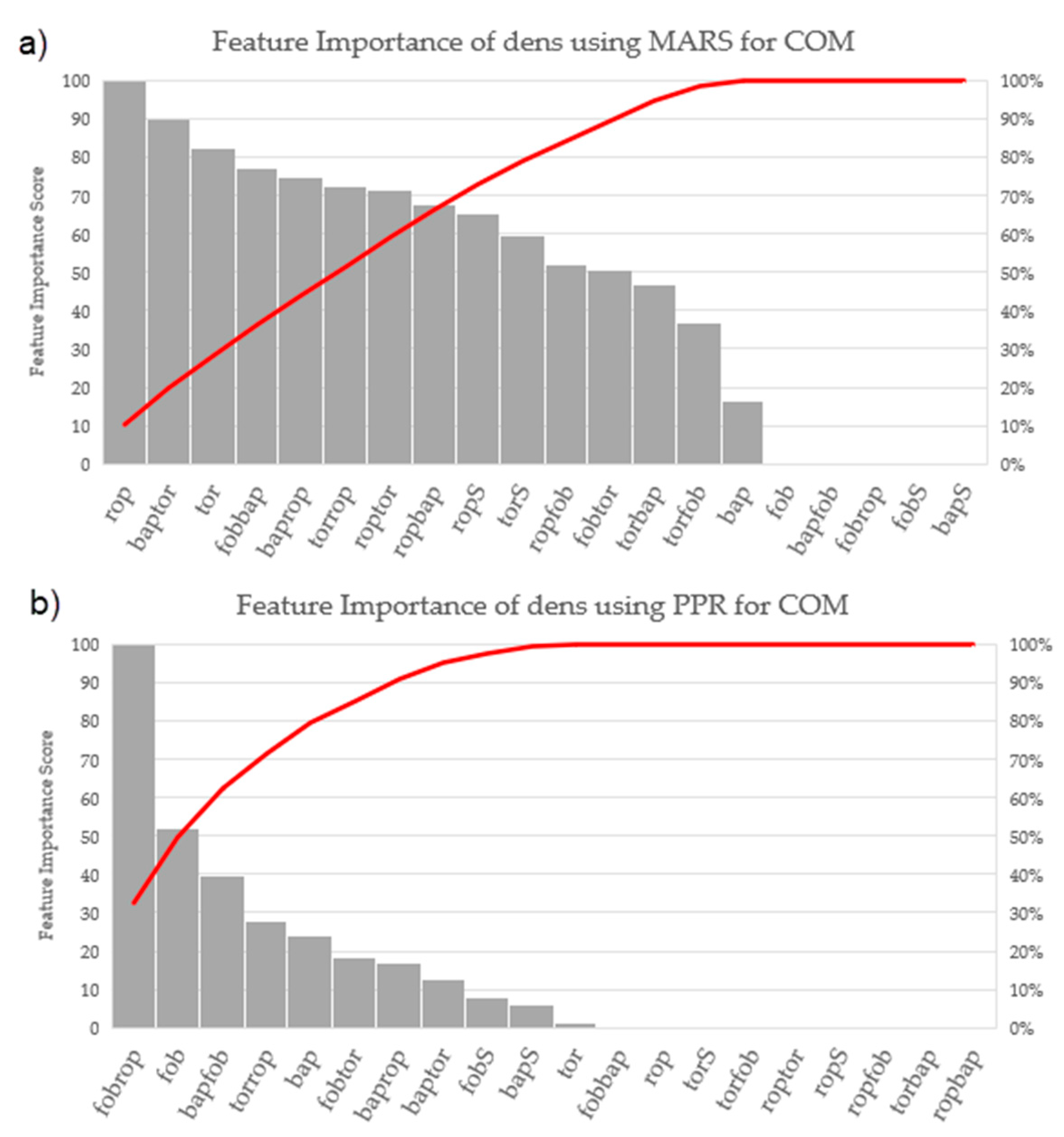

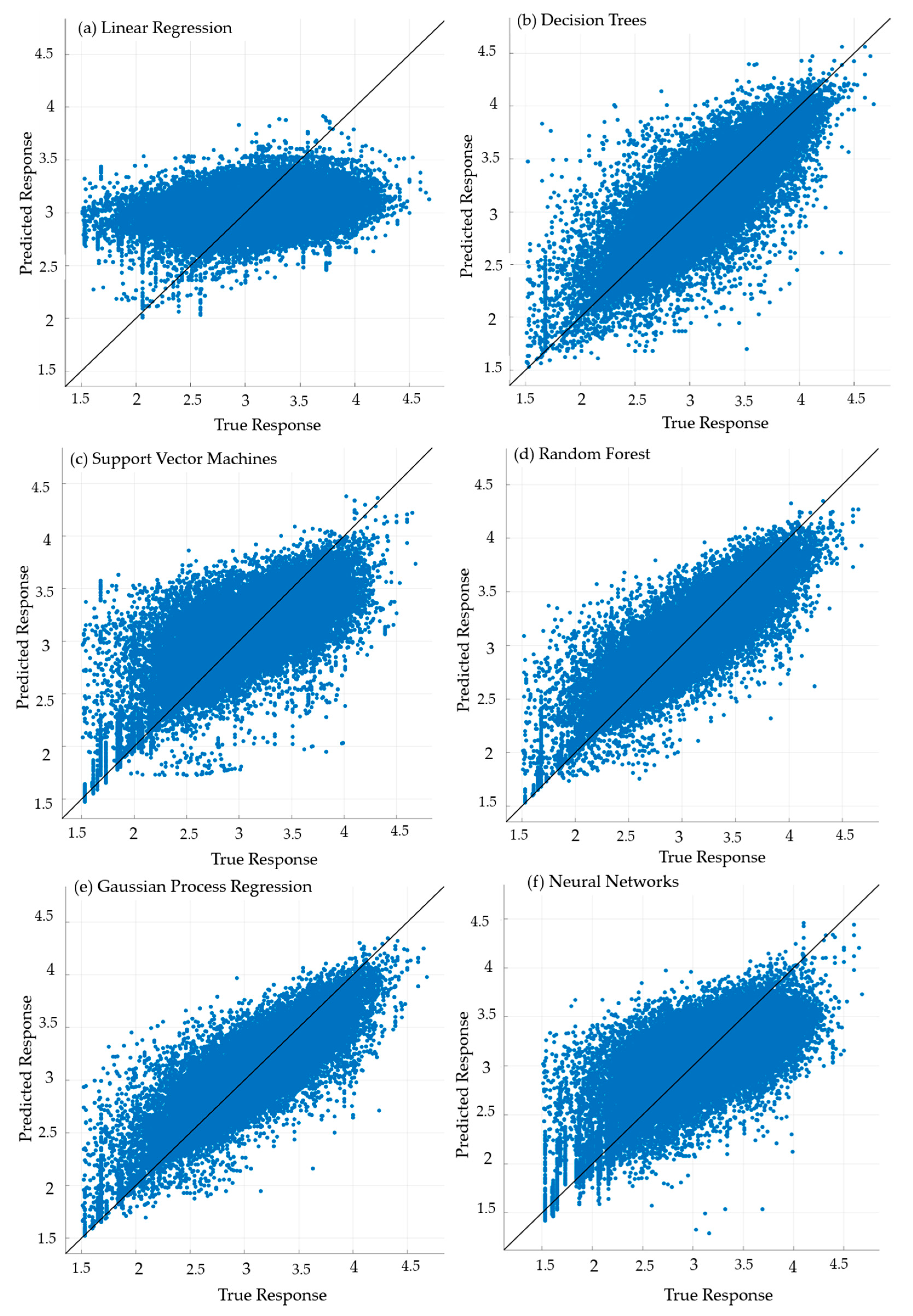
| Geophysical Measurement | Observations | ||
|---|---|---|---|
| BR | MM | COM | |
| Density | 45,813 | 5789 | 51,602 |
| Gamma | 71,126 | 7791 | 78,917 |
| Magnetic Susceptibility | 71,012 | 8261 | 79,273 |
| Resistivity | 3202 | 3798 | 7000 |
| Caliper | 61,666 | 7505 | 69,171 |
| Type | MWD Features | |||
|---|---|---|---|---|
| Recorded | rop | tor | fob | bap |
| Ratio | roptor ropfob ropbap | torrop torfob torbap | fobrop fobtor fobbap | baprop baptor bapfob |
| Standard Deviation | ropS | torS | fobS | bapS |
| Class | Linear Regression (LR) | Decision Trees (DTs) | Support Vector Machines (SVMs) | Random Forests (RFs) | Gaussian Process Regression (GP) | Neural Networks (NNs) |
|---|---|---|---|---|---|---|
| Subclass |
|
|
|
|
|
|
| MWD Feature | Density | Gamma | Magnetic Susceptibility | Resistivity | Caliper | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| MARS n-Terms | 101 (%) | 201 (%) | 101 (%) | 201 (%) | 101 (%) | 201 (%) | 101 (%) | 201 (%) | 101 (%) | 201 (%) |
| rop | 7 | 7 | 10 | 10 | 6 | 6 | 3 | 4 | 11 | 11 |
| tor | 7 | 7 | 9 | 9 | 8 | 8 | 8 | 7 | 0 | 0 |
| fob | 1 | 1 | 0 | 0 | 4 | 4 | 1 | 1 | 0 | 0 |
| bap | 5 | 4 | 2 | 2 | 0 | 0 | 10 | 10 | 0 | 0 |
| roptor | 7 | 7 | 7 | 7 | 6 | 6 | 9 | 9 | 18 | 18 |
| ropbap | 6 | 6 | 7 | 7 | 0 | 0 | 8 | 10 | 0 | 0 |
| ropfob | 6 | 6 | 5 | 5 | 1 | 0 | 6 | 5 | 0 | 0 |
| torrop | 7 | 7 | 8 | 8 | 10 | 10 | 4 | 8 | 2 | 2 |
| torbap | 8 | 8 | 5 | 5 | 5 | 5 | 12 | 12 | 0 | 0 |
| torfob | 6 | 6 | 4 | 4 | 13 | 13 | 5 | 5 | 7 | 7 |
| baprop | 10 | 9 | 8 | 8 | 9 | 9 | 3 | 3 | 15 | 15 |
| baptor | 4 | 4 | 9 | 9 | 10 | 10 | 6 | 8 | 0 | 0 |
| bapfob | 2 | 1 | 0 | 0 | 9 | 9 | 0 | 0 | 0 | 0 |
| fobrop | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 14 | 14 |
| fobtor | 6 | 5 | 5 | 5 | 4 | 4 | 6 | 5 | 7 | 7 |
| fobbap | 9 | 9 | 8 | 8 | 2 | 2 | 10 | 2 | 10 | 10 |
| ropS | 0 | 0 | 7 | 7 | 0 | 0 | 0 | 0 | 0 | 0 |
| torS | 3 | 6 | 6 | 6 | 6 | 6 | 6 | 9 | 5 | 5 |
| fobS | 3 | 3 | 0 | 0 | 2 | 2 | 0 | 0 | 12 | 12 |
| bapS | 3 | 2 | 0 | 0 | 5 | 5 | 0 | 0 | 0 | 0 |
| MWD Feature | Density | Gamma | Magnetic Susceptibility | Resistivity | Caliper | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| PPR n-Terms | 5 (%) | <50 (%) | 5 (%) | <50 (%) | 5 (%) | <50 (%) | 5 (%) | <50 (%) | 5 (%) | <50 (%) |
| rop | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| tor | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| fob | 16 | 18 | 11 | 17 | 21 | 21 | 4 | 8 | 3 | 9 |
| bap | 7 | 4 | 7 | 8 | 5 | 8 | 1 | 18 | 3 | 9 |
| roptor | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ropbap | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ropfob | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| torrop | 19 | 2 | 25 | 9 | 18 | 5 | 9 | 3 | 21 | 12 |
| torbap | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| torfob | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| baprop | 28 | 5 | 29 | 6 | 13 | 12 | 11 | 11 | 49 | 6 |
| baptor | 7 | 4 | 8 | 4 | 8 | 4 | 7 | 4 | 7 | 19 |
| bapfob | 4 | 8 | 3 | 13 | 7 | 10 | 19 | 16 | 3 | 24 |
| fobrop | 11 | 12 | 4 | 33 | 14 | 28 | 11 | 20 | 6 | 14 |
| fobtor | 5 | 37 | 8 | 6 | 9 | 9 | 34 | 1 | 3 | 5 |
| fobbap | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ropS | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| torS | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| fobS | 3 | 9 | 2 | 3 | 5 | 1 | 2 | 17 | 1 | 1 |
| bapS | 0 | 1 | 4 | 2 | 1 | 1 | 2 | 2 | 3 | 1 |
| Geophysical Measurement | BR | MM | COM | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Measured | Additional | Measured | Additional | Measured | Additional | |||||||
| RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | |
| dens | 0.33 | 0.57 | 0.29 | 0.68 | 0.37 | 0.51 | 0.34 | 0.59 | 0.34 | 0.56 | 0.30 | 0.66 |
| gamma | 15.47 | 0.50 | 14.01 | 0.59 | 13.62 | 0.65 | 10.67 | 0.78 | 15.53 | 0.51 | 13.67 | 0.62 |
| magsus | 848 | 0.70 | 701 | 0.80 | 389 | 0.24 | 376 | 0.29 | 845 | 0.68 | 680 | 0.79 |
| res | 582 | 0.27 | 554 | 0.34 | 697 | 0.31 | 705 | 0.29 | 650 | 0.29 | 631 | 0.33 |
| cal | 1.12 | 0.68 | 0.93 | 0.78 | 1.19 | 0.61 | 1.03 | 0.70 | 1.16 | 0.66 | 0.94 | 0.78 |
| Regression-Based ML Class | Regression-Based ML Suclass | BR | MM | COM | |||
|---|---|---|---|---|---|---|---|
| RMSE (t/m3) | R2 | RMSE (t/m3) | R2 | RMSE (t/m3) | R2 | ||
| LR | Linear | 0.49 | 0.06 | 0.49 | 0.13 | 0.50 | 0.05 |
| Interactions | 0.55 | 0.00 | 0.45 | 0.28 | 0.79 | 0.00 | |
| Robust | 0.49 | 0.06 | 0.50 | 0.13 | 0.50 | 0.04 | |
| Stepwise | 0.48 | 0.12 | 0.44 | 0.32 | 0.49 | 0.09 | |
| DTs | Fine | 0.22 | 0.81 | 0.27 | 0.74 | 0.23 | 0.80 |
| Medium | 0.25 | 0.76 | 0.29 | 0.69 | 0.25 | 0.75 | |
| Coarse | 0.29 | 0.68 | 0.34 | 0.59 | 0.30 | 0.66 | |
| SVMs | Linear | 0.49 | 0.05 | 0.50 | 0.12 | 0.50 | 0.04 |
| Quadratic | 0.46 | 0.17 | 0.41 | 0.40 | 0.48 | 0.13 | |
| Cubic | 0.37 | 0.46 | 0.31 | 0.66 | 0.56 | 0.00 | |
| Fine Gaussian | 0.31 | 0.63 | 0.25 | 0.77 | 0.32 | 0.61 | |
| Medium Gaussian | 0.40 | 0.39 | 0.37 | 0.50 | 0.43 | 0.28 | |
| Coarse Gaussian | 0.48 | 0.09 | 0.48 | 0.18 | 0.49 | 0.07 | |
| RFs | Boosted | 0.46 | 0.19 | 0.41 | 0.41 | 0.47 | 0.16 |
| Bagged | 0.21 | 0.83 | 0.24 | 0.80 | 0.21 | 0.82 | |
| GPs | Squared Exponential | 0.28 | 0.70 | 0.23 | 0.81 | 0.27 | 0.72 |
| Matern 5/2 | 0.27 | 0.72 | 0.22 | 0.82 | 0.26 | 0.73 | |
| Exponential | 0.22 | 0.82 | 0.19 | 0.87 | 0.22 | 0.81 | |
| Rational Quadratic | 0.20 | 0.84 | 0.20 | 0.86 | 0.22 | 0.82 | |
| NNs | Narrow | 0.44 | 0.24 | 0.35 | 0.56 | 0.45 | 0.21 |
| Medium | 0.38 | 0.42 | 0.29 | 0.69 | 0.41 | 0.36 | |
| Wide | 0.32 | 0.61 | 0.24 | 0.79 | 0.34 | 0.55 | |
| Bilayered | 0.41 | 0.36 | 0.33 | 0.62 | 0.43 | 0.29 | |
| Trilayered | 0.40 | 0.38 | 0.31 | 0.65 | 0.42 | 0.33 | |
| Regression-Based ML Class | Regression-Based ML Suclass | BR | MM | COM | |||
|---|---|---|---|---|---|---|---|
| RMSE (API) | R2 | RMSE (API) | R2 | RMSE (API) | R2 | ||
| LR | Linear | 21.30 | 0.06 | 20.52 | 0.20 | 21.53 | 0.06 |
| Interactions | 21.53 | 0.04 | 17.81 | 0.40 | 22.38 | 0.00 | |
| Robust | 21.47 | 0.04 | 22.83 | 0.01 | 21.71 | 0.04 | |
| Stepwise | 20.75 | 0.11 | 16.23 | 0.50 | N/A | N/A | |
| DTs | Fine | 10.24 | 0.78 | 0.80 | 0.88 | 10.00 | 0.80 |
| Medium | 11.90 | 0.71 | 8.79 | 0.85 | 11.58 | 0.73 | |
| Coarse | 14.01 | 0.59 | 10.67 | 0.78 | 13.67 | 0.62 | |
| SVMs | Linear | 21.49 | 0.04 | 22.02 | 0.08 | 21.71 | 0.04 |
| Quadratic | 20.39 | 0.14 | 15.45 | 0.55 | 20.70 | 0.13 | |
| Cubic | 18.33 | 0.30 | 10.05 | 0.81 | 27.88 | 0.00 | |
| Fine Gaussian | 16.13 | 0.46 | 7.56 | 0.89 | 16.02 | 0.48 | |
| Medium Gaussian | 18.63 | 0.28 | 12.76 | 0.69 | 19.19 | 0.25 | |
| Coarse Gaussian | 20.96 | 0.09 | 21.03 | 0.16 | 21.24 | 0.08 | |
| RFs | Boosted | 19.92 | 0.18 | 13.86 | 0.63 | 20.03 | 0.18 |
| Bagged | 9.65 | 0.81 | 7.04 | 0.91 | 9.43 | 0.82 | |
| GPs | Squared Exponential | 14.31 | 0.58 | 6.73 | 0.91 | 13.30 | 0.64 |
| Matern 5/2 | 13.72 | 0.61 | 6.52 | 0.92 | 13.24 | 0.64 | |
| Exponential | 10.93 | 0.75 | 6.32 | 0.92 | N/A | N/A | |
| Rational Quadratic | N/A | N/A | 6.51 | 0.92 | N/A | N/A | |
| NNs | Narrow | 19.70 | 0.20 | 11.61 | 0.74 | 19.98 | 0.19 |
| Medium | 18.17 | 0.32 | 8.87 | 0.85 | 18.61 | 0.30 | |
| Wide | 16.03 | 0.47 | 6.88 | 0.91 | 16.22 | 0.47 | |
| Bilayered | 18.92 | 0.26 | 9.34 | 0.83 | 19.19 | 0.25 | |
| Trilayered | 18.84 | 0.26 | 9.41 | 0.83 | 19.28 | 0.24 | |
| Regression-Based ML Class | Regression-Based ML Suclass | BR | MM | COM | |||
|---|---|---|---|---|---|---|---|
| RMSE (m3kg−1) | R2 | RMSE (m3kg−1) | R2 | RMSE (m3kg−1) | R2 | ||
| LR | Linear | 1505 | 0.06 | 435 | 0.05 | 1446 | 0.05 |
| Interactions | 1490 | 0.08 | 388 | 0.24 | 1464 | 0.03 | |
| Robust | 1625 | 0.00 | 453 | 0.00 | 1552 | 0.00 | |
| Stepwise | 1450 | 0.13 | N/A | N/A | 1387 | 0.13 | |
| DTs | Fine | 518 | 0.89 | 260 | 0.66 | 499 | 0.89 |
| Medium | 564 | 0.87 | 291 | 0.57 | 542 | 0.87 | |
| Coarse | 701 | 0.80 | 375 | 0.29 | 680 | 0.79 | |
| SVMs | Linear | 1606 | 0.00 | 450 | 0.00 | 1537 | 0.00 |
| Quadratic | 1498 | 0.07 | 443 | 0.01 | 1468 | 0.03 | |
| Cubic | 1306 | 0.30 | 389 | 0.24 | 1403 | 0.11 | |
| Fine Gaussian | 1081 | 0.52 | 375 | 0.29 | 1105 | 0.45 | |
| Medium Gaussian | 1366 | 0.23 | 438 | 0.03 | 1403 | 0.11 | |
| Coarse Gaussian | 1576 | 0.00 | 450 | 0.00 | 1517 | 0.00 | |
| RFs | Boosted | 1171 | 0.43 | 298 | 0.55 | 1134 | 0.42 |
| Bagged | 486 | 0.90 | 253 | 0.68 | 457 | 0.91 | |
| GPs | Squared Exponential | 668 | 0.82 | 252 | 0.68 | 646 | 0.81 |
| Matern 5/2 | 667 | 0.82 | 254 | 0.68 | 590 | 0.84 | |
| Exponential | 504 | 0.90 | N/A | N/A | 471 | 0.90 | |
| Rational Quadratic | 483 | 0.90 | N/A | N/A | 484 | 0.89 | |
| NNs | Narrow | 1093 | 0.51 | 307 | 0.53 | 1114 | 0.44 |
| Medium | 1019 | 0.57 | 287 | 0.59 | 1030 | 0.52 | |
| Wide | 865 | 0.69 | 262 | 0.66 | 902 | 0.63 | |
| Bilayered | 997 | 0.59 | 295 | 0.56 | 1012 | 0.54 | |
| Trilayered | 971 | 0.61 | 276 | 0.62 | 986 | 0.56 | |
| Regression-Based ML Class | Regression-Based ML Suclass | BR | MM | COM | |||
|---|---|---|---|---|---|---|---|
| RMSE (Ωm) | R2 | RMSE (Ωm) | R2 | RMSE (Ωm) | R2 | ||
| LR | Linear | 21.30 | 0.06 | 20.52 | 0.20 | 21.53 | 0.06 |
| Interactions | 21.53 | 0.04 | 17.81 | 0.40 | 22.38 | 0.00 | |
| Robust | 21.47 | 0.04 | 22.83 | 0.01 | 21.71 | 0.04 | |
| Stepwise | 20.75 | 0.11 | 16.23 | 0.50 | N/A | N/A | |
| DTs | Fine | 10.24 | 0.78 | 0.80 | 0.88 | 10.00 | 0.80 |
| Medium | 11.90 | 0.71 | 8.79 | 0.85 | 11.58 | 0.73 | |
| Coarse | 14.01 | 0.59 | 10.67 | 0.78 | 13.67 | 0.62 | |
| SVMs | Linear | 21.49 | 0.04 | 22.02 | 0.08 | 21.71 | 0.04 |
| Quadratic | 20.39 | 0.14 | 15.45 | 0.55 | 20.70 | 0.13 | |
| Cubic | 18.33 | 0.30 | 10.05 | 0.81 | 27.88 | 0.00 | |
| Fine Gaussian | 16.13 | 0.46 | 7.56 | 0.89 | 16.02 | 0.48 | |
| Medium Gaussian | 18.63 | 0.28 | 12.76 | 0.69 | 19.19 | 0.25 | |
| Coarse Gaussian | 20.96 | 0.09 | 21.03 | 0.16 | 21.24 | 0.08 | |
| RFs | Boosted | 19.92 | 0.18 | 13.86 | 0.63 | 20.03 | 0.18 |
| Bagged | 9.65 | 0.81 | 7.04 | 0.91 | 9.43 | 0.82 | |
| GPs | Squared Exponential | 14.31 | 0.58 | 6.73 | 0.91 | 13.30 | 0.64 |
| Matern 5/2 | 13.72 | 0.61 | 6.52 | 0.92 | 13.24 | 0.64 | |
| Exponential | 10.93 | 0.75 | 6.32 | 0.92 | N/A | N/A | |
| Rational Quadratic | N/A | N/A | 6.51 | 0.92 | N/A | N/A | |
| NNs | Narrow | 19.70 | 0.20 | 11.61 | 0.74 | 19.98 | 0.19 |
| Medium | 18.17 | 0.32 | 8.87 | 0.85 | 18.61 | 0.30 | |
| Wide | 16.03 | 0.47 | 6.88 | 0.91 | 16.22 | 0.47 | |
| Bilayered | 18.92 | 0.26 | 9.34 | 0.83 | 19.19 | 0.25 | |
| Trilayered | 18.84 | 0.26 | 9.41 | 0.83 | 19.28 | 0.24 | |
| Regression-Based ML Class | Regression-Based ML Suclass | BR | MM | COM | |||
|---|---|---|---|---|---|---|---|
| RMSE (cm) | R2 | RMSE (cm) | R2 | RMSE (cm) | R2 | ||
| LR | Linear | 1.92 | 0.07 | 1.70 | 0.20 | 1.92 | 0.06 |
| Interactions | 2.56 | 0.00 | 1.57 | 0.31 | 3.81 | 0.00 | |
| Robust | 2.00 | 0.00 | 1.75 | 0.15 | 1.99 | 0.00 | |
| Stepwise | 1.85 | 0.14 | 1.40 | 0.45 | 1.84 | 0.14 | |
| DTs | Fine | 0.76 | 0.85 | 0.71 | 0.86 | 0.76 | 0.85 |
| Medium | 0.79 | 0.84 | 0.81 | 0.82 | 0.80 | 0.84 | |
| Coarse | 0.93 | 0.78 | 1.03 | 0.70 | 0.94 | 0.78 | |
| SVMs | Linear | 1.98 | 0.01 | 1.76 | 0.14 | 1.97 | 0.01 |
| Quadratic | 1.82 | 0.17 | 1.34 | 0.50 | 1.85 | 0.13 | |
| Cubic | 1.47 | 0.46 | 0.97 | 0.74 | 1.91 | 0.07 | |
| Fine Gaussian | 1.08 | 0.71 | 0.70 | 0.86 | 1.12 | 0.68 | |
| Medium Gaussian | 1.58 | 0.37 | 1.19 | 0.61 | 1.70 | 0.26 | |
| Coarse Gaussian | 1.94 | 0.05 | 1.67 | 0.22 | 1.94 | 0.05 | |
| RFs | Boosted | 1.77 | 0.21 | 1.34 | 0.50 | 1.79 | 0.19 |
| Bagged | 0.71 | 0.87 | 0.62 | 0.89 | 0.70 | 0.87 | |
| GPs | Squared Exponential | 0.85 | 0.82 | 0.63 | 0.89 | 0.83 | 0.82 |
| Matern 5/2 | 0.83 | 0.83 | 0.61 | 0.90 | 0.81 | 0.83 | |
| Exponential | 0.71 | 0.87 | 0.53 | 0.92 | 0.70 | 0.88 | |
| Rational Quadratic | 0.75 | 0.86 | 0.58 | 0.91 | 0.75 | 0.86 | |
| NNs | Narrow | 1.67 | 0.30 | 1.15 | 0.63 | 1.74 | 0.23 |
| Medium | 1.47 | 0.45 | 0.91 | 0.77 | 1.57 | 0.37 | |
| Wide | 1.09 | 0.70 | 0.68 | 0.87 | 1.21 | 0.63 | |
| Bilayered | 1.57 | 0.37 | 1.03 | 0.70 | 1.64 | 0.32 | |
| Trilayered | 1.50 | 0.43 | 1.02 | 0.71 | 1.58 | 0.37 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goldstein, D.; Aldrich, C.; Shao, Q.; O’Connor, L. Unlocking Subsurface Geology: A Case Study with Measure-While-Drilling Data and Machine Learning. Minerals 2025, 15, 241. https://doi.org/10.3390/min15030241
Goldstein D, Aldrich C, Shao Q, O’Connor L. Unlocking Subsurface Geology: A Case Study with Measure-While-Drilling Data and Machine Learning. Minerals. 2025; 15(3):241. https://doi.org/10.3390/min15030241
Chicago/Turabian StyleGoldstein, Daniel, Chris Aldrich, Quanxi Shao, and Louisa O’Connor. 2025. "Unlocking Subsurface Geology: A Case Study with Measure-While-Drilling Data and Machine Learning" Minerals 15, no. 3: 241. https://doi.org/10.3390/min15030241
APA StyleGoldstein, D., Aldrich, C., Shao, Q., & O’Connor, L. (2025). Unlocking Subsurface Geology: A Case Study with Measure-While-Drilling Data and Machine Learning. Minerals, 15(3), 241. https://doi.org/10.3390/min15030241









