Optimizing Strength Prediction for Cemented Paste Backfills with Various Fly Ash Substitution: Computational Approach with Machine Learning Algorithms

Abstract

In cemented paste backfill (CPB), fly ash (FA) can reduce cement costs. However, the chemical compositions of FA and tailings used in the CPB can vary significantly, affecting the strength values of CPBs, which can be determined through laboratory tests and play a crucial role in design operations. Therefore, developing a predictive model would be advantageous in terms of time and cost. The most critical aspect of this study is that machine learning (ML) models demonstrate high accuracy in the performance of strength prediction in experimental studies, especially in nonlinear and complex data structures, and even in the presence of uncertainty in geochemical and geophysical parameters. Among the ML algorithms, random forest (RF), artificial neural network (ANN), linear regression (LR), voting, and extreme gradient boosting (XGBoost) algorithms were used in this study. According to the results obtained, the XGBoost model exhibited the most robust predictive performance, evidenced by the highest correlation coefficient (R) (0.922) and the lowest mean absolute error (0.666). XGBoost also demonstrated its durability and stability by achieving the lowest relative absolute error (18.81%) and root mean square error (41.10%). Therefore, it has been understood that significant time and resource savings can be achieved in important projects by eliminating the need for experimental tests.

1. Introduction

Geological materials that are the raw materials of many industries are produced by mining activities. Ore production in underground mining operations causes the formation of large stopes that can lead to various geotechnical engineering problems, such as collapse and subsidence. In most cases, these stopes are reinforced by filling with an appropriate material to ensure geotechnical stability. The filling process can be carried out using various methods and materials [1,2].

The extracted ores are usually subjected to various mineral processing operations, which result in large amounts of tailings. It is estimated that the amount of tailings produced worldwide exceeds 100 billion tons per year [3,4]. The storage and disposal of tailings is one of the biggest challenges facing the mining industry. These tailings are usually stored in tailings dams; however, this method has disadvantages, including the cost of constructing the tailings dams, the fact that they cover large areas, and the risk of collapse.

Mine tailings are the most preferred filling material and can be applied by various methods. When high filling strengths are needed, the tailing particles forming the filling material can be bound together using cement. This filling material plays a very important role in ensuring the stiffness of the support systems of the cemented mixtures [5]. This method is called cemented paste backfill (CPB). For CPB production, mine tailings (70–85% by weight) are mixed with binders such as cement (2–10% by weight of tailings), and water (15–30% by weight) is added to ensure fluidity [6,7,8,9,10]. Several additives can be also added to the CPB mixture for the desired purposes. One of the most important technical parameters when using cemented paste backfill with fly ash is the transportation of the mixture. Two techniques are suggested for this phenomenon. In the dry waste technique (DWT), the dry waste is transported into the mine pneumatically, mixed underground, and pumped as a thin liquid or paste. In the other method, known as the hydraulic backfill technique (HBT), the mixture is prepared at surface facilities and pumped underground via shafts and pipelines [11].

The primary binder material used in CPB is Portland cement (PC), which constitutes a significant portion of the operational costs. In this context, various studies have been carried out to reduce the cement content of CPB by using natural or artificial pozzolanic materials as secondary binders (substitution materials) while ensuring the desired strength and durability. One of the pozzolanic materials used as a cement substitute is fly ash (FA), which is the fine-sized residue (1–150 μm) of pulverized coal combusted in thermal power plants. Due to increasing energy demands, coal consumption and the resulting amount of FA are also increasing. More than 500 million tons of FA are produced annually worldwide [12].

FA, which is prevented from leaving the chimney with combustion gases by electrostatic filters or cyclones, is stored in silos. Since the very fine-grained amorphous structure containing silicate and alumina in the FA reacts with slaked lime (calcium hydroxide, CaOH₂), fly ash exhibits pozzolanic properties. When the hydration products of cement combines with calcium hydroxide in an aqueous medium, the products develop hydraulic binding features. Therefore, they can be used directly both in the production of Portland-pozzolan-type cement and as a concrete additive. The amount of FA in the concrete mixture can vary between 15% and 50% of the cement weight. Utilizing FA in concrete has advantages such as reducing clinker use, energy consumption, and greenhouse gas emissions [13,14,15].

Therefore, FA can also be used in CPB mixtures as a cement substitute. FAs are divided into two classes, F and C, per the standard of ASTM C 6l8 [16]. The basic compounds of FAs are silica and alumina, and the contents of SiO₂, Al₂O₃, Fe₂O₃, and CaO vary according to the class of the FA. The class of FA, its chemical composition, and its cement substitution ratio affect the strength of CPB considerably. In addition, since the physical and chemical properties of the tailings used in CPBs differ, the interaction of FA with the tailing also varies. For these reasons, there is no standard in terms of the class and substitution ratio that can be used in cement substitution to achieve the desired strength level in the CPB mixture. As a result, the effect of the variables in the CPB mixture on the strength of the CPB is measured by performing separate uniaxial compressive strength (UCS) tests in each condition.

Meanwhile, there have been major developments in the fields of data analysis and computer programming in recent years. In this context, data mining, artificial intelligence (AI), and machine learning (ML) have been successfully applied in the fields of engineering and technology. In the construction sector especially, ML techniques have been used to predict concrete slump flow [17,18], to predict concrete compressive strength [19,20,21,22], and to detect cracks in concrete surfaces [23]. In another study, ML methods were applied to predict the compressive strength of fly ash-added mortar and concrete samples with different properties [24,25]. In addition, ML techniques have been used to predict the fracture toughness of rock structures in the mining discipline [26].

In a recent study, He et al. [27] proposed a novel evolved RF model utilizing a bio-objective optimization approach. Initially, the beetle search algorithm (BAS)-based evolved RF model was created to predict CPB’s uniaxial compressive strength (UCS). Mishra et al. [28] investigated the effects of partially replacing ordinary Portland cement (OPC) with FA on the strength of CPB, aiming to determine the optimal mixture to achieve the required strength (1 MPa at 28 days of curing) cost-effectively using a Bayesian network (BN). Traditional models follow the aleatory principle and are deemed unsuitable for geotechnical engineering. Thus, a BN model was developed and tested. The reliability of two classifiers within the learning model structure was compared, with the naïve Bayes algorithm being identified as the most reliable tool. Qi et al. [29] discussed the applicability of using a deep neural network (DNN) model to predict the UCS of CPB. This study established the first global dataset of UCS values for CPB through a literature review and laboratory studies. Hu et al. [30] noted that the long-short term memory neural network (LSTM) they developed exhibited the highest prediction accuracy for CPB strength compared to other commonly used prediction models under multifactorial conditions. Tran [31] utilized eight ML techniques, including XGBoost, gradient boosting, RF, decision trees (DT), k-nearest neighbor (KNN), support vector machine (SVM), multivariate adaptive regression splines (MARS), and Gaussian process to create a soft-computing model for predicting the yield stress of CPB. Xiong et al. [32] optimized the XGBoost model using the whale optimization algorithm (WOA) to create a hybrid model for predicting the UCS of cemented backfill. Their results indicated that the proposed WOA–XGBoost approach exhibited superior prediction accuracy compared to other ML models, validating WOA’s capability to enhance XGBoost for predicting the fill strength of cemented phosphate tailings. Kurniati et al. [33] evaluated three ML models, a simple linear model, Gaussian process, and an RF model, aiming at predicting the compressive strength of cement pastes containing copper mining tailings, and considering varying amounts of tailings, water-to-binder ratios, and curing time. Hyperparameters in the RF model were fine-tuned using Bayesian optimization. Following a comprehensive evaluation of the models, it was found that the RF model accurately predicted the compressive strength of the cement paste across mixture designs. Additionally, it was noted that cement, ground granulated blast-furnace slag, superplasticizers, and curing times positively influenced compressive strength.

In light of the studies in the literature, this article aims to develop an ML model that effectively and accurately determines the compressive strength of FA-modified CPB samples in terms of time, effort, and cost. For this purpose, the strength results of CPB samples with various proportions of C and F class FA in the study of Tuylu [34] were used. Strength prediction was performed with various ML and ensemble ML (EML) models using a dataset containing observed physical and chemical properties of samples with various FA ratios. The prediction model with the highest accuracy was built based on features such as mixing ratios and curing time related to the constraints of each mixture. Successful results were obtained with ML and EML models, and the prediction performance results were compared. As a result of this study, the predictive success of XGBoost and EML methods has been revealed.

ML methods can make predictions and inferences; however, they require expert input for creating a strategy. These methods require experimental data, and they are particularly useful for assisting decision-making in time-consuming processes like concrete testing. Identifying the right features enhances the accuracy of the predictions. However, interpreting results still necessitates expert intervention to ensure reliable conclusions.

2. Materials and Methods

2.1. UCS Tests

In the study of Tuylu [34], the tailings of a Pb-Zn underground mine located in Balıkesir/Balya (Turkey), where the production is carried out with cut-and-fill method and stopes are generally filled with the cemented tailings, were used. In the production stage of the mine, the tailings are discharged to tailings dams at a 15%–20% solid-in-pulp ratio at the end of the beneficiation circuit, which includes crushing, grinding, flotation, and thickening processes. Tuylu [34] prepared CPB samples by mixing these discharged tailings with various cement-substituted FA materials. CEM-I 42.5 R Portland cement was used as the main binder in CPB production.

In the study of Tuylu [34], FAs were supplied from the various thermal power plants of Turkey, which combust hard coal and lignite at various ranks, namely, Catalagzi-Zonguldak, Soma-Manisa, Yatagan-Mugla, and Tufanbeyli-Adana, and coded as CFA, SFA, YFA, and TFA, respectively, for the experiments. The physical properties and chemical analysis of the CPB components are given in

Table 1. The physical properties of the CPB components.

Component	D10	D30	D50	D60	D90	≤20 μm	>45 μm	>90 μm	Specific Gravity
Balya Tailing	2.5	11.5	30	45	140	42%	40%	12%	3.2
Portland Cement	2.5	8.7	15	20	50	60%	13%	0.1%	3.1
CFA	3.5	9	15	20	120	60%	22%	13%	2.6
SFA	8	15	38	55	145	35%	45%	25%	2.4
YFA	7	15	20	38	155	50%	35%	16%	2.2
TFA	5	20	37	45	90	30%	40%	10%	2.7

and

Table 2. The chemical analysis of the CPB components.

Component (%)	SiO2	Al2O3	Fe2O3	CaO	MgO	K2O	Na2O	* S/** SO3
Balya Tailings	36.2	8.1	13.6	23.3	2.5	2.6	≤0.5	* ~8
Portland Cement	19.9	4.8	3.4	61.6	1.3	0.9	≤0.5	** ~4
CFA	53.4	26.2	6.5	4.1	2.3	4.2	≤0.5	** ~1
SFA	45.1	23.4	4	19.1	1.7	1.3	≤0.5	** ~5
YFA	46.3	23.1	6.5	13	2.8	2.4	≤0.5	** ~3
TFA	33.7	19.8	4.5	22	2.2	1.6	≤0.5	** ~14

* indicates S content, ** indicates SO₃ content.

, respectively.

As stated by Brackebusch [35], one of the important parameters in the pumpability of paste filling is the ratio of the −20 µm particles in the tailing material, which was 42% for the Balya tailings, as seen in Table 1. Meanwhile, it is stated in the standard of EN 196-6 [36] that particles sized greater than 90 µm in cement, which is the most important material affecting strength, should make up less than 14% of the total. Obtaining high strengths at the end of the hydration process depends on the cement particles being active, and this activity is achieved by finely grinding the cement to under 45 μm. Therefore, the same conditions apply to the size of the FA to be used as a substitute material for cement.

These FAs are partially or completely spherical because of melting at high temperatures and subsequent rapid cooling [37]. Their bulk density is 0.994 g/cm³, specific gravity is 2.288, humidity is 3.14%, average particle size is 6.92 μm, and porosity is about 40%–50% [11]. Class F FAs are produced from bituminous coal with a SiO₂ + Al₂O₃ + Fe₂O₃ content of more than 70%. They have pozzolanic properties. On the other hand, Class C FAs are formed from the combustion of lignite or semi-bituminous coals, and the total amount of SiO₂ + Al₂O₃ + Fe₂O₃ is more than 50%. Class C FAs have binding properties as well as pozzolanic properties. FAs also contain the alkali oxides of MgO and SO₃ as minor components [37]. The chemical composition of FAs according to major oxides is given in Table 2.

In Table 2, it is seen that the total SiO₂ + Al₂O₃ + Fe₂O₃ values for CFA, SFA, YFA, and TFA are 86%, 72%, 76%, and 58%, respectively. These values show that CFA, SFA, and YFA are in class F, while TFA is in class C. Meanwhile, these FAs are also divided into three groups related to their chemical structure. Silicate-alumina (SiO₂-Al₂O₃)-based FAs are generally in class F and are sourced from hardcoal. On the other hand, silicate-calcite (SiO₂-CaO)-based class C FAs and sulfur-calcite (CaO-SO₃)-based FAs are mostly in class C, and are generally sourced from lignite. Class C FAs have cement properties as well as pozzolanic properties and can resist the acid potential of mine tailings due to their high calcium content. It is seen in Table 2 that SFA and TFA are closer to each other in terms of their CaO content.

From the slump test [38] results applied to the mixture material with a solids ratio of 70%–85%, the optimum solids ratio for CPB was determined as 80% by Tuylu [34]. Then, the solid material was mixed with cement at ratios of 3, 5, 7, 9, and 11% of its weight to form CPB reference samples. A concrete mixer was used to prepare the mixture of tailing material, binder, and water homogeneously. The mixing process was carried out for 7 min as in Ghirian and Fall [39]. The prepared paste fill mixture was poured into cylindrical sample molds with a diameter of 5 cm and a height of 10 cm. Uniaxial compressive strength (UCS) tests were performed on these reference samples (without FA substitution) according to the standard of ASTM C39 [40] at the end of 28, 56, 90, and 200 days of curing at 80% humidity and 22 °C temperature. Five samples from each mixture were used, and the arithmetic average was reported as the test result (as seen in

Table 3. The UCS test results for the reference CPBs (without FA substitution) at various cement ratios and curing times.

Solids Ratio (%)	Cement Ratio (%)	UCS (MPa) over Curing Time
		28 Days	56 Days	90 Days	200 Days
80	3	0.53	0.94	0.55	0.41
80	5	1.57	1.93	2.36	1.92
80	7	2.55	3.31	3.88	3.37
80	9	3.81	5.59	5.67	5.93
80	11	4.93	8.08	6.38	6.62

).

Mechanical characterization is important to the design and analysis of CPB structures [41]. For the paste filling mixture to provide roof support, the required minimum strength value of 4 MPa was taken into account as in Belem and Benzaazoua [42], and the cement ratios providing these strength values were determined. FA was added in mixtures as a substitution material for cement at ratios of 20, 30, 40, and 50% by weight of the cement. UCS tests were carried out at the end of 28, 56, and 90 days under the same curing conditions as the reference samples. UCS results for CPBs containing 9% and 11% total binder (cement + FA) at various curing times along with the reference UCSs are given in

Table 4. UCS results for CPBs containing 9% total binder (cement + FA) at various curing times, along with the reference UCSs.

FA Subs. Ratio (%)	UCS (MPa) over Curing Time
	28 Days (Reference UCS = 3.81 MPa)				56 Days (Reference UCS = 5.59 MPa)				90 Days (Reference UCS = 5.67 MPa)
	CFA (MPa)	SFA (MPa)	YFA (MPa)	TFA (MPa)	CFA (MPa)	SFA (MPa)	YFA (MPa)	TFA (MPa)	CFA (MPa)	SFA (MPa)	YFA (MPa)	TFA (MPa)
20	2.14	5.27	2.14	3.79	2.31	7.26	5.94	4.18	3.25	6.96	3.95	5.9
30	2.56	5.44	3.2	3.78	2.38	6.22	6.33	4.07	1.69	5.35	4.63	5.81
40	2.46	5.74	3.4	3.07	2.65	6.23	5.78	3.54	2.57	5.49	3.81	5.75
50	1.75	4.85	3.14	2.47	3.66	6.09	3.32	2.87	3.66	6.14	2.82	5.73

and

Table 5. UCS results for CPBs containing 11% total binder (cement + FA) at various curing times along with the reference UCSs.

FA Subs. Ratio (%)	UCS (MPa) over Curing Time
	28 Days (Reference UCS = 4.93 MPa)				56 Days (Reference UCS = 8.08 MPa)				90 Days (Reference UCS = 6.38 MPa)
	CFA (MPa)	SFA (MPa)	YFA (MPa)	TFA (MPa)	CFA (MPa)	SFA (MPa)	YFA (MPa)	TFA (MPa)	CFA (MPa)	SFA (MPa)	YFA (MPa)	TFA (MPa)
20	0.69	4.94	4.86	6.49	4.67	8.13	6.32	7.45	9.82	7.13	4.4	10.33
30	2.97	5.09	5.91	5.55	5.36	6.65	7.65	7.17	8.29	6.37	5.84	10
40	2.7	5.53	4.74	6.73	5.1	9.1	6.28	6.79	6.91	7.35	4.08	9.85
50	1.76	5.86	4.58	6.09	1.73	7.05	6.61	6.55	6.32	6.42	4.27	9.65

, respectively. As seen in the 200-day strength results of the paste materials in Table 3 and the 90-day strength results of the paste materials with 9% and 11% cement substitution in Table 4 and Table 5, the strengths of these materials were very close to each other. Therefore, a maximum of 90 days of curing time was considered in the FA substituted samples. Furthermore, since the binder ratio could not provide sufficient resistance against sulfate attacks that occur in the mixture material in the long term, the 200-day UCSs of the CPBs at 3%, 5%, and 7% cement ratio decreased slightly compared to that of the 90-day UCSs.

2.2. ML Methods

ML methods are primarily used for prediction and inference. However, they cannot independently create strategies without expert intervention. Since these methods learn from experimental data, they require a sufficient dataset to make accurate predictions. ML methods are particularly advantageous in scenarios where rapid decision-making is required, such as in concrete testing, where curing processes are considerably time-consuming. These methods offer various benefits to decision-makers by accelerating workflows. Moreover, if the appropriate features are identified for the related study, the predictive accuracy of the models can be substantially improved. Despite the advancements in modern computational techniques, the interpretation of their results still requires field experts with adequate knowledge of the fundamental discipline to ensure meaningful and reliable conclusions.

In the development of ML models for this study, the Python 3.9 programming language and Scikit-Learn library were used.

2.2.1. Linear Regression (LR)

Linear regression (LR) is a statistical technique that quantifies the relationship between two continuous variables. These variables are referred to as the dependent variable, which is the variable to be predicted, and the independent or predictor variable. The method operates by finding a line that minimizes the squared error for each data point. To express this mathematically, a dataset of $X={\left\{\left(x_i,y_i\right)\right\}}_{i=1 }^l$ where $\left(x_i,y_i\right)ϵR^{n+1}$ should be assumed. The linear relationship between the independent variables of $X={\left\{\left(x_i\right)\right\}}_{i=1}^l$ and the dependent variable “y_i” can be defined as in Equation (1) [43].

$$y_i=x_i^{T}w+{\epsilon }_i$$

(1)

LR aims to minimize the error between the predicted and the actual values. In this regard, the optimization problem can be formulated as in Equation (2).

$$\min {\displaystyle \frac{{\sum }_{i=1}^l{\left(y_i-{\overline{y}}_i\right)}^2}{l}}$$

(2)

2.2.2. Random Forest

Breiman [44] created an ensemble learning method of RF with the primary goal of improving classification and regression trees (CART). By employing a bagging method, this approach aggregates a significant number of decision trees [45]. It also makes it possible to build subtrees that incorporate features that are chosen randomly. Interestingly, the trees that the algorithm creates are not subjected to pruning. Because so many random trees are formed, the random tree algorithm can attain a high accuracy rate in evaluations. This algorithm’s capacity to successfully handle the overfitting issue frequently connected to decision trees is among its most important benefits [46].

However, the main drawback of the RF method is that it may become slow and ineffective for real-time predictions if there are a lot of trees [45]. To lessen overfitting and increase prediction accuracy, RF uses strategies including random feature selection and bagging (bootstrap aggregating). Meanwhile, its guiding concepts can be summarized as follows [44]:

• “B” bootstrap samples are created by randomly selecting “n” samples with replacement from the training dataset.
• “n” randomly chosen and replaced data points from the original dataset make up each bootstrap sample.
• Every bootstrap sample is used to train a decision tree “T_bis”.
• Using “m” features selected randomly from the “p” available features, the optimal split is found at each node.
• Every tree makes a prediction, and the model’s ultimate prediction is the class that receives the most votes overall.

We can summarize the RF algorithm in general with Equation (3).

$$\widehat{y}=mode\left(\left\{{\widehat{y}}_b:b=\mathrm{1,2},\dots ,B\right\}\right)$$

(3)

where $\widehat{y}$ indicates the RF model’s categorization prediction; ${\widehat{y}}_b$ represents the individual prediction made by tree b; b = 1,2,…, B indexes the trees, where B is the number of trees overall; and mode is a statistical metric that chooses the value that appears the most frequently, hence selecting the class that is most frequently predicted out of all trees.

2.2.3. Artificial Neural Networks (ANN)

A computational system that uses linked processing units to solve a problem collectively is called an ANN. Finding patterns in input and output data is its main goal in order to simulate how the human brain works [47]. The brain’s neural structure is the source of the basic idea of ANNs. Multiple interconnected layers of neurons make to a basic ANN architecture. The input layer is the initial layer in which the number of neurons is equal to the number of data features (including bias values). The subsequent layer, known as the hidden layer, plays a critical role in capturing non-linearity. There is no definitive rule for determining the number of neurons in the hidden layer; instead, heuristic methods and statistical approaches are commonly suggested. The final layer in the ANN architecture is called the output layer, where the number of neurons corresponds to the number of output classes [45].

ANNs and biological neural networks also have certain similarities. The many basic processing units, or neurons, that make connections with one another make up a neural network. Every connection is given a particular weight. Because they require fewer assumptions and can accurately describe non-linear interactions with the right activation functions, ANNs have a number of advantages over conventional statistical methods. Similar to humans, who use learned information to make logical conclusions, trained ANNs can generate results even in the absence of sufficient input. The ablation of some neurons does not cause data loss because the data is dispersed throughout the network [47].

The multi-layer perceptron (MLP), one of the most popular and extensively utilized ANN variants nowadays, is made up of many completely connected layers of nodes (neurons). Finding non-linear correlations between inputs and outputs is the main goal of an MLP [48,49]. Feeding the weighted total of input values to each layer is the crucial step. The value of a linear combination of the nodes that came before it is sent to each neuron. The weights are then modified using a technique known as backpropagation training in order to reduce mistakes. Backpropagation has demonstrated encouraging results among the different methods used to assess the performance of ANNs. This technique computes both the total output error and the contribution of each neuron to that error.

2.2.4. Extreme Gradient Boosting (XGBoost)

ANNs are extensively employed across various domains, particularly in classification, modeling, and prediction tasks. Among the advanced algorithms related to neural networks, the XGBoost method stands out as an innovative ML approach. First introduced by Chen and Guestrin [50], the original publication garnered significant attention from data scientists [47].

XGBoost is an optimized extension of the gradient boosting algorithm. While traditional gradient boosting utilizes first-order functions (such as gradients) to compute the loss function, XGBoost leverages second-order functions (Hessians) to achieve more accurate optimization [50]. This refined optimization process is one of the primary factors contributing to the widespread adoption of this method.

In the construction of decision trees, XGBoost imposes limits on the maximum tree depth. When a tree becomes excessively deep, the algorithm performs pruning to mitigate the risk of overfitting [50].

XGBoost operates within the boosting framework, an ensemble technique that sequentially combines multiple weak learners, typically decision trees, to create a strong learner [51]. A key feature of XGBoost is its focus on the optimization of a regularized objective function, which aims to balance the trade-off between model accuracy and complexity [46]. In this framework, f_k refers to the regularization term, expressed as Ω(f_k):

$$\mathsf{\Omega }\left(f_k\right)=\gamma T+\mathrm{½}\lambda {\left|\right|W\left|\right|}^2$$

(4)

where T is the number of leaves in the tree; W is the scores associated with the leaves; γ is a parameter controlling the complexity of the model; and λ is a regularization parameter that controls the magnitude of the leaf weights.

2.2.5. Performance Metrics

In this study, correlation coefficient “R”, root mean square error “RMSE”, mean absolute error “MAE”, relative absolute error “RAE”, and root relative squared error “RRSE” were used as performance metrics to evaluate the prediction accuracy of the proposed models. Performance metrics are described in

Table 6. Performance metrics.

Correlation Coefficient (R): A widely used metric to assess how well the R curve matches the data. When the actual values and the anticipated values coincide perfectly, the values have the same tendency, as indicated by a value of 1.	$R={\displaystyle \frac{n\sum y{y}^{\prime }-\left(\sum y\right)\left(\sum y^{\prime }\right)}{\sqrt{n\left(\sum y^2\right)-{\left(\sum y\right)}^2}\sqrt{n\left(\sum {y^{\prime }}^2\right)-{\left(\sum y^{\prime }\right)}^2}}}$
Mean Absolute Error (MAE): The MAE value is a metric used to assess how well predictions match actual outcomes. By disregarding the direction of the mistakes, it determines the average size of the discrepancies between the expected and actual numbers.	$MAE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}\left|y-y^{\prime }\right|$
Root Mean Square Error (RMSE): To determine the square root of the total value and the square error of the prediction compared to the actual values, RMSE is computed. Thus, it is the mean distance along a vertical line between a data point and the fixed line. This tool effectively identifies undesirable large differences.	$RMSE=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^n\sum {\left(y^{\prime }-y\right)}^2}{n}}}$
Relative Absolute Error (RAE): The ratio of the absolute difference between the actual and anticipated values to the actual values is known as the RAE value.	$RAE={\displaystyle \frac{\left|{y^{\prime }}_1-y_1\right|+\cdots +\left|{y^{\prime }}_n-y_n\right|}{\left|y_1-\overline{y}\right|+\cdots +\left|y_n-\overline{y}\right|}}$
Root Relative Squared Error (RRSE): The square root of the sum of the squares of the differences between the actual and predicted values and the sum of the squares of the differences between the actual and mean values is the correct root square error, or RRSE value.	$RRSE=\sqrt{{\displaystyle \frac{{\left({y^{\prime }}_1-y\right)}^2+\cdots +{\left({y^{\prime }}_n-y_n\right)}^2}{{\left(y_1-\overline{y}\right)}^2+\cdots +{\left(y_n-\overline{y}\right)}^2}}}$

, where $y^{\prime }$ is the predicted value; y is the real value; and n is the number of data samples [52].

2.2.6. Dataset Description and Preparation

In machine learning applications, the quality of input data significantly impacts the accuracy and reliability of the model. To ensure robust predictions, all experiments in this study were conducted in accordance with established standards, ensuring consistency and validity. Additionally, a sufficient amount of experimental data were collected to enable effective data processing and model training. This approach minimizes potential biases and enhances the reliability of the ML model in predicting the strength of CPBs with various fly ash substitutions.

To create a dataset with features such as mixing ratios and different curing times, data obtained from the experimental study of Tuylu [34] were used to predict the strengths. In this context, a dataset containing 116 instances was created from 580 UCS tests containing four different FA materials cured for 28, 56, and 90 days under conditions in accordance with the ASTM C39 [40] standard. The dataset creation process is shown in Figure 1.

Table 7. Dataset of the CPB samples.

Exp.	FA (% of FA + Cement)	FA + Cement (% of Total Mass)	Cement (% of Total Mass)	Water (% of Total Mass)	Tailings (% of Total Mass)	FA (% of Total Mass)	Curing Time (Day)	CFA	SFA	YFA	TFA	Strength (MPa)
1	0	3	3	20	77	0	28	0	0	0	0	0.53
2	0	3	3	20	77	0	56	0	0	0	0	0.94
3	0	3	3	20	77	0	90	0	0	0	0	0.55
4	0	3	3	20	77	0	200	0	0	0	0	0.41
.	.	.	.	.	.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.	.	.	.	.	.
112	50	11	5.5	20	69	5.5	90	0	0	1	0	4.27
113	20	11	8.8	20	69	2.2	90	0	0	0	1	10.33
114	30	11	7.7	20	69	3.3	90	0	0	0	1	10
115	40	11	6.6	20	69	4.4	90	0	0	0	1	9.85
116	50	11	5.5	20	69	5.5	90	0	0	0	1	9.65

shows the experimental dataset used in this study. The water ratio (%) among the 11 available attributes was 20% in all samples, and the FA ratio (%) was not included in the analysis because it was a related value calculated from the FA amount.

One of the most important problems that can be encountered in CPB datasets is the possibility of finding tailings with different chemical compositions originating from different mines. Additionally, the compressive strength of CPB is determined not only by the water/cement ratio, but also by other materials used in the mixture. The multiple components in CPB structures make it difficult to predict the compressive strength. For this reason, LR, RF, ANN, voting, and XGBoost algorithms, which are mentioned in the methodology section of the study and whose estimation success has been proven, were used in the CPB compressive strength prediction model with the prepared dataset. The created data set was examined before the analysis, and it was seen that there were no missing or outlier values.

3. Results and Discussion

3.1. Performance Evaluation of ML Models

The recent studies in the field of ML indicate that XGBoost, ANN, RF, and EML algorithms, which are state-of-the-art and popular algorithms, can provide high accuracy in complex systems. Therefore, XGBoost, ANN, RF, LR, and voting algorithms are used in this study. Statistical metrics such as R, MAE, RMSE, RAE, and RRSE were used to compare the prediction performance results. The performance metric values of RF, ANN, LR, XGBoost, and RF + ANN voting ensemble models are given in

Table 8. Performance metrics of predictive models.

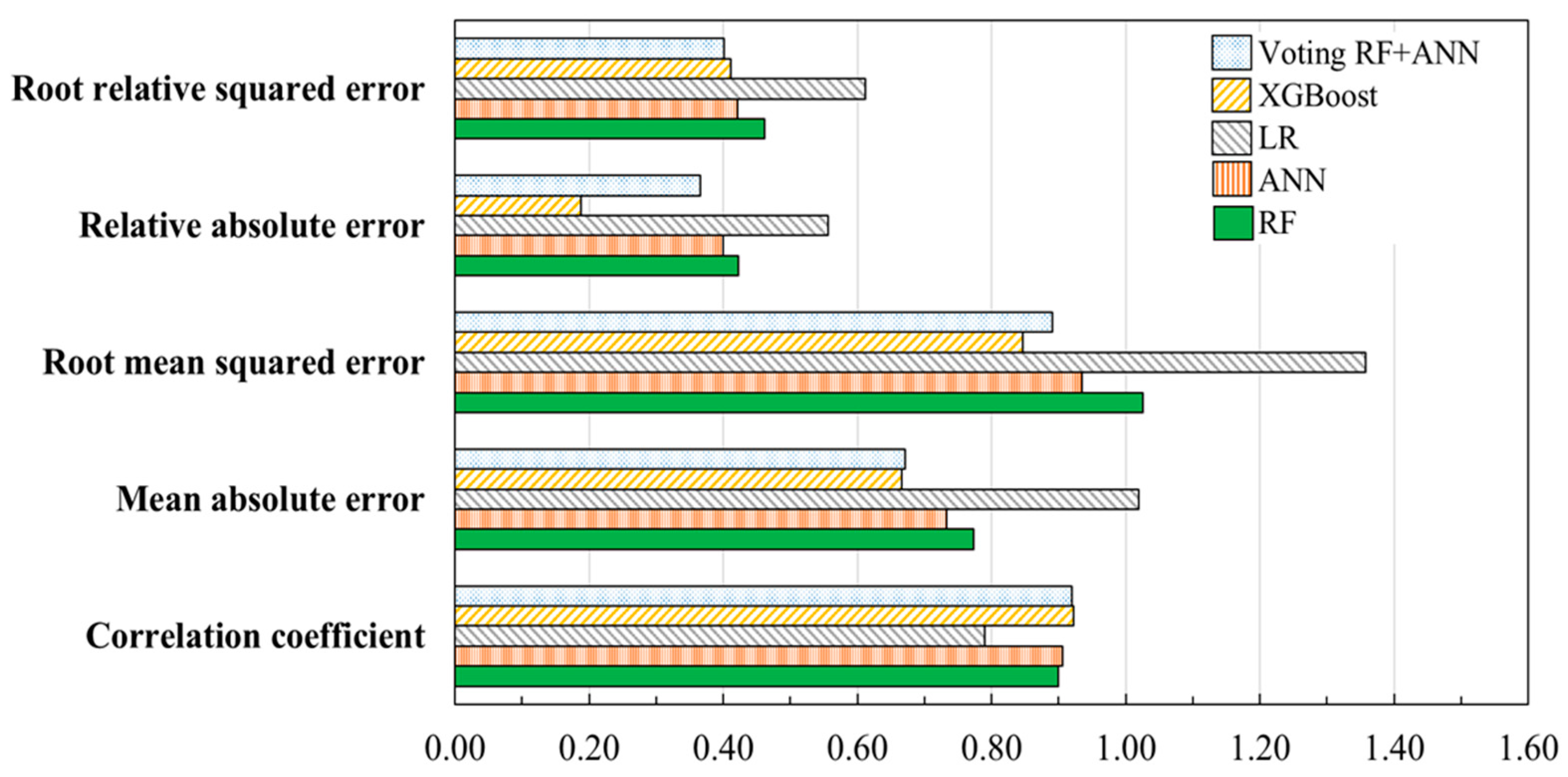
Performance Metrics	RF	ANN	LR	XGBoost	Voting RF + ANN
Correlation coefficient	0.8999	0.9065	0.7902	0.922	0.9192
Mean absolute error	0.7737	0.7333	1.0198	0.666	0.6712
Root mean squared error	1.0263	0.935	1.3571	0.847	0.8903
Relative absolute error (%)	42.23	40.03	55.67	18.81	36.64
Root relative squared error (%)	46.23	42.12	61.13	41.10	40.10
Total number of instances	116	116	116	116	116

.

The XGBoost model showed the strongest prediction performance with the highest correlation coefficient (0.922) and lowest MAE (0.666) values. In addition, XGBoost confirmed its robustness and stability with the lowest relative absolute error (18.81%) and root mean square error (41.10%). According to the obtained outputs, the most accurate results and the lowest error performance values were achieved with the XGBoost model. In this context, the parameters used in the XGBoost model are shown in

Table 9. Parameter values of XGBoost model.

Parameters	Values
tree_method	auto
seed	701,232,104
max_depth	6
booster	gbtree
min_split_loss	0
objective	eg:squarederror
lambda	1
nthread	7
alpha	0
subsample	1
learning_rate	0.3
min_child_weight	1
verbosity	0
Boosting iterations	75

. Optimum parameter values were determined using the grid search method.

The RF + ANN voting ensemble model, which has values very close to the XGBoost model, showed competitive performance with a correlation coefficient of 0.9192 and an MAE of 0.6712. In addition, LR, a traditional modeling approach, was the least successful model with the lowest correlation coefficient (0.7902) and the highest error metrics. As a result, it was revealed that the Boosting and Ensemble methods are valid and reliable in compressive strength prediction.

3.2. Comparison of Actual and Predicted Values

The results of comparing the actual compressive strength values with the predicted values predicted by the modelers are given in

Table 10. Actual and predicted values of each model.

Instance	Actual	RF Predicted	ANN Predicted	LR Predicted	Voting RF + ANN Predicted	XGBoost Predicted
1	1.75	2.864	1.963	1.963	2.413	2.935
2	5.93	4.843	6.388	6.388	5.616	4.998
3	4.18	4.652	3.594	3.594	4.123	4.876
4	7.35	6.532	5.996	5.996	6.264	7.982
5	0.53	1.241	−0.521	−0.521	0.36	0.814
.	.	.	.	.	.	.
.	.	.	.	.	.	.
.	.	.	.	.	.	.
112	3.81	4.231	4.382	4.382	4.307	3.158
113	5.59	5.272	5.774	5.774	5.523	6.027
114	3.66	3.128	2.309	2.309	2.719	3.344
115	7.65	6.297	6.278	6.278	6.287	6.937
116	5.55	6.375	6.24	6.24	6.308	6.209

. The XGBoost model was the model that gave the results closest to the actual values with the lowest error rates. The ANN and RF models also achieved satisfactory results, and the Voting RF + ANN model, which combines the individual strengths of RF and ANN, also predicted reliable results close to the results obtained with the XGBoost method. The performance metric values of the models are shown in Figure 2.

The deviation amounts between the actual and predicted UCS values are given in Figure 3. It is seen from the databased error amount that the traditional algorithms show similar behavior in terms of deviation direction. It is understood from the deviation directions and amounts of the XGBoost algorithm that it makes different and balanced predictions in terms of behavior. This situation has shown that the XGBoost algorithm is particularly sensitive to outliers and has the ability to make reliable and accurate predictions even in complex datasets. Although the RF model could not reach the results obtained with the XGBoost method, it has shown its ability to provide stable solutions in complex, non-linear datasets with its ensemble structure.

This study aimed to optimize the prediction of UCS in CPB by employing various ML models. The results demonstrated that the XGBoost model outperformed other methods with the highest correlation coefficient (R = 0.922) and the lowest mean absolute error (MAE = 0.666). The ensemble RF + ANN model also showed a competitive performance with R = 0.9192. The findings of this study align with the results of Qi et al. [29], who used a DNN model for UCS prediction in CPB and achieved an R-value of 0.989 in training and 0.967 in testing. Their study emphasized that the cement-to-tailings ratio is the most influential factor in UCS prediction, which is consistent with the feature importance analysis in the XGBoost model of this study. Similarly, Kurniati et al. [33] explored ML-based predictions for cement pastes incorporating copper mine tailings (CMT) as supplementary cementitious materials (SCMs). Their results showed that RF models provided reliable UCS values and predictions with respect to curing time and water-binder ratio, supporting our observation that ensemble-based models like RF + ANN improve prediction accuracy. Moreover, He et al. [27] proposed a bi-objective optimization approach using an evolved RF model for the prediction of UCS and cost efficiency in CPB. While our study did not explicitly focus on cost reduction, it focused on the prediction of the UCS by XGBoost at high accuracy.

4. Conclusions

Geotechnical problems can be prevented and the need for storage space on earth for tailing is reduced by the use of cemented paste backfill (CPB) produced with mine tailings. Within the scope of studies carried out to develop this advantageous CPB method, this study aimed to contribute to tailings management in mining by using machine learning (ML) methods, which is a subfield of artificial intelligence.

Considering the costly and time-consuming nature of traditional laboratory tests, artificial intelligence applications may serve as a significant alternative method for determining the compressive strength of CPB. The rapid advancement of artificial intelligence technologies today allows for the acquisition of precise and swift results. This study aimed to predict the compressive strength of CPB using ML based on a specific dataset. A dataset comprising factors influencing CPB strength was prepared and made suitable for analysis. The dataset was modeled and analyzed using linear regression (LR), random forest (RF), artificial neural network (ANN), voting (RF + ANN), and extreme gradient boosting (XGBoost) algorithms.

As a result of this study, the prediction methods modeled with ML methodology have reached satisfactory results, very close to the experimental study results. The highest correlation coefficient and the lowest mean absolute error values were obtained with the XGBoost (R: 0.922, MAE: 0.666), voting RF + ANN (R: 0.9192, MAE: 0.6712), and ANN (R: 0.9065, MAE: 0.7333) models, respectively. These findings demonstrate that the developed ML-based prediction model is highly successful in predicting the compressive strength of fly ash (FA)-substituted CPB. Consequently, artificial intelligence techniques offer opportunities to predict compressive strength results more rapidly and significantly reduce costs. This study proves that ML techniques can generate valuable and potentially productive studies within the framework of the mining engineering discipline.

The findings of this study present a promising method for future research and applications in the field of sustainable mining. The findings provide an innovative approach in the field of predictive modeling, especially in terms of increasing productivity in mining sites and experimental studies. As a result, ML and EML methods such as XGBoost, Voting, and ANN can provide opportunities to researchers and scientists conducting laboratory experiments with their robust and accurate prediction powers, reducing workload, time, and material consumption as a powerful decision support system in their studies. In this way, the developed artificial intelligence-based decision support system provides an opportunity for the minimization of experimental studies.