Next Article in Journal
Advanced 3D Inversion of Airborne EM and Magnetic Data with IP Effects and Remanent Magnetization Modeling: Application to the Mpatasie Gold Belt, Ghana
Previous Article in Journal
Minerals as Windows into Habitability on Lava Tube Basalts: A Biogeochemical Study at Lava Beds National Monument, CA
Previous Article in Special Issue
Crystal Structure Features, Spectroscopic Characteristics and Thermal Conversions of Sulfur-Bearing Groups: New Natural Commensurately Modulated Haüyne Analogue, Na6Ca2−x(Si6Al6O24)(SO42−,HS−,S2●−,S4,S3●−,S52−)2−y
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Minerals
Volume 15
Issue 12
10.3390/min15121304
minerals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Thermal, Structural, and Phase Evolution of the Y2(SO4)3*8H2O–Eu2(SO4)3*8H2O System via Dehydration and Volatilization to Y2(SO4)3–Eu2(SO4)3 and Y2O2(SO4)–Eu2O2(SO4) and Its Thermal Expansion

by
Andrey P. Shablinskii
1,
Olga Y. Shorets
1,
Rimma S. Bubnova
1,
Maria G. Krzhizhanovskaya
2,
Margarita S. Avdontceva
2 and
Stanislav K. Filatov
2,*
1
Grebenchikov Institute of Silicate Chemistry, Makarova Embankment 2, Saint Petersburg 199034, Russia
2
Institute of Earth Sciences, St. Petersburg State University, Universitetskaya Embankment 7/9, Saint Petersburg 199034, Russia
*
Author to whom correspondence should be addressed.
Minerals 2025, 15(12), 1304; https://doi.org/10.3390/min15121304
Submission received: 14 November 2025 / Revised: 9 December 2025 / Accepted: 10 December 2025 / Published: 14 December 2025
(This article belongs to the Special Issue Crystal Chemistry of Sulfate Minerals and Synthetic Compounds)
Browse Figures
Versions Notes

Abstract

The synthesis, crystal structure, phase transformations, and thermal expansion of (Y1−xEux)2(SO4)3*8H2O (where x = 0, 0.17, 0.33, 0.50, 0.66, 0.83, and 1) are presented. (Y1−xEux)2(SO4)3*8H2O solid solutions were synthesized via crystallization from an aqueous solution. (Y1−xEux)2(SO4)3*8H2O (C2/c) ↔ (Y1−xEux)2(SO4)3 (Pbcn) → (Y1−xEux)2O2SO4 (C2/c) and Eu2(SO4)3*8H2O (C2/c) ↔ Eu2(SO4)3 (C2/c) → Eu2O2SO4 (C2/c) phase transformations for all samples were investigated by high-temperature powder X-ray diffraction, differential scanning calorimetry and thermogravimetry in the temperature ranges of 25–750 and 25–1350 °C, respectively. The aim of this work is to identify the structural heredity of the phases formed during thermal transformations of (Y1−xEux)2(SO4)3*8H2O solid solutions, and to study the mechanisms of the thermal deformations of the crystal structure. Structural relations between these phases were found. The crystal structures of YEu(SO4)3*8H2O and (Y0.83Eu0.17)2(SO4)3*8H2O were refined at −173, −123, −73, −23, 27, and 77 °C. Thermal expansion coefficients for (Y1−xEux)2(SO4)3*8H2O, Eu2(SO4)3, (Y1−xEux)2O2SO4 (where x = 0, 0.17, 0.33, 0.50, 0.66, 0.83, and 1) compounds and solid solutions were calculated for the first time. The thermal expansion of Eu2(SO4)3 was highest in the direction approximately coinciding with the c-axis, because the Eu–O chains extended in this direction. As temperature increased, the crystal structure of (Y1−xEux)2(SO4)3*8H2O expanded significantly in the ac plane along directions close to the a and c axes, while thermal expansion along the b axis was relatively low. The distance between layers in the (Y1−xEux)2(SO4)3*8H2O crystal structure increased with increasing temperature, and corrugated layers (parallel to (101) direction) straightened out due to the rotation of the S2O4 tetrahedra. At high temperature, thermal expansion of Y2O2SO4 was highest along the longer diagonal of the ac parallelogram perpendicular to the plane of the oxo-centered 2 ∞ [YO] layers.

Graphical Abstract

1. Introduction

Sulfates are fundamental chemical compounds with significant historical and contemporary relevance across numerous fields, including industry, technology, and environmental science [1]. Sulfates of rare earth elements are widely used in rare earth processing technology at various stages. Sulfuric acid serves as a decomposing agent for raw mineral materials and industrial waste, which are the source of REEs. Aqueous sulfuric acid solutions and rare earth element sulfates are used in rare earth element separation methods [2]. Recently, their optical properties, particularly birefringence in the ultraviolet (UV) region, have garnered significant interest. Sulfates are promising birefringent materials due to their wide transparency window and easy synthesis [3].
Since natural and synthetic sulfates do not form structures based on the polymerization of SO4 tetrahedra (excluding S2O7 pyrogroups), their hierarchy is mainly based on combining SO4 tetrahedra and MO6 octahedra, where M = divalent and trivalent cations. For example, in one of the reviews [4], the following structures were distinguished based on the type of combination of SO4 tetrahedra with MO6 octahedra of di- and trivalent cations: these included structures with unconnected SO4 tetrahedra, structures with finite heteropolyhedral clusters, structures with infinite chains, layered structures of SO4 tetrahedra and octahedra, which were further subdivided into brucite-like and other layers, and heteropolyhedral framework structures. Compounds of SO4 tetrahedra with other polyhedra were also considered. Examples of hydration and dehydration of some sulfate minerals were studied in [5,6].
The structural characterization of rare earth sulfate octahydrates, M2(SO4)3*8H2O, has been largely completed over the past four decades. Early structural determinations of the Sm2(SO4)3*8H2O, Yb2(SO4)3*8H2O, Pr2(SO4)3*8H2O and Nd2(SO4)3*8H2O, Y2(SO4)3*8H2O [7,8,9,10,11] compounds revealed that these octahydrates adopt a single structure type, crystallizing in the centrosymmetric space group C2/c. A comprehensive summary of these and other hydrated rare earth sulfates was later compiled in [2,12]. The thermal decomposition of yttrium and rare earth metal sulfate hydrates was investigated in [13,14,15,16,17,18,19,20]. The cascade of thermal transformations of hydrous sulfates with the release of volatile components is similar to processes that occur in nature, particularly at Kamchatka volcanoes. For example, the discovery of a large number of hydrous sulfate minerals at Tolbachik Volcano [4,5,6] in recent years is associated with sulfate hydration–dehydration processes.
The products of thermal decomposition of the (Y1−xEux)2(SO4)3*8H2O solid solutions exhibit a number of structural similarities with minerals. Y2(SO4)3 sulfate crystallizes in the Al2(WO4)3 structure type; this phase is structurally similar to the garnet crystal structure. These structural relationships are described in detail in [21,22,23]. The removal of the A site from the A3M2(TO4)3 garnet crystal structure results in a framework formed by MO6 octahedra and TO4 tetrahedra. The MO6 octahedra share corners with six TO4 tetrahedra. Therefore, in accordance with [22], the framework of the garnet crystal structure is a distorted form of the Al2(WO4)3 structure type.
The crystal structures of Y2O2(SO4) and Eu2O2(SO4) are closely related to grandreefite Pb2F2SO4 [24]. These crystal structures can be considered in term of anion-centered polyhedra. With this consideration, oxo-centered 2 ∞ [YO] layers of the L12 type can be distinguished in them. Similar layers can be distinguished in the crystal structures of minerals such as litharge PbO, perite PbBiO2Cl, nadorite PbSbO2Cl, bismutite Bi2O2(CO3), bayerite CaBi2O2(CO3), zavaritskite BiOF, bismoclite BiOCl, koechlinite Bi2O2(MoO4), and russellite Bi2O2(WO4) [25].
The aim of this work is to identify the structural heredity of the phases formed during the thermal transformations of (Y1−xEux)2(SO4)3*8H2O solid solutions and to study the mechanisms of thermal deformations of their crystal structures. This paper reports on the synthesis of (Y1−xEux)2(SO4)3*8H2O (x = 0–1) solid solutions, their thermal transformations with the release of volatile components, the thermal evolution of their crystalline structures, and the thermal expansion of their transformation products. The crystal structures of YEu(SO4)3*8H2O and (Y0.83Eu0.17)2(SO4)3*8H2O were refined. The thermal behavior of the samples was studied by high-temperature powder X-ray diffraction (HTPXRD) (25–750 °C), differential-scanning calorimetry (DSC), and thermogravimetry (TG) (25–1350 °C). (Y1−xEux)2(SO4)3*8H2O (C2/c) ↔ (Y1−xEux)2(SO4)3, (Pbcn) → (Y1−xEux)2O2SO4 (C2/c), and Eu2(SO4)3*8H2O (C2/c) ↔ Eu2(SO4)3 (C2/c) → Eu2O2SO4 (C2/c) phase transformations with thermal decompositions were described and structural relations between these phases were investigated. The structural mechanisms of the thermal expansion were described.

2. Materials and Methods

2.1. Synthesis

Seven (Y1−xEux)2(SO4)3·8H2O (where x = 0, 0.17, 0.33, 0.5, 0.66, 0.83, and 1) compounds and solid solutions were synthesized via crystallization from an aqueous solution. Separate supersaturated solutions of Y2(SO4)3 and Eu2(SO4)3 (both 99.99% purity, Vekton, St. Petersburg, Russia) were prepared, mixed in the desired stoichiometric ratios, and allowed to crystallize in Petri dishes. Y2O2(SO4)3 was obtained by heating Y2(SO4)3*8H2O at 1000 °C for 5 h.

2.2. Powder X-Ray Diffraction

Powder X-ray diffraction data for the (Y1−xEux)2(SO4)3*8H2O (where x = 0, 0.17, 0.33, 0.50, 0.66, 0.83, and 1) samples were collected using a Rigaku MiniFlex II diffractometer (Tokyo, Japan) (CuKα, 2θ = 3–60°, step 0.02°, exposition 1s, DS divergence slit 0.625°). Samples were prepared for measurement by precipitation from a heptane suspension. The phase composition was determined using PDXL-integrated X-ray powder diffraction software (Tokyo, Japan) and the PDF-2 2020 (ICDD) database.

2.3. High-Temperature Powder X-Ray Diffraction

In situ HTPXRD measurements were performed on a Rigaku Ultima IV diffractometer (Tokyo, Japan) equipped with an SHT–1500 high-temperature chamber and a PSD DTEX/ULTRA detector. Using CuKα radiation (40 kV, 35 mA) in Bragg–Brentano geometry, patterns were collected over a 2Θ range of 5–70° with a step width of 0.02° and a counting time of ~2 s/step. Samples were heated from 25 to 750 °C at an average rate of 0.4 °C/min.
X-ray phase analysis was conducted using the Rietveld method within the RietveldToTensor software (St. Petersburg, Russia) [26] to refine unit cell parameters at each temperature. The software was subsequently used to calculate the approximation coefficients for the temperature dependence of the unit cell parameters, from which the components, eigenvalues, and figures of the symmetric thermal expansion tensor were derived in a Cartesian crystallophysical coordinate system.
The eigenvalues defined a 3D representation (a second-rank tensor surface) where the length of any radial vector corresponds to the coefficient of thermal expansion in that direction.

2.4. Single Crystal X-Ray Diffraction

The thermal behavior of YEu(SO4)3*8H2O and (Y0.83Eu0.17)2(SO4)3*8H2O was studied by high-temperature single crystal X-ray diffraction analysis using a Rigaku XtaLAB Synergy-S diffractometer (Rigaku, Tokyo, Japan) (MoKα radiation, 50 kV and 1.0 mA) equipped with a high-speed direct-action detector HyPix-6000HE (Rigaku, Tokyo, Japan). The data were collected at −173, −123, −73, −23, 27, and 77 °C. The heating process was controlled by a “Hot Air gas blowers” system (Rigaku, Tokyo, Japan). A single crystal was placed and fixed in quartz capillaries with an approximately 10-micron wall thickness. The hemisphere of diffraction data (frame width 0.5°) was collected for each temperature value. The orientation of the crystals was not changed during all temperature measurements. The CrysAlisPro software (version 1.171.39.44) was used for further processing [27]. An absorption correction was introduced by the SCALE3 ABSPACK algorithm. The crystal structures have been solved and refined using Jana 2006 software [28].

2.5. Differential Scanning Calorimetry

Differential scanning calorimetry (DSC) and thermogravimetry (TG) studies of YEu(SO4)3*8H2O and Eu2(SO4)3*8H2O were performed on NETZSCH STA 429 (NETZSCH, Hanau, Germany) with the use of a standard sample holder for measuring the (DSC) and (TG) curves. The samples, in the form of tablets, were placed in a platinum crucible and heated up to 1350 °C in air at a rate of 20 °C/min. The sample weight was 20 mg. The temperatures of the thermal effects were estimated as onset temperatures. A change in the sample weight was controlled from the TG curves.

2.6. Energy-Dispersive X-Ray Spectroscopy

The chemical composition was studied using a system with focused electron and ion probes, QUANTA 200 3D (FIA, Paris, France), with an energy-dispersive spectroscopy analytical complex, Pegasus 4000 (EDAX, Pleasanton, CA, USA). The analytical spectra were obtained from a smooth crystal surface at an operating voltage of 20 kV, with a beam size of 1 Mm. The samples were coated with carbon. Analytical results are given in Table S7.

3. Results and Discussion

3.1. Powder X-Ray Diffraction of the (Y1−xEux)2(SO4)3*8H2O Solid Solutions

All aqueous samples after synthesis are represented by homogeneous (Y1−xEux)2(SO4)3*8H2O solid solutions. The dependencies of the unit cell parameters and volume of (Y1−xEux)2(SO4)3*8H2O solid solutions as a function of concentration are shown in Figure 1. The unit cell parameters and volume increase with the Eu3+ concentration. A possible reason for this is the difference in ionic radii between the [8]Y3+ (1.159 Å) and [8]Eu3+ (1.206 Å) according to [29].

3.2. Description of the YEu(SO4)3*8H2O and (Y0.83Eu0.17)2(SO4)3*8H2O Crystal Structures

The YEu(SO4)3*8H2O crystal structures were refined to R1 = 0.026, 0.025, and 0.027 at −173, −73, and 77 °C, respectively, and (Y0.83Eu0.17)2(SO4)3*8H2O were refined to R1 = 0.031, 0.033, and 0.035 at −173, −73, and 77 °C, respectively. The crystal structure data and refinement parameters for all modifications are shown in Table 1 and Table 2. The final atomic positional and displacement parameters (Å2) as well as selected bond lengths are given in Tables S1–S6; cifs and checkcifs are in the Supplementary Materials.
The YEu(SO4)3*8H2O and (Y0.83Eu0.17)2(SO4)3*8H2O crystallized into the Pr2(SO4)3*8H2O structure type [7,8,9]. Y and Eu were surrounded by eight O atoms in the range of 2.31–2.49 and 2.28–2.48 Å at 350K, respectively, forming (Y,Eu)O4(H2O)4 polyhedra. These polyhedra shared corners with SO4 tetrahedra, creating (Y,Eu)(S1O4)3(S2O4)(H2O)4 structural units, which are fundamental building blocks (FBB) of this structure. FBBs were linked through the SO4 tetrahedra, forming zig-zag chains along the b axis. These chains were bound through the S2O4 tetrahedra in the layers parallel to the (101) direction. Hydrogen bonds linked these layers in the structure.
Minerals 15 01304 g001
Figure 1. Dependencies of unit cell parameters and volume vs. europium concentration x(Eu3+) in the (Y1−xEux)2(SO4)3*8H2O solid solutions.
Figure 1. Dependencies of unit cell parameters and volume vs. europium concentration x(Eu3+) in the (Y1−xEux)2(SO4)3*8H2O solid solutions.
Minerals 15 01304 g001

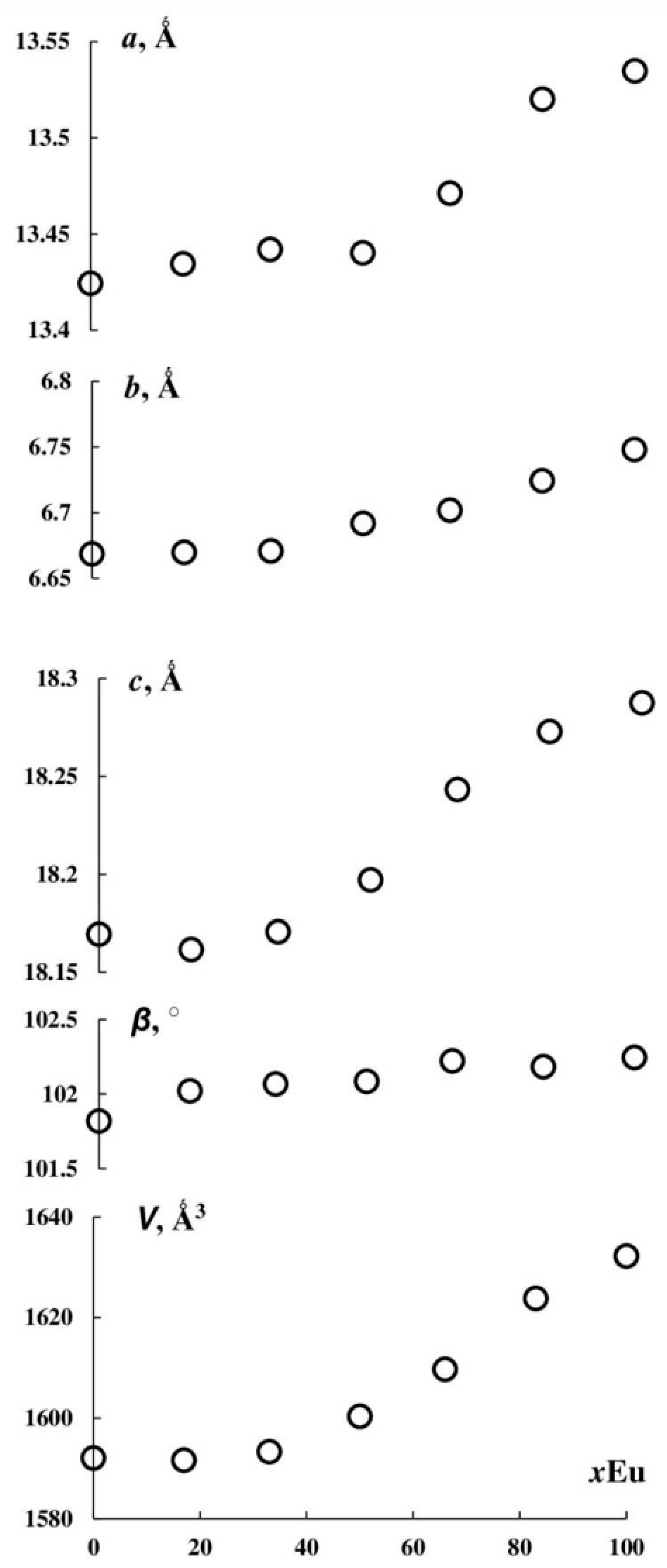
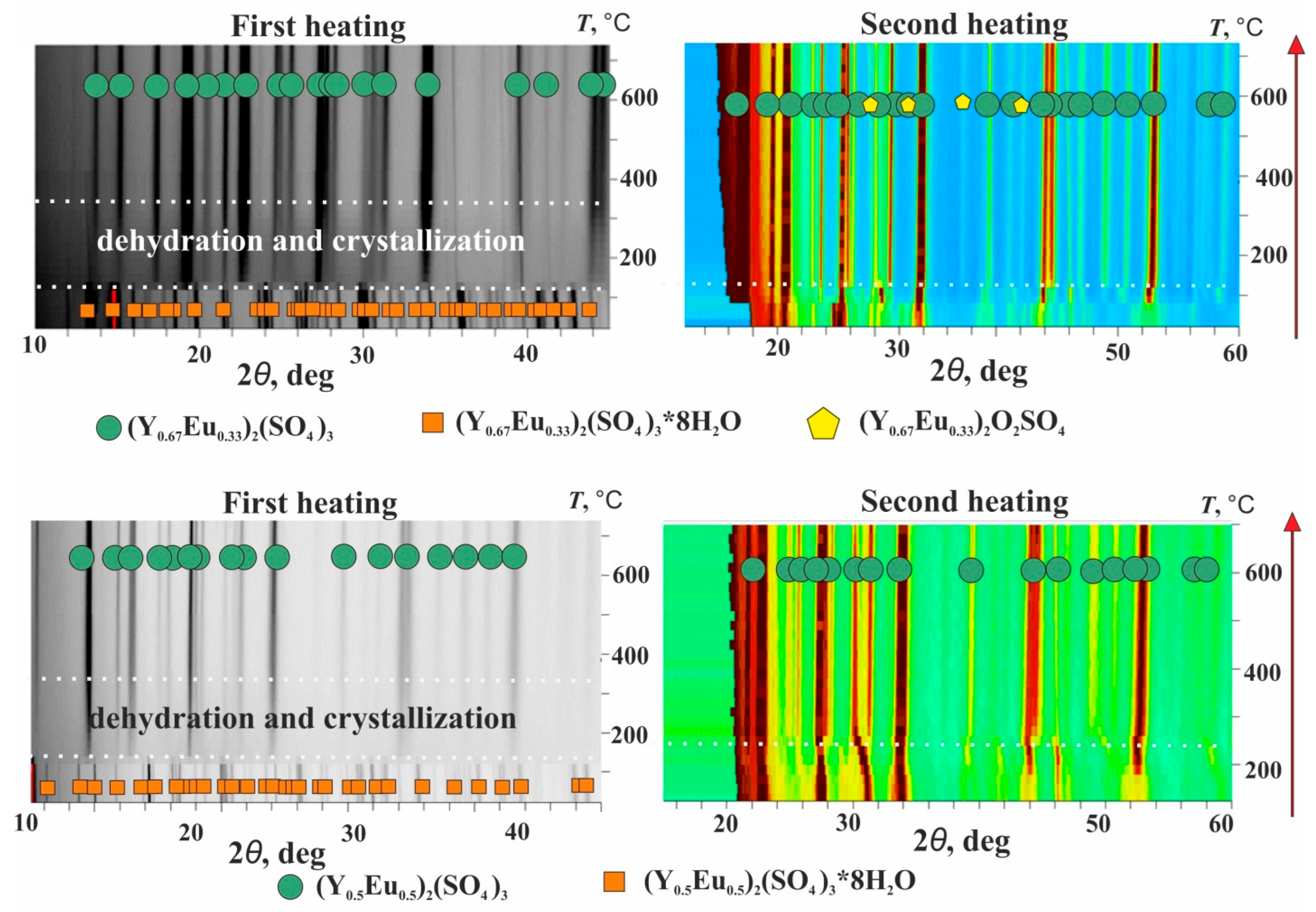
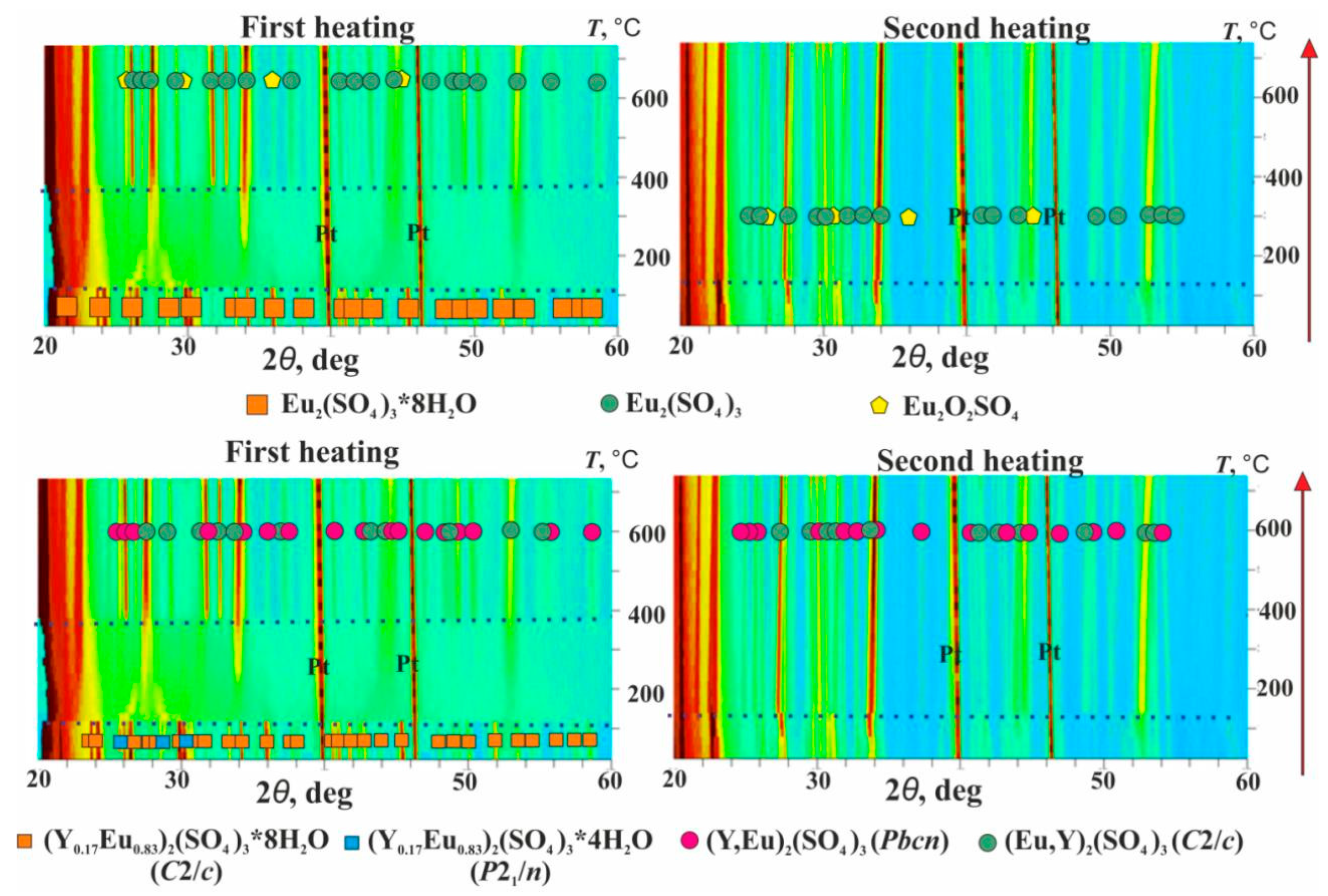
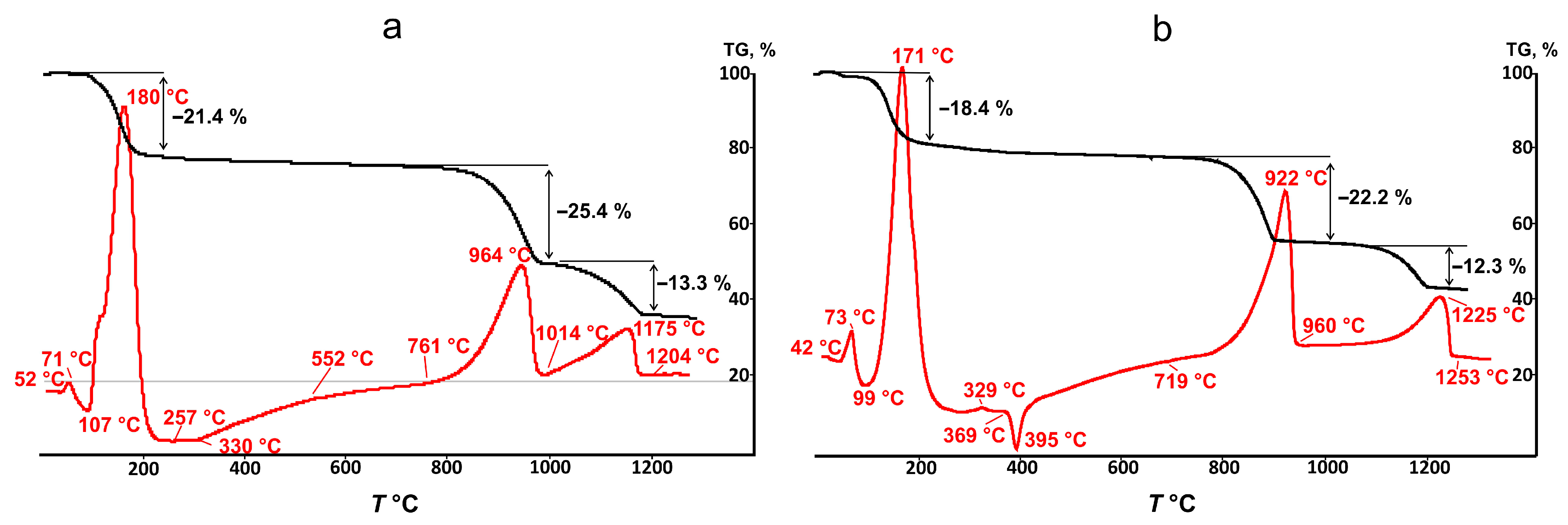
3.3. (Y1−xEux)2(SO4)3*8H2O Thermal Transformations and Thermal Expansion of Products of Its Decomposition

HTXRD study of (Y1−xEux)2(SO4)3*8H2O. Since high-temperature X-ray diffraction (HTXRD) data for samples where x = 0, 0.17, 0.50 were published previously [30], this work focused on a high-temperature X-ray diffraction study of 0.33, 0.66, 0.83, and 1 samples. Figure 2 and Figure 3 show the diffraction patterns of the high-temperature experiment for (Y0.67Eu0.33)2(SO4)3*8H2O and (Y0.50Eu0.50)2(SO4)3*8H2O. As in the previous study, the samples were heated to 600 °C, then cooled to room temperature, and heated again to 750 °C. This approach to the study was motivated by the fact that the dehydration of aqueous sulfates caused the particles to self-disperse and become very small, resulting in a blurred diffraction pattern that remained in the range of 120–380 °C (Figure 2 and Figure 3). Accordingly, dehydration and partial amorphization processes, as well as the thermal expansion of aqueous sulfates, were studied during the first heating. Although the anhydrous sulfates slightly hydrated upon cooling, clear peaks of the main anhydrous phases were present, and during the second heating, the thermal expansion of the anhydrous sulfates was studied. The solid solutions (Y1−xEux)2(SO4)3*8H2O were stable up to approximately 120 °C, and this behavior was similar in all four samples.
Upon the first heating of (Y1−xEux)2(SO4)3*8H2O (x = 0.50 and 0.33), the hydrated sulfate remained stable up to 120 °C. Dehydration occurred between 120 and 160 °C, characterized by a decrease in the (Y1−xEux)2(SO4)3*8H2O peaks and the emergence of weak peaks, corresponding to (Y1−xEux)2(SO4)3 (x = 0.50 and 0.33) anhydrous sulfates. This transformation occurred via a two-phase region, with the anhydrous solid solution fully forming above 160 °C and becoming homogeneous above 350 °C. Upon cooling, the products reversibly absorbed only a minimal amount of water. The crystal structure, or its main character, was apparently preserved, which could be observed by the shift in the peaks during the second heating. The complete dehydration process to form a homogeneous anhydrous sulfate occurred over a broad temperature range of 80–250 °C, above which only the (Y1−xEux)2(SO4)3 phase was stable up to 600 °C. Also, during the second heating of the x = 0.33 sample to above a temperature of 600 °C, thermal decomposition occurred with the formation of the (Y, Eu)2O2(SO4) phase.
Upon the first heating of Eu2(SO4)3*8H2O and (Y0.17Eu0.83)2(SO4)3*8H2O, complete dehydration did not occur until 120 °C. For the x = 0.17 sample, peaks of the phase corresponding to (Y,Eu)2(SO4)3*4H2O (P21/n) [31] were observed from room temperature to 120 °C. After that, an amorphization region occurred up to 380 °C. Above this temperature, crystallization of the Eu2(SO4)3 phase occurred for the x = 1 sample, and crystallization of the (Eu, Y)2(SO4)3 (C2/c) and (Y, Eu)2(SO4)3 (Pbcn) solid solutions occurred for the x = 0.83 sample. Thus, for the x = 0.83 sample, the formation of an immiscibility region of the solid solution occurred through the amorphization region and was caused by the difference in the crystal structure of the end members of the Y2(SO4)3 (Pbcn)–Eu2(SO4)3 (C2/c) solid solutions. In these crystal structures, the coordination numbers of the rare earth metals differed: for the smaller Y, the coordination number was 6, while for the larger Eu, the coordination number was 9. If the x = 1 sample was heated above 600 °C, thermal decomposition would have occurred with the formation of the Eu2O2(SO4) phase.
Upon cooling, the products reversibly absorbed only a minimal amount of water, and the crystal structure, or its main character, was apparently also preserved. Upon reheating the x = 1 sample, complete dehydration occurred at 140 °C and up to 750 °C; only peaks of Eu2(SO4)3 and Eu2O2(SO4) were present. Above 600 °C, the amount of the Eu2O2(SO4) phase gradually increased. Upon reheating the x = 0.83 sample, complete dehydration also occurred at 140 °C, and above 750 °C, only peaks of the (Eu, Y)2(SO4)3 (C2/c) and (Y, Eu)2(SO4)3 (Pbcn) phases were observed.
DSC and TG study of YEu(SO4)3*8H2O and Eu2(SO4)3*8H2O. The heating DSC and TG curves for YEu(SO4)3*8H2O (a) and Eu2(SO4)3*8H2O are shown in Figure 4. The curves are similar to the data on Eu2(SO4)3*8H2O that were published earlier [15,18]. Thermal analysis revealed five thermal effects in the DSC and four mass losses in the TG curves. For both samples, the first very small endoeffects, starting at 52 and 42 °C, with maxima at 71 and 73 °C, respectively, were probably caused by the removal of residual water sorbed by the samples. The next most intense endothermic peak, associated with dehydration, onset at ~107 °C and ~99 °C in the YEu(SO4)3*8H2O and Eu2(SO4)3*8H2O phases, respectively, and peaked at ~180 °C and ~171 °C. The peaks were split and asymmetric, which may have been caused by stepwise dehydration. The DSC curve of YEu(SO4)3*8H2O sulphate exhibited an additional peak at a lower temperature, while Eu2(SO4)3*8H2O exhibited a shoulder at a higher temperature. HTXRD data for YEu(SO4)3*8H2O revealed no traces of phases other than the YEu(SO4)3*8H2O and YEu(SO4)3, while a small amount of Eu2(SO4)3*4H2O (P21/n) phases [31] was observed for the Eu2(SO4)3*8H2O sample in this temperature range. The observed mass losses for this effect were 21.4% and 18.4%, which are consistent with the theoretical values of 21.4% and 19.6% for the loss of eight water molecules from YEu(SO4)3*8H2O and Eu2(SO4)3*8H2O, respectively.
The subsequent very weak exothermic effect at 257 °C and 329 °C with maxima at 330 °C and 395 °C for the corresponding phases was attributed to the onset of crystallization of the YEu(SO4)3 and Eu2(SO4)3 anhydrous sulfates. This crystallization was probably caused by amorphization and self-dispersion of the powder particles after the volatilization of water. Amorphization and subsequent crystallization of the anhydrous phase were clearly visible in the case of Eu2(SO4)3, where amorphization occurred in the wider range of 120–380 °C (Figure 3). One of the probable reasons for such a large difference in the crystallization process was the difference in the crystal structures of YEu(SO4)3 and Eu2(SO4)3 (see Section 3.4).
Upon further heating, the anhydrous sulfates underwent two-stage decomposition with the release of volatile components. The next two broad, asymmetric endothermic peaks on the DSC curve were accompanied by mass losses. The following peak had onset temperatures of 761 °C and 719 °C, with maxima at 964 °C and 922 °C for YEu(SO4)3 and Eu2(SO4)3 sulfates, respectively. These peaks corresponded to mass losses of 25.4% for YEu(SO4)3 and 21.2% for Eu2(SO4)3. This decomposition stage involved the release of SO3 to form oxosulfates according to the following reactions: YEu(SO4)3 → YEuO2(SO4) + 2SO3↑ and Eu2(SO4)3 → Eu2O2(SO4) + 2SO3↑. The presence of peaks of Eu2O2(SO4) oxosulfate in the HTXRD patterns (Figure 3) confirmed the correctness of the reaction equation.
Nevertheless, peaks of the (Y1−xEux)2(SO4)3 phase were observed in practically all of the studied temperature range. The decomposition step was more than 200 °C for each sample, although Eu2(SO4)3 sulphate began to decompose at the lowest temperature (719 °C), followed by the YEu(SO4)3 solid solution (761 °C) and Y2(SO4)3 (787 °C) [30]. The last decomposition stage involved the release of volatile components, either as SO2 + O2 or as SO3, according to the following reactions: (Y,Eu)2O2(SO4) → (Y,Eu)2O3 + SO2↑ + 0.5O2↑ or (Y,Eu)2O2(SO4) → (Y,Eu)2O3 + SO3↑. This interpretation of the endothermic peaks—at 1014 °C, and 960 °C with peak maxima at 1175 °C and 1225 °C for the YEu(SO4)3 and Eu2(SO4)3 sulfates, respectively—is strongly supported by the calculated mass losses of 13.1% and 10.9%, respectively, for these reactions. It is noteworthy that the decomposition stage of the Eu2O2(SO4) sulfate occurred at a higher temperature (1225 °C) than the (Y,Eu)2O2(SO4)3 solid solution (1175 °C) and Y2O2(SO4)3 (1132 °C) [30]. Thus, it can be assumed that in the Y2(SO4)3–Eu2(SO4)3 system the Y2(SO4)3 is the most stable sulfate, while among oxosulfates Eu2O2(SO4) is more stable than the (Y,Eu)2O2(SO4) solid solution and the Y2O2(SO4) compound. Some discrepancies between the thermal analysis and HTXRD data may be due to different heating rates or the fact that the samples were prepared for the study as tablets and powders, respectively.
Thermal expansion. The dependencies of the unit cell parameters and volume of (Y1−xEux)2(SO4)3*8H2O compounds and solid solutions as a function of temperature are shown in Figure 5. The unit cell parameters and volume increase with the Eu3+ concentration and temperature, which is consistent with the known tendency for thermal and compositional deformations to be similar, e.g., [32,33]. The approximation equations and thermal expansion coefficients are given in Table 3 and Table S8.
As described above, the dehydration occurred with increasing temperatures, and (Y1−xEux)2(SO4)3*8H2O (C2/c) solid solutions were transformed into (Y1−xEux)2(SO4)3 (Pbcn) solid solutions, which exhibited negative volumetric thermal expansion in all three directions. Thermal expansion of x = 0, 0.17, and 0.50 was first studied by us earlier, in [30]. After dehydration, the Eu2(SO4)3*8H2O (C2/c) was transformed into Eu2(SO4)3 (C2/c); the temperature dependencies of the Eu2(SO4)3 unit cell parameters are shown in Figure 6.
With a further increase in temperature, the (Y1−xEux)2(SO4)3 (Pbcn) solid solutions decomposed with the release of SO3, resulting in the formation of isotypic solid solutions and compounds (Y1−xEux)2O2(SO4) (C2/c). The Y2O2SO4 compound was synthesized in homogeneous form. The temperature dependencies of the unit cell parameters and the volume of Y2O2SO4 are shown in Figure 7, and the thermal expansion coefficients for the Y2O2SO4, Eu2(SO4)3, and (Y1−xEux)2(SO4)3 compounds and solid solutions are given in Table 4.

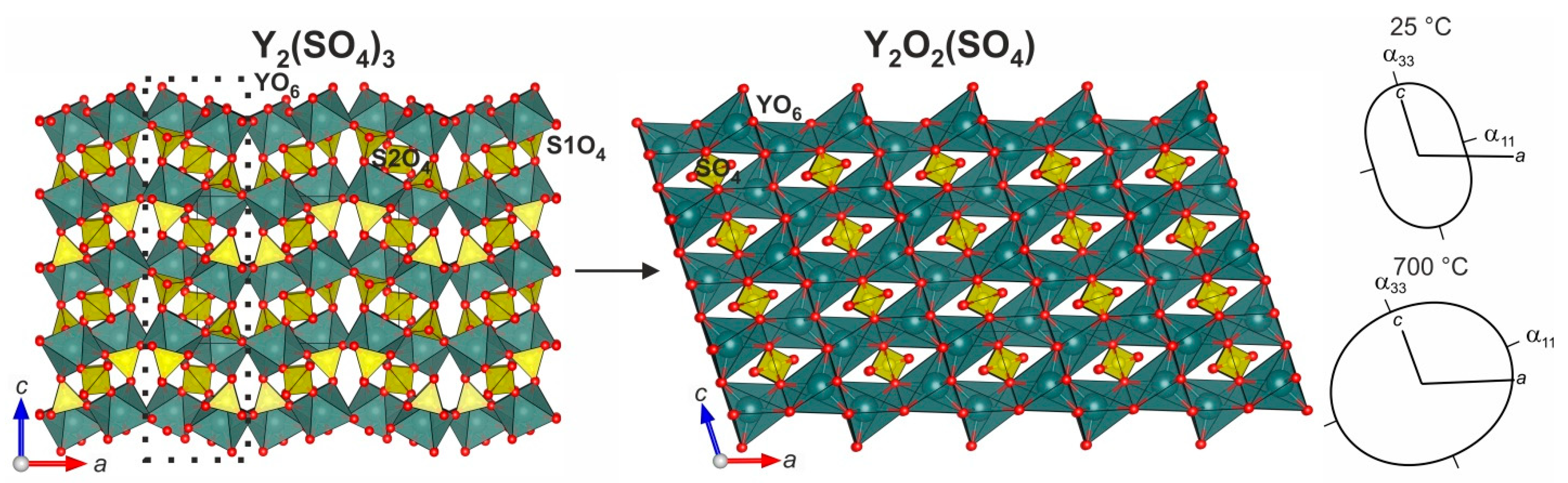
3.4. Crystal Structure Relations

An interesting feature emerged in the transformations of the Eu2(SO4)3*8H2O aqueous sulfate in its decomposition upon heating. Although the end-members and the solid solutions of the(Y1−xEux)2(SO4)3–Eu2(SO4)3*8H2O aqueous system were isotypic, two sequences of transformations were observed. For Eu2(SO4)3*8H2O sulfate, the sequence of transformations was as follows: Eu2(SO4)3*8H2O ↔ Eu2(SO4)3 → Eu2O2SO4. All of these compounds crystallized in the monoclinic C2/c group. The relations of the unit cell parameters are given in Table 5.
The crystal structures of Eu2(SO4)3 and Eu2O2SO4 are shown in Figure 8. In the Eu2(SO4)3 crystal structure, there was one Eu site and two isolated SO4 tetrahedra in an asymmetric unit. Eu is coordinated by nine oxygen atoms to form EuO9 polyhedra. The EuO9 polyhedra are connected by seven SO4 tetrahedra. The fundamental structural unit of Eu2(SO4)3 is the EuO9 polyhedra linked to seven SO4 tetrahedra (Figure 9). These structural units, linked through triangular faces (O3–O4–O1), form chains along the c-axis (Figure 9). These chains are connected by SO4 tetrahedra in a three-dimensional framework.
The crystal structure of Eu2O2SO4 [36] consists of Eu–O layers in the ac plane. The isolated SO4 tetrahedra are located in the interlayer space, forming a mixed heteropolyhedral framework of corner-sharing SO4 tetrahedra and EuO8 polyhedra. The EuO8 polyhedra are linked to each other by edges.
A certain similarity was observed between the crystal structures of the compounds before and after decomposition. For the crystal structures of Eu2(SO4)3*8H2O and Eu2(SO4)3, this was primarily expressed in the similarity of the Eu(S1O4)6(S2O4)3 fundamental structural units and Eu(S1O4)3(S2O4)(H2O)4. Three SO4 tetrahedra were located at a small distance from the EuO8 polyhedra and were linked to the water molecules that coordinated it via hydrogen bonds (Figure 9).
The Eu2(SO4)3 crystal structure is partially uncompensated according to the valence-matching principle [37,38]. The O4, O3, and O1 atoms are coordinated by a sulfur atom and two europium atoms, causing the valence converging on them to be significantly overbonded and to exceed two valence units (Table S9). The bond–valence calculations were performed using empirical parameters taken from [39]. Because of this, the structure was prone to hydration in order to achieve a stable state. Through the three oxygen atoms (O4, O3, and O1), the fundamental building blocks of the Eu2(SO4)3 crystal structure were linked into chains elongated along the c-axis. As a result of hydration, these chains were broken, and water molecules entered these sites in the structure. As a result, weaker chains elongated along the b-axis were preserved, which formed layers elongated along (101), with water molecules located in the interlayer space.
The chain corrugation along the b-axis increased with the introduction of water molecules, but their incorporation did not change the value of the b parameter. The value of the c parameter increased due to the entry of water molecules into the space between the chain links, and the a parameter decreased due to the shift in the broken chains relative to each other along the shorter diagonal of the ac parallelogram.
With a further increase in temperature, the decomposition of Eu2(SO4)3 → Eu2O2SO4 + 2SO3 occurred. Apparently, during the decomposition, sulfur and some oxygen evaporated from the S1O4 tetrahedra, which, due to their multiplicity, were twice as numerous as the S2O4 tetrahedra in the Eu2(SO4)3 crystal structure (Figure 10). As a result, the Eu–O chains elongated along the c-axis were crosslinked into corrugated Eu–O layers through oxygen atoms that were not bonded to S. These layers formed a framework due to the rotation of the S2O4 tetrahedra. The mutual orientation of the crystallographic axes in the structures of these two compounds was practically preserved, and the β angle changed insignificantly. The sharp decrease in the a and b parameters was associated with the volatilization of S and O, and the increase in the c parameter was due to the rotation of S2O4 tetrahedra, one of the edges of which became parallel to the c axis.
The crystal structures of Y2(SO4)3*8H2O and Y2(SO4)3 are closely related, despite crystallizing in different space groups (C2/c and Pbcn, respectively). The relations of the unit cell parameters are given in Table 6. Y2(SO4)3 crystallizes in the orthorhombic Pbcn space group [40]. The asymmetric unit comprises one independent Y atom (8d site), two S atoms (8d and 4c sites), and six O atoms (8d sites). The sulfur atoms are tetrahedrally coordinated by oxygen (S–O bonds ranging from 1.448 to 1.459 Å), while the yttrium atom is octahedrally coordinated (Y–O bonds between 2.20 and 2.24 Å). The crystal structure can be described as a heteropolyhedral framework of corner-sharing YO6 octahedra and SO4 tetrahedra. Since the SO4 tetrahedra are isolated from one another, the framework can be described as being composed of microblocks, where each YO6 octahedron is linked to six surrounding SO4 tetrahedra [41].
As with the Eu2(SO4)3*8H2O ↔ Eu2(SO4)3 transition, the hydration of Y2(SO4)3 induced the separation of the fundamental building blocks, which consisted of YO6 octahedra surrounded by six SO4 tetrahedra; the octahedra were linked to each other through three tetrahedra (Figure 9a). The separation of the fundamental building blocks during hydration resulted in the formation of a layered isotypic structure with Eu2(SO4)3*8H2O (Figure 11a). The framework was destroyed, the metric of the unit cell changed, and layers elongated along (101) were formed. Water molecules were located within the layers and in the interlayer space.
If we consider the fragments in the crystal structure of Y2(SO4)3 (Figure 11b), which formed layers upon hydration (Figure 11c), and the layers in the crystal structure of Y2(SO4)3 (Figure 11d), the similarity is also visible. Thus, in the layers, we can identify chains along the b-axis, formed by YO6 octahedra or Eu(S1O4)3(S2O4)(H2O)4 antiprisms linked through two SO4 tetrahedra (Figure 11e,f). In Y2(SO4)3*8H2O, these chains are shifted by 1/2 translation (b axis) relative to Y2(SO4)3, which causes an increase in the b parameter upon hydration.
Thermal decomposition of Y2(SO4)3 → Y2O2SO4 + 2SO3 occurred upon heating [42]. Similarly to Eu2O2SO4, structural relations between the phases before and after decomposition were observed. As a result of the volatilization of sulfur and oxygen, the slabs (Figure 12) were cross-linked through the edges of the YO6 polyhedra, and by combining through the edges of the YO6 polyhedra and the SO4 tetrahedra, these fragments formed a mixed framework (Figure 12). If the crystal structure was considered to be an oxo-centered polyhedra, then after the transformation, corrugated oxo-centered chains elongated along the c-axis were formed. These chains, linking through the edges of oxo-centered OY4 tetrahedra, form oxo-centered 2 ∞ [YO] layers of the L12 type [25] (Figure 13).
Comparison of the thermal expansion of (Y1−xEux)2(SO4)3*8H2O, Eu2(SO4)3, Y2O2SO4 and Eu2O2SO4 compounds with the crystal structure. We previously interpreted the thermal expansion of Y2(SO4)3 [30]. The thermal expansion of this structure type was also studied in, e.g., [43,44]. The thermal expansion of Eu2(SO4)3 is highest in the direction approximately coinciding with the c-axis, and the expansion increases with increasing temperature (Table 4). Thermal expansion also increases slightly along the b-axis and decreases in the direction close to the a-axis, reaching negative thermal expansion (Figure 8). Similar thermal expansion data were obtained for the isotype Pr2(SO4)3 [20], but the authors did not provide any interpretation of the thermal expansion anisotropy other than that the appearance of a region of negative thermal expansion was associated with a change in the β angle. A structural interpretation of the thermal expansion anisotropy may be developed as follows: the Eu–O chains in the crystal structure are elongated along the c-axis, and the maximum thermal expansion in this direction may be associated with the removal of chain corrugation in this direction, so that the faces linking the EuO9 polyhedra become parallel to each other. Such an expansion in the monoclinic plane causes a decrease in thermal expansion in the direction close to the a-axis, up to negative thermal expansion in accordance with the theory of shear deformations [45,46].
The thermal expansion of (Y1−xEux)2(SO4)3*8H2O can be compared with its crystal structure as follows. The distance between layers in the crystal structure increased with increasing temperatures, and the layer corrugations were also removed due to the rotation of the S2O4 tetrahedra. As a result, the structure expanded sharply in the monoclinic plane along directions close to the a and c axes, while thermal expansion along the b axis was relatively low (Table 4) (Figure 8).
Interpretation of the thermal expansion anisotropy of (Y1−xEux)2O2(SO4) is difficult in terms of cation-centered polyhedra, since the crystal structure is a mixed heteropolyhedral framework of corner-sharing SO4 tetrahedra and (Y, Eu)O8 polyhedra. The (Y, Eu)O8 polyhedra are linked by edges and faces. If we consider the structure in terms of anion-centered polyhedra, the crystal structure consists of oxo-centered 2 ∞ [YO] layers of the L12 type in the bc plane [25]. It is not entirely clear why, at relatively low temperatures, the thermal expansion is highest along the c axis, but with increasing temperature, the thermal expansion perpendicular to the plane of strike of the oxo-centered layers increases, and at high temperature, the thermal expansion was highest in this direction, which is natural, since these layers restrain the thermal expansion in other directions due to strong O–(Y, Eu) bonds (Figure 12 and Figure 13).

4. Conclusions

A series of (Y1−xEux)2(SO4)3*8H2O solid solutions (x = 0, 0.17, 0.33, 0.50, 0.66, 0.83, and 1) was successfully prepared via crystallization from aqueous solutions. The thermal multi-step phase transformations with the formation of new phases were characterized from 25 to 1350 °C, revealing two distinct sequences: (Y1−xEux)2(SO4)3*8H2O (C2/c) ↔ (Y1−xEux)2(SO4)3 (Pbcn) → (Y1−xEux)2O2SO4 (C2/c) and Eu2(SO4)3*8H2O (C2/c) ↔ Eu2(SO4)3 (C2/c) → Eu2O2SO4 (C2/c). Phase transformations for all samples were investigated by high-temperature powder X-ray diffraction, differential scanning calorimetry, and thermogravimetry in the temperature ranges of 25–750 and 25–1350 °C, respectively. The crystal structures of YEu(SO4)3*8H2O and (Y0.83Eu0.17)2(SO4)3*8H2O were refined in a −173 to 87 °C temperature range for the first time. The coefficients of thermal expansion were calculated for the first time for all compounds in the series, including (Y1−xEux)2(SO4)3*8H2O, Eu2(SO4)3, and Y2O2SO4. The thermal expansion of Eu2(SO4)3 was highest in the direction approximately coinciding with the c-axis because of the removal of Eu–O chain corrugation in this direction. The crystal structure of (Y1−xEux)2(SO4)3*8H2O expanded sharply in the ac plane along directions close to the a and c axes, while thermal expansion along the b axis was relatively low. The distance between layers in the (Y1−xEux)2(SO4)3*8H2O crystal structure increased with increasing temperature, and corrugated layers (parallel to (101) direction) straightened out due to the rotation of the S2O4 tetrahedra. At high temperatures, the thermal expansion of Y2O2SO4 was highest along the longer diagonal of the ac parallelogram perpendicular to the plane of strike of the oxo-centered 2 ∞ [YO] layers.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/min15121304/s1, Table S1. Atomic coordinates and isotropic or equivalent displacement parameters (Å2) of YEu(SO4)3*8H2O at 100 K, 200K and 350 K, respectively. Table S2. Atomic coordinates and isotropic or equivalent displacement parameters (Å2) of Y0.83Eu0.17(SO4)3*8H2O at 100K, 200K and 359K, respectively. Table S3. Selected bond lengths for YEu(SO4)3*8H2O at 100 K, 200K and 350 K, respectively. Table S4. Selected bond lengths for Y0.83Eu0.17(SO4)3*8H2O at 100 K, 200K and 359 K, respectively. Table S5. Anisotropic atomic displacement parameters (Å2) of YEu(SO4)3*8H2O at 100 K, 200K and 359 K, respectively. Table S6. Anisotropic atomic displacement parameters (Å2) of Y0.83Eu0.17(SO4)3*8H2O at 100 K, 200K and 359 K, respectively. Table S7. Chemical composition of (Y1−xEux)2(SO4)3 solid solutions (at.%) [24]. Table S8. Temperature dependencies of the unit cell parameters for (Y1−xEux)2(SO4)3*8H2O, (Y1−xEux)2(SO4)3 and (Y1−xEux)2O2(SO4) compounds and solid solutions approximated as quadratic polynomials a0 + a1 × 10−3t + a2 × 10−6t2. Table S9. Bond-valence analysis for Eu2(SO4)3 and Y2(SO4)3 (v.u.).

Author Contributions

Conceptualization, A.P.S., R.S.B., and S.K.F.; methodology, A.P.S., O.Y.S., M.G.K., and S.K.F.; software, A.P.S. and O.Y.S.; validation, A.P.S., R.S.B., M.G.K., O.Y.S., and S.K.F.; formal analysis, A.P.S., R.S.B., and S.K.F.; investigation, O.Y.S., A.P.S., M.G.K., R.S.B., and M.S.A.; resources, S.K.F., R.S.B., M.G.K., and M.S.A.; data curation, R.S.B., M.G.K., and M.S.A.; writing—original draft preparation, A.P.S. and O.Y.S.; writing—review and editing, A.P.S., O.Y.S., R.S.B., M.G.K., and S.K.F.; visualization, O.Y.S., A.P.S., and R.S.B.; supervision, R.S.B. and S.K.F.; project administration, S.K.F.; funding acquisition, S.K.F. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Russian Science Foundation [grant number 22-13-00317-P] (data evaluation and generalization, and XRD experiments), and the Ministry of Science and Higher Education of the Russian Federation within the scientific tasks of the Grebenshikov Institute of Silicate chemistry [project number 1023033000085-7-1.4.3] (synthesis).

Data Availability Statement

The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author.

Acknowledgments

The X-ray diffraction experiments were performed at The Centre for X-ray Diffraction Studies (Saint-Petersburg State University). The authors acknowledge Saint-Petersburg State University for a research project: 125021702335-5.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Schlesinger, W.H.; Bernhardt, E.S. Biogeochemistry: An Analysis of Global Change; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
  2. Komissarova, L.N.; Pyshkina, G.Y.; Schatskiy, V.M.; Znamenskaya, A.S.; Dolgich, V.A.; Syponitskiy, Y.L.; Schacno, I.V.; Pokrovskiy, A.N.; Chizhov, S.M.; Balki, T.I.; et al. Compounds of Rare Earth Elements; Nauka Press: Moscow, Russia, 1986. (In Russian) [Google Scholar]
  3. Shang, Y.; Xu, J.; Sha, H.; Wang, Z.; He, C.; Su, R.; Yang, X.; Long, X. Nonlinear optical inorganic sulfates: The improvement of the phase matching ability driven by the structural modulation. Coord. Chem. Rev. 2023, 494, 215345. [Google Scholar] [CrossRef]
  4. Hawthorne, F.C.; Krivovichev, S.V.; Burns, P.C. The crystal chemistry of sulfate minerals. Rev. Mineral. Geochem. 2000, 40, 1–112. [Google Scholar] [CrossRef]
  5. Siidra, O.I.; Borisov, A.S.; Lukina, E.A.; Depmeier, W.; Platonova, N.V.; Colmont, M.; Nekrasova, D.P. Reversible hydration/dehydration and thermal expansion of euchlorine, ideally KNaCu3O(SO4)3. Phys. Chem. Miner. 2019, 46, 403–416. [Google Scholar] [CrossRef]
  6. Siidra, O.I.; Borisov, A.S.; Charkin, D.O.; Depmeier, W.; Platonova, N.V. Evolution of fumarolic anhydrous copper sulfate minerals during successive hydration/dehydration. Min. Mag. 2021, 85, 262–277. [Google Scholar] [CrossRef]
  7. Podberezskaya, N.V.; Borisov, S.V. Utochnenie kristallicheskoi struktury Sm2(SO4)3(H2O)8. Zhurnal Strukt. Khimii 1976, 17, 186–188. (In Russian) [Google Scholar]
  8. Hiltunen, L.; Niinisto, L. Ytterbium sulfate octahydrate, Yb2(SO4)3(H2O)8. Cryst. Struct. Comm. 1976, 5, 561–566. [Google Scholar]
  9. Gebert, S.E. The structure of Pr2(SO4)3(H2O)8 and La2(SO4)3(H2O)9. J. Solid. State Chem. 1976, 19, 271–279. [Google Scholar]
  10. Bartl, H.; Rodek, E. Untersuchung der Kristallstruktur von Nd2(SO4)3·(H2O)8. Z. Krist. 1983, 162, 13–14. [Google Scholar]
  11. Held, P.; Wickleder, M. Yttrium(III) sulfate octahydrate. Acta Cryst. 2003, 59, 98–100. [Google Scholar] [CrossRef]
  12. Wickleder, M.S. Inorganic Lanthanide Compounds with Complex Anions. Chem. Rev. 2002, 102, 2011–2087. [Google Scholar] [CrossRef] [PubMed]
  13. Wendland, W.W. The thermal decomposition of yttrium and rare earth metal sulfate hydrates. J. Inorg. Nucl. Chem. 1958, 7, 51–54. [Google Scholar] [CrossRef]
  14. Alekseenko, L.A.; Lemenkova, A.F.; Serebrennikov, V.V. On the loss of crystallization water by sulfates of rare earth elements of the cerium group. Russ. J. Inorg. Chem. 1959, 34, 1382–1385. (In Russian) [Google Scholar]
  15. Wendland, W.W.; George, T.D. A differential thermal analysis study of the dehydration of the rare-earth(III) sulfate hydrates. J. Inorg. Nucl. Chem. 1961, 19, 245–250. [Google Scholar] [CrossRef]
  16. Zaitseva, L.L.; Ilyashenko, V.S.; Konarev, M.I.; Konovalov, L.N.; Lipis, L.V.; Chebotarev, N.T. Physicochemical properties of crystal hydrates of rare earth elements of the terbium subgroup. Russ. J. Inorg. Chem. 1965, 10, 1761–1770. (In Russian) [Google Scholar]
  17. Brittain, H.G. Thermal decomposition of Eu2(SO4)3·8H2O studied by high resolution luminescence spectroscopy. J. Less Common Met. 1983, 93, 97–102. [Google Scholar] [CrossRef]
  18. Denisenko, Y.G.; Khritokhin, N.A.; Andreev, O.V.; Basova, S.A.; Sal’nikova, E.I.; Polkovnikov, A.A. Thermal decomposition of europium sulfates Eu2(SO4)3·8H2O and EuSO4. J. Solid. State Chem. 2017, 255, 219–224. [Google Scholar] [CrossRef]
  19. Shizume, K.; Hatada, N.; Uda, T. Experimental study of hydration/dehydration behaviors of metal sulfates M2(SO4)3 (M = Sc, Yb, Y, Dy, Al, Ga, Fe, In) in search of new low-temperature thermochemical heat storage materials. ACS Omega 2020, 5, 13521–13527. [Google Scholar] [CrossRef] [PubMed]
  20. Denisenko, Y.G.; Atuchin, V.V.; Molokeev, M.S.; Sedykh, A.E.; Khritokhin, N.A.; Aleksandrovsky, A.S.; Oreshonkov, A.S.; Shestakov, N.P.; Adichtchev, S.V.; Pugachev, A.M.; et al. Exploration of the crystal structure and thermal and spectroscopic properties of monoclinic praseodymium sulfate Pr2(SO4)3. Molecules 2022, 27, 3966. [Google Scholar] [CrossRef]
  21. Plyasova, L.M.; Borisov, S.V.; Belov, N.V. The garnet pattern in the structure of iron molybdate. Sov. Phys. Crystallogr. 1967, 12, 25–27. [Google Scholar]
  22. Wells, A.F. Structural Inorganic Chemistry, 5th ed.; Oxford University Press: Oxford, UK, 1984; p. 606. [Google Scholar]
  23. Piffard, Y.; Verbaere, A.; Kinoshita, M. β-Zr2(PO4)2SO4: A zirconium phosphato-sulfate with a Sc2(WO4)3 structure. A comparison between garnet, nasicon, and Sc2(WO4)3 structure types. J. Solid State Chem. 1987, 71, 121–130. [Google Scholar] [CrossRef]
  24. Kamf, A.R. Grandreefite, Pb2F2SO4: Crystal structure and relationship to the lanthanide oxide sulfates, Ln2O2SO4. Am. Min. 1991, 76, 278–282. [Google Scholar]
  25. Krivovichev, S.V.; Filatov, S.K. Crystal Chemistry of Minerals and Inorganic Compounds with Complexes of Anion-Centered Tetrahedra; St. Petersburg University Press: St. Petersburg, Russia, 2001. [Google Scholar]
  26. Bubnova, R.S.; Firsova, V.A.; Volkov, S.N.; Filatov, S.K. RietveldToTensor: Program for processing powder X-ray diffraction data under variable conditions. Glass Phys. Chem. 2018, 44, 33–40. [Google Scholar] [CrossRef]
  27. CRYSALISPRO Software System, version 1.171.39.44; Rigaku Oxford Diffraction: Oxford, UK, 2015.
  28. Petricek, V.; Dusek, M.; Palatinus, L. Crystallographic Computing System JANA2006: General Features. Z. Crystallogr. 2014, 229, 345–352. [Google Scholar] [CrossRef]
  29. Shannon, R.D. Revised rffective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. 1976, A32, 751–767. [Google Scholar] [CrossRef]
  30. Shablinskii, A.P.; Shorets, O.Y.; Povotskiy, A.V.; Bubnova, R.S.; Krzhizhanovskaya, M.G.; Janson, S.Y.; Ugolkov, V.L.; Filatov, S.K. Novel Y2(SO4)3:Eu3+ Phosphors with Anti-Thermal Quenching of Luminescence Due to Giant Negative Thermal Expansion. Crystals 2024, 14, 1074. [Google Scholar] [CrossRef]
  31. Choi, M.H.; Kim, M.K.; Jo, V.; Lee, D.W.; Shim, I.W.; Ok, K.M. Hydrothermal syntheses, structures, and characterizations of two lanthanide sulfate hydrates materials, La2(SO4)3·(H2O) and Eu2(SO4)3·4(H2O). Bull. Korean Chem. Soc. 2010, 31, 1077–1080. [Google Scholar] [CrossRef]
  32. Hazen, R.M.; Finger, L.W. Comparative Crystal Chemistry: Temperature, Pressure, Composition and the Variation of Crystal Structure; John Wiley: Chichester, UK; Sons Ltd.: New York, NY, USA, 1982; 231p. [Google Scholar]
  33. Filatov, S.K. High Temperature Crystal Chemistry; Nedra: Leningrad, Russia, 1990. (In Russian) [Google Scholar]
  34. Wei, D.Y.; Zheng, Y.Q. Crystal structure of dieuropium trisulfate octahydrate, Eu2(SO4)3∙8H2O. Z. Krist. 2003, 218, 299–300. [Google Scholar] [CrossRef]
  35. Denisenko, Y.G.; Aleksandrovsky, A.S.; Atuchin, V.V.; Krylov, A.S.; Molokeev, M.S.; Oreshonkov, A.S.; Shestakov, N.P.; Andreev, O.V. Exploration of structural, thermal and spectroscopic properties of self-activated sulfate Eu2(SO4)3 with isolated SO4 groups. J. Ind. Eng. Chem. 2018, 68, 109–116. [Google Scholar] [CrossRef]
  36. Denisenko, Y.G.; Azarapin, N.O.; Khritokhin, N.A.; Andreev, O.V.; Volkova, S.S. Europium oxysulfate Eu2O2SO4 crystal structure. Russ. J. Inorg. Chem. 2019, 64, 7–12. [Google Scholar] [CrossRef]
  37. Brown, I.D. The bond-valence method: An empirical approach to chemical structure and bonding. In Structure and Bonding in Crystals 2; O’Keeffe, M., Navrotsky, A., Eds.; Academic Press: New York, NY, USA, 1981; pp. 1–30. [Google Scholar]
  38. Hawthorne, F.C. The structure hierarchy hypothesis. Min. Mag. 2014, 78, 957–1027. [Google Scholar] [CrossRef]
  39. Gagne, O.C.; Hawthorne, C. Comprehensive derivation of bond-valence parameters for ion pairs involving oxygen. Acta Cryst. 2015, B71, 562–578. [Google Scholar] [CrossRef]
  40. Wickleder, M.S. Wasserfreie Sulfate der Selten-Erd-Elemente: Synthese und Kristallstruktur von Y2(SO4)3 und Sc2(SO4)3. Z. Für Anorg. Allg. Chem. 2000, 626, 1468–1472. [Google Scholar] [CrossRef]
  41. Voronkov, A.A.; Ilyukhin, V.V.; Belov, N.V. Crystal chemistry of mixed frameworks. Principles of their formation. Kristallografiya 1975, 20, 556–566. (In Russian) [Google Scholar]
  42. Oreshonkov, A.S.; Denisenko, Y.G. Structural Features of Y2O2SO4 via DFT Calculations of Electronic and Vibrational Properties. Materials 2021, 14, 3246. [Google Scholar] [CrossRef] [PubMed]
  43. Evans, J.S.O.; Mary, T.A.; Sleight, A.W. Negative thermal expansion in a large molybdate and tungstate family. J. Solid State Chem. 1997, 13, 580–583. [Google Scholar] [CrossRef]
  44. Evans, J.S.O.; Mary, T.A.; Sleight, A.W. Negative thermal expansion in Sc2(WO4)3. J. Solid State Chem. 1998, 137, 148–160. [Google Scholar] [CrossRef]
  45. Filatov, S.K.; Andrianova, L.V.; Bubnova, R.S. Regularities of thermal deformations in monoclinic crystals. Cryst. Res. Technol. 1984, 19, 563–569. [Google Scholar] [CrossRef]
  46. Filatov, S.K. Negative linear thermal expansion of oblique-angle (monoclinic and triclinic) crystals as a common case. Phys. Status Solidi 2008, 245, 2490–2496. [Google Scholar] [CrossRef]
Minerals 15 01304 g002
Figure 2. Thermal phase transformations of (Y0.67Eu0.33)2(SO4)3*8H2O and (Y0.50Eu0.50)2(SO4)3*8H2O. The dotted lines indicate the appearance or disappearance of a phase.
Figure 2. Thermal phase transformations of (Y0.67Eu0.33)2(SO4)3*8H2O and (Y0.50Eu0.50)2(SO4)3*8H2O. The dotted lines indicate the appearance or disappearance of a phase.
Minerals 15 01304 g002
Minerals 15 01304 g003
Figure 3. Thermal phase transformations of Eu2(SO4)3*8H2O and (Y0.17Eu0.83)2(SO4)3*8H2O. The dotted lines indicate the appearance or disappearance of a phase.
Figure 3. Thermal phase transformations of Eu2(SO4)3*8H2O and (Y0.17Eu0.83)2(SO4)3*8H2O. The dotted lines indicate the appearance or disappearance of a phase.
Minerals 15 01304 g003
Minerals 15 01304 g004
Figure 4. DSC and TG data for YEu(SO4)3*8H2O (a) and Eu2(SO4)3*8H2O (b).
Figure 4. DSC and TG data for YEu(SO4)3*8H2O (a) and Eu2(SO4)3*8H2O (b).
Minerals 15 01304 g004
Minerals 15 01304 g005
Figure 5. Temperature dependencies of unit cell parameters and volume for (Y1−xEux)2(SO4)3*8H2O solid solutions.
Figure 5. Temperature dependencies of unit cell parameters and volume for (Y1−xEux)2(SO4)3*8H2O solid solutions.
Minerals 15 01304 g005
Minerals 15 01304 g006
Figure 6. Temperature dependencies of unit cell parameters for Eu2(SO4)3. Dashed lines are marked two-phased regions at low and high temperatures.
Figure 6. Temperature dependencies of unit cell parameters for Eu2(SO4)3. Dashed lines are marked two-phased regions at low and high temperatures.
Minerals 15 01304 g006
Minerals 15 01304 g007
Figure 7. Temperature dependencies of unit cell parameters for Y2O2SO4.
Figure 7. Temperature dependencies of unit cell parameters for Y2O2SO4.
Minerals 15 01304 g007
Minerals 15 01304 g008
Figure 8. Comparison of the ac and ab projections of the crystal structures of Eu2(SO4)3*8H2O (a,b) and Eu2(SO4)3 (c,d). The shaded areas of the tensor figure indicate negative thermal expansion.
Figure 8. Comparison of the ac and ab projections of the crystal structures of Eu2(SO4)3*8H2O (a,b) and Eu2(SO4)3 (c,d). The shaded areas of the tensor figure indicate negative thermal expansion.
Minerals 15 01304 g008
Minerals 15 01304 g009
Figure 9. Comparison of FBB in the Y2(SO4)3 (a), Y2(SO4)3*8H2O (b), Eu2(SO4)3 (c) and Eu2(SO4)3*8H2O (d) crystal structures. Descriptions are given in the text.
Figure 9. Comparison of FBB in the Y2(SO4)3 (a), Y2(SO4)3*8H2O (b), Eu2(SO4)3 (c) and Eu2(SO4)3*8H2O (d) crystal structures. Descriptions are given in the text.
Minerals 15 01304 g009
Minerals 15 01304 g010
Figure 10. Comparison of the ac and ab projections of the crystal structures of Eu2(SO4)3 (a,b) and Eu2O2SO4 (c,d).
Figure 10. Comparison of the ac and ab projections of the crystal structures of Eu2(SO4)3 (a,b) and Eu2O2SO4 (c,d).
Minerals 15 01304 g010
Minerals 15 01304 g011
Figure 11. Comparison of the Y2(SO4)3*8H2O (left) and Y2(SO4)3 (right) crystal structures: (a)—fragment of Y2(SO4)3*8H2O crystal structure, (b)—fragment of Y2(SO4)3 crystal structure, (c)—layer of Y2(SO4)3*8H2O crystal structure, (d)—layer of Y2(SO4)3 crystal structure, (e)—chain in the Y2(SO4)3*8H2O crystal structure, (f)—chain in the Y2(SO4)3 crystal structure.
Figure 11. Comparison of the Y2(SO4)3*8H2O (left) and Y2(SO4)3 (right) crystal structures: (a)—fragment of Y2(SO4)3*8H2O crystal structure, (b)—fragment of Y2(SO4)3 crystal structure, (c)—layer of Y2(SO4)3*8H2O crystal structure, (d)—layer of Y2(SO4)3 crystal structure, (e)—chain in the Y2(SO4)3*8H2O crystal structure, (f)—chain in the Y2(SO4)3 crystal structure.
Minerals 15 01304 g011
Minerals 15 01304 g012
Figure 12. Comparison of Y2(SO4)3 and Y2O2SO4 crystal structures. The crystal structure of Y2O2SO4 is also compared with sections of the thermal expansion tensor figure. Slab in the Y2(SO4)3 crystal structure is marked by a point line.
Figure 12. Comparison of Y2(SO4)3 and Y2O2SO4 crystal structures. The crystal structure of Y2O2SO4 is also compared with sections of the thermal expansion tensor figure. Slab in the Y2(SO4)3 crystal structure is marked by a point line.
Minerals 15 01304 g012
Minerals 15 01304 g013
Figure 13. Oxo-centered layers in the Y2O2SO4 crystal structure in the ac (a) and bc (b) projections.
Figure 13. Oxo-centered layers in the Y2O2SO4 crystal structure in the ac (a) and bc (b) projections.
Minerals 15 01304 g013
Table 1. Crystal data and structure refinement parameters of YEu(SO4)3*8H2O at −173, −73, and 77 °C, respectively.
Table 1. Crystal data and structure refinement parameters of YEu(SO4)3*8H2O at −173, −73, and 77 °C, respectively.
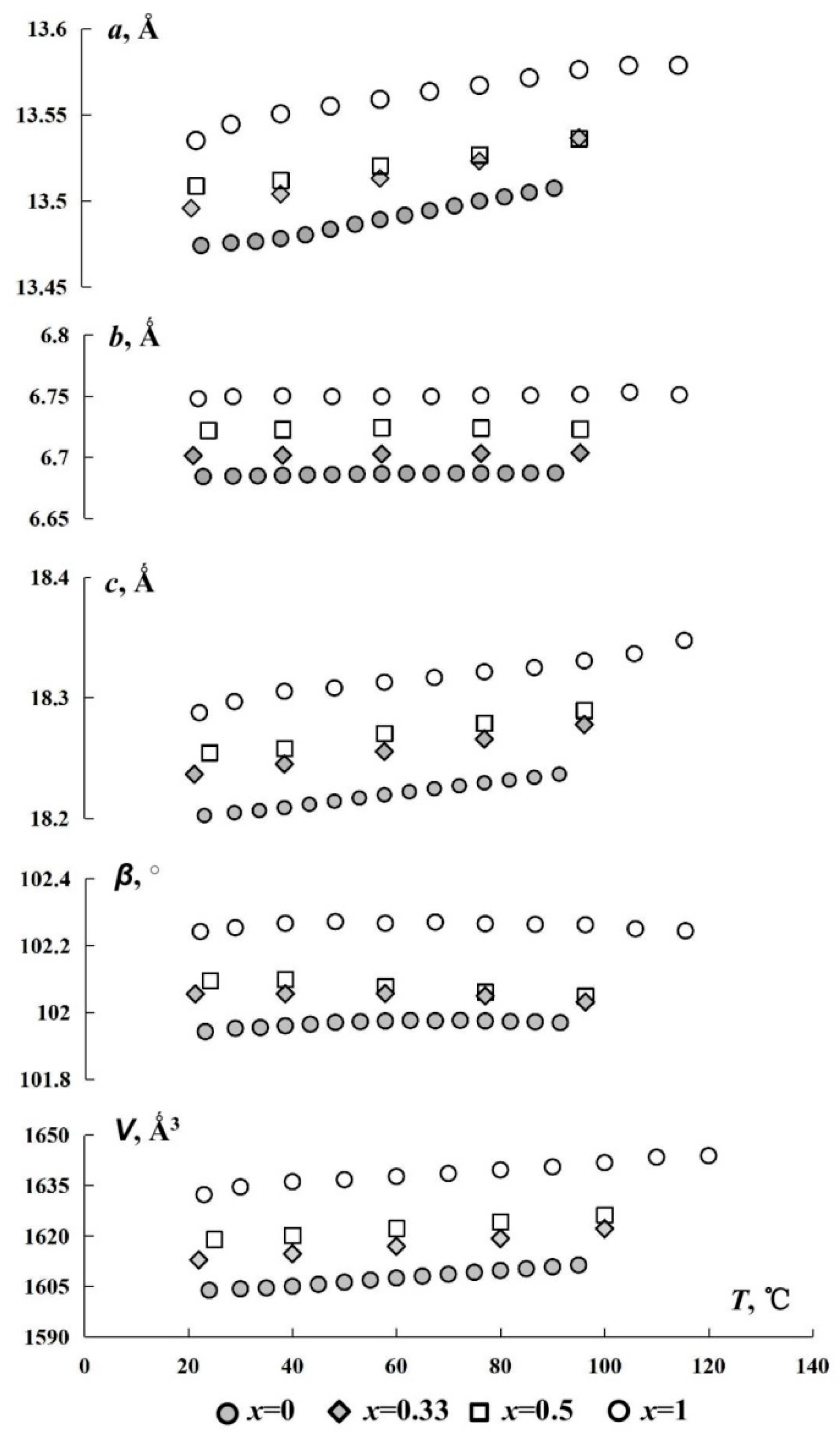
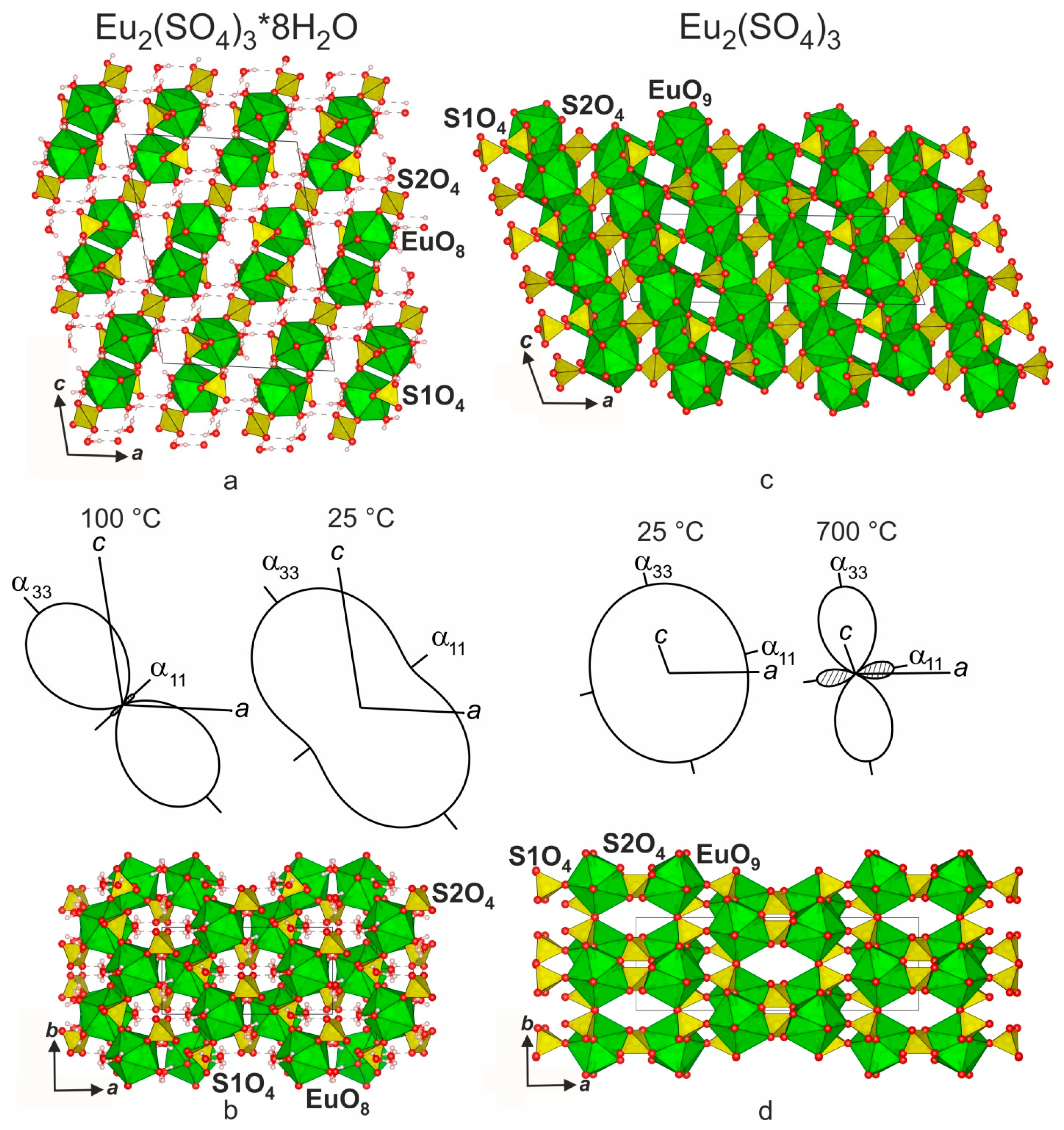
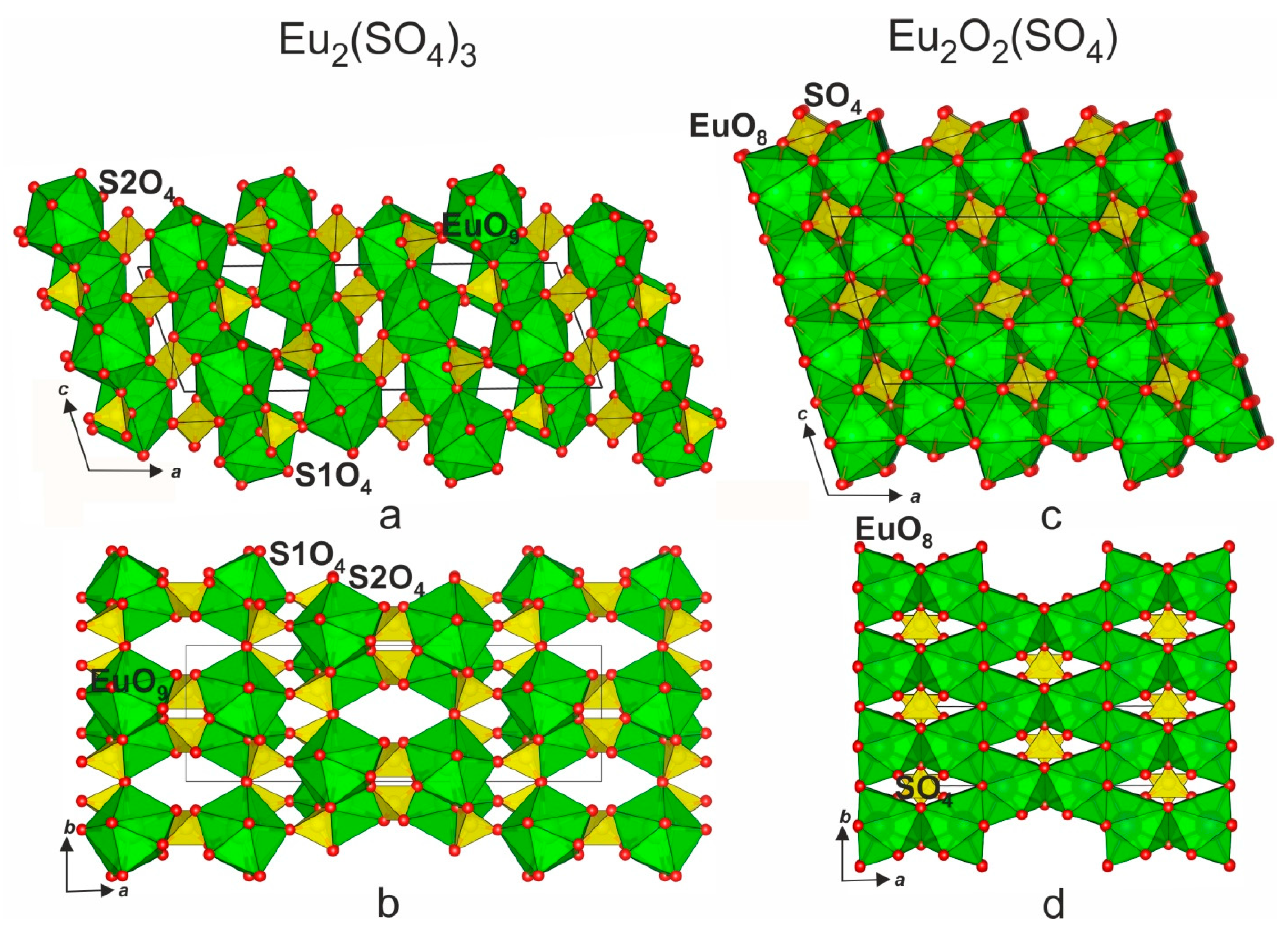
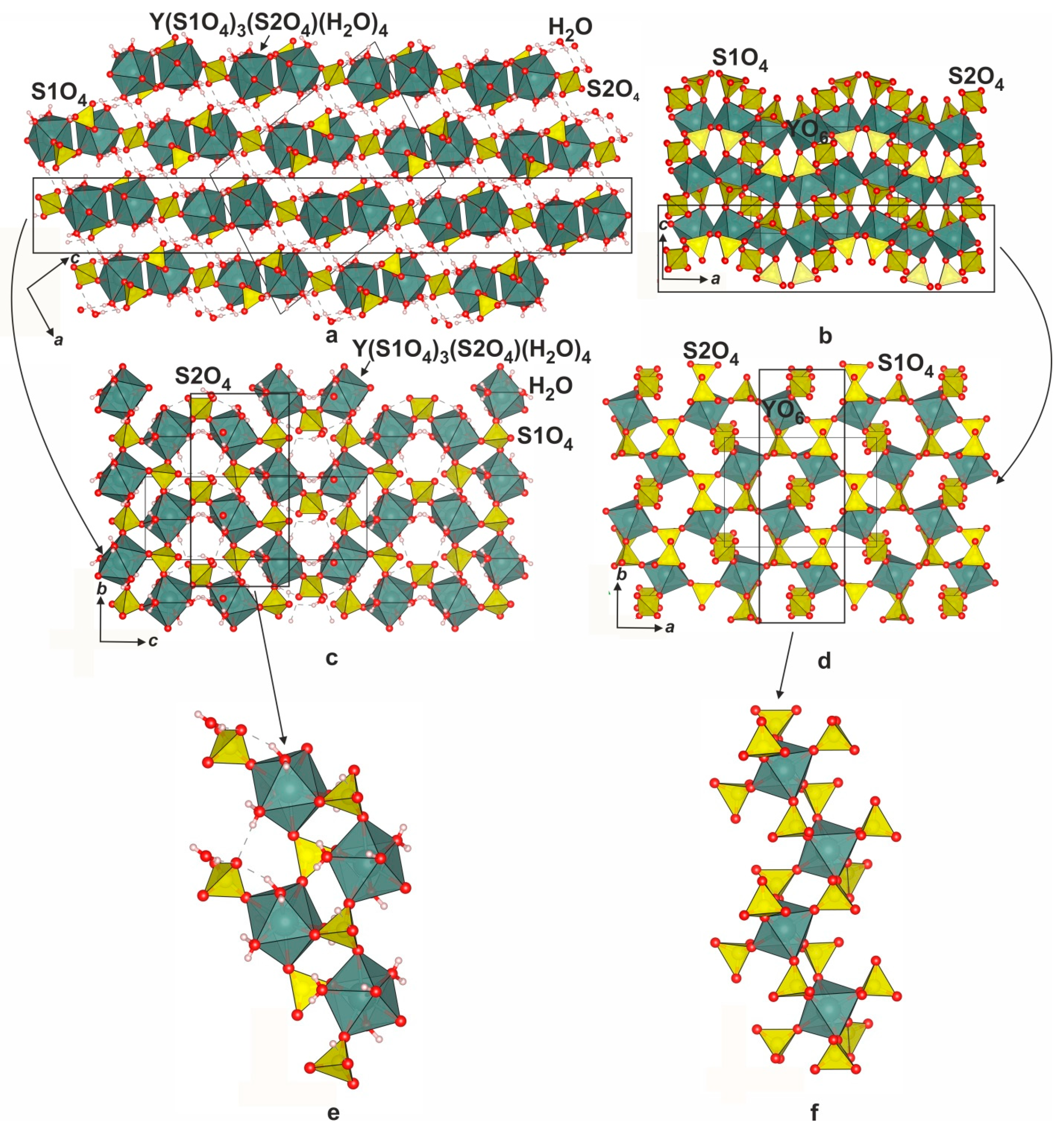
Chemical FormulaY0.98Eu1.02(SO4)3*8H2O
Crystal System, Space GroupMonoclinic, C2/c
Temperature (°C)−173−7377
a, b, c (Å)13.4673 (9), 6.7289 (4), 18.2203 (10)13.4856 (9), 6.7287 (4), 18.2442 (10)13.5343 (9), 6.7250 (4), 18.3136 (10)
β (°)102.148 (7)102.143 (7)102.119 (7)
V (Å3)1614.15 (17)1618.45 (17)1629.72 (18)
Z4
Radiation typeMo Kα
µ (mm−1)7.927.907.85
Crystal size (mm)0.04 × 0.03 × 0.01
DiffractometerXtaLAB Synergy, Single source at home/near, HyPix
Absorption correctionCrysAlis PRO1.171.41.104a Empirical absorption correction using spherical harmonics, implemented in SCALE3 ABSPACK scaling algorithm.
Tmin, Tmax0.565, 10.574, 10.308, 1
No. of measured, independent and
observed [I > 3σ(I)] reflections		13,818, 2839, 247613,846, 2848, 243213,747, 2849, 2351
Rint0.0570.0560.054
(sin θ/λ)max (Å−1)0.7790.7770.777
R(obs), wR(obs), S0.026, 0.032, 1.250.025, 0.031, 1.200.027, 0.031, 1.13
No. of reflections283928482849
No. of parameters147146146
H-atom treatmentAll H-atom parameters refined
Table 2. Crystal data and structure refinement parameters of Y0.83Eu0.17(SO4)3*8H2O at −173, −73 and 77 °C, respectively.
Table 2. Crystal data and structure refinement parameters of Y0.83Eu0.17(SO4)3*8H2O at −173, −73 and 77 °C, respectively.
Chemical formulaY1.89Eu0.11(SO4)3*8H2O
Crystal system, space groupMonoclinic, C2/c
Temperature (°C)−173−7377
a, b, c (Å)13.4358 (9), 6.6941 (4), 18.183 (1)13.4628 (9), 6.6939 (4), 18.1994 (10)13.5130 (9), 6.6953 (4), 18.2531 (10)
β (°)102.030 (7)102.023 (7)101.999 (7)
V (Å3)1599.47 (17)1604.13 (17)1615.34 (17)
Z4
Radiation typeMo Kα
µ (mm−1)7.757.727.67
Crystal size (mm)0.04 × 0.03 × 0.01
DiffractometerXtaLAB Synergy, Single source at home/near, HyPix
Absorption correctionMulti-scan CrysAlis PRO 1.171.42.102a (Rigaku Oxford Diffraction, Abingdon, UK, 2023) Empirical absorption correction using spherical harmonics, implemented in SCALE3 ABSPACK scaling algorithm.
Tmin, Tmax0.758, 10.771, 10.805, 1
No. of measured, independent and
observed [I > 3σ(I)] reflections		9674, 2695, 21709750, 2716, 20519816, 2746, 1998
Rint0.0380.0460.044
(sin θ/λ)max (Å−1)0.7810.7810.779
R(obs), wR(obs), S0.031, 0.042, 1.690.033, 0.040, 1.410.035, 0.043, 1.56
No. of reflections269527162746
No. of parameters147146146
H-atom treatmentAll H-atom parameters refined
Table 3. Thermal expansion coefficients for (Y1−xEux)2(SO4)3*8H2O solid solutions (×10−6 °C−1).
Table 3. Thermal expansion coefficients for (Y1−xEux)2(SO4)3*8H2O solid solutions (×10−6 °C−1).
xT, °Cα11α22 = αbα33αaαcαβμc^α33αV
03050 (1)15 (1)14 (1)41 (1)29 (3)19 (1)41.478 (1)
5043 (1)9 (2)23 (2)41 (1)9 (3)9 (2)32.375 (3)
7041 (2)3 (5)28 (3)40 (2)28 (2)−1 (2)2.471 (4)
10052 (3)−5 (1)20 (2)40 (1)26 (3)−16 (4)26.066 (2)
0.17308 (1)9 (1)25 (1)19 (1)18 (3)9 (1)42.043 (3)
5026 (1)6 (2)16 (2)24 (1)20 (3)5 (2)40.448 (3)
7029 (2)2 (5)22 (3)28 (2)22 (2)2 (2)19.053 (4)
10037 (3)−3 (1)26 (2)35 (1)26 (3)−4 (4)13.960 (2)
0.333019 (1)7 (2)8 (2)17 (1)12 (3)5 (2)35.134 (3)
5029 (2)6 (5)21 (3)29 (2)21 (2)1 (2)10.656 (4)
7043 (1)5 (1)31 (1)41 (1)31 (3)−4 (1)12.478 (3)
10065 (1)4 (2)42 (2)56 (1)46 (3)−11 (2)23.1111 (3)
0.503026 (1)12 (2)18 (2)21 (1)21 (3)−4 (2)39.957 (3)
5032 (2)6 (5)21 (3)25 (2)25 (2)−6 (2)36.959 (4)
7037 (1)0 (1)23 (1)30 (1)28 (3)−7 (1)35.361 (3)
10045 (1)−8 (2)27 (2)36 (1)33 (3)−10 (2)33.864 (3)
0.833028 (1)−12 (1)20 (1)28 (1)22 (3)3 (1)27.436 (3)
5031 (1)−7 (2)25 (2)31 (1)25 (3)1 (2)14.950 (3)
7035 (2)−1 (5)29 (3)34 (2)29 (2)−1 (2)4.663 (4)
10042 (1)7 (1)33 (1)39 (1)35 (3)−4 (1)23.882 (3)
13051 (1)5 (2)31 (2)48 (1)38 (3)9 (2)35.187 (3)
5041 (2)4 (5)29 (3)40 (2)31 (2)4 (2)26.674 (4)
7032 (1)4 (1)24 (1)32 (1)24 (3)0 (1)2.960 (3)
10026 (1)3 (2)11 (2)20 (1)14 (3)−7 (2)27.440 (3)
Table 4. Thermal expansion coefficients for Y2O2SO4, Eu2(SO4)3, and (Y1−xEux)2(SO4)3 compounds and solid solutions (×10−6 °C−1).
Table 4. Thermal expansion coefficients for Y2O2SO4, Eu2(SO4)3, and (Y1−xEux)2(SO4)3 compounds and solid solutions (×10−6 °C−1).
xT, °Ca11a22 = αba33αaαcαβμc3αV
Y2O2SO410010.13 (3)8.40 (3)14.1 (5)10.5 (3)14.1 (2)0.56 (7)0.833 (3)
30012.76 (5)8.62 (1)14.5 (7)11.7 (1)14.5 (1)0.17 (5)3.036 (3)
50015.42 (4)8.86 (3)14.8 (2)14.1 (3)14.7 (2)−0.20 (1)12.839 (2)
70018.00 (1)9.09 (2)15.2 (4)17.6 (4)15.2 (1)−0.593.542 (1)
Y2(SO4)3 [30]300=αa −11 (1)=αc −4 (1)−8 (3)--−23 (2)
400=αa −10 (2)=αc −2 (3)−17 (3)--−29 (2)
500=αa −8 (3)=αc −1 (3)−25 (1)--−34 (3)
(Y0.83Eu0.17)2(SO4)3 [30]300=αa −11 (2)=αc −1 (3)−10 (2)--−22 (1)
400=αa −11 (1)=αc −2 (1)−11 (1)--−23 (1)
500=αa −12 (2)=αc −2 (3)−11 (2)--−24 (1)
(Y0.67Eu0.33)2(SO4)3300=αa −10 (4)=αc −1 (7)−10 (5)--−21 (3)
400=αa −10 (5)=αc −2 (4)−10 (4)--−22 (5)
500=αa −10 (5)=αc −3 (4)−10 (4)--−23 (6)
(Y0.50Eu0.50)2(SO4)3 [30]300=αa −14 (3)=αc −7 (3)−13 (2)--−34 (3)
400=αa −15 (1)=αc −7 (1)−17 (1)--−39 (3)
500=αa −15 (3)=αc −7 (3)−22 (2)--−44 (2)
Eu2(SO4)33004.22 (8)5.6 (1)12.8 (2)4.4 (1)12.8 (2)−0.07 (6)10.122.6 (4)
4001.82 (6)5.7 (2)12.7 (4)2.1 (2)12.7 (4)−0.14 (9)10.420.2 (7)
500−0.58 (4)5.8 (4)12.5 (8)−0.3 (4)12.5 (8)−0.20 (2)10.517 (1)
600−3.0 (3)5.9 (6)12 (1)−2.6 (5)12 (1)−0.26 (2)10.615 (2)
Table 5. Comparison of unit cell parameters of the Eu2(SO4)3*8H2O, Eu2(SO4)3, and Eu2O2SO4 compounds.
Table 5. Comparison of unit cell parameters of the Eu2(SO4)3*8H2O, Eu2(SO4)3, and Eu2O2SO4 compounds.
CompoundEu2(SO4)3*8H2OEu2(SO4)3Eu2O2SO4
Space groupC2/c
a, Å13.555 (2)21.2787 (8)13.6952 (1)
b, Å6.757 (1)6.6322 (3)4.1929 (4)
c, Å18.317 (2)6.8334 (3)8.1393 (2)
β, °102.27 (1)108.002 (2)107.455 (4)
V, Å31639.4 (1)917.16 (6)467.38
Z444
T, °C025–153
References[34][35][36]
Table 6. Comparison of unit cell parameters of Y2(SO4)3*8H2O, Y2(SO4)3, and Y2O2SO4 compounds.
Table 6. Comparison of unit cell parameters of Y2(SO4)3*8H2O, Y2(SO4)3, and Y2O2SO4 compounds.
CompoundY2(SO4)3*8H2OY2(SO4)3Y2O2SO4
Space groupC2/cPbcnC2/c
a, Å13.4802 (9)12.740 (1)13.3076
b, Å6.6846 (4)9.1676 (9)4.1465
c, Å18.216 (1)9.2608 (7)8.0204
β, °101.977 (7)90107.64
V, Å31605.7 (1)1081.6 (1)467.38
Z444
T, °C20200 *
References[11][40][42]
*—calculated.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Shablinskii, A.P.; Shorets, O.Y.; Bubnova, R.S.; Krzhizhanovskaya, M.G.; Avdontceva, M.S.; Filatov, S.K. Thermal, Structural, and Phase Evolution of the Y2(SO4)3*8H2O–Eu2(SO4)3*8H2O System via Dehydration and Volatilization to Y2(SO4)3–Eu2(SO4)3 and Y2O2(SO4)–Eu2O2(SO4) and Its Thermal Expansion. Minerals 2025, 15, 1304. https://doi.org/10.3390/min15121304

AMA Style

Shablinskii AP, Shorets OY, Bubnova RS, Krzhizhanovskaya MG, Avdontceva MS, Filatov SK. Thermal, Structural, and Phase Evolution of the Y2(SO4)3*8H2O–Eu2(SO4)3*8H2O System via Dehydration and Volatilization to Y2(SO4)3–Eu2(SO4)3 and Y2O2(SO4)–Eu2O2(SO4) and Its Thermal Expansion. Minerals. 2025; 15(12):1304. https://doi.org/10.3390/min15121304

Chicago/Turabian Style

Shablinskii, Andrey P., Olga Y. Shorets, Rimma S. Bubnova, Maria G. Krzhizhanovskaya, Margarita S. Avdontceva, and Stanislav K. Filatov. 2025. "Thermal, Structural, and Phase Evolution of the Y2(SO4)3*8H2O–Eu2(SO4)3*8H2O System via Dehydration and Volatilization to Y2(SO4)3–Eu2(SO4)3 and Y2O2(SO4)–Eu2O2(SO4) and Its Thermal Expansion" Minerals 15, no. 12: 1304. https://doi.org/10.3390/min15121304

APA Style

Shablinskii, A. P., Shorets, O. Y., Bubnova, R. S., Krzhizhanovskaya, M. G., Avdontceva, M. S., & Filatov, S. K. (2025). Thermal, Structural, and Phase Evolution of the Y2(SO4)3*8H2O–Eu2(SO4)3*8H2O System via Dehydration and Volatilization to Y2(SO4)3–Eu2(SO4)3 and Y2O2(SO4)–Eu2O2(SO4) and Its Thermal Expansion. Minerals, 15(12), 1304. https://doi.org/10.3390/min15121304

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop