Indentation Size Effects and the Mechanical Properties of Barite Rocks
Abstract
1. Introduction
Theoretical Framework on Dislocation in Rocks and Minerals
2. Materials and Methods
2.1. Collection of Barite Rock Samples
2.2. Sample Preparation
2.3. Experimental Methods
2.3.1. Grid Nanoindentation
2.3.2. Hardness of Barite Rock Materials
2.3.3. Strain Gradient Plasticity
2.3.4. Dislocation Theory
2.3.5. Material Length Scale
2.3.6. Dislocation Spacing—Ashby, Ma and Clarke Models
3. Results
3.1. Rock Samples and Minerals
Mineral Phases and Composition of the Barite Rock-like Materials
3.2. Properties of the Barite Rock Mineral Samples
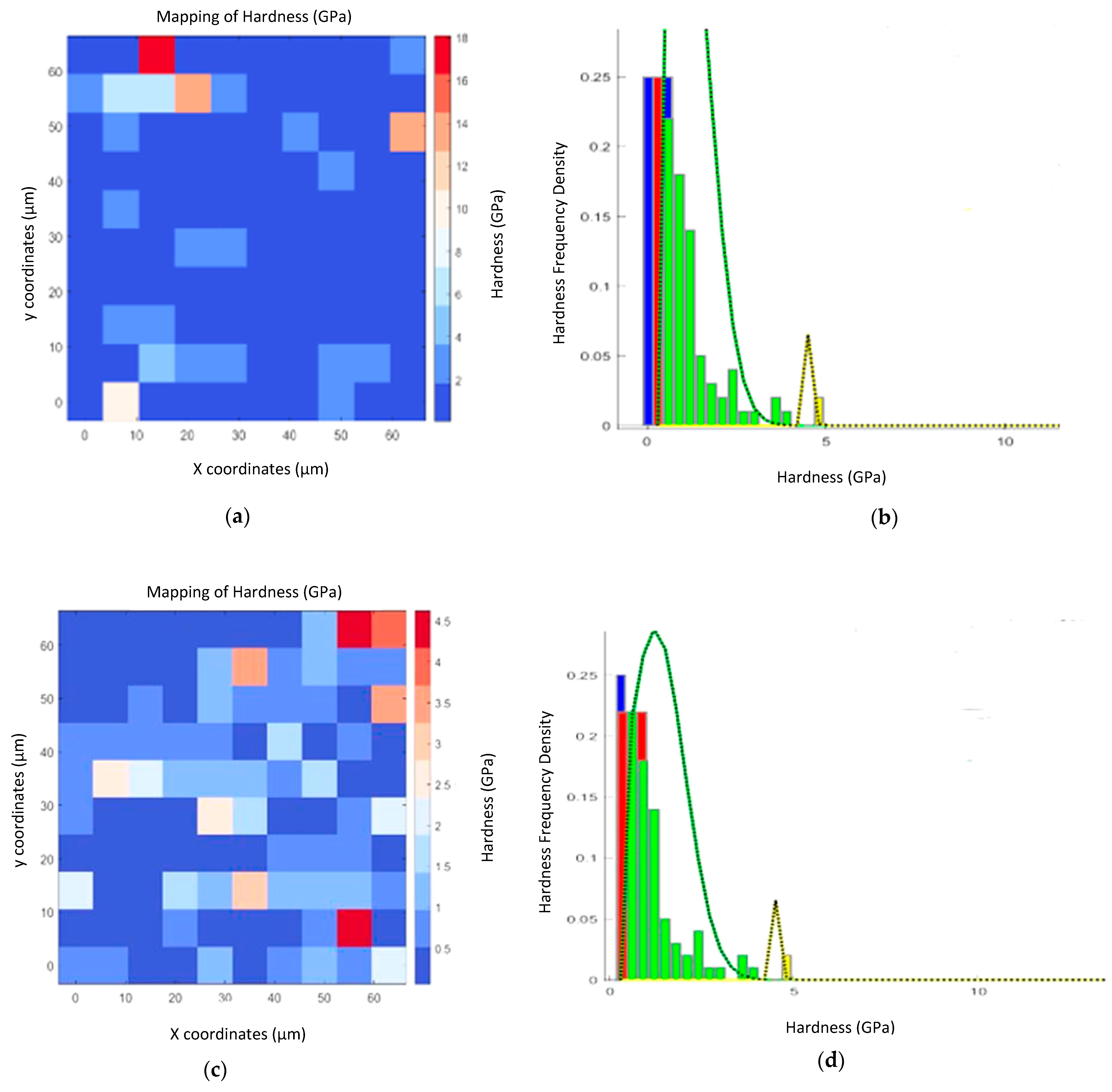
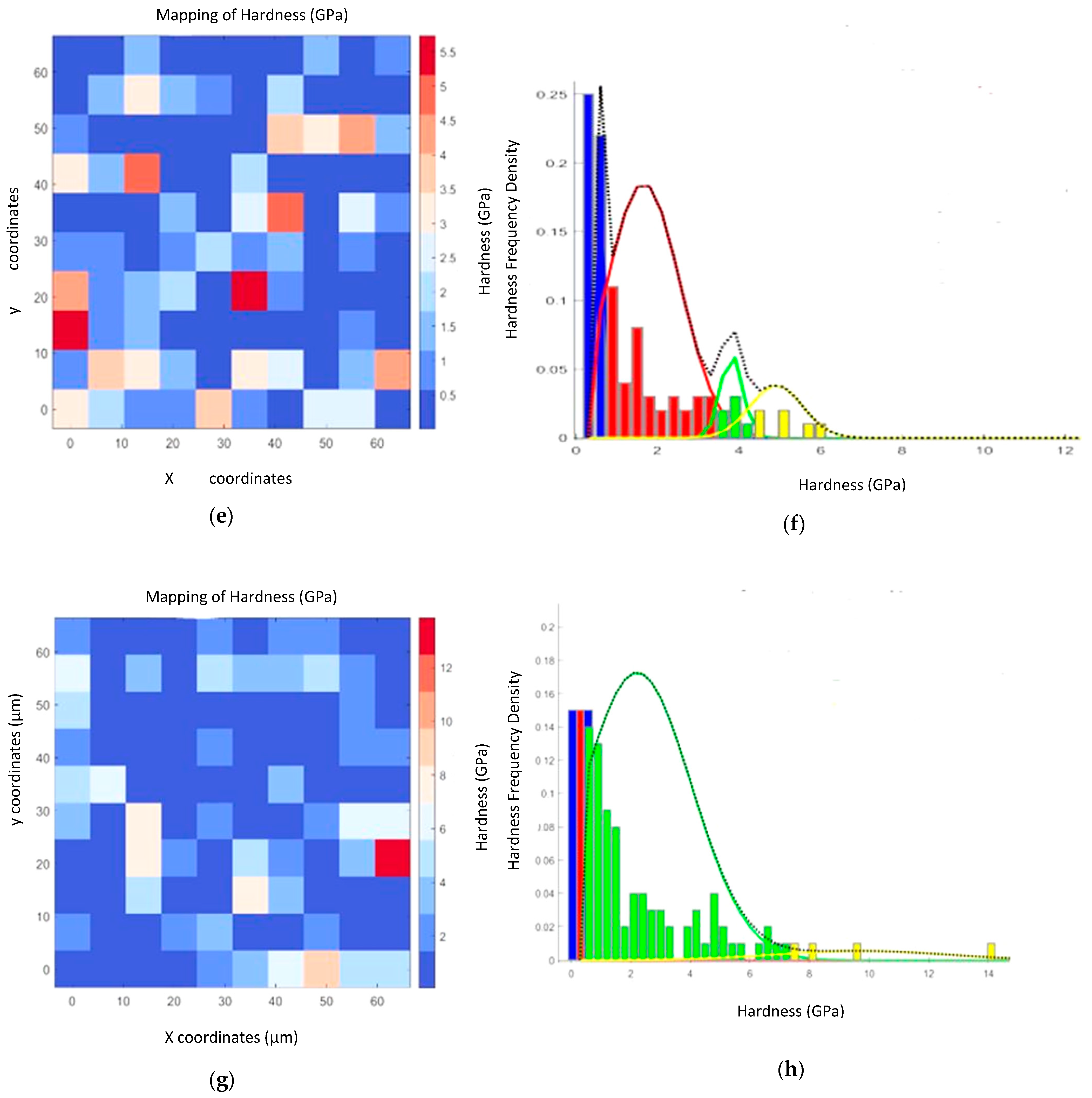
3.2.1. Hardness of the Rock Samples Based on 2D Heat Maps and Statistical Deconvolution
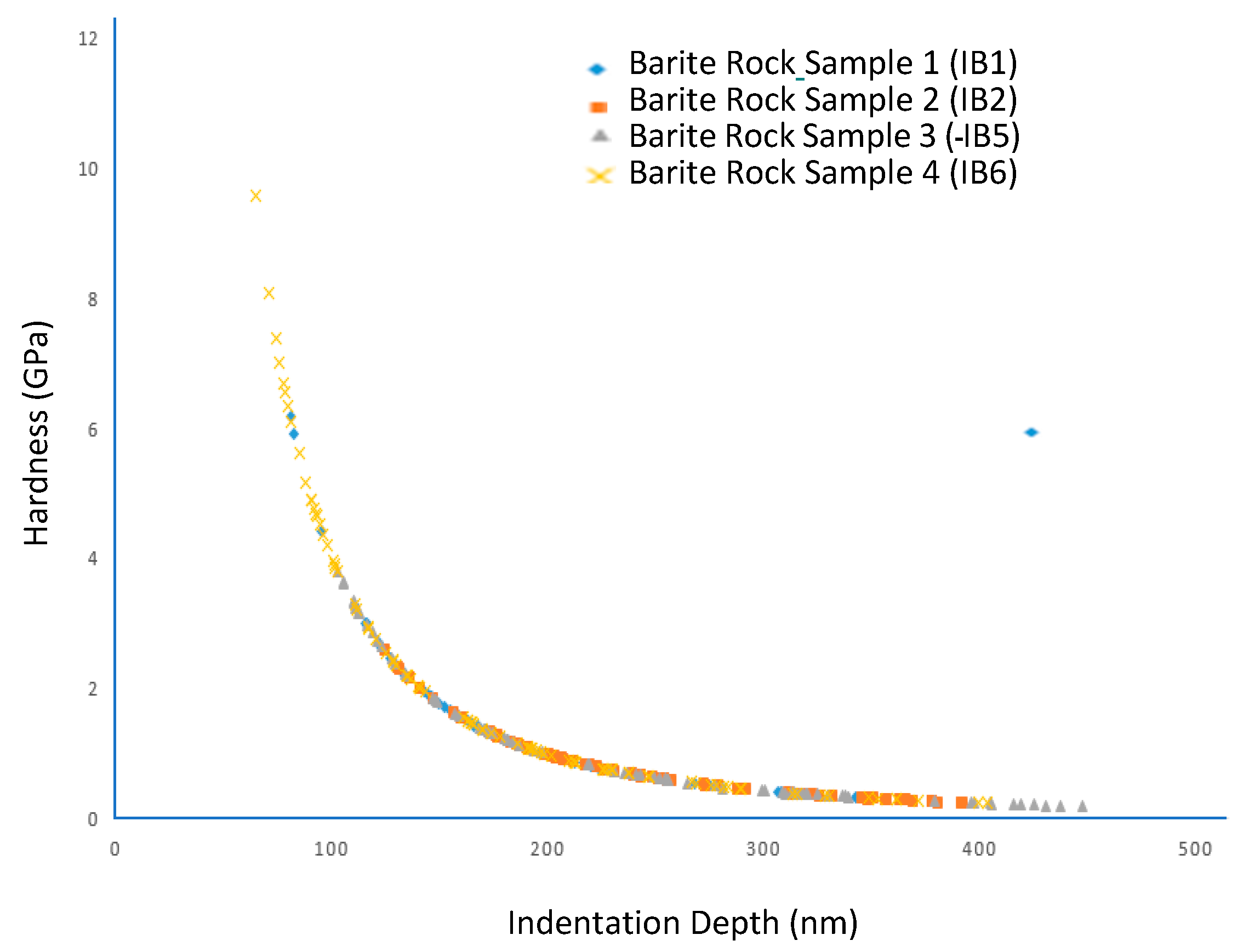
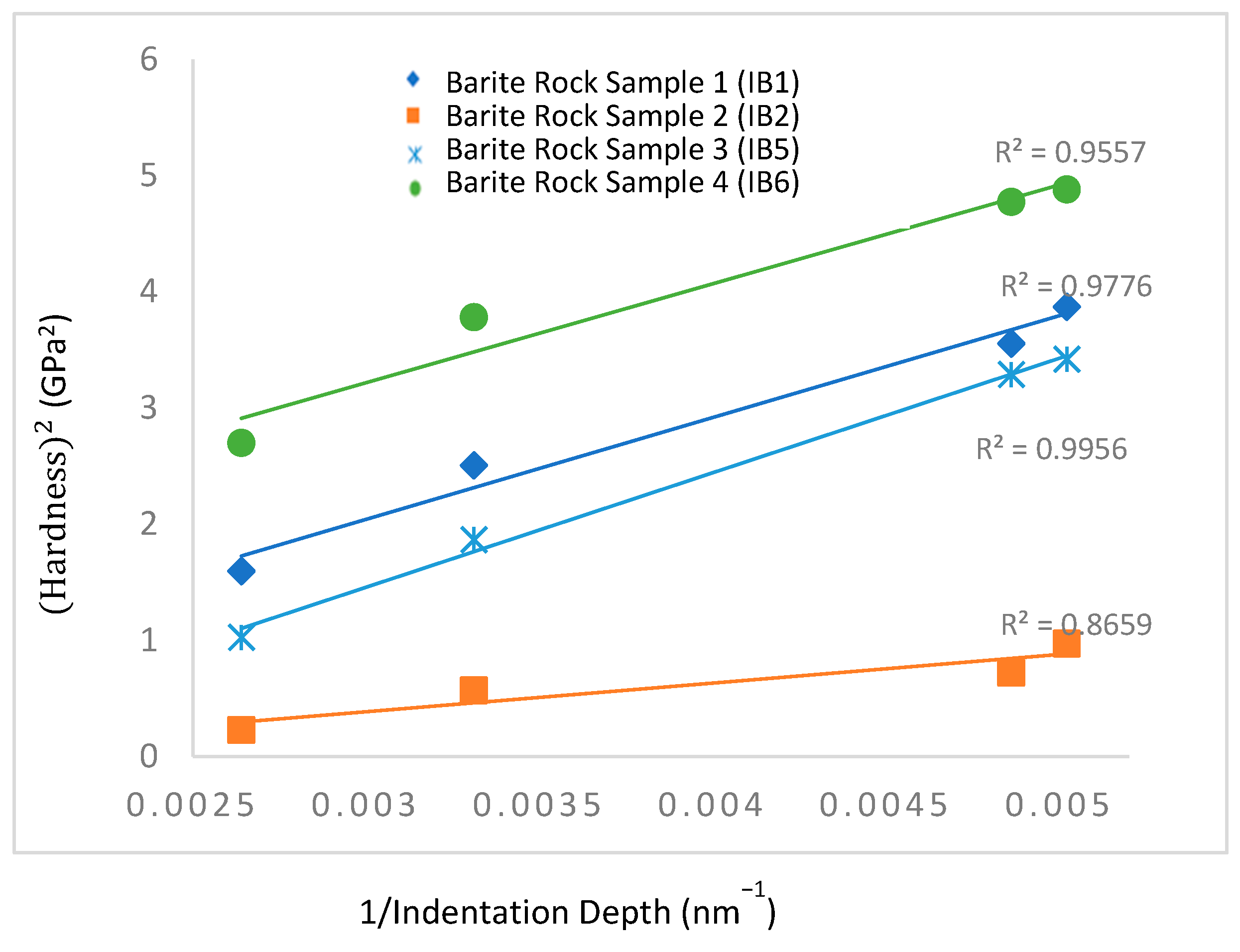
3.2.2. Hardness of the Barite Rock Materials at Different Indentation Depths
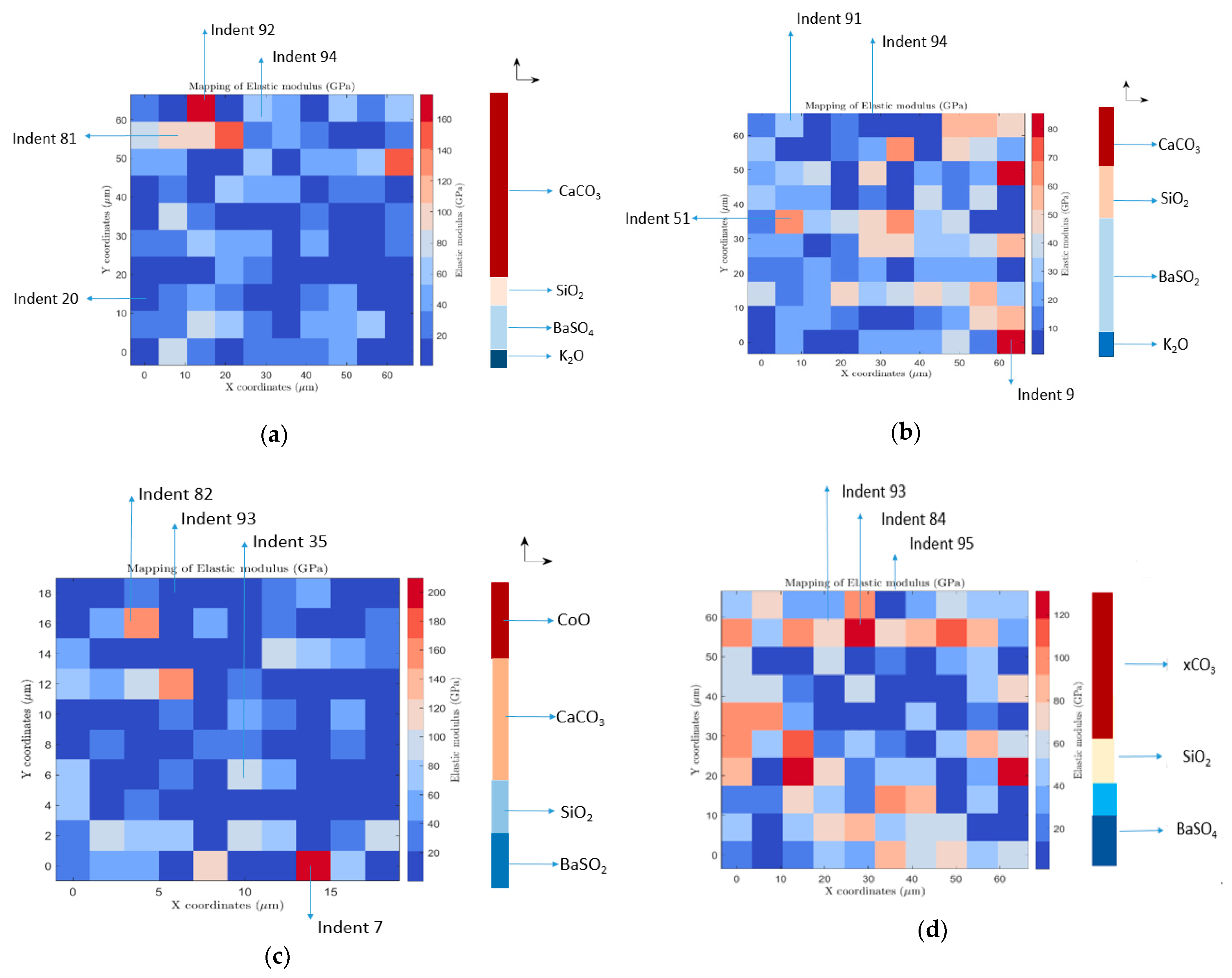
3.2.3. Elastic Moduli (Young’s Moduli) of the Barite Rock Samples
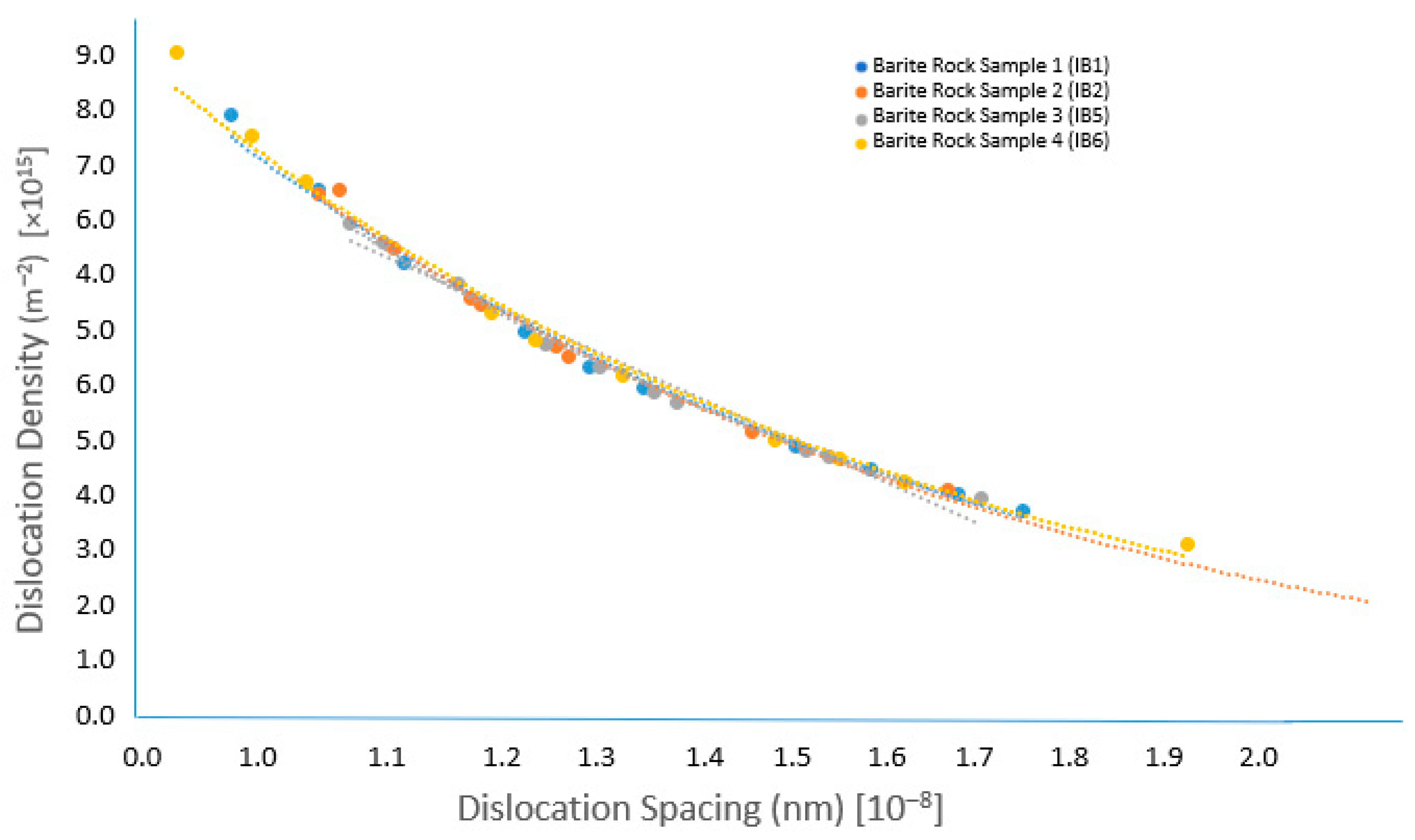
3.3. Dislocation Density
4. Discussion
4.1. Dislocations and Mining Activities with Consequences on Water Contaminations
4.2. Regulations and Environmental Management in Nigerian Barite Mining
5. Conclusions
- The hardness and Young’s moduli values obtained from the barite rocks exhibit spatial variations that are consistent with the presence of multiple phases (barite, quartz, non-barite phases). The statistical deconvolution of the measured hardness and reduced elastic moduli data suggest that the dominant phase in the rocks is barite.
- The indentation size effects obtained from the current study are well described by [53] theory. A combination of [52,53] theory also provided estimates of the densities of geometrically necessary dislocations and statistically stored dislocation densities that are consistent with the trends in the measured hardness data.
- The relatively high dislocation densities obtained in this study suggest that significant plastic deformation is associated with the contact of rocks during the grinding and drilling processes associated with mineral processing and oil/gas extraction. This suggests that strain gradient plasticity models may provide useful tools for the constitutive modeling of barite rock deformation at the nano- and microscales.
- The plasticity length scale parameters obtained from strain gradient plasticity theories provide key insights into the size scales in which the strain gradients are significant. However, the magnitudes of the underlying dislocation densities are perhaps even more important than the plasticity length scales, since they provide estimates of the underlying dislocation strengthening.
- The local variations in the composition of the rock features contributed to the shift in the behavior of rock samples under stress at different indentation depths. Hence, the plasticity or contact deformation and dislocation motion in the barite rock materials are directly impacted by the local variations.
- The heterogeneity of barite rocks is affected by the presence of barite, quartz and other non-barite minerals. However, these represent about 15 vol.% of the total volume. Thus, the behavior of the rocks is dominated by the presence barite.
- The statistically deconvoluted mechanical properties of the barite rock have major implications for the design of comminution and drilling tools that are used in mineral processing and oil and gas extraction. They should, therefore, be considered in the design of mineral processing and oil/gas processing conditions.
- The relationship between hardness of the rock samples and indentation depth provides a good prediction of the effect of local variation in the elemental composition and mineralogy of the rock samples on the plasticity of typical earth-based materials. Hence, the variations observed in some of the rock samples have significant implications for plastic deformation in rock samples.
- The studies identified that traces of non-barite materials, especially cations in barite rocks, are detrimental to human health. While the quantity of the metals was not measured, dusts and sediments rich in heavy metals can initiate chronic diseases in humans and animals over a short or extended period. The findings highlight the implications of the variation in the mechanical response of rocks and the potential environmental risk associated with dislocation sites rich in heavy metals when exposed to water and air, due to the elastic–plastic properties of barite rocks. There is an urgent need for an in-depth materials characterization of barite rocks to ensure a thorough understanding of the implications of their unique properties, thereby facilitating a sustainable approach to barite mining, comminution, and the recovery of heavy metals from air and water. The outlined research provides a roadmap for responsible mining practices and the failure of rock masses during crushing and grinding.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IB1 | Ibi barite sample 1 |
| IB2 | Ibi barite sample 2 |
| IB5 | Ibi barite sample 3 |
| IB6 | Ibi barite sample 4 |
References
- Davarpanah, S.M.; Sharghi, M.; Narimani, S.; Török, Á.; Vásárhelyi, B. Brittle-ductile transition stress of different rock types and its relationship with uniaxial compressive strength and Hoek–Brown material constant (mi). Sci. Rep. 2023, 13, 1186. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, C.; Wang, L.; Feng, X. Effects of Cyclic Loading on the Mechanical Properties of Mature Bedding Shale. Adv. Civ. Eng. 2018, 3, 85973. [Google Scholar] [CrossRef]
- Yu, D.K.; An, Y.; Chen, X. Revealing the cyclic hardening mechanism of an austenitic stainless steel by real-time in situ neutron, diffraction. Scr. Mater. 2014, 89, 45–48. [Google Scholar] [CrossRef]
- Mughrabi, H. The cyclic hardening and saturation behavior of copper singe crystals. Mater. Sci. Eng. 1978, 33, 207–223. [Google Scholar] [CrossRef]
- Hong, S.G.; Yoon, S.; Lee, S.B. The effect of temperature on low-cycle fatigue behavior of prior cold worked 316L stainless steel. Int. J. Fatigue 2003, 25, 1293–1300. [Google Scholar] [CrossRef]
- Hong, S.G.; Lee, S.B. The tensile and low-cycle fatigue behavior of cold worked 316L stainless steel: Influence of dynamic strain aging. Int. J. Fatigue 2004, 26, 899–910. [Google Scholar] [CrossRef]
- Pham, M.S.; Holdsworth, S.R.; Janssens, K.G.F.; Mazza, E. Cyclic plastic deformation response of AISI 316L at room temperature: Mechanical behavior, microstructural evolution, physically-based evoluationary constitutive modelling. Int. J. Plast. 2013, 47, 143–164. [Google Scholar] [CrossRef]
- Stephens, R.I.; Fatemi, A.; Stephens, R.R.; Fuchs, H.O. Metal Fatigue in Engineering, 2nd ed.; John Wiley, Sons, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Galindo-Nava, E.I.; Sietsma, J.; Rivera-Díaz-del-Castillo, P.E.J. Dislocation annihilation in plastic deformation: II. Kocks-Meching analysis. Acta Mater. 2012, 60, 2615–2624. [Google Scholar] [CrossRef]
- Soboyejo, W. 6 Introduction to Dislocation Mechanics. In Mechanical Properties of Engineered Materials; Marcel Dekker: New York, NY, USA, 2003; ISBN 0-8247-8900-8. [Google Scholar]
- Barber, D.J.; Wenk, H.-R.; Gomez-Barreiro, J.; Rybacki, E.; Dresen, G. Basal slip and texture development in calcite: New results from torsion experiments. Phys. Chem. Miner. 2007, 34, 73–84. [Google Scholar] [CrossRef]
- Asenjo, A.; Rojo, J.M. Dislocation generation and motion at the incipient stages of surface plasticity in barite. Philos. Mag. 2007, 87, 3959–3966. [Google Scholar] [CrossRef]
- Verberne, R.; Reddy, S.M.; Saxey, D.W.; Fougerouse, D.; Rickard, W.D.A.; Quadir, Z.; Evans, N.J.; Clark, C. Dislocations in minerals: Fast-diffusion pathways or trace-element traps? Earth Planet. Sci. Lett. 2022, 584, 117517. [Google Scholar] [CrossRef]
- Walker, A.M.; Carrez, P.; Cordier, P. Atomic-scale models of dislocation cores in minerals: Progress and prospects. Mineral. Mag. 2010, 74, 381–413. [Google Scholar] [CrossRef][Green Version]
- Li, X.; Luo, X.; Li, P.; Huang, Y.; Yang, J.; Zhou, Q. Size effect and indenter shape dependence of indentation and scratching behavior for laser melting deposited Ti-6Al-4V alloy. Mater. Sci. Technol. 2025, 41, 443–456. [Google Scholar] [CrossRef]
- Grgic, D.; Al Sahyouni, F.; Golfier, F.; Moumni, M.; Schoumacker, L. Evolution of gas permeability of rock salt under different loading conditions and implications on the underground hydrogen storage in salt caverns. Rock Mech. Rock Eng. 2022, 55, 691–714. [Google Scholar] [CrossRef]
- Grgic, D.; Amitrano, D. Creep of a porous rock and associated acoustic emission under different hydrous conditions. J. Geophys. Res. Solid Earth 2009, 114, B10201. [Google Scholar] [CrossRef]
- Phakey, P.P.; Aly, A.M. Direct observation of dislocations in natural barite (BaSO4). Philos. Mag. 1970, 22, 1217–1225. [Google Scholar] [CrossRef]
- Sakhaei, A.H.; Shafiee, M. Microscale investigation of phase transformation and plasticity in multi-crystalline shape memory alloy using discrete dislocation–transformation method. Contin. Mech. Thermodyn. 2023, 35, 279–297. [Google Scholar] [CrossRef]
- Ord, A. Deformation of rock: A pressure-sensitive, dilatant material. Pure Appl. Geophys. 1991, 137, 337–366. [Google Scholar] [CrossRef]
- Fuenkajorn, K.; Phueakphum, D. Effects of cyclic loading on mechanical properties of Maha Sarakham salt. Eng. Geol. 2010, 112, 43–52. [Google Scholar] [CrossRef]
- Zhou, Y.; Sheng, Q.; Li, N.; Fu, X. Numerical investigation of the deformation properties of rock materials subjected to cyclic compression by the finite element method. Soil Dyn. Earthq. Eng. 2019, 126, 105795. [Google Scholar] [CrossRef]
- Cui, L.; Yu, C.-H.; Jiang, S.; Sun, X.; Peng, R.L.; Lundgren, J.-E.; Moverare, J. A new approach for determining GND and SSD densities based on indentation size effect: An application to additive-manufactured Hastelloy X. J. Mater. Sci. Technol. 2022, 96, 295–307. [Google Scholar] [CrossRef]
- Parapari, P.S. Efficient Mineral Liberation–Multidimensional Investigation of Mechanical Stress and Ore Texture. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2021. [Google Scholar]
- Jakubec, J. Role of defects in rock mass classification. In Ground Support 2013: Proceedings of the Seventh International Symposium on Ground Support in Mining and Underground Construction, Perth, Australia, 13–15 May 2013; Australian Centre for Geomechanics: Crawley, Australia, 2013; pp. 337–344. [Google Scholar]
- Yu, M.; Wang, Z.; Ma, D.; Ge, J.; Wang, Y.; Xie, H.; Wu, G.; Meng, Y. Fracture characteristics and process zone evolution in sandstone under freeze-thaw cycles. Res. Cold Arid. Reg. 2025, 17, 217–228. [Google Scholar] [CrossRef]
- Barber, D.J.; Wenk, H.-R.; Hirth, G.; Kohlstedt, D.L. Dislocations in minerals. Dislocations Solids 2010, 16, 171–232. [Google Scholar]
- Barber, D.J.; Wenk, H.-R. Slip and dislocation behaviour in dolomite. Eur. J. Mineral. 2001, 13, 221–243. [Google Scholar] [CrossRef]
- Hoek, E.; Martin, C.D. Fracture initiation and propagation in intact rock–a review. J. Rock Mech. Geotech. Eng. 2014, 6, 287–300. [Google Scholar] [CrossRef]
- Lei, R.; Zhang, Z.; Ge, Z.; Berto, F.; Wang, G.; Zhou, L. Deformation localization and cracking processes of sandstone containing two flaws of different geometric arrangements. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1959–1977. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Wang, D.; Wu, M.; Yin, G.; Li, M. Mechanical and acoustic emission characteristics of coal at temperature impact. Nat. Resour. Res. 2020, 29, 1755–1772. [Google Scholar] [CrossRef]
- Freund, F.T. Peroxy Defects in Rock-forming Minerals in the Earth’s Crust and their Role in Resolving some of the Longest-Lasting Paradoxes across the Geosciences. AGU Fall Meet. Abstr. 2014, 2014, S51B-4458. [Google Scholar]
- Zhao, F.; Shi, Z.; Yu, S.; Zheng, H. A review of fracture mechanic behaviors of rocks containing various defects. Undergr. Space 2023, 12, 102–115. [Google Scholar] [CrossRef]
- Yang, W.; Wei, B.; Xu, Y. Study on the crack growth law and mechanism of the rock mass with defect combination. Geotech. Geol. Eng. 2021, 39, 1319–1327. [Google Scholar] [CrossRef]
- Hirth, J.P.; Hirth, G.; Wang, J. Disclinations and disconnections in minerals and metals. Proc. Natl. Acad. Sci. USA 2020, 117, 196–204. [Google Scholar] [CrossRef]
- Ashby, M.F. The deformation of plastically non-homogeneous materials. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Muransky, O.; Balogh, L.; Tran, M.; Hamelin, C.J.; Park, J.-S.; Daymond, M.R. On the measurement of dislocations and dislocation substructures using EBSD and HRSD techniques. Acta Mater. 2019, 175, 297–313. [Google Scholar] [CrossRef]
- Zhu, C.; Harrington, T.; Gray, G.T., III; Vecchio, K.S. Dislocation-type evolution in quasi-statically compressed polycrystalline nickel. Acta Mater. 2018, 155, 104–116. [Google Scholar] [CrossRef]
- Birosca, S.; Liu, G.; Ding, R.; Jiang, J.; Simm, T.; Deen, C.; Whittaker, M. The dislocation behaviour and GND development in a nickel based superalloy during creep. Int. J. Plast. 2019, 118, 252–268. [Google Scholar] [CrossRef]
- Cui, L.; Jiang, S.; Xu, J.; Peng, R.L.; Mousavian, R.T.; Moverare, J. Revealing relationships between microstructure and hardening nature of additively manufactured 316L stainless steel. Mater. Des. 2021, 198, 109385. [Google Scholar] [CrossRef]
- Graça, S.; Colaço, R.; Carvalho, P.A.; Vilar, R. Determination of dislocation density from hardness measurements in metals. Mater. Lett. 2008, 62, 3812–3814. [Google Scholar] [CrossRef]
- Kearney, C.; Zhao, Z.; Bruet, B.J.F.; Radovitzky, R.; Boyce, M.C.; Ortiz, C. Nanoscale anisotropic plastic deformation in single crystal aragonite. Phys. Rev. Lett. 2006, 96, 255505. [Google Scholar] [CrossRef] [PubMed]
- Leroux, H. Microstructural shock signatures of major minerals in meteorites. Eur. J. Mineral. 2001, 13, 253–272. [Google Scholar] [CrossRef]
- Monteiro, P.J.M.; Shomglin, K.; Wenk, H.R.; Hasparyk, N.P. Effect of aggregate deformation on alkali-silica reaction. Mater. J. 2001, 98, 179–183. [Google Scholar]
- Nyilas, K.; Couvy, H.; Cordier, P.; Ungár, T. The dislocation structure and crystallite-size in forsterite (olivine) deformed at 14008C by 11 GPa. Z. Fur Krist. Suppl. 2006, 2006, 135–140. [Google Scholar] [CrossRef] [PubMed]
- Wenk, H.-R.; Monteiro, P.J.M.; Shomglin, K. Relationship between aggregate microstructure and mortar expansion. A case study of deformed granitic rocks from the Santa Rosa mylonite zone. J. Mater. Sci. 2008, 43, 1278–1285. [Google Scholar] [CrossRef]
- Wenk, H.-R.; Bulakh, A. Minerals: Their Constitution and Origin; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Durst, K.; Backes, B.; Franke, O.; Göken, M. Indentation size effect in metallic materials: Modeling strength from pop-in to macroscopic hardness using geometrically necessary dislocations. Acta Mater. 2006, 54, 2547–2555. [Google Scholar] [CrossRef]
- De Guzman, M.S.; Neubauer, G.; Flinn, P.; Nix, W.D. The role of indentation depth on the measured hardness of materials. MRS Online Proc. Libr. 1993, 308, 613. [Google Scholar] [CrossRef]
- Tanner, B.K.; Fathers, D.J. Contrast of crystal defects under polarized light. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1974, 29, 1081–1094. [Google Scholar] [CrossRef]
- Mathews, N.G.; Saxena, A.K.; Venkataramani, N.; Dehm, G.; Jaya, B.N. Multiscale characterization of damage tolerance in barium titanate thin films. J. Appl. Phys. 2022, 132, 045302. [Google Scholar] [CrossRef]
- Ma, Q.; Clarke, D.R. Size dependent hardness of silver single crystals. J. Mater. Res. 1995, 10, 853–863. [Google Scholar] [CrossRef]
- Nix, W.D.; Gao, H. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Afolayan, D.O. Characterisation and Processing of Baryte Ores for Oil Drilling Applications. AUST Repos. 2021, 1–184. Available online: https://repository.aust.edu.ng/xmlui/handle/123456789/5032 (accessed on 9 November 2025).
- Ezenwafor, T.; Anye, V.; Madukwe, J.; Amin, S.; Obayemi, J.; Odusanya, O.; Soboyejo, W. Nanoindentation study of the viscoelastic properties of human triple negative breast cancer tissues: Implications for mechanical biomarkers. Acta Biomater. 2023, 158, 374–392. [Google Scholar] [CrossRef] [PubMed]
- Oliver, W.C.; Pharr, G.M. Improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Jamal, M.; Morgan, M.N. Materials characterization part I: Contact area of the Berkovich indenter for nanoindentation tests. Int. J. Adv. Manuf. Technol. 2017, 92, 361–370. [Google Scholar] [CrossRef]
- Yan, W.; Pun, C.L.; Simon, G.P. Conditions of applying Oliver–Pharr method to the nanoindentation of particles in composites. Compos. Sci. Technol. 2012, 72, 1147–1152. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Dhanal, S.V.; Ingale, S. Investigation of nanomechanical properties of Ni-Mn based Heusler alloys using nanoindentation technique. J. Phys. Conf. Ser. 2023, 2604, 012007. [Google Scholar] [CrossRef]
- Constantinides, G.; Chandran, K.S.R.; Ulm, F.J.; Van Vliet, K.J. Grid indentation analysis of composite microstructure and mechanics: Principles and validation. Mater. Sci. Eng. A 2006, 430, 189–202. [Google Scholar] [CrossRef]
- Adamu, H.A.; Olajuyi, S.I.; Bello, A.; Onwualu, P.A.; Ogunmodimu, O.S.O.; Afolayan, D.O. Mechanical Loading of Barite Rocks: A Nanoscale Perspective. Minerals 2025, 15, 779. [Google Scholar] [CrossRef]
- ISO/FDIS 14577-1; Metallic Materials—Instrumented Indentation Test for Hardness and Material Parameter, Part 1: Test Method. ISO—International Organization for Standardization: Geneve, Switzerland, 2002.
- Shen, L.; Wang, L.; Liu, T.; He, C. Nanoindentation and Morphological Studies of Epoxy Nanocomposites. Macromol. Mater. Eng. 2006, 291, 1358–1366. [Google Scholar] [CrossRef]
- Ngasoh, O.F.; Anye, V.C.; Ojo, E.B.; Stanislas, T.T.; Bello, A.; Agyei-Tuffour, B.; Orisekeh, K.; Oyewole, O.K.; Rahbar, N.; Soboyejo, W.O. Mechanical Properties of Epoxy/Clay Composite Coatings on an X65 Steel Substrate. Cogent Eng. 2021, 8, 1944015. [Google Scholar] [CrossRef]
- Cui, Z.; Dai, F.; Liu, Y.; Zhang, B.; Wei, M.; Zhang, Q. Dynamic fracture properties and criterion of cyclic freeze-thaw treated granite subjected to mixed-mode loading. J. Rock Mech. Geotech. Eng. 2024, 16, 4971–4989. [Google Scholar] [CrossRef]
- GB/T50266-2013; Standard for Test Methods of Engineering Rock Mass. China Planning Press: Beijing, China, 2013. (In Chinese)
- D3967-23; Standard Test Method for Splitting Tensile Strength of Intact Rock Core Specimens with Flat Loading Platens. ASTM International: West Conshohocken, PA, USA, 2023.
- Manika, I.; Maniks, J. Size effects in micro-and nanoscale indentation. Acta Mater. 2006, 54, 2049–2056. [Google Scholar] [CrossRef]
- Milman, Y.V.; Golubenko, A.A.; Dub, S.N. Indentation size effect in nanohardness. Acta Mater. 2011, 59, 7480–7487. [Google Scholar] [CrossRef]
- Asumadu, T.K.; Mensah-Darkwa, K.; Gikunoo, E.; Klenam, D.E.P.; Vandadi, M.; Rahbar, N.; Kwofie, S.; Soboyejo, W.O. Strain gradient plasticity phenomenon in surface treated plain carbon steel. Mater. Sci. Eng. A 2023, 871, 144806. [Google Scholar] [CrossRef]
- Hill, R.J. A Further Refinement of the Barite Structure. Can. Mineral. 1977, 15, 522–526. [Google Scholar]
- Paulsen, C.; Galéa-Clolus, V.; Pöttgen, R. Crystal structure of barite from Mine du Pradet (France). Z. Krist. Cryst. Struct. 2023, 238, 611–613. [Google Scholar] [CrossRef]
- Ojo, E.B.; Bello, K.O.; Ngasoh, O.F.; Stanislas, T.T.; Mustapha, K.; Savastano, H., Jr.; Soboyejo, W. Mechanical performance of fiber-reinforced alkali activated un-calcined earth-based composites. Constr. Build. Mater. 2020, 247, 118588. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Yang, C.; Jiang, W.; Li, Y.; Xiong, Y. Modeling the viscoelastic behavior of quartz and clay minerals in shale by nanoindentation creep tests. Geofluids 2022, 2022, 2860077. [Google Scholar] [CrossRef]
- Afolayan, D.O.; Adetunji, A.R.; Onwualu, A.P.; Ogolo, O.; Amankwah, R.K. Characterization of barite reserves in Nigeria for use as weighting agent in drilling fluid. J. Pet. Explor. Prod. Technol. 2021, 11, 2157–2178. [Google Scholar] [CrossRef]
- Ebunu, A.I.; Bayode, B.L.; Olubambi, P.A.; Adetunji, A.R.; Onwualu, A.P. Characterization of barite ores from selected locations in Nigeria for drilling fluid formulation. Sci. Afr. 2021, 14, e01057. [Google Scholar] [CrossRef]
- Ebunu, A.I.; Olanrewaju, Y.A.; Ogolo, O.; Adetunji, A.R.; Onwualu, A.P. Barite as an industrial mineral in Nigeria: Occurrence, utilization, challenges and future prospects. Heliyon 2021, 7, e07365. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Ehirim, C.N.; Ebeniro, J.O.; Ofoegbu, C.O. Baryte mineral exploration in parts of the lower Benue Trough, Nigeria. Int. J. Phys. Sci. 2016, 11, 279–286. [Google Scholar] [CrossRef][Green Version]
- Eseimokumoh, I.B.; Eniye, O. Characterization of Barite (A Case Study of Biase and Yakurr Local Government Areas, Cross River State, Nigeria). Int. Res. J. Mod. Eng. Technol. Sci. 2022, 4, 4324–4335. [Google Scholar]
- de Macedo, G.N.B.M.; Sawamura, S.; Wondraczek, L. Lateral hardness and the scratch resistance of glasses in the Na2O-CaO-SiO2 system. J. Non-Cryst. Solids 2018, 492, 94–101. [Google Scholar] [CrossRef]
- Whitney, D.L.; Broz, M.; Cook, R.F. Hardness, toughness, and modulus of some common metamorphic. Am. Miner. 2007, 92, 281–288. [Google Scholar] [CrossRef]
- Bond, T.; Badmos, A.; Ahmed, R.A.; Obayemi, J.D.; Salifu, A.; Rahbar, N.; Soboyejo, W.O. Indentation size effects in aluminum and titanium alloys. Mater. Sci. Eng. A 2022, 839, 142542. [Google Scholar] [CrossRef]
- de Paula, O.B. Elastic Properties of Carbonates: Measurements and Modelling. Ph.D. Thesis, Curtin University, Perth, Australia, 2011. [Google Scholar]
- Briševac, Z.; Pollak, D.; Maričić, A.; Vlahek, A. Modulus of elasticity for grain-supported carbonates—Determination and estimation for preliminary engineering purposes. Appl. Sci. 2021, 11, 6148. [Google Scholar] [CrossRef]
- Guder, V.; Senturk Dalgic, S. Thermodynamic Properties of Potassium Oxide (K2O) Nanoparticles by Molecular Dynamics Simulations. Acta Phys. Pol. A 2017, 131, 490–494. [Google Scholar] [CrossRef]
- Kudělka, R.; Václavek, L.; Tomáštík, J.; Malecová, S.; Čtvrtlík, R. Laser-induced surface acoustic waves for thin film characterization. Acta Polytech. CTU Proc. 2020, 27, 57–61. [Google Scholar] [CrossRef]
- Ouglova, A.; Berthaud, Y.; François, M.; Foct, F. Mechanical properties of an iron oxide formed by corrosion in reinforced concrete structures. Corros. Sci. 2006, 48, 3988–4000. [Google Scholar] [CrossRef]
- Patel, H.S.; Dabhi, V.A.; Vora, A.M. First principles investigation of electronic and elastic properties of strontium oxide and strontium peroxide phases: Insights into structural stability and phase transitions. Phys. Scr. 2023, 98, 125930. [Google Scholar] [CrossRef]
- Azo Materials. 2025. Available online: https://www.azom.com/article.aspx?ArticleID=1114 (accessed on 1 August 2025).
- Saif, M.T.A.; Zhang, S.; Haque, A.; Hsia, K.J. Effect of native Al2O3 on the elastic response of nanoscale Al films. Acta Mater. 2002, 50, 2779–2786. [Google Scholar] [CrossRef]
- Noinonmueng, T.; Phacheerak, K. Structural and Mechanical Properties of Cubic Na2O: First-Principles Calculations. Res. J. Rajamangala Univ. Technol. Thanyaburi 2020, 19, 17–24. [Google Scholar] [CrossRef]
- Korth Kristalle Company. Magnesium Oxide. 2025. Available online: https://www.korth.de/en/materials/detail/Magnesium%20Oxide (accessed on 1 August 2025).
- Dragoo, A.L.; Spain, I.L. The elastic moduli and their pressure and temperature derivatives for calcium oxide. J. Phys. Chem. Solids 1977, 38, 705–710. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, S.; Liu, J.; Hu, X.; Liu, Y.; He, Y.; He, X.; Wu, X. Geological evolution of offshore pollution and its long-term potential impacts on marine ecosystems. Geosci. Front. 2022, 13, 101427. [Google Scholar] [CrossRef]
- Wuepper, D.; Borrelli, P.; Finger, R. Countries and the Global Rate of Soil Erosion. Nat. Sustain. 2020, 3, 51–55. [Google Scholar] [CrossRef]
- Andersson, L. Soil Loss Estimation Based on the USLE/GIS Approach Through Small Catchments—A Minor Field Study in Tunisia. Master’s Thesis, Lund University, Lund, Sweden, 2010. [Google Scholar]
- Eswaran, H.; Lal, R.; Reich, P. Land Degradation: An Overview. In Response to Land Degradation; CRC Press: Boca Raton, FL, USA, 2019; pp. 20–35. [Google Scholar]
- Emetumah, F.; Okoye, A. Role of Government in Ensuring Safety Consciousness during Mineral Mining Activities in Nigeria. Eur. Sci. J. 2018, 14, 165–184. [Google Scholar] [CrossRef]
- Afolayan, D.O.; Onwualu, A.P.; Eggleston, C.M.; Adetunji, A.R.; Tao, M.; Amankwah, R.K. Safe Mining Assessment of Artisanal Barite Mining Activities in Nigeria. Mining 2021, 1, 224–240. [Google Scholar] [CrossRef]
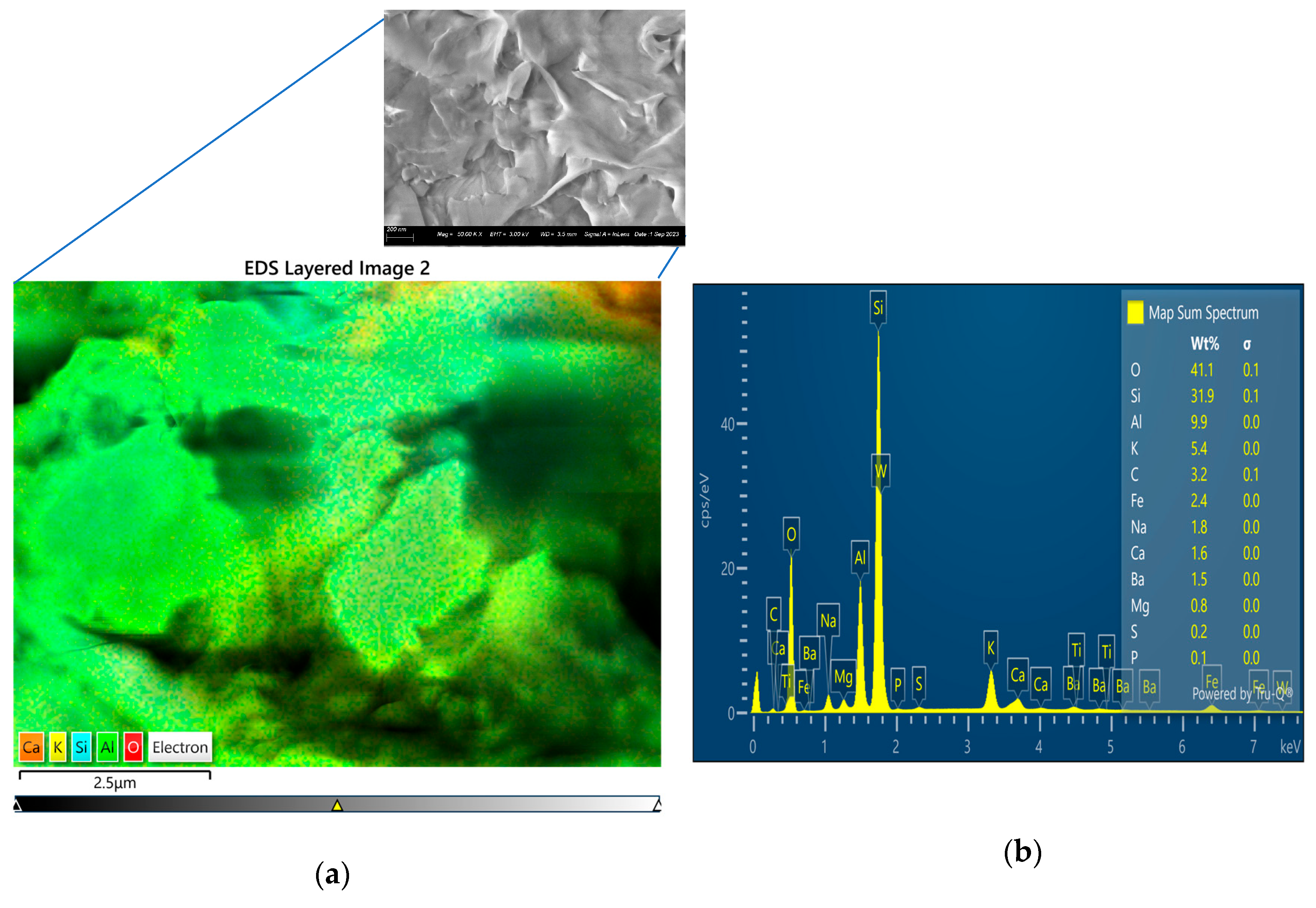
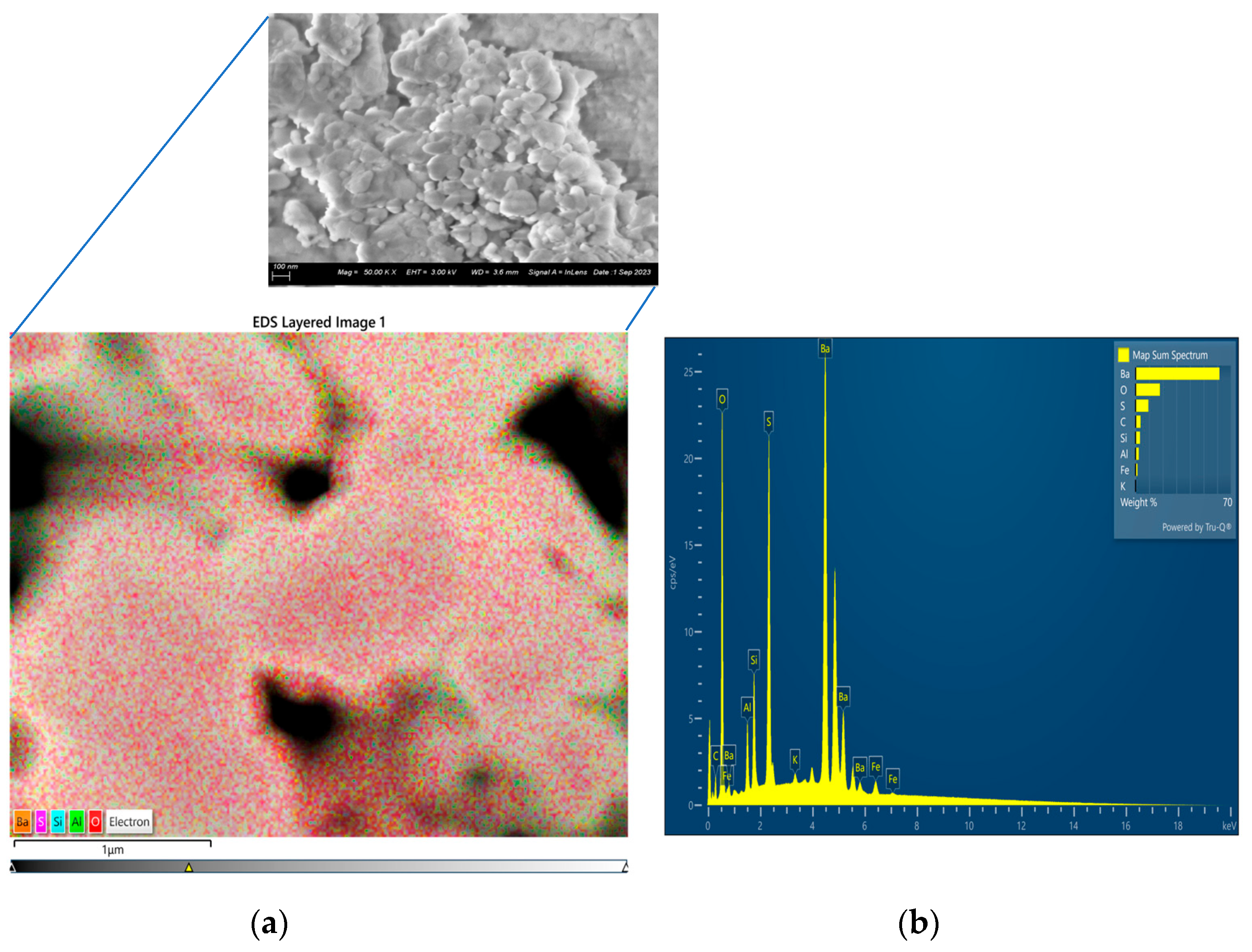
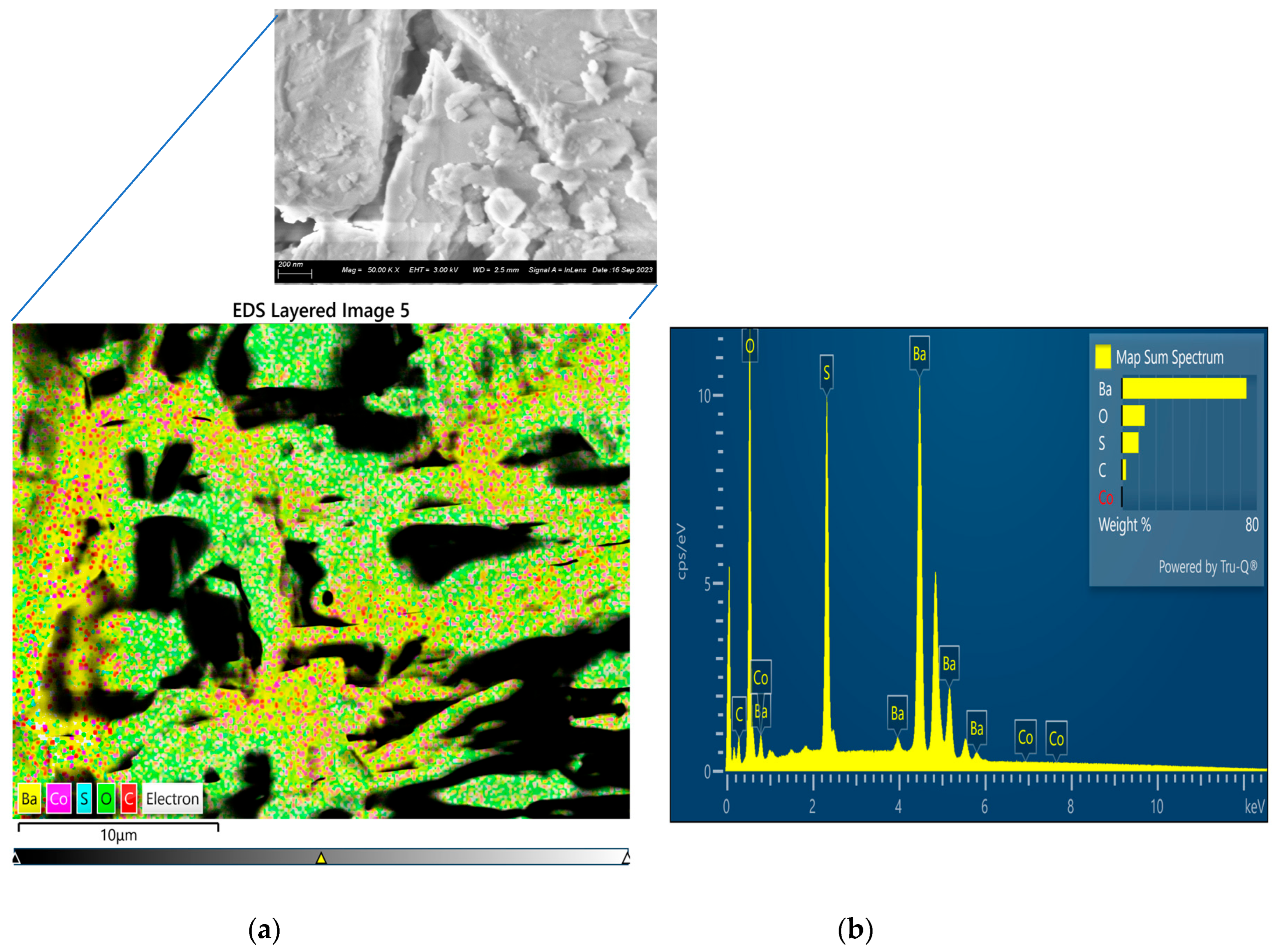
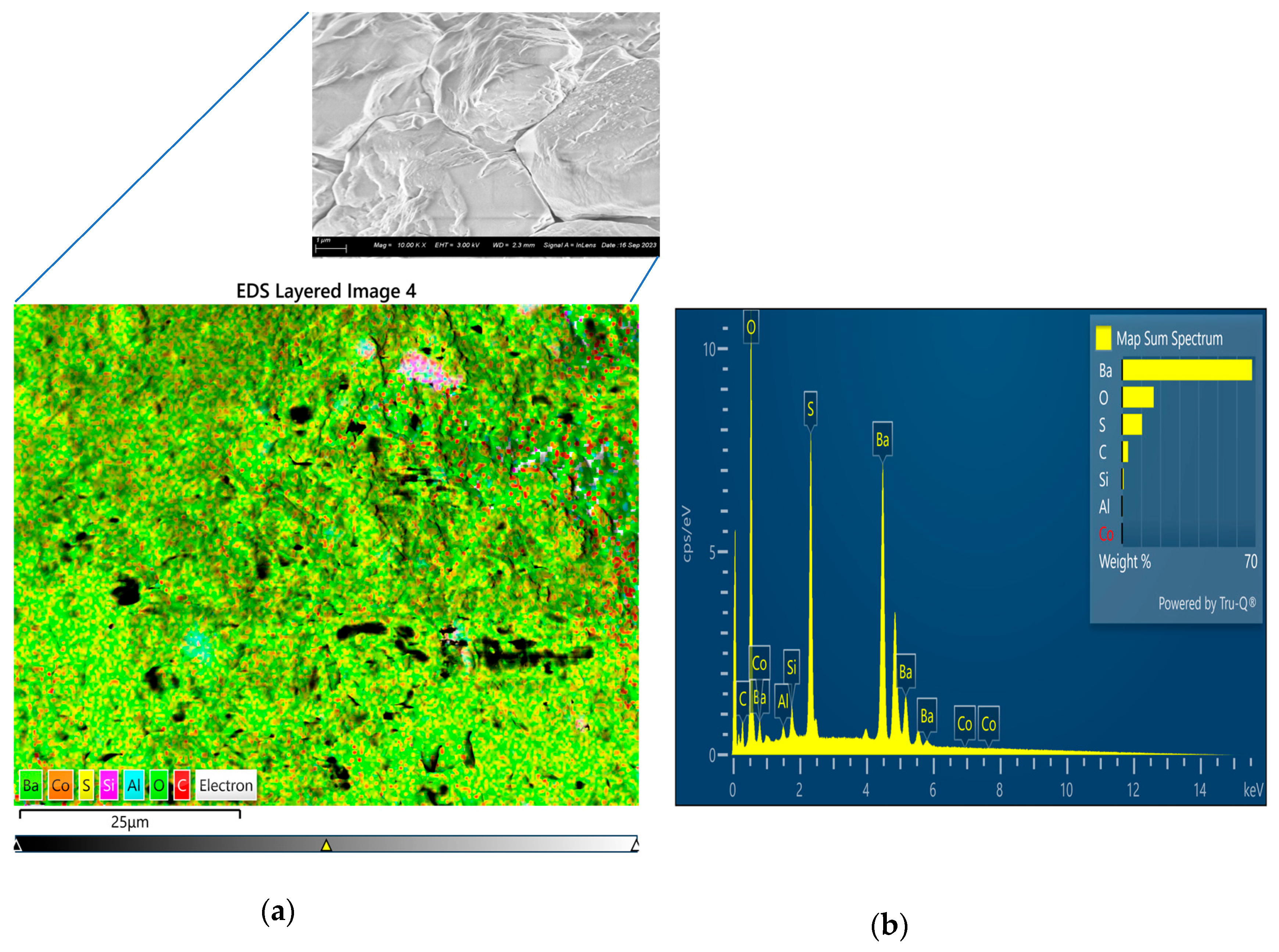
| Serial/N0 | Lattice Parameters of BaSO4 | ||||
|---|---|---|---|---|---|
| a (Å) | b (Å) | c (Å) | Volume (Å3) | A = β = γ = (°) | |
| This study | 5.52 | 7.22 | 8.94 | 356.3 | 90 |
| Hill [72] | 5.46 | 7.16 | 8.88 | 326.0 | |
| Paulsen et al. [73] | 5.45 | 7.16 | 8.88 | 346.6 | |
| S/N | Rock Samples | Mineral Phases (wt%) | |||
|---|---|---|---|---|---|
| 1. | IB1 | Barite (BaSO4)—33.0% | Quartz (SiO2)—56.0% | Chlorite (Mg,Fe)5(Al,Si)5 O10—7.0% | Albite (NaAlSi3O8)—3.3% |
| 2. | IB2 | Quartz (SiO2)—64.0% | Barite (BaSO4)—22.0% | Chlorite (Mg,Fe)5(Al,Si)5 O10—0.2% | Albite (NaAlSi3O8)—14.0% |
| 3. | IB5 | Barite (BaSO4)—37.0% | Quartz (SiO2)—58.0% | Albite (NaAlSi3O8)—1.0% | Chlorite (Mg,Fe)5(Al,Si)5 O10—4.0% |
| 4. | IB6 | Barite (BaSO4)—38.0% | Quartz (SiO2)—42.0% | Chlorite (Mg,Fe)5(Al,Si)5 O10—3.0% | Albite (NaAlSi3O8)—17.0% |
| S/N | Oxides Obtained from EDX Mapping | Modulus (GPa) | Author |
|---|---|---|---|
| 1 | BaSO4 | 36–47 | [62] |
| 2 | SiO2 | 66.3–74.8 | [90] |
| 3 | Al2O3 | Up to 370 | [91] |
| 4 | CO3 | 56–144 38.38 to 93.26 | [84,85] |
| 5 | K2O | 22–70 | [86] |
| 6 | Fe2O3 | 214–350 | [88] |
| 7 | Na2O | 75–93 | [92] |
| 8 | MgO | 248 | [93] |
| 9 | CaO | 226 | [94] |
| S/N | Sample | ρG [m−2] | ρS [m−2] | ρT [m−2] |
|---|---|---|---|---|
| 1 | IB1 | 4.47 × 1015 | 7.68 × 1014 | 5.24 × 1015 |
| 2 | IB2 | 3.35 × 1015 | −1.90 × 1015 | 1.45 × 1015 |
| 3 | IB5 | 2.89 × 1015 | 2.07 × 1015 | 4.96 × 1015 |
| 4 | IB6 | 4.56 × 1015 | 6.21 × 1015 | 1.08 × 1016 |
| Sample | Ho (GPa) | h* (nm) | Length Scale [nm] | ρS Spacing-L [m] | ρG Spacing-L [m] |
|---|---|---|---|---|---|
| IB1 | 2.2 | 96.7 | 878 | 3.61 × 10−8 | 1.50 × 10−8 |
| IB2 | 1.7 | 49.6 | 1359 | −2.29 × 10−8 | 1.73 × 10−8 |
| IB5 | 3.2 | 71.1 | 409 | 2.20 × 10−8 | 1.86 × 10−8 |
| IB6 | 6.1 | 26.5 | 114 | 1.27 × 10−8 | 1.48 × 10−8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adamu, H.A.; Afolayan, D.O.; Ogunmodimu, O.S.O.; Asumadu, T.K.; Olajuyi, S.I.; Dzade, N.Y.; Soboyejo, W.O. Indentation Size Effects and the Mechanical Properties of Barite Rocks. Minerals 2025, 15, 1226. https://doi.org/10.3390/min15111226
Adamu HA, Afolayan DO, Ogunmodimu OSO, Asumadu TK, Olajuyi SI, Dzade NY, Soboyejo WO. Indentation Size Effects and the Mechanical Properties of Barite Rocks. Minerals. 2025; 15(11):1226. https://doi.org/10.3390/min15111226
Chicago/Turabian StyleAdamu, Hassan Abubakar, David Oluwasegun Afolayan, Olumide Samuel Oluwaseun Ogunmodimu, Tabiri Kwayie Asumadu, Seun Isaiah Olajuyi, Nelson Y. Dzade, and Winston O. Soboyejo. 2025. "Indentation Size Effects and the Mechanical Properties of Barite Rocks" Minerals 15, no. 11: 1226. https://doi.org/10.3390/min15111226
APA StyleAdamu, H. A., Afolayan, D. O., Ogunmodimu, O. S. O., Asumadu, T. K., Olajuyi, S. I., Dzade, N. Y., & Soboyejo, W. O. (2025). Indentation Size Effects and the Mechanical Properties of Barite Rocks. Minerals, 15(11), 1226. https://doi.org/10.3390/min15111226








