High-Accuracy Image Segmentation Based on Hybrid Attention Mechanism for Sandstone Analysis
Abstract
1. Introduction
2. Methodology
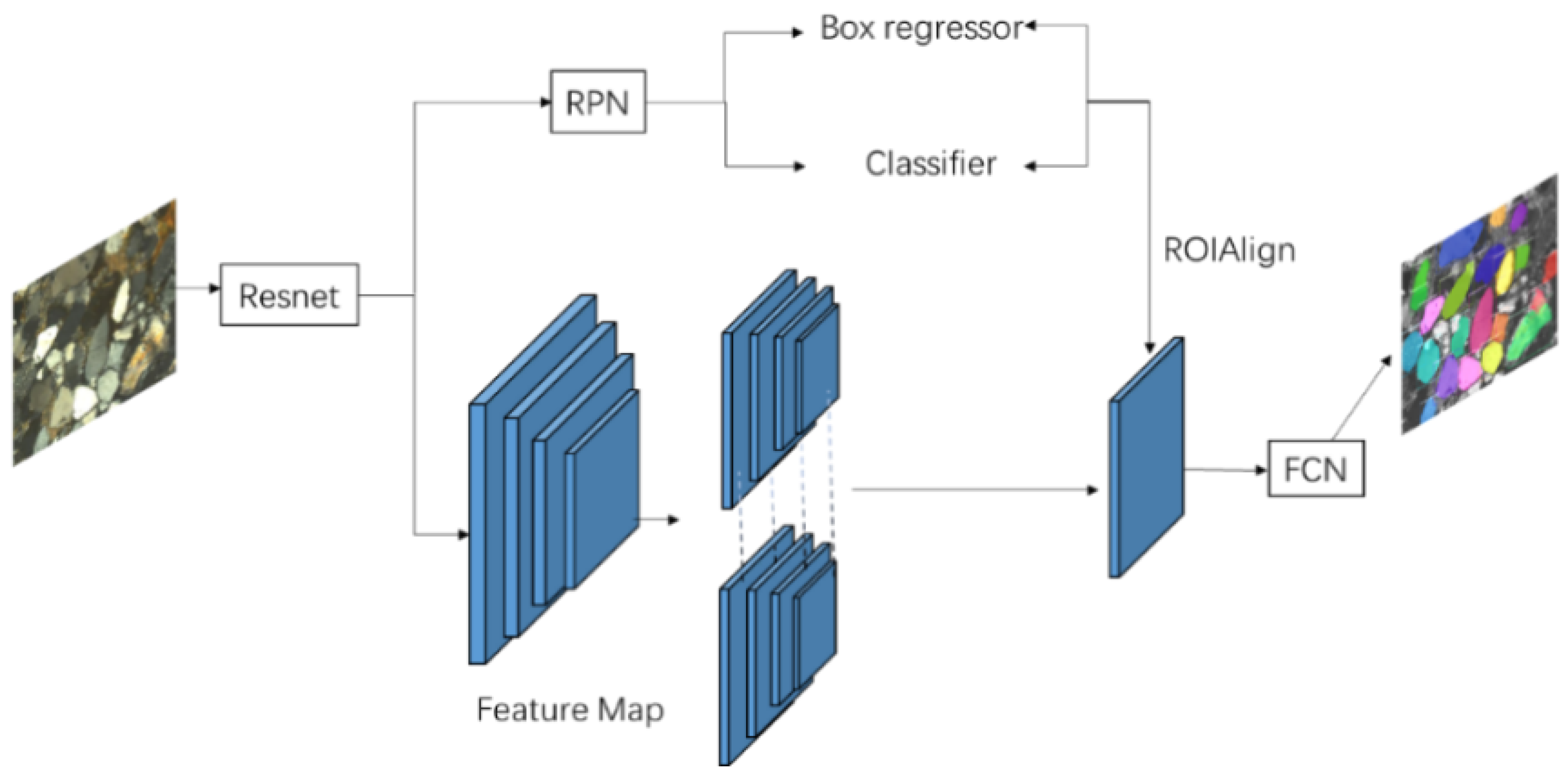
2.1. Mask R-CNN
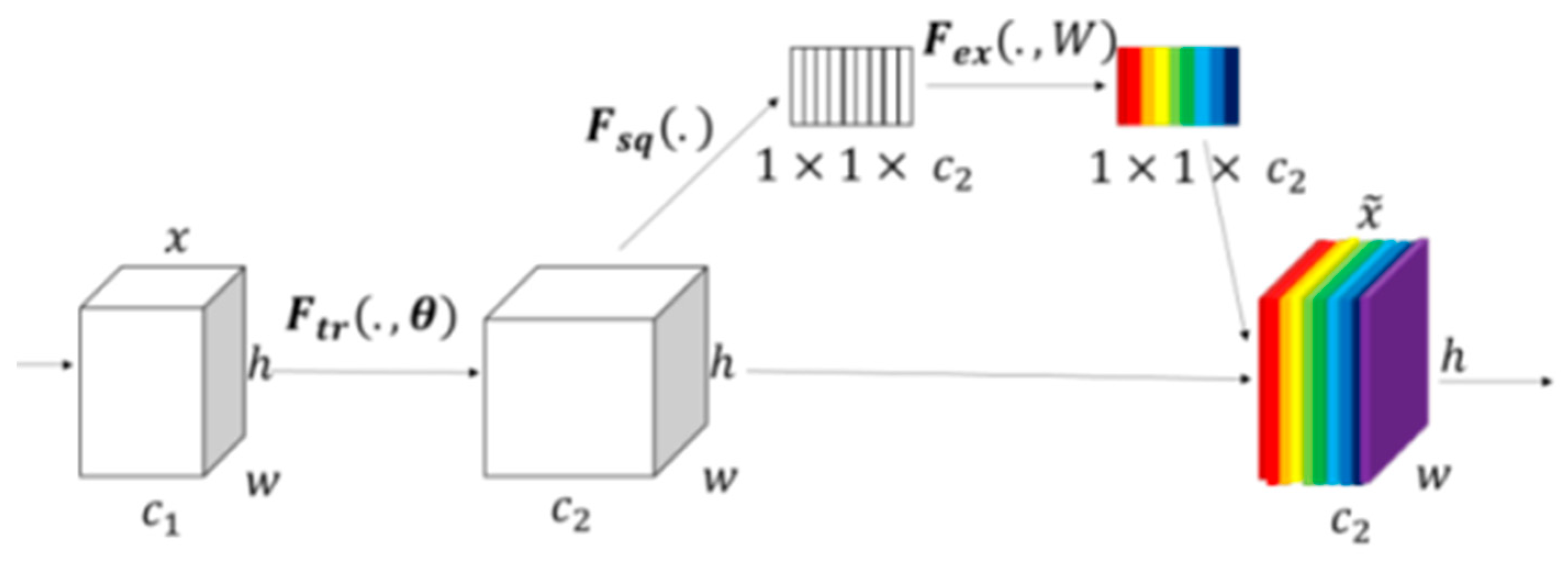
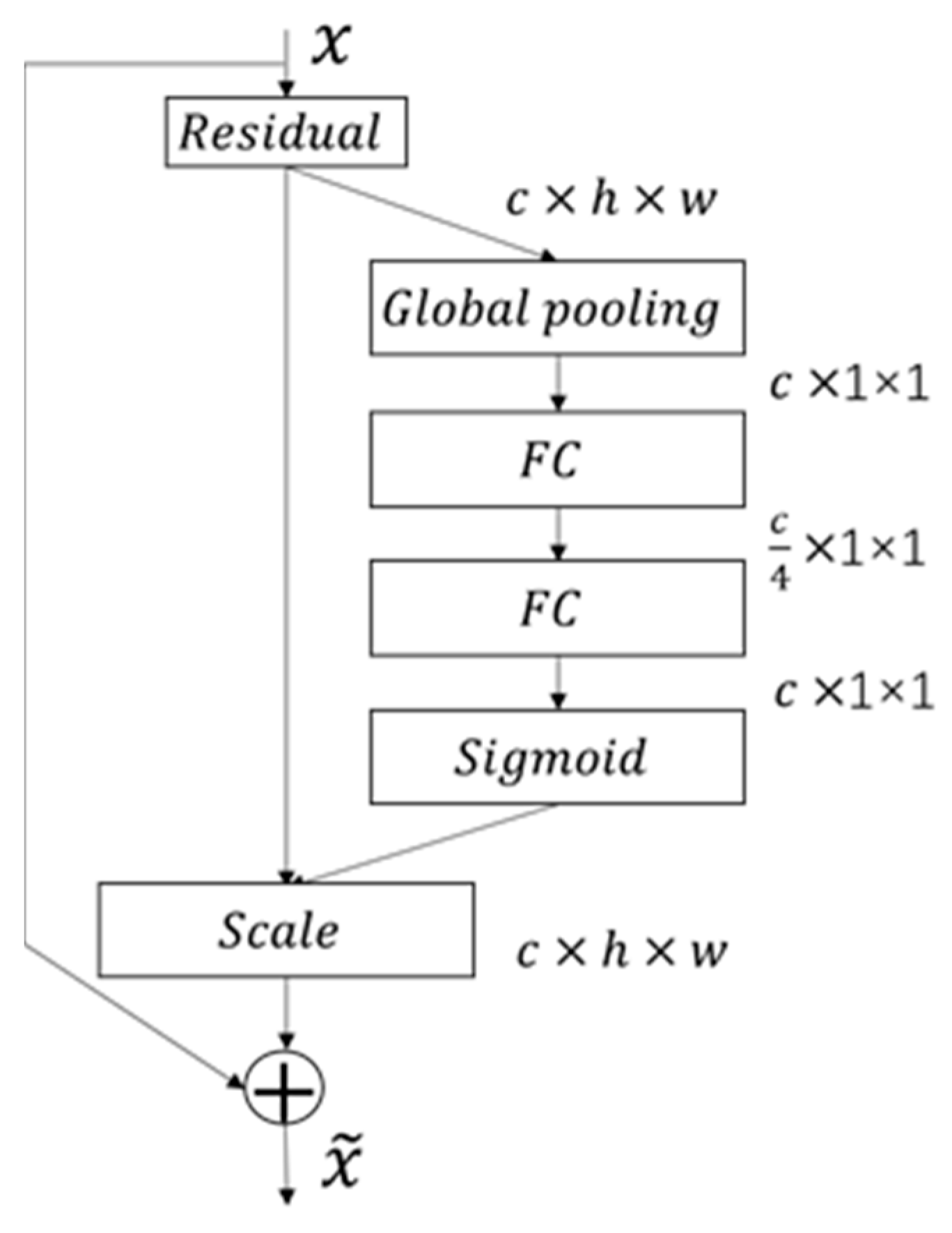
2.2. SE-Net
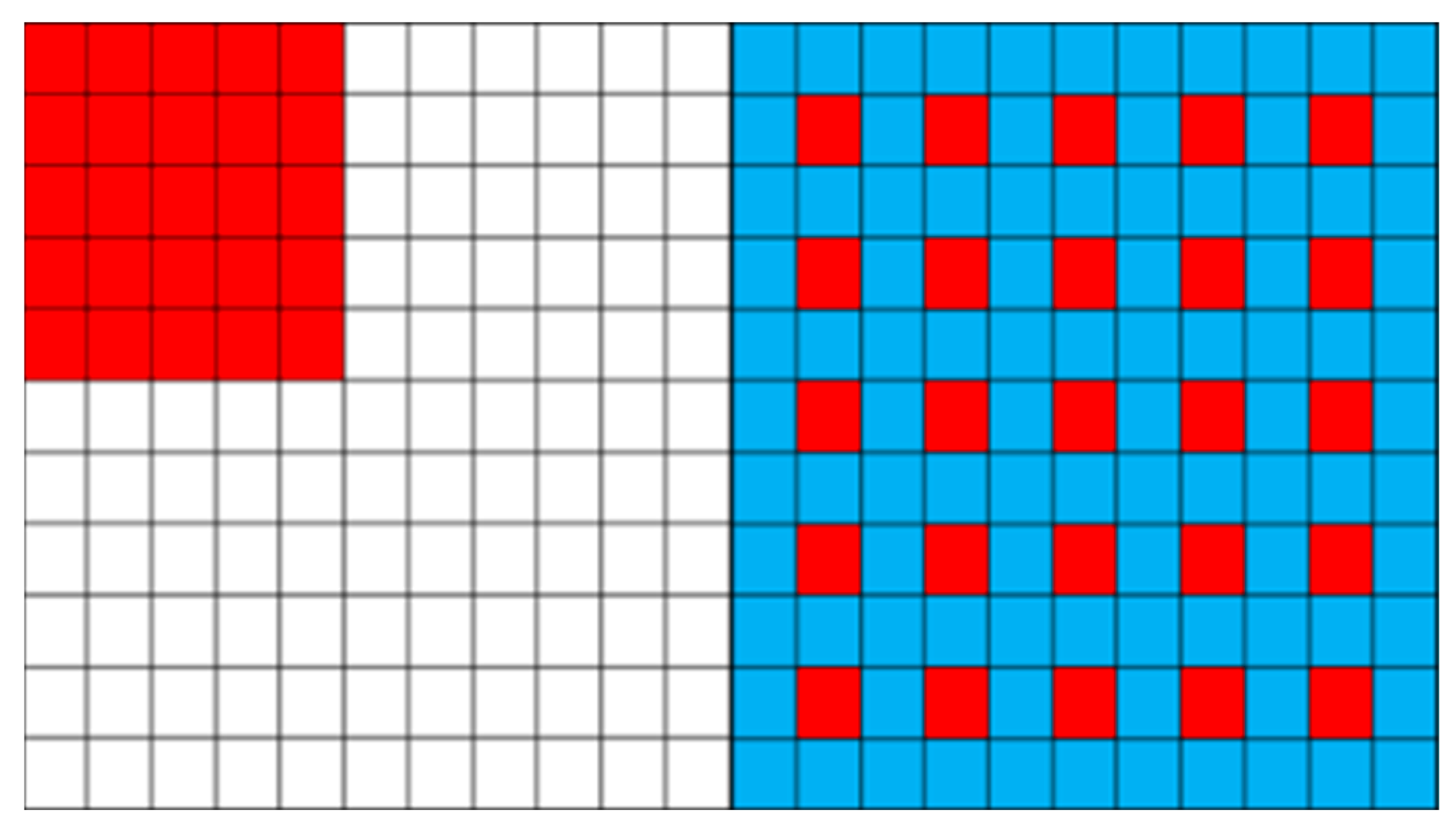
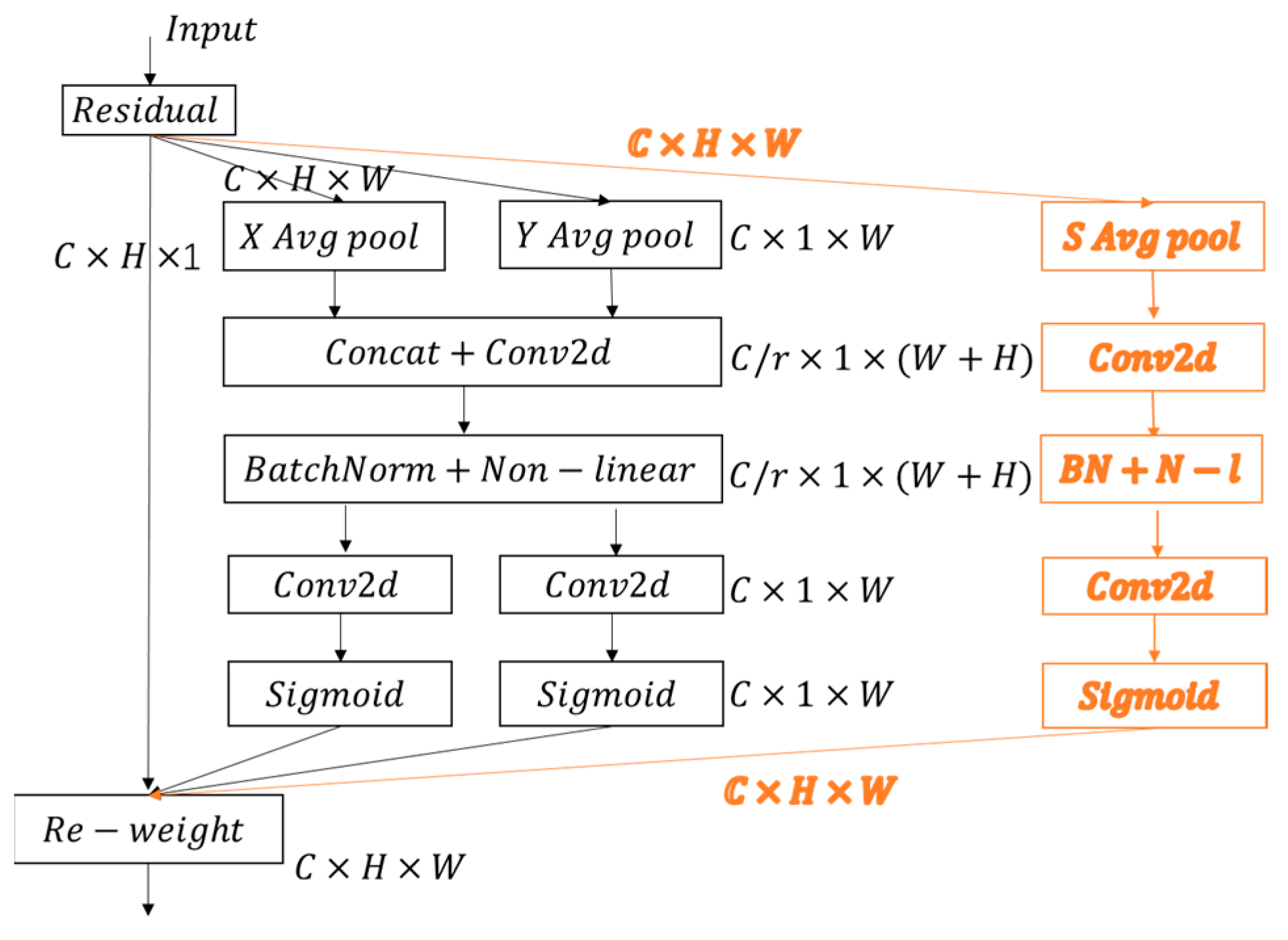
2.3. Coordinate Attention and Spatial Attention
2.4. Dilated Convolution
- Expanding the Mask R-CNN network receptive fields more efficiently while taking into account image resolution;
- Changing the size of the convolution kernel and the perceptual field of the model by adjusting the expansion rate (r) to obtain multi-scale global semantic information.
3. Methods and Materials
3.1. Experimental Methods
3.1.1. Hybrid Attention Mechanism
3.1.2. Loss Function
3.2. Material Preparation
4. Results
4.1. Experiments and Analysis
4.2. Performance Metric
4.2.1. Accuracy and Recall Rate, AP
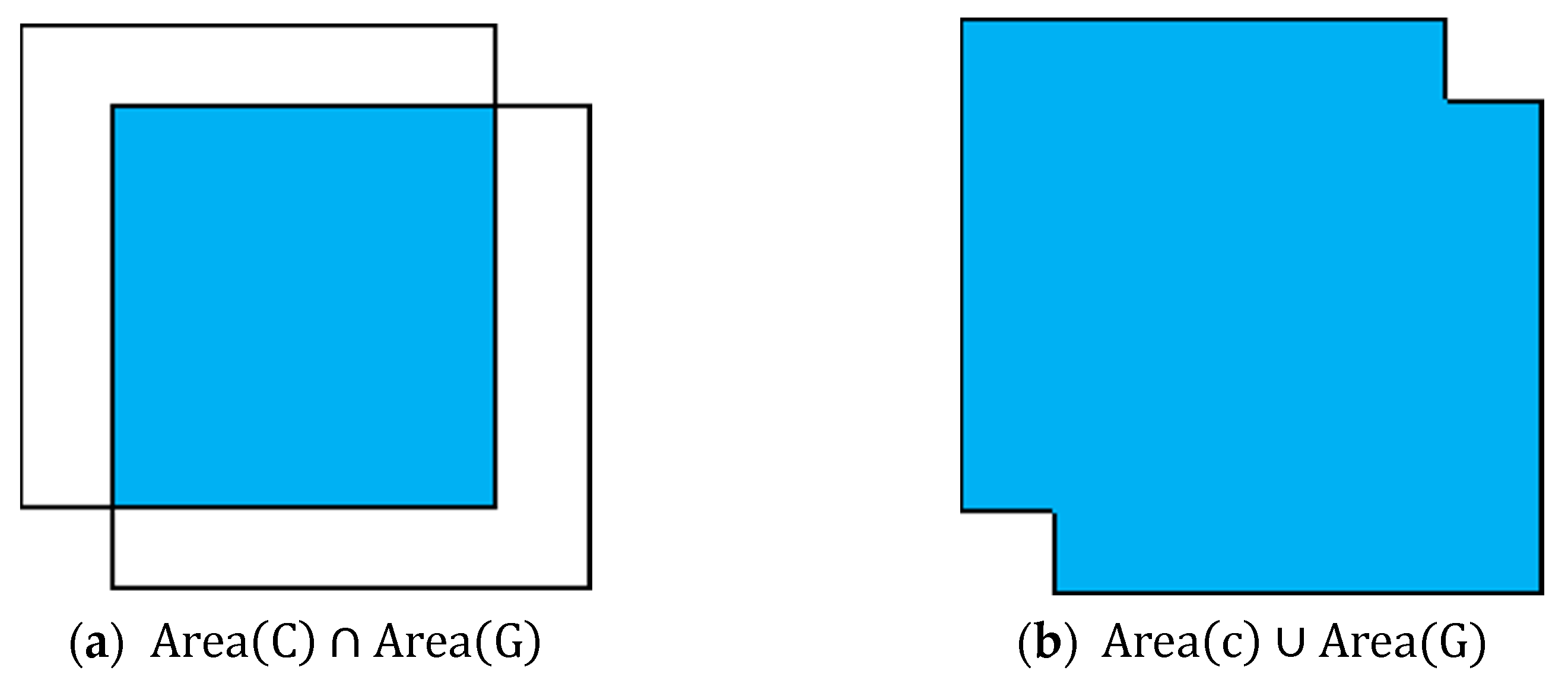
4.2.2. IoU
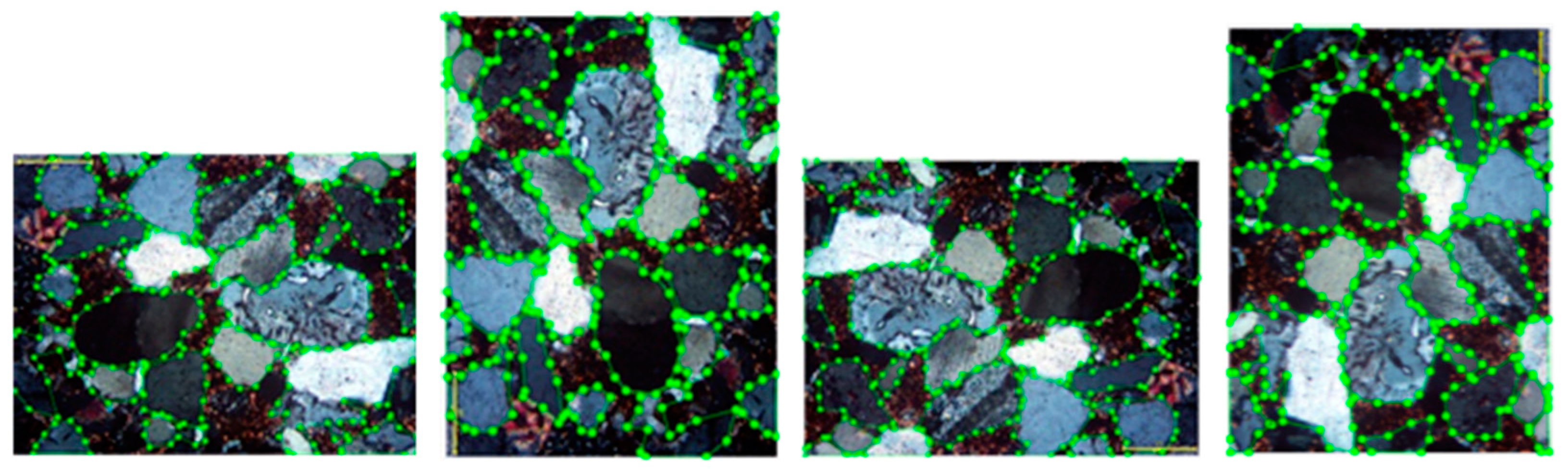
4.2.3. Results and Visualization
Comparison of the Results of the Improved Mask R-CNN Network in Fitting Irregular Sandstone Grain Images
Experiments on the Performance of the Improved Segmentation Network
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taylor, T.R.; Giles, M.R.; Hathon, L.A.; Diggs, T.N.; Braunsdorf, N.R.; Birbiglia, G.V.; Kittridge, M.G.; Macaulay, C.I.; Espejo, I.S. Sandstone diagenesis and reservoir quality prediction: Models, myths, and reality. AAPG Bull. 2010, 94, 1093–1132. [Google Scholar] [CrossRef]
- Milliken, K. Late Diagenesis and Mass Transfer in Sandstone Shale Sequences; Elsevier: Amsterdam, The Netherlands, 2003; Volume 7. [Google Scholar]
- Makowitz, A.; Milliken, K.L. Quantification of brittle deformation in burial compaction, Frio and Mount Simon Formation sandstones. J. Sediment. Res. 2003, 73, 1007–1021. [Google Scholar] [CrossRef]
- Makowitz, A.; Lander, R.; Milliken, K. Diagenetic modeling to assess the relative timing of quartz cementation and brittle grain processes during compaction. AAPG Bull. 2006, 90, 873–885. [Google Scholar] [CrossRef]
- Dutton, S.P.; Loucks, R.G.; Day-Stirrat, R.J. Impact of regional variation in detrital mineral composition on reservoir quality in deep to ultradeep lower Miocene sandstones, western Gulf of Mexico. Mar. Pet. Geol. 2012, 35, 139–153. [Google Scholar] [CrossRef]
- Dutton, S.P.; Loucks, R.G. Diagenetic controls on evolution of porosity and permeability in lower Tertiary Wilcox sandstones from shallow to ultradeep (200–6700 m) burial, Gulf of Mexico Basin, USA. Mar. Pet. Geol. 2010, 27, 69–81. [Google Scholar] [CrossRef]
- McRae, L.; Holtz, M.; Hentz, T. Strategies for Reservoir Characterization and Identification of Incremental Recovery Opportunities in Mature Reservoirs in Frio Fluvial-Deltaic Sandstones, South Texas: An Example from Rincon Field, Starr County; Topical report; U.S. Department of Energy: Washington, DC, USA, 1995. Available online: https://www.osti.gov/servlets/purl/123238 (accessed on 17 March 2024).
- Saxena, N.; Day-Stirrat, R.J.; Hows, A.; Hofmann, R. Application of deep learning for semantic segmentation of sandstone thin sections. Comput. Geosci. 2021, 152, 104778. [Google Scholar] [CrossRef]
- Perez, C.A.; Estévez, P.A.; Vera, P.A.; Castillo, L.E.; Aravena, C.M.; Schulz, D.A.; Medina, L.E. Ore grade estimation by feature selection and voting using boundary detection in digital image analysis. Int. J. Miner. Process. 2011, 101, 28–36. [Google Scholar] [CrossRef]
- Patel, A.K.; Chatterjee, S.; Gorai, A.K. Development of a machine vision system using the support vector machine regression (SVR) algorithm for the online prediction of iron ore grades. Earth Sci. Inform. 2019, 12, 197–210. [Google Scholar] [CrossRef]
- Patel, A.K.; Chatterjee, S.; Gorai, A.K. Development of machine vision-based ore classification model using support vector machine (SVM) algorithm. Arab. J. Geosci. 2017, 10, 1–16. [Google Scholar] [CrossRef]
- Ma, X.-M. A Revised Edge Detection Algorithm Based on Wavelet Transform for Coal Gangue Image. In Proceedings of the 2007 International Conference on Machine Learning and Cybernetics, Hong Kong, China, 19–22 August 2007; pp. 1639–1642. [Google Scholar]
- Xu, D.; Chen, X.; Xie, Y.; Yang, C.; Gui, W. Complex networks-based texture extraction and classification method for mineral flotation froth images. Miner. Eng. 2015, 83, 105–116. [Google Scholar] [CrossRef]
- Chatterjee, S.; Bandopadhyay, S.; Machuca, D. Ore grade prediction using a genetic algorithm and clustering based ensemble neural network model. Math. Geosci. 2010, 42, 309–326. [Google Scholar] [CrossRef]
- Andersson, T.; Thurley, M.J.; Carlson, J.E. A machine vision system for estimation of size distributions by weight of limestone particles. Miner. Eng. 2012, 25, 38–46. [Google Scholar] [CrossRef]
- Delbem, I.; Galéry, R.; Brandão, P.; Peres, A. Semi-automated iron ore characterisation based on optical microscope analysis: Quartz/resin classification. Miner. Eng. 2015, 82, 2–13. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, X.; Le, B.T.; Ji, Z.; Sun, X. An ore image segmentation method based on RDU-Net model. Sensors 2020, 20, 4979. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, Z.; Liu, X.; Wang, L.; Xia, X. Efficient image segmentation based on deep learning for mineral image classification. Adv. Powder Technol. 2021, 32, 3885–3903. [Google Scholar] [CrossRef]
- Baraian, A.; Kellokumpu, V.; Paaso, J.; Koresaar, L.; Kaartinen, J. Computing Particle Size Distribution of Mineral Rocks Using Deep Learning-Based Instance Segmentation. In Proceedings of the 2022 10th European Workshop on Visual Information Processing (EUVIP), Hong Kong, China, 19–22 August 2022; pp. 1–6. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Wu, S.; Wang, Q.; Zeng, Q.; Zhang, Y.; Shao, Y.; Deng, F.; Liu, Y.; Wei, W. Automatic extraction of outcrop cavity based on a multiscale regional convolution neural network. Comput. Geosci. 2022, 160, 105038. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Hou, Q.; Zhou, D.; Feng, J. Coordinate Attention for Efficient Mobile Network Design. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Online, 19–25 June 2021; pp. 13713–13722. [Google Scholar]
- Jaderberg, M.; Simonyan, K.; Zisserman, A. Spatial transformer networks. In Advances in Neural Information Processing Systems, Proceedings of the NIPS 2015, Montreal, Canada, 7–12 December 2015; Neural Information Processing Systems Foundation, Inc. (NeurIPS): La Jolla, CA, USA, 2015; pp. 1–9. [Google Scholar]
- Yu, F.; Koltun, V.; Funkhouser, T. Dilated Residual Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Venice, Italy, 22–29 October 2017; pp. 472–480. [Google Scholar]
- Li, X.; Sun, X.; Meng, Y.; Liang, J.; Wu, F.; Li, J. Dice loss for data-imbalanced NLP tasks. arXiv 2019, arXiv:1911.02855. [Google Scholar]
- Wu, S.; Li, X.; Wang, X. IoU-aware single-stage object detector for accurate localization. Image Vis. Comput. 2020, 97, 103911. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft Coco: Common Objects in Context. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]




| Software/Hardware | Configuration |
|---|---|
| Operating system | Ubuntu 20.04 |
| Memory | 32 GB |
| CPU | Intel(R) Core(TM) i9-10920X CPU @ 3.50 GHz |
| GPU | NVIDIA GeForce RTX 3090 |
| Related software | Python3.8/Torch1.8.0/cuda11.1 |
| Average Precision (AP) | |
| When IoU = 0.50:0.05:0.95 | |
| When IoU = 0.50 | |
| AP When IoU = 0.75 | |
| AP Across Scales | |
| When the grain is small: pixel area < 322 | |
| When the grain is medium: 322 < pixel area < 962 | |
| When the grain is large: pixel area > 962 | |
| Backbone | SMISD (%) | ||
|---|---|---|---|
| ResNet | 15.4 | 37.4 | 41.2 |
| +SE | 18.9 | 38.1 | 42.3 |
| +X attention | 19.3 | 38.9 | 41.9 |
| +Y attention | 19.2 | 38.7 | 42.0 |
| +CA | 20.3 | 39.5 | 43.1 |
| +CA + SP | 20.8 | 39.7 | 43.2 |
| Loss Function | SMISD (%) | ||
|---|---|---|---|
| Lmask | 33.2 | 38.6 | 29.1 |
| Ldice | 36.3 | 41.3 | 37.3 |
| Type | SMISD (%) | ||
|---|---|---|---|
| Original convolution | 33.2 | 38.6 | 29.1 |
| Dilated convolution | 37.9 | 43.2 | 34.2 |
| Dataset | COCO (%) | SMISD (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Algorithm | |||||||||
| Mask R-CNN | 39.6 | 27.2 | 49.0 | 57.7 | 32.3 | 15.4 | 37.4 | 41.2 | |
| HTC | 41.2 | 27.2 | 51.9 | 61.5 | 33.9 | 15.6 | 38.9 | 44.0 | |
| PointRend | 41.1 | 27.8 | 52.0 | 62.0 | 35.1 | 16.3 | 39.9 | 45.7 | |
| RefineMask | 41.8 | 28.6 | 53.1 | 62.8 | 36.7 | 18.0 | 41.1 | 47.3 | |
| Hybrid + Loss | 41.7 | 28.9 | 52.7 | 62.5 | 37.9 | 19.7 | 42.6 | 48.1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, L.; Gui, H.; Yu, X.; Zhang, X.; Xu, M. High-Accuracy Image Segmentation Based on Hybrid Attention Mechanism for Sandstone Analysis. Minerals 2024, 14, 544. https://doi.org/10.3390/min14060544
Dong L, Gui H, Yu X, Zhang X, Xu M. High-Accuracy Image Segmentation Based on Hybrid Attention Mechanism for Sandstone Analysis. Minerals. 2024; 14(6):544. https://doi.org/10.3390/min14060544
Chicago/Turabian StyleDong, Lanfang, Hao Gui, Xiaolu Yu, Xinming Zhang, and Mingyang Xu. 2024. "High-Accuracy Image Segmentation Based on Hybrid Attention Mechanism for Sandstone Analysis" Minerals 14, no. 6: 544. https://doi.org/10.3390/min14060544
APA StyleDong, L., Gui, H., Yu, X., Zhang, X., & Xu, M. (2024). High-Accuracy Image Segmentation Based on Hybrid Attention Mechanism for Sandstone Analysis. Minerals, 14(6), 544. https://doi.org/10.3390/min14060544





