A New Model for Predicting Drag Coefficient and Settling Velocity of Coarse Mineral Particles in Newtonian Fluid
Abstract
1. Introduction
2. Drag Coefficient Model
3. Particle Settling Experiment
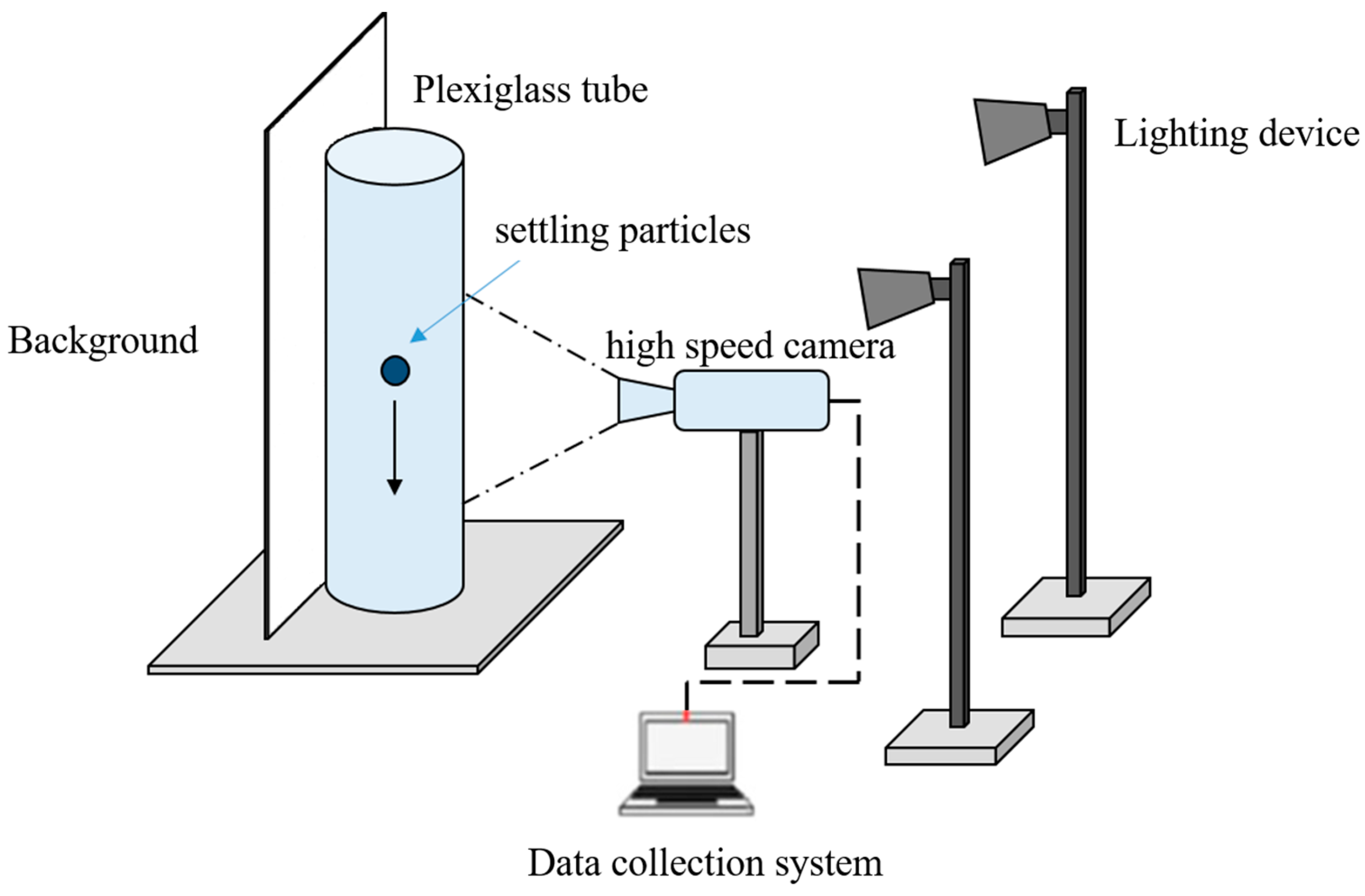
3.1. Experimental Setup and Procedure
3.2. Rheological Parameter Testing of Experimental Materials and Fluids
4. Particle Settling Experiment
5. Coarse Particle Settling Experimental Results and Analysis
- (1)
- The irregular shape of particles, which results in a larger surface area compared to a sphere of the same volume;
- (2)
- The rough surface of particles;
- (3)
- The asymmetry in particle shapes.
6. Conclusions
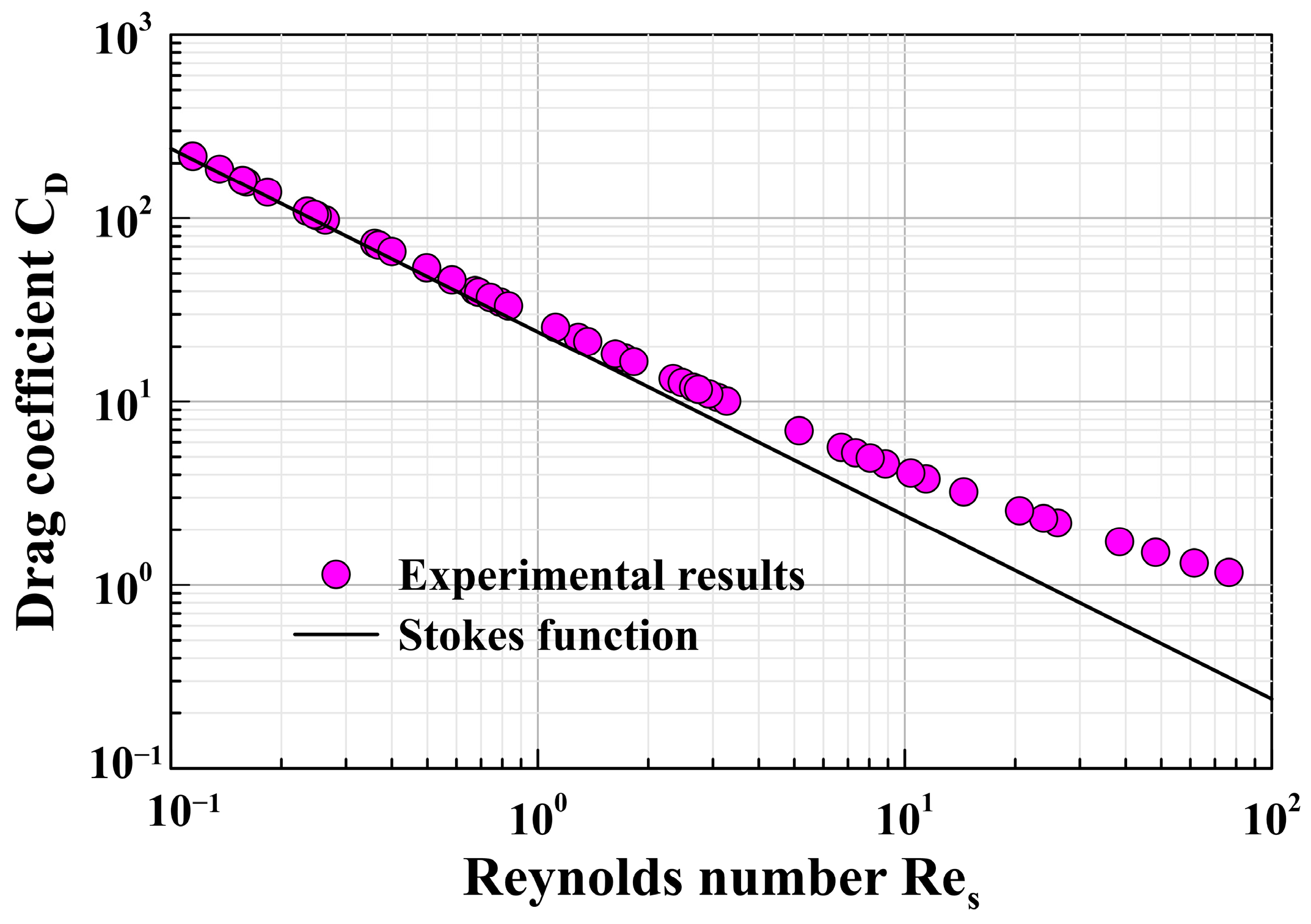
- The experimental data in this study, based on the settling experiments of 64 groups of spherical particles, were compared with four commonly used drag coefficient models. It was found that the errors between the experimental data and the four models were small, confirming the reliability of the experimental equipment and methods.
- Under the same particle Reynolds number conditions, the drag coefficient of coarse mineral particles is greater than that of spherical particles, resulting in a smaller free-settling velocity for coarse mineral particles compared to spherical particles under similar conditions. In instances where the particle Reynolds number is less than 1, the drag coefficient manifests a linear relationship with the particle Reynolds number.
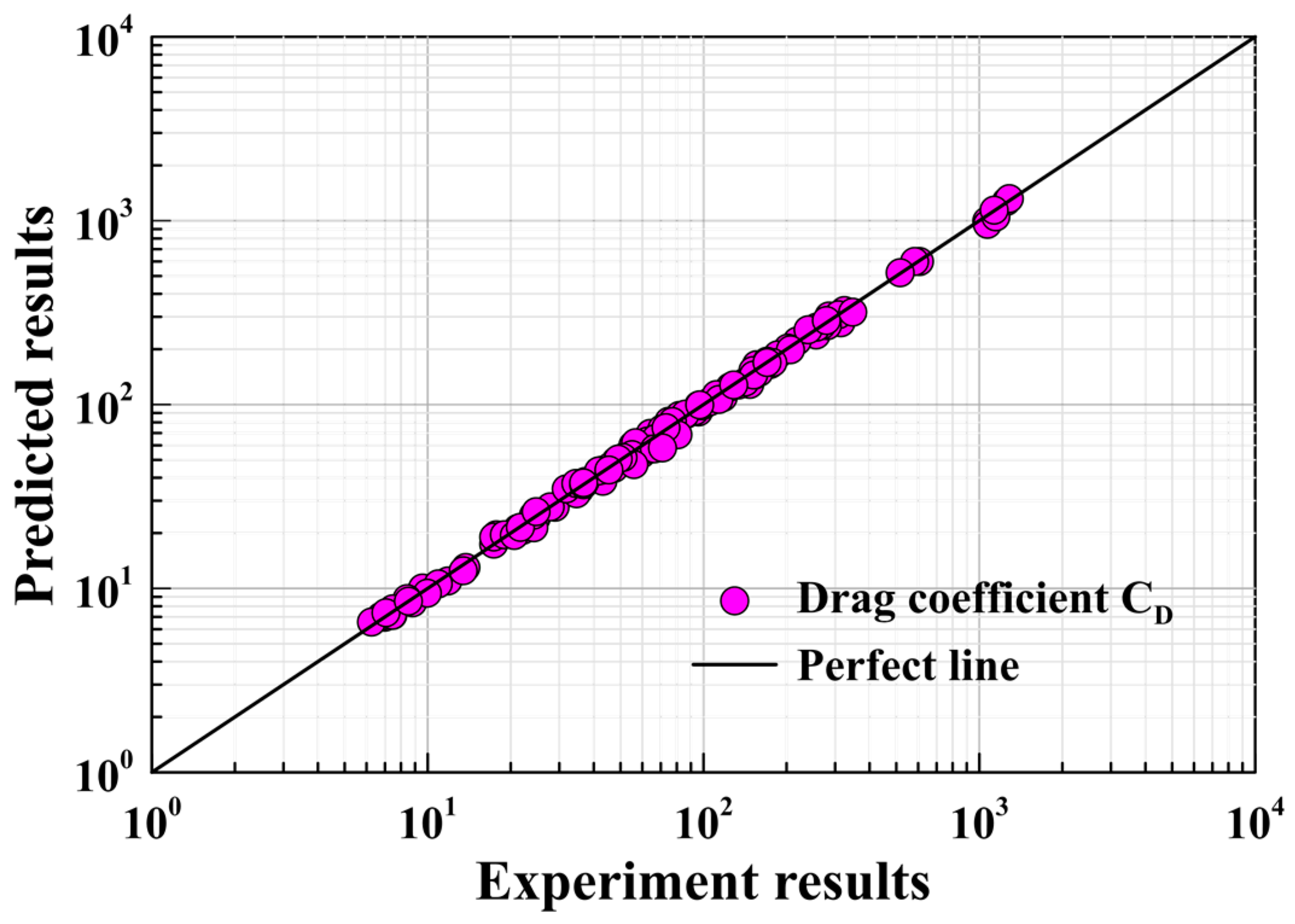
- Utilizing data from 133 groups of settling experiments involving spherical particles, we developed a drag coefficient model for the settling of coarse particles in Newtonian fluids. Additionally, an explicit prediction model for the settling terminal velocity was established. Experimental data verification confirmed the accuracy and reliability of these models, with average relative errors between predicted and experimental values for the drag coefficient and settling terminal velocity being 4.26% and 7.34%, respectively. These predictive models offer valuable theoretical references and guidance for engineering applications in various fields, including chemical engineering, metallurgy, ore filling, deep-sea mining, and pipeline transportation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, T.; Qu, J.Y.; Sun, X.F.; Li, W.; Chen, Y.; Hu, Q.B. A Novel Predictive Model of Drag Coefficient and Settling Velocity of Drill Cuttings in Non-Newtonian Drilling Fluids. Pet. Sci. 2021, 18, 1729–1738. [Google Scholar] [CrossRef]
- Xu, Z.; Song, X.; Li, G.; Pang, Z.; Zhu, Z. Settling Behavior of Non-Spherical Particles in Power-Law Fluids: Experimental Study and Model Development. Particuology 2019, 46, 30–39. [Google Scholar] [CrossRef]
- Hu, X.; Song, X.; Li, G.; Shen, Z.; Lyu, Z.; Shi, Y. Shape Factor of the Flake-like Particle in Thermal Spallation and Its Effects on Settling and Transport Behavior in Drilling Annulus. Powder Technol. 2018, 335, 211–221. [Google Scholar] [CrossRef]
- Hu, Q.; Li, Y.; Sun, X.; Chen, M.; Bu, Q.; Gong, B. Integrating Test Device and Method for Creep Failure and Ultrasonic Response of Methane Hydrate-Bearing Sediments. Rev. Sci. Instrum. 2023, 94, 025105. [Google Scholar] [CrossRef] [PubMed]
- Yan, T.; Qu, J.; Sun, X.; Chen, Y.; Hu, Q.; Li, W.; Zhang, H. Numerical Investigation on Horizontal Wellbore Hole Cleaning with a Four-Lobed Drill Pipe Using CFD-DEM Method. Powder Technol. 2020, 375, 249–261. [Google Scholar] [CrossRef]
- Yan, T.; Xu, R.; Sun, S.-H.; Hou, Z.-K.; Feng, J.-Y. A Real-Time Intelligent Lithology Identification Method Based on a Dynamic Felling Strategy Weighted Random Forest Algorithm. Pet. Sci. 2023. [Google Scholar] [CrossRef]
- Manjula, E.V.P.J.; Ariyaratne, W.K.H.; Ratnayake, C.; Melaaen, M.C. A Review of CFD Modelling Studies on Pneumatic Conveying and Challenges in Modelling Offshore Drill Cuttings Transport. Powder Technol. 2017, 305, 782–793. [Google Scholar] [CrossRef]
- Tang, D.; Xia, J.; Xu, D.; Xiao, H. Research on Variably Accelerated Settling of Coarse Mineral Particles in Still Water. In Proceedings of the ISOPE Ocean Mining and Gas Hydrates Symposium, Kona, HI, USA, 21–26 June 2015; pp. 160–164. [Google Scholar]
- Khan, T.S.; Dai, Y.; Alshehhi, M.S.; Khezzar, L. Experimental Flow Characterization of Sand Particles for Pneumatic Transport in Horizontal Circular Pipes. Powder Technol. 2016, 292, 158–168. [Google Scholar] [CrossRef]
- Xiong, T.; Zhang, X.; Miedema, S.A.; Chen, X. Study of the Characteristics of the Flow Regimes and Dynamics of Coarse Particles in Pipeline Transportation. Powder Technol. 2019, 347, 148–158. [Google Scholar] [CrossRef]
- Rajitha, P.; Chhabra, R.P.; Sabiri, N.E.; Comiti, J. Drag on Non-Spherical Particles in Power Law Non-Newtonian Media. Int. J. Miner. Process. 2006, 78, 110–121. [Google Scholar] [CrossRef]
- Bagheri, G.; Bonadonna, C. On the Drag of Freely Falling Non-Spherical Particles. Powder Technol. 2016, 301, 526–544. [Google Scholar] [CrossRef]
- Tsakalakis, K.G.; Stamboltzis, G.A. Prediction of the Settling Velocity of Irregularly Shaped Particles. Miner. Eng. 2001, 14, 349–357. [Google Scholar] [CrossRef]
- Li, S.; Chen, Z.; Li, W.; Yan, T.; Bi, F.; Tong, Y. An FE Simulation of the Fracture Characteristics of Blunt Rock Indenter Under Static and Harmonic Dynamic Loadings Using Cohesive Elements. Rock Mech. Rock Eng. 2023, 56, 2935–2947. [Google Scholar] [CrossRef]
- Rabinovich, E.; Kalman, H. Phenomenological Study of Saltating Motion of Individual Particles in Horizontal Particle-Gas Systems. Chem. Eng. Sci. 2010, 65, 739–752. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, L.; Wu, Y.; Yang, Q. New Simple Correlation Formula for the Drag Coefficient of Calcareous Sand Particles of Highly Irregular Shape. Powder Technol. 2018, 326, 379–392. [Google Scholar] [CrossRef]
- Agwu, O.E.; Akpabio, J.U.; Dosunmu, A. Artificial Neural Network Model for Predicting Drill Cuttings Settling Velocity. Petroleum 2020, 6, 340–352. [Google Scholar] [CrossRef]
- Goossens, W.R.A. Review of the Empirical Correlations for the Drag Coefficient of Rigid Spheres. Powder Technol. 2019, 352, 350–359. [Google Scholar] [CrossRef]
- Zbib, H.; Ebrahimi, M.; Ein-Mozaffari, F.; Lohi, A. Comprehensive Analysis of Fluid-Particle and Particle-Particle Interactions in a Liquid-Solid Fluidized Bed via CFD-DEM Coupling and Tomography. Powder Technol. 2018, 340, 116–130. [Google Scholar] [CrossRef]
- Loth, E. Drag of Non-Spherical Solid Particles of Regular and Irregular Shape. Powder Technol. 2008, 182, 342–353. [Google Scholar] [CrossRef]
- Levenspiel, O.; Haider, A. Drag Coefficient and Terminal Velocity of Spherical and Nonspherical Particles. Powder Technol. 1989, 58, 63–70. [Google Scholar]
- Song, Z.; Wu, T.; Xu, F.; Li, R. A Simple Formula for Predicting Settling Velocity of Sediment Particles. Water Sci. Eng. 2008, 1, 37–43. [Google Scholar] [CrossRef]
- Cheng, N.S. Comparison of Formulas for Drag Coefficient and Settling Velocity of Spherical Particles. Powder Technol. 2009, 189, 395–398. [Google Scholar] [CrossRef]
- Shahi, S.; Kuru, E. An Experimental Investigation of Settling Velocity of Natural Sands in Water Using Particle Image Shadowgraph. Powder Technol. 2015, 281, 184–192. [Google Scholar] [CrossRef]
- Mohammed, M.A.R. Studying the Factors Affecting the Settling Velocity of Solid Particles in Non-Newtonian Fluids. Al-Nahrain J. Eng. Sci. 2013, 16, 41–50. [Google Scholar]
- Li, Y.; Yu, Q.; Gao, S.; Flemming, B.W. Settling Velocity and Drag Coefficient of Platy Shell Fragments. Sedimentology 2020, 67, 2095–2110. [Google Scholar] [CrossRef]
- Ahmed, R.; Sagheer, M.; Takach, N.; Majidi, R.; Yu, M.; Miska, S.; Rohart, C.; Boulet, J. Experimental Studies on the Effect of Mechanical Cleaning Devices on Annular Cuttings Concentration and Applications for Optimizing ERD Systems. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010. [Google Scholar] [CrossRef]
- Larsson, S.; Prieto, J.M.R.; Heiskari, H.; Jonsén, P. A Novel Particle-Based Approach for Modeling a Wet Vertical Stirred Media Mill. Minerals 2021, 11, 55. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Atif, M.; Ellahi, R.; Sait, S.M. Electromagnetic Flow of SWCNT/MWCNT Suspensions in Two Immiscible Water-and Engine-Oil-Based Newtonian Fluids through Porous Media. Symmetry 2022, 14, 406. [Google Scholar] [CrossRef]
- Sun, X.; Yao, D.; Qu, J.; Sun, S.; Qin, Z.; Tao, L.; Zhao, Y. A Novel Transient Hole Cleaning Algorithm for Horizontal Wells Based on Drift-Flux Model. Geoenergy Sci. Eng. 2024, 233, 212517. [Google Scholar] [CrossRef]
- Dioguardi, F.; Mele, D. A New Shape Dependent Drag Correlation Formula for Non-Spherical Rough Particles. Experiments and Results. Powder Technol. 2015, 277, 222–230. [Google Scholar] [CrossRef]
- Moreira, B.A.; de Oliveira Arouca, F.; Damasceno, J.J.R. Analysis of Suspension Sedimentation in Fluids with Rheological Shear-Thinning Properties and Thixotropic Effects. Powder Technol. 2017, 308, 290–297. [Google Scholar] [CrossRef]
- Mahmoud, H.; Hamza, A.; Nasser, M.S.; Hussein, I.A.; Ahmed, R.; Karami, H. Hole Cleaning and Drilling Fluid Sweeps in Horizontal and Deviated Wells: Comprehensive Review. J. Pet. Sci. Eng. 2020, 186, 106748. [Google Scholar] [CrossRef]
- Hsu, W.Y.; Liu, C.M.; Hwung, H.; Yang, R.Y.; Shugan, I.V. Settling Process and Shock Wave of Cohesive Sediment. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Osaka, Japan, 21–26 June 2009; Volume 1, pp. 122–127. [Google Scholar]
- Wang, Y.; Zhou, L.; Yang, Q. Hydro-Mechanical Analysis of Calcareous Sand with a New Shape-Dependent Fluid-Particle Drag Model Integrated into CFD-DEM Coupling Program. Powder Technol. 2019, 344, 108–120. [Google Scholar] [CrossRef]
- Schiller, L.; Neumann, A. A Drag Coefficient Correlation. Zeit. Ver. Deutsch 1933, 77, 318–320. [Google Scholar]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Zhong, W.; Yu, A.; Liu, X.; Tong, Z.; Zhang, H. DEM/CFD-DEM Modelling of Non-Spherical Particulate Systems: Theoretical Developments and Applications. Powder Technol. 2016, 302, 108–152. [Google Scholar] [CrossRef]
- Breakey, D.E.S.; Vaezi, G.F.; Masliyah, J.H.; Sanders, R.S. Side-View-Only Determination of Drag Coefficient and Settling Velocity for Non-Spherical Particles. Powder Technol. 2018, 339, 182–191. [Google Scholar] [CrossRef]
- Li, Y.; Tang, B.; Jiao, S.; Su, Q. Snake Optimization-Based Variable-Step Multiscale Single Threshold Slope Entropy for Complexity Analysis of Signals. IEEE Trans. Instrum. Meas. 2023, 72, 3317908. [Google Scholar] [CrossRef]
- Li, Y.; Tang, B.; Jiao, S.; Zhou, Y. Optimized Multivariate Multiscale Slope Entropy for Nonlinear Dynamic Analysis of Mechanical Signals. Chaos Solitons Fractals 2024, 179, 114436. [Google Scholar] [CrossRef]






| Experimental Materials | Particle Equivalent Diameter/(mm) | Density/(kg/m3) |
|---|---|---|
| Stainless steel | 1~5 | 7930 |
| Zirconia | 1~5 | 6080 |
| Glass | 1~5 | 2500 |
| Coarse particles | 1.8~6.4 | 2500 |
| The Mass Concentration of Glycerol Solution (%) | Temperature (°C) | Density (kg/m3) | Fluid Viscosity (Pa.s) |
|---|---|---|---|
| 100 | 22.1 | 1260 | 0.665 |
| 95 | 22.4 | 1250 | 0.438 |
| 90 | 23.2 | 1230 | 0.215 |
| 80 | 21.0 | 1210 | 0.038 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Shen, K.; Zhang, K.; Guo, N.; Li, Z. A New Model for Predicting Drag Coefficient and Settling Velocity of Coarse Mineral Particles in Newtonian Fluid. Minerals 2024, 14, 150. https://doi.org/10.3390/min14020150
Xu Z, Shen K, Zhang K, Guo N, Li Z. A New Model for Predicting Drag Coefficient and Settling Velocity of Coarse Mineral Particles in Newtonian Fluid. Minerals. 2024; 14(2):150. https://doi.org/10.3390/min14020150
Chicago/Turabian StyleXu, Zhenqiang, Kaixiang Shen, Kewei Zhang, Nana Guo, and Zijian Li. 2024. "A New Model for Predicting Drag Coefficient and Settling Velocity of Coarse Mineral Particles in Newtonian Fluid" Minerals 14, no. 2: 150. https://doi.org/10.3390/min14020150
APA StyleXu, Z., Shen, K., Zhang, K., Guo, N., & Li, Z. (2024). A New Model for Predicting Drag Coefficient and Settling Velocity of Coarse Mineral Particles in Newtonian Fluid. Minerals, 14(2), 150. https://doi.org/10.3390/min14020150





