Abstract
Efficient transport in vertical pipeline hydraulic lifting systems is vital for coarse-grained ore, necessitating a deep comprehension of the settling traits of coarse mineral particles. In this study, we conducted a series of settling experiments on individual coarse particles in Newtonian fluids with varying viscosities, employing a self-designed and manufactured settling apparatus. A total of 133 sets of experimental data on the free settling of coarse particles in Newtonian fluids were obtained by recording the particle settling process with a high-speed camera and applying image processing techniques. A mechanical model was employed to perform statistical analysis on the experimental data and establish a predictive model for the drag coefficient and an explicit predictive model for the settling terminal velocity of coarse-grained ore in Newtonian fluids. The average relative errors between the predicted values and experimental values of the drag coefficient and settling terminal velocity models are 4.26% and 7.34%, respectively. This confirms the reliability of the provided predicted model, providing a theoretical foundation for determining the hydraulic lifting speed of coarse mineral particles in vertical pipelines for deep mining.
1. Introduction
The drag coefficient plays a crucial role in studying the interaction between particles, particle aggregates, and liquids. It has extensive applications in fields such as chemical engineering, medicine, geotechnical engineering, geology, petroleum engineering, fluid mechanics, and aerospace [1,2,3,4,5,6]. The hydraulic lifting system for coarse particle ore in a vertical pipeline involves the fundamental issue of particle–fluid two-phase flow. Compared to alternative transportation methods, this system offers advantages such as low transportation cost, high transport capacity, efficiency, minimal footprint, unrestricted pipeline layout, no pollution, and enhanced safety, making it an economical, safe, efficient, and reliable advanced transportation technology [7].
In deep mining hydraulic lifting systems for deep well ore pulp, the lifting speed stands out as a crucial parameter in the ore hoisting system [8]. It must ensure the continuous ascent of coarse particle ore while achieving the required ore particle transport quantity. Excessive lifting speed increases friction and drag losses on the pipe wall, leading to higher lifting costs and substantial energy consumption. However, a low lifting speed may cause irregular movement of the ore pulp, resulting in particle retention and aggregation in the pipeline, leading to blockage [5,9,10]. Therefore, the free settling velocity of individual coarse particles becomes a pivotal factor in determining the hydraulic lifting speed in deep mining coarse particle ore vertical pipeline systems [11,12,13,14].
The exploration of free settling patterns of coarse particles begins with studying spherical particle settling, as spherical particles have a simple shape [15,16,17], and the research does not involve the influence of shape factors, making variable control relatively simple. Currently, there is extensive exploration in this field. Past investigators have undertaken numerous theoretical and practical examinations to scrutinize the settling features of spherical particles in Newtonian fluids. They have established dozens of models predicting drag coefficients with high precision [18,19,20,21,22,23]. However, the highly irregular shape of coarse particles raises doubts about the applicability of previously proposed models. The settling characteristics of coarse particles in Newtonian fluids differ from those of spheres in Newtonian fluids.
Therefore, this study conducts settling experiments on spherical particles in Newtonian fluids, performs regression analysis on the settling test data, establishes a prediction model, and compares it with existing influential models to verify the accuracy of the experiments. Based on this, the equivalent diameter of particles is introduced to characterize particle size, and a model for coarse particles in Newtonian fluids is established [24,25,26,27]. The average relative error between the calculated settling velocity and the measured settling velocity is analyzed to confirm the accuracy of the model predictions. Compared to other similar studies, what sets this paper apart is the introduction of a drag coefficient prediction model that does not rely on specific three-dimensional shape descriptor parameters. This model demonstrates a high level of application precision, making it more adaptable for use in real-world environments. The research conclusions provide a theoretical basis and engineering application guidance for subsequent studies on hydraulic lifting speed, aiding in determining the optimal hydraulic lifting speed for deep mining coarse particle ore. Additionally, it holds high theoretical reference value and practical engineering significance for projects in chemical engineering, metallurgy, ore filling, deep-sea mining, and pipeline transport.
2. Drag Coefficient Model
The sedimentation of spherical particles in Newtonian fluids forms the foundation for particle settling analysis, owing to the simplicity of characterizing spherical particle shapes and the rheological properties of Newtonian fluids [28,29]. In quiescent fluid, the settling of spherical particles involves two forces: drag force and buoyant force. As spherical particles commence settling, acceleration occurs when the buoyant force exceeds the drag force, and simultaneously, the drag force acting on the particles continuously increases [30]. When the drag force acting on the particles equals the buoyant force, acceleration reduces to zero, and the particles maintain a constant settling velocity, referred to as the final settling velocity [12,31,32].
During the hydraulic lifting of coarse ore in a vertical pipeline, if the fluid velocity in the pipeline is maintained to be larger than the free settling velocity of lifting coarse ore, the coarse ore will be carried away by the fluid in the pipeline, thereby achieving hydraulic lifting of coarse ore. The ratio of fluid viscous force to particle kinetic energy during particle settling is referred to as the drag coefficient, a key parameter describing particle settling behavior [32,33,34]. The calculation of the drag coefficient based on the properties of both the fluid and particles, as well as the settling velocity:
Among them,
where CD is the drag coefficient; ρl is the fluid density; g is the gravitational acceleration; Vt is the settling velocity; de is the equivalent diameter of particles (when particles are spherical, de equals the diameter); mp is the mass of particles; ρs is the density of particles.
For a smooth, spherical object, the drag coefficient is solely a function of the particle Reynolds number:
The Reynolds number stands as another pivotal parameter delineating the settling characteristics of particles. For Newtonian fluids, the expression for the particle Reynolds number is given by [35]:
Spherical particle shapes are simple, and studies generally do not involve the influence of shape factors. Controlling variables is relatively straightforward. Therefore, both domestically and internationally, research in this area has been extensive and in-depth. Dozens of drag coefficient formulas have been established, providing a rich set of tools and theoretical foundations for predicting multiphase fluid flow in the academic and industrial fields. For example, the model proposed by Schiller–Naumann [36] is shown in Equation (5):
Based on the model proposed by Schiller–Naumann, the improved model suggested by Clift–Gauvin [37] is expressed as Equation (6):
The model proposed by Haider–Levenspiel [21] is represented by Equation (7):
Cheng’s model [23] is presented by Equation (8):
The mentioned model not only possesses high predictive accuracy but has also undergone extensive validation and application. Its accuracy has been verified in various research and practical engineering contexts, making it a crucial tool in practical engineering applications across fields such as mining, chemical industry, pharmaceuticals, geotechnical engineering, geological exploration, fluid mechanics, and aerospace.
So far, most studies have assumed rock fragments to be ideal spheres. This is because the spherical particle shape is simple, requiring only one parameter, the sphere diameter [2,38,39]. Additionally, the settling characteristics of spheres are relatively convenient, with mature models available to predict. However, the universality of the formulas provided for coarse granular materials under specific test conditions is limited. This implies that these formulas may struggle to accurately predict or describe the settling behavior of coarse particles in certain situations, necessitating further research for their refinement to enhance their applicability, including introducing some three-dimensional shape descriptor parameters or more advanced optimization algorithms [39,40,41].
3. Particle Settling Experiment
3.1. Experimental Setup and Procedure
The settling test apparatus is shown in Figure 1. The apparatus is an organic glass cylinder with an inner diameter of 100 mm and a height of 1500 mm. The apparatus employs a high-speed camera (Revealer 2F04C) to capture the settling trajectory of rock fragments. The image capture area is set at 300 mm above the bottom of the cylinder, ensuring that the coarse particles have reached their settling terminal velocity and avoiding the influence of end effects on settling velocity [12].
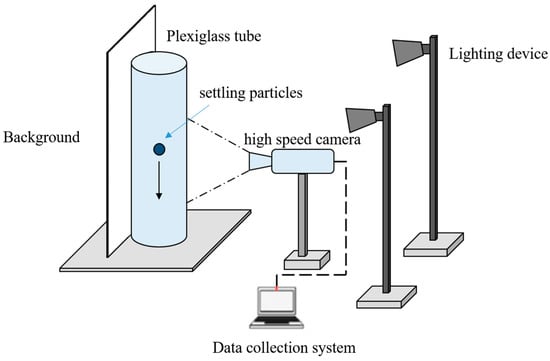
Figure 1.
Instruments and equipment for the particle settling experiment.
The experiment excludes particles with strong eccentricity and intense rolling. Particles that approximately fall along the central axis are chosen. Figure 2 shows the instantaneous position changes of particles at one-second intervals. The time is displayed below the image from left to right in minutes, seconds, and frames. Using the bottom pixel point of the particle as a reference, the settling distance is read out with steel rulers on both sides, and the particle’s descent velocity is calculated.

Figure 2.
Instantaneous position images of individual coarse particles settling.
3.2. Rheological Parameter Testing of Experimental Materials and Fluids
It can be observed from Equation (4) that Res is related to the settling terminal velocity, particle equivalent diameter, and fluid properties. Therefore, to validate the accuracy of the experiment and expand the applicability range of the prediction model at higher particle Reynolds numbers, three materials—stainless steel, zirconia, and glass—were selected for spherical particle settling experiments.
Additionally, coarse river sand particles with large diameters were chosen for coarse particle settling experiments (see Figure 3). First, place the coarse particles to be measured in a small LED photo studio, exposing them to a digital camera (Nikon Z5) positioned above the studio. Each photo has a resolution of 5568 × 3712 pixels. Subsequently, convert the original RGB-format digital images captured by the camera into 8-bit grayscale images.

Figure 3.
Coarse particulate materials were used for the experiments.
To mitigate the impact of wall effects on the experiment, the ratio of particle diameter to the diameter of the experimental circular tube was kept at a low level. The physical properties obtained in the laboratory are listed in Table 1.

Table 1.
Particle property parameters for experiments.
Various concentrations of aqueous glycerol solutions served as the foundational fluid for Newtonian fluid, encompassing mass fractions spanning from 80% to 100%. The rheological properties were tested using an advanced rheometer (Anton Paar MCR 92) under experimental temperature conditions, and the rheological parameters were fitted according to the rheological model of Newtonian fluids. The rheological model for Newtonian fluids is as follows:
where τ is fluid stress, μ is fluid viscosity, and γ is shear rate.
The temperature is controlled using the Anton Paar advanced rheometer (MCR 92) temperature control system to maintain consistency with the temperature during the test (Figure 4).

Figure 4.
Advanced rheometer was used in the experiment (Anton Paar MCR 92).
The experimental solution’s rheological and physical parameters can be found in Table 2.

Table 2.
Physical parameters and rheological parameters of a glycerol aqueous solution with different concentrations.
4. Particle Settling Experiment
First, sedimentation experiments were conducted on spherical particles, establishing the relationship between CD and Res for 64 sets of spherical particles. The relationship between CD and Res was plotted on logarithmic coordinates (as seen in Figure 5). The circular data points represent the combination of particle Reynolds number Res calculated using Formula (4) and drag coefficient CD calculated using Formula (1).
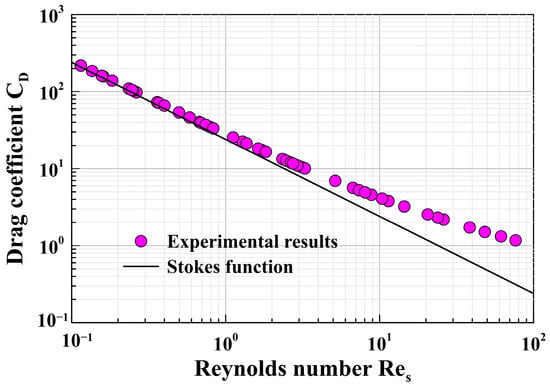
Figure 5.
CD-Res relationship of 64 groups of spheres.
The graph further features data points represented by the inclined line, an outcome derived from the application of Stokes formula calculations. These data points consist of particle Reynolds numbers (Res) calculated with precision using Equation (6) and corresponding drag coefficients (CD) obtained through the application of the Stokes formula (CD = 24/Res). Notably, the drag coefficient demonstrates a discernible decrease with an ascending particle Reynolds number. Interestingly, the rate of this decrease gradually decelerates as the Reynolds number increases. In instances where the particle Reynolds number is less than 1, the drag coefficient manifests a linear relationship with the particle Reynolds number [2].
As seen from Figure 5, it can be observed that, at low Reynolds numbers, the Stokes formula can predict the settling drag coefficient of a spherical particle in a Newtonian fluid well. However, at higher Reynolds numbers, there is a significant error when using the Stokes formula (CD = 24/Res) to predict the settling drag coefficient of spherical particles in a Newtonian fluid. For instance, under Res < 0.1 conditions, the MRE between the settling test results and the Stokes formula predictions is approximately 1.61%. However, under Res > 1 conditions, the MRE between the settling test results and the Stokes formula predictions is about 16.47%. This indicates that fluid–particle interactions have a significant impact at high Reynolds numbers. In such cases, using the Stokes formula to calculate the drag coefficient of a spherical particle in a Newtonian fluid under high Reynolds number conditions will result in a significant error, requiring the adoption of semi-empirical models to predict the particle settling drag coefficient and settling velocity under high Reynolds number conditions.
In this paper, the semi-empirical models proposed by Schiller–Naumann, Clift–Gauvin, Haider–Levenspiel, and Cheng are employed to predict the settling drag coefficients under the experimental conditions of this study. The drag coefficient results predicted by the four models are compared with the experimentally obtained settling drag coefficients to quantitatively assess the accuracy of the experiments.
The comparative analysis, graphically depicted in Figure 6, serves as a crucial tool for evaluating the efficacy of each model in capturing the nuances of particle settling. The obtained results reveal minute variations between the predicted and experimentally measured settling drag coefficients, showcasing the models’ high predictive accuracy. Specifically, the prediction errors for the Schiller–Naumann, Clift–Gauvin, Haider–Levenspiel, and Cheng models for spherical particles stand at 1.51%, 1.43%, 1.86%, and 3.62%, respectively. These low prediction errors reinforce the robustness of the models and underscore their ability to reliably estimate settling behavior under the given experimental conditions, thus validating the precision of the experimental measurements.
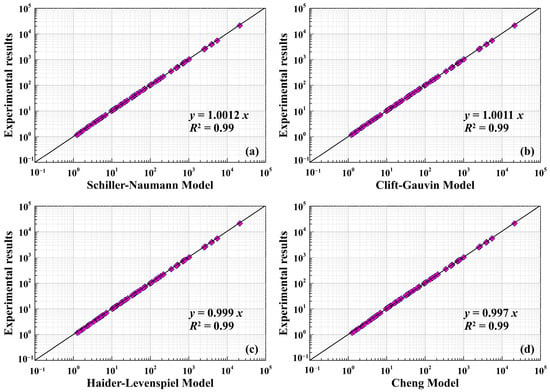
Figure 6.
Experimental results are compared with the drag coefficient results predicted by different models. (a) Schiller–Naumann model; (b) Clift–Gauvin model; (c) Haider–Levenspiel model; (d) Cheng model.
5. Coarse Particle Settling Experimental Results and Analysis
Currently, many researchers have provided various individual spherical particle-free settling velocity calculation formulas based on their specific experimental conditions. However, these fitted empirical formulas are only suitable for specific experimental conditions (such as extremely regular spherical particles), and their general applicability is poor, thus limiting their application in different fields and practical engineering.
In practical engineering applications, almost all particles exhibit irregular shapes rather than regular spherical shapes. Therefore, the free-settling velocity formula for spherical particles cannot be directly applied. The primary distinctions between irregular and spherical particles lie in:
- (1)
- The irregular shape of particles, which results in a larger surface area compared to a sphere of the same volume;
- (2)
- The rough surface of particles;
- (3)
- The asymmetry in particle shapes.
According to the characteristics of irregular coarse particles and the analysis of drag theory for moving objects, it can be deduced that these features of irregular coarse ore particles lead to increased drag during particle motion. Specifically, the drag experienced by irregular coarse ore particles surpasses that encountered by spherical particles, consequently yielding a diminished free settling velocity for irregular coarse ore particles in comparison to their spherical counterparts.
Notwithstanding the aforementioned disparities between irregular coarse ore particles and spherical particles, their settling motion adheres to fundamentally analogous laws. The only requisite adjustment lies in introducing the equivalent particle diameter of irregular ore particles into the free-settling velocity formula designed for spherical particles. This substitution facilitates a preliminary computation of the free-settling velocity applicable to irregular coarse ore particles. This nuanced approach takes into account the irregularities in particle shape, providing a more comprehensive understanding of their settling dynamics within the broader framework of drag theory.
As seen in Figure 7, the relationship between the particle Reynolds number and the drag coefficient of 133 sets of coarse particles settling in a Newtonian fluid is obtained. The figure also presents the drag coefficient model proposed by the Haider–Levenspiel model. As mentioned earlier, using the drag coefficient formula for spherical particles to predict the settling drag coefficient of coarse particles results in significant errors. The average relative error between the experimentally measured drag coefficient of coarse particle settling and the predicted values by the Haider–Levenspiel model is 23.0%.
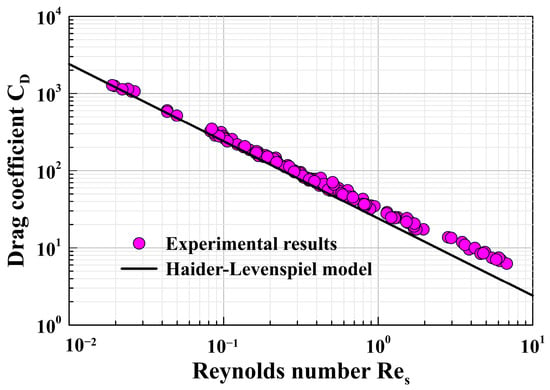
Figure 7.
CD-Res relationship of 133 groups of coarse particles.
In this paper, adopting Cheng’s proposed five-parameter model for fitting the settling drag coefficient formula, with its expression as:
The first term on the right side of Equation (10) is used to characterize the rapid decrease trend of drag coefficient under low Reynolds numbers, and the second term is used to represent the slow decrease trend of drag coefficient under high Reynolds numbers. A predictive model for the settling drag coefficient (CD) of coarse particles in Newtonian fluids was established through fitting regression analysis of 133 sets of settling experimental data, as shown in Equation (11):
Usually, the calculation of particle settling velocity relies on the formula for the drag coefficient during particle settling. It involves employing a trial-and-error approach to determine the ultimate settling velocity, leading to the necessity for iterative calculations and causing a decrease in computational efficiency. To swiftly derive an explicit formula for the settling velocity of large particles in a Newtonian fluid, following Cheng’s model, we establish a distinct formula for the settling velocity of coarse particles. The formulated expression is [22]:
Based on 133 sets of coarse particle settling data obtained in Figure 7, a data fitting was conducted using Equation (12) to derive a novel predictive model for the settling velocity of coarse particles in a Newtonian fluid. The expression is as follows:
Utilizing three statistical parameters, namely the average relative error (δMRE), maximum average relative error (δMMRE), and root mean square logarithmic error (δRMSLE), the predictive accuracy of the proposed correlations was assessed.
The calculation methods for δMRE and δRMSLE are as follows:
where N is the total number; CD,c is the predicted value; and CD,m is the experimentally measured value.
In accordance with the suggested framework for forecasting the drag coefficient of larger particles (as outlined in Equation (12)), calculations are conducted for the drag coefficient, CD, and the settling velocity, Vt, of particles undergoing settling. This information is depicted in Figure 8 and Figure 9, respectively.
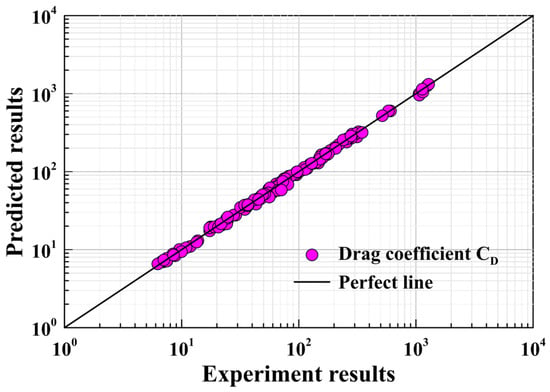
Figure 8.
Comparison between the predicted values of the settling drag coefficient for coarse particles and experimental measurements.
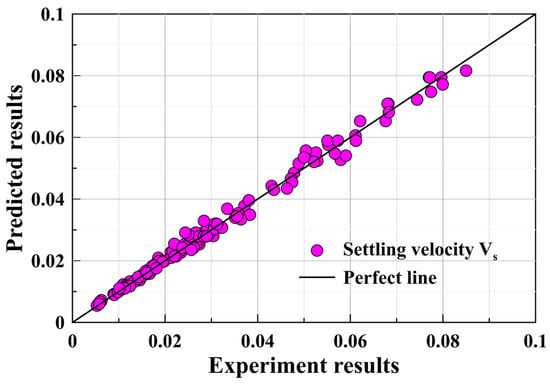
Figure 9.
Comparison between the predicted values of the terminal settling velocity for coarse particles and experimental measurements.
The predicted values of the settling drag coefficient prediction model (Equation (11)) for coarse particles proposed in this paper in a Newtonian fluid are close to the experimental values, with an average relative error of 4.26%, a root mean square logarithmic error of 0.0189, and a maximum relative error of 17.90%. If the model from the literature [23] is employed for calculation, the average error between experimental and predicted values is 14.56%. These outcomes affirm that the model effectively forecasts the settling drag coefficient, demonstrating substantial concurrence with the measurements obtained through experimentation.
From Figure 9, it can be observed that the predicted values of the explicit settling velocity prediction model (Equation (14)) proposed in this paper for coarse particles in a Newtonian fluid are close to the experimental values. The average relative error of the settling velocity is 7.34%, the root mean square logarithmic error is 0.0212, and the maximum relative error is 19.43%. If the model from the literature [22] is employed for calculation, the average error between experimental and predicted values is 14.47%, indicating a good agreement between the model-predicted settling final velocity and the experimental measurements.
During the free-settling experiments of coarse ore particles, it was observed that the majority of the free-settling motion of coarse ore particles occurs near the center of the pipeline, with minimal movement near the pipe wall. The particle’s trajectory in the pipeline is complex, exhibiting behaviors such as jumping, rotating, and swinging during the motion. Consequently, there is a certain degree of fluctuation between predicted and experimental settling velocities, leading to an increase in experimental error.
6. Conclusions
This paper investigates the settling characteristics of spherical particles and coarse mineral particles in Newtonian fluids through experimental studies. The settling characteristics of particles were observed through high-speed photography, including 64 sets of effective experiments for spherical particle settling and 133 sets for coarse particle settling. Models were developed to predict the drag coefficient during settling and explicitly determine the terminal velocity of coarse particles in Newtonian fluids. The outcomes derived under the parameters investigated in this research lead to the following deductions:
- The experimental data in this study, based on the settling experiments of 64 groups of spherical particles, were compared with four commonly used drag coefficient models. It was found that the errors between the experimental data and the four models were small, confirming the reliability of the experimental equipment and methods.
- Under the same particle Reynolds number conditions, the drag coefficient of coarse mineral particles is greater than that of spherical particles, resulting in a smaller free-settling velocity for coarse mineral particles compared to spherical particles under similar conditions. In instances where the particle Reynolds number is less than 1, the drag coefficient manifests a linear relationship with the particle Reynolds number.
- Utilizing data from 133 groups of settling experiments involving spherical particles, we developed a drag coefficient model for the settling of coarse particles in Newtonian fluids. Additionally, an explicit prediction model for the settling terminal velocity was established. Experimental data verification confirmed the accuracy and reliability of these models, with average relative errors between predicted and experimental values for the drag coefficient and settling terminal velocity being 4.26% and 7.34%, respectively. These predictive models offer valuable theoretical references and guidance for engineering applications in various fields, including chemical engineering, metallurgy, ore filling, deep-sea mining, and pipeline transportation.
Author Contributions
Conceptualization, Z.X.; data curation, N.G.; investigation, K.Z.; methodology, K.S.; writing—original draft, Z.X. and K.S.; writing—review and editing, K.Z. and Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Marine Economy Development Foundation of Guangdong Province (GDNRC [2022]44) and the Guangdong Major Project of Basic and Applied Basic Research (NO.2020 B0301030003).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Nana Guo are employees of CCCC-FHDI Engineering Co., Ltd. The paper reflects the views of the scientists and not the company.
References
- Yan, T.; Qu, J.Y.; Sun, X.F.; Li, W.; Chen, Y.; Hu, Q.B. A Novel Predictive Model of Drag Coefficient and Settling Velocity of Drill Cuttings in Non-Newtonian Drilling Fluids. Pet. Sci. 2021, 18, 1729–1738. [Google Scholar] [CrossRef]
- Xu, Z.; Song, X.; Li, G.; Pang, Z.; Zhu, Z. Settling Behavior of Non-Spherical Particles in Power-Law Fluids: Experimental Study and Model Development. Particuology 2019, 46, 30–39. [Google Scholar] [CrossRef]
- Hu, X.; Song, X.; Li, G.; Shen, Z.; Lyu, Z.; Shi, Y. Shape Factor of the Flake-like Particle in Thermal Spallation and Its Effects on Settling and Transport Behavior in Drilling Annulus. Powder Technol. 2018, 335, 211–221. [Google Scholar] [CrossRef]
- Hu, Q.; Li, Y.; Sun, X.; Chen, M.; Bu, Q.; Gong, B. Integrating Test Device and Method for Creep Failure and Ultrasonic Response of Methane Hydrate-Bearing Sediments. Rev. Sci. Instrum. 2023, 94, 025105. [Google Scholar] [CrossRef] [PubMed]
- Yan, T.; Qu, J.; Sun, X.; Chen, Y.; Hu, Q.; Li, W.; Zhang, H. Numerical Investigation on Horizontal Wellbore Hole Cleaning with a Four-Lobed Drill Pipe Using CFD-DEM Method. Powder Technol. 2020, 375, 249–261. [Google Scholar] [CrossRef]
- Yan, T.; Xu, R.; Sun, S.-H.; Hou, Z.-K.; Feng, J.-Y. A Real-Time Intelligent Lithology Identification Method Based on a Dynamic Felling Strategy Weighted Random Forest Algorithm. Pet. Sci. 2023. [Google Scholar] [CrossRef]
- Manjula, E.V.P.J.; Ariyaratne, W.K.H.; Ratnayake, C.; Melaaen, M.C. A Review of CFD Modelling Studies on Pneumatic Conveying and Challenges in Modelling Offshore Drill Cuttings Transport. Powder Technol. 2017, 305, 782–793. [Google Scholar] [CrossRef]
- Tang, D.; Xia, J.; Xu, D.; Xiao, H. Research on Variably Accelerated Settling of Coarse Mineral Particles in Still Water. In Proceedings of the ISOPE Ocean Mining and Gas Hydrates Symposium, Kona, HI, USA, 21–26 June 2015; pp. 160–164. [Google Scholar]
- Khan, T.S.; Dai, Y.; Alshehhi, M.S.; Khezzar, L. Experimental Flow Characterization of Sand Particles for Pneumatic Transport in Horizontal Circular Pipes. Powder Technol. 2016, 292, 158–168. [Google Scholar] [CrossRef]
- Xiong, T.; Zhang, X.; Miedema, S.A.; Chen, X. Study of the Characteristics of the Flow Regimes and Dynamics of Coarse Particles in Pipeline Transportation. Powder Technol. 2019, 347, 148–158. [Google Scholar] [CrossRef]
- Rajitha, P.; Chhabra, R.P.; Sabiri, N.E.; Comiti, J. Drag on Non-Spherical Particles in Power Law Non-Newtonian Media. Int. J. Miner. Process. 2006, 78, 110–121. [Google Scholar] [CrossRef]
- Bagheri, G.; Bonadonna, C. On the Drag of Freely Falling Non-Spherical Particles. Powder Technol. 2016, 301, 526–544. [Google Scholar] [CrossRef]
- Tsakalakis, K.G.; Stamboltzis, G.A. Prediction of the Settling Velocity of Irregularly Shaped Particles. Miner. Eng. 2001, 14, 349–357. [Google Scholar] [CrossRef]
- Li, S.; Chen, Z.; Li, W.; Yan, T.; Bi, F.; Tong, Y. An FE Simulation of the Fracture Characteristics of Blunt Rock Indenter Under Static and Harmonic Dynamic Loadings Using Cohesive Elements. Rock Mech. Rock Eng. 2023, 56, 2935–2947. [Google Scholar] [CrossRef]
- Rabinovich, E.; Kalman, H. Phenomenological Study of Saltating Motion of Individual Particles in Horizontal Particle-Gas Systems. Chem. Eng. Sci. 2010, 65, 739–752. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, L.; Wu, Y.; Yang, Q. New Simple Correlation Formula for the Drag Coefficient of Calcareous Sand Particles of Highly Irregular Shape. Powder Technol. 2018, 326, 379–392. [Google Scholar] [CrossRef]
- Agwu, O.E.; Akpabio, J.U.; Dosunmu, A. Artificial Neural Network Model for Predicting Drill Cuttings Settling Velocity. Petroleum 2020, 6, 340–352. [Google Scholar] [CrossRef]
- Goossens, W.R.A. Review of the Empirical Correlations for the Drag Coefficient of Rigid Spheres. Powder Technol. 2019, 352, 350–359. [Google Scholar] [CrossRef]
- Zbib, H.; Ebrahimi, M.; Ein-Mozaffari, F.; Lohi, A. Comprehensive Analysis of Fluid-Particle and Particle-Particle Interactions in a Liquid-Solid Fluidized Bed via CFD-DEM Coupling and Tomography. Powder Technol. 2018, 340, 116–130. [Google Scholar] [CrossRef]
- Loth, E. Drag of Non-Spherical Solid Particles of Regular and Irregular Shape. Powder Technol. 2008, 182, 342–353. [Google Scholar] [CrossRef]
- Levenspiel, O.; Haider, A. Drag Coefficient and Terminal Velocity of Spherical and Nonspherical Particles. Powder Technol. 1989, 58, 63–70. [Google Scholar]
- Song, Z.; Wu, T.; Xu, F.; Li, R. A Simple Formula for Predicting Settling Velocity of Sediment Particles. Water Sci. Eng. 2008, 1, 37–43. [Google Scholar] [CrossRef]
- Cheng, N.S. Comparison of Formulas for Drag Coefficient and Settling Velocity of Spherical Particles. Powder Technol. 2009, 189, 395–398. [Google Scholar] [CrossRef]
- Shahi, S.; Kuru, E. An Experimental Investigation of Settling Velocity of Natural Sands in Water Using Particle Image Shadowgraph. Powder Technol. 2015, 281, 184–192. [Google Scholar] [CrossRef]
- Mohammed, M.A.R. Studying the Factors Affecting the Settling Velocity of Solid Particles in Non-Newtonian Fluids. Al-Nahrain J. Eng. Sci. 2013, 16, 41–50. [Google Scholar]
- Li, Y.; Yu, Q.; Gao, S.; Flemming, B.W. Settling Velocity and Drag Coefficient of Platy Shell Fragments. Sedimentology 2020, 67, 2095–2110. [Google Scholar] [CrossRef]
- Ahmed, R.; Sagheer, M.; Takach, N.; Majidi, R.; Yu, M.; Miska, S.; Rohart, C.; Boulet, J. Experimental Studies on the Effect of Mechanical Cleaning Devices on Annular Cuttings Concentration and Applications for Optimizing ERD Systems. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010. [Google Scholar] [CrossRef]
- Larsson, S.; Prieto, J.M.R.; Heiskari, H.; Jonsén, P. A Novel Particle-Based Approach for Modeling a Wet Vertical Stirred Media Mill. Minerals 2021, 11, 55. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Atif, M.; Ellahi, R.; Sait, S.M. Electromagnetic Flow of SWCNT/MWCNT Suspensions in Two Immiscible Water-and Engine-Oil-Based Newtonian Fluids through Porous Media. Symmetry 2022, 14, 406. [Google Scholar] [CrossRef]
- Sun, X.; Yao, D.; Qu, J.; Sun, S.; Qin, Z.; Tao, L.; Zhao, Y. A Novel Transient Hole Cleaning Algorithm for Horizontal Wells Based on Drift-Flux Model. Geoenergy Sci. Eng. 2024, 233, 212517. [Google Scholar] [CrossRef]
- Dioguardi, F.; Mele, D. A New Shape Dependent Drag Correlation Formula for Non-Spherical Rough Particles. Experiments and Results. Powder Technol. 2015, 277, 222–230. [Google Scholar] [CrossRef]
- Moreira, B.A.; de Oliveira Arouca, F.; Damasceno, J.J.R. Analysis of Suspension Sedimentation in Fluids with Rheological Shear-Thinning Properties and Thixotropic Effects. Powder Technol. 2017, 308, 290–297. [Google Scholar] [CrossRef]
- Mahmoud, H.; Hamza, A.; Nasser, M.S.; Hussein, I.A.; Ahmed, R.; Karami, H. Hole Cleaning and Drilling Fluid Sweeps in Horizontal and Deviated Wells: Comprehensive Review. J. Pet. Sci. Eng. 2020, 186, 106748. [Google Scholar] [CrossRef]
- Hsu, W.Y.; Liu, C.M.; Hwung, H.; Yang, R.Y.; Shugan, I.V. Settling Process and Shock Wave of Cohesive Sediment. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Osaka, Japan, 21–26 June 2009; Volume 1, pp. 122–127. [Google Scholar]
- Wang, Y.; Zhou, L.; Yang, Q. Hydro-Mechanical Analysis of Calcareous Sand with a New Shape-Dependent Fluid-Particle Drag Model Integrated into CFD-DEM Coupling Program. Powder Technol. 2019, 344, 108–120. [Google Scholar] [CrossRef]
- Schiller, L.; Neumann, A. A Drag Coefficient Correlation. Zeit. Ver. Deutsch 1933, 77, 318–320. [Google Scholar]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Zhong, W.; Yu, A.; Liu, X.; Tong, Z.; Zhang, H. DEM/CFD-DEM Modelling of Non-Spherical Particulate Systems: Theoretical Developments and Applications. Powder Technol. 2016, 302, 108–152. [Google Scholar] [CrossRef]
- Breakey, D.E.S.; Vaezi, G.F.; Masliyah, J.H.; Sanders, R.S. Side-View-Only Determination of Drag Coefficient and Settling Velocity for Non-Spherical Particles. Powder Technol. 2018, 339, 182–191. [Google Scholar] [CrossRef]
- Li, Y.; Tang, B.; Jiao, S.; Su, Q. Snake Optimization-Based Variable-Step Multiscale Single Threshold Slope Entropy for Complexity Analysis of Signals. IEEE Trans. Instrum. Meas. 2023, 72, 3317908. [Google Scholar] [CrossRef]
- Li, Y.; Tang, B.; Jiao, S.; Zhou, Y. Optimized Multivariate Multiscale Slope Entropy for Nonlinear Dynamic Analysis of Mechanical Signals. Chaos Solitons Fractals 2024, 179, 114436. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).