Modelling Flocculation in a Thickener Feedwell Using a Coupled Computational Fluid Dynamics–Population Balance Model
Abstract
1. Introduction
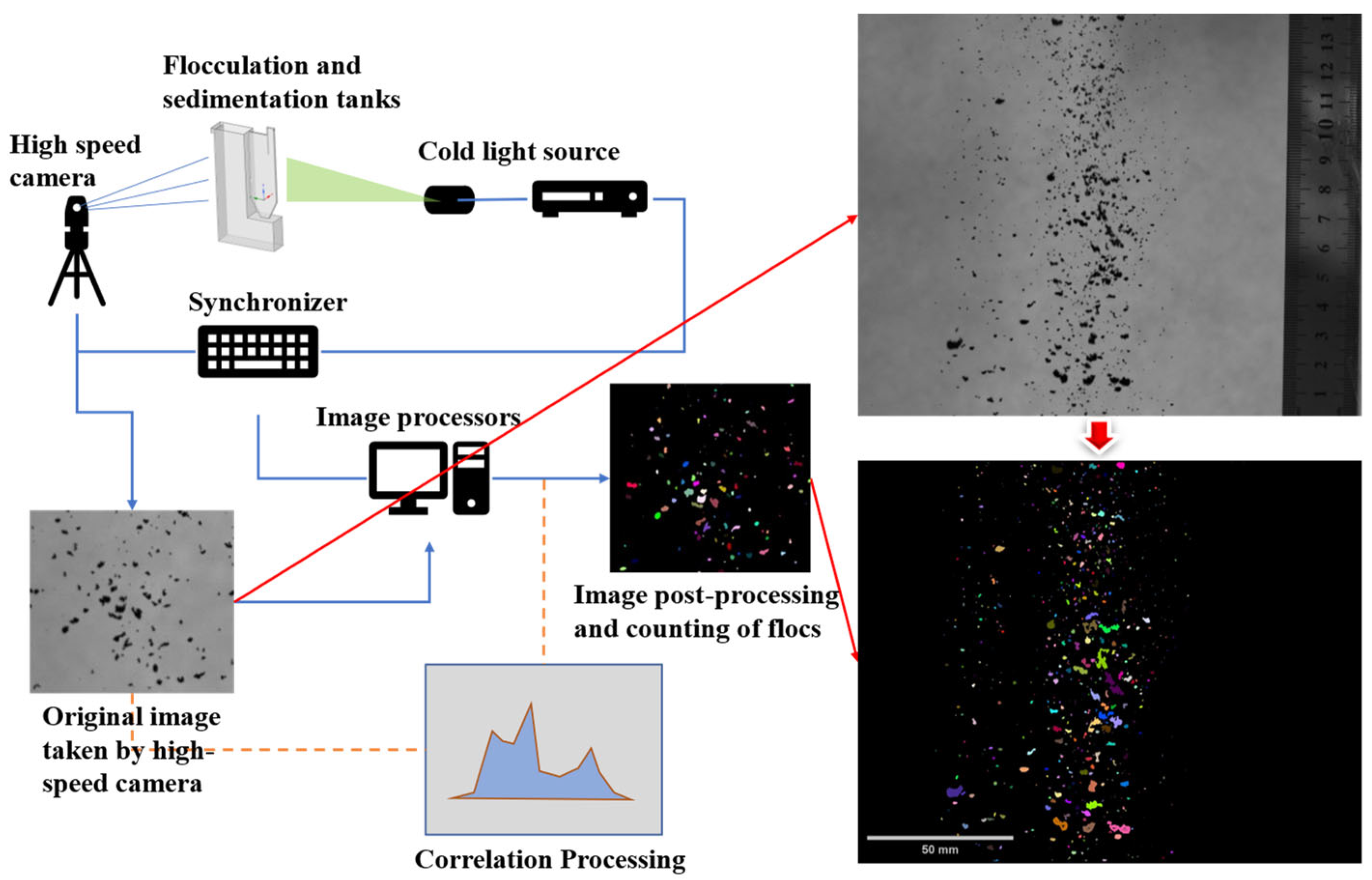
2. Materials and Methods
2.1. Mathematical Model
2.1.1. Multiphase Flow Model
2.1.2. Turbulence Model
2.1.3. Aggregation Kernel in the PBM
2.1.4. Breakage Kernel in the PBM
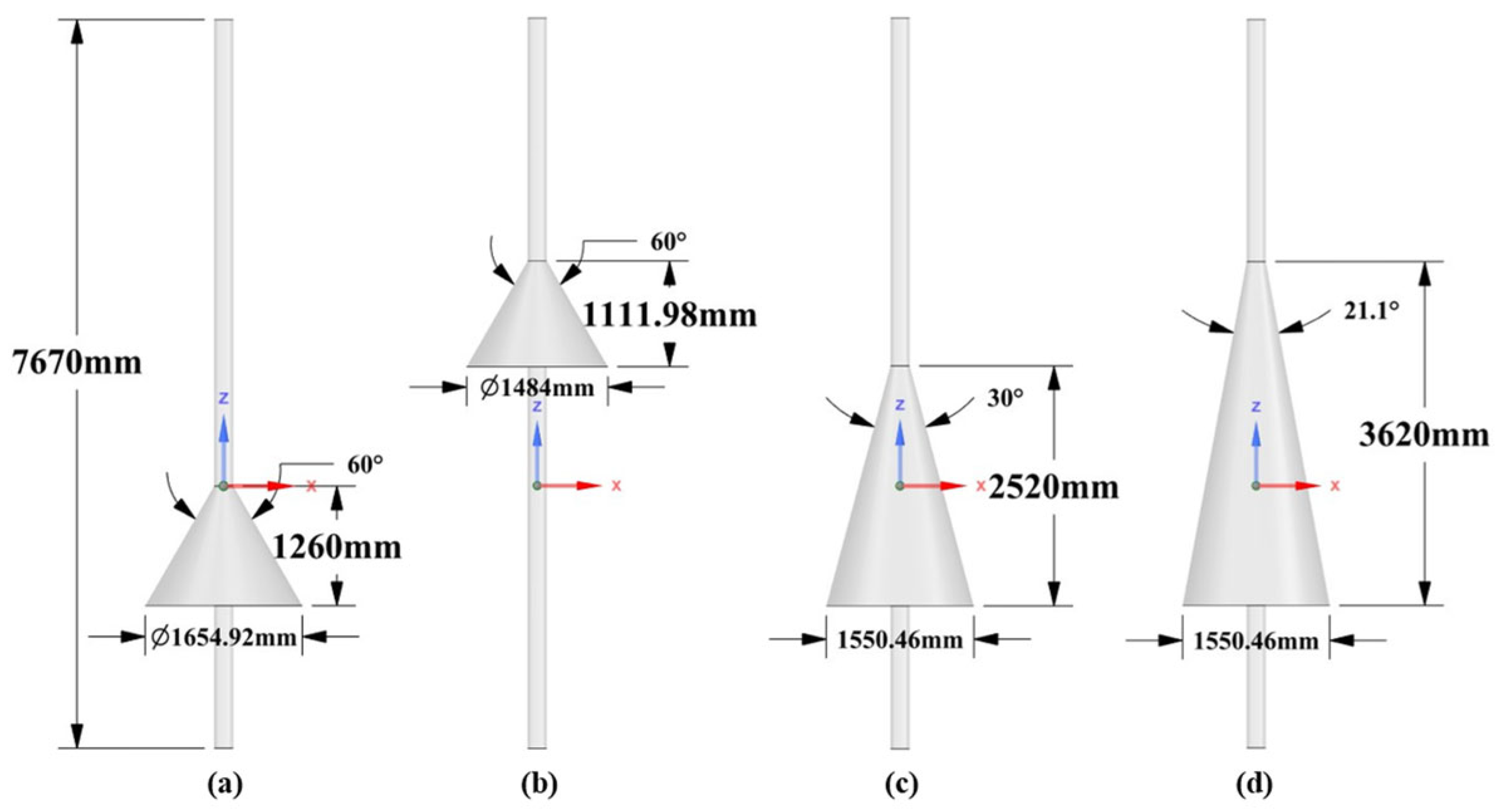
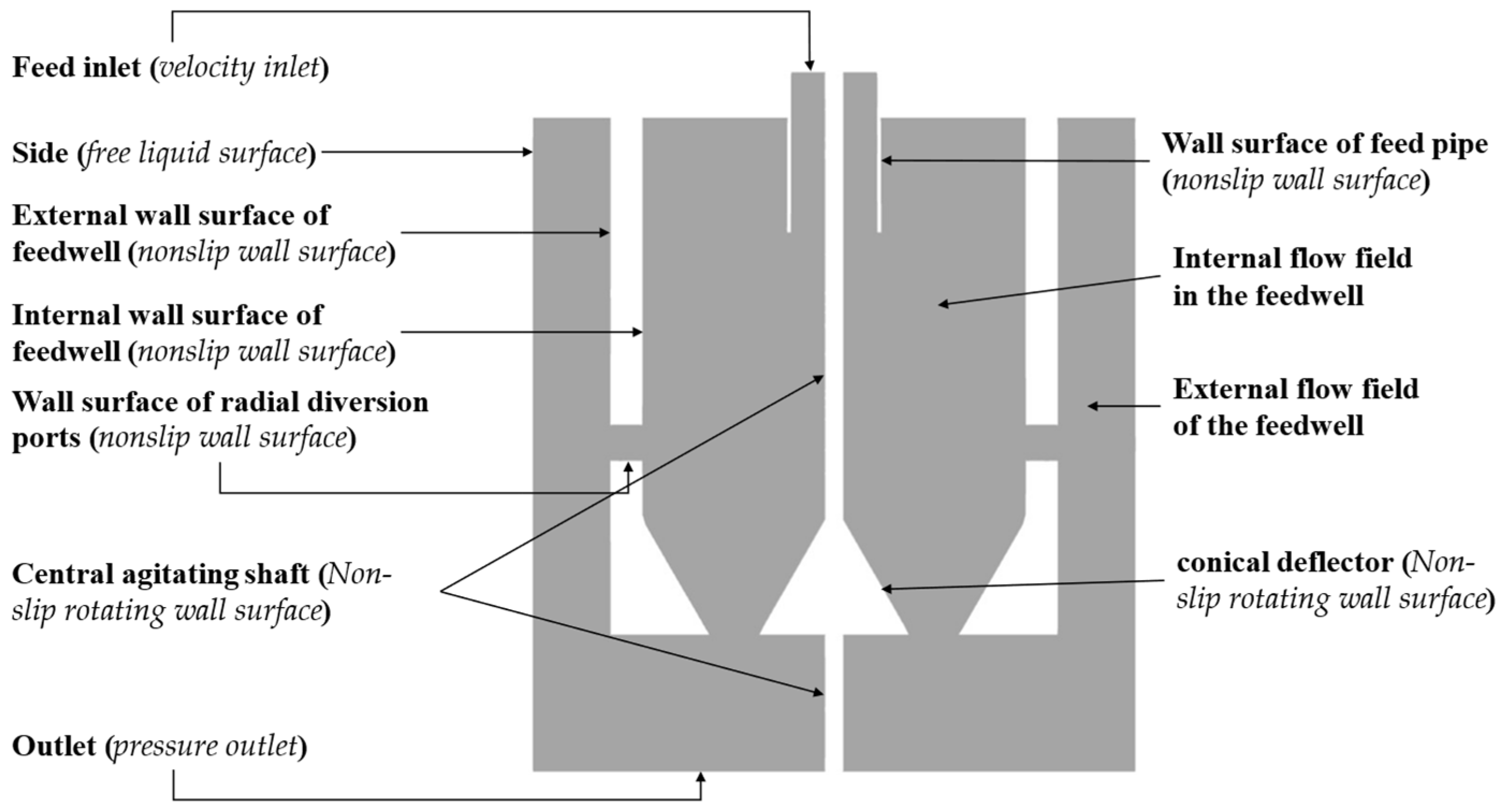
2.2. Structure and Meshing
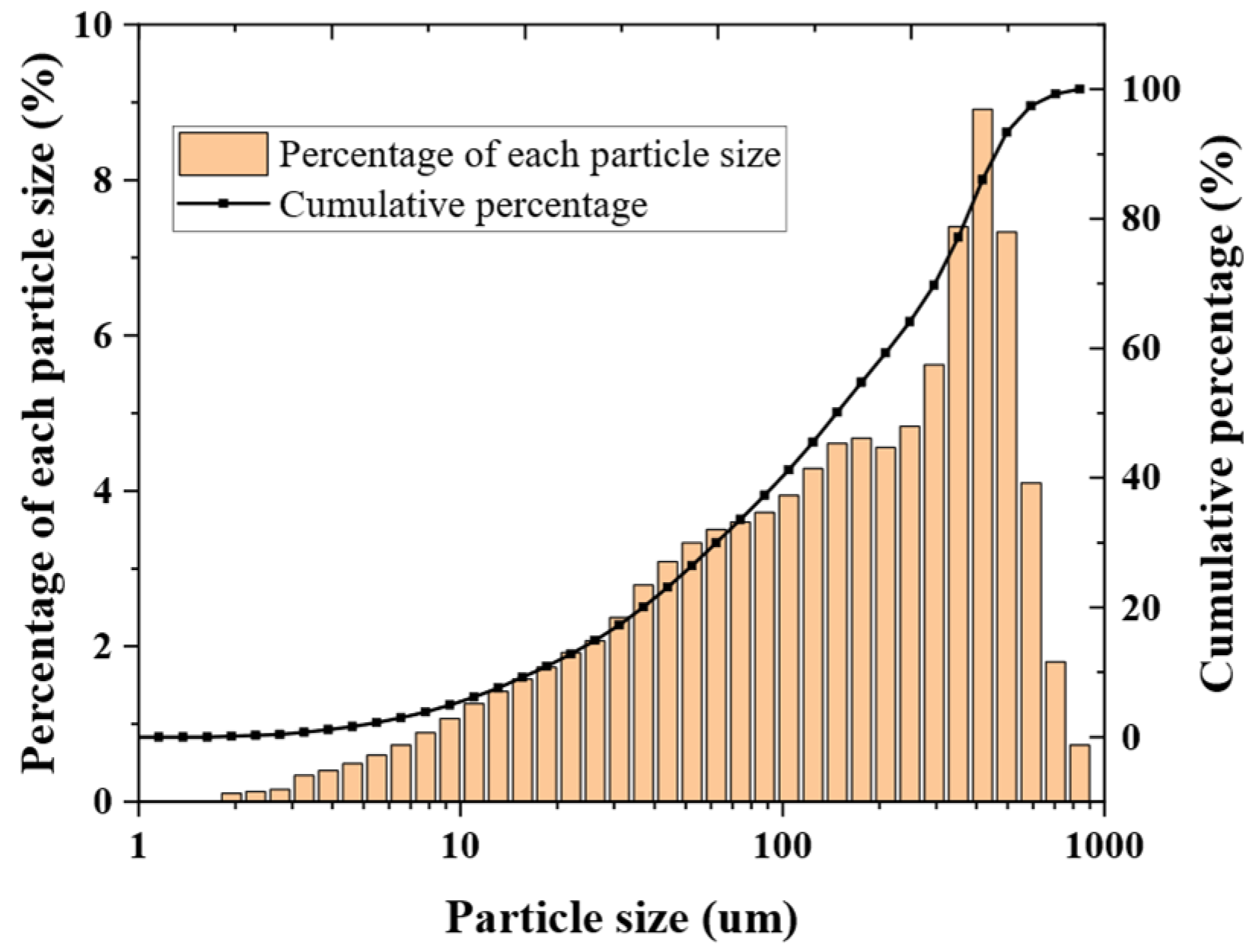
2.3. Initial Parameters
2.4. Boundary Conditions
3. Results
3.1. Turbulence Characteristics
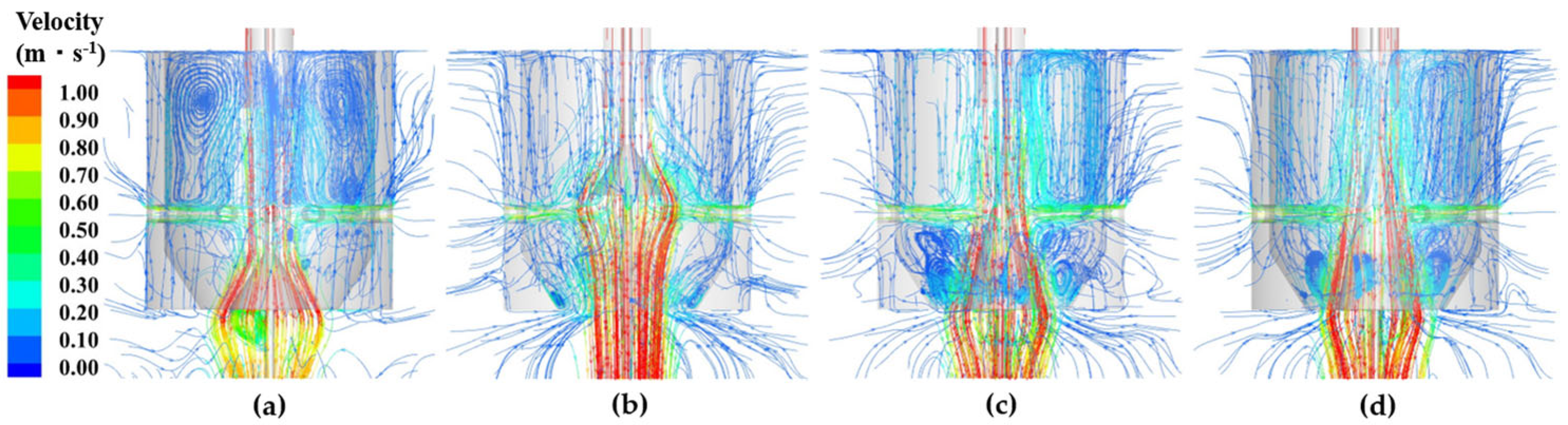
3.1.1. Flow-Field Distribution and Velocity Characteristics
3.1.2. Evolution Characteristics of Macro-Vortices in the Central Feedwell
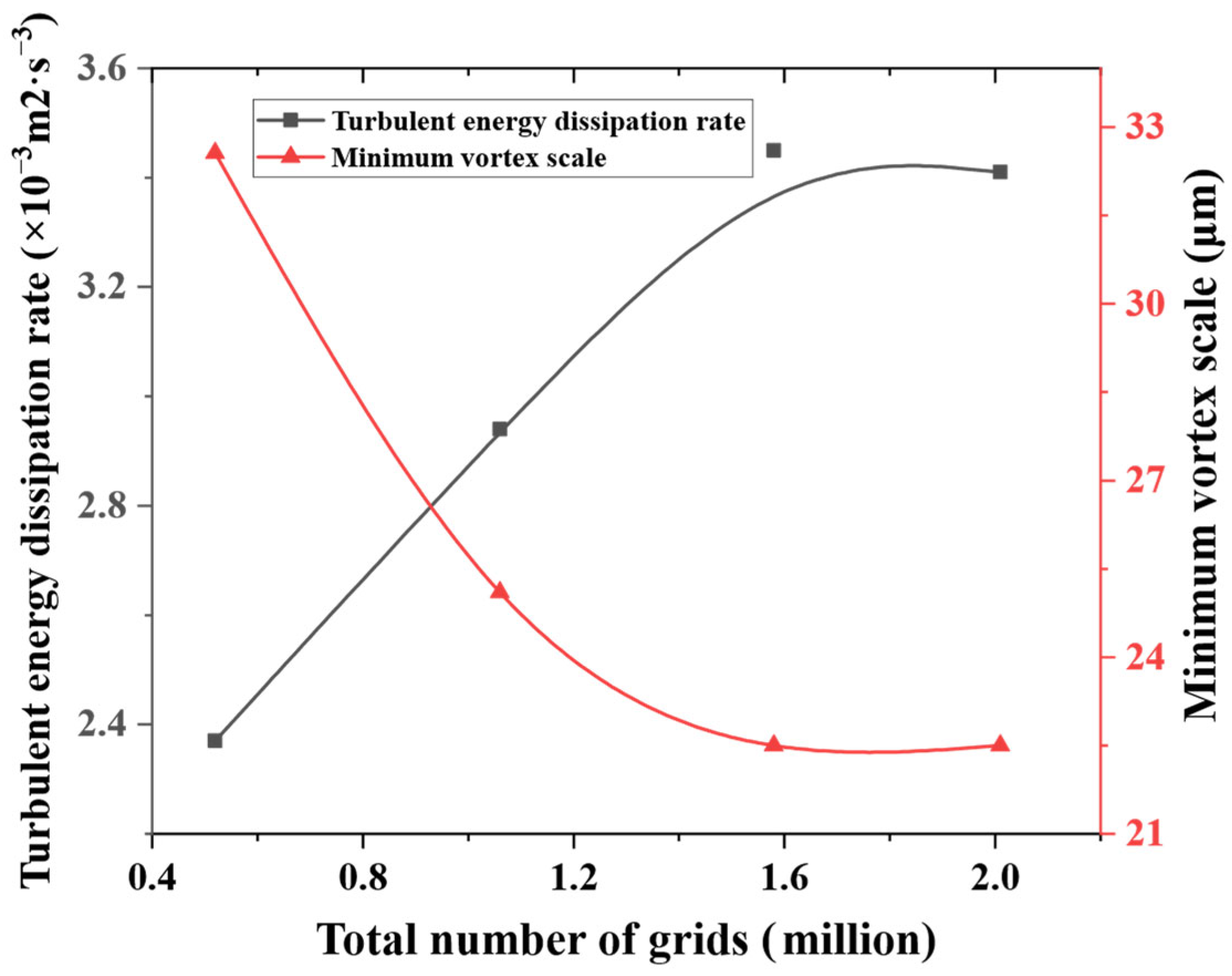
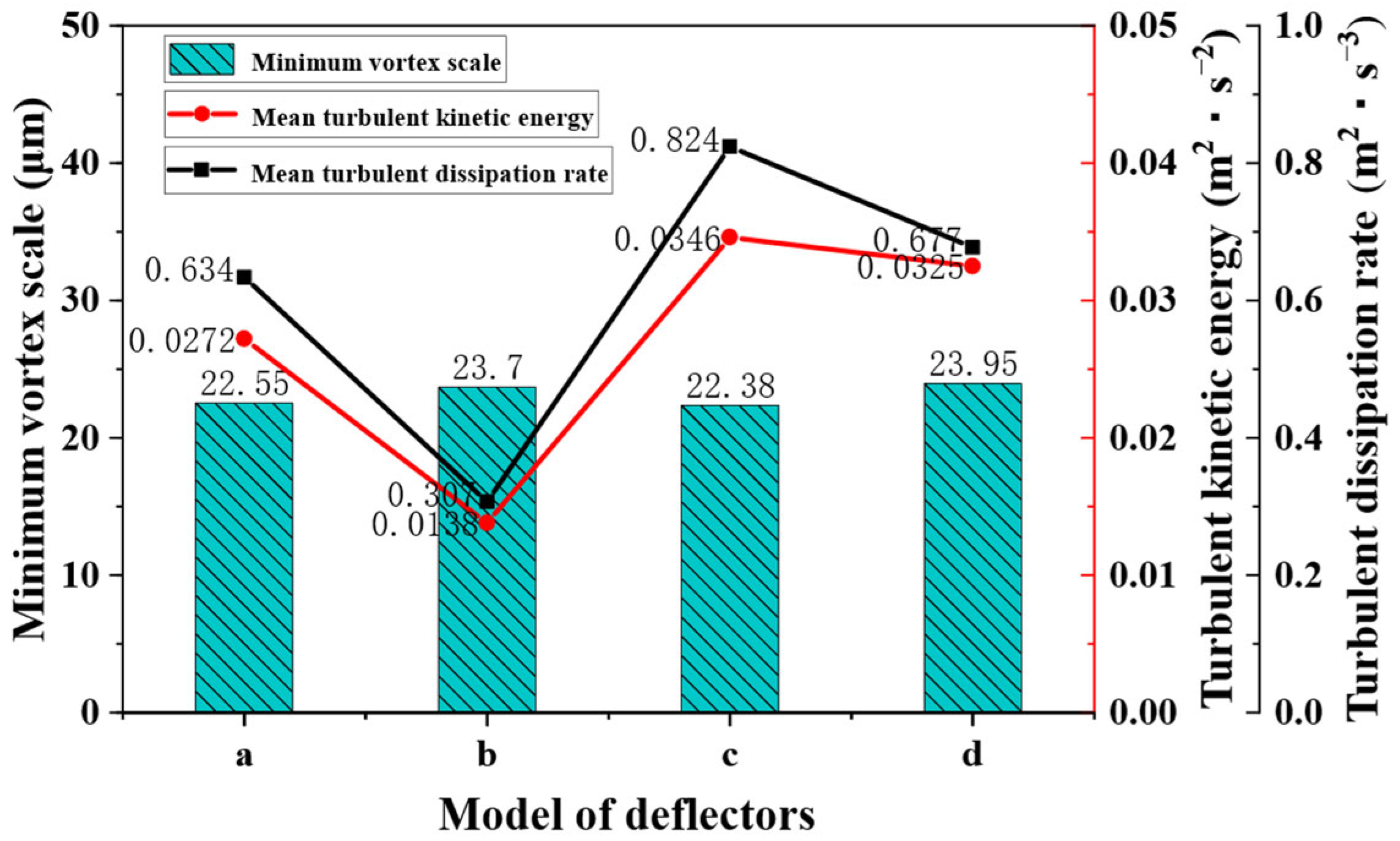
3.1.3. Minimum Vortex Scale
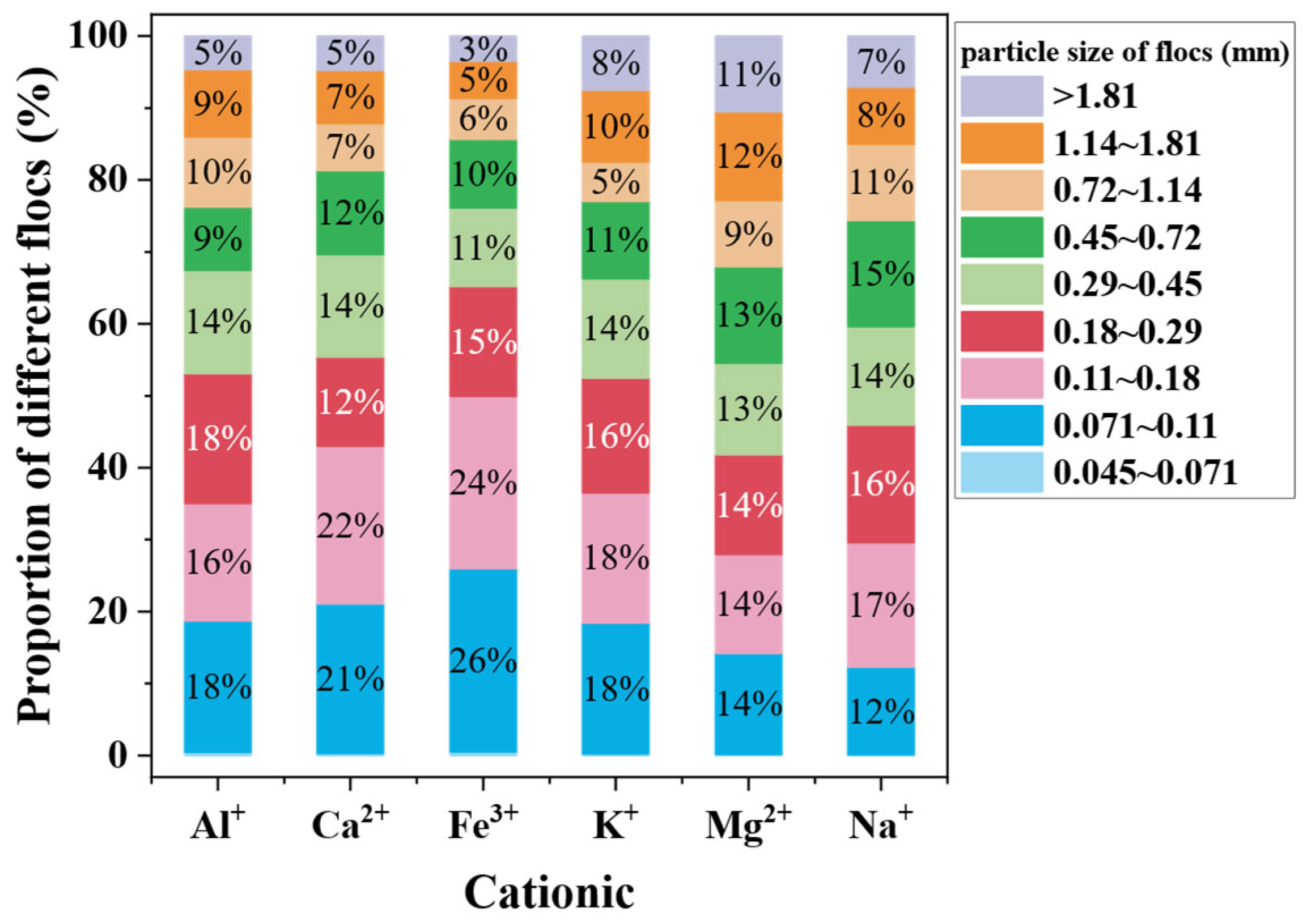
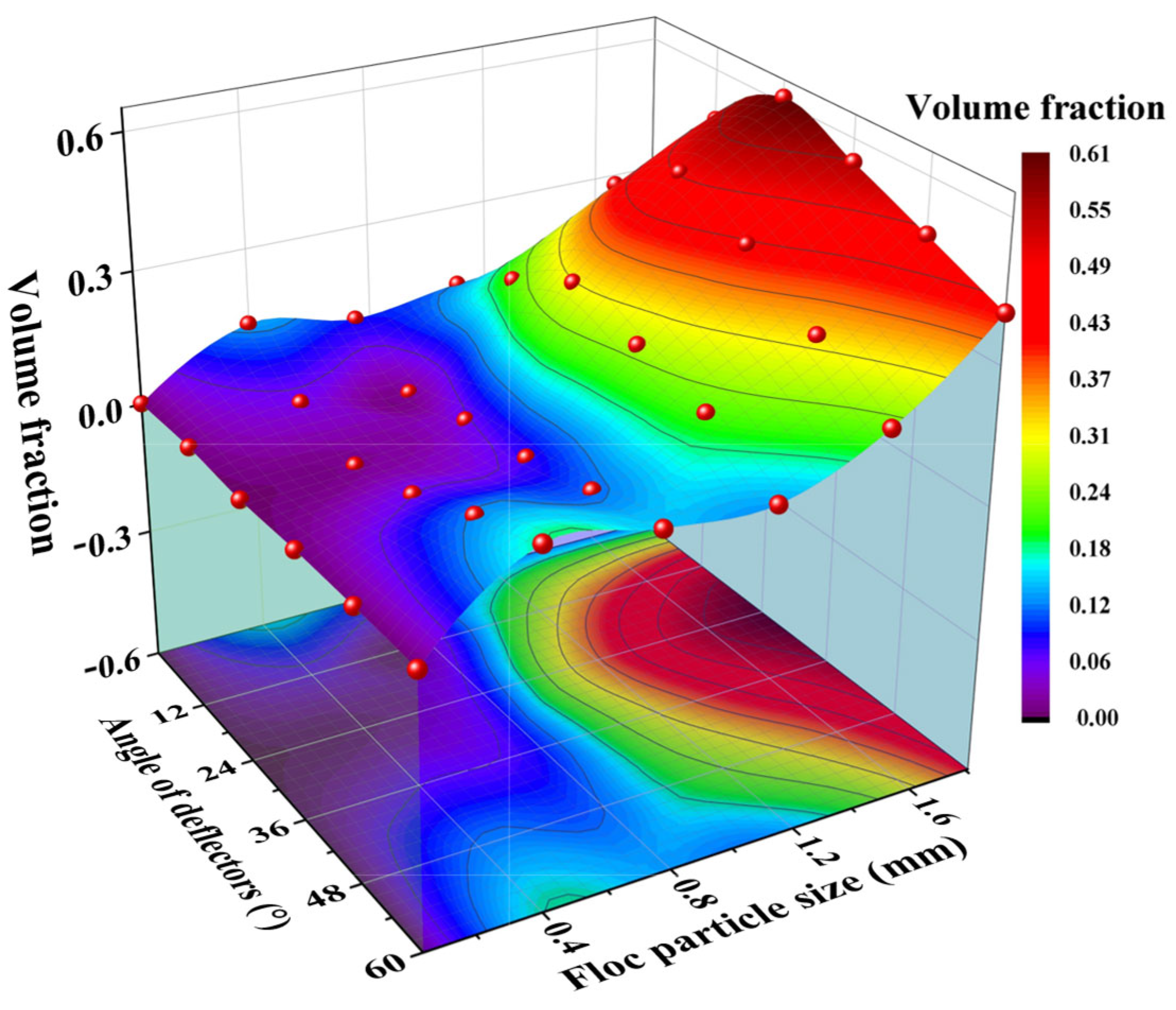
3.2. Effect of Deflector on Flocculation Performance
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Min, F.; Chen, J.; Peng, C.; Chen, C. Promotion of Coal Slime Water Sedimentation and Filtration via Hydrophobic Coagulation. International J. Coal Prep. Util. 2021, 41, 815–829. [Google Scholar] [CrossRef]
- Bedell, D.; Slottee, S.; Shoenbrunn, F.; Fawell, P. Chapter 7—Thickening. In Paste and Thickened Tailings—A Guide, 3rd ed.; Jewell, R.J., Fourie, A.B., Eds.; Australian Centre for Geomechanics: Nedlands, Australia, 2015; pp. 113–134. [Google Scholar]
- Saini, N.; Kleinstreuer, C. A New Collision Model for Ellipsoidal Particles in Shear Flow. J. Comput. Phys. 2019, 376, 1028–1050. [Google Scholar] [CrossRef]
- Šulc, R.; Ditl, P. Scale-up Rules for Flocculation. Int. J. Miner. Process. 2017, 167, 79–85. [Google Scholar] [CrossRef]
- Šulc, R.; Ditl, P. The Effect of Process Conditions on the Flocculation Process Occurring in an Agitated Vessel. Pol. J. Chem. Technol. 2012, 14, 88–96. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Farrow, J.B.; Smith, J.; Fawell, P.D. Design and Development of a Novel Thickener Feedwell Using Computational Fluid Dynamics. J. South. Afr. Inst. Min. Metall. 2012, 112, 939–948. [Google Scholar]
- Chadwick, J.R. Zaldivar. Min. Mag. 1994, 171, 271–277. [Google Scholar]
- Taylor, D. Thickener. US5015392(A), 1989-11-15. Available online: https://worldwide.espacenet.com/publicationDetails/originalDocument?CC=US&NR=5015392&KC=&FT=E (accessed on 20 November 2022).
- Gong, T.; Courtenay, S. Case Study: Advantages of High Rate Thickening at TISCO Jianshan Iron Mine. In Proceedings of the XXIV International Mineral Processing Congress, Beijing, China, 24–28 September 2008; pp. 4171–4175. [Google Scholar]
- Arabadzhi, Y.N.; Olennikov, A.S.; Kurchukov, A.M.; Likhachova, T.A. Thickening equipment modernazation with supaflo process (Outotec) at Talnakh Concentrator. Tsvetnye Metally 2018, 2018, 38–43. [Google Scholar] [CrossRef]
- Watanabe, Y. Flocculation and Me. Water Res. 2017, 114, 88–103. [Google Scholar] [CrossRef]
- Heath, A.R.; Bahri, P.A.; Fawell, P.D.; Farrow, J.B. Polymer Flocculation of Calcite: Population Balance Model. AIChE J. 2006, 52, 1641–1653. [Google Scholar] [CrossRef]
- Ge, L.H.; Evans, G.M.; Moreno-Atanasio, R. CFD-DEM Investigation of the Interaction Between a Particle Swarm and a Stationary Bubble: Particle-Bubble Collision Efficiency. Powder Technol. 2020, 366, 641–652. [Google Scholar] [CrossRef]
- Fawell, P.D.; Nguyen, T.V.; Solnordal, C.B.; Stephens, D.W. Enhancing Gravity Thickener Feedwell Design and Operation for Optimal Flocculation through the Application of Computational Fluid Dynamics. Miner. Process. Extr. Metall. Rev. 2021, 42, 496–510. [Google Scholar] [CrossRef]
- Johnston, R.R.M.; Nguyen, T.W.; Schwarz, M.P.; Simic, K. Fluid Flow and Natural Dilution in Open-type Thickener Feedwells. In Proceedings of the 4th International Alumina Quality Workshop, Darwin, Australia, 2–7 June 1996; pp. 468–475. [Google Scholar]
- Tanguay, M.; Fawell, P.; Adkins, S. Modelling the Impact of Two Different Flocculants on the Performance of a Thickener Feedwell. Appl. Math. Model. 2014, 38, 4262–4276. [Google Scholar] [CrossRef]
- Nguyen, T.; Heath, A.; Witt, P. Population Balance-CFD Modelling of Fluid Flow, Solids Distribution and Flocculation in Thickener Feedwells. In Proceedings of the Fifth International Conference on CFD in the Process Industries Melbourne, Melbourne, Australia, 13–15 December 2006; p. 1. [Google Scholar]
- Owen, A.T.; Nguyen, T.V.; Fawell, P.D. The Effect of Flocculant Solution Transport and Addition Conditions on Feedwell Performance in Gravity Thickeners. Int. J. Miner. Process. 2009, 93, 115–127. [Google Scholar] [CrossRef]
- Rau, M.J.; Ackleson, S.G.; Smith, G.B. Effects of Turbulent Aggregation on Clay Floc Breakup and Implications for the Oceanic Environment. PLoS ONE 2018, 13, e0207809. [Google Scholar] [CrossRef]
- Kostoglou, M.; Karapantsios, T.D.; Oikonomidou, O. A Critical Review on Turbulent Collision Frequency/Efficiency Models in Flotation: Unravelling the Path from General Coagulation to Flotation. Adv. Colloid Interface Sci. 2020, 279, 102158. [Google Scholar] [CrossRef]
- Nguyen, A.V.; An-Vo, D.-A.; Tran-Cong, T.; Evans, G.M. A Review of Stochastic Description of the Turbulence Effect on Bubble-Particle Interactions in Flotation. Int. J. Miner. Process. 2016, 156, 75–86. [Google Scholar] [CrossRef]
- Yunus, A.C.; John, M.C. Fluid Mechanics Fundamentals and Applications; McGraw-Hill: New York, NY, USA, 2013; pp. 134–391. [Google Scholar]
- Vlieghe, M.; Frances, C.; Coufort-Saudejaud, C.; Liné, A. Morphological Properties of Flocs Under Turbulent Break-up and Restructuring Processes. AIChE J. 2017, 63, 3706–3716. [Google Scholar] [CrossRef]
- Sun, H.; Wu, Y.; Xu, C. Pressure Fluctuation in the Submerged Circulative Impinging Stream Reactor. Chin. J. Chem. Eng. 2006, 14, 428–434. [Google Scholar] [CrossRef]
- Yacoubi, A.E.; Xu, S.; Wang, Z.J. A New Method for Computing Particle Collisions in Navier–Stokes Flows. J. Comput. Phys. 2019, 399, 108919. [Google Scholar] [CrossRef]
- Wang, X.; Cui, B.; Wei, D.; Song, Z.; He, Y.; Bayly, A.E. CFD-PBM Modelling of Tailings Flocculation in a Lab-scale Gravity Thickener. Powder Technol. 2022, 396, 139–151. [Google Scholar] [CrossRef]
- Fawell, P.; Farrow, J.; Heath, A.; Nguyen, T.; Owen, A.; Paterson, D.; Rudman, M.; Scales, P.; Simic, K.; Stephens, D.; et al. 20 years of AMIRA P266 ‘Improving Thickener Technology’—How Has It Changed the Understanding of Thickener Performance? In Proceedings of the Twelfth International Seminar on Paste and Thickened Tailings, Australian Centre for Geomechanics, Viña del Mar, Chile, 21–24 April 2009; pp. 59–68. [Google Scholar]
- Jeldres, R.I.; Fawell, P.D.; Florio, B.J. Population Balance Modelling to Describe the Particle Aggregation Process: A Review. Powder Technol. 2018, 326, 190–207. [Google Scholar] [CrossRef]
- Frungieri, G.; Vanni, M. Aggregation and breakup of colloidal particle aggregates in shear flow: A combined Monte Carlo-Stokesian dynamics approach. Powder Technol. 2021, 388, 357–370. [Google Scholar] [CrossRef]
- Frungieri, G.; Boccardo, G.; Buffo, A.; Karimi-Varzaneh, H.A.; Vanni, M. CFD-DEM characterization and population balance modelling of a dispersive mixing process. Chem. Eng. Sci. 2022, 260, 117859. [Google Scholar] [CrossRef]
- An, M.; Guan, X.; Yang, N. Modeling the Effects of Solid Particles in CFD-PBM Simulation of Slurry Bubble Columns. Chem. Eng. Sci. 2020, 223, 115743. [Google Scholar] [CrossRef]
- Yan, P.; Jin, H.; He, G.; Guo, X.; Ma, L.; Yang, S.; Zhang, R. Numerical Simulation of Bubble Characteristics in Bubble Columns with Different Liquid Viscosities and Surface Tensions Using a CFD-PBM Coupled Model. Chem. Eng. Res. Des. 2020, 154, 47–59. [Google Scholar] [CrossRef]
- Guo, K.; Wang, T.; Liu, Y.; Wang, J. CFD-PBM Simulations of a Bubble Column with Different Liquid Properties. Chem. Eng. J. 2017, 329, 116–127. [Google Scholar] [CrossRef]
- Rave, K.; Hermes, M.; Wirz, D.; Hundshagen, M.; Friebel, A.; von Harbou, E.; Bart, H.-J.; Skoda, R. Experiments and Fully Transient Coupled CFD-PBM 3D Flow Simulations of Disperse Liquid–Liquid Flow in a Baffled Stirred Tank. Chem. Eng. Sci. 2022, 253, 117518. [Google Scholar] [CrossRef]
- Valdés, J.P.; Asuaje, M.; Ratkovich, N. Study of an ESP’s Performance Handling Liquid–Liquid Flow and Unstable O-W Emulsions Part II: Coupled CFD-PBM Modelling. J. Pet. Sci. Eng. 2021, 198, 108227. [Google Scholar] [CrossRef]
- Thaker, A.H.; Buwa, V.V. Separation of Liquid–Liquid Dispersion in a Batch Settler: CFD-PBM Simulations Incorporating Interfacial Coalescence. AIChE J. 2020, 66, e16983. [Google Scholar] [CrossRef]
- Zhou, H.; Yu, X.; Wang, B.; Jing, S.; Lan, W.; Li, S. CFD–PBM Simulation of Liquid–Liquid Dispersions in a Pump-Mixer. Ind. Eng. Chem. Res. 2021, 60, 1926–1938. [Google Scholar] [CrossRef]
- Cai, L.; Liu, Z.; Mi, S.; Luo, C.; Ma, K.; Xu, A.; Yang, S. Investigation on Flow Characteristics of Ice Slurry in Horizontal 90° Elbow Pipe by a CFD-PBM Coupled Model. Adv. Powder Technol. 2019, 30, 2299–2310. [Google Scholar] [CrossRef]
- Xu, D.; Liu, Z.; Cai, L.; Tang, Y.; Yu, Y.; Xu, A. A CFD-PBM Approach for Modeling Ice Slurry Flow in Horizontal Pipes. Chem. Eng. Sci. 2018, 176, 546–559. [Google Scholar] [CrossRef]
- Li, L.; Zhao, Y.; Lian, W.; Han, C.; Liu, Y.; Li, P.; Zhang, Q.; Huang, W. Insight into the Effect of Particle Density and Size on the Hydrodynamics of a Particular Slurry Bubble Column Reactor by CFD-PBM Approach. Powder Technol. 2022, 400, 117264. [Google Scholar] [CrossRef]
- Wang, X.; Cui, B.; Wei, D.; Song, Z.; He, Y.; Bayly, A.E. Effect of Feed Solid Concentration on Tailings Slurry Flocculation in a Thickener by a Coupled CFD-PBM Modelling Approach. J. Environ. Chem. Eng. 2021, 9, 106385. [Google Scholar] [CrossRef]
- Lee, J.L.; Lim, E.W.C. Comparisons of Eulerian-Eulerian and CFD-DEM Simulations of Mixing Behaviors in Bubbling Fluidized Beds. Powder Technol. 2017, 318, 193–205. [Google Scholar] [CrossRef]
- Xiao, H.; Cinnella, P. Quantification of Model Uncertainty in RANS Simulations: A Review. Prog. Aerosp. Sci. 2019, 108, 1–31. [Google Scholar] [CrossRef]
- Ashraf Ali, B.; Pushpavanam, S. Analysis of Unsteady Gas–Liquid Flows in a Rectangular Tank: Comparison of Euler–Eulerian and Euler–Lagrangian Simulations. Int. J. Multiph. Flow 2011, 37, 268–277. [Google Scholar] [CrossRef]
- Prat, O.P.; Ducoste, J.J. Simulation of Flocculation in Stirred Vessels Lagrangian Versus Eulerian. Chem. Eng. Res. Des. 2007, 85, 207–219. [Google Scholar] [CrossRef]
- Ding, J.; Gidaspow, D. A bubbling fluidization model using kinetic theory of granular flow. AIChE J. 1990, 36, 523–538. [Google Scholar] [CrossRef]
- Lebowitz, J.L. Exact Solution of Generalized Percus-Yevick Equation for a Mixture of Hard Spheres. Phys. Rev. 1964, 133, A895–A899. [Google Scholar] [CrossRef]
- Lun, C.K.K.; Savage, S.B.; Jeffrey, D.J.; Chepurniy, N. Kinetic theories for granular flow: Inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J. Fluid Mech. 1984, 140, 223–256. [Google Scholar] [CrossRef]
- Gidaspow, D.B.; Bezburua, R.; Ding, J. Hydrodynamics of Circulating Fluidized Beds: Kinetic Theory Approach. In Proceedings of the 7th Engineering Foundation Conference on Fluidization, Chicago, IL, USA, 1 January 1991; pp. 75–82. [Google Scholar]
- Ogawa, S.; Umemura, A.; Oshima, N. On the Equations of Fully Fluidized Granular Materials. Z. Für Angew. Math. Und Phys. ZAMP 1980, 31, 483–493. [Google Scholar] [CrossRef]
- Wen, C.; Yu, Y. Mechanics of Fluidization. Chem. Eng. Prog. Symp. Ser. 1966, 62, 100–111. [Google Scholar]
- Richardson, J.F.; Zaki, W.N. Sedimentation and Fluidisation: Part I. Chem. Eng. Res. Des. 1997, 75, S82–S100. [Google Scholar] [CrossRef]
- Heath, A.; Koh, P.T.L. Combined Population Balance and CFD Modeling of Particle Aggregation by Polymeric Flocculants. In Third International Conference on CFD in the Minerals and Process Industries; CSIRO: Melbourne, Australia, 2003. [Google Scholar]
- White, R.B.; Sutalo, I.D.; Nguyen, T. Fluid Flow in Thickener Feedwell Models. Miner. Eng. 2003, 16, 145–150. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows. In Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; pp. 185–188. [Google Scholar]
- Saffman, P.G.; Turner, J.S. On the Collision of Drops in Turbulent Clouds. J. Fluid Mech. 1956, 1, 16–30. [Google Scholar] [CrossRef]
- Abrahamson, J. Collision Rates of Small particles in a Vigorously Turbulent Fluid. Chem. Eng. Sci. 1975, 30, 1371–1379. [Google Scholar] [CrossRef]
- Ghadiri, M.; Zhang, Z. Impact Attrition of Particulate Solids. Part 1: A Theoretical Model of Chipping. Chem. Eng. Sci. 2002, 57, 3659–3669. [Google Scholar] [CrossRef]
- Moreno-Atanasio, R.; Ghadiri, M. Mechanistic Analysis and Computer Simulation of Impact Breakage of Agglomerates: Effect of Surface Energy. Chem. Eng. Sci. 2006, 61, 2476–2481. [Google Scholar] [CrossRef]
- Hou, D.; Zhao, Q.; Cui, B.; Wei, D.; Song, Z.; Feng, Y. The effects of solid shear stress and wall roughness on the simulation of cylindrical hydrocyclone classification. Powder Technol. 2021, 393, 184–204. [Google Scholar] [CrossRef]
- Hunt, J.; Wray, A.; Moin, P. Eddies, Streams, and Convergence Zones in Turbulent Flows. Stud. Turbul. Using Numer. Simul. Databases 1988, 1, 193–208. [Google Scholar]
- Hayashi, Y. Asymptotic behavior of the node degrees in the ensemble average of adjacency matrix. Netw. Sci. 2016, 4, 385–399. [Google Scholar] [CrossRef]
- Gao, H.; Stenstrom, M.K. Evaluation of three turbulence models in predicting the steady state hydrodynamics of a secondary sedimentation tank. Water Res. 2018, 143, 445–456. [Google Scholar] [CrossRef]







| Parameter | Value |
|---|---|
| Bins | 9 |
| Ratio exponent | 2 |
| Min. Diameter (mm) | 0.045 |
| Max. Diameter (mm) | 1.814 |
| Designation | Bin 0 | Bin 1 | Bin 2 | Bin 3 | Bin 4 | Bin 5 | Bin 6 | Bin 7 | Bin 8 |
|---|---|---|---|---|---|---|---|---|---|
| Equivalent diameter (mm) | 1.810 | 1.140 | 0.720 | 0.450 | 0.290 | 0.190 | 0.110 | 0.071 | 0.045 |
| Volume fraction | 0.105 | 0.124 | 0.092 | 0.134 | 0.127 | 0.139 | 0.137 | 0.140 | 0.001 |
| Parameter | Value |
|---|---|
| Inlet velocity (m·s−1) | 1.44 |
| Solid density (kg·m−3) | 1440 |
| Angular speed of stirring shaft (rpm) | 1.6 |
| Inlet hydraulic diameter (mm) | 575 |
| Underflow port hydraulic diameter (mm) | 3700 |
| Free liquid surface hydrodynamic diameter on the side (mm) | 3585 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, H.; Fan, Y.; Ma, X.; Dong, X.; Chang, M.; Li, N. Modelling Flocculation in a Thickener Feedwell Using a Coupled Computational Fluid Dynamics–Population Balance Model. Minerals 2023, 13, 309. https://doi.org/10.3390/min13030309
Tang H, Fan Y, Ma X, Dong X, Chang M, Li N. Modelling Flocculation in a Thickener Feedwell Using a Coupled Computational Fluid Dynamics–Population Balance Model. Minerals. 2023; 13(3):309. https://doi.org/10.3390/min13030309
Chicago/Turabian StyleTang, Hailong, Yuping Fan, Xiaomin Ma, Xianshu Dong, Ming Chang, and Na Li. 2023. "Modelling Flocculation in a Thickener Feedwell Using a Coupled Computational Fluid Dynamics–Population Balance Model" Minerals 13, no. 3: 309. https://doi.org/10.3390/min13030309
APA StyleTang, H., Fan, Y., Ma, X., Dong, X., Chang, M., & Li, N. (2023). Modelling Flocculation in a Thickener Feedwell Using a Coupled Computational Fluid Dynamics–Population Balance Model. Minerals, 13(3), 309. https://doi.org/10.3390/min13030309






