Abstract
Filtration is crucial for separating solids and liquids in various industries. Understanding slurry properties and filter cake structures is essential for optimising filtration performance. Conventional methods focus on interpreting filtration data to improve the understanding of filtration mechanisms. However, examining fragile filter cakes is challenging, and current techniques often alter their structure. Conventional methods only provide an average representation of cake porosity, neglecting variations in porosity and pore distribution across the cake thickness. This study introduces the Digital cake analysis, a non-destructive technique for evaluating filter cake structure. Filtration experiments using a custom-built unit were conducted on coal slurries to obtain filter cake samples. X-ray-microcomputed tomography (µCT) imaging was utilized for cake analysis. Image enhancement techniques were employed to improve the quality of the µCT images. The enhanced images were segmented into three phases (resolved pore, subresolution pore, and solid phases) for quantitative analysis. This segmentation technique allocated partial pore volume to voxels in the subresolution phase based on their intermediate grey-scale intensity, enabling more accurate porosity calculations. Unlike conventional methods, this approach computed porosity values for resolved (100% void) and subresolution (partially void) pores. This image segmentation technique facilitated accurate computations of porosity, pore size distribution, and pore properties, significantly advancing the understanding of cake structures. Digital cake analysis produced porosity measurements similar to the experimental results.
1. Introduction
Filtration is the most practised solid–liquid separation technique for recovering either a solid product (e.g., coal dewatering) or a liquid product (e.g., water clarification) from a solid–liquid mixture. A filter cake structure is essentially a network of capillary tubes that are formed by the deposition of particles/flocs []. The void spaces between solid grains provide travel pathways for the liquid flow. Filtration kinetics can be evaluated using well known equations: Laplace–Young equations and Darcy’s law. The former describes the relationship between the pressure drop and the capillary radius, while the latter relates the fluid flowrate and permeability to the pressure drop. It is also common to see the utilisation of the Kozeny–Carman equation to interpret filtration results [,,,]. The Kozeny–Carman equation transforms the filtration curve recorded from experiments into a linear equation, where the gradient and the intercept of the linear equation are used to evaluate some filtration parameters, such as the specific cake resistance and medium resistance. These parameters are representative of the filtration kinetics during filtration. They govern the filtration performance, i.e., the fluid velocity, flowrate, and cake resistance, which are strongly related to the porosity of the cake [,,].
The conventional methods of filter cake structure evaluation usually examine the properties of the cake by considering it a piece of a consolidated object [,,,], i.e., the cake structure is generally evaluated as a whole piece, and only the average values are taken. For example, the filter cake porosity measurement, either using intrusive porosimetry or volume difference estimation, only provides the average porosity value of the cake. Such porosity measurements hardly provide information about porosity and/or pore size distribution throughout the cake thickness, which is generally non-uniform. The bottom of the cake (i.e., the side closer to the filtrate outlet) is usually more porous than the top due to larger particles/flocs deposited at the early stage of cake formation. Moreover, the variations in the porosity across cake thickness may be significant depending on the properties of the slurry. The cake might contain very fine pores at the top section and very large pores at the bottom section. In such cases, the average porosity measurement might neither be suitable for cake structure evaluations nor advanced analysis such as flow simulation. Furthermore, intrusive porosimetry measurements, which involve the pressurisation of helium or mercury to intrude into the pores, might disrupt the cake structure depending on the compactness and the properties of the solid materials, resulting in inaccurate results. This structural interference is known as pore collapsing [,]. Another way of estimating the cake porosity is to calculate the volume loss of a wet cake after drying and back-calculate the volume fraction of the porosity []. However, such an estimation may also produce inaccurate results due to uncertainties regarding the degree of cake saturation. Moreover, the abovementioned methods only measure the effective porosity, i.e., the porosity of connected pores, whereas the isolated pores that are disconnected from the effective pore network are disregarded, resulting in the total porosity estimation being inaccurate.
There are also non-destructive means for the structural examination and visualisation of materials. Digital rock technology, in the form of the application of non-destructive X-ray-microcomputed tomography (µCT) imaging technique to rocks, is becoming a routine tool in engineering modelling. Digital Rock technology uses µCT images of rocks for modelling and simulations to compute rock properties. Digital Rock technology is shown to be able to provide a relatively accurate estimation of petrophysical rock properties, including porosity. It also provides extensive details on sample features, e.g., pores, fractures and solid particles and their special distribution [,,,,]. However, the application of µCT to the visualisation, modelling, and analysis of filter cakes has received limited attention. Limited studies have explored the capacity of µCT imaging technique for coal cake analysis, and it is still in its infancy [,,,,]. These studies usually adopt binarisation, a 2-phase segmentation technique to separate the pore and solid phases, and do not consider the subresolution pore phase (intermediate phase). The subresolution pore phase refers to the void spaces with a size below the µCT resolution limit or those at or above the resolution limit but not resolved with the µCT imaging technique []. The subresolution pore phase, in many cases, is disregarded or mislabelled during image segmentation and analysis, which ultimately results in inaccuracies in the estimation of the cake structure. Although there are methods with nano-scale accuracy, such as synchrotron radiation microscopy [,], the scale of the examination is usually localised, e.g., synchrotron radiation microscopy is commonly seen in body cell investigations that are focused on small regions of interest (cell-scale), and can be very time consuming and demanding for computational resources investigating samples with bigger sizes. Furthermore, although nano-CT has been demonstrated to show extreme resolutions (with a pore diameter examinable up to 1 nm) for coal specimens, which granted abundant details of mesopores and micropores that are un-examinable using the micro-CT technique, the specimens, however, were usually thin slices cut from a coal piece or just few particles [,,,]. Furthermore, the examination of coal filter cake using nano-scale microscopy has been barely attempted, possibly due to the complex structure of filter cakes, because they usually involve significantly wide variations in the size and shape of the pores, and the pore structure of the cake can be largely subjective to the properties of the feeding slurry (i.e., particle density, particle size, viscosity, slurry pH) and the filtration technique [,,,]. Thus, a nano-scale analysis of the filter cake focused on a few small regions might not be representative of the filter cake property.
This study uses the non-destructive µCT imaging technique for filter cake analysis, Digital cake analysis, and specifically for filter cake structure evaluation. Like the Digital Rock technique, the Digital cake analysis produces a digital version of the sample cake, which is examinable with computer software. The aim of this work is to establish a technique is that is non-destructive through a time- and cost-efficient methodology suitable for the structural analysis of filter cakes made of fine particles. This work also demonstrates the capability of the adopted technique, which allows for the extraction of valuable information from the Digital cake, such as pore distribution along the cake thickness and an analysis of individual pore size, which has been barely elaborated on in previous filter cake studies. To validate the method, filtration experiments were carried out first to produce filter cakes using a custom-built filtration unit. The filter cakes were then imaged using a µCT scanner to produce Digital cakes, which were processed and analysed. The pore structure of the filter cake samples obtained from the Digital cakes was analysed and compared with the experimental results.
2. Experimental
2.1. Materials
The coal sample used in this study was obtained as a flotation product from a coal processing plant located in Queensland, Australia. The size distribution and ultimate and proximate analyses were conducted on the sample. The size distribution of the particles was measured by wet sieving using laboratory sieves by MRS Scientific. Wet sieving was repeated 3 times, and the average cumulative particle size distribution of the sample is shown in Figure 1. The sieve sizes used are 20 µm, 50 µm, 63 µm, 125 µm, 250 µm, 300 µm, and 500 µm. The sample had a d80 of approximately 184 µm and an average ash value of 5.4%. In this study, d80 is used to represent the particle size value at which 80% of the particles are smaller, where “d” represents diameter and “80” indicates the cumulative distribution. Using “d80” provides a succinct and accurate way to communicate the particle size distribution. The sample contained about 26% of fines less than 20 µm, with a relatively high ash value (8.8%), whereas the ash values in the other size classes were below 6%. It should be noted that not all of the particles passed the 500 µm sieve; thus, the percentage passing did not reach 100%. However, only the −500 µm fraction of the particles was considered for the particle size distribution analysis in this study.
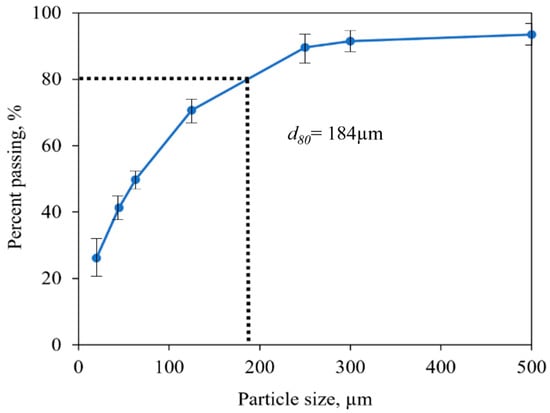
Figure 1.
Cumulative particle size distribution of the sample used in the study.
The proximate and ultimate analyses results are provided in Table 1. The analyses were performed on dried samples in accordance with the Australian Standard (AS1038.3–2000).

Table 1.
Results of proximate and ultimate analyses.
This study used two concentrations of NaCl solutions, 2 mM and 200 mM, to explore Digital cake analysis capabilities. The NaCl solutions were produced by dissolving a laboratory grade NaCl powder obtained from Sigma-Aldrich (St. Louis, MO, USA) in Milli-Q water by Merck Reverse Osmosis System (Darmstadt, Germany). The pH was controlled at 8.5 by adding pH modifiers, HCl (from Sigma-Aldrich) and NaHCO3 ( AJAX FineChem, Brisbane, Australia), for acidity and alkalinity, respectively. The selections of the salt concentrations and pH were based on previous studies [,], where the conductivity and the pH of water were found to vary seasonally from 4 mS/cm to 16 mS/cm and 7.5 to 9.5, respectively, in industrial practices. Table 2 shows the conditions of the slurry samples prepared.

Table 2.
Conditions of slurries prepared for filtration experiments.
Flocculation was used for comparing the changes in filter cake structure with and without flocculation. An anionic flocculant, SNF FloPAM AN923SH, which is currently used in the specific coal processing plant where the sample came from, was used. The flocculant was received as a dry powder. A stock solution was first prepared by dissolving the polymer to a concentration of 0.25% (w/w) with Milli-Q water, which was then further diluted to a 0.025% (w/w) concentration. The designated flocculant dosages were 0 and 90 g/t (grams of flocculant per ton of coal) for the comparison of their effects on cake structure.
2.2. Slurry Preparation and Filtration
A 200 g slurry with a 7% solid concentration (i.e., particle weight was 7% of the slurry weight) was prepared for each filtration experiment. The solid particles were suspended in the NaCl solution (solution concentration was subjected to the designated NaCl concentration, i.e., 2 or 200 mM) and stirred for 2 min using a propeller stirrer at 350 rpm for proper wetting of particle surface and dispersion. The slurry pH was then adjusted to the desired level, as previously mentioned, using the pH modifiers. The slurry was sampled, and flocculation was carried out with the addition of the diluted flocculant of the selected dosage. After the addition of the flocculant, the suspension was gently shaken by hand 5 times to avoid a rupture of the floc structure.
Filtration experiments were carried out using a custom-built filtration unit schematically shown in Figure 2. A Büchner funnel with a perforated filter disc was used, and the filtrate was collected into a filter flask. The filtration was driven by a vacuum pump at constant vacuum pressure. The filtrate mass was constantly monitored by a loadcell under the flask, and real-time filtrate mass data were recorded on a computer at 1 Hz. The software used for monitoring and exporting the filtration data was LabView 2022, developed by National Instrument.
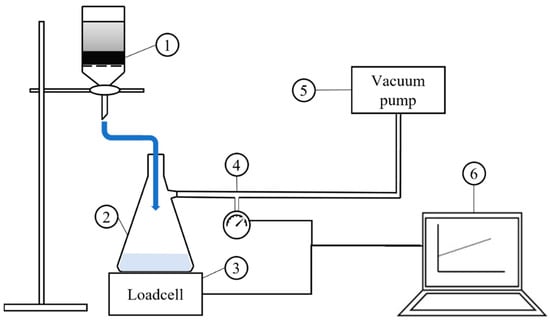
Figure 2.
Schematic illustration of the filtration setup: (1) Büchner funnel and filter paper, (2) filtration flask, (3) loadcell, (4) vacuum gauge, (5) vacuum pump, (6) computer for pressure and filtrate collection logging.
2.3. Filter Cake Sampling
The filter cake samples were collected using a 10 mm inner diameter transparent Perspex tube. The tube was placed at the centre of the filter paper before pouring the slurry into the funnel. The slurry was then filtered, as demonstrated in Figure 3a. Subsequently, the tube and the filter paper beneath it were removed to form the sample for µCT imaging (Figure 3b). To determine the thickness of the filter cake samples, a Vernier caliper with an accuracy of two decimal points in millimetres was used. Measurements were taken at four different locations on the cake, and the recorded thicknesses were averaged to obtain the representative thickness of the cake. The thickness of the cakes varied between 6.4 mm to 7.2 mm. Moreover, the cross-sectional area of the cakes was identical to that of the sampling tube, which measured at 78.5 mm2.

Figure 3.
Filter cake sampling procedures: (a) sample acquisition from filtration, (b) sample removal and sealing.
2.4. Experimental Porosity Measurement Method
Meeten []’s method (Equation (1)) was used to estimate the filter cake porosity based on the measurements of the cake volume loss (determined from the weight loss of the moisture held by the pores), where the ratio of the volume loss of saturated cake after drying, Vp, to the total volume of the saturated cake, VT, was used as an indicator of the cake porosity.
The porosity measured by this method is only capable of providing an average porosity value of the cake as a whole piece. Thus, the distribution of the pores and the variations in the porosity across the cake body cannot be estimated with this method.
2.5. Digital Cake Analysis Methods
2.5.1. µCT Imaging
For Digital cake analysis, two filter cake samples were extracted from the cakes produced by the two specified slurry conditions (refer to Table 2). The imaging of the samples was conducted with a HeliScan µCT scanner (Figure 4), located at the UNSW Tyree X-ray Facility. The configuration of the scanner can be observed in A; a double-helix acquisition trajectory was used for µCT imaging, which is shown to provide high-quality images with relatively uniform resolution [,].

Figure 4.
High cone-angle helical scanner at UNSW.
Table 3 provides the scanning parameters used in this study. The radiographic field of vision is 18 mm × 43 mm with a 3040 × 3040 display. The detector panel has a pixel size of 139 µm. The acquisition time is determined by the size of the sample. Smaller samples require less time, e.g., 12 h, while larger samples necessitate longer acquisition times. Each revolution executed 2520 projections with an angular step width of 0.14 °C. The X-ray source emits a polychromatic beam onto the specimen, which is absorbed, scattered, diffracted, refracted, or transmitted through the material []. The attenuated radiations, an array of attenuation coefficients, are received by the detector unit. The attenuated intensity, I, after the X-rays have passed through the sample, is calculated using Lambert–Beer’s Law:
where µ is the linear attenuation coefficient measured during imaging, x is the thickness of the sample object, and I0 is the incident radiation intensity []. It should be noted that the attenuation coefficient is closely related to the type and the density of the of the sample material. Denser materials, e.g., minerals, tend to prohibit the penetration of X-ray radiation through the sample object; thus, the images obtained can be blurry and contain less structural features, as the internal structure cannot be fully scanned []. The number of projections refers to the number of times the X-ray source emits the X-ray beam onto the sample object during the 360-degree scanning process. Each projection takes approximately 2.87 s. These projections pass through the sample from different angles, and the attenuated X-ray radiation is captured by the detector panel to record the radiograph from that specific angle. It is important to clarify that the detector pixel size mentioned here pertains to the detectable pixel size of the radiographic field of vision by the detector panel and not the image pixel size.

Table 3.
Imaging parameters and specifications of the µCT scanner used in this study.
The data collected by the detector unit are processed to generate a radiograph. A number of radiographs are recorded from the specimen at different angles, covering the full 360°. The radiographs (projections) characterise the cumulative attenuation of the X-ray beam through the specimen. The projections are then used to reconstruct a 3D grey-scale tomogram, which is generally displayed in a 16-bit grey-scale image, in which 65,536 grey values (0, 65,535) are possible.
2.5.2. Image Quality Enhancement
A bimodal intensity histogram is ideal for 2-phase segmentation, where the peaks represent voids and solids. However, realistically, µCT images contain features below instrument resolutions, or at or above the resolution limit but not resolved with the µCT technique, resulting in an intermediate phase. The intermediate phase is mainly due to the partial volume effect [,,] and the averaging generated by the non-zero size of the X-ray focal spot and/or detectors, which causes the material in one voxel to have an effect on its neighbouring voxels []. A comparison between the raw and enhanced images can be found in Figure 5. The raw images usually contain blurry boundaries between phases and features, which can result in inaccurate phase separation. Furthermore, these blurred features are generally distributed heterogeneously across the intensity histogram, making image segmentation challenging. Previous works have demonstrated that coherence-enhanced anisotropic diffusion could satisfactorily enhance the quality of 3D µCT images [,,]. With the anisotropic diffusion (AD) filter, intra-region smoothing is promoted over edge smoothing, and regions with similar grey-scale intensities are connected. Such smoothing sometimes causes image blurring []; thus, it is often followed by an image sharpening or blur removal method. Nevertheless, there is no general routine for image sharpening []. In this study, the unsharp mask (UM) filter [] was applied, following the AD filter, to enhance the quality of the images, which has been previously demonstrated to be able to achieve satisfactory results for 3D µCT images [,,,]. The UM filter is less sensitive to noises in the tomographic image; thus, the high-frequency components are not exaggerated [].

Figure 5.
Comparison of raw image and smoothed image. (a) Raw image from reconstruction; (b) enhanced image after the application of anisotropic diffusion and unsharp mask filters.
2.5.3. Image Segmentation
Image segmentation is the process of labelling the image into well-defined, homogeneous regions (phases), with each phase representing a different class of material. The converging active contour (CAC) method [] was used for image segmentation in this study. The CAC method is based on a combination of the watershed method [] and the active contour method []. It uses the intensity (grey-scale) gradient and intensity information simultaneously [,], which has been demonstrated to be capable of the segmentations of cubic sample images of up to 20003 voxels [,,,,,,,]. The gradient-based segmentation is a well-established technique that has been applied in many fields [,,,,,,,]. It uses the thresholds defined by user or automation (e.g., auto-selection by AI boundary recognition) for object separation and selection, thus allowing for the regions of interest to be further processed [,,,]. The CAC method, as a derived form of gradient-based segmentation, works on two user-defined thresholds based on a detailed inspection of the grey-scale intensity histogram. The voxels with grey-scale intensity values below the lower threshold are tagged as voids, the voxels with grey-scale intensity values higher than the upper threshold are tagged as solids, and the voxels with intermediate grey-scale intensity values are tagged as unallocated. The algorithm simultaneously expands the tagged regions towards each other within the unallocated region. The phase boundaries are eventually placed when the two expanding contours join and stop expanding [,].
Here, using CAC, the Images were segmented into three phases: (1) resolved voids, including the fractures and pores that are resolved using the µCT technique; (2) subresolution pores and fractures that are below the image resolution or exist at or above the resolution but are unresolved by the µCT technique; and (3) solid phase, including both the coal macerals and the mineral matters. Figure 6 shows a grey-scale image and its segmented image. A total of 1356 images (278 (x-axis) × 278 (y-axis) × 800 (z-axis) slices) were used for the 3D rendering of the region of interest on each cake, which correspond to the physical dimension of 2 mm × 2 mm × 5.7 mm. The cake images were first segmented using the MANGO software toolkit developed by the Australian National University, and the 3D visualisations were carried out in AVIZO 3D 2021.2 from Thermo Fisher ScientificTM (Waltham, MA, USA).
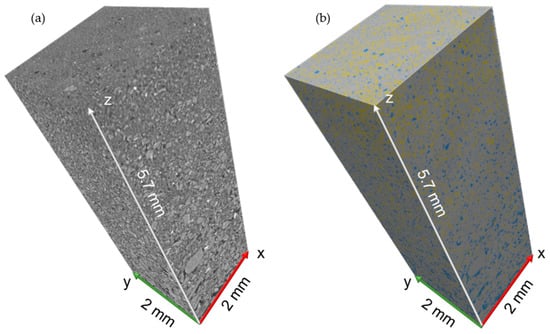
Figure 6.
A 3D visualisation of Digital cake: (a) Grey-scale representation of the cake µCT image, (b) representation of the 3-phase segmented image (blue: resolved pore phase; yellow: subresolution phase; grey: solid phase).
2.5.4. Crack Isolation
The dilation and erosion filters were shown to be effective in the separation of features with different morphologies [,]. In the phase of interest, the erosion filter shrinks the image features and removes features with a radius less than the kernel, whereas the dilation filter expands features, and, thus, the undesired gaps in the image are closed []. Both the erosion and the dilation modules are reiterative, i.e., the repetition of an erosion or dilation of size 1 N times has the same effect as performing a single operation with a structuring element of size N. The morphological operations have been shown to be able to successfully extract fractures from 3D digital rocks []. In this study, morphological operations were used to separate the cracks from pore spaces in the cake. The neighbouring particles around the crack were first removed by the erosion module. Then, the shrunken crack feature was dilated to satisfactorily isolate the crack from the segmented image.
2.5.5. Imaged-Based Cake Analyses
The ratio of the number of voxels in the resolved pore phase to the total number of Digital cake voxels was used to calculate the resolved porosity. Assuming that the intensity (grey-scale value) of each voxel in the intermediate phase was linearly correlated to the void fraction of the voxel, the voxels within the subresolution (intermediate) pore phase were divided into 102 levels, building a porosity map where each voxel in the subresolution pore phase was assigned a porosity value based on a linear interpolation between a minimum and maximum attenuation value corresponding to 100% pore and 100% solid, respectively []. The porosity value assigned to each intermediate grey-scale bin was then used as a microporosity multiplier and applied to all the subresolution voxels to calculate the subresolution porosity. Figure 7 shows how the grey-scale intensity value was converted into the microporosity multiplier, Vpore. The volume fraction of each voxel from the subresolution pore phase needed to be multiplied by the microporosity multiplier to calculate the actual porosity attributed to that voxel.
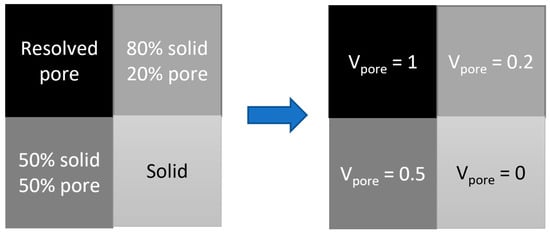
Figure 7.
Illustration of the conversion of the grey-scale intensity to the microporosity multiplier on voxels with resolved and intermediate grey-scale intensities.
On the other hand, the resolved pores that were connected were further analysed by employing the separation function in AVIZO. A marker extending the value of 2 voxels was defined for the pore boundaries. The adjacent faces were set to 6, which evaluates objects (e.g., pores) with 6 neighbouring connected faces that are to be separated. The separated pores were given unique ID values (pore ID) and colour labels. Thus, the unique pore IDs could be used to analyse the distribution of key pore properties, such as the number of pores, pore volume, and pore diameter, as a function of the cake thickness. The distributions of these properties are very difficult to be measured by conventional cake analysis techniques and usually require some degree of destruction in the cake structure.
3. Results and Discussions
3.1. Filter Cake Porosity
Cake porosities (ε), measured by Meeten []’s method, are shown in Table 4, along with the porosity computed from the Digital cakes.

Table 4.
Comparison of the porosity estimated from 2-phase segmentation, 3-phase segmentation, and laboratory estimation.
A good consistency between the porosity computed from the 3-phase segmented Digital cake (the summation of the resolved porosity (2-phase) and the subresolution porosity) and the lab measurements was observed. The inclusion and computation of the subresolution porosity were observed to produce more accurate results than the 2-phase segmentation (Table 4). This is because, with 2-phase segmentation, the only porosity computed was from the resolved porosity, which resulted in a significant underestimation of the porosities of the cakes. This is particularly more pronounced in cake A, which contains a significant fraction of voxels within the intermediate phase. These results are consistent with the observation of Ramandi et al. [], who computed the porosity of a coal lump using the same method. They showed that their imaged-based porosity computation result was in the range of their experimental porosity measurements when they accounted for subresolution porosity.
3.2. Crack Isolation
In the filter cake structure, the pores are formed simultaneously as the particles deposit; hence, the voids primarily represent pores. However, it is possible that the cake becomes fractured due to the mishandling of the sample, such as inadequate solid concentration and pressure or a deformation of the sample during transportation [,,].
As shown in Figure 8, a crack was observed on one of the cake samples (Cake A), which was successfully isolated from the pore space using morphological operations, i.e., erosion–dilation operations. This crack-removal technique is very useful when examining a cake with a macro-crack, i.e., a crack that penetrates across two faces of the cake [,]. This macro-cracking usually occurs due to human error when the sample is mishandled during sampling/transportation. Macro-cracks are usually larger than the micro-crack observed in this study, which could account for a significantly large void space if not removed. Furthermore, cracks are difficult to measure in terms of size, as they might expand within the cake structure. Estimating the size of a crack usually requires a means of destruction for the cake sample [,,,], whereas, with the Digital cake analysis, cracks can be isolated and analysed and also non-destructively removed. In this work, for instance, there was only one micro-crack observed on Cake A, which was found to occupy less than 0.1% of the total cake porosity due to its insignificant size. However, removing the cracks would make the results more accurate, as it is necessary to avoid miscalculating the actual porosity from the pore spaces. Thus, all the porosity analyses shown in this study were shown with the crack fraction excluded from the porosity.
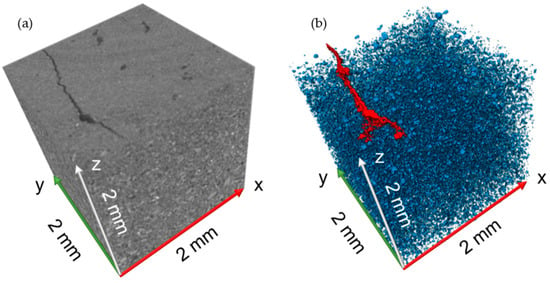
Figure 8.
(a) Crack observed from cake sample A, and (b) a 3D visualisation of the crack and the pores (red: the isolated crack; blue: pores, with coal particles being transparent).
3.3. Porosity Profile
One of the limitations of total porosity measurement, both in the lab and digitally, is that it represents the cake properties as a whole, which may not be representative of the properties of different cake layers due to variations in the cake structure. The Digital cake analysis method allows for an analysis of the variations in porosity across the cake thickness, which can provide structural information that cannot be obtained using conventional methods. Here the porosity along the z-axes was computed for cakes A and B and shown in Figure 9, along with 3D visualisations of the cake specimens. In both cakes, the porosity increases from top to bottom, indicating that the bottom layer of the cake is more porous than the upper section of the cake. Furthermore, the resolved pores were the predominant pore fraction in the lower sections of the cakes, whereas the subresolution pores were relatively more abundant in the upper sections of the cakes. It appears that the pore size decreases as the cake is formed, which aligns with observations from previous works [,,,,].
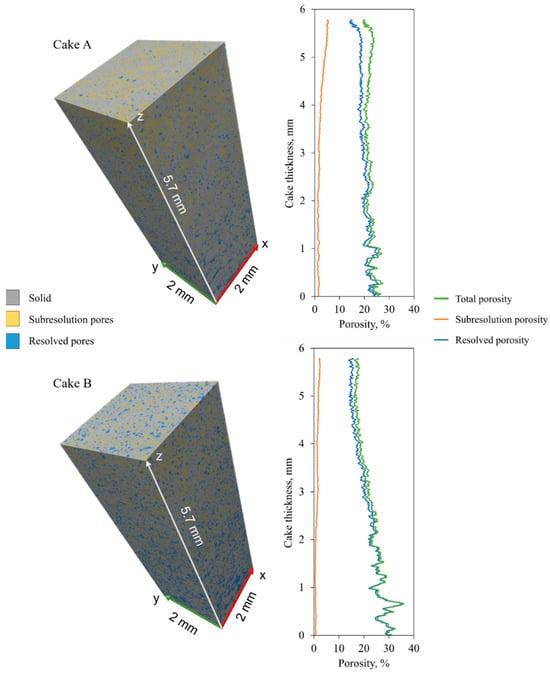
Figure 9.
Different filter cake 3D visualisations and porosity distributions along the z-axis.
It is worth mentioning that, in this study, the subresolution pore phase was exclusively analysed with respect to subresolution porosity (Figure 10). Note that, because the subresolution pore phase obtained from the 3-phase segmentation technique was initially recognised as an individual phase with resolved porosities, it represents the volume fraction of the voxels with intermediate grey-scale intensities and is not directly representative of the actual porosity. Thus, the porosity multiplier values obtained using the microporosity analysis method were used to obtain the corresponding porosities of the subresolution pore phase, which is represented by the orange series in Figure 10. The subresolution pore phase (blue series) is the volume fraction of the intermediate phase from image segmentation, which should be multiplied by the microporosity multiplier to obtain the actual porosity of that phase. In addition, as shown in Figure 10, cake A showed more distinct variations between the subresolution pore phase and the subresolution porosity calculated from the microporosity analysis. The reason is that the image of cake A contains more voxels with intermediate grey-scale intensities, especially at the upper section of the cake. On the other hand, the image of cake B showed a relatively lower divergence between the subresolution pore phase and subresolution porosity, because it contains less voxels with intermediate grey-scale intensities.
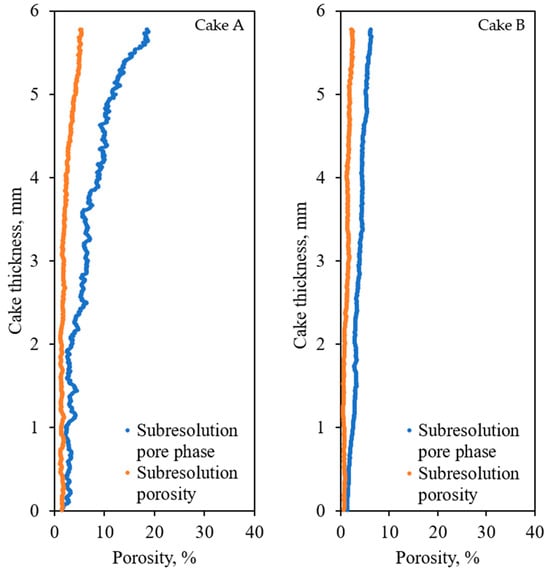
Figure 10.
A comparison of the subresolution pore phase (blue) and the subresolution porosity (orange) with porosity value assigned based on the microporosity analysis for cakes A and B.
As previously mentioned, some studies used a 2-phase segmentation technique to separate the pore phase and the solid phase [,], which might be acceptable for images that contain an insignificant fraction of subresolution pores. However, the Digital cake analysis used in this work granted higher accuracy in porosity analysis. Figure 11 shows the percentage error in the porosity estimation in comparison to the experimental measurements. The error shown in Figure 11 represents the cumulative error based on the fraction of pores on voxels with intermediate grey-scale intensities. The fraction of the pore space was calculated by first analysing the grey-scale histogram of the image. As previously mentioned, the intermediate grey-scale intensities were split into 102 bins, and the percentage of the pore in each bin could be calculated by applying the microporosity multiplier assigned to each bin. Then, the cumulative error was calculated based on the difference of porosity estimation with the application of the microporosity multiplier and experimental value. It can be seen that the cumulative error in porosity was reduced when there was a higher fraction of pore in the subresolution voxels. For example, at about a 10% pore fraction, the estimation error would be relatively large compared to the porosity measured at around −5% for both cakes. As the pore fraction increases, the error simultaneously reduces. When the full range of the intermediate grey-scale intensity was calibrated, the estimation error was reduced to around ±3% in both cakes. However, it is worth mentioning that the fraction of grey-scale intensity is not only subjected to the material type but also the quality of the image and the scanning configuration. For example, a significant amount of subresolution pores were observed in Cake A. These pores are of small sizes and mostly distributed within the 0 to 20% porosity range (x-axis in Figure 11). Thus the error observed within this range showed more variance, as these voxels actually do not possess “full porosity”. On the other hand, for Cake B, there are less subresolution pores, which are more evenly distributed across the grey-scale intensity range; thus, the error was found to be less significant and the change in the error was found to be smoother. With a limited number of samples, a generalised standard cannot be provided here in this study. Nonetheless, almost all of the µCT images contain the subresolution phase (intermediate grey-scale voxels). This phase is unavoidable and should not be neglected in analysis. The technique presented in this study can be a valuable tool for accurately analysing the intermediate phase. More importantly, the technique is not only applicable to Digital cakes but also to images of all other materials.
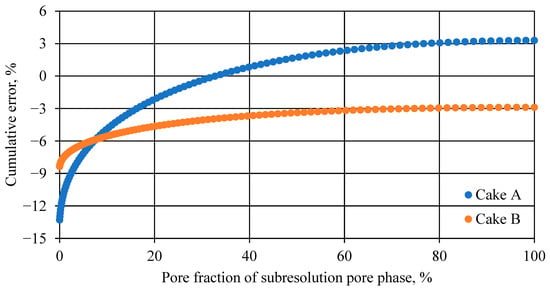
Figure 11.
Changes in porosity estimation errors against the fraction of pore in the subresolution pore phase.
The results from the microporosity analysis indicate that, as the cake formation continues, a smaller proportion of the sub-resolution phase contains pore spaces—i.e., finer pores exist at the top section of the cake so that the majority of each sub-resolution voxel contains solids. Again, this is in agreement with previous works indicating the dominance of finer pores in the upper section, which occupied available spaces within the cake structure and limited the formation of larger pores [,,]. The results also demonstrated the great capacity of Digital cake analysis for detailed structural analysis and the providing of new insights into cake formation. With the properly segmented Digital cake, more advanced analysis can be carried out. For example, the connected pores can be separated and further analysed pore by pore. The distribution of the separated pores (resolved only) from the two cakes obtained from this study can be found in Figure 12. To differentiate each separated pore from one another, a distinct colour was assigned to each pore based on the pore ID. It should be clarified that the colour labelling of the pores is only used for distinguishing separated pores. There are no properties associated with colour code; thus, a code is not provided in Figure 12. It is possible to observe that the pore distributions were different between the two cake samples, which could be attributed to the cake formation mechanisms, as larger pores are formed from the flocculation treatment applied to sample B. The increased particle size resulted in the cake containing larger pores; thus, more resolved pores could be recognised during imaging. With the pores separated and labelled, the number of connected resolved pores on each cake sample across the cake thickness could be computed. It was found that most of the resolved pores were distributed at the lower section of Cake A, since the void spaces at the upper section of Cake A were mainly sub-resolved pores. On the other hand, resolved pores were more evenly distributed on Cake B. The difference in the pore distribution is due to the size of the pores, as Cake A mostly contained fine pores with subresolution porosity, and Cake B contained a greater number of larger pores with resolved resolution.
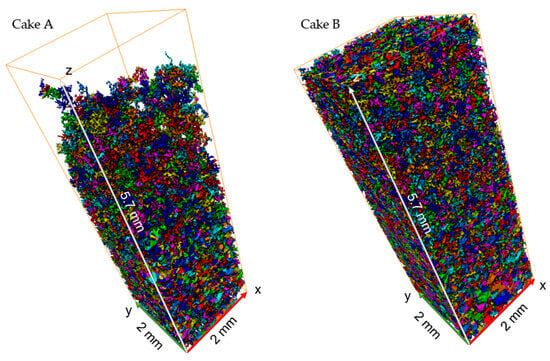
Figure 12.
A 3D visualisation of the separated resolved pores for cakes A and B.
Digital cake analysis showed a great capability for extracting useful structural information from the digitally restored cake sample. Digital cake analysis encompassed both the resolved pores and subresolution pores, a feat that conventional cake analysis techniques cannot achieve. With the applied image segmentation technique, it was possible to accurately calculate the porosity, pore size distribution, and properties of the pores, marking a significant advancement in our current understanding of cake structure. Although this work only demonstrated the means of image segmentation and extraction of some basic cake structure, there is great potential for future development. Moreover, the interactive rendering and visualization of the cake structure facilitated an easy identification of features and optimization of segmentation techniques. Some other advanced analyses, such as pore shape analysis, pore size analysis, pore surface area analysis, pore network modelling, and fluid flow simulation could be very beneficial for relevant research fields. Nonetheless, this current study is focused on introducing a technique for obtaining Digital cake and accurately conducting image segmentation and porosity estimation. An analysis of the segmented images could provide a significant amount of information and is worth a full publication of its own; therefore, it will not be further elaborated here and will be presented in another study that the authors are currently working on.
4. Conclusions
This study aimed to present a non-destructive methodology for analysing the pore structure of filtration cakes composed of fine particles. To achieve this goal, a novel technique called Digital cake analysis was employed. This technique involved using a 3-phase segmentation of filter cake images obtained from µCT imaging, followed by the computation of the segmented cake image with porosity and pore-scale analyses. Two filter cake samples obtained from different slurry conditions were studied in this work, with experimental measurements taken and then analysed using the Digital cake analysis technique. It was possible to successfully demonstrate the accuracy of the Digital cake analysis technique, as it demonstrated very good consistency with laboratory measurements.
The 3-phase segmentation method is more accurate in determining porosity compared to the 2-phase method due to its ability to address the limitations of CT imaging (i.e., some voxels on the scanned image are only partially void or below the maximum resolution of the image). Therefore, using the 2-phase segmentation would result in either overestimating or underestimating the porosity. The 3-phase segmentation method assigns microporosity values to voxels with intermediate grey-scale intensities, resulting in higher accuracy. While the structural information from the 3-phase Digital cake may not be as detailed as advanced nano-scale techniques, it offers advantages in efficiency, larger sample size, and relatively high accuracy. The Digital cake analysis technique is also capable of identifying and, if needed, eliminating structural defects from the sample image. In this study, one of the cakes had a micro-crack on its surface. Although the crack only minimally affected porosity, its removal could enhance porosity estimation and aid subsequent analyses. Given that the occurrence and size of such cracks are unpredictable, and they may not be visible from the outside, the crack removal technique introduced here could be a valuable tool when undertaking Digital cake analysis (extendable to other types of sample, e.g., lumps and cores), allowing the user to eliminate undesired defects. Pore distribution and pore size analyses provided deeper insights into the structure of filtration cakes, providing valuable information on liquid extraction and the impact of chemical reagents on filtration responses.
Author Contributions
Conceptualization, S.A., G.B. and H.L.R.; methodology, F.Z.; data curation; F.Z. and H.L.R.; formal analysis, F.Z.; validation, F.Z. and H.L.R.; writing—original draft preparation, F.Z.; writing—review and editing, S.A., G.B. and H.L.R.; resources, S.A.; funding acquisition, S.A.; project administration, S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by ACARP grant number [C26013x].
Data Availability Statement
Data is contained within the article.
Acknowledgments
The authors would like to thank ACARP for funding this project, providing the samples, and sharing knowledge on industrial practices.
Conflicts of Interest
The authors confirm that there are no personal circumstances or interest that may be perceived as inappropriately influencing the representation or interpretation of reported research results.
References
- Lin, C.; Miller, J. Pore structure and network analysis of filter cake. Chem. Eng. J. 2000, 80, 221–231. [Google Scholar] [CrossRef]
- Tien, C.; Ramarao, B.V. Can filter cake porosity be estimated based on the Kozeny–Carman equation? Powder Technol. 2013, 237, 233–240. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Xia, W.; Xie, G. Filtration of kaolinite and coal mixture suspension: Settling behavior and filter cake structure analysis. Powder Technol. 2021, 381, 122–128. [Google Scholar] [CrossRef]
- Condie, D.J.; Hinkel, M.; Veal, C.J. Modelling the vacuum filtration of fine coal. Filtr. Sep. 1996, 33, 825–834. [Google Scholar] [CrossRef]
- Feng, Z.; Fan, Y.; Dong, X.; Ma, X.; Chen, R. Permeability estimation in filter cake based on X-ray microtomography and Lattice Boltzmann method. Sep. Purif. Technol. 2021, 275, 119114. [Google Scholar] [CrossRef]
- Kozeny, J. Uber kapillare leitung der wasser in boden. R. Acad. Sci. Vienna Proc. Cl. I 1927, 136, 271–306. [Google Scholar]
- Carman, P. Fundamental principles of industrial filtration (A critical review of present knowledge). Trans. Inst. Chem. Eng. 1938, 16, 168–188. [Google Scholar]
- Carman, P.C. Fluid flow through granular beds. Trans. Inst. Chem. Eng. 1937, 15, 150–166. [Google Scholar] [CrossRef]
- Tien, C. Introduction to Cake Filtration: Analyses, Experiments and Applications; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Esser, S.; Löwer, E.; Peuker, U. Network model of porous media–Review of old ideas with new methods. Sep. Purif. Technol. 2021, 257, 117854. [Google Scholar] [CrossRef]
- Foley, G. A review of factors affecting filter cake properties in dead-end microfiltration of microbial suspensions. J. Membr. Sci. 2006, 274, 38–46. [Google Scholar] [CrossRef]
- Pirard, R.; Alié, C.; Pirard, J.-P. Porosimetry: Collapse and Intrusion. In Handbook of Sol-Gel Science and Technology; 2. Characterization and properties of sol-gel materials and products; Springer Science & Business Media: New York, NY, USA, 2005; Volume 2, p. 211. [Google Scholar]
- Lawrence, G. Measurement of pore sizes in fine-textured soils: A review of existing techniques. J. Soil Sci. 1977, 28, 527–540. [Google Scholar] [CrossRef]
- Meeten, G. A dissection method for analysing filter cakes. Chem. Eng. Sci. 1993, 48, 2391–2398. [Google Scholar] [CrossRef]
- Wildenschild, D.; Sheppard, A.P. X-ray imaging and analysis techniques for quantifying pore-scale structure and processes in subsurface porous medium systems. Adv. Water Resour. 2013, 51, 217–246. [Google Scholar] [CrossRef]
- Sheppard, A.P.; Sok, R.M.; Averdunk, H. Techniques for image enhancement and segmentation of tomographic images of porous materials. Phys. A Stat. Mech. Its Appl. 2004, 339, 145–151. [Google Scholar] [CrossRef]
- Yang, B.; Wu, A.; Miao, X.; Liu, J. 3D characterization and analysis of pore structure of packed ore particle beds based on computed tomography images. Trans. Nonferrous Met. Soc. China 2014, 24, 833–838. [Google Scholar] [CrossRef]
- Mathews, J.P.; Campbell, Q.P.; Xu, H.; Halleck, P. A review of the application of X-ray computed tomography to the study of coal. Fuel 2017, 209, 10–24. [Google Scholar] [CrossRef]
- Ramandi, H.L.; Mostaghimi, P.; Armstrong, R.T.; Saadatfar, M.; Pinczewski, W.V. Porosity and permeability characterization of coal: A micro-computed tomography study. Int. J. Coal Geol. 2016, 154, 57–68. [Google Scholar] [CrossRef]
- Fan, Y.; Ma, X.; Dong, X.; Feng, Z.; Dong, Y. Characterisation of floc size, effective density and sedimentation under various flocculation mechanisms. Water Sci. Technol. 2020, 82, 1261–1271. [Google Scholar] [CrossRef]
- Li, Y.; Xia, W.; Wen, B.; Xie, G. Filtration and dewatering of the mixture of quartz and kaolinite in different proportions. J. Colloid Interface Sci. 2019, 555, 731–739. [Google Scholar] [CrossRef]
- Feng, Z.; Dong, X.; Fan, Y.; Li, H.; Dong, Y.; Ma, X.; Chen, R. Use of X-ray microtomography to quantitatively characterize the pore structure of three-dimensional filter cakes. Miner. Eng. 2020, 152, 106275. [Google Scholar] [CrossRef]
- Ramandi, H.L.; Mostaghimi, P.; Armstrong, R.T. Digital rock analysis for accurate prediction of fractured media permeability. J. Hydrol. 2017, 554, 817–826. [Google Scholar] [CrossRef]
- Andrews, J.C.; Almeida, E.; van der Meulen, M.C.; Alwood, J.S.; Lee, C.; Liu, Y.; Chen, J.; Meirer, F.; Feser, M.; Gelb, J. Nanoscale X-ray microscopic imaging of mammalian mineralized tissue. Microsc. Microanal. 2010, 16, 327–336. [Google Scholar] [CrossRef] [PubMed]
- Peyrin, F. Investigation of bone with synchrotron radiation imaging: From micro to nano. Osteoporos. Int. 2009, 20, 1057–1063. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Sun, Y.; Yuan, L.; Xu, Q. Impact of nanopore structure on coal strength: A study based on synchrotron radiation nano-CT. Results Phys. 2020, 17, 103029. [Google Scholar] [CrossRef]
- Zhao, Y.; Peng, L.; Liu, S.; Cao, B.; Sun, Y.; Hou, B. Pore structure characterization of shales using synchrotron SAXS and NMR cryoporometry. Mar. Pet. Geol. 2019, 102, 116–125. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, Y.; Liu, S.; Chen, Z.; Yuan, L. Pore structure characterization of coal by synchrotron radiation nano-CT. Fuel 2018, 215, 102–110. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, S.; Elsworth, D.; Jiang, Y.; Zhu, J. Pore Structure Characterization of Coal by Synchrotron Small-Angle X-ray Scattering and Transmission Electron Microscopy. Energy Fuels 2014, 28, 3704–3711. [Google Scholar] [CrossRef]
- Sørensen, B.L.; Sørensen, P.B. Structure compression in cake filtration. J. Environ. Eng. 1997, 123, 345–353. [Google Scholar] [CrossRef]
- Stamatakis, K.; Tien, C. Cake formation and growth in cake filtration. Chem. Eng. Sci. 1991, 46, 1917–1933. [Google Scholar] [CrossRef]
- Kakwani, R.M.; Gala, H.B.; Chiang, S.H.; Klinzing, G.E.; Tierney, J.W. Dewatering of fine coal—Micrographic analysis of filter cake structure. Powder Technol. 1985, 41, 239–250. [Google Scholar] [CrossRef]
- Shirato, M.; Aragaki, T.; Ichimura, K.; Norio, O. Porosity variation in filter cake under constant-pressure filtration. J. Chem. Eng. Jpn. 1971, 4, 172–177. [Google Scholar] [CrossRef]
- Bournival, G.; Yoshida, M.; Cox, N.; Lambert, N.; Ata, S. Analysis of a coal preparation plant. Part 1. Changes in water and coal quality, coal seam, and plant performance. Fuel Process. Technol. 2019, 190, 67–80. [Google Scholar] [CrossRef]
- Manono, M.S.; Corin, K.; Wiese, J. Water quality effects on a sulfidic PGM ore: Implications for froth stability and gangue management. Physicochem. Probl. Miner. Process. 2018, 54, 1253–1265. [Google Scholar]
- Varslot, T.; Kingston, A.; Myers, G.; Sheppard, A. Considerations for high-magnification high-cone-angle helical micro-CT. In Developments in X-ray Tomography VIII; SPIE: Bellingham, WA, USA, 2012; pp. 259–268. [Google Scholar]
- Latham, S.J.; Kingston, A.M.; Recur, B.; Myers, G.R.; Sheppard, A.P. Multi-resolution radiograph alignment for motion correction in x-ray micro-tomography. In Developments in X-ray Tomography X; SPIE: Bellingham, WA, USA, 2016; pp. 50–61. [Google Scholar]
- Wildenschild, D.; Vaz, C.M.P.; Rivers, M.L.; Rikard, D.; Christensen, B.S.B. Using X-ray computed tomography in hydrology: Systems, resolutions, and limitations. J. Hydrol. 2002, 267, 285–297. [Google Scholar] [CrossRef]
- Worden, R.H. A Review of Particle Size Analysis with X-ray CT. Materials 2023, 16, 1259. [Google Scholar]
- Ketcham, R.A. Computational methods for quantitative analysis of three-dimensional features in geological specimens. Geosphere 2005, 1, 32–41. [Google Scholar] [CrossRef]
- Karimpouli, S.; Tahmasebi, P.; Ramandi, H.L. A review of experimental and numerical modeling of digital coalbed methane: Imaging, segmentation, fracture modeling and permeability prediction. Int. J. Coal Geol. 2020, 228, 103552. [Google Scholar] [CrossRef]
- Weickert, J. Coherence-enhancing diffusion filtering. Int. J. Comput. Vis. 1999, 31, 111–127. [Google Scholar] [CrossRef]
- Frangakis, A.S.; Hegerl, R. Noise reduction in electron tomographic reconstructions using nonlinear anisotropic diffusion. J. Struct. Biol. 2001, 135, 239–250. [Google Scholar] [CrossRef]
- Pratt, W.K. Introduction To Digital Image Processing; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Ramandi, H.L.; Liu, M.; Tadbiri, S.; Mostaghimi, P. Impact of dissolution of syngenetic and epigenetic minerals on coal permeability. Chem. Geol. 2018, 486, 31–39. [Google Scholar] [CrossRef]
- Sakellariou, A.; Arns, C.H.; Sheppard, A.P.; Sok, R.M.; Averdunk, H.; Limaye, A.; Jones, A.C.; Senden, T.J.; Knackstedt, M.A. Developing a virtual materials laboratory. Mater. Today 2007, 10, 44–51. [Google Scholar] [CrossRef]
- Vincent, L.; Soille, P. Watersheds in digital spaces: An efficient algorithm based on immersion simulations. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 583–598. [Google Scholar] [CrossRef]
- Caselles, V.; Kimmel, R.; Sapiro, G. Geodesic active contours. Int. J. Comput. Vis. 1997, 22, 61–79. [Google Scholar] [CrossRef]
- Schlüter, S.; Sheppard, A.; Brown, K.; Wildenschild, D. Image processing of multiphase images obtained via X-ray microtomography: A review. Water Resour. Res. 2014, 50, 3615–3639. [Google Scholar] [CrossRef]
- Golab, A.; Ward, C.R.; Permana, A.; Lennox, P.; Botha, P. High-resolution three-dimensional imaging of coal using microfocus X-ray computed tomography, with special reference to modes of mineral occurrence. Int. J. Coal Geol. 2013, 113, 97–108. [Google Scholar] [CrossRef]
- Qajar, J.; Francois, N.; Arns, C.H. Microtomographic characterization of dissolution-induced local porosity changes including fines migration in carbonate rock. SPE J. 2013, 18, 545–562. [Google Scholar] [CrossRef]
- Ramandi, H.L.; Armstrong, R.T.; Mostaghimi, P.; Saadatfar, M.; Pinczewsk, W.V. X-ray micro-computed tomography imaging for coal characterization. In SPE Asia Pacific Unconventional Resources Conference and Exhibition; OnePetro: Richardson, TX, USA, 2015. [Google Scholar]
- Saadatfar, M.; Francois, N.; Arad, A.; Madadi, M.; Cruikshank, R.; Alizadeh, M.; Sheppard, A.; Kingston, A.; Limay, A.; Senden, T. 3D mapping of deformation in an unconsolidated sand: A micro mechanical study. In SEG Technical Program Expanded Abstracts 2012; Society of Exploration Geophysicists: Houston, TX, USA, 2012; pp. 1–6. [Google Scholar]
- Saadatfar, M.; Mukherjee, M.; Madadi, M.; Schröder-Turk, G.; Garcia-Moreno, F.; Schaller, F.; Hutzler, S.; Sheppard, A.; Banhart, J.; Ramamurty, U. Structure and deformation correlation of closed-cell aluminium foam subject to uniaxial compression. Acta Mater. 2012, 60, 3604–3615. [Google Scholar] [CrossRef]
- Sok, R.M.; Varslot, T.; Ghous, A.; Latham, S.; Sheppard, A.P.; Knackstedt, M.A. Pore scale characterization of carbonates at multiple scales: Integration of micro-CT, BSEM, and FIBSEM. Petrophysics 2010, 51, 379–387. [Google Scholar]
- Miletić, M.; Kumar, L.M.; Arns, J.-Y.; Agarwal, A.; Foster, S.J.; Arns, C.; Perić, D. Gradient-based fibre detection method on 3D micro-CT tomographic image for defining fibre orientation bias in ultra-high-performance concrete. Cem. Concr. Res. 2020, 129, 105962. [Google Scholar] [CrossRef]
- Alhammadi, A.M.; Gao, Y.; Akai, T.; Blunt, M.J.; Bijeljic, B. Pore-scale X-ray imaging with measurement of relative permeability, capillary pressure and oil recovery in a mixed-wet micro-porous carbonate reservoir rock. Fuel 2020, 268, 117018. [Google Scholar] [CrossRef]
- Hermanek, P.; Rathore, J.S.; Aloisi, V.; Carmignato, S. Principles of X-ray computed tomography. In Industrial X-ray Computed Tomography; Springer: Berlin/Heidelberg, Germany, 2018; pp. 25–67. [Google Scholar]
- Baveye, P.C.; Pot, V.; Garnier, P. Accounting for sub-resolution pores in models of water and solute transport in soils based on computed tomography images: Are we there yet? J. Hydrol. 2017, 555, 253–256. [Google Scholar] [CrossRef]
- Shah, S.; Gray, F.; Crawshaw, J.; Boek, E. Micro-computed tomography pore-scale study of flow in porous media: Effect of voxel resolution. Adv. Water Resour. 2016, 95, 276–287. [Google Scholar] [CrossRef]
- Herrmann, H.; Pastorelli, E.; Kallonen, A.; Suuronen, J.-P. Methods for fibre orientation analysis of X-ray tomography images of steel fibre reinforced concrete (SFRC). J. Mater. Sci. 2016, 51, 3772–3783. [Google Scholar] [CrossRef]
- Michael, G. X-ray computed tomography. Phys. Educ. 2001, 36, 442. [Google Scholar] [CrossRef]
- Serra, J. Introduction to mathematical morphology. Comput. Vis. Graph. Image Process. 1986, 35, 283–305. [Google Scholar] [CrossRef]
- Quackenbush, L.J. A review of techniques for extracting linear features from imagery. Photogramm. Eng. Remote Sens. 2004, 70, 1383–1392. [Google Scholar] [CrossRef]
- Wiedemann, T.; Stahl, W. Experimental investigation of the shrinkage and cracking behaviour of fine participate filter cakes. Chem. Eng. Process. 1996, 35, 35–42. [Google Scholar] [CrossRef]
- Anlauf, H.; Bott, R.; Stahl, W.; Krebber, A. The formation of shrinkage cracks in filter cakes during dewatering of fine sized ores. Alc~ Ereit~ Mgstechnik 1985, 4, 188–196. [Google Scholar]
- Wakeman, R. The role of internal stresses in filter cake cracking. Filtr. Sep. 1974, 11, 357–360. [Google Scholar]
- Pham, T.H. Experimental Investigation on Crack Formation in Filter Cakes with Wide Particle Size Distribution. Maschinenbau, Verfahrens- Und Energietechnik. Ph.D. Thesis, Technische Universität Bergakademie Freiberg, Freiberg, Germany, 2021. [Google Scholar]
- Barua, A.; Eagles, W.; Giorgio, G.; Ricard, F.; Stepanek, F. Experimental Study of Filter Cake Cracking during Deliquoring. Sci. Pharm. 2010, 78, 661. [Google Scholar] [CrossRef]
- Zhuo, Q.; Liu, W.; Xu, H.; Wang, D. Effect of particle size distribution on filter cake pore structure and coal slurry dewatering process. Int. J. Coal Prep. Util. 2020, 42, 1879–1894. [Google Scholar] [CrossRef]
- Hu, P.; Liang, L.; Xie, G.; Zhou, S.; Peng, Y. Effect of slurry conditioning on flocculant-aided filtration of coal tailings studied by low-field nuclear magnetic resonance and X-ray micro-tomography. Int. J. Min. Sci. Technol. 2020, 30, 859–864. [Google Scholar] [CrossRef]
- Hieke, M.; Ruland, J.; Anlauf, H.; Nirschl, H. Analysis of the porosity of filter cakes obtained by filtration of colloidal suspensions. Chem. Eng. Technol. Ind. Chem.-Plant Equip.-Process Eng.-Biotechnol. 2009, 32, 1095–1101. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).