Simulation and Validation of Discrete Element Parameter Calibration for Fine-Grained Iron Tailings
Abstract
1. Introduction
2. Experiments to Calibrate Parameters
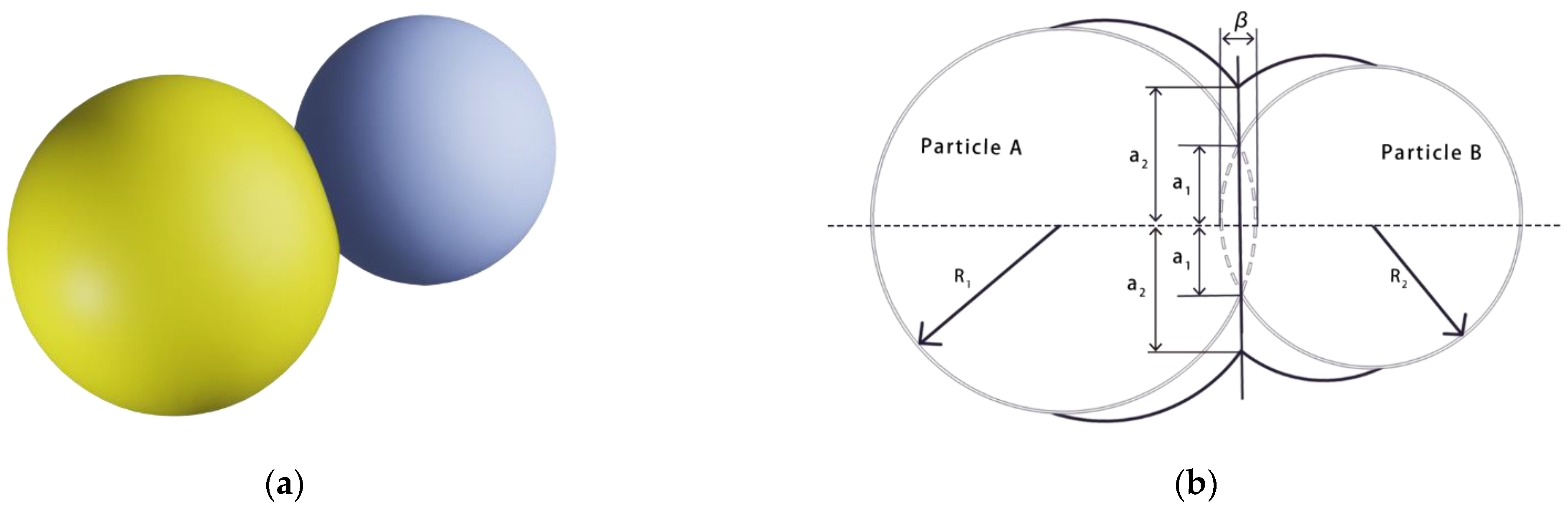
2.1. JKR Contact Discrete Element Model
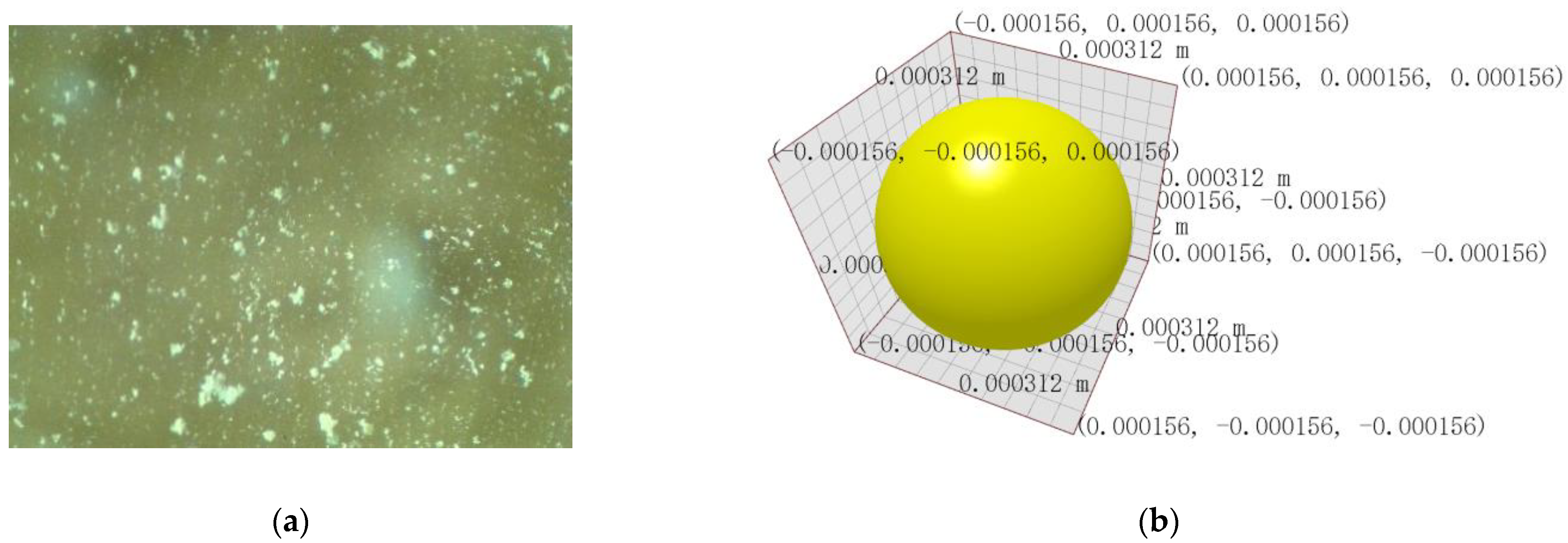
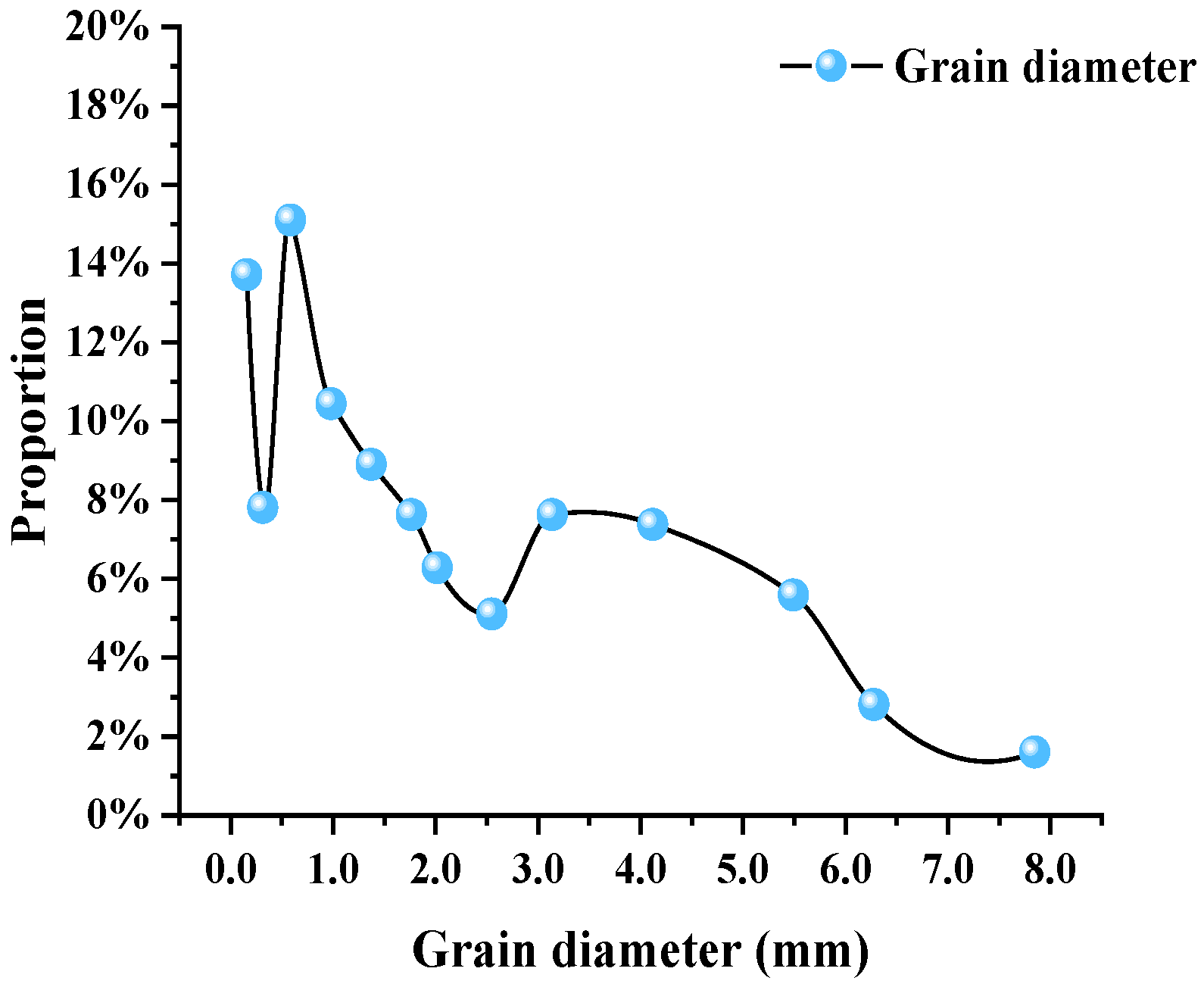
2.2. Sizing for Discrete Element Models
2.3. Determination of the Angle of Repose
2.4. Particle Modeling with Discrete Elements
3. Designing and Analyzing Studies for Parameter Calibration
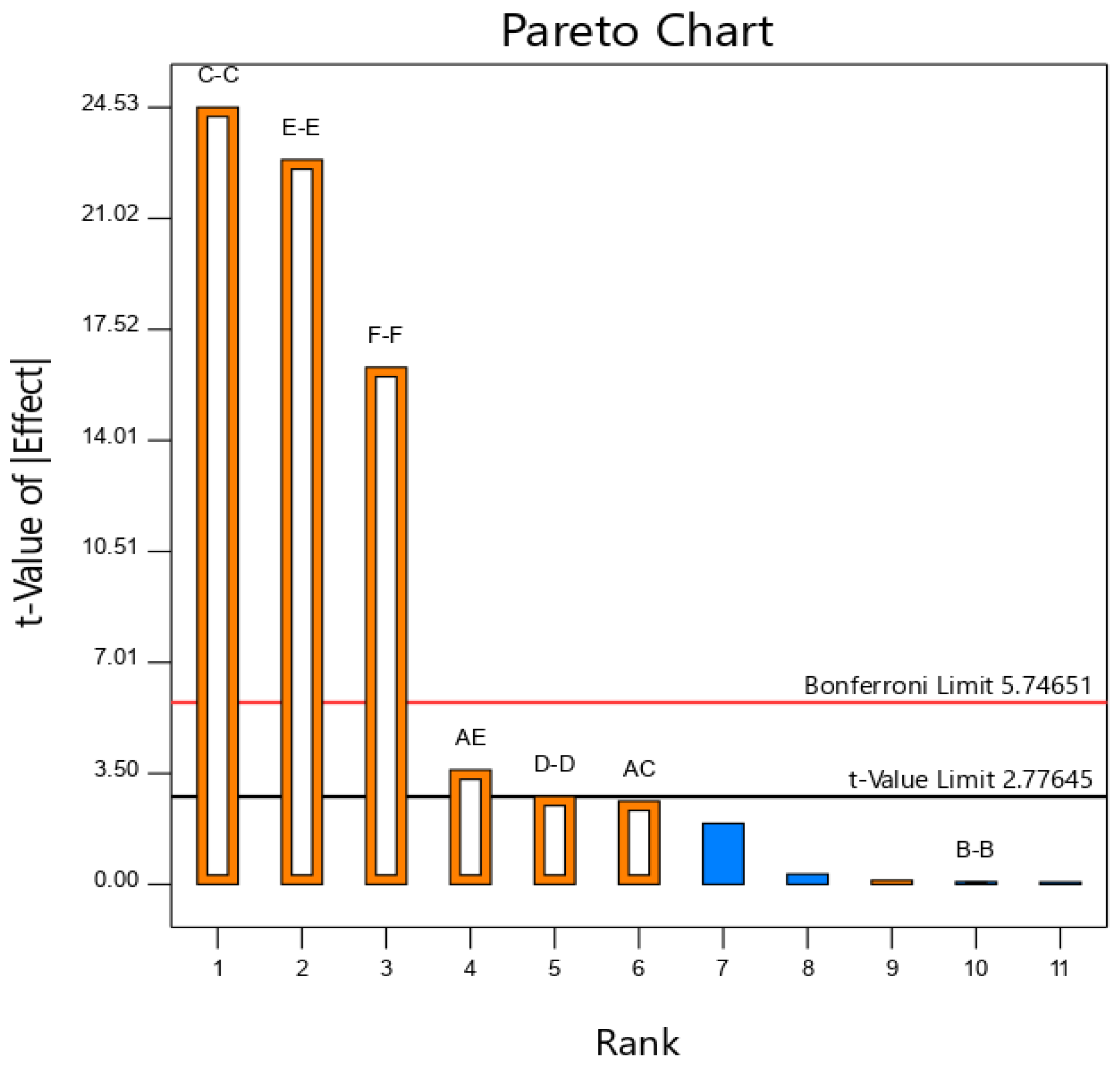
3.1. Plackett-Burman Experimental Design Importance
3.2. Box-Behnken Response Surface Analysis
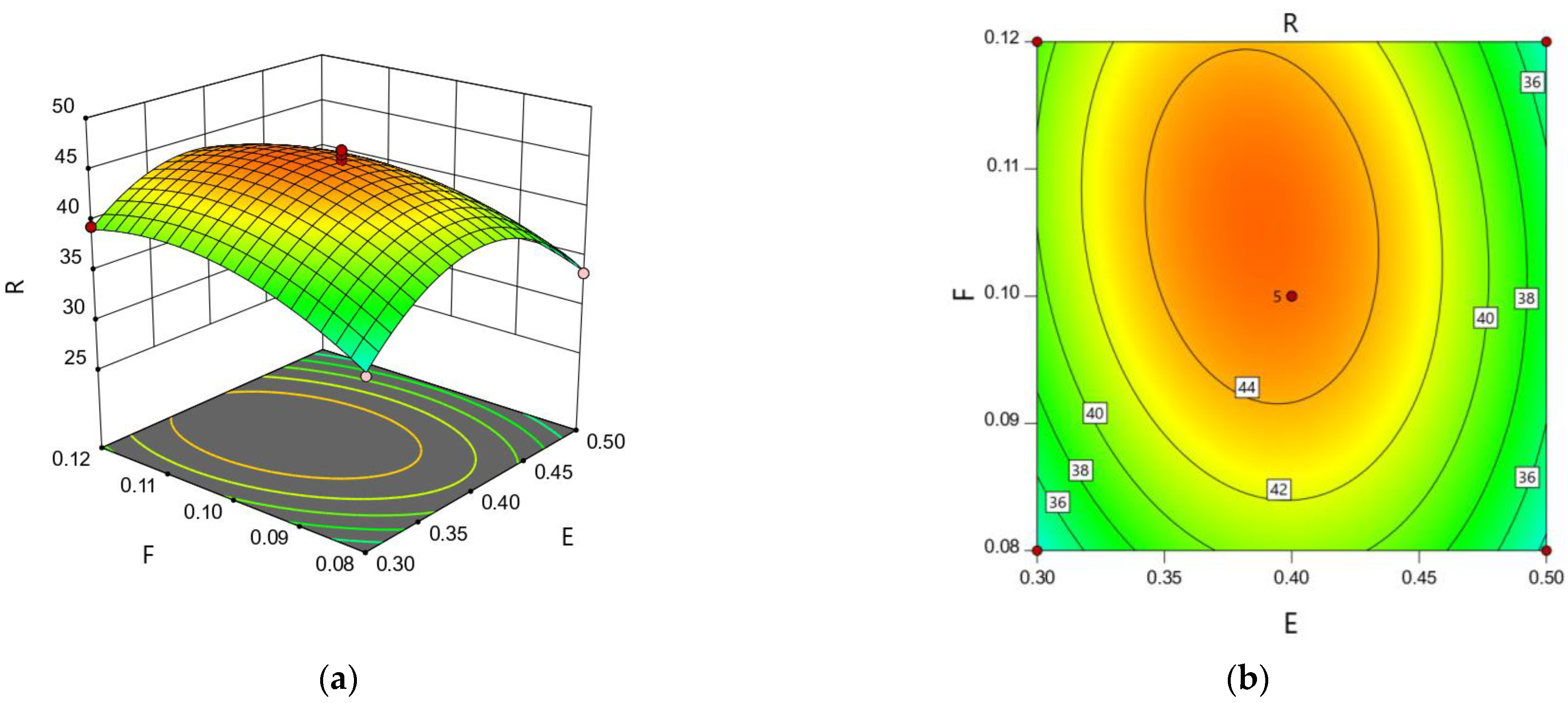
3.3. Regression Model Interaction Effect Analysis
4. Determination of the Optimal Combination of Parameters and Validation of the Simulation
5. Conclusions
- (1)
- The computational performance of the numerical simulation was improved by increasing the discrete element of fine-grained iron tailings’ particle size by 1.959708 mm, with an average particle size of 24.15 um, and using 500,000 particles as the maximum.
- (2)
- The contact characteristics of the amplified particles were calibrated using the JKR contact model in discrete elements. The Plackett-Burman tests were used to determine the factors that significantly affect the resting angle of the amplified particles of microfine-grained iron tailings. These factors included the surface energy JKR coefficient, particle-particle static friction coefficient and particle-particle dynamic friction coefficient.
- (3)
- The Box-Behnken test revealed that, in contrast to the simulated particle rest angle of 44.81° for fine-grained iron tailings particles at 0.459, 0.393 and 0.106, respectively, the relative error of the surface energy JKR coefficient, particle-particle static friction coefficient and particle-particle kinetic friction coefficient in the EDEM discrete element software was only 2.18%; this proves the viability of response surface experiments for the discrete element particle system. It was shown that it was possible to calibrate the particle coefficients for discrete elements.
- (4)
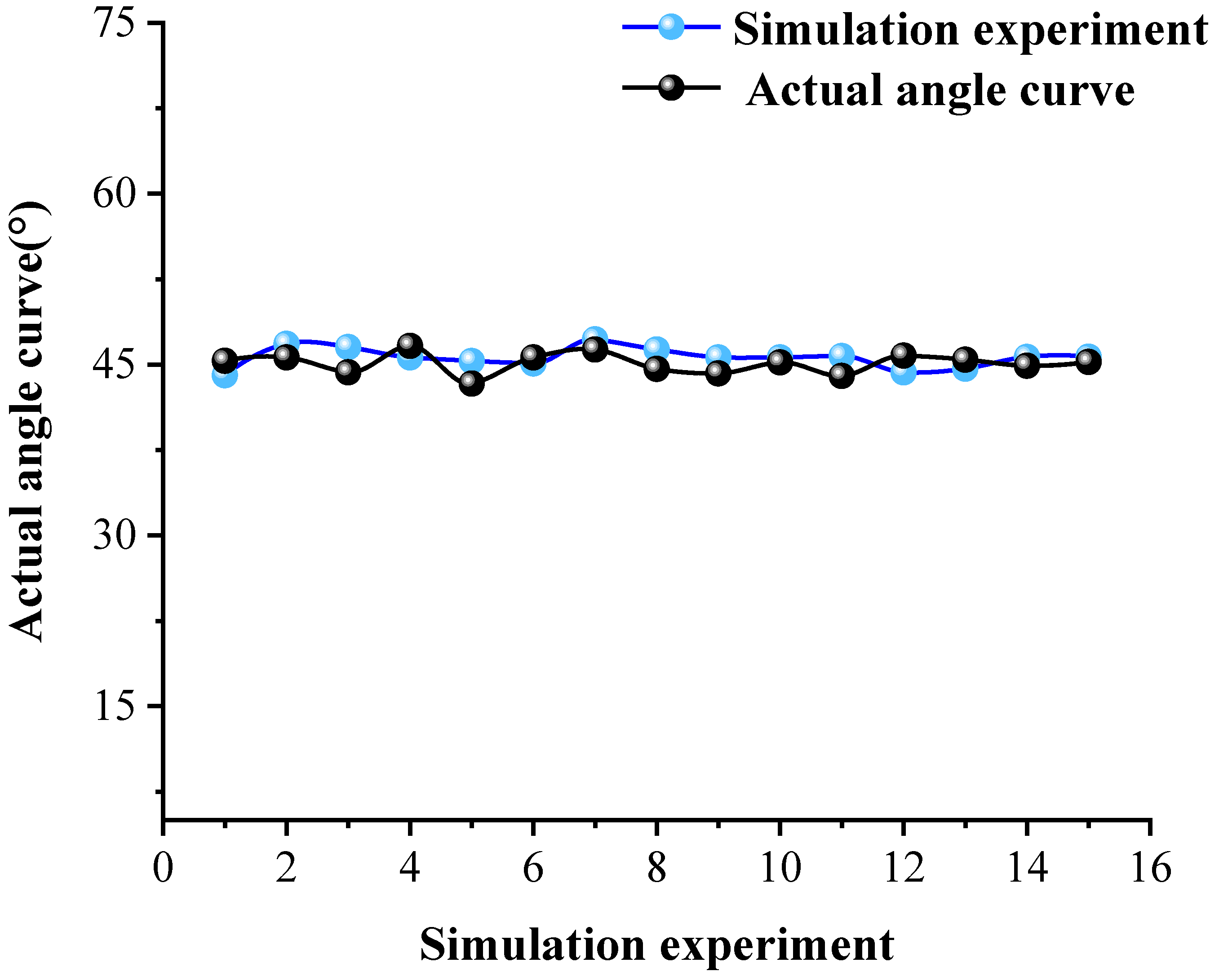
- The best experimentally obtained parameters were entered into discrete element software, where the mean resting angle was calculated to be 45.823°. This was compared to the mean angle from physical experiments, which was 45.119°, and the error was calculated to be 1.56%, which was not significantly different. This proves that the contact parameters obtained from the particle size scaling coefficient calibration trials satisfy the numerical simulation’s requirements, and serve as a reference for the discrete element model used to simulate the numerical behavior of fine-grained iron tailings particles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, J. Discussion on comprehensive utilization technology of tailings. Copp. Eng. 2021, 167, 45–47. [Google Scholar]
- Shi, X.; Du, G.; Zhang, M.; Du, J.; Gao, J. Problems and suggestions of tailings comprehensive utilization industry. Mod. Min. 2022, 38, 38–40+44. [Google Scholar]
- Zhang, J.; Zhu, L. Characterization of heavy metal pollution in tin mine tailing ponds. Min. Metall. 2022, 31, 122–126. [Google Scholar]
- Ren, M.; Xie, X.; Li, B.; Hu, S.; Chen, T.; Zhu, H.; Tong, X. Research progress of comprehensive utilization of iron tailings. Miner. Conserv. Util. 2022, 42, 155–168. [Google Scholar] [CrossRef]
- Fu, Y.; Hou, Y.; Wang, R.; Wang, Y.; Yang, X.; Dong, Z.; Liu, J.; Man, X.; Yin, W.; Yang, B.; et al. Detailed insights into improved chlorite removal during hematite reverse flotation by sodium alginate. Miner. Eng. 2021, 173, 107191. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, Q.; Sun, Y.; Gao, P.; Han, Y. Pilot-scale extraction of iron from flotation tailings via suspension magnetization roasting in a mixture of CO and H2 followed by magnetic separation. Resour. Conserv. Recycl. 2021, 172, 105680. [Google Scholar] [CrossRef]
- Nakamura, H.; Fujii, H.; Watano, S. Scale-up of high shear mixer-granulator based on discrete element analysis. Powder Technol. 2013, 236, 149–156. [Google Scholar] [CrossRef]
- Kim, K.C.; Jiang, T.; Kim, N.I.; Kwon, C. Effects of ball-to-powder diameter ratio and powder particle shape on EDEM simulation in a planetary ball mill. J. Indian Chem. Soc. 2022, 99, 100300. [Google Scholar] [CrossRef]
- Han, W.; Wang, S.Z.; Zhang, Q.; Tian, Y.H. Parameter calibration of discrete elements for micron-sized particles based on JKR contact model. China Powder Technol. 2021, 27, 60–69. [Google Scholar] [CrossRef]
- Han, Z.; Shi, W.; Xiao, Y.; Li, L. Linear Adhesive Contact Analysis of Rough Cylindrical Surface Based on JKR Model. J. Mech. Eng. 2016, 52, 116–122. [Google Scholar] [CrossRef]
- Li, Y.; Li, F.; Xu, X.; Shen, C.; Meng, K.; Chen, J.; Chang, D. Discrete element parameter calibration of wheat flour based on particle scaling. J. Agric. Eng. 2019, 35, 320–327. [Google Scholar]
- Roessler, T.; Katterfeld, A. Scaling of the angle of repose test and its influence on the calibration of DEM parameters using upscaled particles. Powder Technol. 2018, 330, 58–66. [Google Scholar] [CrossRef]
- Marigo, M.; Stitt, E.H. Discrete Element Method (DEM) for Industrial Applications: Comments on Calibration and Validation for the Modelling of Cylindrical Pellets. KONA Powder Part. J. 2015, 32, 236–252. [Google Scholar] [CrossRef]
- Ma, G.; Sun, Z.; Ma, H.; Li, P.; Černý, R. Calibration of Contact Parameters for Moist Bulk of Shotcrete Based on EDEM. Adv. Mater. Sci. Eng. 2022, 2022, 6072303. [Google Scholar] [CrossRef]
- Saruwatari, M.; Nakamura, H. Coarse-grained discrete element method of particle behavior and heat transfer in a rotary kiln. Chem. Eng. J. 2022, 428, 130969. [Google Scholar] [CrossRef]
- Li, J.W.; Tong, J.; Hu, B.; Wang, H.; Mao, C.; Ma, Y. Calibration of discrete element simulation parameters for the interaction between clayey heavy black soils with different water content and contact soil components. J. Agric. Eng. 2019, 35, 130–140. [Google Scholar]
- Kishida, N.; Nakamura, H.; Takimoto, H.; Ohsaki, S.; Watano, S. Coarse-grained discrete element simulation of particle flow and mixing in a vertical high-shear mixer. Powder Technol. 2021, 390, 1–10. [Google Scholar] [CrossRef]
- Soltanbeigi, B.; Podlozhnyuk, A.; Papanicolopulos, S.A.; Kloss, C.; Pirker, S.; Ooi, J.Y. DEM study of mechanical characteristics of multi-spherical and superquadric particles at micro and macro scales. Powder Technol. 2018, 329, 288–303. [Google Scholar] [CrossRef]
- Feng, Y.T.; Owen, D.R.J. Discrete element modelling of large scale particle systems-I: Exact scaling laws. Comput. Part. Mech. 2014, 390, 159–168. [Google Scholar] [CrossRef]
- He, Y.; Xiang, W.; Wu, M.; Quan, W.; Chen, C. Calibration of discrete element parameters for loamy soils based on stacking tests. J. Hunan Agric. Univ. 2018, 44, 216–220. [Google Scholar] [CrossRef]
- Zhao, T.T.; Feng, Y.T. Accurate scaling and coarse-grained discrete element methods for large-scale granular systems. J. Comput. Mech. 2022, 39, 365–372. [Google Scholar]
- Qiu, Y.; Guo, Z.; Jin, X.; Zhang, P.; Si, S.; Guo, F. Calibration and Verification Test of Cinnamon Soil Simulation Parameters Based on Discrete Element Method. Agriculture 2022, 12, 1082. [Google Scholar] [CrossRef]
- Niu, F.; Zhang, H.; Zhang, J. Three-dimensional Reconstruction of hematite flocs SEM image using MATLAB software. China Min. Ind. 2021, 30, 62–67. [Google Scholar]
- Luo, S.; Yuan, Q.; Gouda, S.; Yang, L. Parameter calibration of discrete element method for earthworm manure substrate based on JKR bonding model. J. Agric. Mach. 2018, 49, 343–350. [Google Scholar]
- Ren, J.; Zhou, L.; Han, L.; Zhou, J.; Yan, M. Discrete simulation of vertical screw conveying based on particle scaling theory. J. Process Eng. 2017, 17, 936–943. [Google Scholar]
- Xin, X.; Zhang, J.; Feng, H. Optimization of selective leaching process of zinc-containing dust and mud by response surface method. Compr. Util. Miner. Resour. 2021, volume, 146–151. [Google Scholar]
- Weinhart, T.; Labra, C.; Luding, S.; Ooi, J.Y. Influence of coarse-graining parameters on the analysis of DEM simulations of silo flow. Powder Technol. 2016, 293, 138–148. [Google Scholar] [CrossRef]
- Zhang, Y. Study on the vibration characteristics of fluid-solid coupling of vibrating inclined plate thickener. Kunming Univ. Technol. 2021, volume, page. [Google Scholar] [CrossRef]
- Xia, R.; Li, B.; Wang, X.; Li, T.; Yang, Z. Measurement and calibration of the discrete element parameters of wet bulk coal. Measurement 2019, 142, 84–95. [Google Scholar] [CrossRef]
- Huang, Z.H.; Li, D.T. Plackett-Burman test method combined with star point design-response surface method to optimize the purification process of Phellodendron spp. leaves. Chin. Med. Mater. 2020, 43, 682–686. [Google Scholar] [CrossRef]
- Wang, W.; Cai, D.; Xie, J.; Zhang, C.; Liu, L.; Chen, L. Calibration of discrete element model parameters for dense forming of corn straw. J. Agric. Mach. 2021, 52, 127–134. [Google Scholar]
- Xu, X.; Li, F.; Shen, C.; Li, Y.; Chang, D. Optimization design and experiment of isometric screw feeding device for wheat flour. J. Agric. Mach. 2020, 51, 150–157. [Google Scholar]
- Xu, X.; Li, F.; Li, Y.; Shen, C.; Meng, K.; Chen, J. Design and experiment of fixed-volume variable-pitch spiral structure. J. Agric. Mach. 2019, 50, 89–97. [Google Scholar]
- Feng, F.; Hu, P.; Tao, X.K. Mulberry leaf polysaccharide extracted by response surface methodolog suppresses the proliferation, invasion and migration of MCF-7 breast cancer cells. Food Sci. Technol. 2022, 42, page. [Google Scholar] [CrossRef]
- Wei, S.Y.; Wei, H.; Saxen, H.; Yu, Y.W. Numerical Analysis of the Relationship between Friction Coefficient and Repose Angle of Blast Furnace Raw Materials by Discrete Element Method. Materials 2022, 15, 903. [Google Scholar] [CrossRef]








| Simulation Parameters | Level | ||
|---|---|---|---|
| Low Level | High Level | ||
| Particle Poisson’s ratio | A | 0.3 | 0.5 |
| Coefficient of shear elasticity (pa) | B | 2.40 × 109 | 2.40 × 1010 |
| JKR surface energy coefficient (J/m2) | C | 0.3 | 0.6 |
| Collision recovery factor (particles) | D | 0.1 | 0.3 |
| Coefficient of static friction (particles) | E | 0.3 | 0.5 |
| Coefficient of dynamic friction (particles) | F | 0.08 | 0.12 |
| Serial Number | A | B (pa) | C (J/m3) | D | E | F | Repose Angle (°) |
|---|---|---|---|---|---|---|---|
| 1 | 0.50 | 2.40 × 1010 | 0.3 | 0.3 | 0.50 | 0.12 | 35.41 |
| 2 | 0.30 | 2.40 × 1010 | 0.6 | 0.1 | 0.50 | 0.12 | 40.29 |
| 3 | 0.50 | 2.40 × 109 | 0.6 | 0.3 | 0.30 | 0.12 | 35.53 |
| 4 | 0.30 | 2.40 × 1010 | 0.3 | 0.3 | 0.50 | 0.08 | 30.12 |
| 5 | 0.30 | 2.40 × 109 | 0.6 | 0.1 | 0.50 | 0.12 | 40.25 |
| 6 | 0.30 | 2.40 × 109 | 0.3 | 0.3 | 0.30 | 0.12 | 30.94 |
| 7 | 0.50 | 2.40 × 109 | 0.3 | 0.1 | 0.50 | 0.08 | 29.18 |
| 8 | 0.50 | 2.40 × 1010 | 0.3 | 0.1 | 0.30 | 0.12 | 27.03 |
| 9 | 0.50 | 2.40 × 1010 | 0.6 | 0.1 | 0.30 | 0.08 | 29.18 |
| 10 | 0.30 | 2.40 × 1010 | 0.6 | 0.3 | 0.30 | 0.08 | 30.96 |
| 11 | 0.50 | 2.40 × 109 | 0.6 | 0.3 | 0.50 | 0.08 | 37.85 |
| 12 | 0.30 | 2.40 × 109 | 0.3 | 0.1 | 0.30 | 0.08 | 24.35 |
| Factors | Sum of Squares | F-Value | p-Value | Effect |
|---|---|---|---|---|
| Models | 293.48 | 106.54 | <0.0001 | |
| A | 0.6211 | 1.35 | 0.2973 | −0.2275 |
| B | 2.18 | 4.74 | 0.0814 | −0.425833 |
| C | 114.27 | 248.88 | <0.0001 | 3.08583 |
| D | 9.24 | 20.13 | 0.0065 | 0.8775 |
| E | 102.73 | 223.74 | <0.0001 | 2.92583 |
| F | 64.45 | 140.37 | <0.0001 | 2.3175 |
| Residual | 2.30 | |||
| Total deviation | 295.78 |
| Serial Number | C (J/m2) | E | F | Repose Angle (°) |
|---|---|---|---|---|
| 1 | 0.30 | 0.40 | 0.08 | 34.36 |
| 2 | 0.45 | 0.40 | 0.10 | 45.88 |
| 3 | 0.30 | 0.40 | 0.12 | 34.11 |
| 4 | 0.45 | 0.30 | 0.08 | 33.32 |
| 5 | 0.45 | 0.40 | 0.10 | 44.13 |
| 6 | 0.60 | 0.40 | 0.08 | 29.19 |
| 7 | 0.45 | 0.40 | 0.10 | 44.12 |
| 8 | 0.45 | 0.40 | 0.10 | 45.34 |
| 9 | 0.45 | 0.30 | 0.12 | 39.45 |
| 10 | 0.30 | 0.30 | 0.10 | 28.13 |
| 11 | 0.30 | 0.50 | 0.10 | 30.13 |
| 12 | 0.60 | 0.40 | 0.12 | 35.13 |
| 13 | 0.45 | 0.40 | 0.10 | 46.34 |
| 14 | 0.60 | 0.30 | 0.10 | 29.23 |
| 15 | 0.45 | 0.50 | 0.12 | 34.45 |
| 16 | 0.60 | 0.50 | 0.10 | 25.19 |
| 17 | 0.45 | 0.50 | 0.08 | 33.34 |
| Source of Variance | Sum of Squares | Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Models | 637.64 | 9 | 70.85 | 66.47 | <0.0001 |
| C | 272.84 | 1 | 272.84 | 255.99 | <0.0001 |
| E | 13.47 | 1 | 13.47 | 12.64 | 0.0093 |
| F | 18.30 | 1 | 18.30 | 17.17 | 0.0043 |
| C × E | 22.09 | 1 | 22.09 | 20.73 | 0.0026 |
| C × F | 7.18 | 1 | 7.18 | 6.74 | 0.0356 |
| E × F | 6.30 | 1 | 6.30 | 5.91 | 0.0453 |
| C2 | 29.09 | 1 | 29.09 | 27.29 | 0.0012 |
| E2 | 205.64 | 1 | 205.64 | 192.94 | <0.0001 |
| F2 | 38.75 | 1 | 38.75 | 36.35 | 0.0005 |
| Residual | 7.46 | 7 | 1.07 | ||
| Lack of fit | 3.38 | 3 | 1.13 | 1.10 | 0.4458 |
| Pure error | 4.09 | 4 | 1.02 | ||
| Sum | 645.10 | 16 | |||
| R2 = 0.9884 | R2adj = 0.9736 | R2pre = 0.9064 | Adep Precision = 24.6778 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Chang, Z.; Niu, F.; Chen, Y.; Wu, J.; Zhang, H. Simulation and Validation of Discrete Element Parameter Calibration for Fine-Grained Iron Tailings. Minerals 2023, 13, 58. https://doi.org/10.3390/min13010058
Zhang J, Chang Z, Niu F, Chen Y, Wu J, Zhang H. Simulation and Validation of Discrete Element Parameter Calibration for Fine-Grained Iron Tailings. Minerals. 2023; 13(1):58. https://doi.org/10.3390/min13010058
Chicago/Turabian StyleZhang, Jinxia, Zhenjia Chang, Fusheng Niu, Yuying Chen, Jiahui Wu, and Hongmei Zhang. 2023. "Simulation and Validation of Discrete Element Parameter Calibration for Fine-Grained Iron Tailings" Minerals 13, no. 1: 58. https://doi.org/10.3390/min13010058
APA StyleZhang, J., Chang, Z., Niu, F., Chen, Y., Wu, J., & Zhang, H. (2023). Simulation and Validation of Discrete Element Parameter Calibration for Fine-Grained Iron Tailings. Minerals, 13(1), 58. https://doi.org/10.3390/min13010058








