Control Structure Design Using Global Sensitivity Analysis for Mineral Processes under Uncertainties
Abstract
1. Introduction
2. Materials and Methods
2.1. Uncertainty Analysis (UA)
2.2. Sensitivity Analysis (SA)
2.3. Solving the Model in MATLAB–Simulink
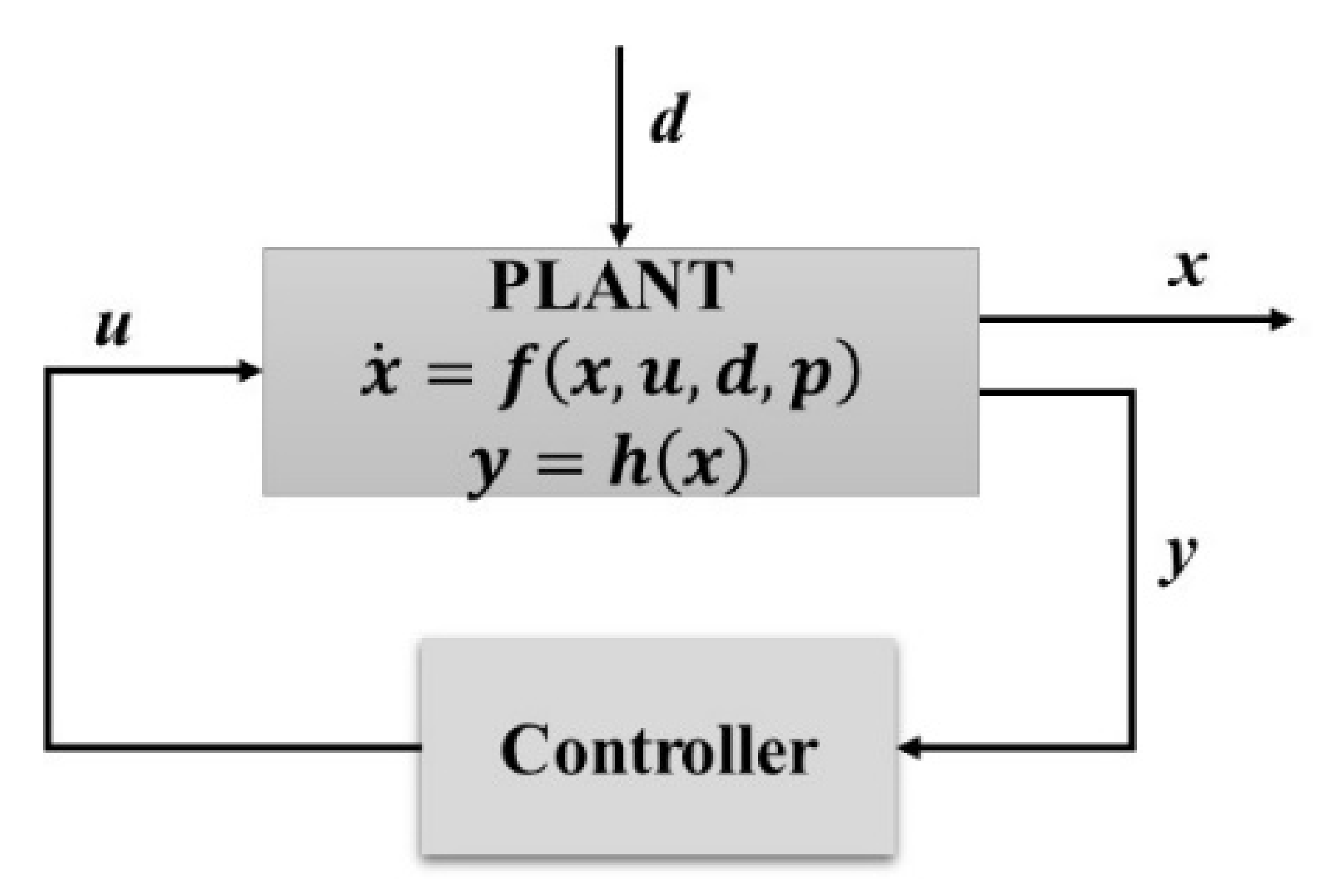
2.4. Methodology for Control Structure Design (CSD)
3. Results
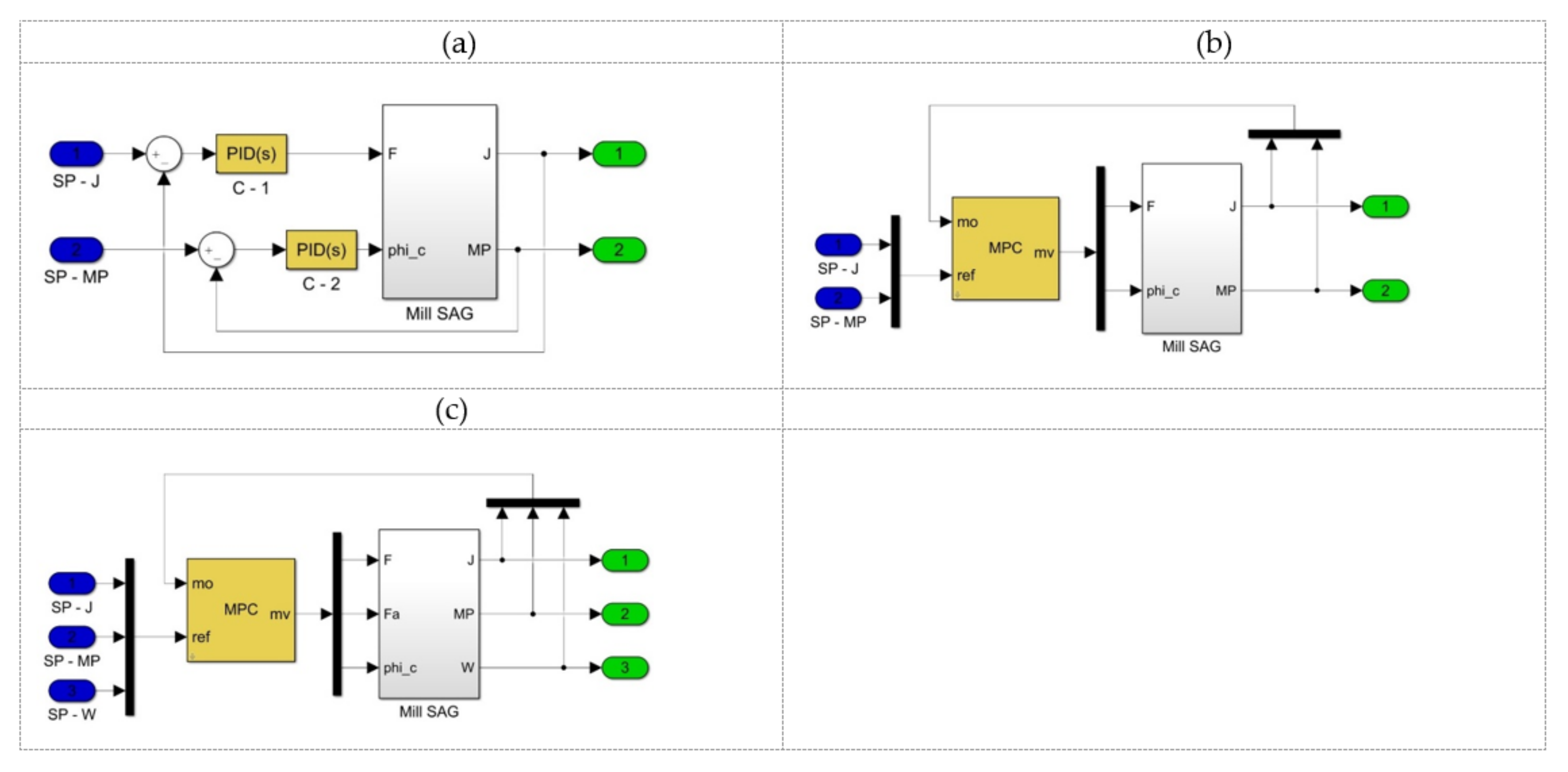
3.1. Semi-Autogenous Grinding (SAG)
3.2. Solvent Extraction (SX) Process
- (a)
- A traditional structure (4 × 5) reported previously [24], with = 4 and = 5:
- (b)
- A reduced structure (3 × 3) obtained in step 2, with = = 3:
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| For SAG model: | |
| ore impact breakage parameter | |
| parameter of specific breakage rate model | |
| parameter of specific breakage rate model | |
| cumulative breakage distribution function | |
| values of input variables that provide desired behavior of output milling model | |
| values of input variables that provide unwanted behavior of output milling model | |
| ore impact breakage parameter | |
| breakage distribution function | |
| number of species present in fresh feed | |
| mass flow recirculated internally by grill | |
| classification efficiency of internal grid mill | |
| solid weight percentage in mill charge | |
| mill diameter | |
| comminution specific energy (kWh/t) | |
| fresh ore flux fed to mill, t/h | |
| fraction of fresh ore flux fed to mill | |
| fraction of mill filling | |
| percentage of mill volume occupied by steel balls | |
| specific breakage rate | |
| mill length | |
| parameter of classification efficiency model | |
| mill power consumption | |
| total number of input variables in model | |
| total number of simulations | |
| first-order sensitivity index for input variable | |
| total sensitivity index for input variable | |
| mill volume | |
| total number of simulations | |
| variance of model | |
| mass retained in mill | |
| water in mill charge | |
| ratio between ore mass and water mass retained inside mill | |
| weight fraction of retained mass in mill | |
| percentage of solids in discharge mill | |
| parameter of specific breakage rate model | |
| particle size of species present in fresh feed | |
| parameter of classification efficiency model | |
| parameter of classification efficiency model | |
| characteristic parameter of material | |
| parameter of specific breakage rate model | |
| parameter of specific breakage rate model | |
| fraction of fines produced in a single fracture event | |
| parameter of classification efficiency model | |
| parameter of cumulative breakage distribution function | |
| parameter of specific breakage rate model | |
| parameter of specific breakage rate model | |
| parameter of cumulative breakage distribution function | |
| percentage of critical speed | |
| parameter of classification efficiency model | |
| For SX model: | |
| flow inputs to process, pregnant leach solution (PLS) | |
| flow inputs to process, pregnant leach solutions (PLS) | |
| solution with a copper concentration | |
| poor electrolyte flow | |
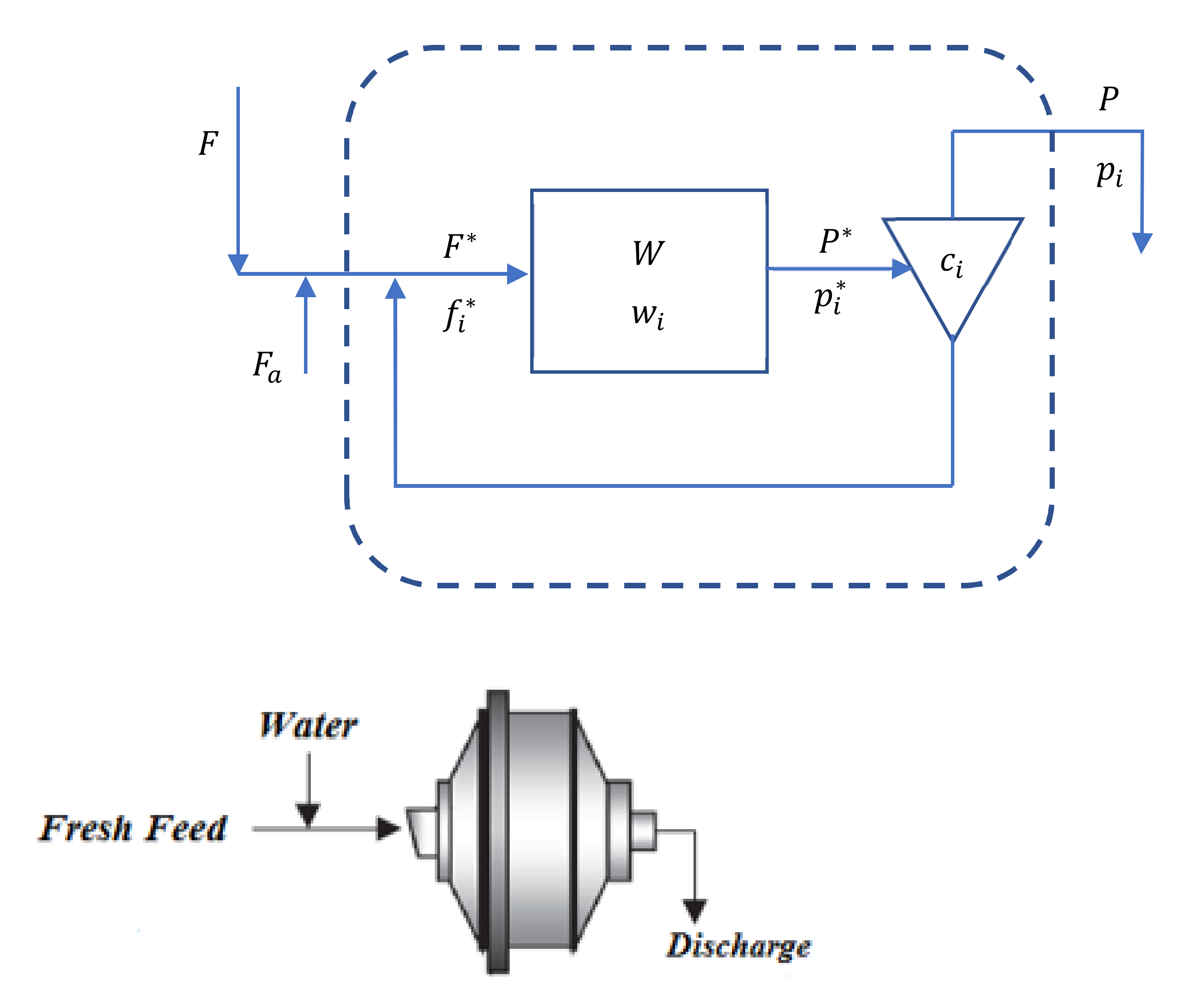
Appendix A. SAG Model
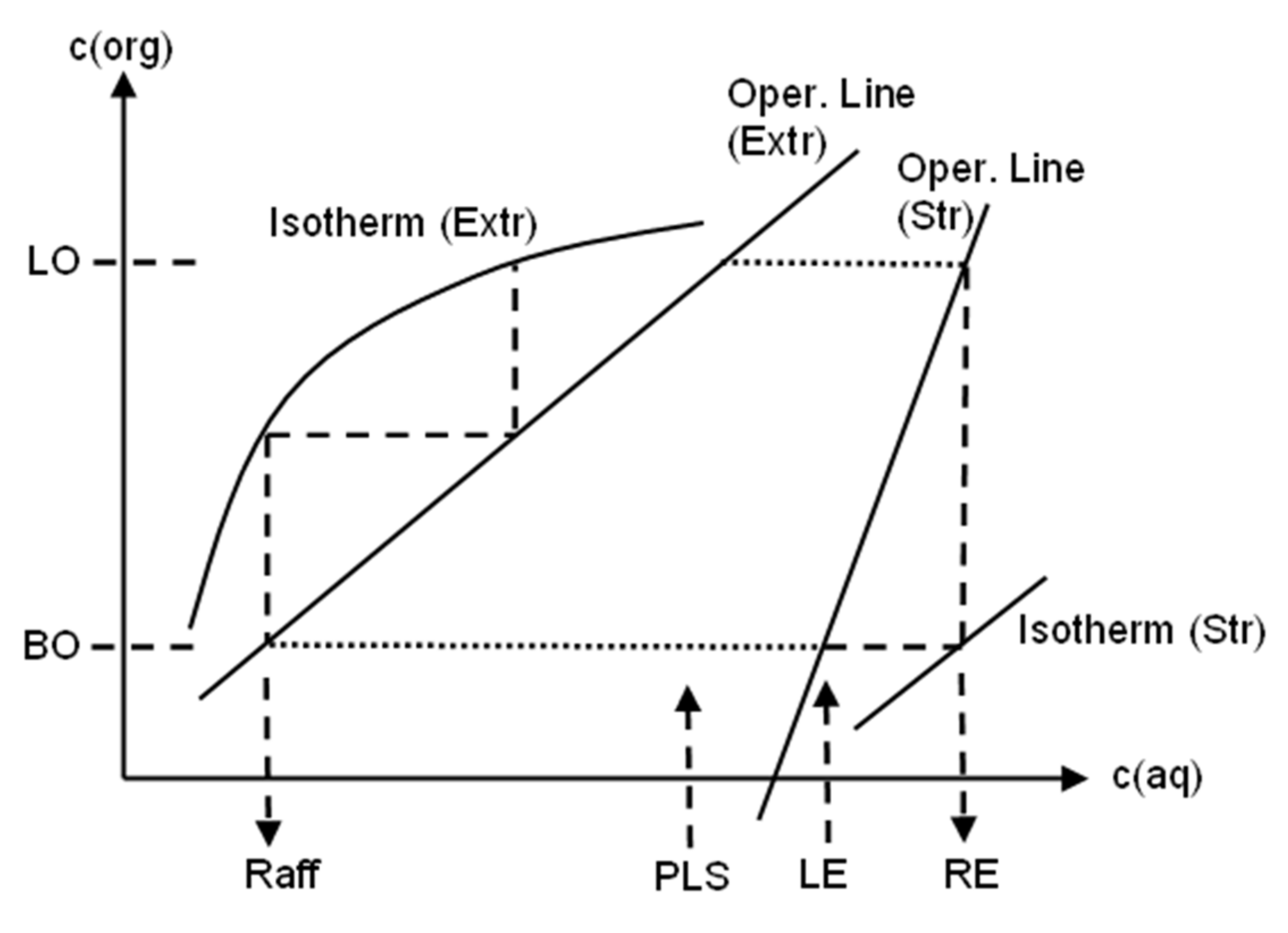
Appendix B. SX Model
References
- Liu, G.; Wang, Z.; Mei, C.; Ding, Y. A Review of Decoupling Control Based on Multiple Models. In Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 1077–1081. [Google Scholar]
- Xiong, Q.; Cai, W.J.; He, M.J. A Practical Loop Pairing Criterion for Multivariable Processes. J. Process Control 2005, 15, 741–747. [Google Scholar] [CrossRef]
- Vaes, D.; Swevers, J.; Sas, P. Optimal Static Decoupling to Simplify and Improve Multivariable Control Design. Mediterr. J. Meas. Control 2006, 2, 48–62. [Google Scholar]
- Liu, L.; Tian, S.; Xue, D.; Zhang, T.; Chen, Y.Q.; Zhang, S. A Review of Industrial MIMO Decoupling Control. Int. J. Control Autom. Syst. 2019, 17, 1246–1254. [Google Scholar] [CrossRef]
- Hanuma, R.; Ashok, D.; Anjaneyulu, K. Control Configuration Selection and Controller Design for Multivariable Processes Using Normalized Gain. Int. J. Electr. Comput. Eng. 2014, 8, 1–5. [Google Scholar] [CrossRef]
- Castaño Arranz, M.; Birk, W.; Nikolakopoulos, G. A Survey on Control Configuration Selection and New Challenges in Relation to Wireless Sensor and Actuator Networks. In Proceedings of the IFAC-PapersOnLine, Touluse, France, 10–14 July 2017; Volume 50, pp. 8810–8825. [Google Scholar]
- Jain, A.; Babu, B.V. Relative Response Array: A New Tool for Control Configuration Selection. Int. J. Chem. Eng. Appl. 2015, 6, 356–362. [Google Scholar] [CrossRef][Green Version]
- Niederlinski, A. A Heuristic Approach to the Design of Linear Multivariable Interacting Control Systems. Automatica 1971, 7, 691–701. [Google Scholar] [CrossRef]
- Zhu, Z.X. Variable Pairing Selection Based on Individual and Overall Interaction Measures. Ind. Eng. Chem. Res. 1996, 35, 4091–4099. [Google Scholar] [CrossRef]
- Kinnaert, M. Interaction Measures and Pairing of Controlled and Manipulated Variables for Multiple-Input Multiple-Output Systems: A Survey. Journal A 1995, 16, 15–23. [Google Scholar]
- Mc Avoy, T.; Arkun, Y.; Chen, R.; Robinson, D.; Schnelle, P.D. A New Approach to Defining a Dynamic Relative Gain. Control Eng. Pract. 2003, 11, 907–914. [Google Scholar] [CrossRef]
- Salgado, M.E.; Conley, A. MIMO Interaction Measure and Controller Structure Selection. Int. J. Control 2004, 77, 367–383. [Google Scholar] [CrossRef]
- Wittenmark, B.; Salgado, M.E. Hankel-Norm Based Interaction Measure for Input-Output Pairing. In Proceedings of the IFAC Proceedings Volumes (IFAC-PapersOnline), Barcelona, Spain, 21–26 July 2002; Volume 15, pp. 429–434. [Google Scholar]
- Hanzon, B. The Area Enclosed by the (Oriented) Nyquist Diagram and the Hilbert-Schmidt-Hankel Norm of a Linear System. IEEE Trans. Autom. Control 1992, 37, 835–839. [Google Scholar] [CrossRef]
- Birk, W.; Medvedev, A. A Note on Gramian-Based Interaction Measures. In Proceedings of the European Control Conference (ECC), Cambridge, UK, 1–4 September 2003; pp. 2625–2630. [Google Scholar]
- Halvarsson, B.; Carlsson, B.; Wik, T. A New Input/Output Pairing Strategy Based on Linear Quadratic Gaussian Control. In Proceedings of the 2009 IEEE International Conference on Control and Automation (ICCA), Christchurch, New Zealand, 9–11 December 2009; pp. 978–982. [Google Scholar]
- Jain, A.; Babu, B.V. Sensitivity of Relative Gain Array for Processes with Uncertain Gains and Residence Times. In Proceedings of the IFAC-PapersOnLine, Tiruchirappalli, India, 1–5 February 2016; Volume 49, pp. 486–491. [Google Scholar]
- Coetzee, L.C.; Craig, I.K.; Kerrigan, E.C. Robust Nonlinear Model Predictive Control of a Run-of-Mine Ore Milling Circuit. IEEE Trans. Control Syst. Technol. 2010, 18, 1–86. [Google Scholar] [CrossRef]
- Craig, I.K.; MacLeod, I.M. Specification Framework for Robust Control of a Run-of-Mine Ore Milling Circuit. Control Eng. Pract. 1995, 3, 621–630. [Google Scholar] [CrossRef]
- Olivier, L.E.; Craig, I.K. Model-Plant Mismatch Detection and Model Update for a Run-of-Mine Ore Milling Circuit under Model Predictive Control. In Proceedings of the Journal of Process Control, Cape Town, South Africa, 24–29 August 2014; Volume 23, pp. 100–107. [Google Scholar]
- Olivier, L.E.; Huang, B.; Craig, I.K. Dual Particle Filters for State and Parameter Estimation with Application to a Run-of-Mine Ore Mill. J. Process Control 2012, 22, 710–717. [Google Scholar] [CrossRef]
- Karelovic, P.; Putz, E.; Cipriano, A. Dynamic Hybrid Modeling and Simulation of Grinding-Flotation Circuits for the Development of Control Strategies. Miner. Eng. 2016, 93, 65–79. [Google Scholar] [CrossRef]
- Bauer, M.; Brooks, K.; Burchell, J.; Coetzee, L.; le Roux, D.; McCoy, J.; Miskin, J.; Winter, D. The Use of a Semi-Rigorous SAG Mill Model for a Hands-on Workshop. In Proceedings of the IFAC-PapersOnLine, Berlin, Germany, 11–17 July 2020; Volume 53. [Google Scholar]
- Komulainen, T.; Doyle III, F.J.; Rantala, A.; Jämsä-Jounela, S.-L. Control of an Industrial Copper Solvent Extraction Process. J. Process Control 2009, 19, 2–15. [Google Scholar] [CrossRef]
- Maldonado, M.; Desbiens, A.; Villar, D.R. Decentralized Control of a Pilot Flotation Column: A 3×3 System. Can. Metall. Q. 2008, 47, 377–385. [Google Scholar] [CrossRef]
- Guo, N.; Zheng, H.; Zou, T.; Jia, Y. Integration of Numerical Simulation and Control Scheme for Energy Conservation of Aluminum Melting Furnaces. IEEE Access 2019, 7, 114659–114669. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis. The Primer; John Wiley & Sons, Ltd.: Chichester, UK, 2007; ISBN 9780470725184. [Google Scholar]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance Based Sensitivity Analysis of Model Output. Design and Estimator for the Total Sensitivity Index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Homma, T.; Saltelli, A. Importance Measures in Global Sensitivity Analysis of Nonlinear Models. Reliab. Eng. Syst. Saf. 1996, 52, 1–17. [Google Scholar] [CrossRef]
- Lucay, F.A.; Gálvez, E.D.; Salez-Cruz, M.; Cisternas, L.A. Improving Milling Operation Using Uncertainty and Global Sensitivity Analyses. Miner. Eng. 2019, 131, 249–261. [Google Scholar] [CrossRef]
- Mellado, M.; Cisternas, L.; Lucay, F.; Gálvez, E.; Sepúlveda, F. A Posteriori Analysis of Analytical Models for Heap Leaching Using Uncertainty and Global Sensitivity Analyses. Minerals 2018, 8, 44. [Google Scholar] [CrossRef]
- Helton, J.C.; Burmaster, D.E. Treatment of Aleatory and Epistemic Uncertainty in Performance Assesments for Complex Systems. Reliab. Eng. Syst. Saf. 1996, 54, 91–94. [Google Scholar] [CrossRef]
- Zio, E.; Pedroni, N. Methods for Representing Uncertainty—A Literature Review. Found. Ind. Saf. Cult. (FonCSI) 2013, 5, 77–88. [Google Scholar]
- Saltelli, A. Sensitivity Analysis for Importance Assessment. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef]
- Reuter, U.; Liebscher, M. Global Sensitivity Analysis in View of Nonlinear Structural Behavior. LS-Dyna Users Conf. 2008, 56, 903–915. [Google Scholar]
- Lilburne, L.; Tarantola, S. Sensitivity Analysis of Spatial Models. Int. J. Geogr. Inf. Sci. 2009, 23, 151–168. [Google Scholar] [CrossRef]
- Sepúlveda, F.D.; Lucay, F.; González, J.F.; Cisternas, L.A.; Gálvez, E.D. A Methodology for the Conceptual Design of Flotation Circuits by Combining Group Contribution, Local/Global Sensitivity Analysis, and Reverse Simulation. Int. J. Miner. Process. 2017, 164, 56–66. [Google Scholar] [CrossRef]
- Lucay, F.A.; Cisternas, L.A.; Gálvez, E.D. An LS-SVM Classifier Based Methodology for Avoiding Unwanted Responses in Processes under Uncertainties. Comput. Chem. Eng. 2020, 138, 106860. [Google Scholar] [CrossRef]
- Calisaya-Azpilcueta, D.; Herrera-Leon, S.; Lucay, F.A.; Cisternas, L.A. Assessment of the Supply Chain under Uncertainty: The Case of Lithium. Minerals 2020, 10, 604. [Google Scholar] [CrossRef]
- Lucay, F.A.; Lopez-Arenas, T.; Sales-Cruz, M.; Gálvez, E.D.; Cisternas, L.A. Performance Profiles for Benchmarking of Global Sensitivity Analysis Algorithms. Rev. Mex. Ing. Quim. 2020, 19, 423–444. [Google Scholar] [CrossRef]
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Li, S.; Wu, Q. Why so Many Published Sensitivity Analyses Are False: A Systematic Review of Sensitivity Analysis Practices. Environ. Model. Softw. 2019, 114, 29–39. [Google Scholar] [CrossRef]
- Velez, C. Global Sensitivity and Uncertainty Analysis (GSUA). Available online: https://www.mathworks.com/matlabcentral/fileexchange/47758-global-sensitivity-and-uncertainty-analysis-gsua (accessed on 5 May 2022).
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity Analysis of Environmental Models: A Systematic Review with Practical Workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Austin, L.G.; Barahona, C.A.; Weymont, N.P.; Suryanarayanan, K. An Improved Simulation Model for Semi-Autogenous Grinding. Powder Technol. 1986, 47, 265–283. [Google Scholar] [CrossRef]
- Austin, L.G.; Menacho, J.M.; Pearcy, F. A General Model for Semi-Autogenous and Autogenous Milling. In Proceedings of the Twentieth International Symposium on the Application of Computers and Mathematics in the Mineral Industries APCOM 87, Johannesburg, South Africa, 19–23 October 1987; pp. 107–126. [Google Scholar]
- Barani, K.; Balochi, H. First-Order and Second-Order Breakage Rate of Coarse Particles in Ball Mill Grinding. Physicochem. Probl. Miner. Process. 2016, 52, 268–278. [Google Scholar] [CrossRef]
- Fuerstenau, D.W.; De, A.; Kapur, P.C. Linear and Nonlinear Particle Breakage Processes in Comminution Systems. Int. J. Miner. Process. 2004, 74, S317–S327. [Google Scholar] [CrossRef]
- Magne, L.; Améstica, R.; Barría, J.; Menacho, J. Modelización Dinámica de Molienda Semiautógena Basada En Un Modelo Fenomenológico Simplificado. Rev. Metal. 1995, 31, 97–105. [Google Scholar] [CrossRef]
- Magne, L.; Barría, J.; Améstica, R.; Menacho, J. Evaluación de Variables de Operación En Molienda Semiautógena. In Proceedings of the Segundo Congreso en Metalurgia e Ingeniería de Materiales, IBEROMET II, Ciudad de Mexico, Mexico, 8–14 November 1992; Available online: https://www.revistas.usach.cl/ojs/index.php/remetallica/article/view/1701/1581 (accessed on 5 May 2022).
- Tripathy, S.K.; Murthy, Y.R.; Singh, V.; Srinivasulu, A.; Ranjan, A.; Satija, P.K. Performance Optimization of an Industrial Ball Mill for Chromite Processing. J. S. Afr. Inst. Min. Met. 2017, 117, 75–81. [Google Scholar] [CrossRef][Green Version]
- Xu, Y. The Fractal Evolution of Particle Fragmentation under Different Fracture Energy. Powder Technol. 2018, 323, 337–345. [Google Scholar] [CrossRef]
- Helton, J.C.; Oberkampf, W.L. Alternative Representations of Epistemic Uncertainty. Engineering and System Safety. Reliab. Eng. Syst. Saf. 2004, 85, 1–10. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0951832004000481?via%3Dihub (accessed on 5 May 2022). [CrossRef]
- Salazar, J.L.; Valdés-González, H.; Vyhmesiter, E.; Cubillos, F. Model Predictive Control of Semiautogenous Mills (Sag). Miner. Eng. 2014, 64, 92–96. [Google Scholar] [CrossRef]
- César, G.Q.; Daniel, S.H. Multivariable Model Predictive Control of a Simulated SAG Plant. IFAC Proc. Vol. 2009, 42, 37–42. [Google Scholar] [CrossRef]
- Kämpjärvi, P.; Jämsä-Jounela, S.L. Level Control Strategies for Flotation Cells. Miner. Eng. 2003, 16, 1061–1068. [Google Scholar] [CrossRef]
- Komulainen, T.; Pekkala, P.; Rantala, A.; Jämsä-Jounela, S.L. Dynamic Modelling of an Industrial Copper Solvent Extraction Process. Hydrometallurgy 2006, 81, 52–61. [Google Scholar] [CrossRef]



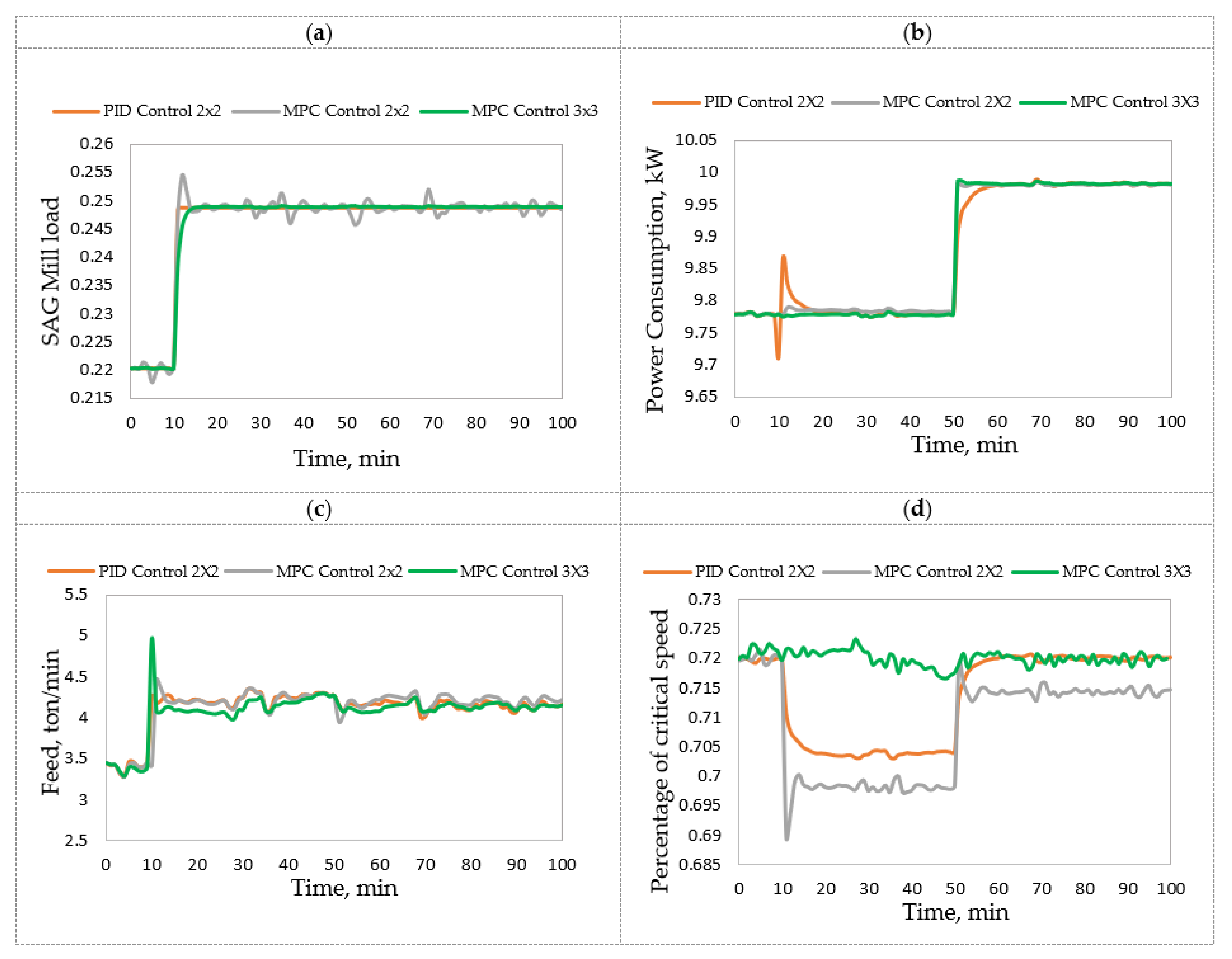

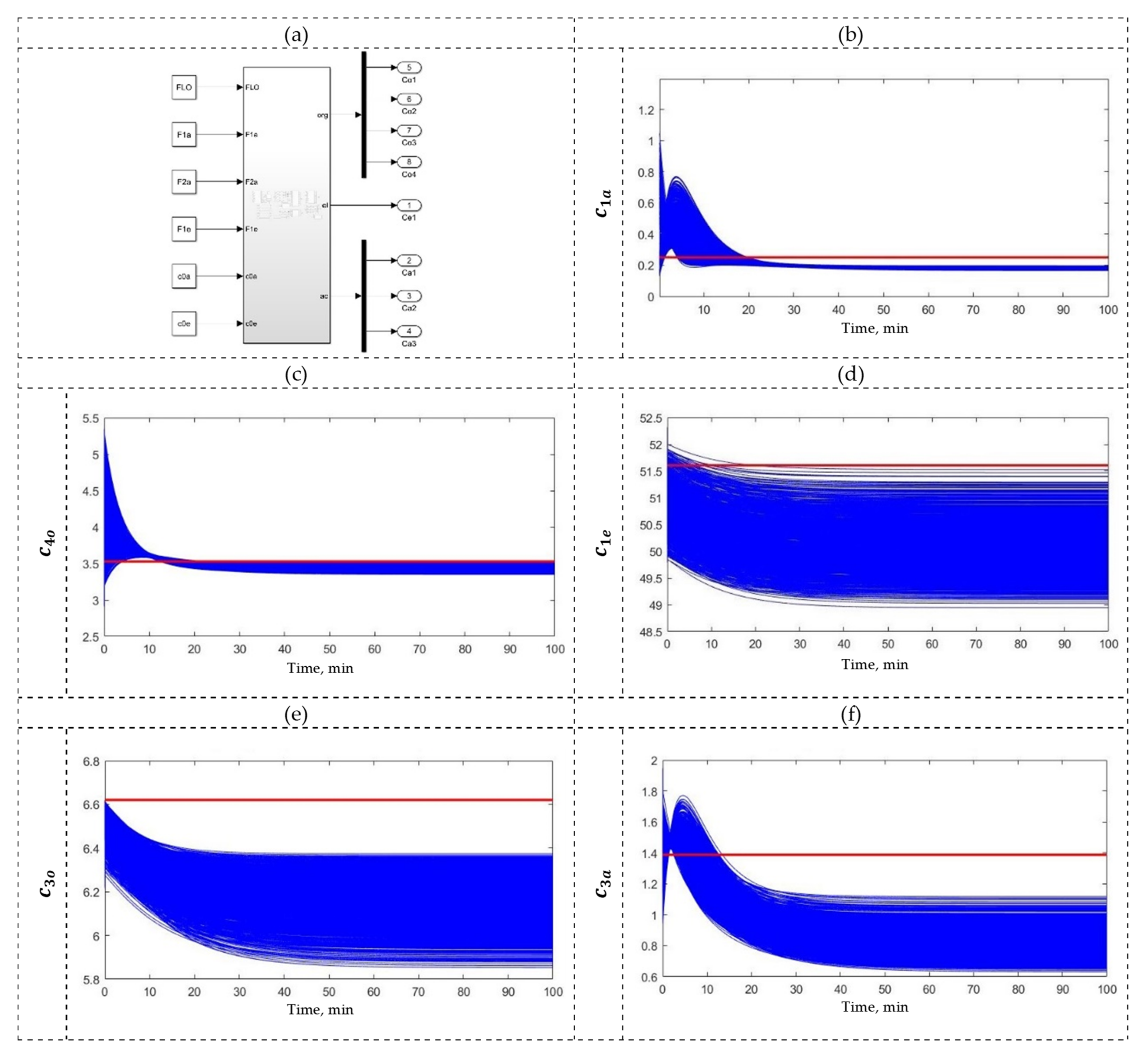
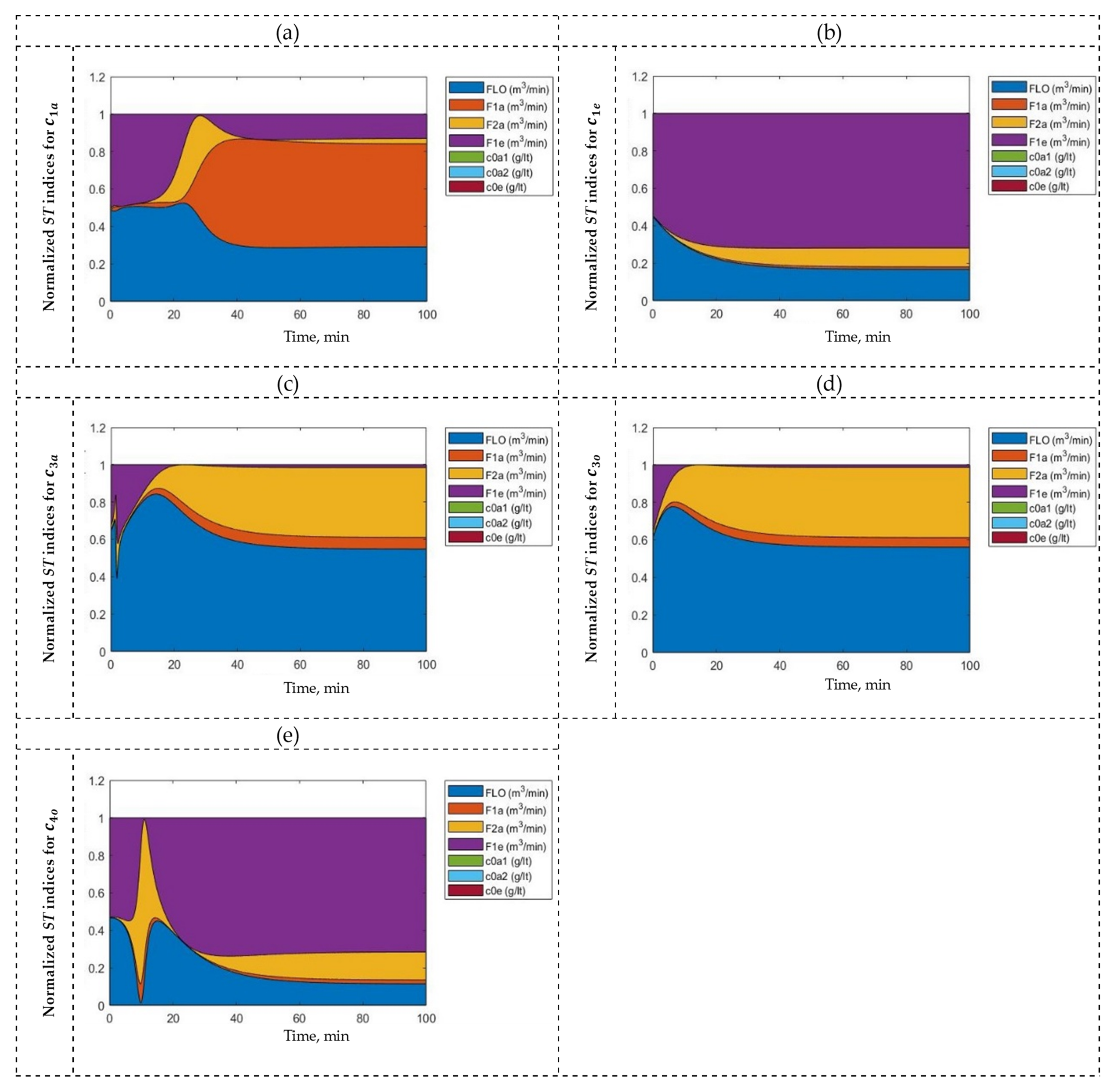
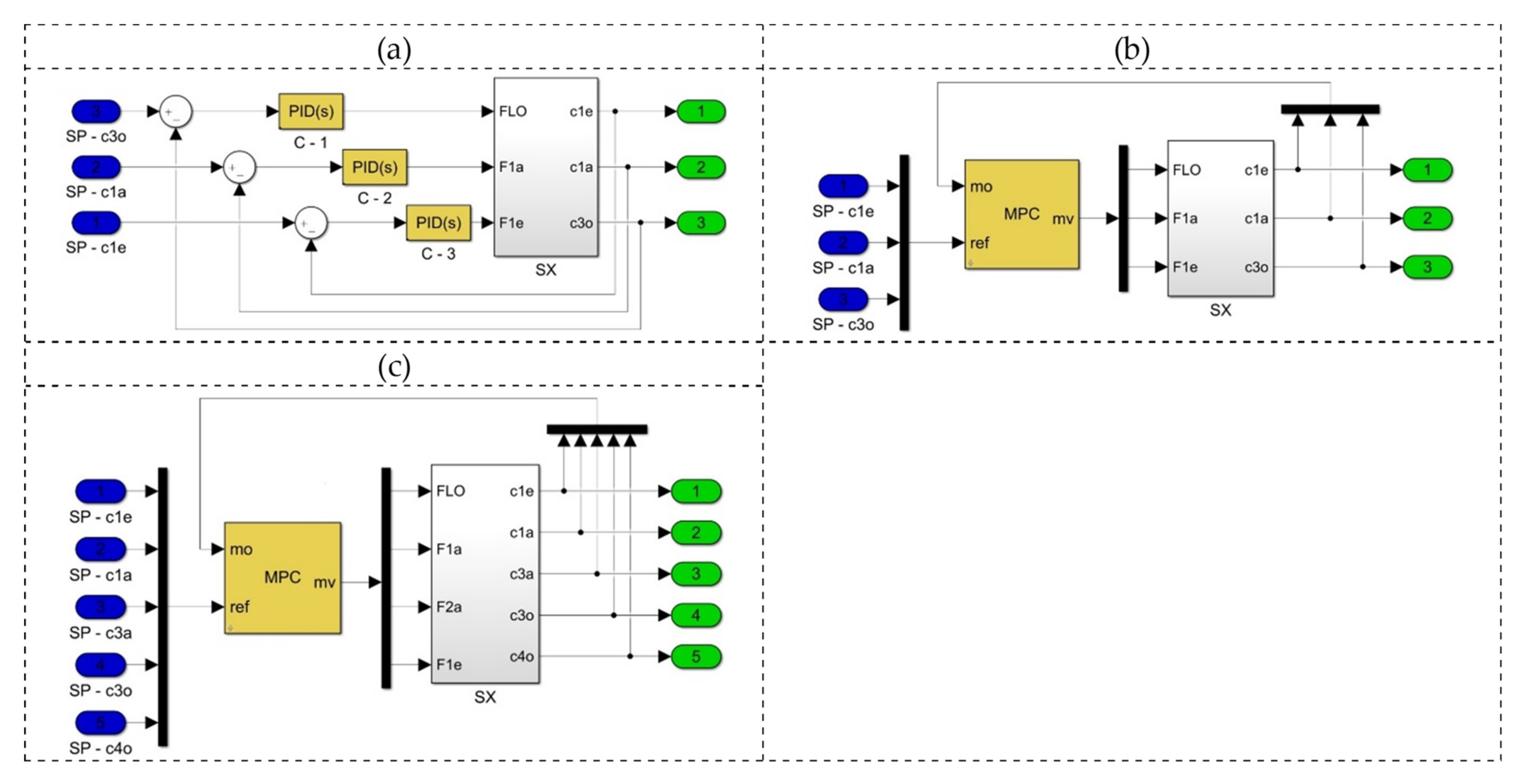

| Control | Controlled Variables | Manipulated Variables | |||
|---|---|---|---|---|---|
| IAE | |||||
| High performance | PID 2 × 2 | MPC 3 × 3 | PID 2 × 2 | PID 2 × 2 | |
| 0.001 | 0.111 | 6.437 | 0.793 | ||
| Good performance | MPC 3 × 3 | MPC 2 × 2 | MPC 3 × 3 | MPC 3 × 3 | |
| 0.020 | 0.299 | 6.081 | 0.240 | ||
| Sufficient performance | MPC 2 × 2 | PID 2 × 2 | MPC 2 × 2 | MPC 2 × 2 | |
| 0.075 | 0.630 | 9.594 | 0.995 | ||
| Reference | Open-loop | ||||
| 0.255 | 11.536 | ||||
| Control | Controlled Variables | Manipulated Variables | |||||
|---|---|---|---|---|---|---|---|
| High performance | PID 3 × 3 | PID 3 × 3 | PID 3 × 3 | MPC 3 × 3 | MPC 3 × 3 | MPC 3 × 3 | |
| 0.008 | 0.072 | 0.001 | 2.300 | 9.088 | 9.365 | ||
| Good performance | MPC 3 × 3 | MPC 3 × 3 | MPC 3 × 3 | PID 3 × 3 | PID 3 × 3 | PID 3 × 3 | |
| 0.096 | 0.090 | 0.060 | 2.545 | 10.230 | 10.660 | ||
| Sufficient performance | MPC 4 × 5 | MPC 4 × 5 | MPC 4 × 5 | MPC 4 × 5 | MPC 4 × 5 | MPC 4 × 5 | |
| 0.112 | 2.234 | 2.636 | 21.598 | 85.689 | 110.112 | ||
| Reference | Open-loop | ||||||
| 2.180 | 0.099 | 0.605 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mamani-Quiñonez, O.; Cisternas, L.A.; Lopez-Arenas, T.; Lucay, F.A. Control Structure Design Using Global Sensitivity Analysis for Mineral Processes under Uncertainties. Minerals 2022, 12, 736. https://doi.org/10.3390/min12060736
Mamani-Quiñonez O, Cisternas LA, Lopez-Arenas T, Lucay FA. Control Structure Design Using Global Sensitivity Analysis for Mineral Processes under Uncertainties. Minerals. 2022; 12(6):736. https://doi.org/10.3390/min12060736
Chicago/Turabian StyleMamani-Quiñonez, Oscar, Luis A. Cisternas, Teresa Lopez-Arenas, and Freddy A. Lucay. 2022. "Control Structure Design Using Global Sensitivity Analysis for Mineral Processes under Uncertainties" Minerals 12, no. 6: 736. https://doi.org/10.3390/min12060736
APA StyleMamani-Quiñonez, O., Cisternas, L. A., Lopez-Arenas, T., & Lucay, F. A. (2022). Control Structure Design Using Global Sensitivity Analysis for Mineral Processes under Uncertainties. Minerals, 12(6), 736. https://doi.org/10.3390/min12060736








