Improving Inversion Quality of IP-Affected TEM Data Using Dual Source
Abstract
:1. Introduction
2. Materials and Methods
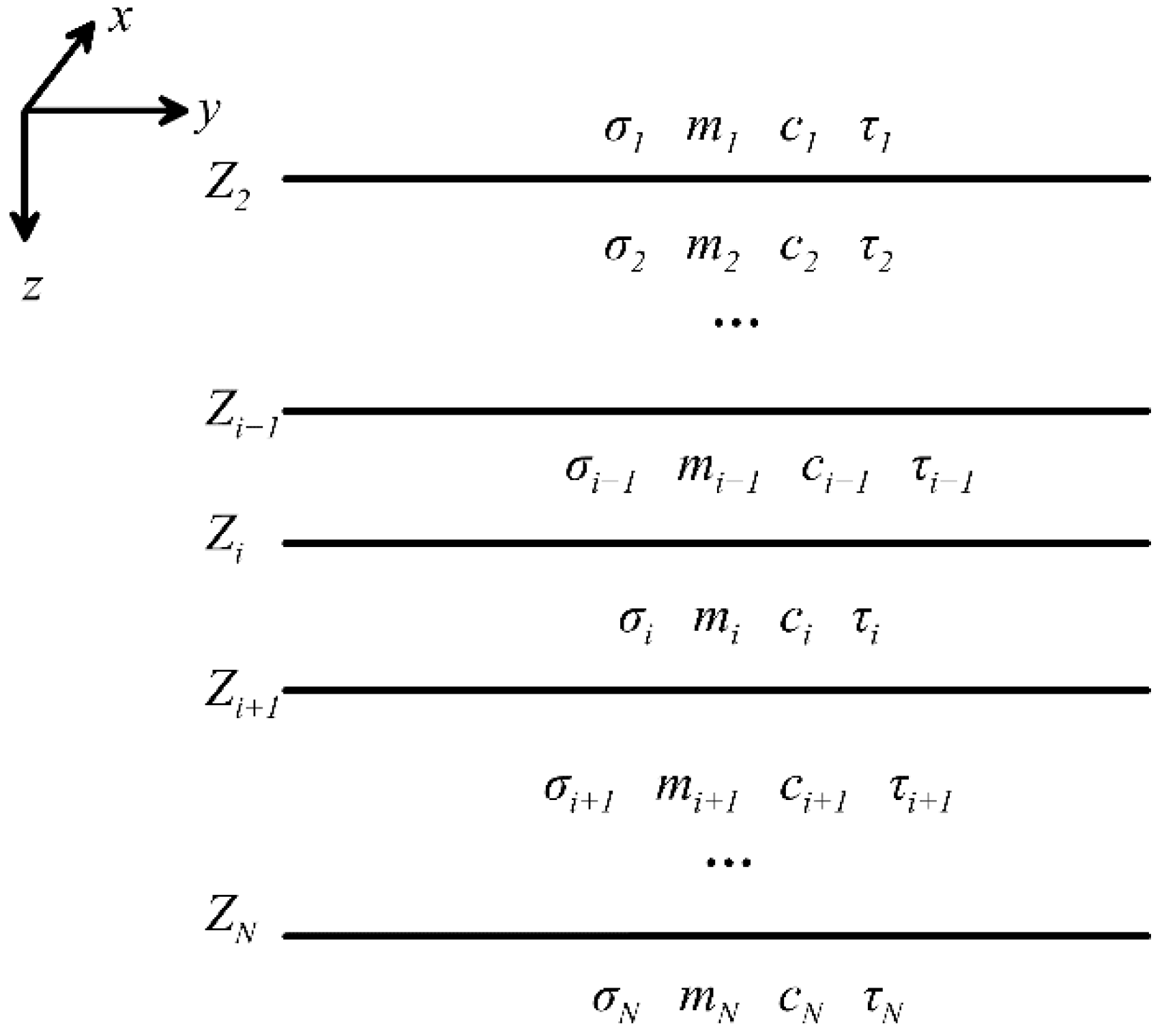
2.1. Forward Modeling of IP-Affected TEM Response
2.2. Singularity of IP-Affected TEM Data Inversion
2.3. TEM Data Acquisition Using Dual Source
2.4. Joint Inversion of Dual-Source TEM Responses
3. Results
3.1. Synthetic Data Test
3.2. A Field Example: Baiyun Gold Deposit
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nabighian, M.N.; Macnae, J.C. Time Domain Electromagnetic Prospecting Methods. In Electromagnetic Methods in Applied Geophysics: Volume 2, Application, Parts A and B; SEG: Tulsa, OK, USA, 1991; pp. 427–520. [Google Scholar]
- Asten, M.W.; Duncan, A.C. The quantitative advantages of using B-field sensors in time-domain EM measurement for mineral exploration and unexploded ordnance search. Geophysics 2012, 77, WB137–WB148. [Google Scholar] [CrossRef]
- Yang, D.K.; Oldenburg, D.W. Three-dimensional inversion of airborne time-domain electromagnetic data with applications to a porphyry deposit. Geophysics 2012, 77, B23–B34. [Google Scholar] [CrossRef]
- Chen, W.; Xue, G.Q.; Zhou, N.N.; Tang, D.M.; Hou, D.Y.; He, Y.M.; Lei, K.X.; Chen, K.; Li, H. Delineating ore-forming rock using a frequency domain controlled-source electromagnetic method. Ore Geol. Rev. 2019, 115, 103167. [Google Scholar] [CrossRef]
- Di, Q.Y.; Zhu, R.X.; Xue, G.Q.; Yin, C.C.; Li, X. New development of the Electromagnetic (EM) methods for deep exploration. Chin. J. Geophys. 2019, 62, 2128–2138. [Google Scholar] [CrossRef]
- Di, Q.Y.; Xue, G.Q.; Yin, C.C.; Li, X. New methods of controlled-source electromagnetic detection in China. Sci. China Earth Sci. 2020, 63, 1268–1277. [Google Scholar] [CrossRef]
- Guo, Z.W.; Xue, G.Q.; Liu, J.X.; Wu, X. Electromagnetic methods for mineral exploration in China: A review. Ore Geol. Rev. 2020, 118, 103357. [Google Scholar] [CrossRef]
- Li, R.H.; Hu, X.Y.; Xu, D.; Liu, Y.; Yu, N. Characterizing the 3D hydrogeological structure of a debris landslide using the transient electromagnetic method. J. Appl. Geophys. 2020, 175, 103991. [Google Scholar] [CrossRef]
- Lee, T.J.; Thomas, L. A Review of the Application of Analytical Methods to the Prediction of Transient Electromagnetic Field Responses. Explor. Geophys. 1988, 19, 423–434. [Google Scholar] [CrossRef]
- Swidinsky, A.; Hölz, S.; Jegen, M. On mapping seafloor mineral deposits with central loop transient electromagnetics. Geophysics 2012, 77, E171–E184. [Google Scholar] [CrossRef] [Green Version]
- Raiche, A.P. Comparison of apparent resistivity functions for transient electromagnetic methods. Geophysics 1983, 48, 787–789. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Li, X.; Yao, W.H.; Zhi, Q.Q.; Li, J. Multi-component full field apparent resistivity definition of multi-source ground-airborne transient electromagnetic method with galvanic sources. Chin. J. Geophys. 2015, 58, 2745–2758. [Google Scholar] [CrossRef]
- Spies, B.R.; Eggers, D.E. The use and misuse of apparent resistivity in electromagnetic methods. Geophysics 1986, 51, 1462–1471. [Google Scholar] [CrossRef]
- Xue, G.Q.; Li, H.; He, Y.M.; Xue, J.J.; Wu, X. Development of the Inversion Method for Transient Electromagnetic Data. IEEE Access 2020, 8, 146172–146181. [Google Scholar] [CrossRef]
- Xue, G.Q.; Zhang, L.B.; Zhou, N.N.; Chen, W.Y. Developments measurements of TEM sounding in China. Geol. J. 2020, 55, 1636–1643. [Google Scholar] [CrossRef]
- Christensen, N.B. Fast approximate 1D modelling and inversion of transient electromagnetic data. Geophys. Prospect. 2016, 64, 1620–1631. [Google Scholar] [CrossRef]
- Lu, X.S.; Farquharson, C.; Miehé, J.M.; Harrison, G.; Ledru, P. Computer modeling of electromagnetic data for mineral exploration: Application to uranium exploration in the Athabasca Basin. Lead. Edge 2021, 40, 139a1–139a10. [Google Scholar] [CrossRef]
- Engebretsen, K.W.; Zhang, B.; Fiandaca, G.; Madsen, L.M.; Auken, E.; Christiansen, A.V. Accelerated 2.5-D inversion of airborne transient electromagnetic data using reduced 3-D meshing. Geophys. J. Int. 2022, 230, 643–653. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef] [Green Version]
- Pelton, W.H.; Ward, S.H.; Hallof, P.G.; Sill, W.R.; Nelson, P.H. Mineral discrimination and removal of inductive coupling with multifrequency IP. Geophysics 1978, 43, 588–609. [Google Scholar] [CrossRef]
- Merriam, J.B. Induced polarization and surface electrochemistry. Geophysics 2007, 72, F157–F166. [Google Scholar] [CrossRef]
- Gurin, G.; Titov, K.; Ilyin, Y.; Tarasov, A. Induced polarization of disseminated electronically conductive minerals: A semi-empirical model. Geophys. J. Int. 2015, 200, 1555–1565. [Google Scholar] [CrossRef] [Green Version]
- Zhdanov, M.; Endo, M.; Cox, L.; Sunwall, D. Effective-Medium Inversion of Induced Polarization Data for Mineral Exploration and Mineral Discrimination: Case Study for the Copper Deposit in Mongolia. Minerals 2018, 8, 68. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Xue, G.Q.; He, Y.M. Decoupling induced polarization effect from time domain electromagnetic data in a Bayesian framework. Geophysics 2019, 84, A59–A63. [Google Scholar] [CrossRef]
- Zhou, N.N.; Lei, K.X.; Xue, G.Q.; Chen, W. Induced polarization effect on grounded-wire transient electromagnetic data from transverse electric and magnetic fields. Geophysics 2020, 85, E111–E120. [Google Scholar] [CrossRef]
- Raiche, A.P. Negative transient voltage and magnetic field responses for a half-space with a Cole-Cole impedance. Geophysics 1983, 48, 790–791. [Google Scholar] [CrossRef]
- Spies, B.R. A field occurrence of sign reversals with the transient electromagnetic method. Geophys. Prospect. 1980, 28, 620–632. [Google Scholar] [CrossRef]
- Raiche, A.P.; Bennett, L.A.; Clark, P.J.; Smith, R.J. The use of Cole–Cole impedances to interpret the TEM response of layered earths. Explor. Geophys. 1985, 16, 271–273. [Google Scholar] [CrossRef]
- Smith, R.S.; West, G.F. Inductive interaction between polarizable conductors: An explanation of a negative coincident-loop transient electromagnetic response. Geophysics 1988, 53, 677–690. [Google Scholar] [CrossRef]
- Flis, M.F.; Newman, G.A.; Hohmann, G.W. Induced-polarization effects in time-domain electromagnetic measurements. Geophysics 1989, 54, 514–523. [Google Scholar] [CrossRef] [Green Version]
- Lee, T. Transient electromagnetic response of a polarizable ground. Geophysics 1981, 46, 1037–1041. [Google Scholar] [CrossRef]
- Knight, J.H.; Raiche, A.P. Transient electromagnetic calculations using the Gaver-Stehfest inverse Laplace transform method. Geophysics 1982, 47, 47–50. [Google Scholar] [CrossRef]
- Yin, C.C.; Liu, B. The research on the 3D TDEM modeling and IP effect. Chin. J. Geophys. 1994, 37, 486–492. [Google Scholar]
- Marchant, D.; Haber, E.; Oldenburg, D.W. Three-dimensional modeling of IP effects in time-domain electromagnetic data. Geophysics 2014, 79, E303–E314. [Google Scholar] [CrossRef]
- Smith, R.S.; Klein, J. A special circumstance of airborne induced-polarization measurements. Geophysics 1996, 61, 66–73. [Google Scholar] [CrossRef]
- Yu, C.T.; Liu, H.F.; Zhang, X.J.; Yang, D.Y.; Li, Z.H. The analysis on IP signals in TEM response based on SVD. Appl. Geophys. 2013, 10, 79–87. [Google Scholar] [CrossRef]
- Flores, C.; Peralta-Ortega, S.A. Induced polarization with in-loop transient electromagnetic soundings: A case study of mineral discrimination at El Arco porphyry copper, Mexico. J. Appl. Geophys. 2009, 68, 423–436. [Google Scholar] [CrossRef]
- Zhi, Q.Q.; Deng, X.H.; Wu, J.J.; Li, X.; Wang, X.C.; Yang, Y.; Zhang, J. Inversion of IP-Affected TEM Responses and Its Application in High Polarization Area. J. Earth Sci. 2021, 32, 42–50. [Google Scholar] [CrossRef]
- Kozhevnikov, N.O.; Antonov, E.Y. Joint inversion of IP-affected TEM data. Russ. Geol. Geophys. 2009, 50, 136–142. [Google Scholar] [CrossRef]
- Kozhevnikov, N.O.; Antonov, E.Y. Inversion of IP-affected TEM responses of a two-layer earth. Russ. Geol. Geophys. 2010, 51, 708–718. [Google Scholar] [CrossRef]
- Key, K. 1D inversion of multicomponent, multifrequency marine CSEM data: Methodology and synthetic studies for resolving thin resistive layers. Geophysics 2009, 74, F9–F20. [Google Scholar] [CrossRef]
- Wu, J.J.; Zhi, Q.Q.; Deng, X.H.; Wang, X.C.; Yang, Y.; Zhang, J.; Dai, P. Exploration of Deep Geological Structure of Baiyun Gold Deposit in Eastern Liaoning Province with TEM. Earth Sci. 2020, 45, 4027–4037. [Google Scholar]









| Model | σ (S/m) | τ (s) | c | 1 − m |
|---|---|---|---|---|
| Lornex | 7.90 × 10−3 | 1.00 × 10−4 | 0.160 | 0.540 |
| Copper cities | 6.45 × 10−3 | 6.90 × 10−3 | 0.280 | 0.580 |
| Kidd Creek | 6.40 × 10−2 | 3.08 × 10−2 | 0.306 | 0.089 |
| Parameters | h (m) | ρ (Ω·m) | m | c | τ (s) |
|---|---|---|---|---|---|
| Layer 1 | 100 | 400 | 0.06 | 0.55 | 10−2 |
| Layer 2 | 50 | 100 | 0.06 | 0.55 | 10−2 |
| Layer 3 | - | 800 | 0.60 | 0.55 | 10−2 |
| Parameters | h (m) | ρ (Ω·m) | m | c | τ (s) |
|---|---|---|---|---|---|
| Layer 1 | 100 | 517 | 0.70 | 0.06 | 3.96 × 10−3 |
| Layer 2 | 50 | 195 | 0.66 | 0.36 | 3.98 × 10−3 |
| Layer 3 | - | 251 | 0.26 | 0.26 | 3.26 × 10−3 |
| Parameters | h (m) | ρ (Ω·m) | m | c | τ (s) |
|---|---|---|---|---|---|
| Layer 1 | 100 | 800 | 0.05 | 0.55 | 10−3 |
| Layer 2 | 50 | 100 | 0.30 | 0.55 | 10−3 |
| Layer 3 | - | 800 | 0.05 | 0.55 | 10−3 |
| Terms | Parameters | Terms | Parameters |
|---|---|---|---|
| Instrument | SMARTem24 | Receiver type | Crone probe |
| Current | 23 A | Receiver area | 3850 m2 |
| Time Base | 50 ms | Stack times | 512 |
| Ramp time | 122 μs | Receive signal | dBz/dt |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhi, Q.; Wu, J.; Li, X.; Wang, X.; Deng, X. Improving Inversion Quality of IP-Affected TEM Data Using Dual Source. Minerals 2022, 12, 684. https://doi.org/10.3390/min12060684
Zhi Q, Wu J, Li X, Wang X, Deng X. Improving Inversion Quality of IP-Affected TEM Data Using Dual Source. Minerals. 2022; 12(6):684. https://doi.org/10.3390/min12060684
Chicago/Turabian StyleZhi, Qingquan, Junjie Wu, Xiu Li, Xingchun Wang, and Xiaohong Deng. 2022. "Improving Inversion Quality of IP-Affected TEM Data Using Dual Source" Minerals 12, no. 6: 684. https://doi.org/10.3390/min12060684
APA StyleZhi, Q., Wu, J., Li, X., Wang, X., & Deng, X. (2022). Improving Inversion Quality of IP-Affected TEM Data Using Dual Source. Minerals, 12(6), 684. https://doi.org/10.3390/min12060684






