Rod Mill Product Control and Its Relation to Energy Consumption: A Case Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Particle Size Distribution Determination
2.2. Experimental Design
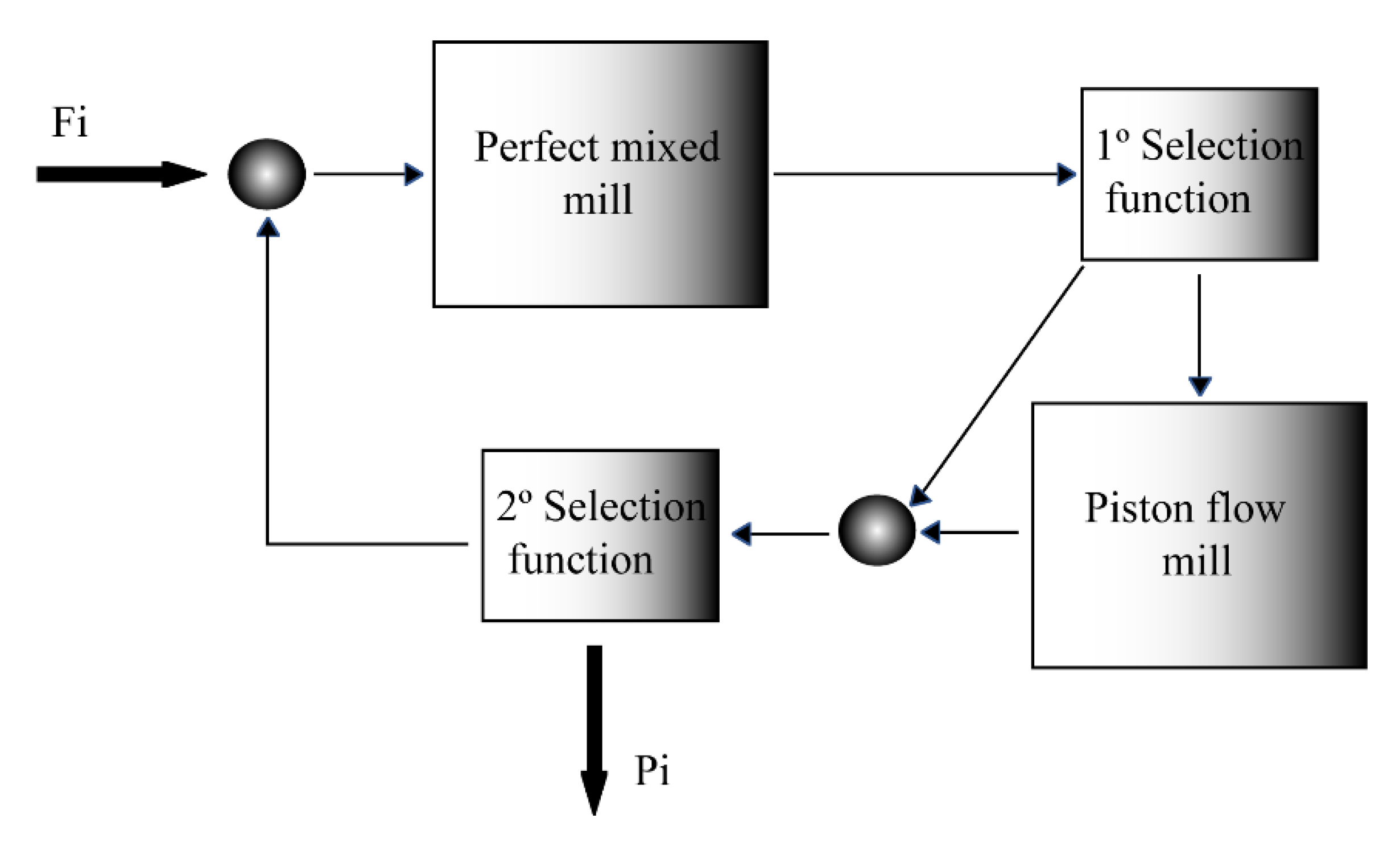
2.3. Mathematical Modeling for Optimization
3. Results
3.1. Particle Size Distribution and Energy Consumption Determination
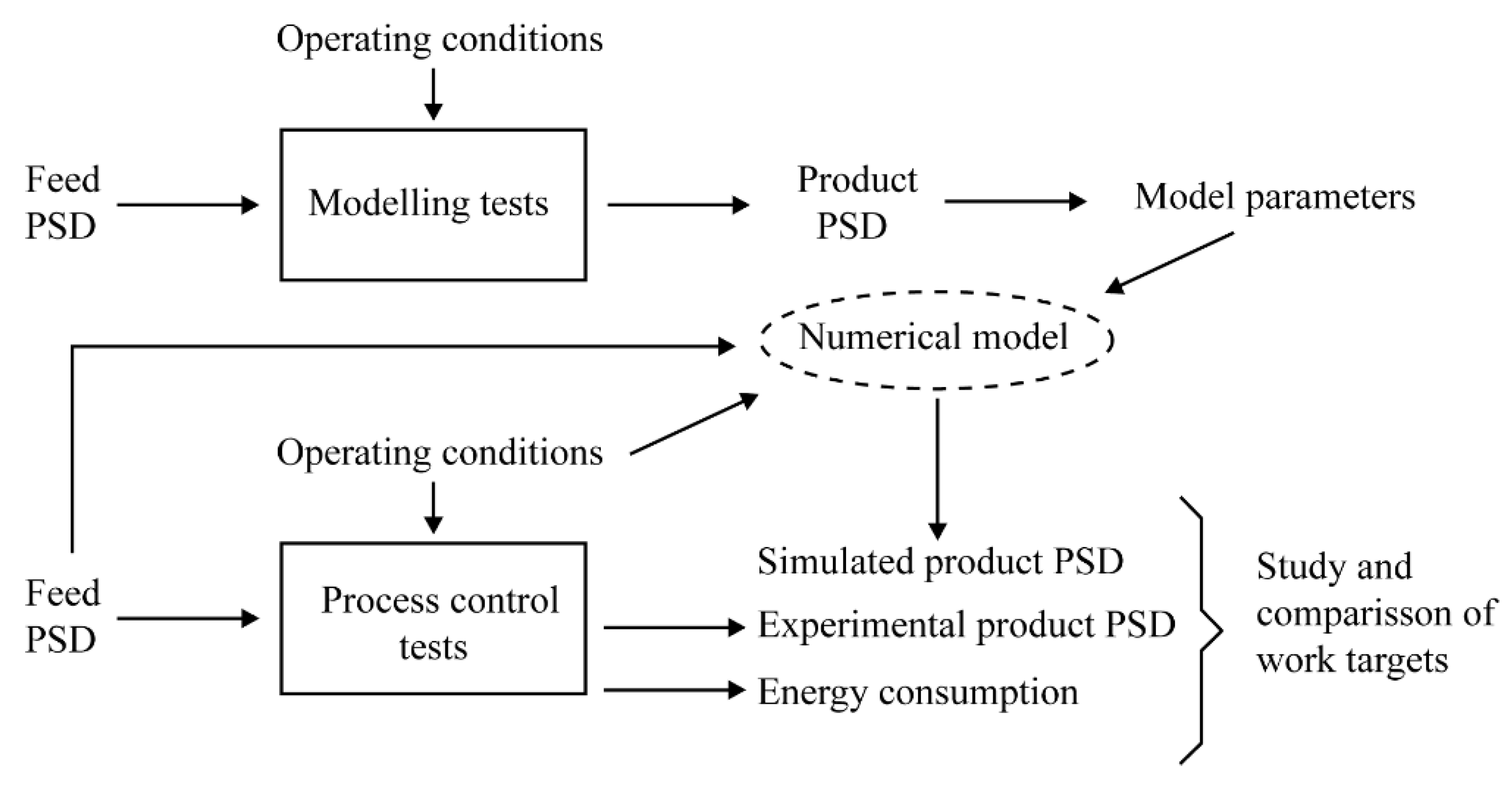
3.2. Numerical Simulation
4. Discussion
5. Conclusions
- -
- It was shown that by varying the percentage of critical mill speed or grinding media charge, the impact on reducing energy consumption becomes noticeable.
- -
- This work will take on more significance when it is necessary to reach mineral liberation while preventing overgrinding phenomena. In this sense, varying the solid/water ratio may well control excessive fine particle generation. Without being the best action to reduce energy consumption, some improvement in this respect can be observed.
- -
- It was also demonstrated how it is possible to control the particle size of the product by varying the feed rate, and lifter and rod geometry, while keeping energy utilization constant. By applying one or a combination of these criteria, it is possible to achieve both objectives, to control grinding without excessive energy consumption.
- -
- In the overall process, considering comminution as the most expensive module, an improvement in energy consumption efficiency could lead to subsequent savings for companies. A 20% reduction in media charge could lead to a 12% reduction in energy bill, which would be a remarkable milestone. Modeling and prediction approaches can also be used to manage production and energy issues, as simulation could express the product size, considering the parameters that affect the milling process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gupta, A.; Yan, D. Mineral Processing Design and Operation; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Zeng, Y.; Forssberg, E. Effects of mill feed on product fineness and energy consumption in coarse grinding. Miner. Eng. 1992, 4, 599–609. [Google Scholar] [CrossRef]
- Shoji, K.; Austin, L.G. A model for batch rod milling. Powder Technol. 1974, 10, 29–35. [Google Scholar] [CrossRef]
- Gaudin, A.M.; Schuhmann, R.; Schlechten, A.W. Flotation Kinetics. II. The Effect of Size on the Behavior of Galena Particles. J. Phys. Chem. 1942, 46, 902–910. [Google Scholar] [CrossRef]
- Crawford, R.; Ralston, J. The influence of particle size and contact angle in mineral flotation. Int. J. Miner. Process. 1987, 23, 1–24. [Google Scholar] [CrossRef]
- Derjaguin, B.V.; Dukhin, S. Theory of flotation of small and medium-size particles. Prog. Surf. Sci. 1993, 43, 241–266. [Google Scholar] [CrossRef]
- Bruckard, W.J.; Sparrow, G.J.; Woodcock, J.T. A review of the effects of the grinding environment on the flotation of copper sulphides. Int. J. Miner. Process. 2011, 100, 1–13. [Google Scholar] [CrossRef]
- Jeswiet, J.; Szekeres, A. Energy consumption in mining comminution. Procedia CIRP 2016, 48, 140–145. [Google Scholar] [CrossRef] [Green Version]
- Musa, F.; Morrison, R. A more sustainable approach to assessing comminution efficiency. Miner. Eng. 2009, 22, 593–601. [Google Scholar] [CrossRef]
- Heyes, G.W.; Kelsall, D.F.; Stewart, P.S.B. Continuous grinding in a small wet rod mil; Part I, comparison with a small ball mil. Powder Technol. 1972, 7, 235–319. [Google Scholar] [CrossRef]
- Li, Z.; Fu, Y.; Yang, C.; Yu, W.; Liu, L.; Qu, J.; Zhao, W. Mineral liberation analysis on coal component separated using typical comminution methods. Miner. Eng. 2018, 126, 74–81. [Google Scholar] [CrossRef]
- Devaswithin, A.; Pitchumani, B.; De Silva, S.R. Modified back-calculation method to predict particle size distribution for batch grinding in a ball mill. Ind. Eng. Chem. Res. 1988, 27, 723–726. [Google Scholar] [CrossRef]
- Austin, L.G.; Luckie, P.T. Methods of Determination of Breakage Distribution Parameters. Powder Technol. 1972, 5, 215–222. [Google Scholar] [CrossRef]
- Austin, L.G.; Shoji, K.; Bhatia, V.; Jindal, V.; Savage, K. Some Results on the Description of Size Reduction as a Rate Process in Various Mills. Ind. Eng. Chem. Process Des. Dev. 1976, 15, 187–196. [Google Scholar] [CrossRef]
- Lee, H.; Klima, M.S.; Saylor, P. Evaluation of a laboratory rod mill when grinding bituminous coal. Fuel 2012, 92, 116–121. [Google Scholar] [CrossRef]
- Hoşten, Ç.; Özbay, C. Technical note: A comparison of particle bed breakage and rod mill grinding with regard to mineral liberation and particle shape effects. Miner. Eng. 1998, 11, 871–874. [Google Scholar] [CrossRef]
- Wills, B.A. Mineral Processing Technology; Butterworth-Heineman: Oxford, UK, 1997. [Google Scholar]
- Soleymani, M.M.; Fooladi Mahani, M.; Rezaeizadeh, M. Experimental study the impact forces of tumbling mills. J. Process Mech. Eng. 2015, 231, 283–293. [Google Scholar] [CrossRef]
- Guasch, E.; Anticoi, H.; Hamid, S.A.; Oliva, J.; Alfonso, P.; Escobet, T.; Sanmiquel, L.; Bascompta, M. New approach to ball mill modelling as a piston flow process. Miner. Eng. 2018, 116, 82–87. [Google Scholar] [CrossRef]
- Usman, H.; Taylor, P.; Spiller, D.E. The Effects of Lifter Configurations and Mill Speeds on the Mill Power Draw and Performance. AIP Conf. Proc. 2017, 1805, 050001. [Google Scholar]
- Gupta, V.K.; Zouit, H.; Hodouin, D. The effect of ball and mill diameters on grinding rate parameters in dry grinding operation. Powder Technol. 1985, 42, 199–208. [Google Scholar] [CrossRef]
- Hasegawa, M.; Honma, T.; Kanda, Y. Effect of mil diameter on the rate of initial grinding in vibration balls mills. Powder Technol. 1990, 60, 259–264. [Google Scholar] [CrossRef]
- Powell, M.S. The effect of liner design on the motion of the outer grinding elements in a rotary mill. Int. J. Miner. Process. 1991, 31, 163–193. [Google Scholar] [CrossRef]
- Takalamide, M. Evaluating the Influence of Lifter Face Angle on the Trajectory of Particles in a Tumbling Mill Using PEPT. Master’s Thesis, University of Cape Town, Cape Town, South Africa, 2014. [Google Scholar]
- Yin, Z.; Peng, Y.; Zhu, Z.; Yu, Z.; Li, T. Impact Load behavior between Different Charge and Lifter in a Laboratory-Scale Mill. Materials 2017, 10, 882. [Google Scholar] [CrossRef] [PubMed]
- Yin, Z.; Peng, Y.; Li, T.; Wu, G. DEM Investigation of Mill Speed and Lifter Face Angle on Charge Behavior in Ball Mills. In Proceedings of the 5th International Conference on Advanced Composite Materials and Manufacturing Engineering, Jinan, China, 16–17 June 2018. [Google Scholar]
- Li, Z.; Wang, Y.; Li, K.; Lin, W.; Tong, X. Study on the performance of a ball mill with liner structure based on DEM. J. Eng. Technol. Sci. 2018, 50, 157–178. [Google Scholar] [CrossRef]
- Broussaud, A.; Albera, F. Selection of a model for the simulation of a pilot plant rod mill. Autom. Min. Miner. Met. Process. 1986, 20, 193–198. [Google Scholar] [CrossRef]
- Annapragada, A.; Adjei, A. Numerical simulation of milling processes as an aid to process design. Int. J. Pharm. 1996, 136, 1–11. [Google Scholar] [CrossRef]
- Foszcz, D.; Krawczykowski, D.; Gawenda, T.; Kasinska-Pilut, E.; Pawlos, W. Analysis of process of grinding efficiency in ball and rod mills with various feed parameters. IOP Conf. Ser. Mater. Sci. Eng. 2018, 427, 012031. [Google Scholar] [CrossRef]
- Pratseya, A.; Mawadati, A.; Putri, A.; Petrus, H. Study on Sumbawa gold ore liberation using rod mill: Effect of rod-number and rotational speed on particle size distribution. IOP Conf. Ser. Mater. Sci. Eng. 2018, 52, 012024. [Google Scholar]
- Góralczyk, M.; Krot, P.; Zimroz, R.; Ogonowski, S. Increasing energy efficiency and productivity of the comminution process in tumbling mills by indirect measurments of internal dynamics-An overview. Energies 2020, 13, 6735. [Google Scholar] [CrossRef]
- Mayer-Laigle, C.; Rajaonarivony, R.K.; Blanc, N.; Rouau, X. Comminution of dry lignocellulosic biomass: Part II. Technologies, improvement of milling performances and security issues. Bioengineering 2018, 5, 50. [Google Scholar] [CrossRef] [Green Version]
- Lau, L.; Fan, J. Laundry performance of fabric garments. Eng. Appar. Fabr. Garments 2009, 1, 339–360. [Google Scholar]
- ASTM International. Standard Specification for Woven Wire Test Sieve Cloth and Test Sieves; ASTM: West Conshohocken, PA, USA, 2020; pp. E11–E20. [Google Scholar]
- Austin, L.G.; Menacho, J.M.; Pearcy, F. A general model for semi-autogeneous and autogenous milling. APCON. In Proceedings of the Twentieth International Symposium on the Application of Computers and Mathematics in the Mineral Industries, Metallurgy, SAIMM, Johannesburg, South Africa, 19–23 October 1987; Volume 2, pp. 107–126. [Google Scholar]
- Whiten, W.J.; Walter, G.W.; White, M.E. A breakage function suitable for crusher models. In Proceedings of the 4th Tewkesbury Symposium, Melbourne, Australia, 12–14 February 1979; pp. 19.1–19.3. [Google Scholar]
- Kelly, E.G.; Spottiswood, D.J. The breakage function; what is it really? Miner. Eng. 1990, 3, 405–414. [Google Scholar] [CrossRef]
- Anticoi, H.; Guasch EHamid, S.; Oliva JAlfonso, P.; Garcia-Valles, M.; Escobet, T.; Sanmiquel, L.; Bascompta, M.; De Felipe, J.J.; Parcerisa, D.; Peña, E. Breakage function for HPGR: Mineral and mechanical characterization of tantalum and tungsten ores. Minerals 2018, 8, 170. [Google Scholar] [CrossRef] [Green Version]
- King, R.P. Modeling and Simulation of Mineral Processing Systems; Elsevier: Amsterdam, The Netherlands, 2001; ISBN 978-0-08-051184-9. [Google Scholar]
- Reid, K.J. A solution to the batch grinding equation. Chem. Eng. Sci. 1965, 20, 953–963. [Google Scholar] [CrossRef]
- Roy, K.; Das, R.N.; Ambure, P.; Aher, R. Be aware of error measures. Further studies on validation of predictive QSAR models. Chem. Intell. Lab. Syst. 2016, 152, 18–33. [Google Scholar] [CrossRef]
- Rogovin, Z.; Casali, A.; Herbst, A. Tracer study of mass transport and grinding in a rod mill. Int. J. Miner. Process. 1988, 22, 149–167. [Google Scholar] [CrossRef]
- Ghassa, S.; Gharabaghi, M.; Azadmehr, A.R.; Nasrabadi, M. Effects of Flow rate, slurry solid content, and feed size distribution on rod mill efficiency. Part. Sci. Technol. 2016, 34, 533–539. [Google Scholar] [CrossRef]
- Minin, I.; Dedyalkov, P.; Savov, S. Research of the charge load influence over the tumbling mill characteristics through general utility function. J. Chem. Metall. 2021, 56, 819–826. [Google Scholar]
- Bazin, C.; Obiang, P. Should the slurry density in a grinding mill be adjusted as a function of grinding media size. Miner. Eng. 2007, 20, 810–815. [Google Scholar] [CrossRef]
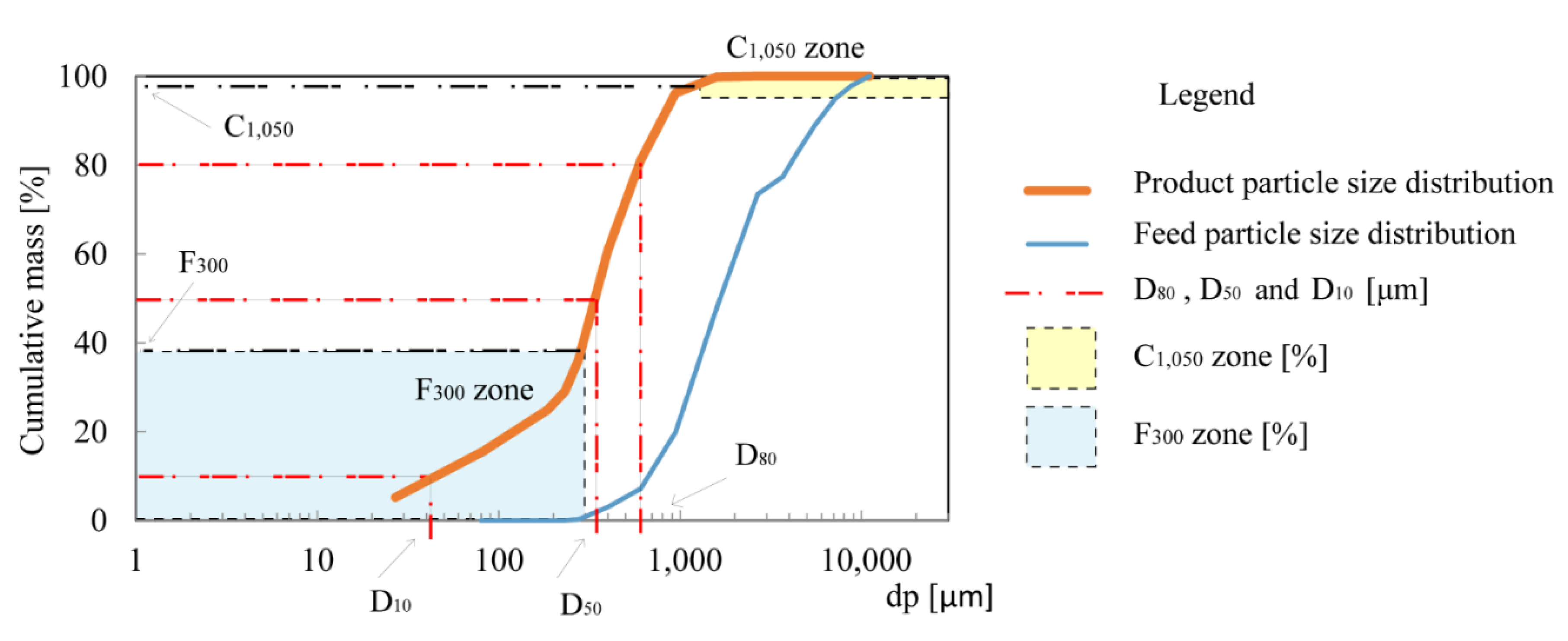
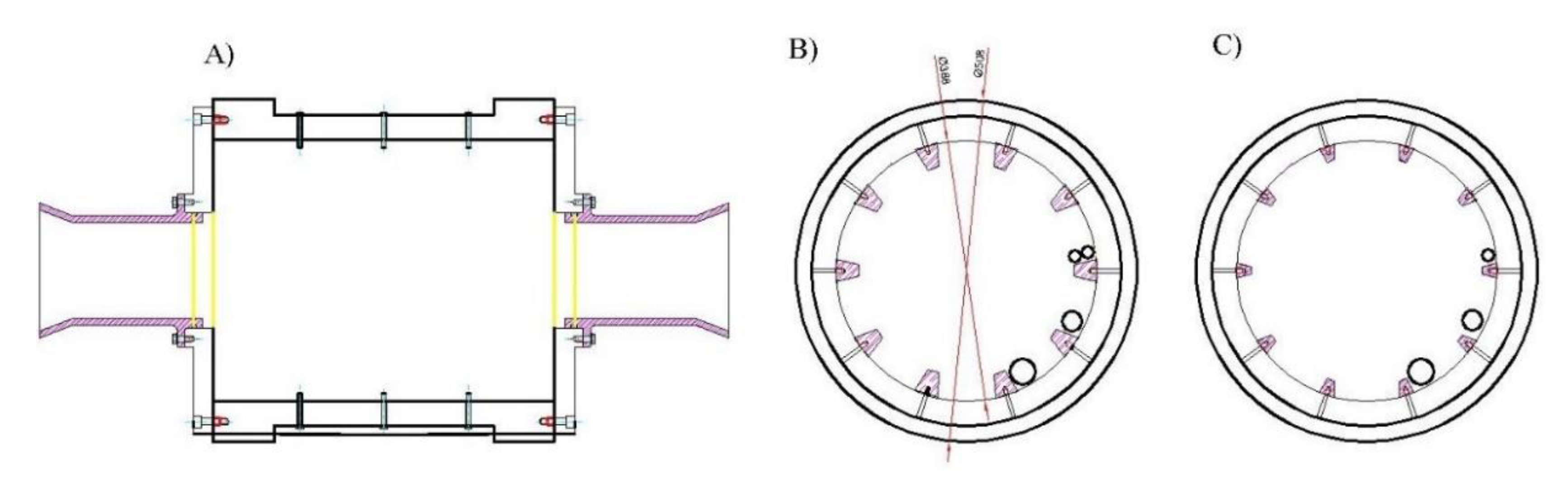
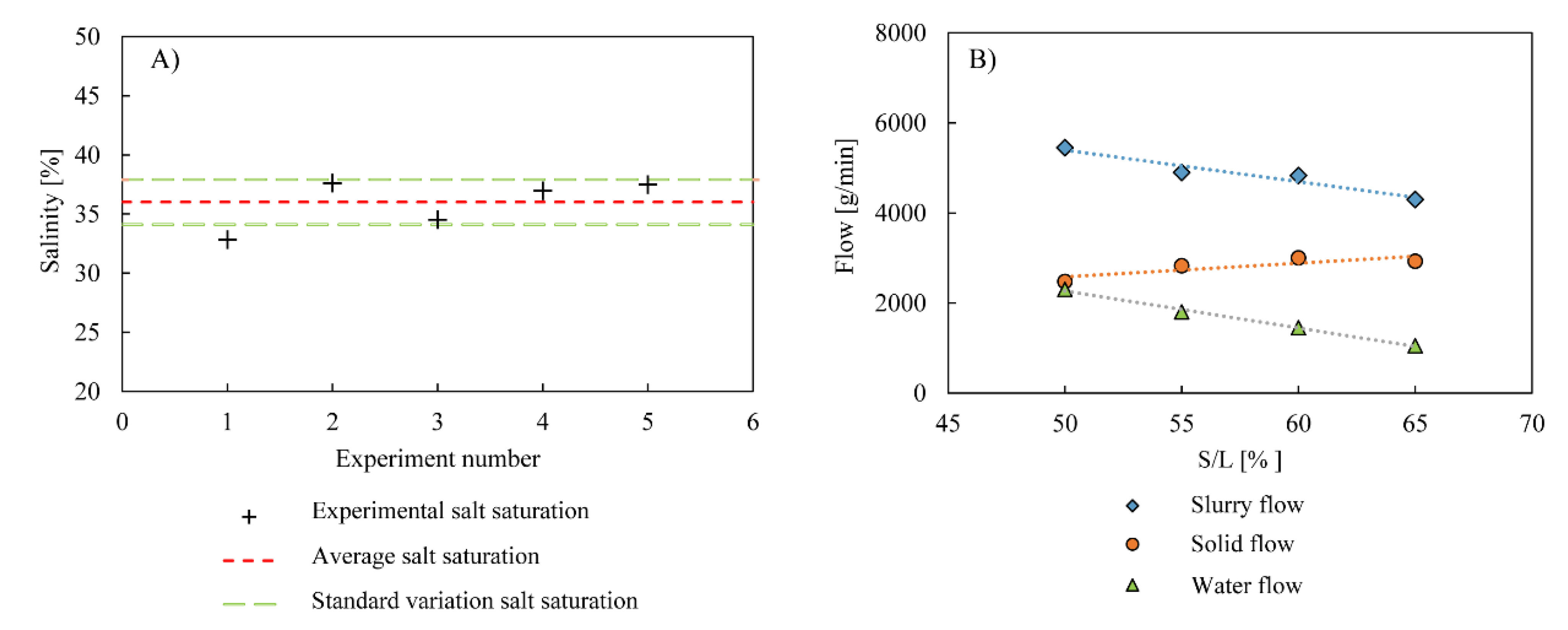

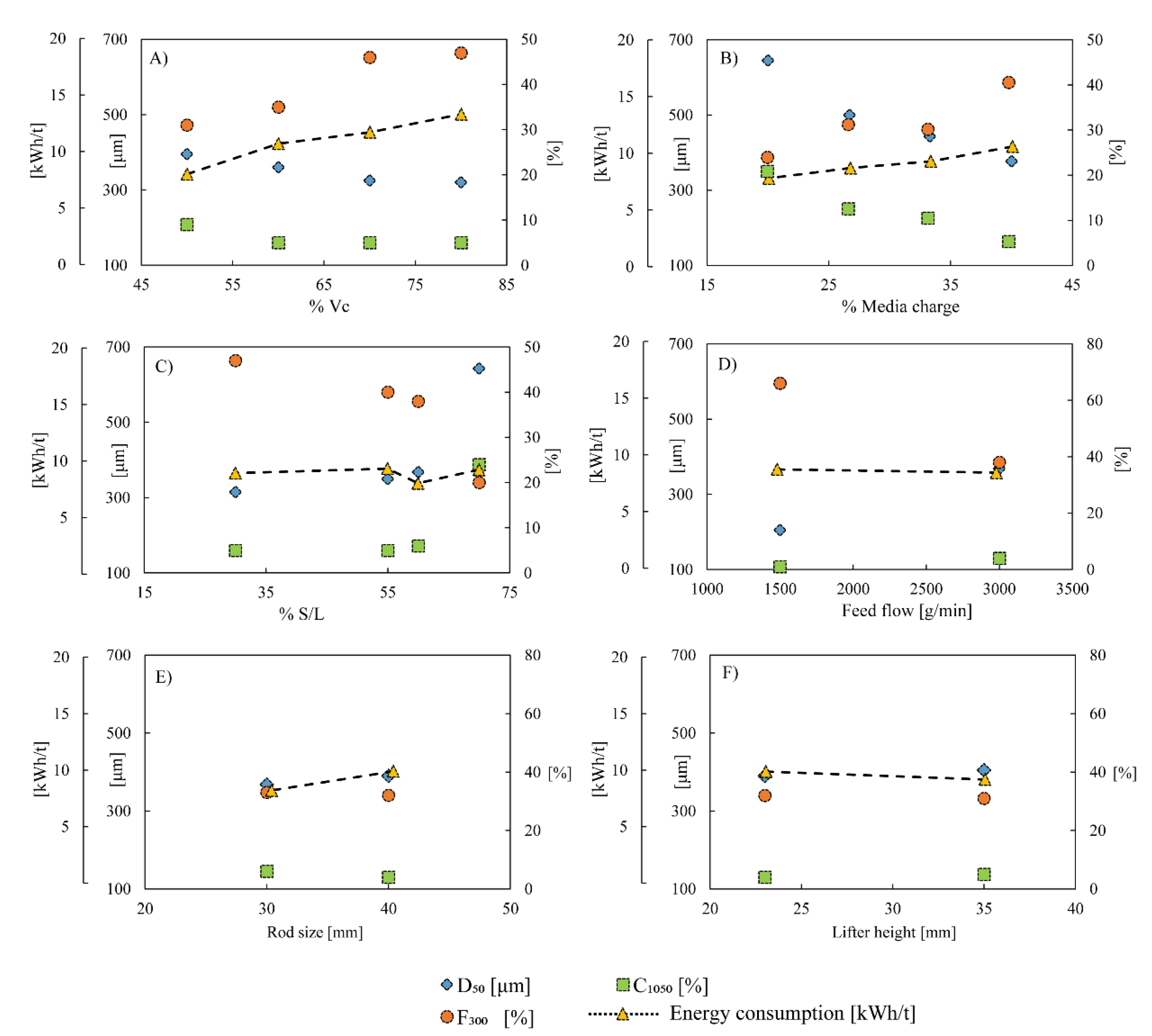
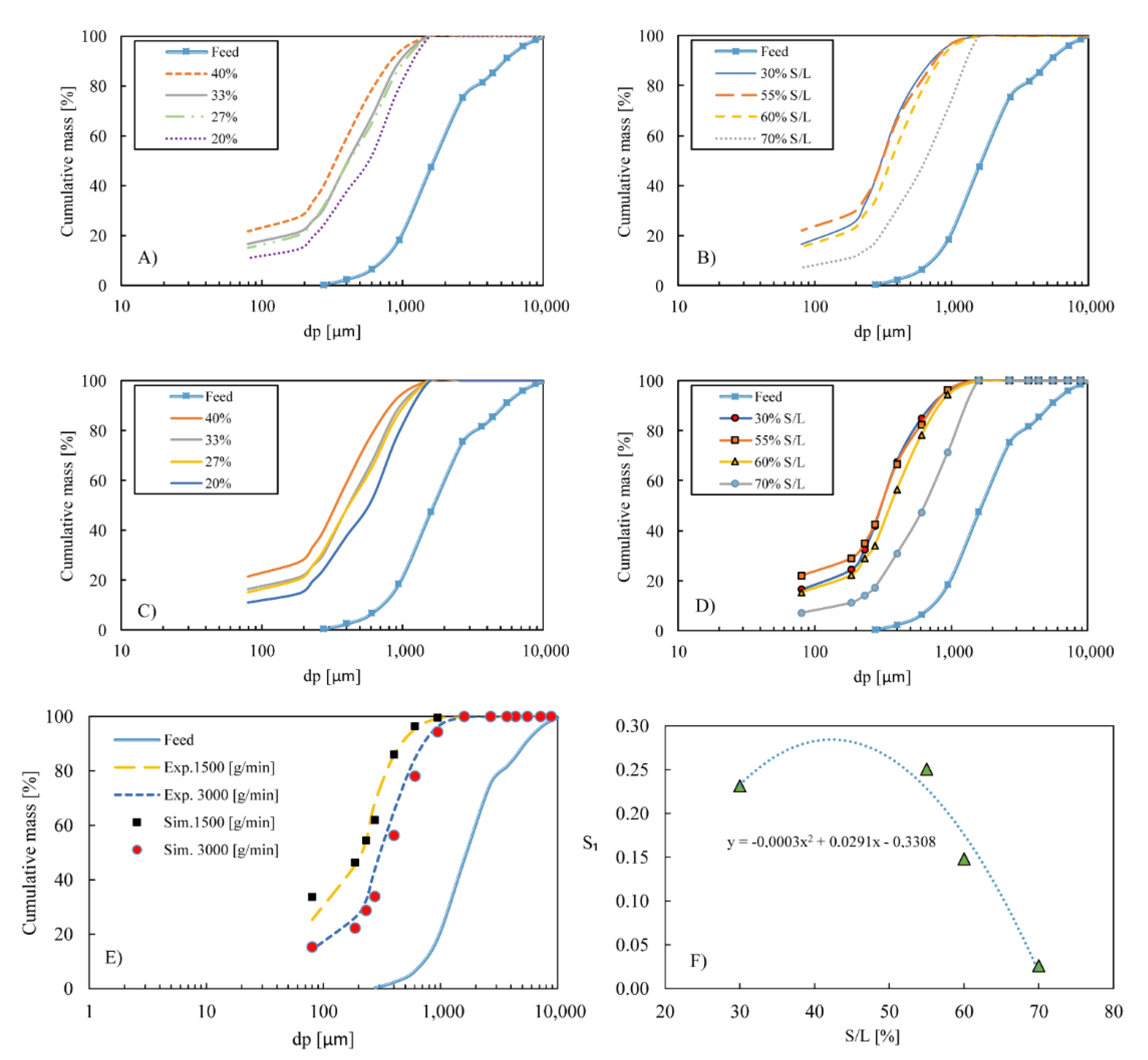
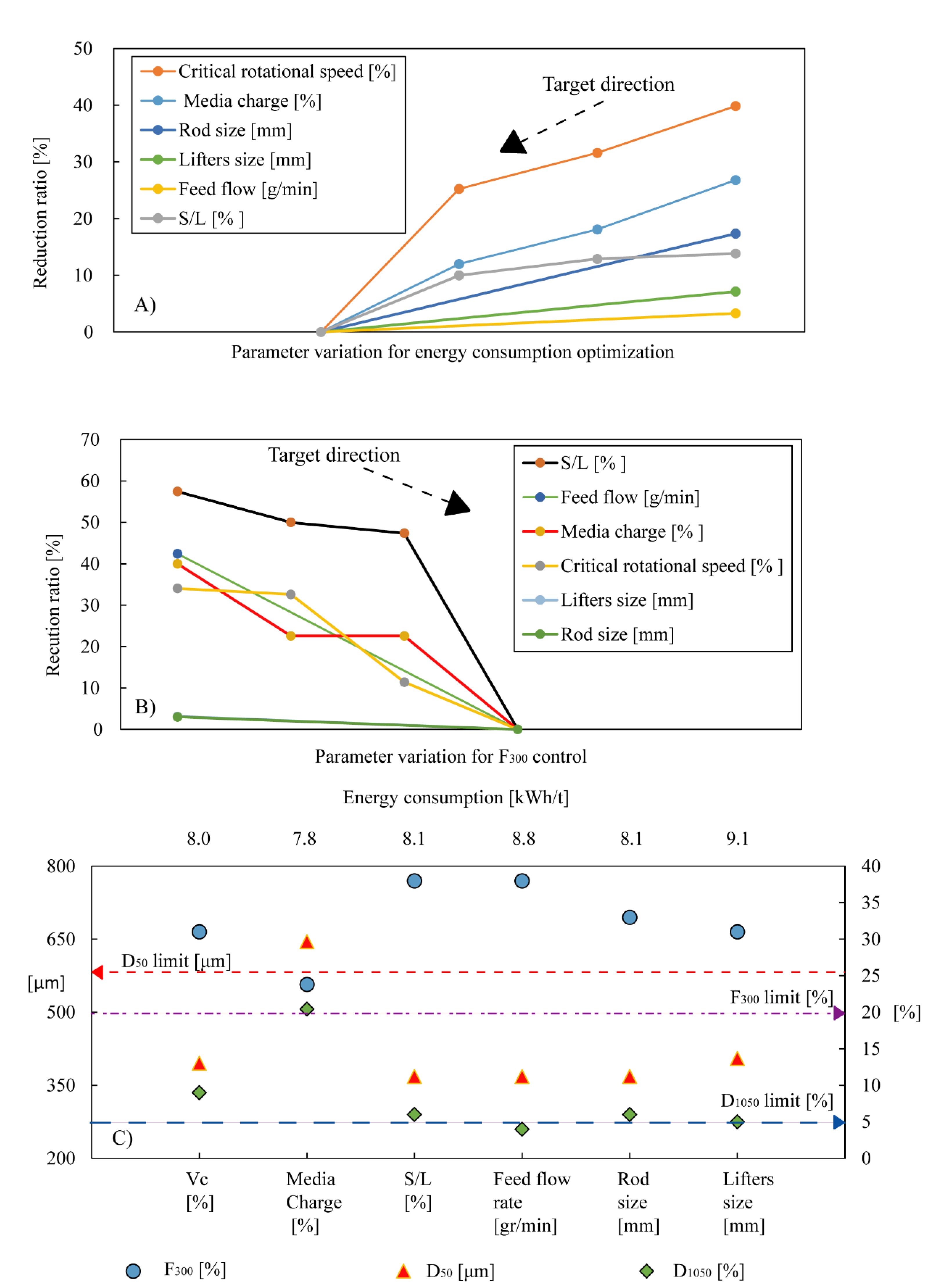
| Parameter | Meaning |
|---|---|
| D10 | 10% of the particles are under this size |
| D50 | 50% of the particles are under this size |
| D80 | 80% of the particles are under this size |
| F300 | Percentage of particles less than 300 μm |
| C1050 | Percentage of particles larger than 1050 μm |
| Feature | Value | Units |
|---|---|---|
| Internal diameter | 388 | mm |
| Internal length | 506 | mm |
| Rod media charge | 40, 33, 27, and 20 | % |
| Rod diameter | 30 and 40 | mm |
| Critical speed (Vc) | 71.2 | rpm |
| Engine power | 4 | kW |
| Tests | Vc | Media Charge | S/L |
|---|---|---|---|
| (%) | (%) | (%) | |
| A | 50 | 40 | 50–55–60–65 |
| B | 60 | 40 | 50–55–60–65 |
| C | 70 | 40 | 50–55–60–65 |
| D | 80 | 40 | 35–55–60–65 |
| Test | Vc | Media Charge | S/L | Solid Feed Flow | Rod Dimensions | Lifter Dimensions |
|---|---|---|---|---|---|---|
| (%) | (%) | (%) | (g/min) | (mm) | (mm) | |
| V1 | 50 | 40 | 60 | 3000 | 30 | 23 |
| V2 | 60 | |||||
| V3 | 70 | |||||
| V4 | 80 | |||||
| M1 | 60 | 40 | 60 | 3000 | 30 | 23 |
| M2 | 33 | |||||
| M3 | 27 | |||||
| M4 | 20 | |||||
| S1 | 60 | 40 | 30 | 3000 | 30 | 23 |
| S2 | 55 | |||||
| S3 | 60 | |||||
| S4 | 70 | |||||
| F1 | 60 | 40 | 60 | 1500 | 30 | 23 |
| F2 | 3000 | |||||
| R | 60 | 40 | 60 | 3000 | 40 | 23 |
| L | 60 | 40 | 60 | 3000 | 40 | 35 |
| Evaluated Parameter | Energy Consumption (kWh/t) | D50 (μm) | F300 (%) | C1050 (%) | |
|---|---|---|---|---|---|
| Critical rotational speed [%] | 50 | 8.0 | 395 | 31 | 9 |
| 60 | 10.7 | 360 | 35 | 5 | |
| 70 | 11.7 | 325 | 46 | 5 | |
| 80 | 13.3 | 320 | 47 | 5 | |
| Media charge [%] | 20 | 7.8 | 645 | 24 | 21 |
| 27 | 8.7 | 500 | 31 | 13 | |
| 33 | 9.3 | 443 | 31 | 11 | |
| 40 | 10.6 | 377 | 40 | 6 | |
| Solid/water rate S/L [%] | 30 | 9.0 | 315 | 47 | 5 |
| 55 | 9.4 | 350 | 40 | 5 | |
| 60 | 8.1 | 368 | 38 | 6 | |
| 70 | 9.3 | 643 | 20 | 24 | |
| Feed flow [g/min] | 1500 | 9.1 | 205 | 66 | 1 |
| 3000 | 8.8 | 368 | 38 | 4 | |
| Rod size [mm] | 30 | 8.1 | 368 | 33 | 6 |
| 40 | 9.8 | 390 | 32 | 4 | |
| Lifter size [mm] | 23 | 9.8 | 390 | 32 | 4 |
| 35 | 9.1 | 405 | 31 | 5 | |
| Parameter | Value |
|---|---|
| k | 0.500 |
| n1 | 1.022 |
| n2 | 1.500 |
| S1 | - |
| α | 3.204 |
| ω1 | 0.005 |
| β1 | 2.970 |
| ω2 | 0.005 |
| β2 | 4.372 |
| Experimental | Simulated | |||||
|---|---|---|---|---|---|---|
| Parameter | F300 (%) | C1050 (%) | D50 (μm) | F300 (%) | C1050 (%) | D50 (μm) |
| Critical rotational speed | 31 | 9 | 395 | 34 | 8.5 | 410 |
| 35 | 5 | 360 | 39 | 5.0 | 365 | |
| 46 | 5 | 325 | 47 | 4.0 | 320 | |
| 47 | 5 | 320 | 46 | 4.0 | 325 | |
| Media charge [%] | 40 | 6 | 377 | 41 | 4.0 | 340 |
| 30 | 11 | 443 | 31 | 9.0 | 420 | |
| 31 | 13 | 500 | 30 | 9.0 | 425 | |
| 24 | 21 | 645 | 21 | 17.0 | 580 | |
| Solid/water Rate S/L [%] | 20 | 24 | 643 | 20 | 21.0 | 640 |
| 38 | 6 | 368 | 41 | 5.0 | 360 | |
| 40 | 5 | 350 | 49 | 3.0 | 340 | |
| 47 | 5 | 315 | 48 | 3.0 | 316 | |
| Feed flow [g/min] | 66 | 1 | 205 | 72 | 1.0 | 210 |
| 38 | 4 | 368 | 40 | 4.5 | 355 | |
| Rod size [mm] | 32 | 4 | 390 | 37 | 6.0 | 380 |
| 33 | 6 | 368 | 40 | 4.5 | 360 | |
| Lifter size [mm] | 32 | 4 | 390 | 39 | 4.5 | 380 |
| 31 | 5 | 405 | 35 | 5.5 | 400 | |
| RMSE | 4.1 | 1.9 | 26.6 | |||
| % Media Charge | Energy (kWh/t) | Energy Red. (%) |
|---|---|---|
| 40 | 10.6 | 0 |
| 33 | 9.3 | 12.1 |
| 27 | 8.7 | 18.1 |
| 20 | 7.8 | 26.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anticoi, H.; Guasch, E.; Pérez-Álvarez, R.; de Luis-Ruiz, J.M.; Oliva, J.; Hoffman Sampaio, C. Rod Mill Product Control and Its Relation to Energy Consumption: A Case Study. Minerals 2022, 12, 183. https://doi.org/10.3390/min12020183
Anticoi H, Guasch E, Pérez-Álvarez R, de Luis-Ruiz JM, Oliva J, Hoffman Sampaio C. Rod Mill Product Control and Its Relation to Energy Consumption: A Case Study. Minerals. 2022; 12(2):183. https://doi.org/10.3390/min12020183
Chicago/Turabian StyleAnticoi, Hernan, Eduard Guasch, Rubén Pérez-Álvarez, Julio Manuel de Luis-Ruiz, Josep Oliva, and Carlos Hoffman Sampaio. 2022. "Rod Mill Product Control and Its Relation to Energy Consumption: A Case Study" Minerals 12, no. 2: 183. https://doi.org/10.3390/min12020183
APA StyleAnticoi, H., Guasch, E., Pérez-Álvarez, R., de Luis-Ruiz, J. M., Oliva, J., & Hoffman Sampaio, C. (2022). Rod Mill Product Control and Its Relation to Energy Consumption: A Case Study. Minerals, 12(2), 183. https://doi.org/10.3390/min12020183











