An Effective Algorithm for 2D Marine CSEM Modeling in Anisotropic Media Using a Wavelet Galerkin Method
Abstract
:1. Introduction
2. Methodology
2.1. MCSEM Field Governing Equations
2.2. WGM
2.3. WGM Analysis
2.4. Boundary Conditions
3. Model Study Results
3.1. Simple Model for Verification Algorithm
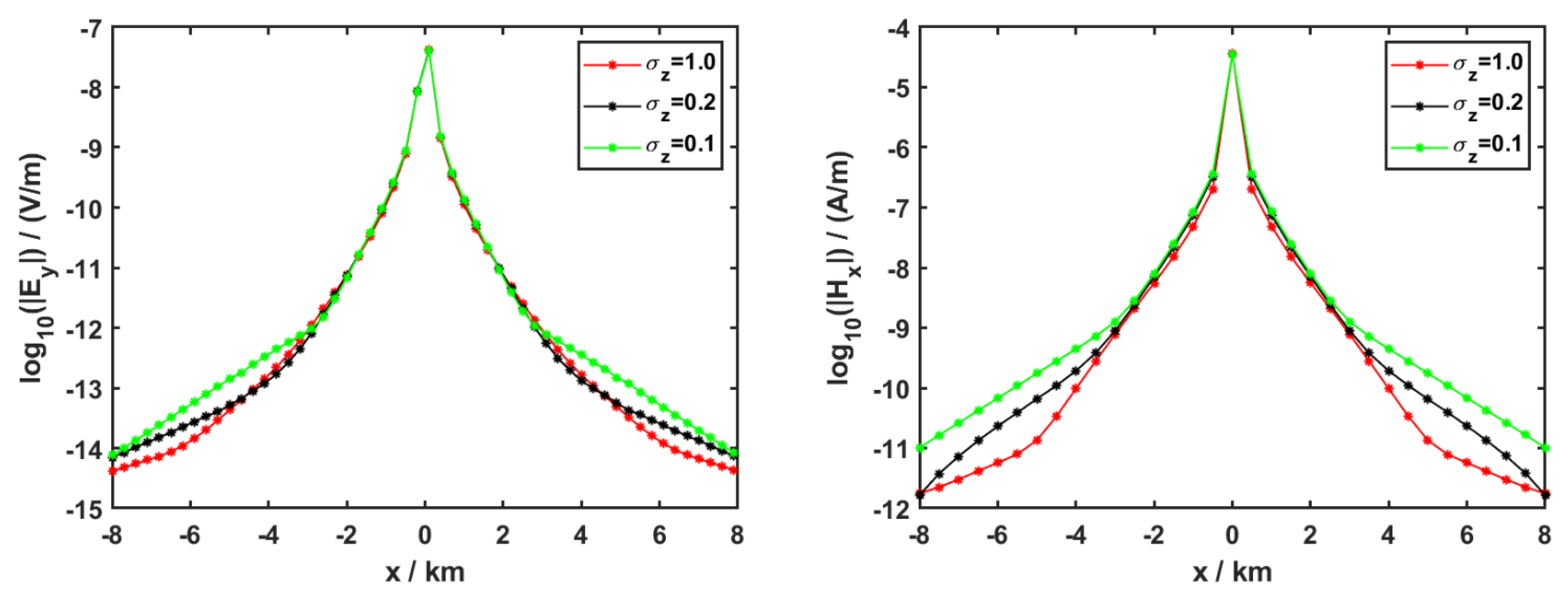
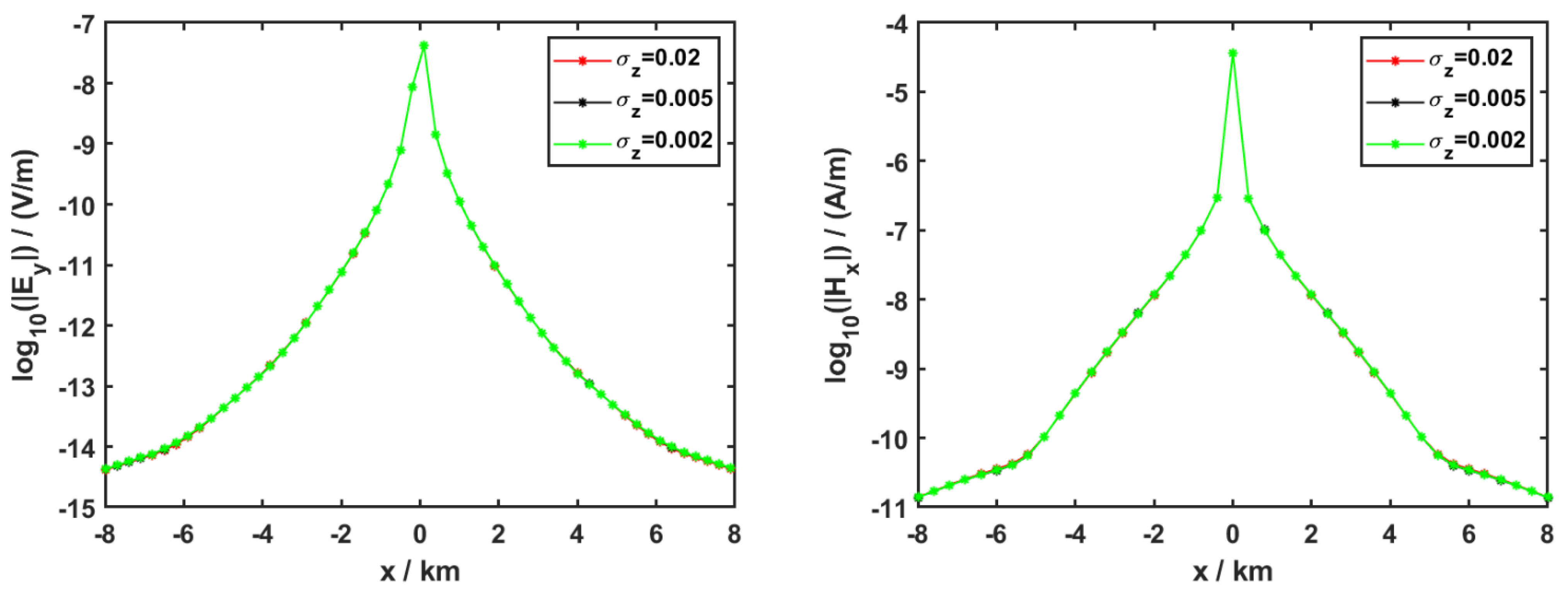
3.2. Anisotropy in the Sediment
3.3. Anisotropy in the Reservoir
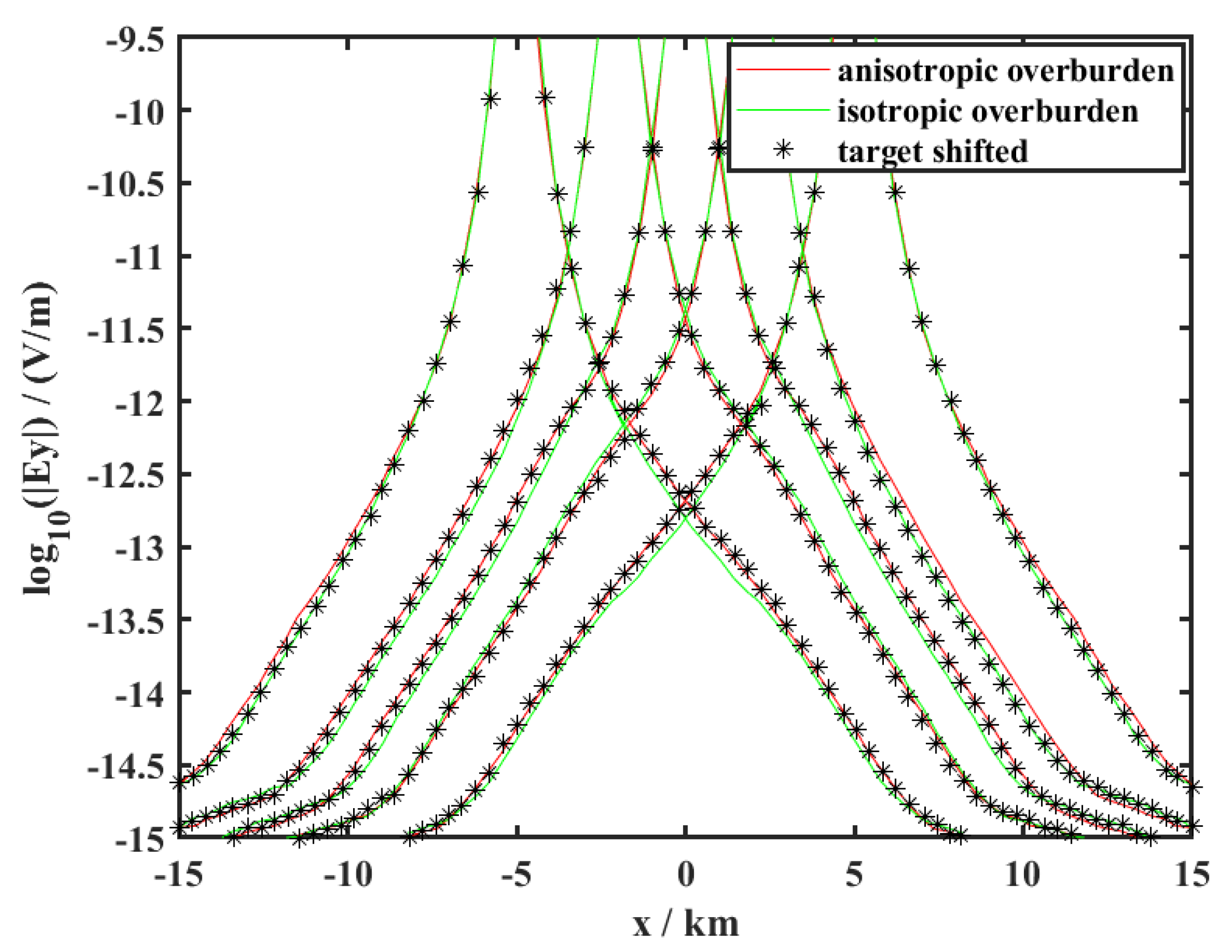
3.4. Effect of Isotropic and Anisotropic Overburdens on Underlying Targets
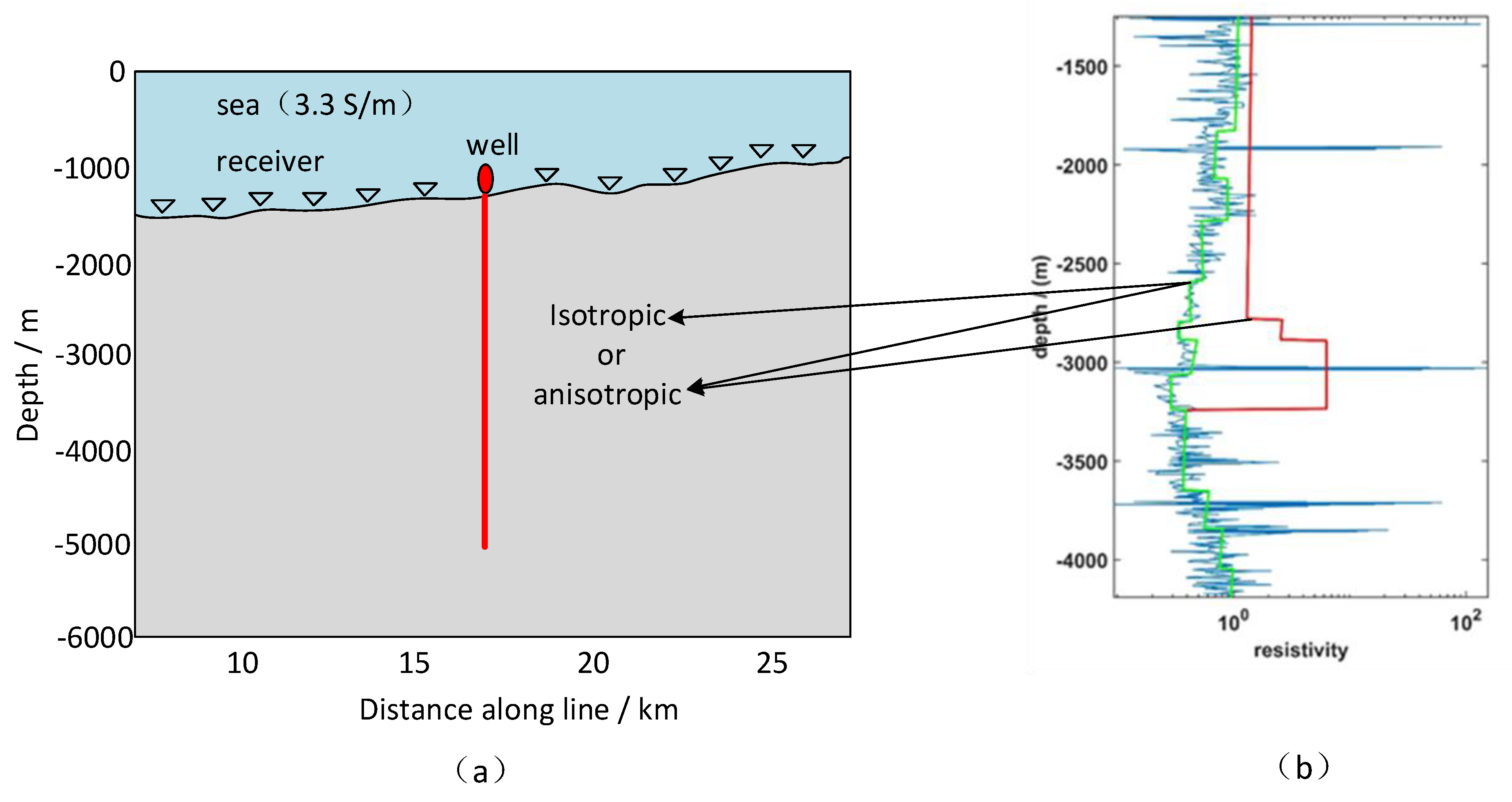
3.5. Real Data
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Srnka, L.J.; Carazzone, J.J.; Ephron, M.S.; Eriksen, E.A. Remote reservoir resistivity mapping. Lead. Edge 2006, 25, 972–975. [Google Scholar] [CrossRef]
- Constable, S.; Srnka, L.J. An introduction to marine controlled-source electromagnetic methods for hydrocarbon exploration. Geophysics 2007, 72, WA3–WA12. [Google Scholar] [CrossRef]
- Li, Y.; Key, K. 2D marine controlled-source electromagnetic modeling, Part 1: An adaptive finite-element algorithm. Geophysics 2007, 72, WA51–WA62. [Google Scholar] [CrossRef] [Green Version]
- Yuji, M. 2-D electromagnetic modeling by finite-element method with a dipole source and topography. Geophysics 2012, 65, 465–475. [Google Scholar]
- Kerry, K. MARE2DEM: A 2-D inversion code for controlled-source electromagnetic and magneto telluric data. Geophys. J. Int. 2016, 207, 571–588. [Google Scholar]
- Josef, P.; Tomáš, V. Finite-difference modelling of magnetotelluric fields in two-dimensional anisotropic media. Geophys. J. Int. 1997, 128, 505–521. [Google Scholar]
- Arash, J.G.; Hiroshi, T. Efficient FDTD algorithm for plane-wave simulation for vertically heterogeneous attenuative media. Geophysics 2007, 72, H43–H53. [Google Scholar]
- Aria, A.; Peter, M.V.D.; Tarek, M.H. An integral equation approach for 2.5-dimensional forward and inverse electromagnetic scattering. Geophys. J. Int. 2006, 165, 744–762. [Google Scholar]
- Daubechies, I. Orthonormal bases of compactly supported wavelet. Commun. Pure Appl. Math. 1988, 41, 906–996. [Google Scholar] [CrossRef] [Green Version]
- Moller, N.O. Wavelets in Scientific Computing. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 1998. [Google Scholar]
- Hussaina, N.; Karsitia, M.N.; Yahyaa, N.; Jeotia, V.; Yahyab, N. 2D wavelets Galerkin method for the computation of EM field on seafloor excited by a point source. Int. J. Appl. Electromagn. Mech. 2017, 53, 631–644. [Google Scholar] [CrossRef]
- Chen, H.B.; Li, T.L. 3D Marine Controlled-Source electromagnetic modeling in an Anisotropic Medium Using a Wavelet-Galerkin Method with a Secondary Potential Formulation. Geophys. J. Int. 2019, 219, 373–393. [Google Scholar] [CrossRef]
- Ramananjaona, C.; MacGregor, L.; Andréis, D. Sensitivity and inversion of marine electromagnetic data in a vertically anisotropic stratified earth. Geophys. Prospect. 2011, 110, 341–360. [Google Scholar] [CrossRef]
- Brown, V.; Hoversten, M.; Key, K.; Chen, J. Resolution of reservoir scale electrical anisotropy from marine CSEM data. Geophysics 2012, 77, E147–E158. [Google Scholar] [CrossRef]
- Newman, G.A.; Commer, M.; Carazzone, J.J. Imaging CSEM data in the presence of electrical anisotropy. Geophysics 2010, 75, F51–F61. [Google Scholar] [CrossRef]
- Kong, F.N.; Johnstad, S.E.; Rosten, T.; Westerdahl, H. A 2.5D finite-element modeling difference method for marine CSEM modeling in stratified anisotropic media. Geophysics 2008, 73, F9–F19. [Google Scholar] [CrossRef]
- Weiss, C.J.; Newman, G.A. Electromagnetic induction in a fully 3D anisotropic earth. Geophysics 2002, 67, 104–114. [Google Scholar] [CrossRef]
- Freund, R.W.; Nachtigal, N.M. QMR: A quasi-minimal residual method for non-Hermitian linear systems. Numer. Math. 1991, 60, 315–339. [Google Scholar] [CrossRef] [Green Version]
- Debnath, L.; Shah, F.A. Multiresolution Analysis and Construction of Wavelets. In Wavelet Transforms and Their Applications; Birkhäuser: Boston, MA, USA, 2015; Volume 45, pp. 375–440. [Google Scholar]
- Li, B.; Chen, X. Wavelet-based numerical analysis: A review and classification. Finite Elem. Anal. Des. 2014, 81, 14–31. [Google Scholar] [CrossRef]
- Latto, A. The Evaluation of Connection Coefficients of Compactly Supported Wavelets; Princeton: New York, NY, USA, 1991. [Google Scholar]
- Keller, G.V.; Frischknecht, F.C. Electrical Methods in Geophysical Prospecting; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Christensen, N.B. Difficulties in determining electrical anisotropy in subsurface investigations. Geophys. Prospect. 2000, 48, 1–19. [Google Scholar] [CrossRef]
- Aissaoui, R.; Bounif, A.; Zeyen, H.; Messaoudi, S.A. Evaluation of resistivity anisotropy parameters in the Eastern Mitidja basin, Algeria, using azimuthal electrical resistivity tomography. Near Surf. Geophys. 2019, 17, 359–378. [Google Scholar] [CrossRef]
- Ramananjaona, C.; Macgregor, L. 2.5D inversion of CSEM data in a vertically anisotropic earth. J. Phys. Conf. Ser. 2010, 255, 012004. [Google Scholar] [CrossRef]
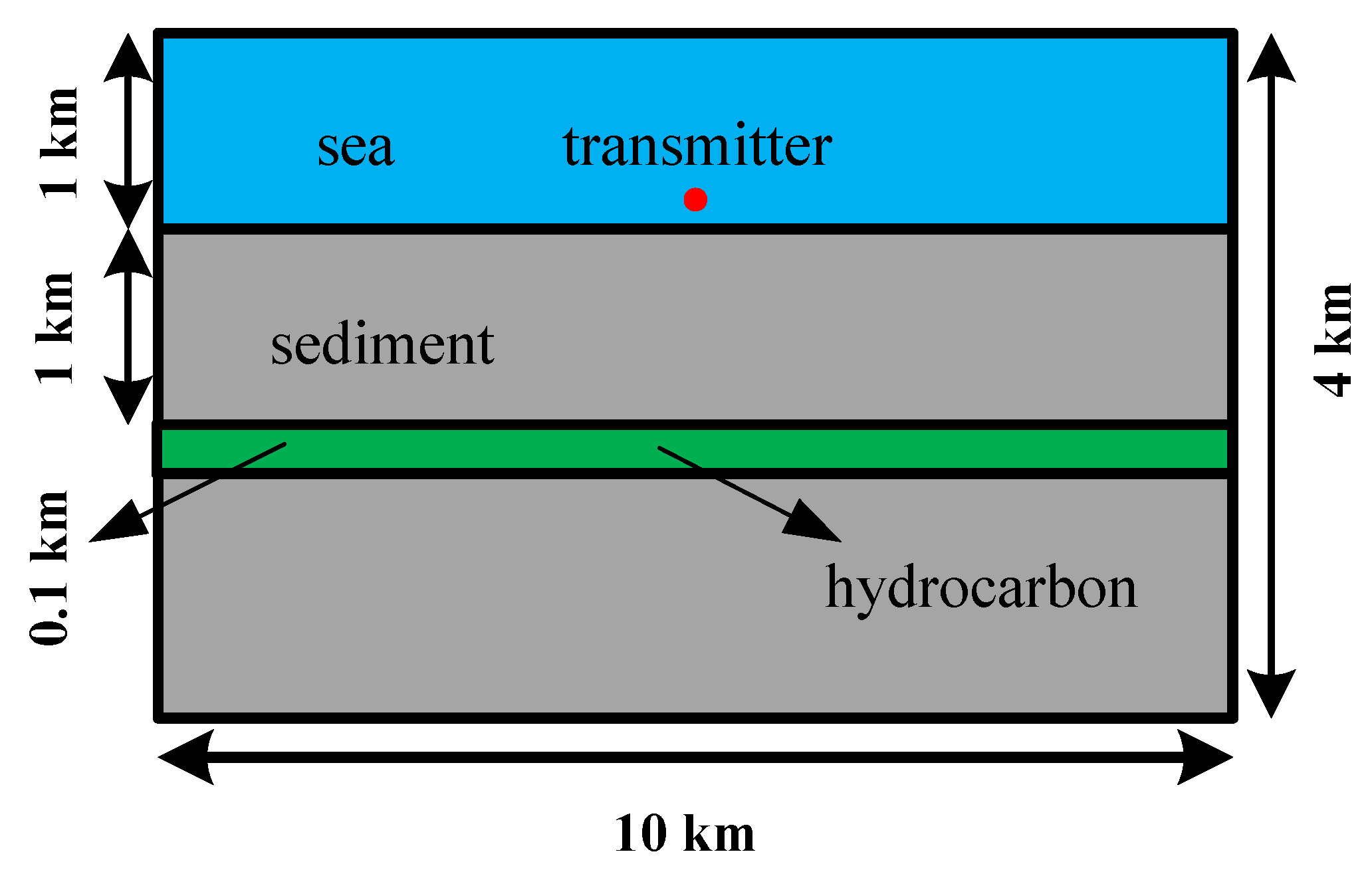
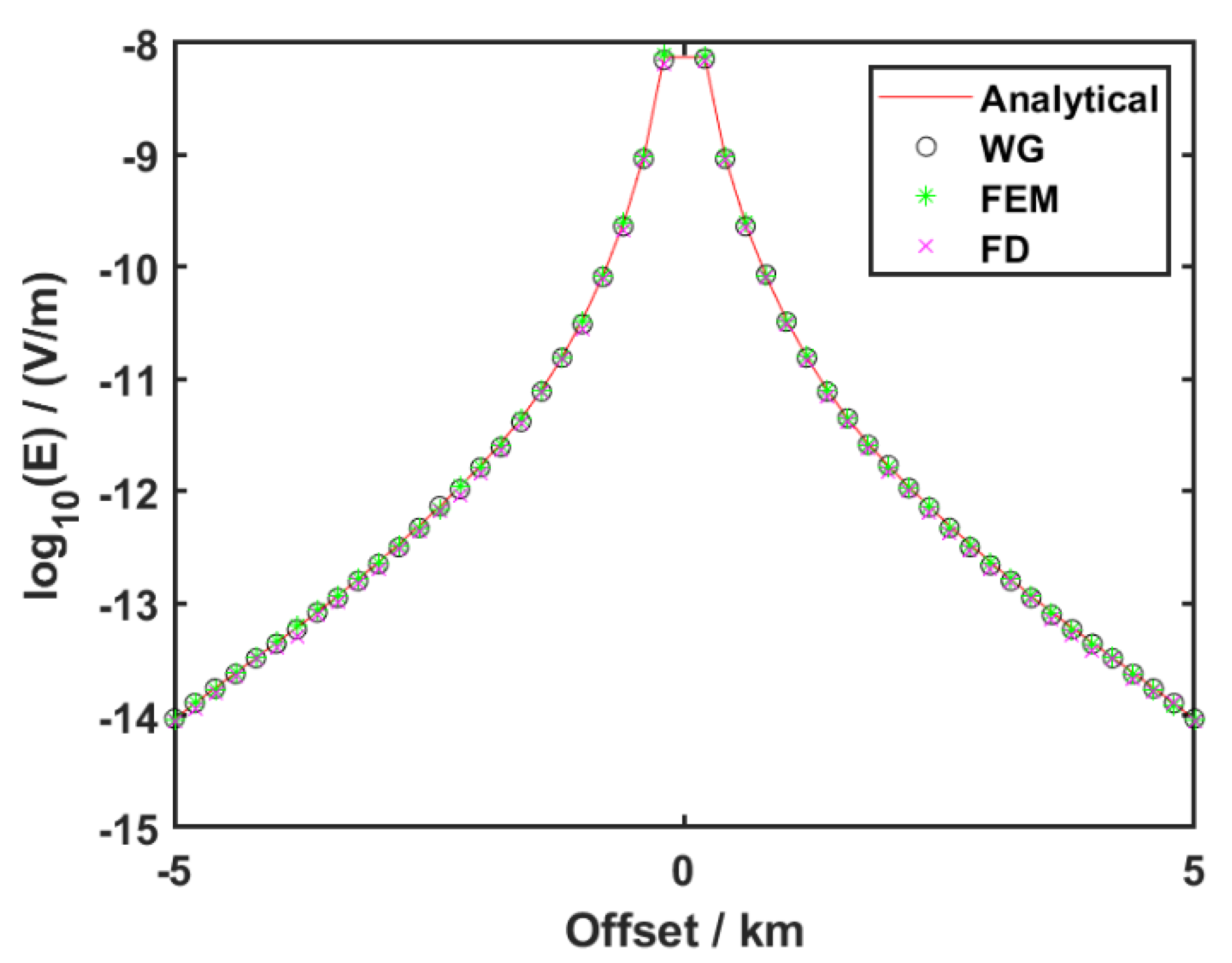

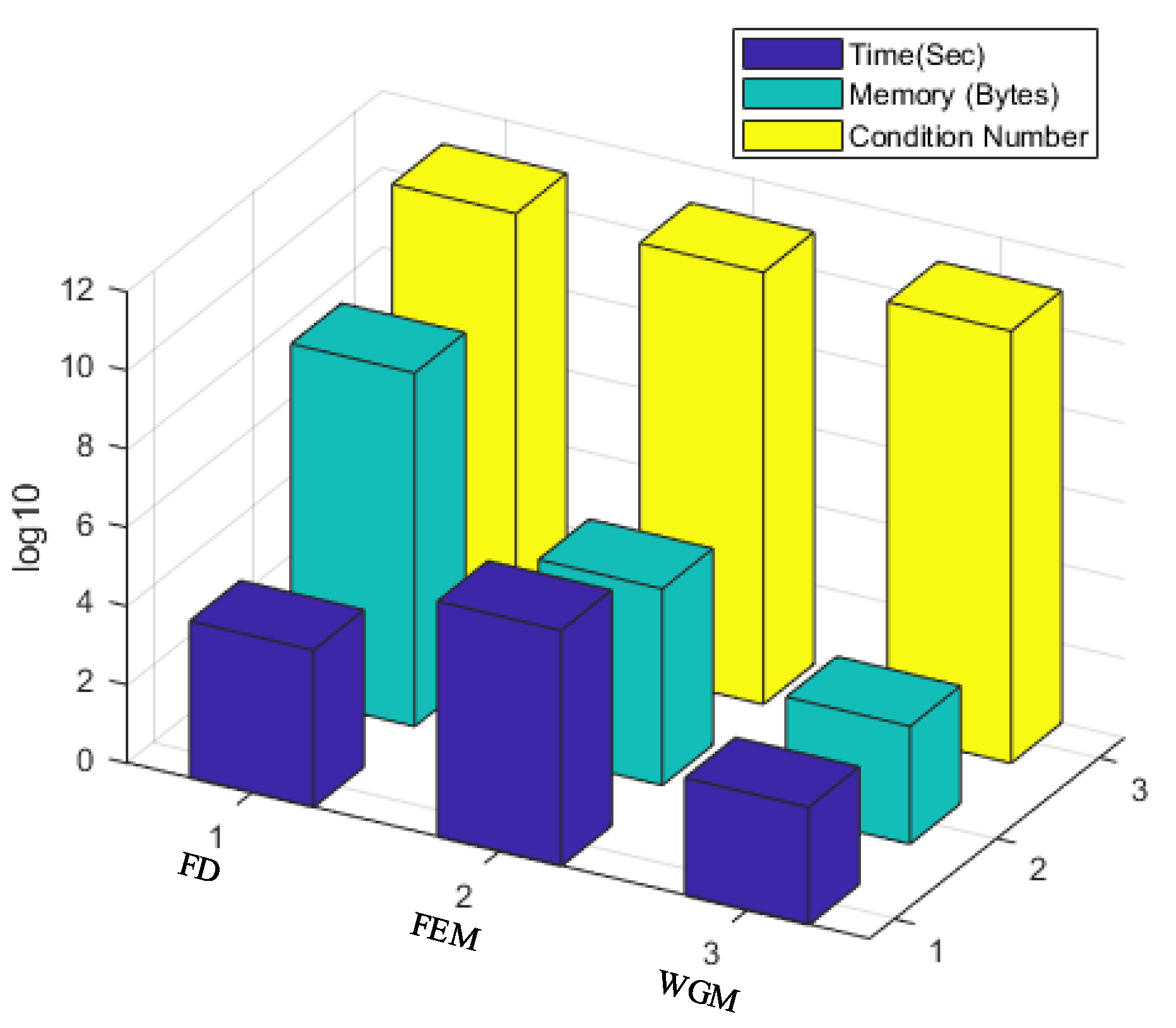

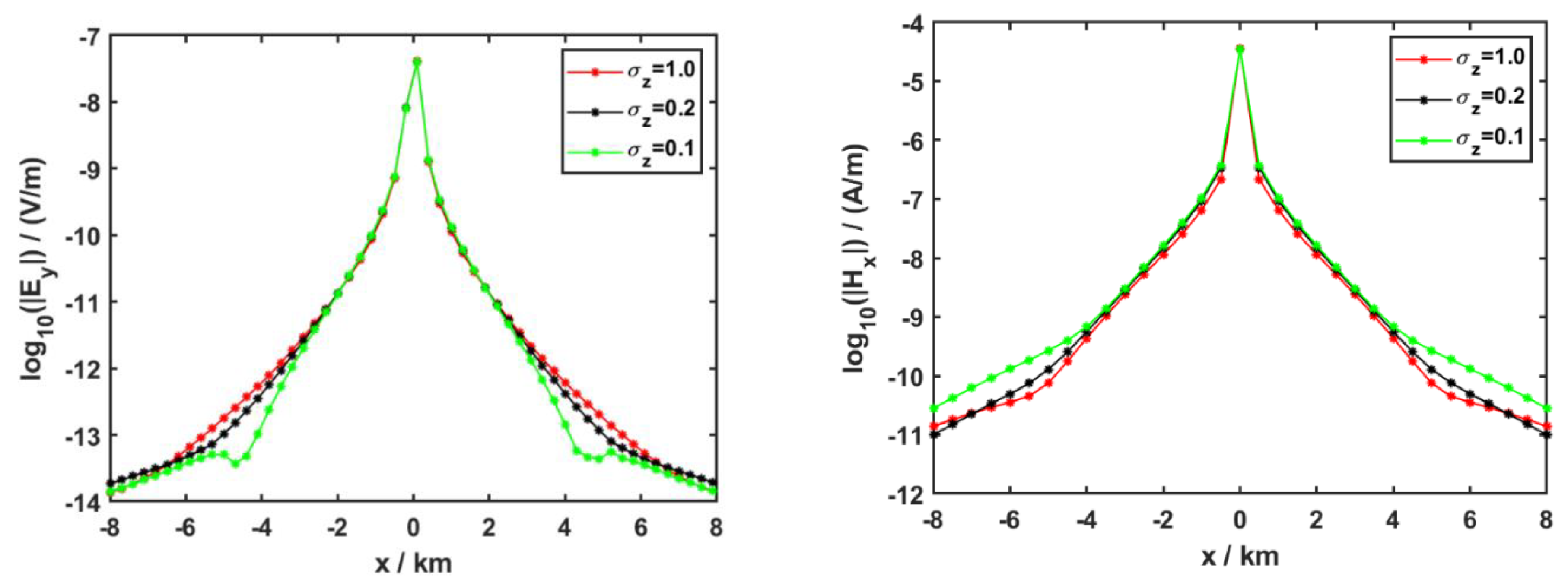





| Parameters | Symbols | Magnitude |
|---|---|---|
| Frequency | f | 0.5 Hz |
| Air | S/m | |
| Seawater | 3.30 S/m | |
| Sediment | 1.0 S/m | |
| Hydrocarbon | 0.1 S/m |
| Parameters | |||
|---|---|---|---|
| Air | 1 × 10−8 | 1 × 10−8 | 1 × 10−8 |
| Seawater | 3.3 | 3.3 | 3.3 |
| Sediment | 1.0 | 1.0 | 1.0, 0.2, 0.1 |
| Reservoir | 0.02 | 0.02 | 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Xiong, B.; Han, Y. An Effective Algorithm for 2D Marine CSEM Modeling in Anisotropic Media Using a Wavelet Galerkin Method. Minerals 2022, 12, 124. https://doi.org/10.3390/min12020124
Chen H, Xiong B, Han Y. An Effective Algorithm for 2D Marine CSEM Modeling in Anisotropic Media Using a Wavelet Galerkin Method. Minerals. 2022; 12(2):124. https://doi.org/10.3390/min12020124
Chicago/Turabian StyleChen, Hanbo, Bin Xiong, and Yu Han. 2022. "An Effective Algorithm for 2D Marine CSEM Modeling in Anisotropic Media Using a Wavelet Galerkin Method" Minerals 12, no. 2: 124. https://doi.org/10.3390/min12020124
APA StyleChen, H., Xiong, B., & Han, Y. (2022). An Effective Algorithm for 2D Marine CSEM Modeling in Anisotropic Media Using a Wavelet Galerkin Method. Minerals, 12(2), 124. https://doi.org/10.3390/min12020124





