A Novel Method for Evaluation of Ore Minerals Based on Optical Microscopy and Image Analysis: Preliminary Results
Abstract
1. Introduction
2. Materials and Methods
2.1. White and Dark Calibration
2.2. Color Spaces and Features Extraction
2.3. Self-Organized Maps
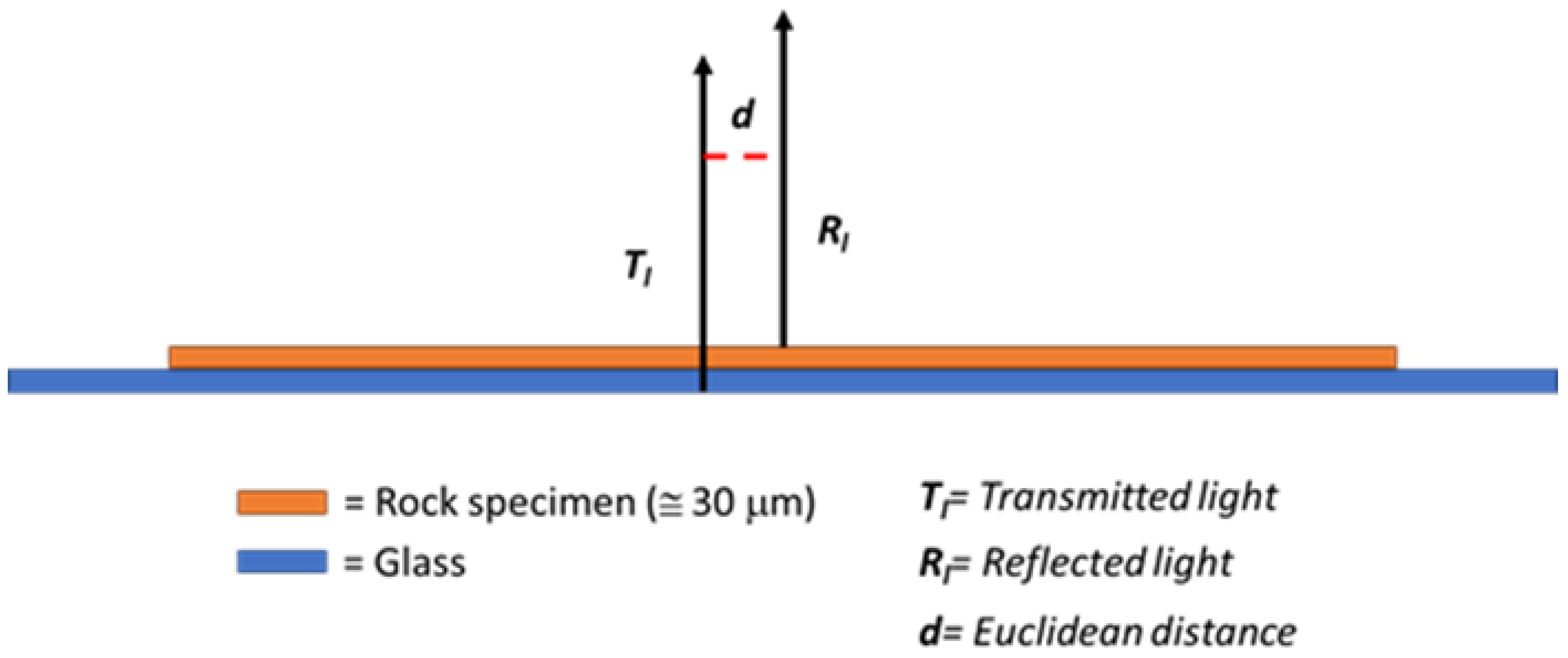
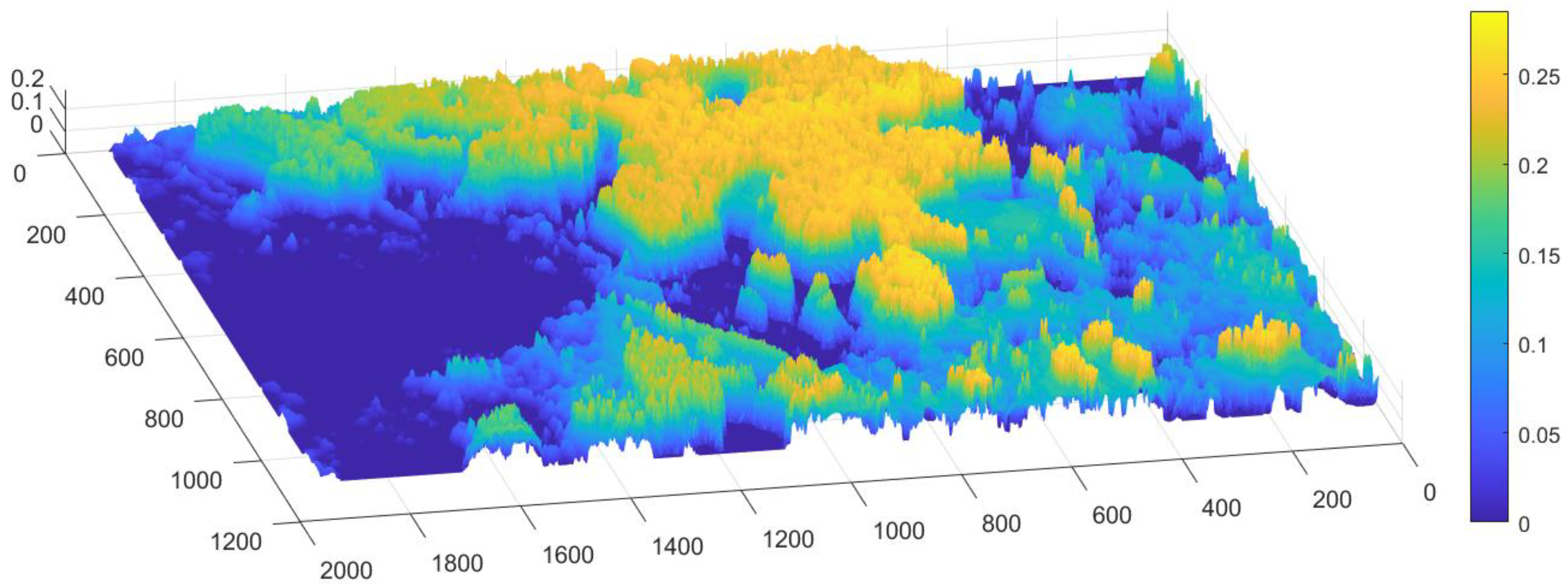
2.4. The Pseudo-3D Surface
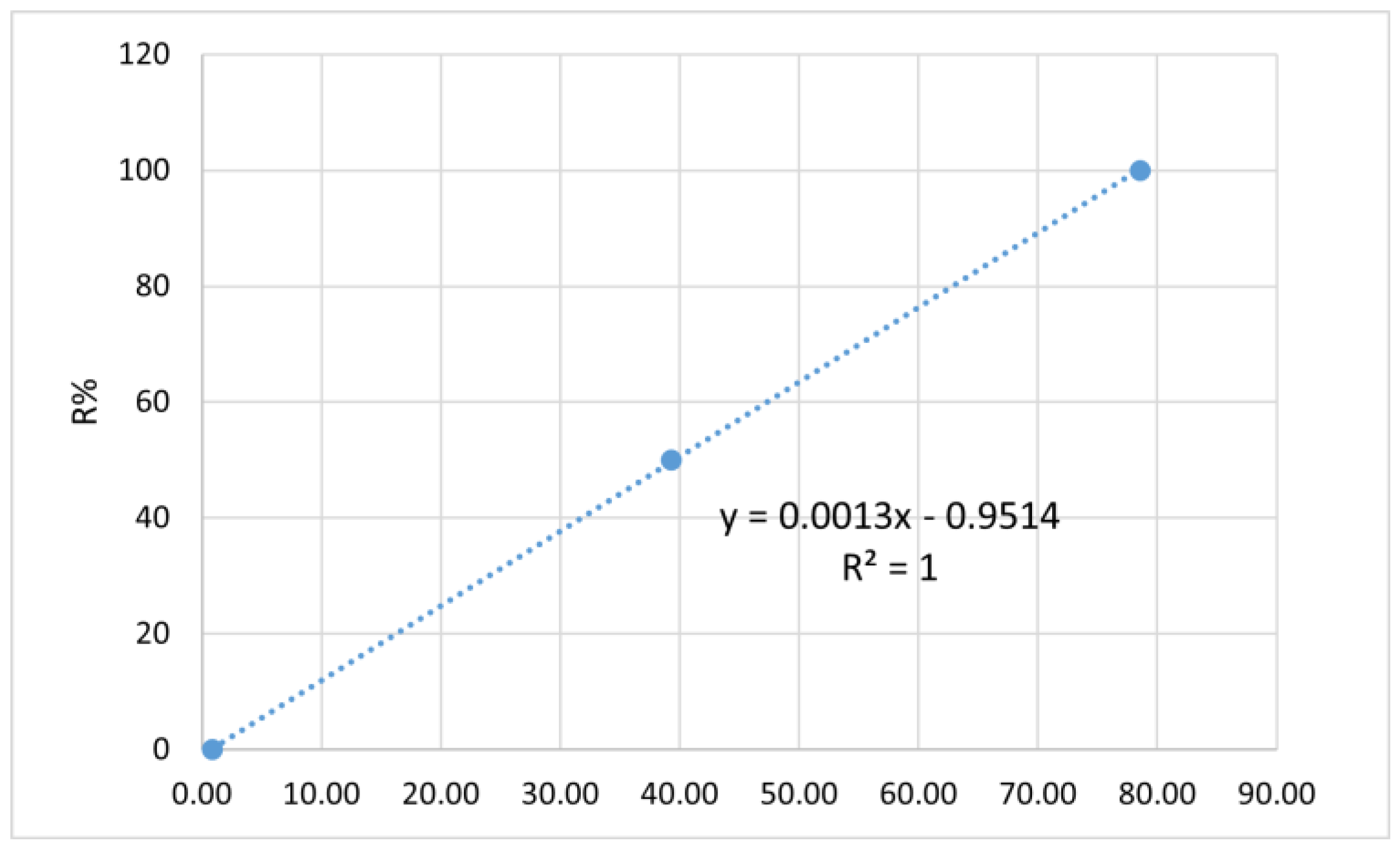
2.5. Calibration Curve and Reflectivity
3. SEM Validation
4. Results and Discussion
5. Conclusions and Recommendations
Additional Comments
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Clarke, A.; Eberhardt, C.; Eberhardt, C.N. Microscopy Techniques for Materials Science; Woodhead Publishing: Boca Raton, FL, USA, 2002. [Google Scholar]
- Hrstka, T.; Gottlieb, P.; Skala, R.; Breiter, K.; Motl, D. Automated mineralogy and petrology-applications of TESCAN Integrated Mineral Analyzer (TIMA). J. Geosci. 2018, 63, 47–63. [Google Scholar] [CrossRef]
- Maloy, A.K.; Treiman, A.H. Evaluation of image classification routines for determining modal mineralogy of rocks from X-ray maps. Am. Mineral. 2007, 92, 1781–1788. [Google Scholar] [CrossRef]
- Schulz, B.; Sandmann, D.; Gilbricht, S. SEM-based automated mineralogy and its application in geo-and material sciences. Minerals 2020, 10, 1004. [Google Scholar] [CrossRef]
- Schofield, P.F.; Knight, K.S.; Covey-Crump, S.J.; Cressey, G.; Stretton, I.C. Accurate quantification of the modal mineralogy of rocks when image analysis is difficult. Mineral. Mag. 2002, 66, 189–200. [Google Scholar] [CrossRef]
- McSween, H.Y., Jr.; McGlynn, I.O.; Rogers, A.D. Determining the modal mineralogy of Martian soils. J. Geophys. Res. Planets 2010, 115, E00F12. [Google Scholar] [CrossRef]
- Koch, P.-H.; Lund, C.; Rosenkranz, J. Automated drill core mineralogical characterization method for texture classification and modal mineralogy estimation for geometallurgy. Miner. Eng. 2019, 136, 99–109. [Google Scholar] [CrossRef]
- Koh, E.J.Y.; Amini, E.; McLachlan, G.J.; Beaton, N. Utilising convolutional neural networks to perform fast automated modal mineralogy analysis for thin-section optical microscopy. Miner. Eng. 2021, 173, 107230. [Google Scholar] [CrossRef]
- Hoal, K.O.; Stammer, J.G.; Appleby, S.K.; Botha, J.; Ross, J.K.; Botha, P.W. Research in quantitative mineralogy: Examples from diverse applications. Miner. Eng. 2009, 22, 402–408. [Google Scholar] [CrossRef]
- Sorby, H.C. XII. On the microscopical structure of meteorites. Proc. R. Soc. Lond. 1864, 13, 333–334. [Google Scholar]
- Hammond, C. The contribution of Henry Clifton Sorby to the study of reflected light microscopy of iron and steel. Hist. Metall. 1989, 23, 1–8. [Google Scholar]
- Hardwick, D.A.; Williams, W.M. The birth of metallography- The work of Henry Clifton Sorby (1826–1908). Bull. Can. Inst. Min. Metall. 1980, 73, 143–144. [Google Scholar]
- Perrin, L. Henry Clifton Sorby and the Beginnings of Microscopial Metallography. Doctoral Dissertation, Oxford University, Oxford, UK, 1976. [Google Scholar]
- Ramdohr, P. The Ore Minerals and Their Intergrowths; Elsevier Ltd.: Oxford, UK, 2013. [Google Scholar]
- Chryssoulis, S.L.; McMullen, J. Mineralogical investigation of gold ores. Dev. Miner. Process. 2005, 15, 21–71. [Google Scholar]
- Piller, H. Colour measurements in ore-microscopy. Miner. Depos. 1966, 1, 175–192. [Google Scholar] [CrossRef]
- Ineson, P.R. Introduction to Practical Ore Microscopy; Routledge, Taylor & Francis Group: London, UK; New York, NY, USA, 2014. [Google Scholar]
- Bowie, S.H.U.; Taylor, K. A System of Ore Mineral Identification; Geological Survey: London, UK, 1959. [Google Scholar]
- Craig, J.R.; Vaughan, D.J.; Hagni, R.D. Ore Microscopy and Ore Petrography; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Uytenbogaardt, W.; Burke, E.A.J. Tables for Microscopic Identification of Ore Minerals; Courier Corporation: New York, NY, USA, 1985. [Google Scholar]
- Sánchez-Ramos, S.; Doménech-Carbó, A.; Gimeno-Adelantado, J.V.; Peris-Vicente, J. Analytical and mineralogical studies of ore and impurities from a chromite mineral using X-ray analysis, electrochemical and microscopy techniques. Talanta 2008, 74, 1592–1597. [Google Scholar] [CrossRef]
- Kahn, H.; Mano, E.S.; Tassinari, M. Image analysis coupled with a SEM-EDS applied to the characterization of a partially weathered Zn-Pb ore. J. Miner. Mater. Charact. Eng. 2002, 1, 1–9. [Google Scholar]
- Donskoi, E.; Manuel, J.R.; Austin, P.; Poliakov, A.; Peterson, M.J.; Hapugoda, S. Comparative study of iron ore characterisation using a scanning electron microscope and optical image analysis. Appl. Earth Sci. 2013, 122, 217–229. [Google Scholar] [CrossRef]
- Reyes, F.; Lin, Q.; Udoudo, O.; Dodds, C.; Lee, P.D.; Neethling, S.J. Calibrated X-ray micro-tomography for mineral ore quantification. Miner. Eng. 2017, 110, 122–130. [Google Scholar] [CrossRef]
- Mohanan, S.; Bhoja, S.K.; Kumar, C.R.; Kumar, A.; Venugopalan, T. Estimation of ore mineralogy from analytical analysis of iron ore. Min. Metall. Explor. 2015, 32, 97–101. [Google Scholar] [CrossRef]
- Gu, Y. Automated scanning electron microscope based mineral liberation analysis an introduction to JKMRC/FEI mineral liberation analyser. J. Miner. Mater. Charact. Eng. 2003, 2, 33–41. [Google Scholar] [CrossRef]
- Fandrich, R.; Gu, Y.; Burrows, D.; Moeller, K. Modern SEM-based mineral liberation analysis. Int. J. Miner. Process. 2007, 84, 310–320. [Google Scholar] [CrossRef]
- Gottlieb, P.; Wilkie, G.; Sutherland, D.; Ho-Tun, E.; Suthers, S.; Perera, K.; Jenkins, B.; Spencer, S.; Butcher, A.; Rayner, J. Using quantitative electron microscopy for process mineralogy applications. JOM 2000, 52, 24–25. [Google Scholar] [CrossRef]
- Pirrie, D.; Butcher, A.R.; Power, M.R.; Gottlieb, P.; Miller, G.L. Rapid quantitative mineral and phase analysis using automated scanning electron microscopy (QemSCAN); potential applications in forensic geoscience. Geol. Soc. Lond. Spec. Publ. 2004, 232, 123–136. [Google Scholar] [CrossRef]
- Graham, S.D.; Brough, C.; Cropp, A. An introduction to ZEISS mineralogic mining and the correlation of light microscopy with automated mineralogy: A case study using BMS and PGM analysis of samples from a PGE-bearing chromite prospect. In Proceedings of the Precious Metals’15, Falmouth, UK, 13–14 May 2015; pp. 1–12. [Google Scholar]
- Ayling, B.; Rose, P.; Petty, S.; Zemach, E.; Drakos, P. QEMSCAN (Quantitative evaluation of minerals by scanning electron microscopy): Capability and application to fracture characterization in geothermal systems. In Proceedings of the Thirty-Seventh Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 30 January–1 February 2012. [Google Scholar]
- Andersen, J.C.Ø.; Rollinson, G.K.; Snook, B.; Herrington, R.; Fairhurst, R.J. Use of QEMSCAN® for the characterization of Ni-rich and Ni-poor goethite in laterite ores. Miner. Eng. 2009, 22, 1119–1129. [Google Scholar] [CrossRef]
- Donskoi, E.; Manuel, J.; Austin, P.; Poliakov, A.; Peterson, M.; Hapugoda, S. Comparative study of iron ore characterisation by optical image analysis and QEMSCAN (TM). In Proceedings of the Iron Ore 2011, Perth, WA, Australia, 11–13 July 2011. [Google Scholar]
- Gu, Y.; Schouwstra, R.P.; Rule, C. The value of automated mineralogy. Miner. Eng. 2014, 58, 100–103. [Google Scholar] [CrossRef]
- Harmon, R.S.; Lawley, C.J.M.; Watts, J.; Harraden, C.L.; Somers, A.M.; Hark, R.R. Laser-induced breakdown spectroscopy—An emerging analytical tool for mineral exploration. Minerals 2019, 9, 718. [Google Scholar] [CrossRef]
- Nikonow, W.; Rammlmair, D.; Meima, J.A.; Schodlok, M.C. Advanced mineral characterization and petrographic analysis by μ-EDXRF, LIBS, HSI and hyperspectral data merging. Mineral. Petrol. 2019, 113, 417–431. [Google Scholar] [CrossRef]
- Lawley, C.J.M.; Somers, A.M.; Kjarsgaard, B.A. Rapid geochemical imaging of rocks and minerals with handheld laser induced breakdown spectroscopy (LIBS). J. Geochem. Explor. 2021, 222, 106694. [Google Scholar] [CrossRef]
- El Haddad, J.; de Lima Filho, E.S.; Vanier, F.; Harhira, A.; Padioleau, C.; Sabsabi, M.; Wilkie, G.; Blouin, A. Multiphase mineral identification and quantification by laser-induced breakdown spectroscopy. Miner. Eng. 2019, 134, 281–290. [Google Scholar] [CrossRef]
- Senesi, G.S.; Capitelli, F. Compositional, mineralogical and structural investigation of meteorites by XRD and LIBS. In Hypersonic Meteoroid Entry Physics; IOP Publishing: Bristol, UK, 2019. [Google Scholar] [CrossRef]
- Haavisto, O.; Kauppinen, T.; Häkkänen, H. Laser-induced breakdown spectroscopy for rapid elemental analysis of drillcore. IFAC Proc. Vol. 2013, 46, 87–91. [Google Scholar] [CrossRef]
- Mohamed, N.; Rifai, K.; Selmani, S.; Constantin, M.; Doucet, F.R.; Özcan, L.Ç.; Sabsabi, M.; Vidal, F. Chemical and Mineralogical Mapping of Platinum-Group Element Ore Samples Using Laser-Induced Breakdown Spectroscopy and Micro-X-ray Fluorescence. Geostand. Geoanal. Res. 2021, 45, 539–550. [Google Scholar] [CrossRef]
- Paradis, M.-C.M.; Doucet, F.R.; Rifai, K.; Özcan, L.Ç.; Azami, N.; Vidal, F. ECORE: A new fast automated quantitative mineral and elemental core scanner. Minerals 2021, 11, 859. [Google Scholar] [CrossRef]
- Rifai, K.; Michaud Paradis, M.-C.; Swierczek, Z.; Doucet, F.; Özcan, L.; Fayad, A.; Li, J.; Vidal, F. Emergences of new technology for ultrafast automated mineral phase identification and quantitative analysis using the CORIOSITY Laser-Induced Breakdown Spectroscopy (LIBS) system. Minerals 2020, 10, 918. [Google Scholar] [CrossRef]
- Ross, L.; Russ, J.C. The image processing handbook. Microsc. Microanal. 2011, 17, 843. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Neurocomputing 1998, 21, 1–6. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organization and Associative Memory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Jiang, D.; Yang, Y.; Xia, M. Research on intrusion detection based on an improved SOM neural network. In Proceedings of the 2009 Fifth International Conference on Information Assurance and Security, Xi’an, China, 18–20 August 2009; pp. 400–403. [Google Scholar]
- Chen, L.-P.; Liu, Y.-G.; Huang, Z.-X.; Shi, Y.-T. An improved SOM algorithm and its application to color feature extraction. Neural Comput. Appl. 2014, 24, 1759–1770. [Google Scholar] [CrossRef][Green Version]
- Smits, J.R.M.; Melssen, W.J.; Buydens, L.M.C.; Kateman, G. Using artificial neural networks for solving chemical problems: Part I. Multi-layer feed-forward networks. Chemom. Intell. Lab. Syst. 1994, 22, 165–189. [Google Scholar] [CrossRef]
- Livingstone, D.J. Artificial Neural Networks: Methods and Applications; Springer: Totowa, NJ, USA, 2008. [Google Scholar]
- Zupan, J. Introduction to artificial neural network (ANN) methods: What they are and how to use them. Acta Chim. Slov. 1994, 41, 327. [Google Scholar]
- Ng, H.P.; Ong, S.H.; Foong, K.W.C.; Goh, P.S.; Nowinski, W.L. Medical image segmentation using k-means clustering and improved watershed algorithm. In Proceedings of the 2006 IEEE Southwest Symposium on Image Analysis and Interpretation, Denver, CO, USA, 26–28 March 2006; pp. 61–65. [Google Scholar]
- Akinin, M.V.; Taganov, A.I.; Nikiforov, M.B.; Sokolova, A.V. Image segmentation algorithm based on self-organized Kohonen’s neural maps and tree pyramidal segmenter. In Proceedings of the 2015 4th Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 14–18 June 2015; pp. 168–170. [Google Scholar]
- Lee, Y.-K.; Rhodes, W.T. Nonlinear image processing by a rotating kernel transformation. Opt. Lett. 1990, 15, 1383–1385. [Google Scholar] [CrossRef]
- Thum, C. Measurement of the entropy of an image with application to image focusing. Opt. Acta Int. J. Opt. 1984, 31, 203–211. [Google Scholar] [CrossRef]
- Chang, D.-C.; Wu, W.-R. Image contrast enhancement based on a histogram transformation of local standard deviation. IEEE Trans. Med. Imaging 1998, 17, 518–531. [Google Scholar] [CrossRef] [PubMed]
- Ranganath, A.; Senapati, M.R.; Sahu, P.K. Estimating the fractal dimension of images using pixel range calculation technique. Vis. Comput. 2021, 37, 635–650. [Google Scholar] [CrossRef]
- Wood, B.J.; Strens, R.G.J. Diffuse reflectance spectra and optical properties of some sulphides and related minerals. Mineral. Mag. 1979, 43, 509–518. [Google Scholar] [CrossRef]
- Poliakov, A.; Donskoi, E. Automated relief-based discrimination of non-opaque minerals in optical image analysis. Miner. Eng. 2014, 55, 111–124. [Google Scholar] [CrossRef]








| Element | Goethite | Magnetite | Quartz | Tourmaline | |||
|---|---|---|---|---|---|---|---|
| Point 1 | Point 2 | Point 3 | Point 4 | Point 5 | Point 6 | Point 7 | |
| wt% | |||||||
| O | 25.82 | 26.07 | 29.24 | 29.45 | 53.3 | 34.91 | 35.17 |
| Al | 0.6 | 0.55 | 0.56 | 13.39 | 13.46 | ||
| Na | 0.16 | 1.3 | 1.18 | ||||
| Mg | 4.31 | 5.27 | |||||
| Si | 1.2 | 1.28 | 1.56 | 0.83 | 46.69 | 16.63 | 16.96 |
| P | 0.76 | 0.68 | |||||
| Ca | 0.09 | 0.45 | 0.22 | 1.56 | 1.7 | ||
| Ti | 0.25 | 0.57 | |||||
| Fe | 53.32 | 53.98 | 68.12 | 69.5 | 19.61 | 19.15 | |
| Sr | 0.24 | ||||||
| Total | 81.78 | 82.8 | 100 | 100 | 99.99 | 91.95 | 93.46 |
| Segments | R% in Air with Craig et al. [19] Equation (3) | R% in Air with Our Calibration |
|---|---|---|
| seg 1 | 13.9 | 15.2 |
| seg 2 | 0.4 | 1.4 |
| seg 3 | 10.1 | 11.3 |
| seg 4 | 0.9 | 1.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santoro, L.; Lezzerini, M.; Aquino, A.; Domenighini, G.; Pagnotta, S. A Novel Method for Evaluation of Ore Minerals Based on Optical Microscopy and Image Analysis: Preliminary Results. Minerals 2022, 12, 1348. https://doi.org/10.3390/min12111348
Santoro L, Lezzerini M, Aquino A, Domenighini G, Pagnotta S. A Novel Method for Evaluation of Ore Minerals Based on Optical Microscopy and Image Analysis: Preliminary Results. Minerals. 2022; 12(11):1348. https://doi.org/10.3390/min12111348
Chicago/Turabian StyleSantoro, Licia, Marco Lezzerini, Andrea Aquino, Giulia Domenighini, and Stefano Pagnotta. 2022. "A Novel Method for Evaluation of Ore Minerals Based on Optical Microscopy and Image Analysis: Preliminary Results" Minerals 12, no. 11: 1348. https://doi.org/10.3390/min12111348
APA StyleSantoro, L., Lezzerini, M., Aquino, A., Domenighini, G., & Pagnotta, S. (2022). A Novel Method for Evaluation of Ore Minerals Based on Optical Microscopy and Image Analysis: Preliminary Results. Minerals, 12(11), 1348. https://doi.org/10.3390/min12111348









