The Effect of Freeze-Thaw Cycling and the Initial Mass of Water on the Unfrozen Water Content of Calcium Bentonites Modified by Copper Ions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Chemical Preparatory Procedures of the Samples
2.2.2. Determination of the Mineral Composition and Physicochemical Properties
2.2.3. The DSC Method and Calculating the Unfrozen Water Content
3. Results and Analysis
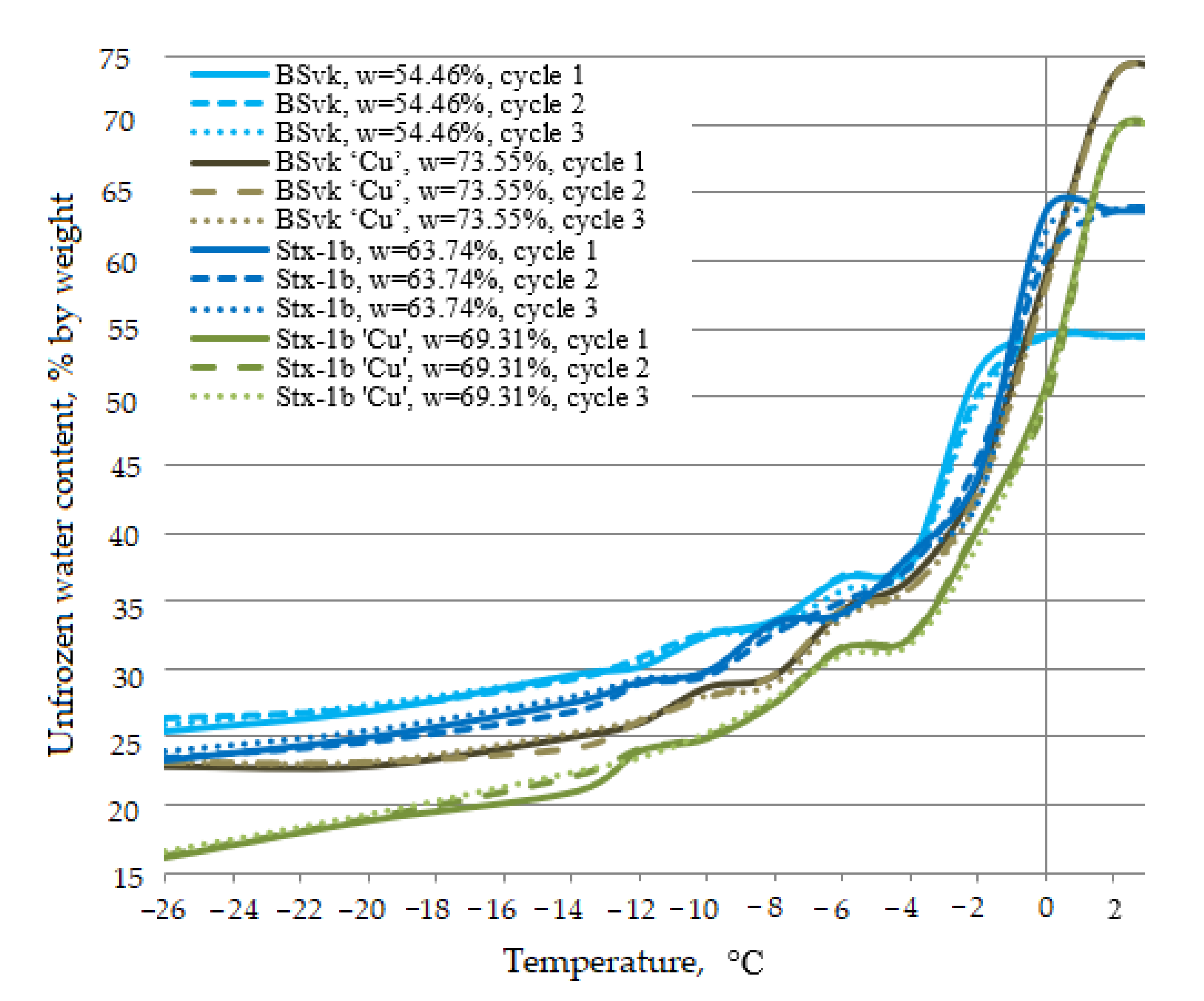
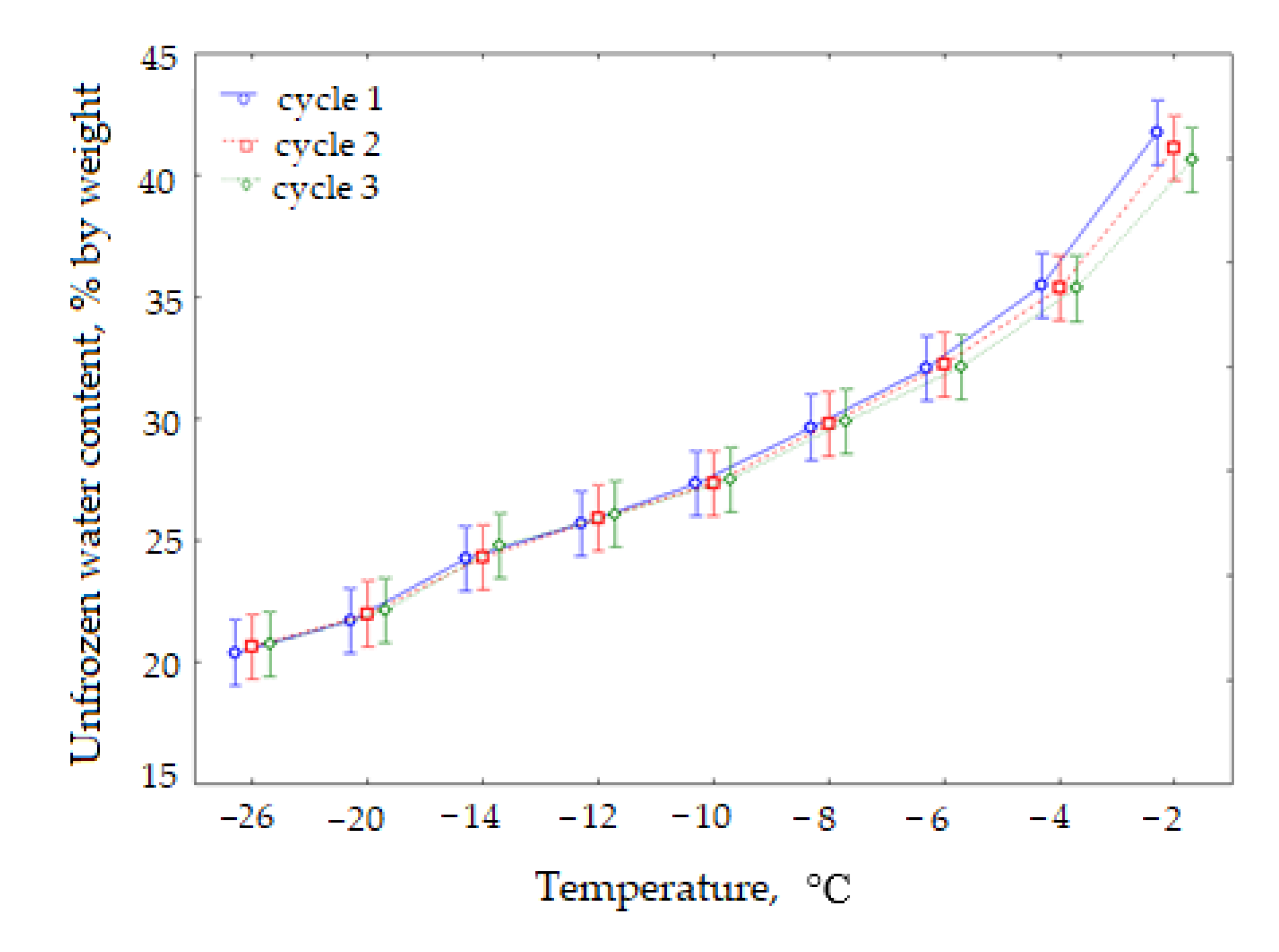
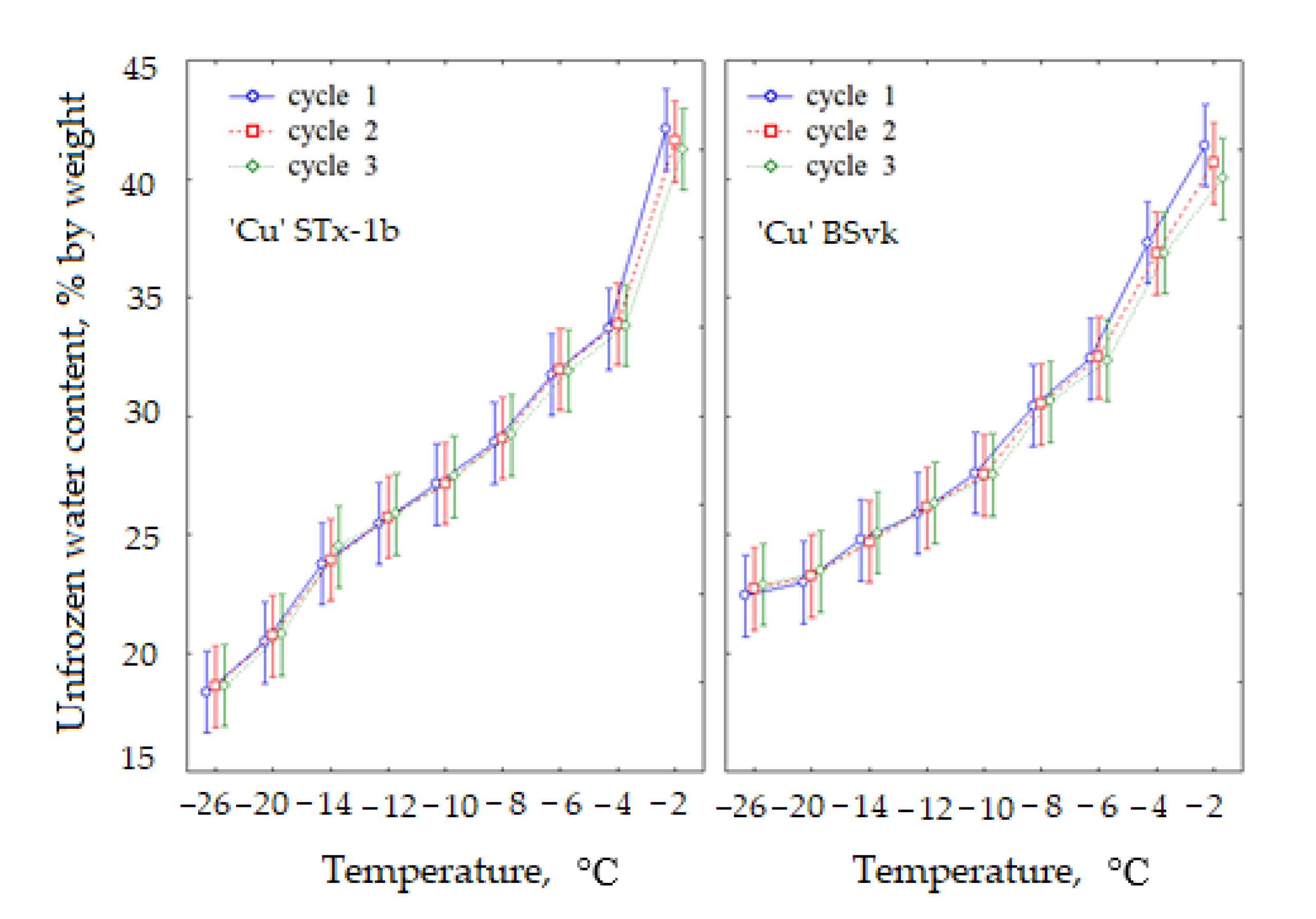
3.1. The Effect of the Freeze-Thaw Cycles
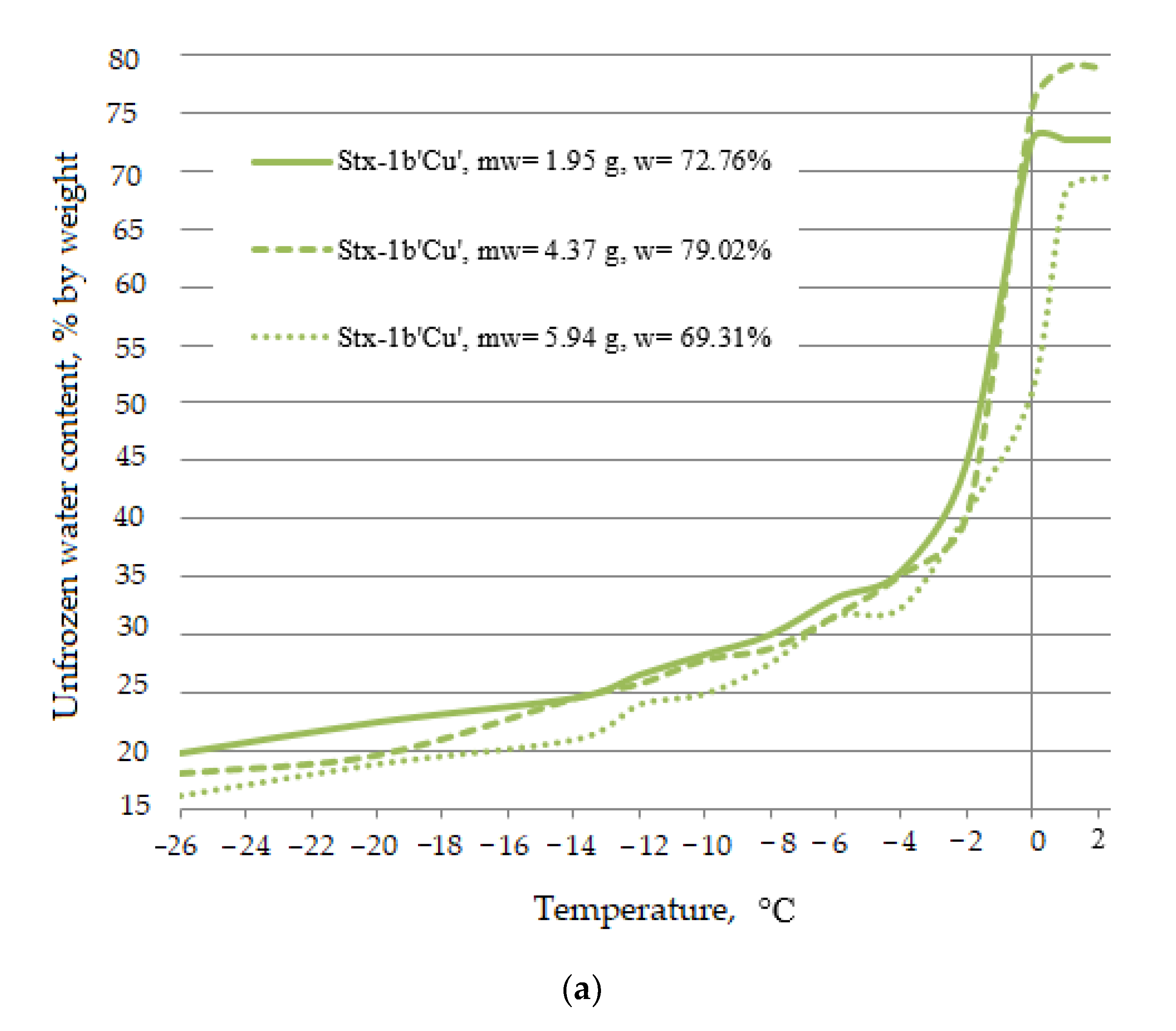
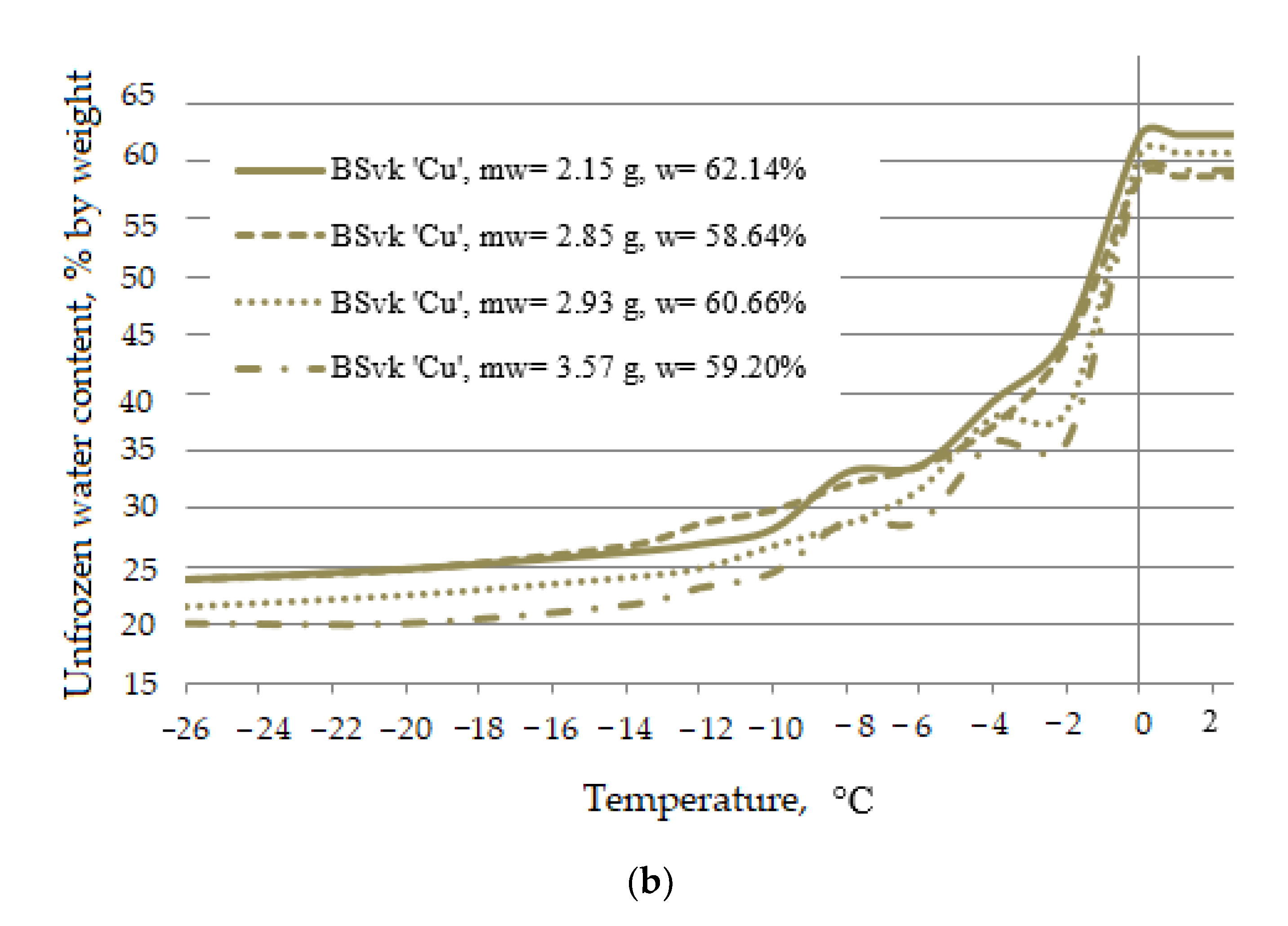
3.2. The Effect of the Initial Mass of Water
4. Discussion
5. Conclusions
- The effect of the cyclic freezing on the unfrozen water content in bentonites (≥75% smectite) contaminated with copper ions, frozen in a closed system, was determined to be statistically insignificant.
- The most important factors impacting the unfrozen water content in the examined bentonites included: the temperature, the initial mass of the water contained in the clay, and the clay type.
- In the case of the clays with a similar moisture content at a given negative temperature, the unfrozen water content was higher and the lower the initial mass of the water in the clay sample. Research should be continued in order to optimise the drainage processes on the clays contaminated with copper ions.
- It was observed that in the case of the clays with higher contents of copper ions, there was a higher unfrozen water content at a given negative temperature. Research should be continued on a wider range of metal concentrations, in order to establish this correlation and use it as a basis for the creation of a tool for evaluating the migration of copper ions in the contaminated clays.
- The unfrozen water content determined via the DSC method in the bentonites contaminated with copper ions can be expressed as a simple linear function with R~0.96, depending on the initial mass of the water contained in the clay determined with the use of the gravimetric method.
- Only significant correlations for the unfrozen water and the mass of the dry soil were obtained at the temperature of −2 °C. As a result, an empirical model was proposed that was determined to be better suited to the experimental data than the model with the mass of the water.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anderson, D.M.; Tice, A.R. The unfrozen interfacial phase in frozen soil water systems. In Physical Aspects of Soil Water and Salts in Ecosystems. Ecological Studies (Analysis and Synthesis); Hadas, A., Swartzendruber, D., Rijtema, P.E., Fuchs, M., Yaron, B., Eds.; Springer: Berlin/Heidelberg, Germany, 1973; Volume 4. [Google Scholar] [CrossRef]
- Andersland, O.; Ladanyi, B. Frozen Ground Engineering, 2nd ed.; John Wiley & Sons: Chichester, UK, 2004; pp. 1–75. [Google Scholar]
- Taber, S. Frost heaving. J. Geol. 1929, 37, 428–461. [Google Scholar] [CrossRef]
- Li, T.; Kong, L.; Guo, A. The deformation and microstructure characteristics of expansive soil under freeze–thaw cycles with loads. Cold Reg. Sci. Technol. 2021, 192, 103393. [Google Scholar] [CrossRef]
- Melnikov, A.; Kut, A.; Zhang, Z.; Rochev, V. Carbonate Soil Cryogenesis in South Yakutia (Russia). Minerals 2021, 11, 800. [Google Scholar] [CrossRef]
- Zhai, J.; Zhang, Z.; Melnikov, A.; Zhang, M.; Yang, L.; Jin, D. Experimental Study on the Effect of Freeze—Thaw Cycles on the Mineral Particle Fragmentation and Aggregation with Different Soil Types. Minerals 2021, 11, 913. [Google Scholar] [CrossRef]
- Krupskaya, V.V.; Zakusin, S.V.; Tyupina, E.A.; Dorzhieva, O.V.; Zhukhlistov, A.P.; Belousov, P.E.; Timofeeva, M.N. Experimental study of montmorillonite structure and transformation of its properties under treatment with inorganic acid solutions. Minerals 2017, 7, 49. [Google Scholar] [CrossRef]
- Nartowska, E.; Kozłowski, T.; Kolankowska, M. The changes in the microstructure of ion-exchanged clays. E3 Web Conf. 2017, 17, 00063. [Google Scholar] [CrossRef] [Green Version]
- Nartowska, E.; Kozłowski, T.; Gawdzik, J. Assessment of the influence of copper and zinc on the microstructural parameters and hydraulic conductivity of bentonites on the basis of SEM tests. Heliyon 2019, 5, 7. [Google Scholar] [CrossRef] [Green Version]
- Podlech, C.; Matschiavelli, N.; Peltz, M.; Kluge, S.; Arnold, T.; Cherkouk, A.; Meleshyn, A.; Grathoff, G.; Warr, L.N. Bentonite Alteration in Batch Reactor Experiments with and without Organic Supplements: Implications for the Disposal of Radioactive Waste. Minerals 2021, 11, 932. [Google Scholar] [CrossRef]
- Ren, J.; Vanapalli, S.K. Effect of freeze–thaw cycling on the soil-freezing characteristic curve of five Canadian soils. Vadose Zone J. 2020, 19, e20039. [Google Scholar] [CrossRef]
- Liu, S.; Wang, J.; Zhou, G.; Chen, T.; Zhou, Y.; Wang, T.; Mu, Y.; Liang, H. Effects of different freezing rates on purification efficiency of sandy soil contaminated by heavy metal copper. Cold Reg. Sci. Technol. 2019, 163, 1–7. [Google Scholar] [CrossRef]
- Du, L.; Dyck, M.; Shotyk, W.; He, H.; Ly, J.; Cuss, C.W.; Bie, J. Lead immobilization processes in soils subjected to freeze-thaw cycles. Ecotoxicol. Environ. Saf. 2020, 192, 110288. [Google Scholar] [CrossRef]
- Foose, G.; Thomson, R.A., Jr. Effect of freeze-thaw cycling on the hydraulic conductivity of soil-bentonite mixtures. In Proceedings of the 11th International Conference on Cold Regions Engineering, Anchorage, AK, USA, 20–22 May 2002. [Google Scholar] [CrossRef]
- Sun, B.; Ren, F.; Ding, W.; Zhang, G.; Huang, J.; Li, J.; Zhang, L. Effects of freeze-thaw on soil properties and water erosion. Soil Water Res. 2021, 16, 205–216. [Google Scholar] [CrossRef]
- Wei, C.; You, S.; Jichun, W.; Yaling, C.; Erxing, P.; Leonid, G. Soil hydrological process and migration mode influenced by the freeze-thaw process in the activity layer of permafrost regions in Qinghai-Tibet Plateau. Cold Reg. Sci. Technol. 2021, 184, 103236. [Google Scholar] [CrossRef]
- Ren, J.; Vanapalli, S.K.; Han, Z.; Omenogor, K.O.; Bai, Y. The resilient moduli of five Canadian soils under wetting and freeze-thaw conditions and their estimation by using an artificial neural network. Cold Reg. Sci. Technol. 2019, 168. [Google Scholar] [CrossRef]
- Zhang, M.; Lu, J.; Zhang, X.; Pei, W. Analysis of volumetric unfrozen water contents in freezing soils. Exp. Heat Transf. 2018, 32, 426–438. [Google Scholar] [CrossRef]
- Nartowska, E.; Kozłowski, T.; Kolankowska, M. Exchangeable cations (Cu2+, Zn2+) effects on unfrozen water content in clay-water system using 1H NMR method. Cold Reg. Sci. Technol. 2021, 192, 103403. [Google Scholar] [CrossRef]
- Kozłowski, T.; Rusin, A.; Nartowska, E. The specific heat of dry homoionic forms of bentonites SWy-2 and Stx-1b: An effect of the fraction of particles less than 2 μm. Appl. Clay Sci. 2014, 101, 82–89. [Google Scholar] [CrossRef]
- Teng, J.; Kou, J.; Yan, X.; Zhang, S.; Sheng, D. Parameterization of soil freezing characteristic curve for unsaturated soils. Cold Reg. Sci. Technol. 2020, 170, 102928. [Google Scholar] [CrossRef]
- Timofeev, A.M.; Kravtsova, O.N.; Protodyakonova, N.A. Temperature dependence of unfrozen water quantity in clay soil with different moisture content. IOP Conf. Ser. Mater. Sci. Eng. 2020, 753, 052002. [Google Scholar] [CrossRef]
- Kozłowski, T. Temperature dependence of the solidification enthalpy as experimentally determined between 245 and 203 K for montmorillonite-water systems. Thermochim. Acta 2016, 634, 12–25. [Google Scholar] [CrossRef]
- Kozłowski, T.; Nartowska, E. Unfrozen water content in representative bentonites of different origin subjected to cyclic freezing and thawing. Vadose Zone J. 2013, 12, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Chipera, S.J.; Bish, D.L. Baseline studies of the clay minerals society source clays: Powder X-ray diffraction analyses. Clay Clay Miner. 2001, 49, 398–409. [Google Scholar] [CrossRef]
- Górniak, K. Bentonite from the Central Slovakia Volcanic Field—A Prospective Raw Material for Polish Industry. Mineralogia 2017, 48, 23–38. [Google Scholar] [CrossRef]
- Stępkowska, E.T. Simple method of crystal phase water. Specific surface and clay mineral content estimation in natural clays. Stud. Geotech. 1973, 2, 21–36. [Google Scholar]
- Sare, E.J.; Moynihan, C.T.; Angell, C.A. Proton magnetic resonance chemical shifts and the hydrogen bond in concentrated aqueous electrolyte solutions. J. Phys. Chem. 1973, 77, 1869–1876. [Google Scholar] [CrossRef]
- Wang, H.; Shibue, T.; Komine, H. Hydration and dehydration of water of bentonite: A solid-state 1H magic-angle spinning NMR study. Chem. Phys. 2020, 536, 110796. [Google Scholar] [CrossRef]
- Kozłowski, T. Some factors affecting supercooling and the equilibrium freezing point in soil–water systems. Cold Reg. Sci. Technol. 2009, 59, 25–33. [Google Scholar] [CrossRef]
- Kozłowski, T. A comprehensive method of determining the soil unfrozen water curves: 1. Application of the term of convolution. Cold Reg. Sci. Technol. 2003, 36, 71–79. [Google Scholar] [CrossRef]
- Kozłowski, T. Low temperature exothermic effects on cooling of homoionic clays. Cold Reg. Sci. Technol. 2011, 68, 139–149. [Google Scholar] [CrossRef]
- Nartowska, E. The effects of potentially toxic metals (copper and zinc) on selected physical and physico-chemical properties of bentonites. Heliyon 2019, 5, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bing, H.; He, P.; Zhang, Y. Cyclic freeze–thaw as a mechanism for water and salt migration in soil. Environ. Earth Sci. 2015, 74, 675–681. [Google Scholar] [CrossRef] [Green Version]
- Kruse, A.M.; Darrow, M.M. Adsorbed cation effects on unfrozen water in fine-grained frozen soil measured using pulsed nuclear magnetic resonance. Cold Reg. Sci. Technol. 2017, 142, 42–54. [Google Scholar] [CrossRef]
- Qiu, E.; Wan, X.; Qu, M.; Zheng, L.; Zhong, C.; Gong, F.; Liu, L. Estimating Unfrozen Water Content in Frozen Soils Based on Soil Particle Distribution. J. Cold Reg. Eng. 2020, 34, 2. [Google Scholar] [CrossRef]
- Shang, J.Q.; Lo, K.Y.; Quigley, R.M. Quantitative determination of potential distribution in Stern–Gouy double-layer model. Can. Geotech. J. 1994, 31, 5. [Google Scholar] [CrossRef]
- Martin, R.T. Water vapor sorption on kaolinite: Entropy of adsorption. Clays Clay Miner. 1960, 8, 102–114. [Google Scholar] [CrossRef]
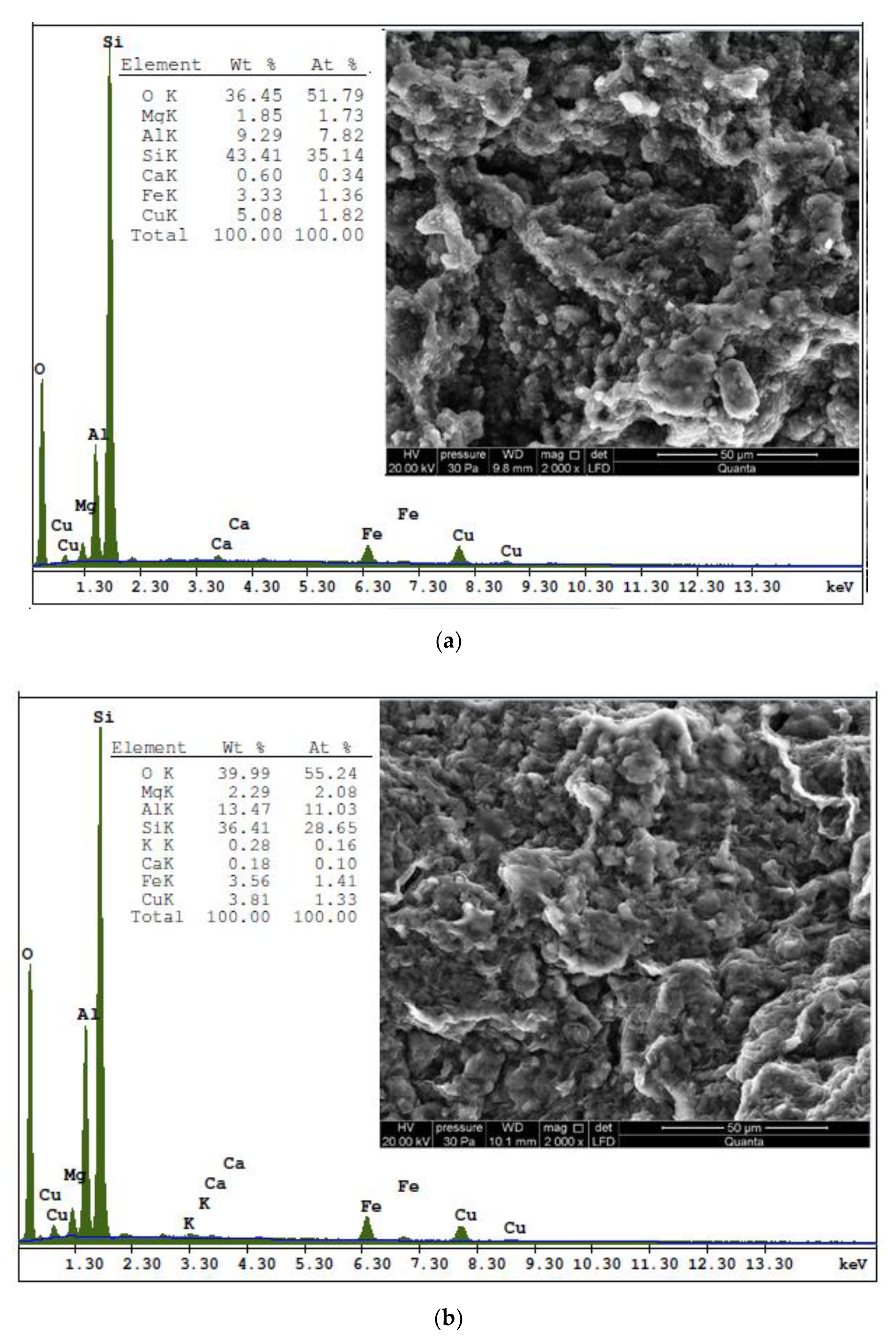
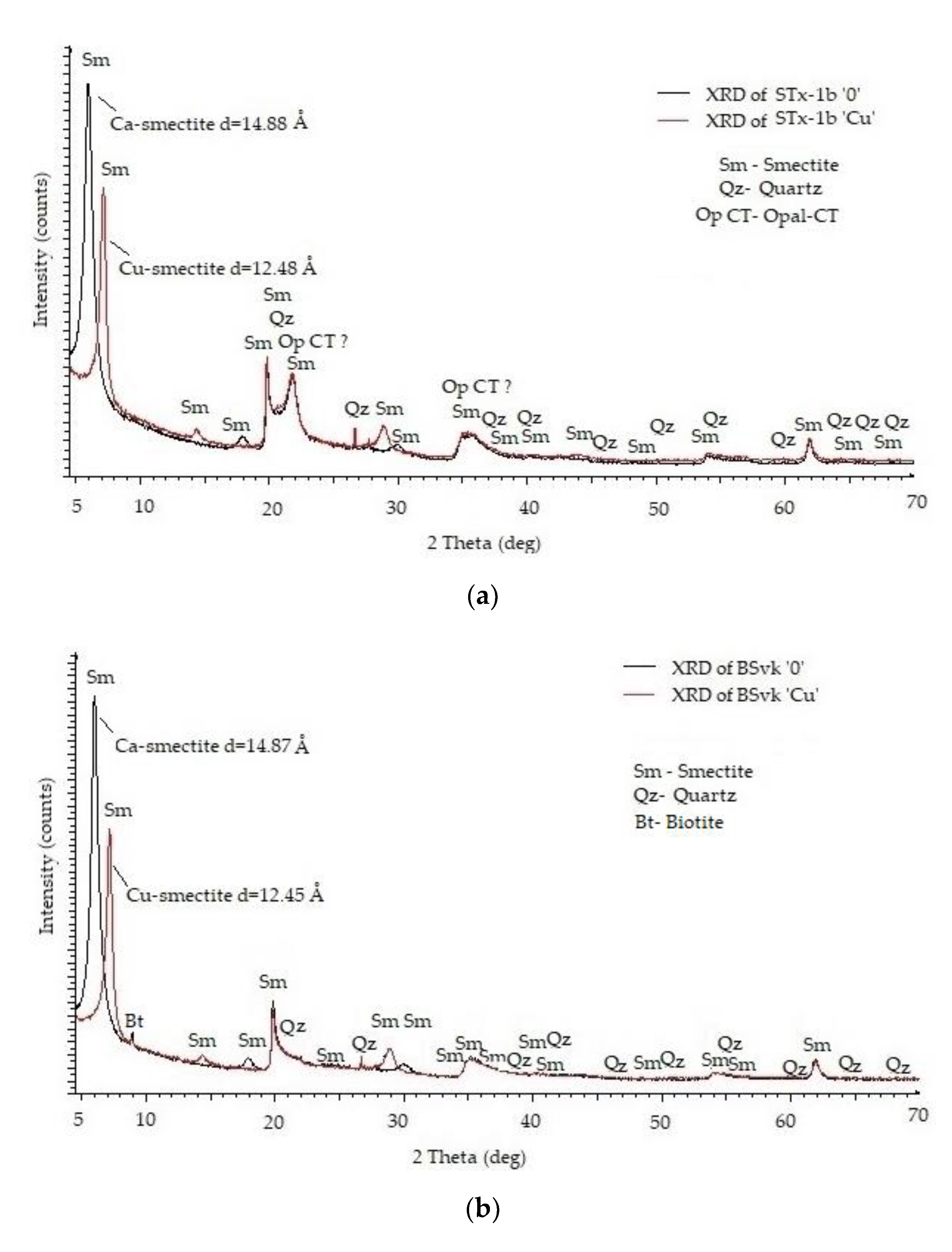
| Symbol | Description | Characteristics of the Samples | ||
|---|---|---|---|---|
| Water Content w (%) | Mass of Water mw (g) | Mass of Dry Soil ms (g) | ||
| Stx-1b | Natural calcium bentonite from Texas, USA (the Clay Minerals Society Source Clay) | 76.99 | 3.58 | 4.65 |
| 63.74 | 2.90 | 4.55 | ||
| 64.86 | 4.06 | 6.26 | ||
| 81.72 | 5.9 | 7.22 | ||
| 85.21 | 4.61 | 5.41 | ||
| Stx-1b ‘Cu’ | Homoionic form of bentonite from Texas saturated with copper ions | 72.76 | 1.95 | 2.68 |
| 85.83 | 4.18 | 4.87 | ||
| 88.02 | 2.94 | 3.34 | ||
| 69.31 | 5.94 | 8.57 | ||
| 79.02 | 4.37 | 5.53 | ||
| BSvk | Natural calcium bentonite from Stará Kremnička—Jelšový Potok, Slovakia | 125.0 | 4.05 | 3.24 |
| 90.94 | 5.22 | 5.74 | ||
| 54.46 | 1.77 | 3.25 | ||
| 48.70 | 1.87 | 3.84 | ||
| 70.06 | 3.44 | 4.91 | ||
| BSvk ‘Cu’ | Homoionic form of the bentonite from Slovakia saturated with copper ions | 62.14 | 2.15 | 3.46 |
| 58.64 | 2.85 | 4.86 | ||
| 60.66 | 2.93 | 4.83 | ||
| 59.20 | 3.57 | 6.03 | ||
| 73.55 | 5.59 | 7.6 | ||
| Property | Stx-1b | BSvk | |||
|---|---|---|---|---|---|
| ‘0’ | ‘Cu’ | ‘0’ | ‘Cu’ | ||
| Content of elements in the dry clay matrix(mg/kg dry of clay) a | Ca | 11,802 ± 129 | 1491 ± 14.1 | 11,945 ± 140 | 1598 ± 28 |
| K | 661 ± 10.7 | 198.5 ± 5 | 959 ± 9.3 | 522 ± 18.4 | |
| Mg | 5609 ± 68 | 2702 ± 48 | 5348 ± 60.5 | 2819 ± 10.7 | |
| Na | 1970 ± 39 | 363 ± 6.8 | 1151 ± 9 | 412.57 ± 4.8 | |
| Fe | 2493 ± 36 | 3764 ± 48 | 3582 ± 46 | 4443 ± 32 | |
| Cd | 0.25 ± 0.002 | 0.5 ± 0.1 | 0.27 ± 0.002 | 0.63 ± 0.003 | |
| Cr | 13.95 ± 0.34 | 17.5 ± 0.3 | 10.09 ± 0.11 | 22.88 ± 0.17 | |
| Ni | 7.57 ± 0.14 | 16.2 ± 0.08 | 7.22 ± 0.21 | 22.02 ± 0.09 | |
| Pb | 2.59 ± 0.04 | 6.07 ± 0.1 | 17.02 ± 0.01 | 17.93 ± 0.18 | |
| Zn | 73.68 ± 0.27 | 92.96 ± 2.9 | 64.54 ± 0.69 | 95.61 ± 0.72 | |
| Co | 0.27 ± 0.03 | 0.1 ± 0.005 | 1.26 ± 0.01 | 0.11 ± 0.06 | |
| Cu | 8.97 ± 0.13 | 5427 ± 43 | 6.28 ± 0.06 | 7677 ± 70 | |
| Mineral composition b | Estimated quantity | ≈ 75% smectite (20% opal CT; 5% quartz) | ≈ 92% smectite (5% quartz; 3% biotite) | ||
| According to the literaturefor ‘0’ clays | ≈67% smectite ((30% opal CT, 3% )quartz + feldspar + kaolinite + talc(?)) c | ≈85% smectite (5% opal C/CT, 5% feldspar, 3% biotite, 2% quartz) d | |||
| Clay/Silt fraction (%) e | 12/88 | 14/84 | 11/89 | 13/87 | |
| Specific surface area S (m2/g) f | 568 | 414 | 671 | 460 | |
| Clay | Cycle | Mean Unfrozen Water Content (% by Weight) by Temperature (°C) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| −2 | sd | −4 | sd | −6 | sd | −8 | sd | −10 | sd | ||
| Stx-1b | 1 | 43.19 | 3.95 | 38.56 | 1.51 | 34.54 | 1.31 | 32.81 | 1.31 | 29.98 | 0.46 |
| 2 | 42.81 | 3.50 | 37.97 | 1.29 | 34.65 | 1.17 | 32.48 | 1.01 | 29.97 | 0.90 | |
| 3 | 42.11 | 2.95 | 38.18 | 1.27 | 34.33 | 0.87 | 32.35 | 0.98 | 30.00 | 0.59 | |
| Stx-1b ‘Cu’ | 1 | 42.09 | 1.85 | 33.68 | 1.57 | 31.73 | 1.65 | 28.87 | 1.13 | 27.13 | 1.71 |
| 2 | 41.60 | 1.50 | 33.86 | 1.63 | 31.97 | 1.11 | 29.06 | 1.17 | 27.15 | 1.63 | |
| 3 | 41.24 | 1.65 | 33.82 | 1.97 | 31.91 | 1.36 | 29.19 | 1.20 | 27.46 | 1.88 | |
| BSvk | 1 | 46.88 | 5.07 | 39.02 | 1.05 | 35.44 | 2.03 | 33.02 | 1.26 | 30.47 | 1.85 |
| 2 | 45.71 | 4.85 | 38.71 | 1.33 | 34.93 | 2.28 | 33.10 | 1.18 | 30.4 | 2.20 | |
| 3 | 46.03 | 4.87 | 38.33 | 0.89 | 35.22 | 1.97 | 32.95 | 1.72 | 30.41 | 2.21 | |
| BSvk ‘Cu’ | 1 | 41.4 | 4.07 | 37.31 | 1.38 | 32.42 | 2.21 | 30.43 | 2.03 | 27.59 | 2.08 |
| 2 | 40.67 | 3.59 | 36.86 | 1.45 | 32.48 | 2.09 | 30.50 | 1.88 | 27.51 | 1.87 | |
| 3 | 40.02 | 3.47 | 36.88 | 1.38 | 32.35 | 1.94 | 30.62 | 2.14 | 27.52 | 1.89 | |
| Clay | Cycle | Mean Unfrozen Water Content (% by Weight) by Temperature (°C) | |||||||||
| −12 | sd | −14 | sd | −20 | sd | −26 | sd | −35 | sd | ||
| Stx-1b | 1 | 28.82 | 0.99 | 27.43 | 0.51 | 24.90 | 0.89 | 23.44 | 1.06 | 22.21 | 1.24 |
| 2 | 28.59 | 0.88 | 27.17 | 0.67 | 24.73 | 0.93 | 23.41 | 0.94 | 22.46 | 1.37 | |
| 3 | 28.56 | 0.88 | 27.44 | 0.41 | 24.79 | 0.79 | 23.35 | 0.79 | 22.52 | 1.11 | |
| Stx-1b ‘Cu’ | 1 | 25.46 | 1.78 | 23.76 | 2.18 | 20.46 | 1.74 | 18.36 | 1.76 | 18.36 | 1.76 |
| 2 | 25.72 | 1.42 | 23.93 | 1.88 | 20.73 | 1.51 | 18.60 | 1.88 | 18.60 | 1.88 | |
| 3 | 25.86 | 1.87 | 24.48 | 2.17 | 20.79 | 1.63 | 18.64 | 2.05 | 18.64 | 2.05 | |
| BSvk | 1 | 28.78 | 1.94 | 28.13 | 1.56 | 25.58 | 1.58 | 24.84 | 1.23 | 24.54 | 1.30 |
| 2 | 29.08 | 2.00 | 27.84 | 1.79 | 25.76 | 1.39 | 25.14 | 1.29 | 24.75 | 1.12 | |
| 3 | 29.04 | 1.86 | 27.98 | 1.91 | 25.85 | 1.59 | 24.98 | 1.24 | 24.74 | 1.29 | |
| BSvk ‘Cu’ | 1 | 25.91 | 2.14 | 24.78 | 2.05 | 22.98 | 1.96 | 22.43 | 1.66 | 22.43 | 1.66 |
| 2 | 26.14 | 2.08 | 24.69 | 1.90 | 23.25 | 1.97 | 22.71 | 1.68 | 22.71 | 1.68 | |
| 3 | 26.33 | 2.07 | 25.07 | 1.90 | 23.47 | 2.19 | 22.88 | 1.63 | 22.88 | 1.63 | |
| The Unfrozen Water Content | Sum of Squares | Degrees of Freedom | Mean Square | F-Test Value | p-Value | Statistical Significance |
|---|---|---|---|---|---|---|
| Intercept | 223,262.2 | 1 | 223,262.2 | 58,366.21 | 0.0000 | *** |
| Temperature (T) | 10,565.9 | 8 | 1320.7 | 345.27 | 0.0000 | *** |
| Type of clay (S) | 131.8 | 1 | 131.8 | 34.45 | 0.0000 | *** |
| Cycle (C) | 0.4 | 2 | 0.2 | 0.06 | 0.9441 | NS |
| T × S | 157.6 | 8 | 19.7 | 5.15 | 0.000007 | *** |
| T × C | 10.7 | 16 | 0.7 | 0.17 | 0.999878 | NS |
| S × C | 0.6 | 2 | 0.3 | 0.08 | 0.927128 | NS |
| T × S × C | 1.0 | 16 | 0.1 | 0.02 | 1.000000 | NS |
| Error | 826.2 | 216 | 3.8 |
| The Unstandardized Beta (β) | Std. Error β | The Standardized Beta (β) | Std. Error β | t Test Value | p-Value | Significance | |
|---|---|---|---|---|---|---|---|
| N = 270 | Dependent Variable: Unfrozen Water at the Temperatures −26 °C, −20 °C, −14 °C, −12 °C, −10 °C, −8 °C, −6 °C, −4 °C, and −2 °C | ||||||
| R = 0.89 | R2 = 0.79 | adj. R2 = 0.78 | Std. Error of Estimate: 3.06 | ||||
| Intercept | −186.026 | 62.53284 | −2.97485 | 0.003202 | ** | ||
| Mass of water | −0.133708 | 0.029177 | −0.683 | 0.14896 | −4.58271 | 0.000007 | *** |
| The water content | 0.106366 | 0.046153 | 0.068 | 0.02945 | 2.30463 | 0.021960 | * |
| Type of clay | 0.165678 | 0.045589 | 2.181 | 0.60006 | 3.63419 | 0.000335 | ** |
| Temperature | 0.869839 | 0.028360 | 0.784 | 0.02556 | 30.67115 | 0.000000 | *** |
| Parameter | Estimate | SE | t | p | Statistical Significance | Confidence Limits | ||
|---|---|---|---|---|---|---|---|---|
| Lower | Upper | |||||||
| a1 | 49.340 | 0.475 | 103.825 | 0.000 | *** | 48.405 | 50.276 | |
| a2 | −0.705 | 0.088 | −7.964 | 0.000 | *** | −0.880 | −0.531 | |
| a3 | −8.258 | 0.151 | −54.697 | 0.000 | *** | −8.554 | −7.960 | |
| Temperature (°C) | −2 | −4 | −6 | −8 | −10 | −12 | −14 | −20 | −26 |
|---|---|---|---|---|---|---|---|---|---|
| Equation (4) | 5.7 | 2.8 | 3.6 | 2.4 | 2.1 | 3.1 | 3.3 | 3.1 | 4.7 |
| Equation (5) | 6.3 | 2.3 | 3.6 | 2.2 | 3.8 | 3.7 | 3.8 | 2.6 | 4.0 |
| Equation (6) | 5.2 | 3.2 | 3.6 | 2.6 | 2.2 | 3.1 | 3.3 | 3.5 | 4.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nartowska, E.; Kozłowski, T. The Effect of Freeze-Thaw Cycling and the Initial Mass of Water on the Unfrozen Water Content of Calcium Bentonites Modified by Copper Ions. Minerals 2022, 12, 66. https://doi.org/10.3390/min12010066
Nartowska E, Kozłowski T. The Effect of Freeze-Thaw Cycling and the Initial Mass of Water on the Unfrozen Water Content of Calcium Bentonites Modified by Copper Ions. Minerals. 2022; 12(1):66. https://doi.org/10.3390/min12010066
Chicago/Turabian StyleNartowska, Edyta, and Tomasz Kozłowski. 2022. "The Effect of Freeze-Thaw Cycling and the Initial Mass of Water on the Unfrozen Water Content of Calcium Bentonites Modified by Copper Ions" Minerals 12, no. 1: 66. https://doi.org/10.3390/min12010066
APA StyleNartowska, E., & Kozłowski, T. (2022). The Effect of Freeze-Thaw Cycling and the Initial Mass of Water on the Unfrozen Water Content of Calcium Bentonites Modified by Copper Ions. Minerals, 12(1), 66. https://doi.org/10.3390/min12010066






