Comparison of Semirigorous and Empirical Models Derived Using Data Quality Assessment Methods
Abstract
:1. Introduction
- The modes of the PID loops in the past are not known.
- The data are correlated and cannot be used.
- There is too much data to look through to find regions where model identification can be used.
- Either store the modes, or calculate them from the setpoint, process value, and output behaviour.
- Modern identification techniques can handle a certain amount of cross-correlation in the data.
- In this era of big data, can we not write a routine that partitions the data for us?
2. Data Quality Assessment Method
Multivariate Data Segmentation Algorithm
- Preprocessing: The data set is first loaded and preprocessed. Often preprocessing consists of scaling and centering the data.
- Mode Changes: Any known mode changes should be given to the algorithm. This will allow for better segmentation of the data set. The modes could be based the state of the process control system, for example, whether certain PID loops are in cascade, automatic of manual mode, or the mode may refer to an operating mode of the plant such as low or high throughput mode.
- Correlation Detection: For each mode, determine which of the parameters are correlated with each other. This problem can quickly become intractable if time delays in the problem are considered. For each of the correlated variables, only a subset of these parameters can be selected for analysis. Otherwise, the methods will all return the result that there is no viable model, as the regression matrix will not be invertible [6].
- Segmentation: For each mode, perform the following steps:
- (a)
- Initialization: Initialize the mode counter to the current data value, that is, set .
- (b)
- Computation: Compute the variances of the signals and the condition number of the information matrix.
- (c)
- Comparison: Compare the variances, the condition number, and the significance of the parameters against the thresholds.
- (d)
- Failure: Should the thresholds fail to be met, then go to the next data point, that is, set , and go to Step 4.b.
- (e)
- Success: Otherwise, set , and go to Step 4.c. The “good” data region is then .
- Termination: The procedure ends when k equals N, that is, the total number of data points for the given mode.
- Simplification: Compare adjacent regions, and determine if they belong to the same model using an appropriate metric such as an entropy-based metric. It happens that the method may be too anxious to split adjacent regions on the slightest of changes [13].
3. Process and Modeling
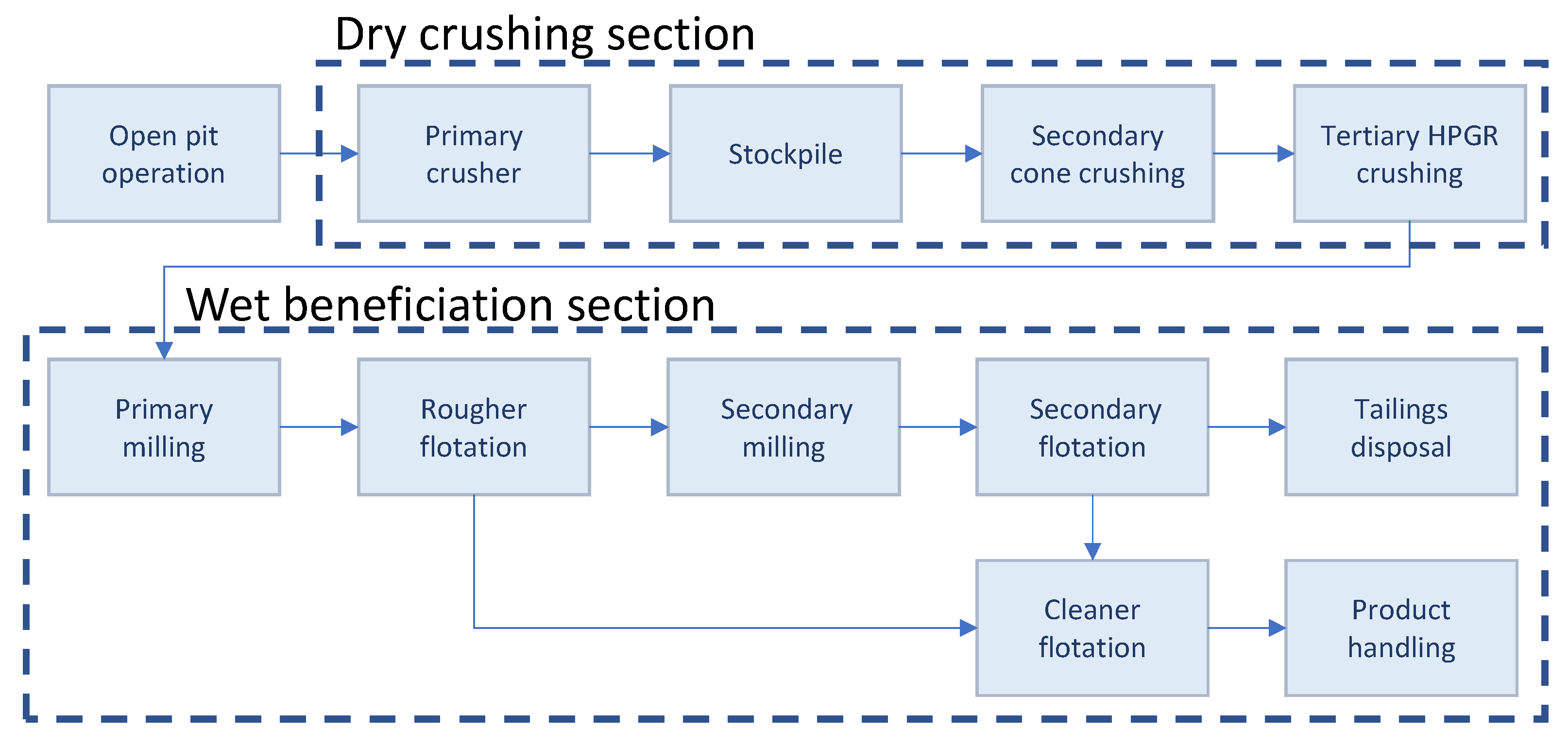
3.1. Process Description
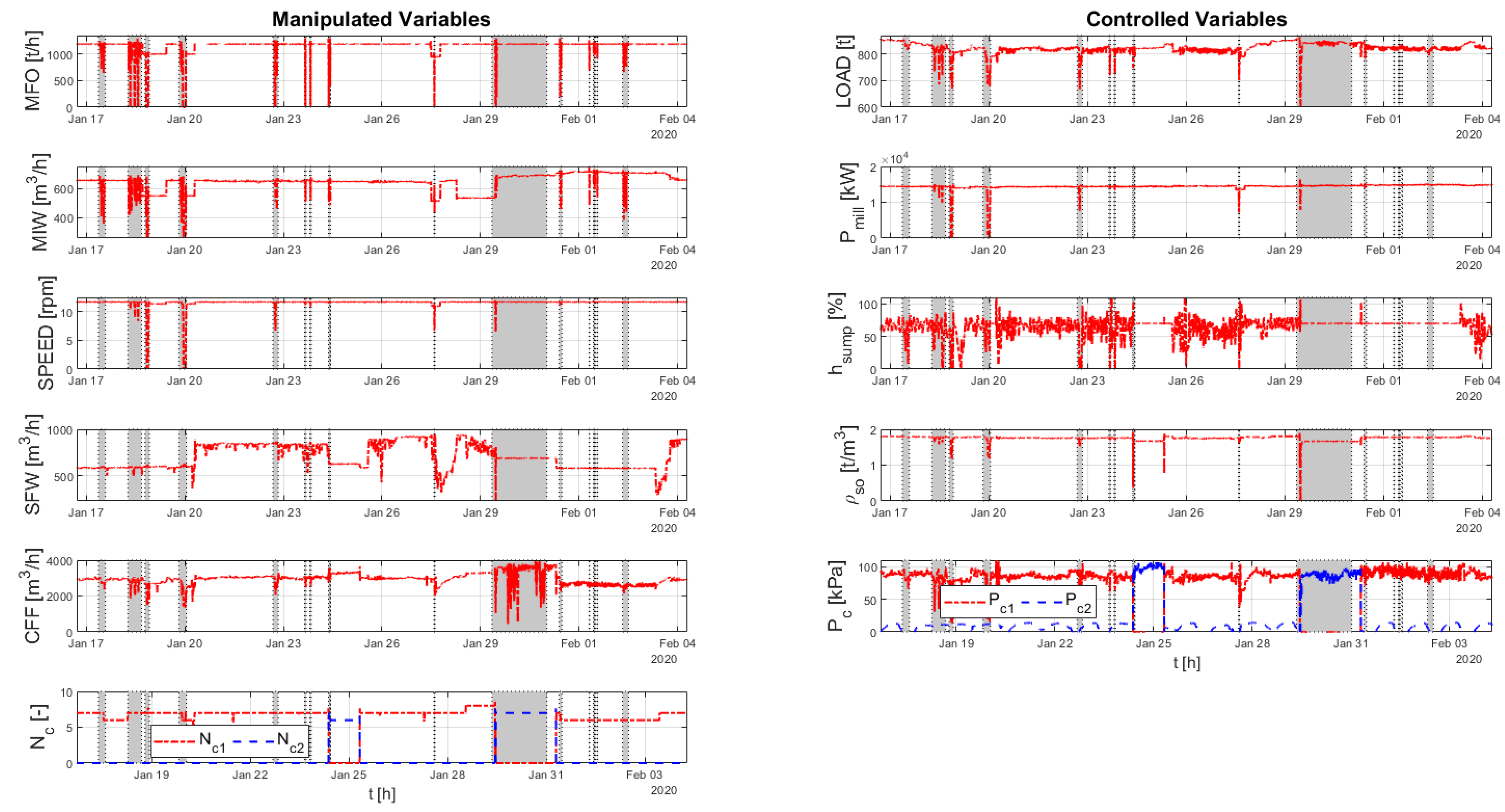
3.2. Process Data
3.3. Linear Empirical Models
Linear Model Identification
- Finite Impulse Response (FIR),
- Autoregressive with exogenous inputs (ARX) and
- subspace modeling (SS).
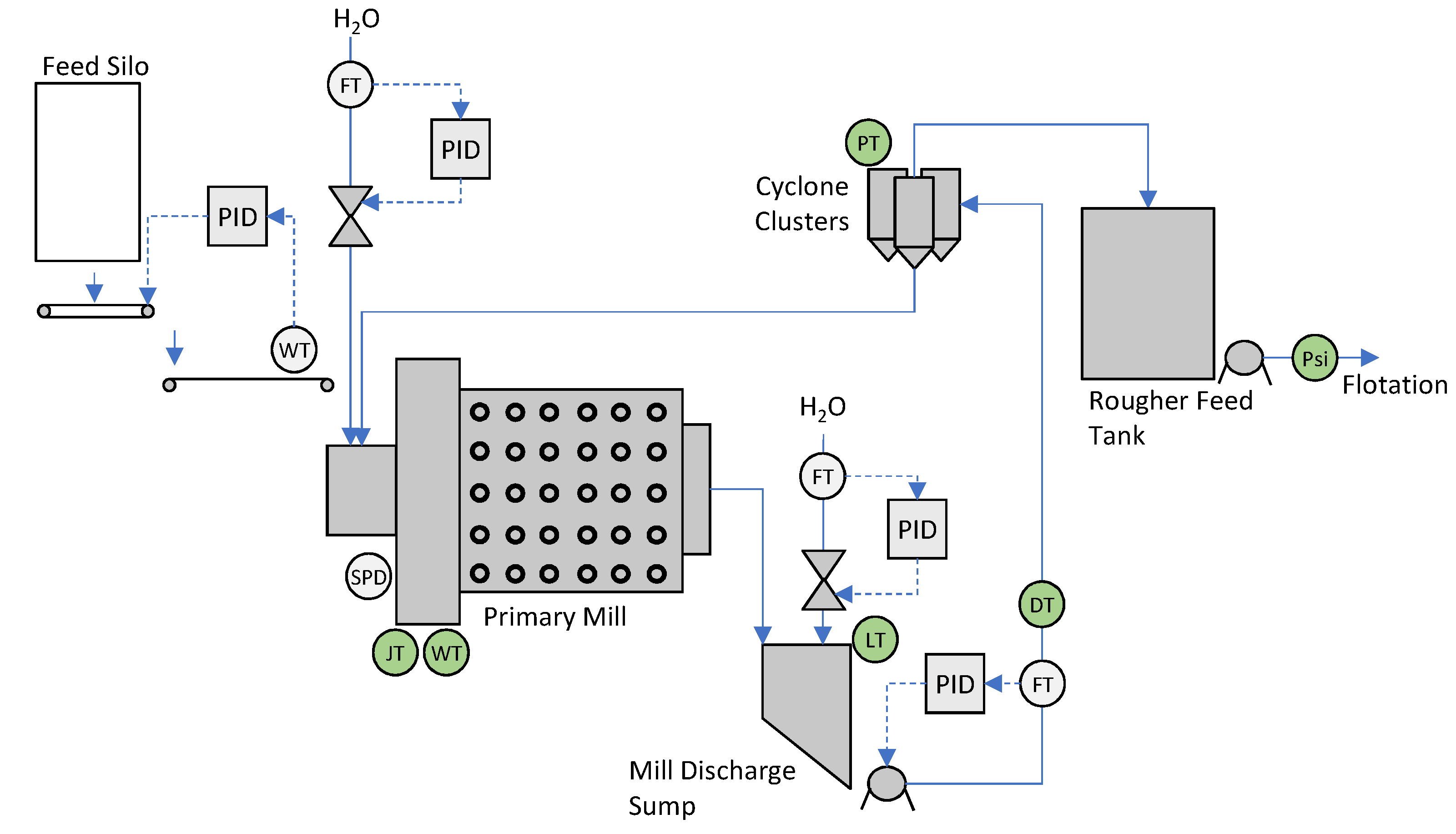
3.4. Semirigorous Mill Circuit Model
3.4.1. Mill Model
3.4.2. Sump Model
3.4.3. Cyclone Cluster Model
4. Data Quality Assessment Results
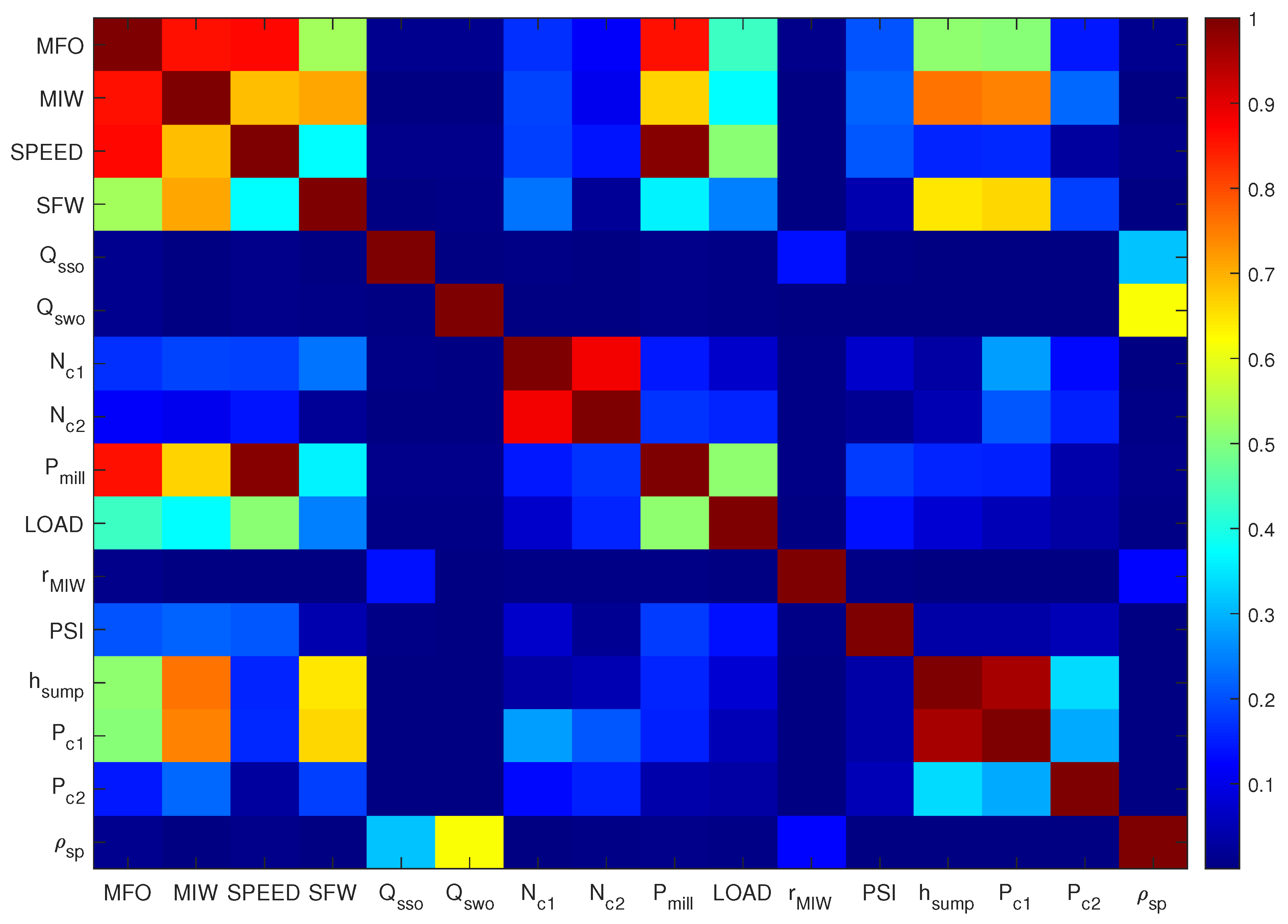
4.1. Analysis of the Complete Data Set
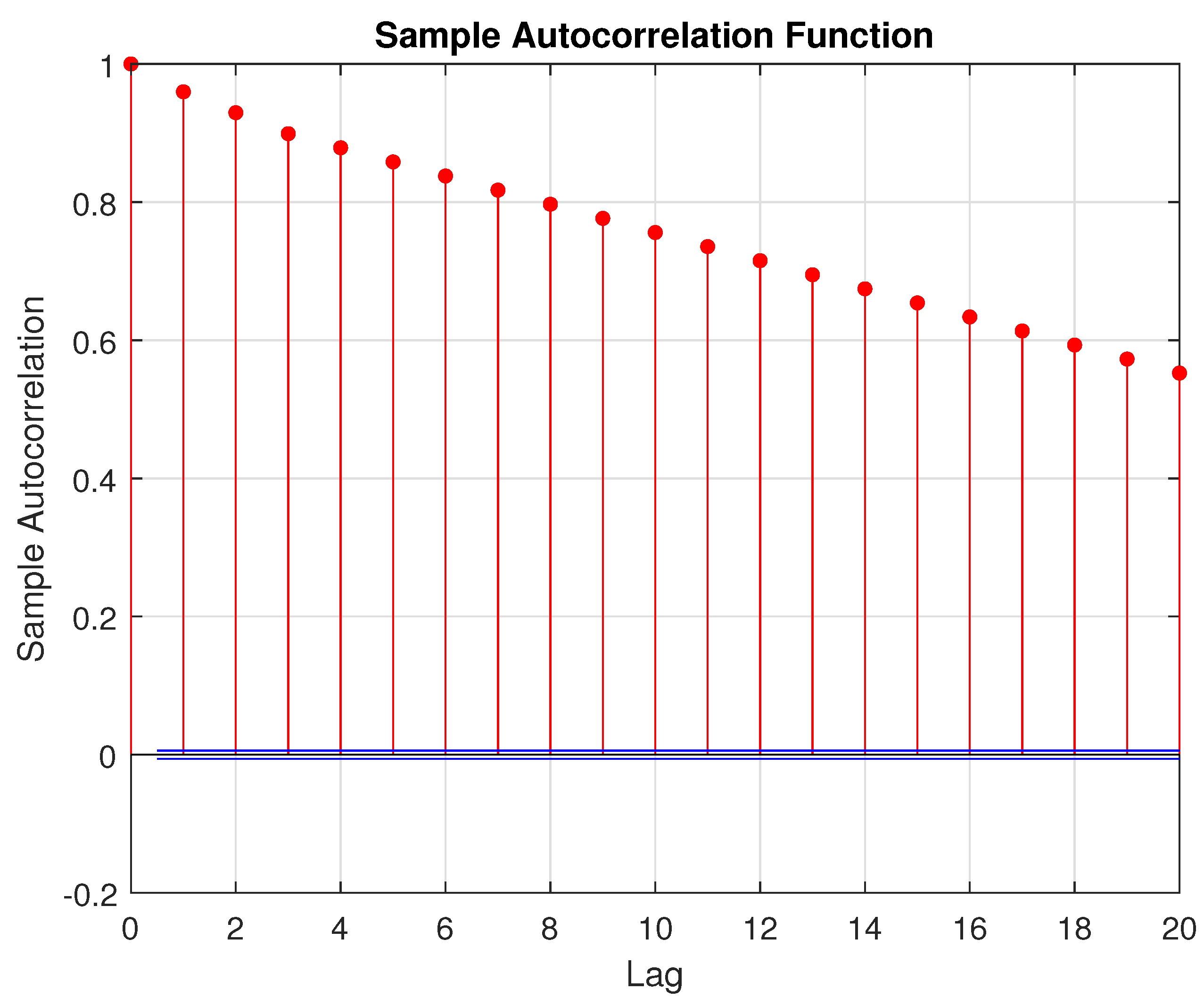
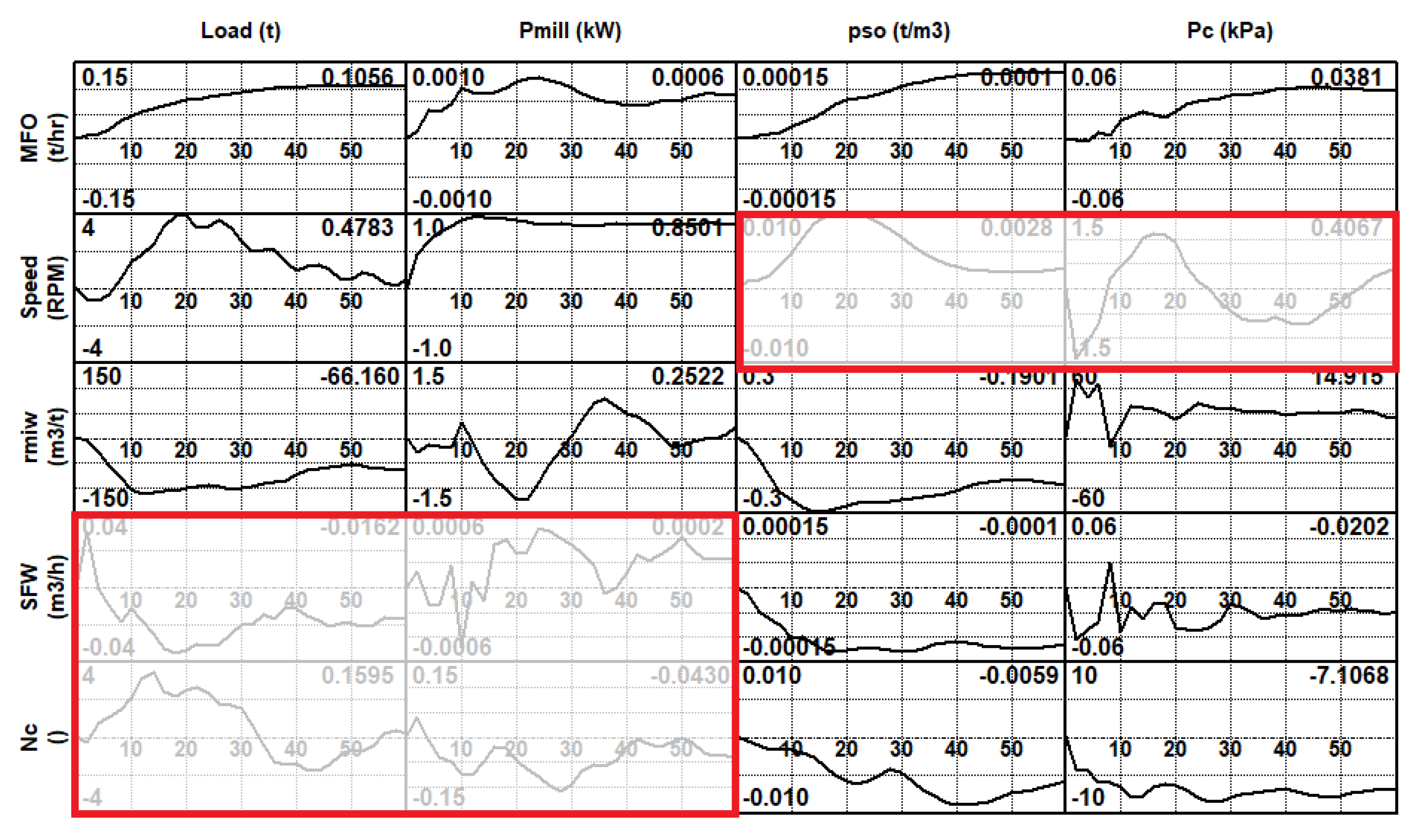
4.1.1. Correlation Analysis of the Complete Data Set
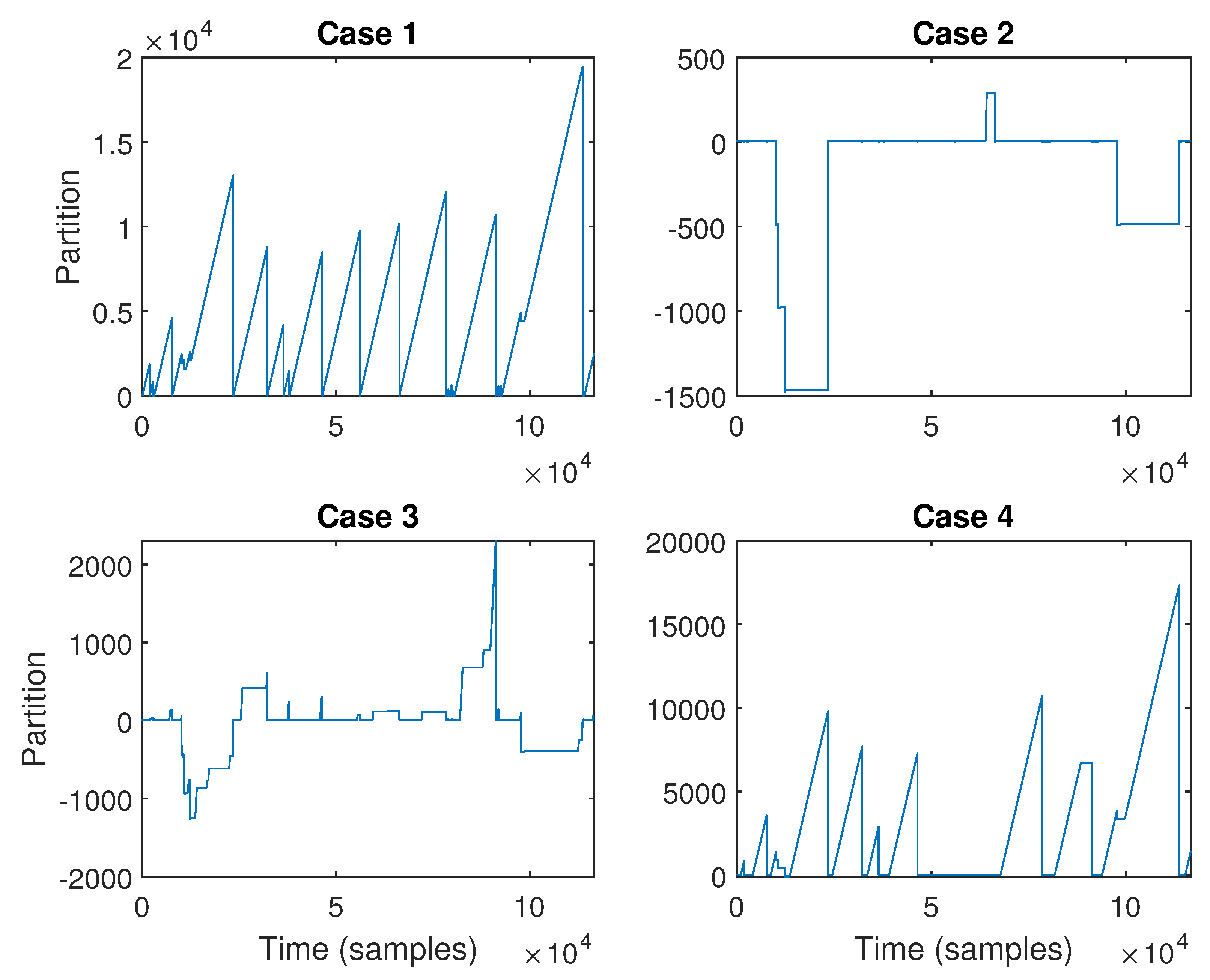
4.1.2. Data Segmentation for the Complete Data Set
- Case 1: Here the partitioning will be performed using , , , and (that is, the first four variables).
- Case 2: Here the partitioning will be performed using only .
- Case 3: Here the partitioning will be performed using only , , and .
- Case 4: Here the partitioning will be performed using only , which is a quasi-integrating variable.
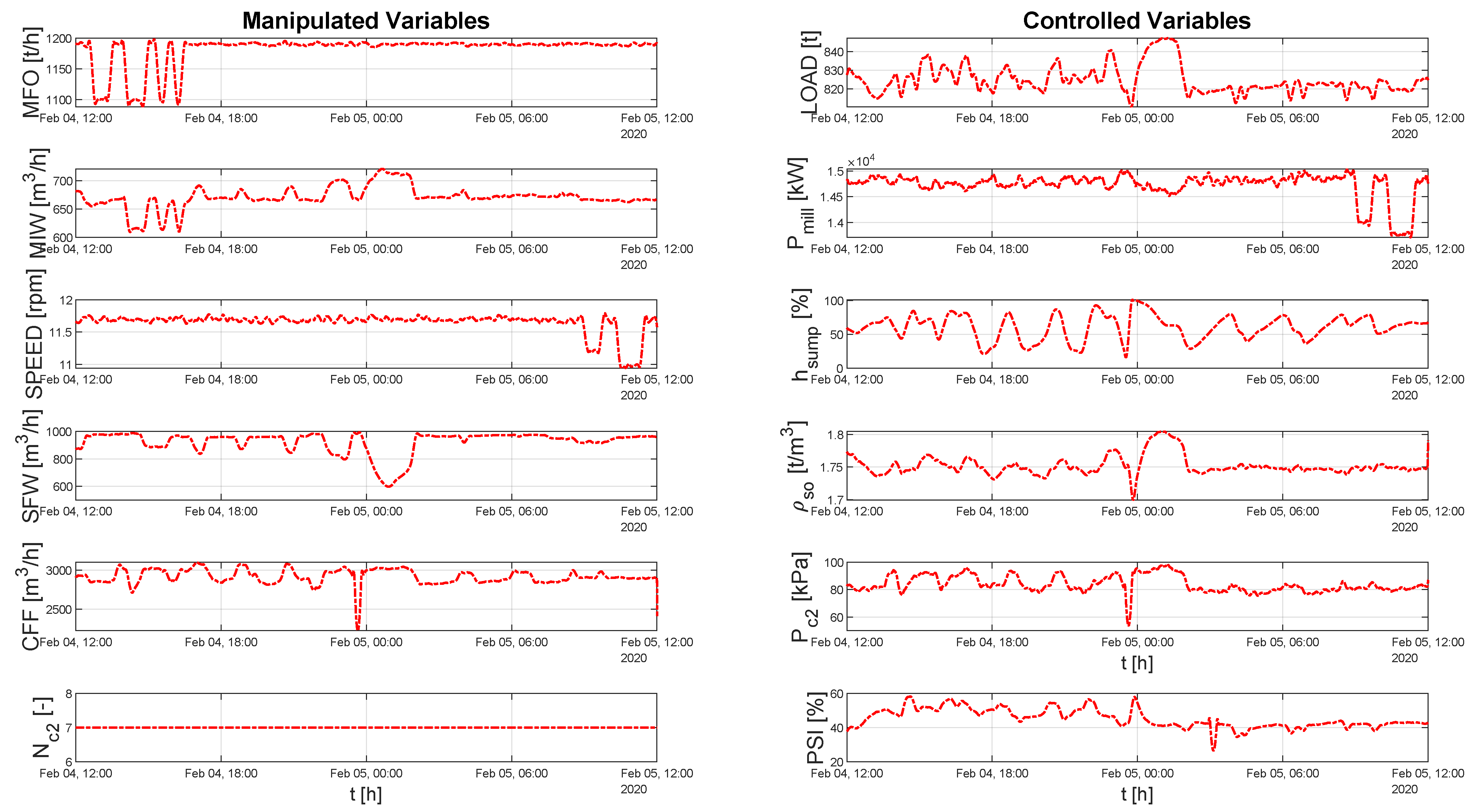
4.2. Data Quality Assessment for the Step Data Set
5. Results
5.1. Results from the Routine Operating Data
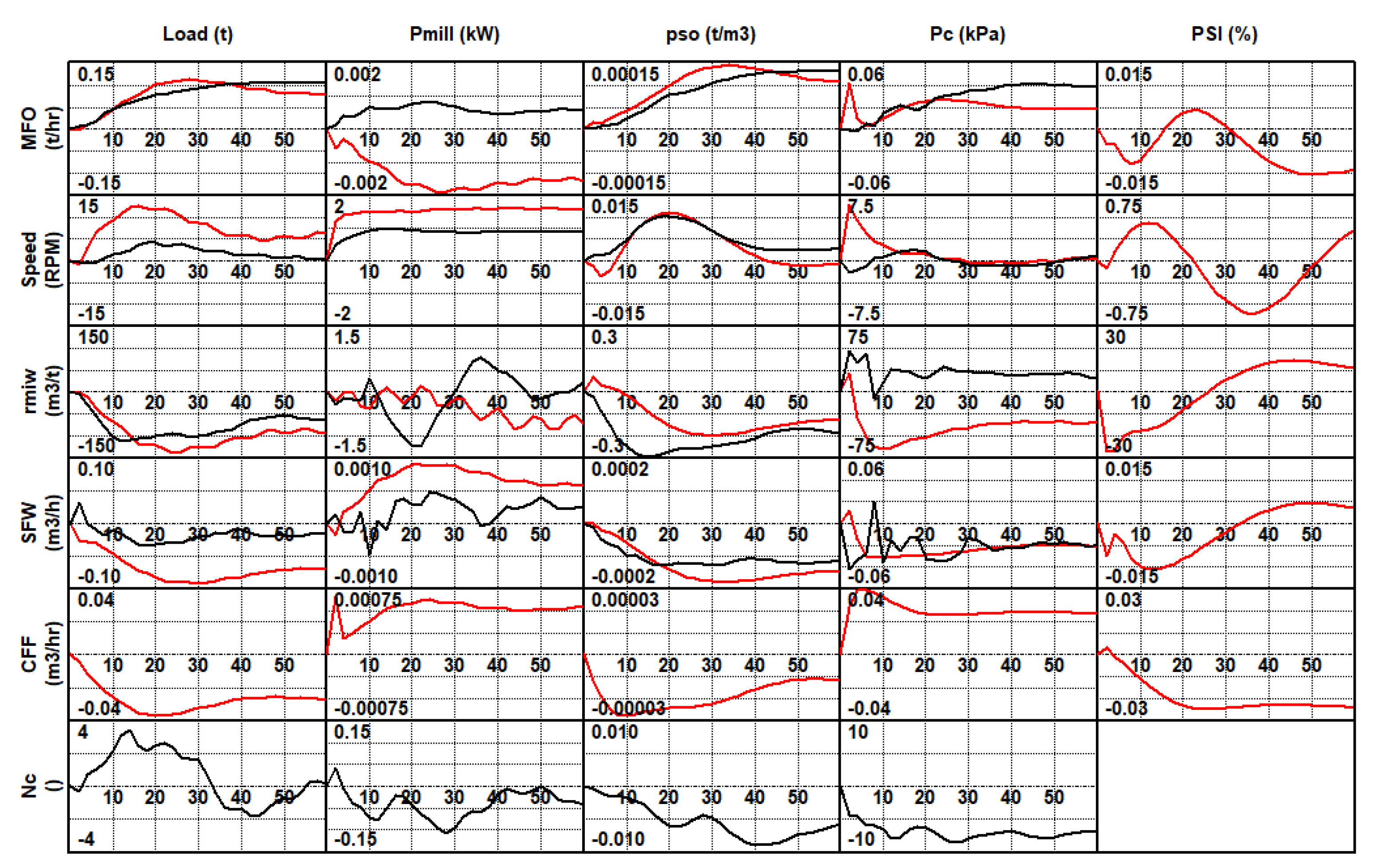
5.1.1. Results Using the Linear Empirical Models
5.1.2. Results Using the Semirigorous Mill Circuit Model
5.2. Results from the Planned Step Tests
5.2.1. Results Using the Linear Empirical Model
5.2.2. Results Using the Semirigorous Mill Circuit Model
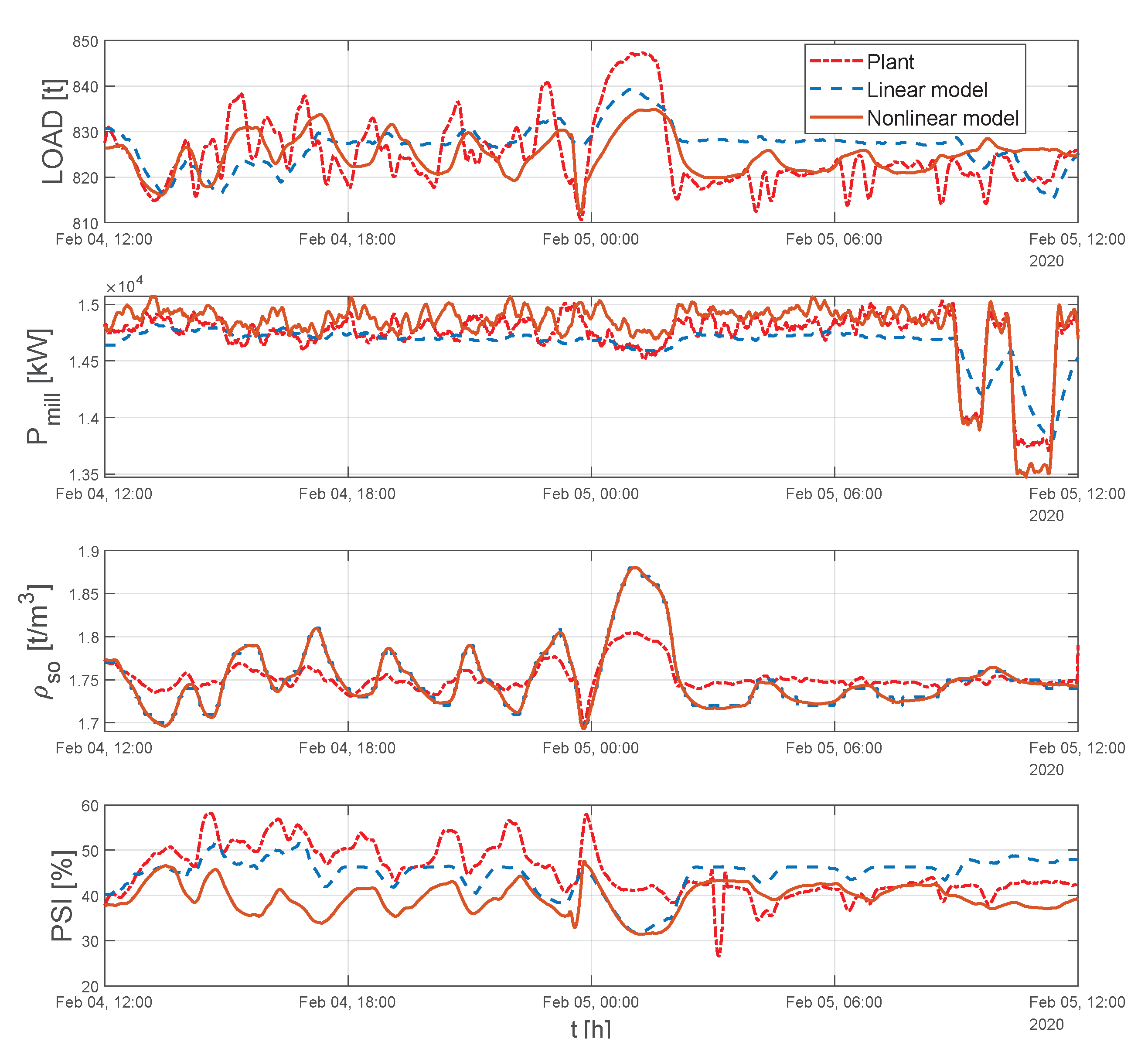
5.3. Comparison of the Linear and Nonlinear Models
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| APC | Advanced Process Control |
| ARX | Autoregressive with exogenous inputs |
| CVA | Canonical Variable Analysis |
| CV | Controlled Variable |
| DQA | Data Quality Assessment |
| FIR | Finite Impulse Response |
| I/O | Input/Output |
| MIMO | Multi-input, Multi-output |
| MISO | Multi-input, Single-Output |
| MPC | Model Predictive Control |
| MSE | Mean Squared Error |
| MV | Manipulated Variable |
| PID | Proportional, Integral, Derivative |
| SS | Subspace |
| TTSS | Time to steady state |
| SCADA | Supervisory Control and Data Acquisition |
| VSD | Variable Speed Drive |
References
- Ge, Z.; Song, Z.; Ding, S.X.; Huang, B. Data Mining and Analytics in the Process Industry: The Role of Machine Learning. IEEE Access 2017, 5, 20590–20616. [Google Scholar] [CrossRef]
- McCoy, J.; Auret, L. Machine learning applications in minerals processing: A review. Miner. Eng. 2019, 132, 95–109. [Google Scholar] [CrossRef]
- Lidwell, W.; Holden, K.; Butler, J. Universal Principles of Design, Revised and Updated: 125 Ways to Enhance Usability, Influence Perception, Increase Appeal, Make Better Design Decisions, and Teach through Design; Rockport Pub: Beverly, MA, USA, 2010. [Google Scholar]
- Qin, S.J. Process data analytics in the era of big data. AIChE J. 2014, 60, 3092–3100. [Google Scholar] [CrossRef]
- Ljung, L. System Identification: Theory for the User; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Shardt, Y.A.W. Statistics for Chemical and Process Engineers; Springer: Berlin, Germany, 2015. [Google Scholar]
- Peretzki, D.; Isaksson, A.; Carvalho Bittencourt, A.; Forsman, K. Data Mining of Historic Data for Process Identification; Linköping University Electronic Press: Linköping, Sweden, 2011. [Google Scholar]
- Shardt, Y.A.W.; Huang, B. Data quality assessment of routine operating data for process identification. Comput. Chem. Eng. 2013, 55, 19–27. [Google Scholar] [CrossRef]
- Arengas, D.; Kroll, A. A data selection method for large databases based on recursive instrumental variables for system identification of MISO models. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 357–362. [Google Scholar]
- Shardt, Y.A.; Yang, X.; Brooks, K.; Torgashov, A. Data Quality Assessment for System Identification in the Age of Big Data and Industry 4.0. IFAC-PapersOnLine 2020, 53, 104–113. [Google Scholar] [CrossRef]
- Shardt, Y.A.W. Data Quality Assessment for Closed-Loop System Identification and Forecasting with Application to Soft Sensors. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2012. [Google Scholar]
- Shardt, Y.A.W.; Brooks, K.S. Automated system identification in mineral processing industries: A case study using the zinc flotation cell. IFAC-PapersOnLine 2018, 51, 132–137. [Google Scholar] [CrossRef]
- Shah, S.; Shardt, Y.A.W. Segmentation methods for model identification from historical process data. IFAC-PapersOnLine 2014, 47, 2836–2841. [Google Scholar]
- Steyn, C.W.; Brooks, K.S.; De Villiers, P.G.R.; Muller, D.; Humphries, G. A holistic approach to control and optimization of an industrial run-of-mine ball milling circuit. IFAC Proc. Vol. 2010, 43, 137–141. [Google Scholar] [CrossRef]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Kalafatis, A.; Patel, K.; Harmse, M.; Zheng, Q.; Craik, M. Multivariable step testing for MPC projects reduces crude unit testing time. Hydrocarb. Process. 2006, 85, 93–100. [Google Scholar]
- Nieto, L.; Olivares, J.; Gatica, J.; Ramos, B.; Olmos, H. Implementation of a multivariable controller for grinding-classification process. IFAC Proc. Vol. 2009, 42, 55–60. [Google Scholar] [CrossRef]
- Jamaludin, I.; Wahab, N.; Khalid, N.; Sahlan, S.; Ibrahim, Z.; Rahmat, M.F. N4SID and MOESP subspace identification methods. In Proceedings of the 2013 IEEE 9th International Colloquium on Signal Processing and its Applications, Kuala Lumpur, Malaysia, 8–10 March 2013; pp. 140–145. [Google Scholar]
- Zhao, H.; Harmse, M.; Guiver, J.; Canney, W.M. Subspace identification in industrial APC applications—A review of recent progress and industrial experience. IFAC Proc. Vol. 2006, 39, 1074–1079. [Google Scholar] [CrossRef]
- Larimore, W.E. Automated multivariable system identification and industrial applications. In Proceedings of the 1999 American Control Conference (Cat. No. 99CH36251), San Diego, CA, USA, 2–4 June 1999; Volume 2, pp. 1148–1162. [Google Scholar]
- Le Roux, J.D.; Craig, I.K.; Hulbert, D.G.; Hinde, A.L. Analysis and validation of a run-of-mine ore grinding mill circuit model for process control. Miner. Eng. 2013, 43–44, 121–134. [Google Scholar] [CrossRef] [Green Version]
- Powell, M.S.; Van der Westhuizen, A.P.; Mainza, A.N. Applying grindcurves to mill operation and optimisation. Miner. Eng. 2009, 22, 625–632. [Google Scholar] [CrossRef]
- Apelt, T.A.; Asprey, S.P.; Thornhill, N.F. Inferential measurement of SAG mill parameters. Miner. Eng. 2001, 14, 575–591. [Google Scholar] [CrossRef]
- Le Roux, J.D.; Steinboeck, A.; Kugi, A.; Craig, I.K. Steady-state and dynamic simulation of a grinding mill using grind curves. Miner. Eng. 2020, 152, 106208. [Google Scholar] [CrossRef]
- Botha, S.; Craig, I.K.; Le Roux, J.D. Hybrid non-linear model predictive control of a run-of-mine ore grinding mill circuit. Miner. Eng. 2018, 123, 49–62. [Google Scholar] [CrossRef] [Green Version]


| Variable | Unit | Description |
|---|---|---|
| Manipulated Variables | ||
| t/h | Fresh mill feed ore tonnage | |
| m3/h | Mill inlet water | |
| m3/t | Mill inlet water to feed ore ratio | |
| rpm | Mill speed | |
| m3/h | Sump feed water | |
| m3/h | Cyclone feed flow-rate | |
| integer | Number of cyclones in operation for cluster 1 | |
| integer | Number of cyclones in operation for cluster 2 | |
| Controlled Variables | ||
| ton | Mill load | |
| MW | Mill power | |
| % | Percentage of sump filled with slurry | |
| t/m3 | Sump outflow density | |
| kPa | Cyclone cluster 1 pressure | |
| kPa | Cyclone cluster 2 pressure | |
| % pass 75 mm | Product particle size passing 75 m | |
| Parameter | Unit | Description |
|---|---|---|
| General | ||
| t/m3 | Density of ore | |
| t/m3 | Density of water | |
| Mill | ||
| - | Mass fraction of fines in the feed ore | |
| - | Mass fraction of rocks in the feed ore | |
| D | m | Internal mill diameter |
| - | Power parameter for fraction solids in the mill | |
| - | Power parameter for volume of mill filled | |
| h | Discharge rate | |
| - | Rheology normalization factor | |
| - | Fraction of mill volume filled at maximum power draw | |
| MWh/t | Fines production factor | |
| - | Fractional change in fines production factor per change in fractional mill filling | |
| MWh/t | Rock consumption factor | |
| MW | Maximum mill power draw parameters | |
| m3 | Mill volume | |
| Sump | ||
| m3 | Sump volume | |
| Cyclone cluster | ||
| - | Parameter related to fraction solids in cyclone underflow | |
| - | Cyclone model constant | |
| m3/h | Parameter related to coarse split at cyclone | |
| 1.35 | −0.36 | 1.24 | 2.03 | |
| 0.08 | 0.54 | N/A | N/A | |
| 0.70 | −0.34 | 1.45 | −0.42 | |
| N/A | N/A | 0.80 | 0.93 |
| Average | 824.9 | 14.73 | 1.752 | 0.447 |
| MSE—Nonlinear model | 6.17 | 0.14 | 0.002 | 0.082 |
| —Nonlinear model | 0.32 | 0.86 | 0.98 | 0.05 |
| MSE—Linear Model | 7.06 | 0.10 | 0.028 | 0.055 |
| —Linear Model | 0.22 | 0.87 | 0.79 | 0.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brooks, K.; le Roux, D.; Shardt, Y.A.W.; Steyn, C. Comparison of Semirigorous and Empirical Models Derived Using Data Quality Assessment Methods. Minerals 2021, 11, 954. https://doi.org/10.3390/min11090954
Brooks K, le Roux D, Shardt YAW, Steyn C. Comparison of Semirigorous and Empirical Models Derived Using Data Quality Assessment Methods. Minerals. 2021; 11(9):954. https://doi.org/10.3390/min11090954
Chicago/Turabian StyleBrooks, Kevin, Derik le Roux, Yuri A. W. Shardt, and Chris Steyn. 2021. "Comparison of Semirigorous and Empirical Models Derived Using Data Quality Assessment Methods" Minerals 11, no. 9: 954. https://doi.org/10.3390/min11090954
APA StyleBrooks, K., le Roux, D., Shardt, Y. A. W., & Steyn, C. (2021). Comparison of Semirigorous and Empirical Models Derived Using Data Quality Assessment Methods. Minerals, 11(9), 954. https://doi.org/10.3390/min11090954






