1. Introduction
Comminution is the progressive reduction in size of run-of-mine (ROM) ore, and its initial stage is consists of primary crushing [
1]. Gyratory crushers are the most common machine used in the primary crushing in the copper mining industry of Chile and worldwide, and they are designed for large tonnage throughput. Notably, Chile has produced almost one-third of global copper mine production, and this industry is one of the most important industries for this country [
2].
Currently, there is a strong interest to study the operating parameters of primary and secondary crushers in order to optimize their performance [
3]. For this reason, different models have been developed to predict the operating conditions of gyratory crushers. These models can be classified as empirical [
4] and mechanistic models [
5,
6]: of the latter, some of them can be solved numerically, such as with the discrete element method.
The discrete element method (DEM) is an explicit numerical scheme utilized to simulate the dynamical behavior of granular flow. The interaction of the particles is monitored contact by contact, and the motion is modeled for each particle [
7]. It was first proposed by Cundall [
8], and then it was expanded to three dimensions by Hart and Cundall [
9,
10]. The particles in the system interact with one another through forces calculated by contact models, allowing the computation of the interactions between particles and between particles and walls. For all the time steps, the equations of motion for each particle are numerically solved, and the new position of the particles is acquired and updated for the new time step.
DEM has been used by engineers and scientists in an extensive range of fields, in particularly, DEM has become one of the most important tools for simulating the behavior of machines and processes in mineral processing and grinding [
11]. DEM simulations deliver dynamic information, such as the transient forces for each particle, that is extremely complicated if not impossible to obtain through physical experiments with current scientific and experimental development [
12]. To simulate comminution equipment, it is necessary to use a proper breakage model to represent the particle size distribution (PSD) of the progeny particles and the specific energy consumption.
Several gyratory and cone crushers have been simulated with DEM. Litcher et al. proposed a two-way coupling DEM-PBM (Population Balance Model) model of cone crushers [
13], where the PBM was used to represent the size reduction in the particles. A B90 cone crusher and a HP100 cone crusher were simulated, and the particle size distribution of the product was validated. Li et al. [
14] presented a DEM model of a cone crusher by using the particle replacement method (PRM) to represent the breakage of rocks. They studied the effect of closed side setting and eccentric speed on the size distribution of the products with DEM simulations. Delaney et al. [
15] simulated an industrial-scale cone crusher with DEM employing super-quadrics particles, and a DEM breakage model was proposed where the particles were broken when the contact energy reaches a maximum value. The progeny size distribution of this breakage model was obtained with data from the Julius Kruttschnitt Mineral Research Centre (JKRMC) Drop Weight Test. Quist et al. [
16] investigated an industrial-scale Svedala H6000 cone crusher using DEM and experiments. The commercial software EDEM 2.5 (provided by DEM Solutions Ltd., Edinburgh, Scotland, UK) was employed with a bonded particle model (BPM) to describe the particle breakage. Throughput capacity, power draw, and product particle size distribution were calculated in the simulations and then compared with experimental data. For throughput capacity, relative errors of 34.6% and 1.97% were obtained for closed side settings equal to 34 mm and 50 mm, respectively. Using the same DEM code, Johansson et al. [
3] presented a DEM simulation of a Morgårdshammar B90 laboratory cone crusher, and the results were compared with laboratory experiments. Two case simulations had been performed for investigating the influence of eccentric speed at 10 Hz and 20 Hz. The PSD of the product matched the experimental results relatively well with the corresponding coarse region. Comparing the mass flow rate, a relative error of 1.36% was achieved for the simulation at 10 Hz, and 56.4% was achieved for the simulation at 20 Hz. Chen et al. performed a DEM simulation and parameter optimization of a gyratory crusher by utilizing the bonded-particle model to represent particle breakage [
17]. These simulations were performed with the EDEM software in a CG810i SANDVIK gyratory crusher, and a full sensibility analysis was accomplished. André and Tavares published simulations of a laboratory-scale cone crusher by adopting a novel breakage model [
18]. Their results provided good agreement with experiments for throughput with a relative error of 9.6, 10.4, and 37.9% for the three cases presented, but the findings reported a deviation up to a 50% for specific energy and product size. A multibody dynamic and discrete element method was presented to analyze the performance of the GYP1200 inertia cone crusher, and it was contrasted with experimental data, obtaining a 4% of relative error in both power draw and throughput for the 400 rpm case, 11% error in power draw, and a 22% error in throughput for the 600 rpm case [
19]. Complete research of comminution modeling was presented by Cleary et al., focusing on recent advances in particle-based modeling of crushing [
20]. Three machines were analyzed: twin roll crusher, cone crusher, and vertical shaft impactor (VSI). Between the challenges that they proposed, an industrial-scale validation of DEM models of crushers is highlighted. A crushing chamber optimization with DEM (EDEM 2018) was performed by using a genetic algorithm [
21]. The particle breakage was modeled by BPM, modeling the particles as a cube shape ore of 300 mm of edge formed by spherical particles of 30 mm of radius. After the optimization, an increase of 36% and 26% was reported in productivity and power density (mass flow rate per unit of power), respectively. Another chamber optimization was performed by adopting a dual-objective optimization of productivity and product quality in a C900 cone crusher [
22]. The productivity was determined with an analytical model and numerically with DEM. Optimization of the angular speed of the mantle consisted of the following: the length of the parallel zone; the bottom angle of the mantle; the eccentric angle; the eccentricity; and the engagement angle. The productivity and the percentage of crushed products were increased by about 2% and 2.1%, respectively.
In this paper, a Metso 60-110 gyratory crusher of 1500 kW nominal power operating in a Chilean copper mine is modeled and simulated by using the discrete element method in order to study the crushing power and crushing torque under different operational conditions. The software Rocky DEM is employed with polyhedral particles, a hysteretic contact model, and the Tavares’ breakage model [
23]. The simulations are validated by utilizing the nominal and experimental data of throughput, product size, and crushing power, being an important contribution to comminution modeling [
20]. A complete force analysis of the loading force distribution acting on the crusher’s mantle and the torque in the mantle geometry is performed with a moving frame of reference in polar coordinates. With this variable change, a planar force and torque distribution can be obtained, as can be observed in a previous work [
21] and machines such as jaw crushers [
24]. As a novelty, a calculation procedure for the crushing power of crushers is proposed where the torque is computed with radial forces because only these forces are transmitted to the eccentric.
2. Gyratory Crusher
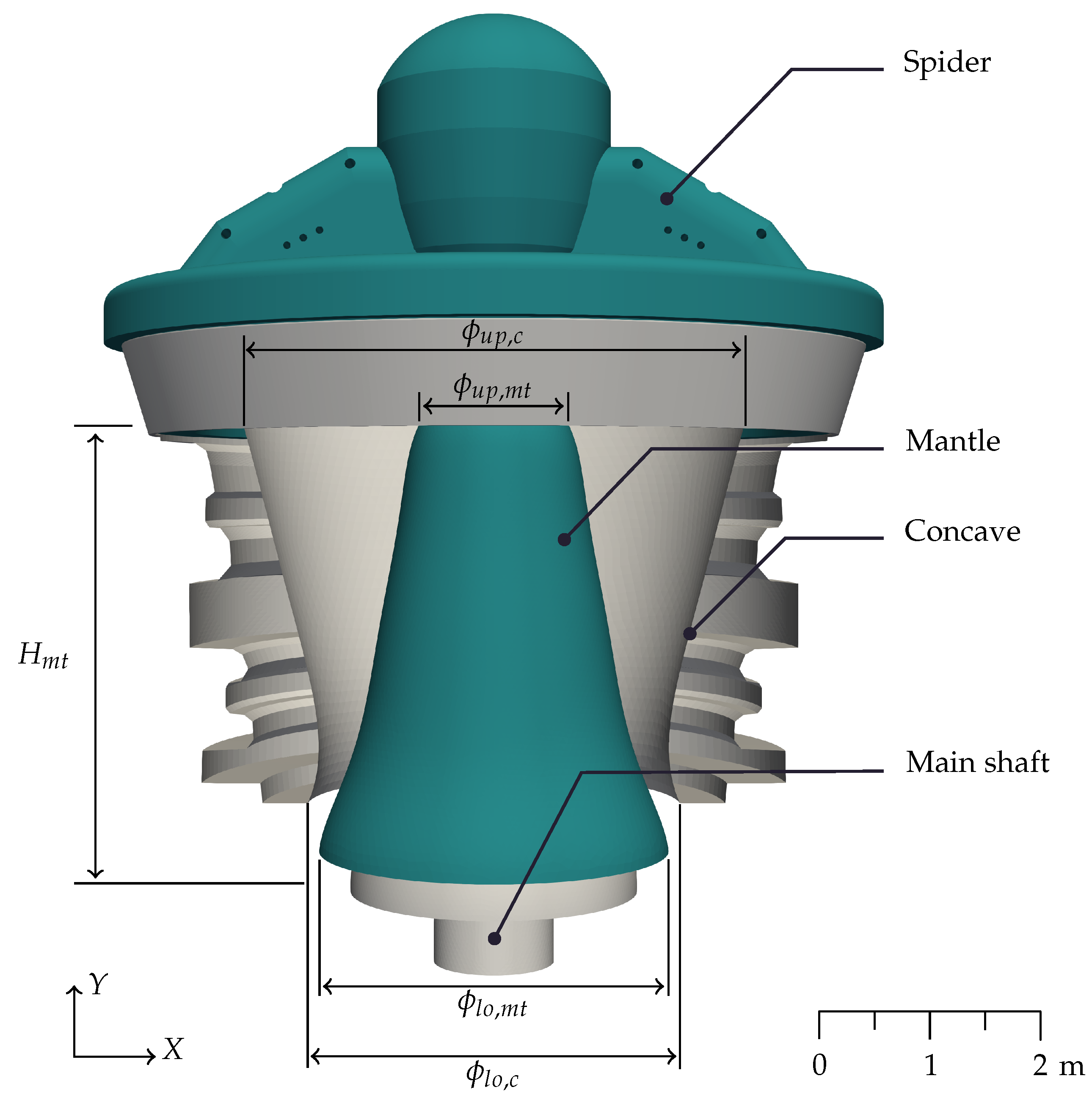
A gyratory crusher consists of a movable and truncated conical head and a fixed concave shell, as is presented in
Figure 1. The head is integral with the main shaft, and it is covered by an element of wear named
mantle. The set of these parts is the main shaft assembly. The external element is denominated
concave and is fixed on the main frame of the machine. The main shaft is supported by the spider at the top and by the main shaft position system (a hydraulic system of vertical adjustment) and eccentric bushing at the bottom.
The functional principle of the machine is to compress the ore among the mantle and the concave. To achieve particle compression, the main shaft rotates eccentrically, allowing a periodic approach and receding of the mantle regarding the concave. This means that, for a given angular and vertical position, the distance between the mantle and the concave periodically changes with each rotation of the main shaft. The eccentric, as its name indicates, allows the eccentric motion. This motion is produced by an electric motor coupled to the pinion shaft, which is connected to the eccentric by a helical gear.
The closed side setting,
, is defined as the smallest distance between the mantle and the concave, and the open side setting,
, is defined as the greatest distance at the same height [
16]. Due to the eccentric motion, if at a given vertical position this distance is the
, the
will be in the diametrically opposite position. The rotational speed of the eccentric is between 85 and 150 rpm [
25].
The classical empirical approach to estimate the crushing power,
P, is by using Equation (1), derived from Bond’s equation [
26]:
where
is the mass flow rate of the product,
is a constant of the machine,
is the work index, and
and
are the size of the cumulative percentage lower to 80% in the product and feed, respectively. The power draw is obtained by adding the no-load power, which can be measured empirically.
On the other hand, by utilizing data from DEM simulations, the crushing power can be calculated with the contact information between particles and the mantle in terms of the crushing torque [
16]. In the same manner as Bond’s equation, the no-load or idle power must be added to the crushing power in order to obtain the overall power to operate this machine [
27].
Let us consider a force
between a particle and the mantle applied in the
i-node or point
A of the mantle, as can be observed in
Figure 2 where all the following geometrical parameters are shown in that illustration. A fixed
and a moving
frame of reference are used. The frame
follows the motion of the main shaft rotating at the same speed
and with
, where
t is time. The
Y-axis is the axis of the eccentric, and the
-axis is the axis of the main shaft. A polar coordinate system is also utilized, where
is measured regarding the
x-axis and the
is always at
or point
C. The position of point
A is represented with the vector
and angles
and
.
The contact force is decomposed into three components: , , and . The radial r and transverse components are the projection in a horizontal plane of the contact force between the particle and the mantle in polar coordinates. The Y-component is the vertical component of this force.
As the main shaft is mounted in a full lubricated eccentric bushing, the power and torque needed to break the ore are evaluated only with the particle-mantle radial force,
. The torque produced by the transverse forces,
, on the mantle is not transmitted to the eccentric assembly and only produces a rotation about the main shaft’s axis, which is also called
head spin,
[
3]. Radial forces are those that compress the particles. The vertical force
is supported by the main shaft position system, and it does not produce torque.
The dashed line presented in
Figure 2 graphically represents the radial direction, which joins the intersection between the main shaft’s axis and the horizontal plane, point
and point
A. This direction is mathematically expressed with the unit vector,
; therefore, the radial component in the horizontal plane of the contact force is as follows:
Subsequently, the crushing torque,
T, in the
Y-axis of the
N nodes of the mantle in the instant
t is calculated with the following equation:
where
is the vector starting at point
O and finishing at point
A. Point
O corresponds to the intersection between the horizontal plane and the central axis of the eccentric, which is the
Y-axis. Then, by using the definition of work expressed with torque and the angular speed in the
Y-axis of the eccentric being equal to
, the crushing power is described as follows:
If the angular speed is constant, the crushing power, , is only time-dependent in terms of the crushing torque, . Gyratory crushers operate when it reaches the constant angular speed and with a frequency converter; consequently, the angular velocity in operation is generally constant.
In some DEM applications such as ball mill [
28], jaw crusher [
24], high pressure roll grinding [
29,
30], agitated drum dryer [
31], V-blender [
32], and screw conveyor [
33], the calculation of power draw is expressed by the sum of the scalar product of the force applied on the
i-node and the velocity vector of the same node,
, with the following expression:
Notwithstanding, the definitions of power with force (4) and torque (5) are equivalent, Equation (5) is not correct for gyratory crushers since it considers the tangential forces and head spin. If we consider a simple case of a rectangular plate rotating around a vertical axis
Y as the mixer shown in
Figure 3a, both Equations (4) and (5) deliver the same result because only forces perpendicular to the rectangular plate provides work. By knowing that the torque is
and that the velocity of any point in the plate is equal to
and is perpendicular to the rectangular plate, the statement can be verified.
For gyratory crushers, if we use (5), the power will consider the work performed by transverse forces.
Figure 3b presents a part of a cross-section of the mantle at a height
Y. A force vector
applied on the mantle and the velocity,
, of the
i-node is provided. If the head spin is null, the velocity
is the same in all cross-sections of the mantle, perpendicular to the
x-axis, and with magnitude equal to
, where
e is the eccentricity at that height
Y. As the velocity is parallel to the
z-axis, only the component in the same axis performs work,
; therefore, by utilizing Equation (5), the crushing power will be described as follows:
Figure 3c,d describes the rectangular decomposition of the contact force in radial and transverse direction, and
x and
z, respectively. A change in the transverse component will generate a variation in the
z-component. As
depends on the transverse component of the contact force, the power calculation with Equation (5) will consider the work of transverse forces; thus, it is not convenient for this application and the power will be overestimated.
Furthermore, if the head spin is not null, the velocity in the node i changes to , changing the magnitude and direction of the velocity of the node. This change in the direction of the velocity will affect the scalar product of (4), and consequently that equation is not recommended.
The polar coordinate system proposed in
Figure 2 can be used to analyze the torque produced by radial forces over the mantle. With the geometry presented in
Figure 3b we can define the following:
where
r is the mantle’s radius, and
and
belong to the
x-axis and
z-axis, respectively. Then, the crushing torque (3) in polar coordinates is expressed as in Equation (10).
As e is a function of the height Y, Equation (10) depends on r and . With that expression, we can find the maximum and minimum of the torque by considering the contact force as constant. A critical point was not observed by studying the first partial derivative regarding and r. By analyzing the boundary, it was found that the torque was maximum in and , and it was minimum in and , where is the maximum radius of the mantle located at the bottom. Moreover, there is a change in the sign of the torque. If we consider the torque positive in , in the torque will be negative. Besides, from (10) it is possible to note that the torque is zero for and because the moment arm of the radial force is null.
3. DEM Model
In the discrete element method, particles and boundaries are simulated, such as rigid bodies. Contact forces are modeled as damping spring systems by considering an overlap distance between them. The normal contact force is modeled with the hysteretic linear spring model proposed by Walton and Braun [
34] and the linear spring Coulomb limit for the tangential component of the force. The implementation of the normal contact model in Rocky is time-dependent, as described by the following set of equations for the time step
j:
where
and
are the normal elastic-plastic contact forces at the current time,
, and at the previous time,
, respectively.
is the change in the contact normal overlap during the current time.
and
are the normal overlap values at the current and at the previous time, respectively.
and
are the values of loading and unloading contact stiffnesses, respectively.
is a dimensionless stabilization constant parameter; its value in Rocky DEM is 0.001. The use of ensures that, during the unloading, the normal force will return to zero when the overlap decreases to zero.
The tangential forces,
, are represented by the linear spring Coulomb limit model:
where
is the tangential force given by (14), and
is the coefficient of friction. The following is described:
with
being the value of the tangential force at the previous time,
denotes the tangential relative displacement of the particles during the time step, and
is the tangential stiffness. The stiffnesses can be calculated as is described in
Appendix A.1 in accordance with the material parameters.
For the purpose of establish the normal
and tangential direction
in contact, a contact plane is utilized, and the normal direction is thereby perpendicular to that plane. For example, the contact plane in the interaction between two spherical particles is defined as the plane perpendicular to the line that connects the centers of these particles. For polyhedral particles, the particle–boundary contact algorithm uses the closest points of the particle and a triangle of the meshed boundary or two points with the maximum overlap distance to create a line and then a plane perpendicular to this line [
34].
To accurately describe the physical phenomenon in the gyratory crusher, a breakage model is needed to ensure particle flow through the machine. In the selected software, there are two of these models: Ab-T10 and Tavares. Both models are a particle replacement scheme (PRM), changing the polyhedral parent particle in polyhedral progeny particles, and preserve both mass and volume in the resulting fragments in a breakage event. The Tavares model is selected to represent the breakage of the particles because it has extensive material characterization. This breakage model can characterize body breakage of polyhedral convex particles, and the particles will break in depending on the energy dissipated in a contact when they are under stress [
23]. If the energy is not enough to break the particle, the particle will weaken, decreasing its strength.
The fragments of a broken particle are generated following the Voronoi fracture algorithm [
35] according to a size distribution. Rocky has two different models available for the size distribution: Gaudin–Schumann and incomplete beta function [
36]. The last one was selected in this work, and the details of the calculation procedure of the breakage model are presented in
Appendix A.2.
5. Results
The results of the DEM simulations of the gyratory crusher are presented. It begins with the validation of the model, then the effects of the operational parameters such as and are presented. Finally, the results of the simulation of the non-uniform filling case are shown and compared with the base case.
5.1. Model Validation
Table 6 provides the efficiency and performance of the crusher changing the
. The crushing power for
mm, base case, is close to the experimental value, 1329.4 kW, and the behavior of the other configurations is as expected. The model correctly predicts the throughput of the crusher because all the mass flow rates of the product calculated in the simulations performed,
, are quite close to that indicated by the manufacturer
. The error is less than 20% between
mm and 200 mm, and the error is less than 10% between 215 mm and 250 mm, which is low compared with the values obtained in the literature [
3,
16,
18]. The product size, represented by the
value, is near
, as indicated by the manufacturer [
43]. As the throughput, product size, and power are close to the ones reported by the manufacturer and the experimental data, the simulation is considered validated.
5.2. Base Case
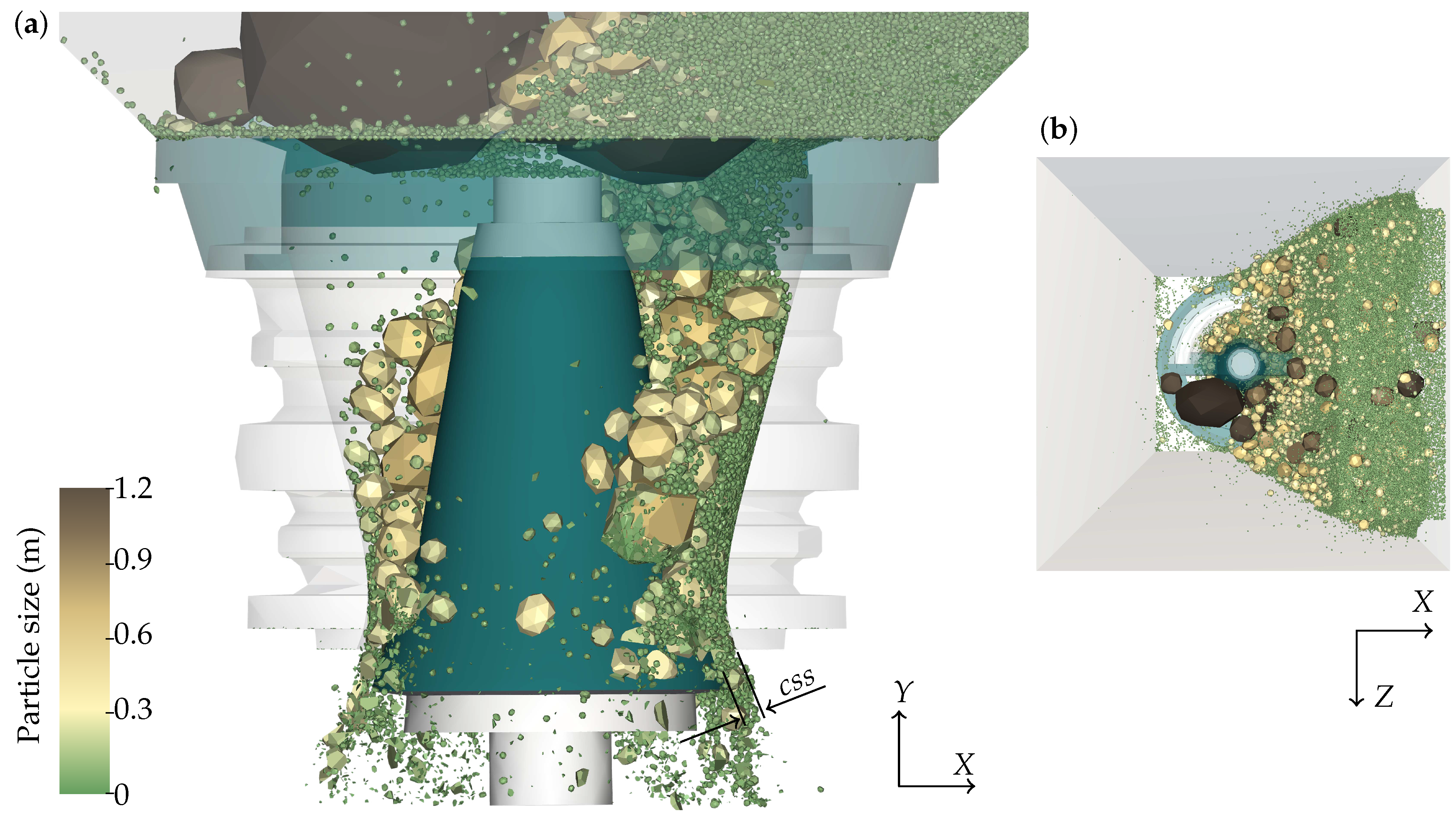
Figure 7 presents a snapshot of the DEM simulation of the gyratory crusher with
mm and
rpm, the base case, at simulation time
s. At that time, the crushing chamber is full of particles with a total mass of 66,410 kg. In the crushing chamber there are 75,000 particles and there are between 100,000 and 200,000 particles in the entire domain. The median mass flow rate of the product is 8473.0 t/h. At the top of the crusher cavity, the mean particle velocity in the vertical direction is 0.48 m/s, and it is 2.02 m/s at the bottom. As the total particle mass in the chamber and the median mass flow rate of the product remain with low variations, it is considered to be in a steady state.
The particle size distribution of the feed and product are exhibited in
Figure 8. Comparing the
and the feed PSD, more than half of the particles can pass through the crushing chamber without being broken. In the
Figure 7, several fine particles with sizes less than 70 mm can be observed in the chamber. For the time
s, 8.64% of the mass of fine particles are located in the crusher cavity without been crushed. All the particles of the product have a size less than 400 mm and a
equal to 116.43 mm.
The simulated root-mean-square crushing power calculated with all the forces is 1703.3 kW and determined when the torque of the radial forces is 1430.8 kW. Both values of power are quite close to the measured crushing power, with an error of 28.1% and 7.6%, respectively. As was mentioned earlier, this difference is due to the work performed by the transverse forces. The RMS crushing torque is 91.25 kNm.
A complete force distribution analysis acting on the crusher’s mantle is performed. The force profile is exported from Rocky DEM to MATLAB (version R2021a provided by MathWorks, Natick, MA, USA) and Paraview (version 5.9.0 provided by Kitware Inc., Clifton Park, NY, USA). With these post-processing software, it is studied the spatial force distribution over the mantle and the generated torque.
Figure 9 illustrates an example of the prediction of forces on the mantle of the gyratory crusher with the DEM simulation in steady state. Each vector represents the nodal force in the mantle for the given time step. Half of the concave is shown, the hidden part of the concave corresponds to the section where the compression is carried out. The location of the
distance is also drawn. As the main shaft rotates in the negative
Y direction, the position of the
moves in the same direction. The forces cover a surface of half of the mantle (where the concave is hidden) and increase its magnitude when the mantle approaches the concave. A particle–boundary contact can generate more of one nodal force depending on the geometry of the contact, and that is why the nodal forces can be observed to be grouped together.
High magnitude compression forces are presented due to individual compression events. These forces can generate peaks in the power, as it can be observed, both in numerical results [
18] and experiments [
44].
For the purpose of achieve a representative force distribution that is comparable in different time steps, a moving frame of reference in polar coordinates relative to main shaft is used, as described in
Section 2. A planar force distribution in polar coordinates can be obtained, and all the mantle surface can be analyzed in a simple surface plot instead of a 3D graphical representation. This type of graphics can be extracted in all DEM software in terms of normal or shear stress [
15], but it is not good for calculating power in the gyratory crusher because only radial forces must be considered in power and torque calculations.
In
Figure 10a, the force distribution in polar coordinates of the base case is illustrated. The angle
was previously defined and represented the relative position of a node’s mantle regarding the
position. The radial coordinate,
r, of this polar plot is the radius of the mantle. Additionally, to locate any point in a vertical position of the mantle, a scale of the vertical coordinate,
, is added. Both scales are displayed at the bottom. The relationship between
r and
is the mantle profile shown in
Figure 1 and as is not linear, the scale of
is non-linear. In this plot, the lower mantle diameter is at the base of the mantle
m, and the upper mantle diameter,
m, is at the top
m. The center of this polar plot corresponds to the geometrical center of the mantle, point
. The positive direction of the radial forces is defined by the opposite direction of the unit radial vector,
, presented in
Figure 2. Since only compression forces were applied over the particles and since there was no adhesion force, all the vectorial components of the forces calculated in these simulations were greater than zero. The radial force distribution is principally concentrated between
rad and
rad, where the mantle is approaching to concave.
With this force distribution, the crushing torque is determined with Equations (2) and (3). This torque is evaluated regarding the center of the eccentric, located to the left of the center of this polar plot. The positive direction of the torque is defined in the opposite direction of the vertical axis Y coming out of the plane of the graph. Then, the positive radial forces between 0 and produce positive torque, and they produce negative torque between 0 and .
In the torque plot shown in
Figure 10b, as it was mentioned before, a drastic change in the value can be observed at
rad. The positive torque is principally present between
and to
where the torque is negative. Between
and 0, the mantle moves away from the concave; thus, the forces presented are particles that are in decompression. These forces that produce negative torque are acting for a short period of time.
Comparing the radial force and torque distribution, it can be observed that the torque value depends on the magnitude of the radial force, the vertical position, and the angular position. The lower values of , the greater the eccentricity; therefore, the greater the moment arm will be. For values close to , the moment arm is negligible, and the torque will be close to zero.
5.3. Effect of Open Side Setting
In this subsection, the simulations obtained by changing the
are presented. As it is expected, the increase in
generates a rise in the discharge mass flow rate due to the flow area is greater.
Figure 11a indicates a decrease in the specific energy consumption due to the larger particle size in the discharge, as evidenced by the comparison of the corresponding
. This variation in mass flow rate and energy consumption also agrees with data provided by different authors [
18,
45]. The crushing torque follows the same trend as the crushing power because
is fixed.
The PSD of the product is characterized by the
, which is illustrated in
Figure 11d. All these curves of distribution are similar to the one presented in
Figure 8. The
is computed with the cumulated product of the crusher in the steady state. The relationship between the
and
is almost linear, with
.
The crushing power computed by DEM with both approaches shown in
Table 6 presents a clear difference. Those calculated only with transverse force are less than those calculated with all the forces. Moreover, the calculated with (5) does not have a strict decreasing behavior for
equals 200 mm and 240 mm. The power calculated only with radial forces is considered in the following analyses.
A comparison is performed between the power values determined with the discrete element method and those calculated using Bond’s model for different
. For Bond’s model, only manufacturer data were used, and the product size
was modeled as
[
43]. The machine parameter,
, was fitted to the power of the base case, and the result was 1.286.
Figure 11b shows a comparison between the power evaluated with Bond’s and DEM models. It can be observed that both models can predict the increase in power as the
decreases, but the slope in absolute value of the DEM model is significantly greater. Bond’s model is more conservative in calculating power, and the linear fit is almost horizontal, as the difference in power between each
is less than 200 kW. The power is almost constant because this model cannot predict high variations. When the
changes between 190 mm and 250 mm, the power only changes by 7.9%. On the other hand, in the DEM model for the same change in the
, the power varies by 44.5%. Moreover, the power calculated with Bond’s equation for
mm is an outlier being the lowest value obtained, and it interrupts the increase in power for
mm. These differences can be explained mathematically by the relationship between the throughput that the manufacturer indicates and the
. For
mm, the difference with the following data is 1410 t/h, and there is a difference of 710 t/h for
mm with the previous one, while the other differences remain lesser than 400 t/h.
In
Figure 11c, the variation of the head spin regarding the open side setting is presented. The relationship between the head spin and
decreases, as it is represented by the linear fit. This behavior can be explained because there are more particles in contact with the mantle when
is lower, producing more tangential forces on the mantle. As these results are less than 20 rpm as the manufacturer indicates in no-load conditions, they are considered viable.
5.4. Effect of Eccentric Speed
The effect of the eccentric speed between 100 and 200 rpm on a specific energy consumption is provided in
Figure 12a. The specific energy consumption decreased by 55.1% as the eccentric rotation speed decreased by 33.3%. The lowest specific energy consumption was achieved for 100 rpm eccentric speed. This point also increases the mass flow rate in the discharge by 12.8% with respect to the nominal operating conditions and decreases the crushing torque by 26.1%.
The power consumption is highly influenced by the eccentric speed; with an increase in the eccentric rotation speed from 100 to 200 rpm, a 171.4% increase in crushing power was calculated. The torque follows the same tendency, increasing at 35.6% between 100 and 200 rpm.
The mass flow rate in the discharge is maximized when working at 200 rpm. However, it is not recommended to work at this speed since the specific energy consumption increases by 109.1% regarding the 100 rpm simulation.
To choose the rotation speed of the eccentric, it is also important to consider the granulometry in the discharge.
Figure 12d presents the 80th percentile of the product size distribution. The complete PSD follows the same trend as the particle size distribution of the base case, shown in
Figure 8. The lowest value of
was acquired for 150 rpm. On the other hand, by decreasing the rotation speed of the eccentric from 150 to 100 rpm, an increase of 6.91% in the value of
was obtained.
A comparison is generated between the power values computed with the discrete element method and those determined by using Bond’s model for different
. As the eccentric velocity is not an input parameter of Bond’s model, it is represented by the throughput and product size calculated by DEM simulations. The values utilized here and the resulting findings are presented in the
Table 7.
Figure 12b presents a comparison between the power evaluated with Bond and the DEM model for different
. In these results, Bond’s model is also more conservative. According to the DEM model, doubling the rotational speed of the main shaft increases the power by 271.4%, while the equation of Bond only yielded an increase of 29.3%.
In
Figure 12c, the variation of the head spin about the angular speed of the eccentric is plotted. The higher the rotation speed of the eccentric, the higher the head spin, achieving a value of 4.25 rpm at 200 rpm of the eccentric. As the head spin is related to the tangential forces over the mantle with higher
, the relative velocities of the mantle and particles are greater and so are the tangential forces. Moreover, more particles are flowing through the crushing chamber, generating more interactions with the mantle. As the particles are moving faster, there are more interactions with the mantle. The linear fit is
. In the same manner as the previous results, they are considered viable as they are less than 20 rpm.
5.5. Effect of Non-Uniform Feeding
Figure 13 presents an image of the distribution of the particles for the simulation of non-uniform feeding. The truck feeds the crusher from the right side, as can be observed for the concentration of the particles in the top-right corner and in the top view in
Figure 13b. Large rocks are in one input of the crusher (the input in the positive
z-axis) while the side of the negative
Z-axis has an unobstructed entrance, and the particles pass through the right side into the crushing chamber. As the simulation progresses, the left side of the chamber becomes partially filled.
As the particles have greater freedom to move within the chamber, it can be observed that larger particles reach lower areas of the chamber, as it is illustrated in
Figure 7 and
Figure 13a. To clarify this statement, the
is calculated for different vertical positions,
Y, of the crushing chamber and is exposed in
Figure 14. In general, the non-uniform feeding simulation has greater
than the base simulation. This can produce greater torque because, in a lower position, the mantle’s eccentricity is greater. For example, the
are 245.0 mm and 288.3 mm for
m for the base and non-uniform feeding simulation, respectively. The difference in size is 18% with respect to the base case. If we determine the maximum torque that both particle sizes can produce at that height by using
mm, the difference in torque will be 38%.
The unbalance of particles in the chamber will affect the power consumption. In
Figure 15a, the crushing powers of the non-uniform filling simulation and the base simulation are presented. As the crushing chamber is not perfectly filled, the crushing power of the non-uniform filling simulation shows cycles of loading and unloading with frequency 2.5 Hz, one per revolution, due to the ore being on one side of the crusher cavity. It is expected that the power shows these oscillations, and it does not represent an issue in the machine. When the base case reaches its steady state and the chamber is full of particles, the non-uniform feeding simulation has only one-third of the chamber full at about 9 s, with the total particle mass equal to 22,500 kg. However, both simulations can reach an instantaneous crushing power of 2000 kW. The variance in the crushing power in the base simulation is 0.113 MW
, meanwhile, the variance is 0.291 MW
in the non-uniform filling simulation.
In these conditions and in some time steps, NUF power peaks are found to be greater than when the chamber is fed uniformly. The mean value of the NUF peaks is 2005 kW, and some valley values of the base case are lower than 1000 kW. This behavior is not expected because the chamber of the base case is full of particles; therefore, the power should be close to the peaks values of the NUF case at all times. This difference in power is because some particles generate negative torque on the mantle when the crushing chamber is full of particles, decreasing the torque value in comparison with the NUF condition.
In the
Table 8, a comparison between the base and the non-uniform feeding simulation is carried out. This comparison aims to contrast both simulations when the base case is in steady state starting from 9 s, and the non-uniform filling case is still filling up at this point. If we use data for
s, the base case has more particles than the non-uniform filling case, and hence the power is greater. On the other hand, if we utilize
, the non-uniform case will be full of particles and both simulations will be almost the same.
Table 8 reports the power draw of both simulations, calculated by adding the no-load power to the crushing power. According to the ones presented in
Figure 15a, the power draw in the base case is greater than the non-uniform filling case, principally because it has more particles in contact with the mantle. For the same reason, the throughput is greater in the base case. This throughput is calculated with the cumulative particle mass of the product plotted in
Figure 15b. However, the specific energy is less in the base case; thus, the non-uniform filling case requires more energy to process the same mass of ore. The particle size distribution of the product is affected, the
of the NUF case is coarser than the base case. This can be compared with non-choke feed conditions, where the particles have greater freedom of movement. Under these conditions, coarser particles were found experimentally in the product [
46]. On the other hand, the head spin increases to more than double in the non-uniform feeding case. This is due to there being an imbalance of tangential forces that allows free rotation of the main shaft.
If we extrapolate the data to the complete process, i.e., the crusher fed by two trucks with 293 tons of copper ore in each one, the total crushing time and energy consumption can be determined. The non-uniform filling case takes twice the time and the energy consumption is 23% greater, as it is summarized in
Table 8.
In
Figure 16, the polar distributions of force and torque are presented. Compared to the base case, it can be observed that zones with non-zero forces are smaller due to the lower number of particles in contact. In
Figure 10, it can be observed that there are forces that perform negative torque; meanwhile, the same cannot be detected in the non-uniform feeding case. This brings about an increment in the crushing power, which is shown in
Figure 15a, where the non-uniform feeding case with fewer particles can achieve almost the same value of power.
In
Figure 16b it is possible to observe that the particles generate torque principally in the first 180
of the mantle. In
, there is a zone with force greater than zero in
Figure 16a, but the torque is null in
Figure 16b. As the moment arm is null, there will be no torque. Furthermore, when the forces are close to
, the torque is greater, as can be noticed in the torque between
and
.