Ultrafast X-ray Diffraction Study of a Shock-Compressed Iron Meteorite above 100 GPa
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation and Characterization
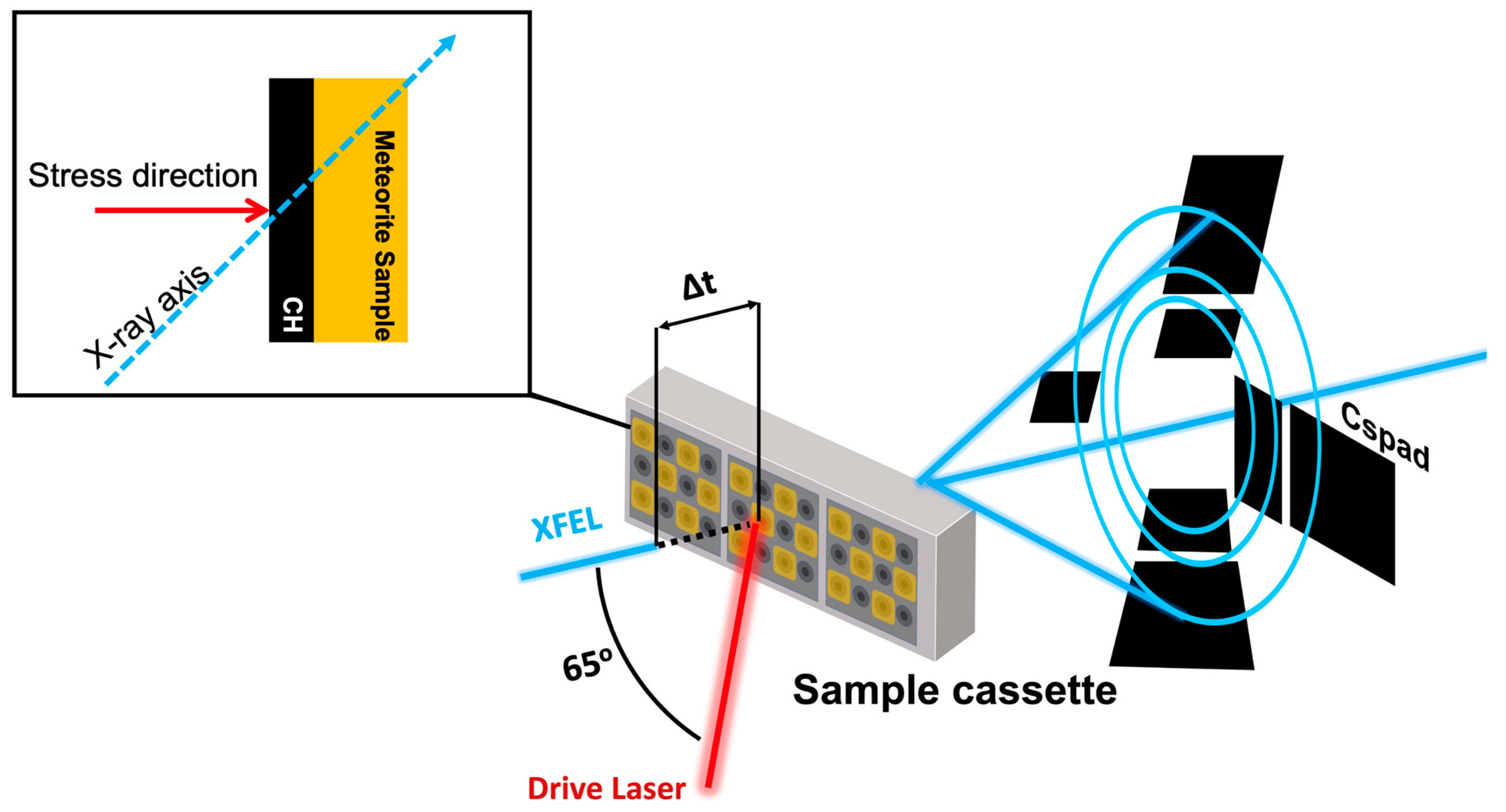
2.2. Experimental Setup
3. Results
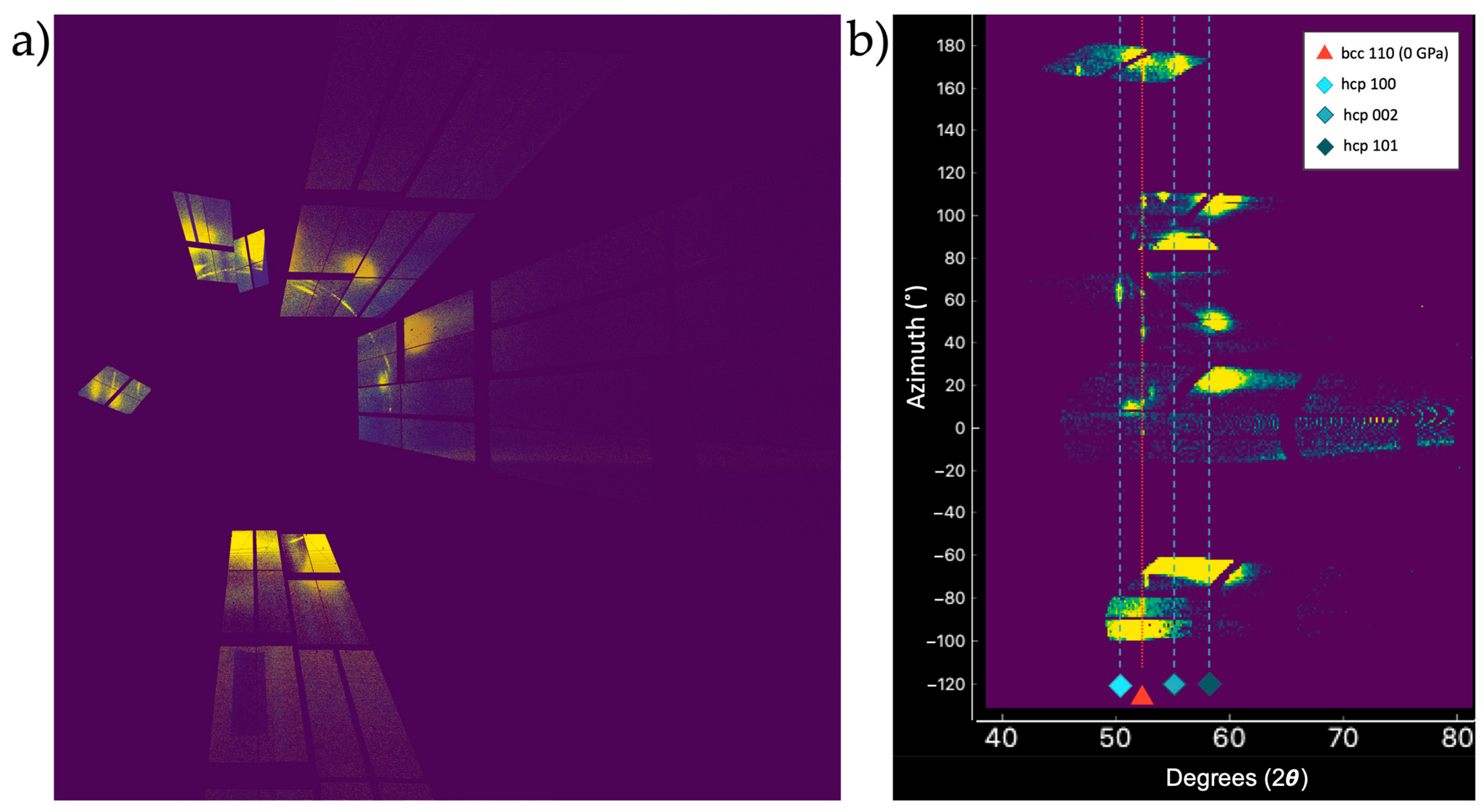
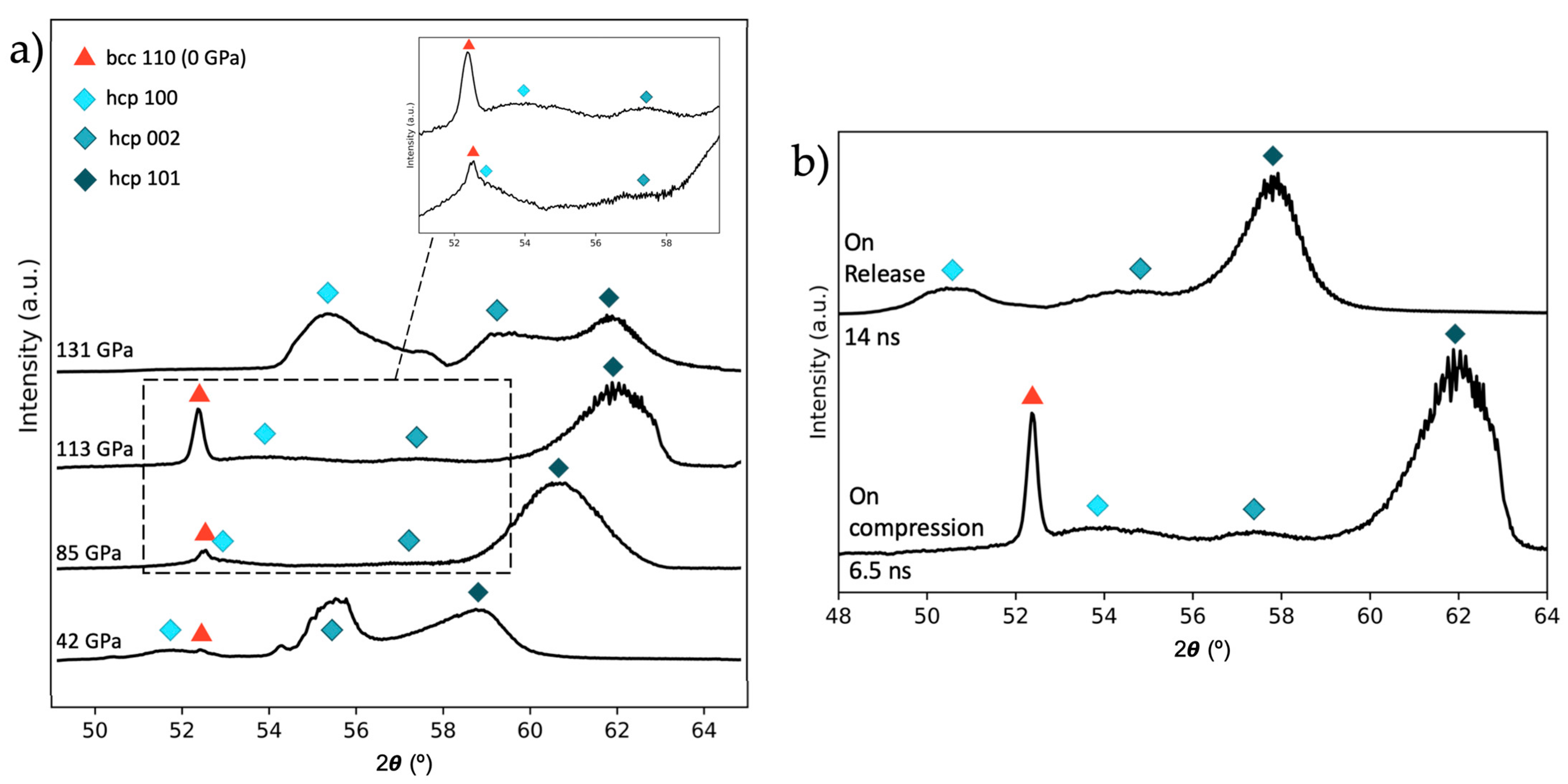
3.1. X-ray Diffraction
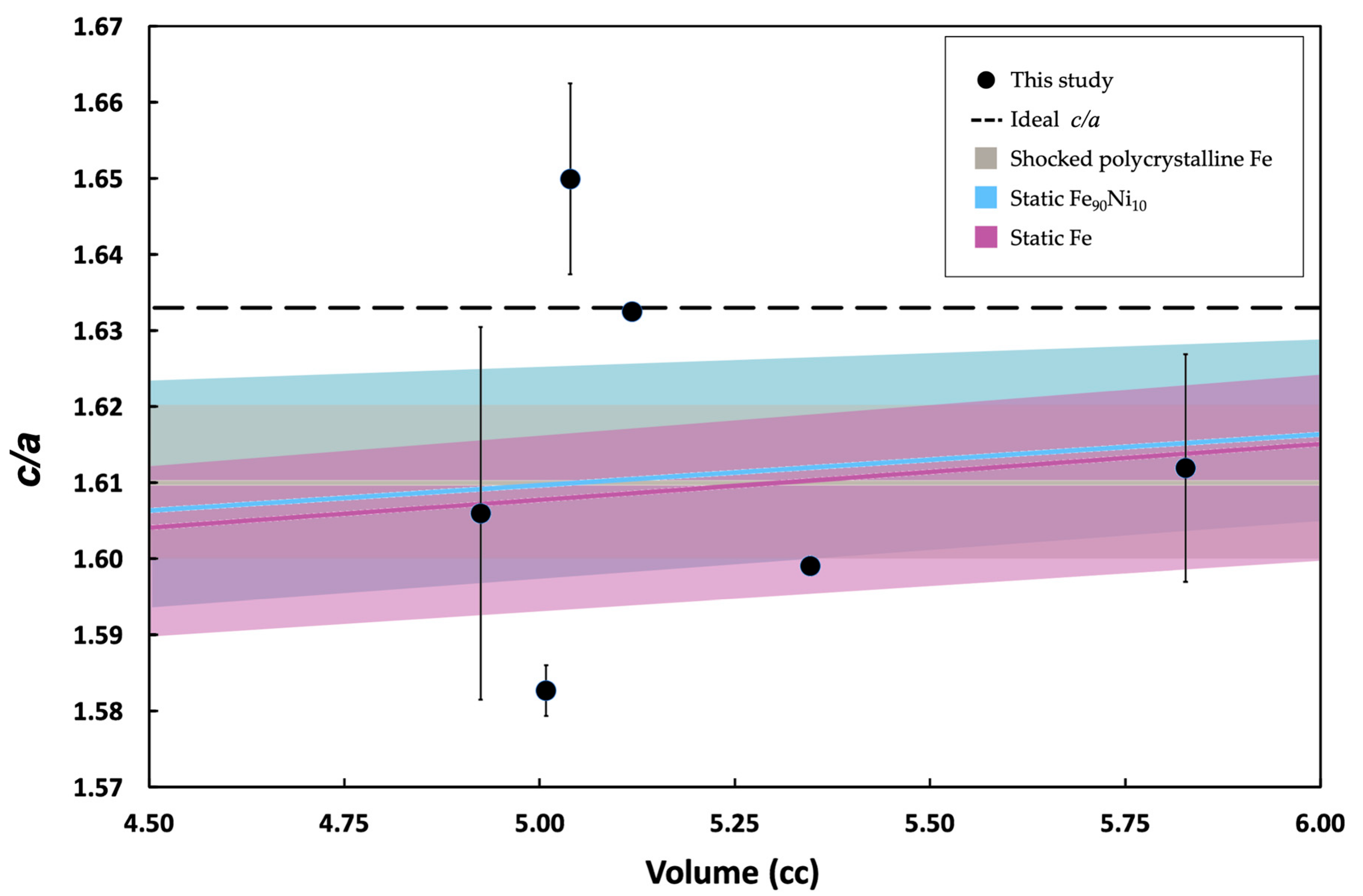
3.2. Axial c/a Ratio
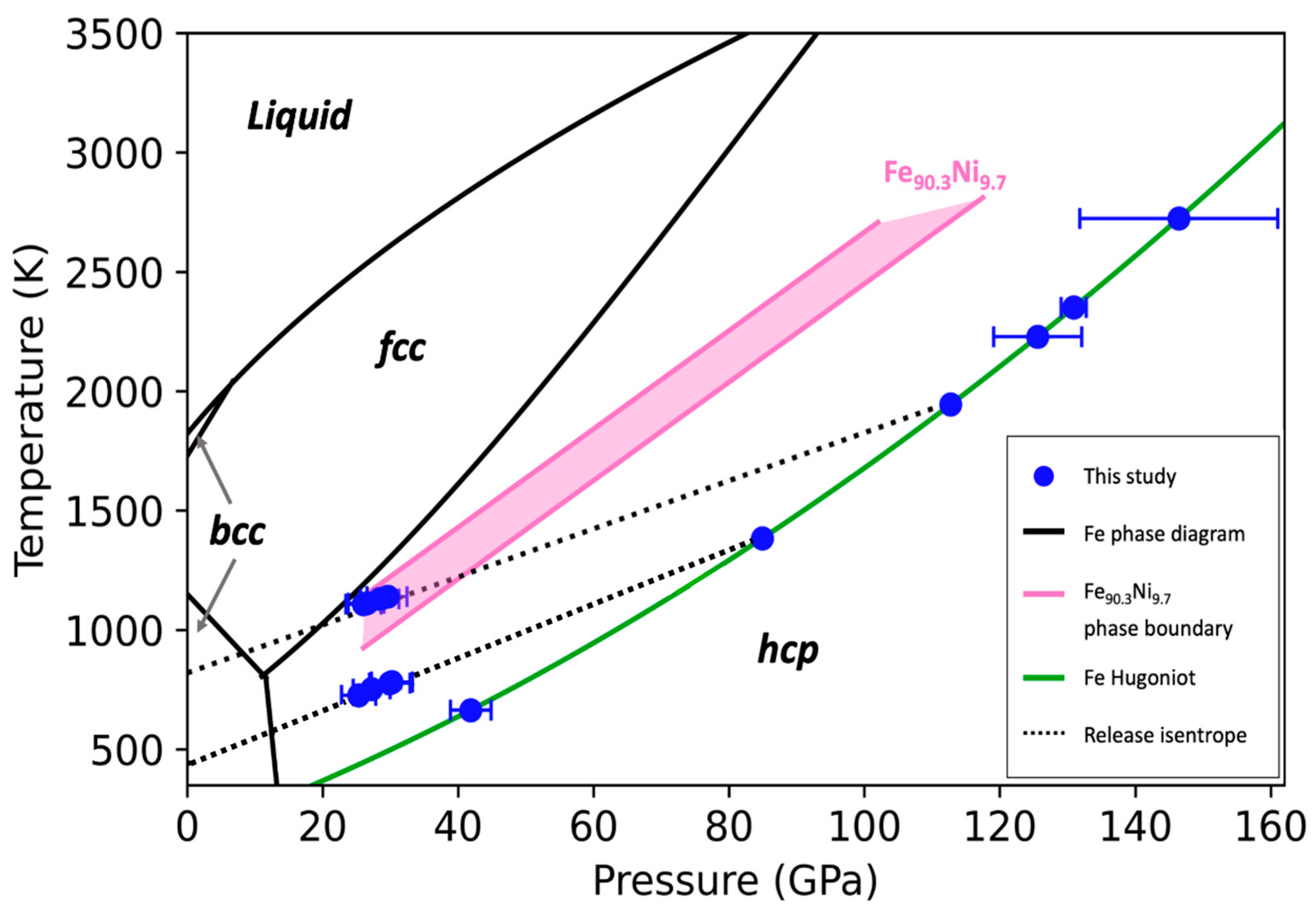
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Asphaug, E. Interiors of small bodies and moons. Nat. Commun. 2020, 11, 10–12. [Google Scholar] [CrossRef]
- Goldstein, J.I.; Scott, E.R.D.; Chabot, N.L. Iron meteorites: Crystallization, thermal history, parent bodies, and origin. Geochemistry 2009, 69, 293–325. [Google Scholar] [CrossRef]
- Buchwald, V.F. Handbook of Iron Meteorites. Their History, Distribution, Composition and Structure; Danmarks Tekniske Hojskole: Lyngby, Denmark, 1975. [Google Scholar]
- Oh, D.Y.; Goebel, D.; Polanskey, C.; Snyder, S.; Carr, G.; Collins, S.M.; Lantoine, G.; Landau, D.; Elkins-Tanton, L.; Lord, P.; et al. Psyche: Journey to a metal world. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016; p. 4541. [Google Scholar] [CrossRef]
- Burbine, T.H.; Meibom, A.; Binzel, R.P. Mantle material in the main belt: Battered to bits? Meteorit. Planet. Sci. 1996, 31, 607–620. [Google Scholar] [CrossRef]
- Yang, J.; Goldstein, J.I.; Scott, E.R.D.; Michael, J.R.; Kotula, P.G.; Pham, T.; Mccoy, T.J. Thermal and impact histories of reheated group IVA, IVB, and ungrouped iron meteorites and their parent asteroids. Meteorit. Planet. Sci. 2011, 46, 1227–1252. [Google Scholar] [CrossRef]
- McKeehan, L.W. The crystal structure of iron-nickel alloys. Phys. Rev. 1923, 21, 402–407. [Google Scholar] [CrossRef]
- Owen, E.A.; Yates, E.L.; Sully, A.H. An X-ray investigation of pure iron-nickel alloys. Part 4: The variation of lattice-parameter with composition. Proc. Phys. Soc. 1937, 49, 315–322. [Google Scholar] [CrossRef]
- Purdy, G.R. Widmanstätten Structures. In Encyclopedia of Materials: Science and Technology; Elsevier: Amsterdam, The Netherlands, 2001; pp. 9575–9578. [Google Scholar]
- Johnson, A.A.; Remo, J.L. A new interpretation of the mechanical properties of the Gibeon Meteorite. J. Geophys. Res. 1974, 79, 1142–1146. [Google Scholar] [CrossRef]
- He, Y.; Godet, S.; Jacques, P.J.; Jonas, J.J. Crystallographic relations between face- and body-centred cubic crystals formed under near-equilibrium conditions: Observations from the Gibeon meteorite. Acta Mater. 2006, 54, 1323–1334. [Google Scholar] [CrossRef]
- Jeanloz, R. The nature of the Earth’s core. Annu. Rev. Earth Planet. Sci. 1990, 18, 357–386. [Google Scholar] [CrossRef]
- Hawreliak, J.; Colvin, J.D.; Eggert, J.H.; Kalantar, D.H.; Lorenzana, H.E.; Stölken, J.S.; Davies, H.M.; Germann, T.C.; Holian, B.L.; Kadau, K.; et al. Analysis of the x-ray diffraction signal for the α- transition in shock-compressed iron: Simulation and experiment. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 74, 184107. [Google Scholar] [CrossRef]
- Anzellini, S.; Dewaele, A.; Mezouar, M.; Loubeyre, P.; Morard, G. Melting of Iron at Earth’s Inner Core Boundary Based on Fast X-ray Diffraction. Science 2013, 340, 464–466. [Google Scholar] [CrossRef] [PubMed]
- Hwang, H.; Galtier, E.; Cynn, H.; Eom, I.; Chun, S.H.; Bang, Y.; Hwang, G.C.; Choi, J.; Kim, T.; Kong, M.; et al. Subnanosecond phase transition dynamics in laser-shocked iron. Sci. Adv. 2020, 6, 5132–5137. [Google Scholar] [CrossRef]
- Mao, W.L.; Campbell, A.J.; Heinz, D.L.; Shen, G. Phase relations of Fe-Ni alloys at high pressure and temperature. Phys. Earth Planet. Inter. 2006, 155, 146–151. [Google Scholar] [CrossRef]
- Steinle-Neumann, G.; Stixrude, L.; Cohen, R.E.; Gülseren, O. Elasticity of iron at the temperature of the Earth’s inner core. Nature 2001, 413, 57–60. [Google Scholar] [CrossRef]
- Mao, H.K.; Wu, Y.; Chen, L.C.; Shu, J.F.; Jephcoat, A.P. Static compression of iron to 300 GPa and Fe0.8Ni0.2 alloy to 260 GPa: Implications for composition of the core. J. Geophys. Res. 1990, 95, 21737–21742. [Google Scholar] [CrossRef]
- Hawreliak, J.A.; El-Dasher, B.; Lorenzana, H.; Kimminau, G.; Higginbotham, A.; Nagler, B.; Vinko, S.M.; Murphy, W.J.; Whitcher, T.; Wark, J.S.; et al. In situ x-ray diffraction measurements of the c/a ratio in the high-pressure ε phase of shock-compressed polycrystalline iron. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 83, 1–6. [Google Scholar] [CrossRef]
- Morrison, R.A.; Jackson, J.M.; Sturhahn, W.; Zhang, D.; Greenberg, E. Equations of State and Anisotropy of Fe-Ni-Si Alloys. J. Geophys. Res. Solid Earth 2018, 123, 4647–4675. [Google Scholar] [CrossRef]
- Reagan, M.M.; Gleason, A.E.; Liu, J.; Krawczynski, M.J.; Van Orman, J.A.; Mao, W.L. The effect of nickel on the strength of iron nickel alloys: Implications for the Earth’s inner core. Phys. Earth Planet. Inter. 2018, 283, 43–47. [Google Scholar] [CrossRef]
- Schoelmerich, M.O.; Tschentscher, T.; Bhat, S.; Bolme, C.A.; Cunningham, E.; Farla, R.; Galtier, E.; Gleason, A.E.; Harmand, M.; Inubushi, Y.; et al. Evidence of shock-compressed stishovite above 300 GPa. Sci. Rep. 2020, 10, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Duffy, T.S.; Smith, R.F. Ultra-high pressure dynamic compression of geological materials. Front. Earth Sci. 2019, 7, 23. [Google Scholar] [CrossRef]
- Coleman, A.L.; Gorman, M.G.; Briggs, R.; McWilliams, R.S.; McGonegle, D.; Bolme, C.A.; Gleason, A.E.; Fratanduono, D.E.; Smith, R.F.; Galtier, E.; et al. Identification of Phase Transitions and Metastability in Dynamically Compressed Antimony Using Ultrafast X-Ray Diffraction. Phys. Rev. Lett. 2019, 122, 255704. [Google Scholar] [CrossRef] [PubMed]
- Tracy, S.J.; Smith, R.F.; Wicks, J.K.; Fratanduono, D.E.; Gleason, A.E.; Bolme, C.A.; Prakapenka, V.B.; Speziale, S.; Appel, K.; Fernandez-Pañella, A.; et al. In situ observation of a phase transition in silicon carbide under shock compression using pulsed x-ray diffraction. Phys. Rev. B 2019, 99, 214106. [Google Scholar] [CrossRef]
- Gleason, A.E.; Bolme, C.A.; Lee, H.J.; Nagler, B.; Galtier, E.; Kraus, R.G.; Sandberg, R.; Yang, W.; Langenhorst, F.; Mao, W.L. Time-resolved diffraction of shock-released SiO2 and diaplectic glass formation. Nat. Commun. 2017, 8, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Nagler, B.; Arnold, B.; Bouchard, G.; Boyce, R.F.; Boyce, R.M.; Callen, A.; Campell, M.; Curiel, R.; Galtier, E.; Garofoli, J.; et al. The Matter in Extreme Conditions instrument at the Linac Coherent Light Source. J. Synchrotron Radiat. 2015, 22, 520–525. [Google Scholar] [CrossRef]
- Blaj, G.; Caragiulo, P.; Carini, G.; Carron, S.; Dragone, A.; Freytag, D.; Haller, G.; Hart, P.; Hasi, J.; Herbst, R.; et al. X-ray detectors at the Linac Coherent Light Source. J. Synchrotron Radiat. 2015, 22, 577–583. [Google Scholar] [CrossRef]
- Bolme, C. Bolmian XRD Projection Software; LA-UR-15-25840, US DOE Copyright; Los Alamos National Laboratory: Los Alamos, NM, USA, 2015. [Google Scholar]
- Prescher, C.; Prakapenka, V.B. DIOPTAS: A program for reduction of two-dimensional X-ray diffraction data and data exploration. High Press. Res. 2015, 35, 223–230. [Google Scholar] [CrossRef]
- Wojdyr, M. Fityk: A general-purpose peak fitting program. J. Appl. Crystallogr. 2010, 43, 1126–1128. [Google Scholar] [CrossRef]
- Brown, J.M.; McQueen, G. Phase transitions, Grüneisen parameter, and elasticity. J. Geophys. Res. 1986, 91, 7485–7494. [Google Scholar] [CrossRef]
- Marsh, S.P. LASL Shock Hugoniot Data; University of California Press: Berkeley, CA, USA, 1980; ISBN 0-520-04008-2. [Google Scholar]
- Huser, G.; Koenig, M.; Benuzzi-Mounaix, A.; Henry, E.; Vinci, T.; Faral, B.; Tomasini, M.; Telaro, B.; Batani, D. Temperature and melting of laser-shocked iron releasing into an LiF window. Phys. Plasmas 2005, 12, 1–4. [Google Scholar] [CrossRef]
- Dorogokupets, P.I.; Dymshits, A.M.; Litasov, K.D.; Sokolova, T.S. Thermodynamics and Equations of State of Iron to 350 GPa and 6000 K. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Komabayashi, T.; Hirose, K.; Ohishi, Y. In situ X-ray diffraction measurements of the fcc-hcp phase transition boundary of an Fe-Ni alloy in an internally heated diamond anvil cell. Phys. Chem. Miner. 2012, 39, 329–338. [Google Scholar] [CrossRef]
- Wells, A.F. Structural Inorganic Chemistry; Oxford University Press: Oxford, UK, 1984; Volume 168. [Google Scholar]
- Fischer, R.A.; Campbell, A.J. The axial ratio of hcp Fe and Fe-Ni-Si alloys to the conditions of Earth’s inner core. Am. Mineral. 2015, 100, 2718–2724. [Google Scholar] [CrossRef]
- Kalantar, D.H.; Belak, J.F.; Collins, G.W.; Colvin, J.D.; Davies, H.M.; Eggert, J.H.; Germann, T.C.; Hawreliak, J.; Holian, B.L.; Kadau, K.; et al. Direct observation of the α-ε Transition in shock-compressed iron via nanosecond X-ray diffraction. Phys. Rev. Lett. 2005, 95, 075502. [Google Scholar] [CrossRef] [PubMed]
- Merkel, S.; Lincot, A.; Petitgirard, S. Microstructural effects and mechanism of bcc-hcp-bcc transformations in polycrystalline iron. Phys. Rev. B 2020, 102, 104103. [Google Scholar] [CrossRef]
- Boehler, R.; Santamaría-Pérez, D.; Errandonea, D.; Mezouar, M. Melting, density, and anisotropy of iron at core conditions: New x-ray measurements to 150 GPa. J. Phys. Conf. Ser. 2008, 121. [Google Scholar] [CrossRef]
- Fischer, R.A.; Campbell, A.J.; Shofner, G.A.; Lord, O.T.; Dera, P.; Prakapenka, V.B. Equation of state and phase diagram of FeO. Earth Planet. Sci. Lett. 2011, 304, 496–502. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ito, E.; Yoshino, T.; Yoneda, A.; Guo, X.; Zhang, B.; Sun, W.; Shimojuku, A.; Tsujino, N.; Kunimoto, T.; et al. P-V-T equation of state for ε-iron up to 80 GPa and 1900 K using the Kawai-type high pressure apparatus equipped with sintered diamond anvils. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Ono, S.; Kikegawa, T.; Hirao, N.; Mibe, K. High-pressure magnetic transition in hcp-Fe. Am. Mineral. 2010, 95, 880–883. [Google Scholar] [CrossRef]
- Tateno, S.; Hirose, K.; Ohishi, Y.; Tatsumi, Y. The structure of iron in earth’s inner core. Science 2010, 330, 359–361. [Google Scholar] [CrossRef] [PubMed]
- Uchida, T.; Wang, Y.; Rivers, M.L.; Sutton, S.R. Stability field and thermal equation of state of ε-iron determined by synchrotron X-ray diffraction in a multianvil apparatus. J. Geophys. Res. Solid Earth 2001, 106, 21799–21810. [Google Scholar] [CrossRef]
- Sakai, T.; Ohtani, E.; Hirao, N.; Ohishi, Y. Stability field of the hcp-structure for Fe, Fe-Ni, and Fe-Ni-Si alloys up to 3 Mbar. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Dewaele, A.; Loubeyre, P.; Occelli, F.; Mezouar, M.; Dorogokupets, P.I.; Torrent, M. Quasihydrostatic equation of state of Iron above 2 Mbar. Phys. Rev. Lett. 2006, 97, 215504. [Google Scholar] [CrossRef] [PubMed]
- Tateno, S.; Hirose, K.; Komabayashi, T.; Ozawa, H.; Ohishi, Y. The structure of Fe-Ni alloy in Earth’s inner core. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Lin, J.F.; Heinz, D.L.; Campbell, A.J.; Devine, J.M.; Mao, W.L.; Shen, G. Iron-nickel alloy in the Earth’s core. Geophys. Res. Lett. 2002, 29, 109-1–109-3. [Google Scholar] [CrossRef]
- Hok, S.; Gleason, A.E.; Bolme, C.; Rittman, D.; Merkel, S.; Ramos, K.J.; Morrow, B.; Lee, H.J.; Nagler, B.; Galtier, E.; et al. In situ strength measurement of shock-compressed iron via time-resolved X-ray diffraction. AGUFM 2019, 2019, DI23B-0043. [Google Scholar]
- Dewaele, A.; Denoual, C.; Anzellini, S.; Occelli, F.; Mezouar, M.; Cordier, P.; Merkel, S.; Véron, M.; Rausch, E. Mechanism of the α-ε Phase transformation in iron. Phys. Rev. B Condens. Matter Mater. Phys. 2015, 91, 174105. [Google Scholar] [CrossRef]
- Komabayashi, T.; Fei, Y. Internally consistent thermodynamic database for iron to the Earth’s core conditions. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Wang, J.; Smith, R.F.; Eggert, J.H.; Braun, D.G.; Boehly, T.R.; Reed Patterson, J.; Celliers, P.M.; Jeanloz, R.; Collins, G.W.; Duffy, T.S. Ramp compression of iron to 273 GPa. J. Appl. Phys. 2013, 114. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tecklenburg, S.; Colina-Ruiz, R.; Hok, S.; Bolme, C.; Galtier, E.; Granados, E.; Hashim, A.; Lee, H.J.; Merkel, S.; Morrow, B.; et al. Ultrafast X-ray Diffraction Study of a Shock-Compressed Iron Meteorite above 100 GPa. Minerals 2021, 11, 567. https://doi.org/10.3390/min11060567
Tecklenburg S, Colina-Ruiz R, Hok S, Bolme C, Galtier E, Granados E, Hashim A, Lee HJ, Merkel S, Morrow B, et al. Ultrafast X-ray Diffraction Study of a Shock-Compressed Iron Meteorite above 100 GPa. Minerals. 2021; 11(6):567. https://doi.org/10.3390/min11060567
Chicago/Turabian StyleTecklenburg, Sabrina, Roberto Colina-Ruiz, Sovanndara Hok, Cynthia Bolme, Eric Galtier, Eduardo Granados, Akel Hashim, Hae Ja Lee, Sébastien Merkel, Benjamin Morrow, and et al. 2021. "Ultrafast X-ray Diffraction Study of a Shock-Compressed Iron Meteorite above 100 GPa" Minerals 11, no. 6: 567. https://doi.org/10.3390/min11060567
APA StyleTecklenburg, S., Colina-Ruiz, R., Hok, S., Bolme, C., Galtier, E., Granados, E., Hashim, A., Lee, H. J., Merkel, S., Morrow, B., Nagler, B., Ramos, K., Rittman, D., Walroth, R., Mao, W. L., & Gleason, A. E. (2021). Ultrafast X-ray Diffraction Study of a Shock-Compressed Iron Meteorite above 100 GPa. Minerals, 11(6), 567. https://doi.org/10.3390/min11060567






