Particle Size Distribution of Various Soil Materials Measured by Laser Diffraction—The Problem of Reproducibility
Abstract
1. Introduction
2. Materials and Methods
2.1. Soils
2.2. LDM Measurements
2.3. Statistical Analysis
3. Results
3.1. Reproducibility of LDM Results
3.2. Verification of the Normality of Distributions
4. Discussion
4.1. Comparison of the PSD Obtained by Hydrometed and Laser Diffraction Methods
4.2. Reproducibility of LDM Results
4.3. Verification of the Normality of Distributions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lamorski, K.; Pachepsky, Y.; Sławiński, C.; Walczak, R.T. Using Support Vector Machines to Develop Pedotransfer Functions for Water Retention of Soils in Poland. Soil Sci. Soc. Am. J. 2008, 72, 1243–1247. [Google Scholar] [CrossRef]
- Szypłowska, A.; Lewandowski, A.; Jones, S.B.; Sabouroux, P.; Szerement, J.; Kafarski, M.; Wilczek, A.; Skierucha, W. Impact of Soil Salinity, Texture and Measurement Frequency on the Relations between Soil Moisture and 20 MHz–3 GHz Dielectric Permittivity Spectrum for Soils of Medium Texture. J. Hydrol. 2019, 579, 124155. [Google Scholar] [CrossRef]
- Zhao, B.; Li, L.; Zhao, Y.; Zhang, X. Thermal Conductivity of a Brown Earth Soil as Affected by Biochars Derived at Different Temperatures: Experiment and Prediction with the Campbell Model. Int. Agrophys. 2020, 34, 433–439. [Google Scholar] [CrossRef]
- Farhadi-Machekposhti, M.; Valdes-Abellan, J.; Pla, C.; Benavente, D.; Pachepsky, Y. Impact of Marble Powder Amendment on Hydraulic Properties of a Sandy Soil. Int. Agrophys. 2020, 34, 223–232. [Google Scholar] [CrossRef]
- Usowicz, B.; Lukowski, M.; Lipiec, J. The SMOS-Derived Soil Water EXtent and Equivalent Layer Thickness Facilitate Determination of Soil Water Resources. Sci. Rep. 2020, 10, 18330. [Google Scholar] [CrossRef]
- Kiani-Harchegani, M.; Sadeghi, S.H.; Singh, V.P.; Asadi, H.; Abedi, M. Effect of Rainfall Intensity and Slope on Sediment Particle Size Distribution during Erosion Using Partial Eta Squared. CATENA 2019, 176, 65–72. [Google Scholar] [CrossRef]
- Fernández-Raga, M.; Palencia, C.; Keesstra, S.; Jordán, A.; Fraile, R.; Angulo-Martínez, M.; Cerdà, A. Splash Erosion: A Review with Unanswered Questions. Earth Sci. Rev. 2017, 171, 463–477. [Google Scholar] [CrossRef]
- Rochette, P.; Angers, D.A.; Chantigny, M.H.; Bertrand, N. Nitrous Oxide Emissions Respond Differently to No-Till in a Loam and a Heavy Clay Soil. Soil Sci. Soc. Am. J. 2008, 72, 1363–1369. [Google Scholar] [CrossRef]
- Abdalla, K.; Chivenge, P.; Ciais, P.; Chaplot, V. No-Tillage Lessens Soil CO2 Emissions the Most under Arid and Sandy Soil Conditions: Results from a Meta-Analysis. Biogeosciences 2016, 13, 3619–3633. [Google Scholar] [CrossRef]
- Walkiewicz, A.; Kalinichenko, K.; Kubaczyński, A.; Brzezińska, M.; Bieganowski, A. Usage of Biochar for Mitigation of CO2 Emission and Enhancement of CH4 Consumption in Forest and Orchard Haplic Luvisol (Siltic) Soils. Appl. Soil Ecol. 2020, 156, 103711. [Google Scholar] [CrossRef]
- Balashov, E.; Kren, J.; Prochazkova, B. Influence of Plant Residue Management on Microbial Properties and Water-Stable Aggregates of Two Agricultural Soils. Int. Agrophys. 2010, 24, 9–13. [Google Scholar]
- Navarro-García, F.; Casermeiro, M.Á.; Schimel, J.P. When Structure Means Conservation: Effect of Aggregate Structure in Controlling Microbial Responses to Rewetting Events. Soil Biol. Biochem. 2012, 44, 1–8. [Google Scholar] [CrossRef]
- Oszust, K.; Frąc, M.; Lipiec, J. Soil Microbial Functionality in Response to Dairy Sewage Sludge and Mineral Fertilisers Application under Winter Rape. Int. J. Environ. Sci. Technol. 2015, 12, 3675–3684. [Google Scholar] [CrossRef]
- Frąc, M.; Lipiec, J.; Usowicz, B.; Oszust, K.; Brzezińska, M. Structural and Functional Microbial Diversity of Sandy Soil under Cropland and Grassland. PeerJ 2020, 8, e9501. [Google Scholar] [CrossRef]
- International Organisation for Standarisation ISO 11277. Soil Quality—Determination of Particle Size Distribution in Mineral Soil Material—Method by Sieving and Sedimentation; International Organization for Standarisation: Geneva, Switzerland, 2020. [Google Scholar]
- Ryżak, M.; Bartmiński, P.; Bieganowski, A. Metody Wyznaczania Rozkładu Granulometrycznego Gleb Mineralnych; Intytut Agrofizyki im, Bohdana Dobrzańskiego PAN w Lublinie: Lublin, Poland, 2009; Volume 175. [Google Scholar]
- Polakowski, C.; Sochan, A.; Bieganowski, A.; Ryzak, M.; Földényi, R.; Tóth, J. Influence of the Sand Particle Shape on Particle Size Distribution Measured by Laser Diffraction Method. Int. Agrophys. 2014, 28, 195–200. [Google Scholar] [CrossRef]
- Shang, Y.; Kaakinen, A.; Beets, C.J.; Prins, M.A. Aeolian Silt Transport Processes as Fingerprinted by Dynamic Image Analysis of the Grain Size and Shape Characteristics of Chinese Loess and Red Clay Deposits. Sediment. Geol. 2018, 375, 36–48. [Google Scholar] [CrossRef]
- Kandler, K.; Schneiders, K.; Ebert, M.; Hartmann, M.; Weinbruch, S.; Prass, M.; Pöhlker, C. Composition and Mixing State of Atmospheric Aerosols Determined by Electron Microscopy: Method Development and Application to Aged Saharan Dust Deposition in the Caribbean Boundary Layer. Atmos. Chem. Phys. 2018, 18, 13429–13455. [Google Scholar] [CrossRef]
- Kaszubkiewicz, J.; Papuga, K.; Kawałko, D.; Woźniczka, P. Particle Size Analysis by an Automated Dynamometer Method Integrated with an X-y Sample Changer. Measurement 2020, 157, 107680. [Google Scholar] [CrossRef]
- Durner, W.; Iden, S.C.; von Unold, G. The Integral Suspension Pressure Method (ISP) for Precise Particle-Size Analysis by Gravitational Sedimentation: ISP METHOD FOR PARTICLE-SIZE ANALYSIS. Water Resour. Res. 2017, 53, 33–48. [Google Scholar] [CrossRef]
- Faé, G.S.; Montes, F.; Bazilevskaya, E.; Añó, R.M.; Kemanian, A.R. Making Soil Particle Size Analysis by Laser Diffraction Compatible with Standard Soil Texture Determination Methods. Soil Sci. Soc. Am. J. 2019, 83, 1244–1252. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, L.; Wendroth, O.; Liu, B.; Cheng, C.; Huang, T.; Shi, Y. Is the Laser Diffraction Method Reliable for Soil Particle Size Distribution Analysis? Soil Sci. Soc. Am. J. 2019, 83, 276. [Google Scholar] [CrossRef]
- Vodyanitskii, Y.N.; Savichev, A.T.; Morgun, E.G. Towards a New and General Method for Decoding the Soil Texture from Laser Diffraction Spectra. Environ. Earth Sci. 2020, 79, 266. [Google Scholar] [CrossRef]
- Makó, A.; Szabó, B.; Rajkai, K.; Szabó, J.; Bakacsi, Z.; Labancz, V.; Hernádi, H.; Barna, G. Evaluation of Soil Texture Determination Using Soil Fraction Data Resulting from Laser Diffraction Method. Int. Agrophys. 2019, 33, 445–454. [Google Scholar] [CrossRef]
- Joint Committee for Guides in Metrology JCGM 100:2008. GUM 1995 Ewaluacja Danych Pomiarowych Przewodnik Wyrażania Niepewności Pomiaru. In Évaluation Des Données de Mesure—Guide Pour L’Expression de L’Incertitude de Mesure; JCGM: Sèvres, France, 2010. [Google Scholar]
- Goossens, D. Techniques to Measure Grain-Size Distributions of Loamy Sediments: A Comparative Study of Ten Instruments for Wet Analysis. Sedimentology 2008, 55, 65–96. [Google Scholar] [CrossRef]
- Tavares, L.D.F.; Carvalho, A.M.X.D.; Machado, L.G. An Evaluation of the Use of Statistical Procedures in Soil Science. Rev. Bras. Ciência Solo 2016, 40. [Google Scholar] [CrossRef]
- Bieganowski, A.; Ryżak, M.; Sochan, A.; Barna, G.; Hernádi, H.; Beczek, M.; Polakowski, C.; Makó, A. Laser Diffractometry in the Measurements of Soil and Sediment Particle Size Distribution. Adv. Agron. 2018, 15, 215–279. [Google Scholar]
- FAO. World Reference Base for Soil Resources 2014: International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; Update 2015; FAO: Rome, Italy, 2015; ISBN 978-92-5-108369-7. [Google Scholar]
- Lamorski, K.; Sławiński, C.; Moreno, F.; Barna, G.; Skierucha, W.; Arrue, J.L. Modelling Soil Water Retention Using Support Vector Machines with Genetic Algorithm Optimisation. Sci. World J. 2014, 2014, 740521. [Google Scholar] [CrossRef]
- Sperazza, M.; Moore, J.N.; Hendrix, M.S. High-Resolution Particle Size Analysis of Naturally Occurring Very Fine-Grained Sediment Through Laser Diffractometry. J. Sediment. Res. 2004, 74, 736–743. [Google Scholar] [CrossRef]
- Fisher, P.; Aumann, C.; Chia, K.; Halloran, N.O.; Chandra, S. Adequacy of Laser Diffraction for Soil Particle Size Analysis. PLoS ONE 2017, 12, e0176510. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Q.; Li, X.; Jia, X.; Wei, X.; Shao, M. Determination of Soil Texture by Laser Diffraction Method. Soil Sci. Soc. Am. J. 2015, 79, 1556. [Google Scholar] [CrossRef]
- Igaz, D.; Aydin, E.; Šinkovičová, M.; Šimanský, V.; Tall, A.; Horák, J. Laser Diffraction as An Innovative Alternative to Standard Pipette Method for Determination of Soil Texture Classes in Central Europe. Water 2020, 12, 1232. [Google Scholar] [CrossRef]
- Buurman, P.; Pape, T.; Reijneveld, J.A.; de Jong, F.; van Gelder, E. Laser-Diffraction and Pipette-Method Grain Sizing of Dutch Sediments: Correlations for Fine Fractions of Marine, Fluvial, and Loess Samples. Neth. J. Geosci. 2001, 80, 49–57. [Google Scholar] [CrossRef]
- Konert, M.; Vandenberghe, J. Comparison of Laser Grain Size Analysis with Pipette and Sieve Analysis: A Solution for the Underestimation of the Clay Fraction. Sedimentology 1997, 44, 523–535. [Google Scholar] [CrossRef]
- Roberson, S.; Weltje, G.J. Inter-Instrument Comparison of Particle-Size Analysers. Sedimentology 2014, 61, 1157–1174. [Google Scholar] [CrossRef]
- Polakowski, C.; Ryżak, M.; Bieganowski, A.; Sochan, A.; Bartmiński, P.; Dębicki, R.; Stelmach, W. The Reasons for Incorrect Measurements of the Mass Fraction Ratios of Fine and Coarse Material by Laser Diffraction. Soil Sci. Soc. Am. J. 2015, 79, 30–36. [Google Scholar] [CrossRef]
- Sochan, A.; Bieganowski, A.; Ryżak, M.; Dobrowolski, R.; Bartmiński, P. Comparison of Soil Texture Determined by Two Dispersion Units of Mastersizer 2000. Int. Agrophys. 2012, 26, 99–102. [Google Scholar] [CrossRef]
- Deng, Y.; Cai, C.; Xia, D.; Ding, S.; Chen, J. Fractal Features of Soil Particle Size Distribution under Different Land-Use Patterns in the Alluvial Fans of Collapsing Gullies in the Hilly Granitic Region of Southern China. PLoS ONE 2017, 12, e0173555. [Google Scholar] [CrossRef]
- Kondrlova, E.; Igaz, D.; Horak, J. Effect of Calculation Models on Particle Size Distribution Estimated by Laser Diffraction. In Proceedings of the 9th International Soil Science Congress on “The Soul of Soil and Civilization”, Side, Antalya, Turkey, 14–16 October 2014; pp. 21–27. [Google Scholar]
- Murray, M. Is Laser Particle Size Determination Possible for Carbonate Rick Lake Sediments? J. Paleolimnol. 2002, 27, 173–183. [Google Scholar] [CrossRef]
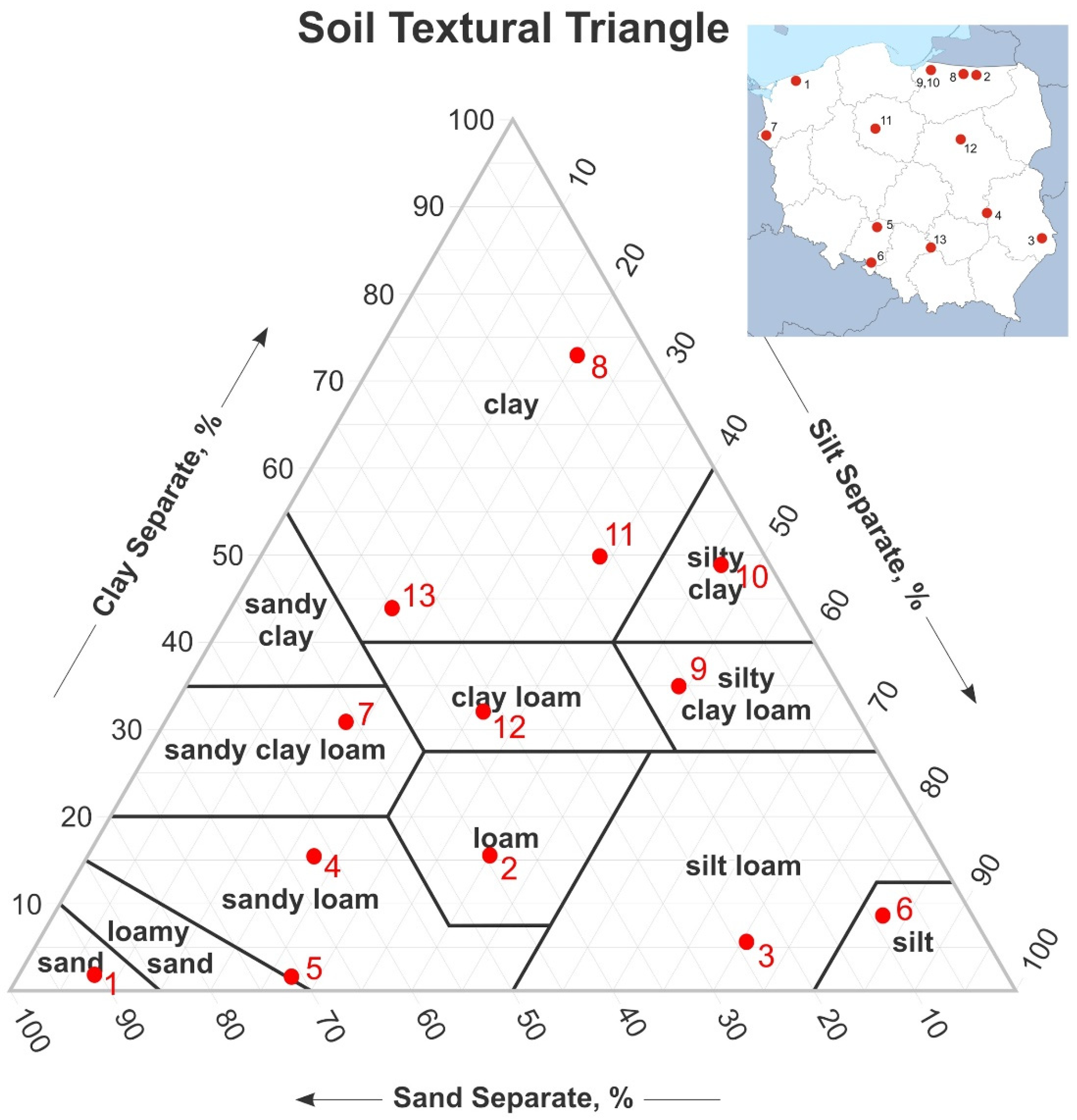
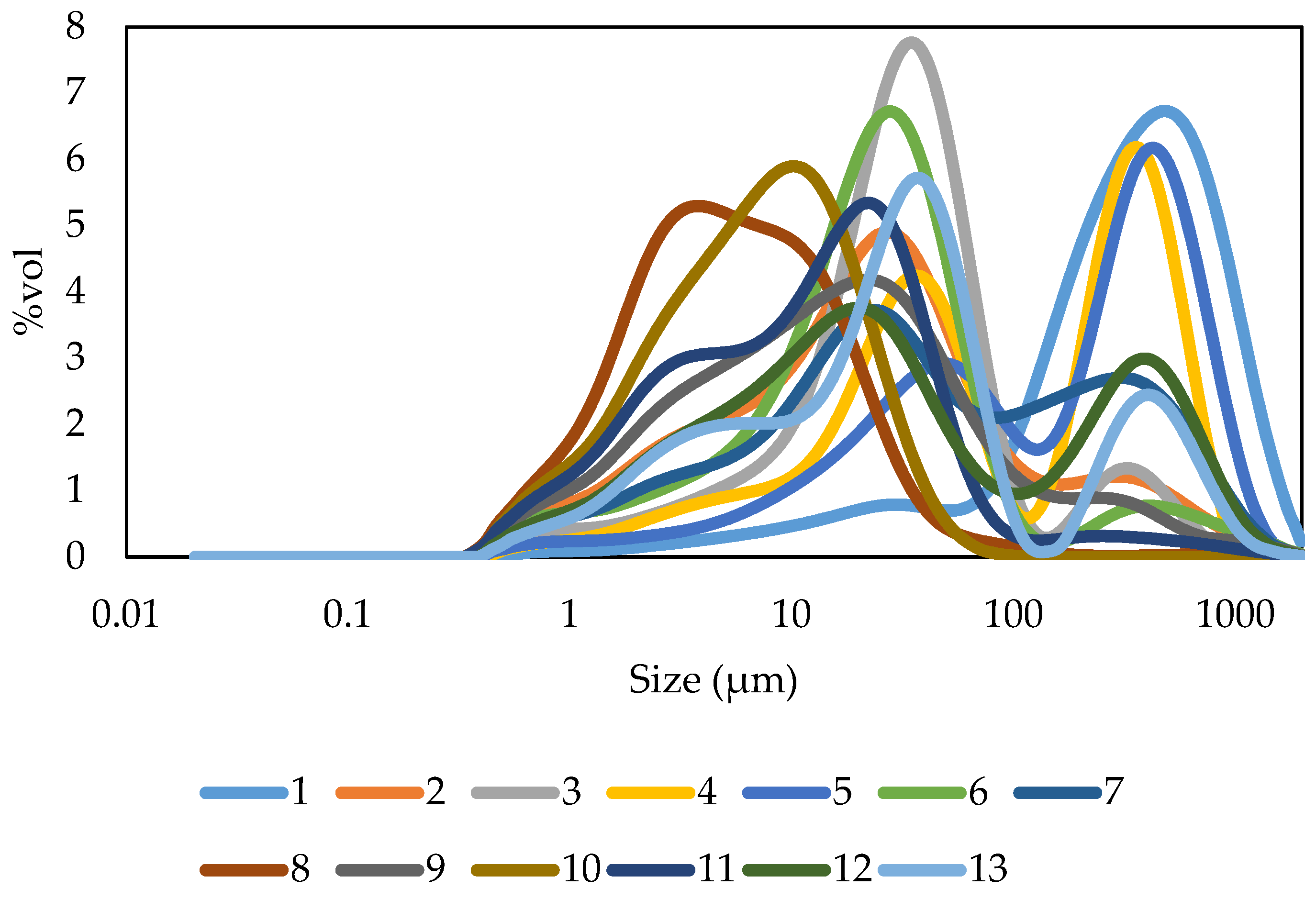
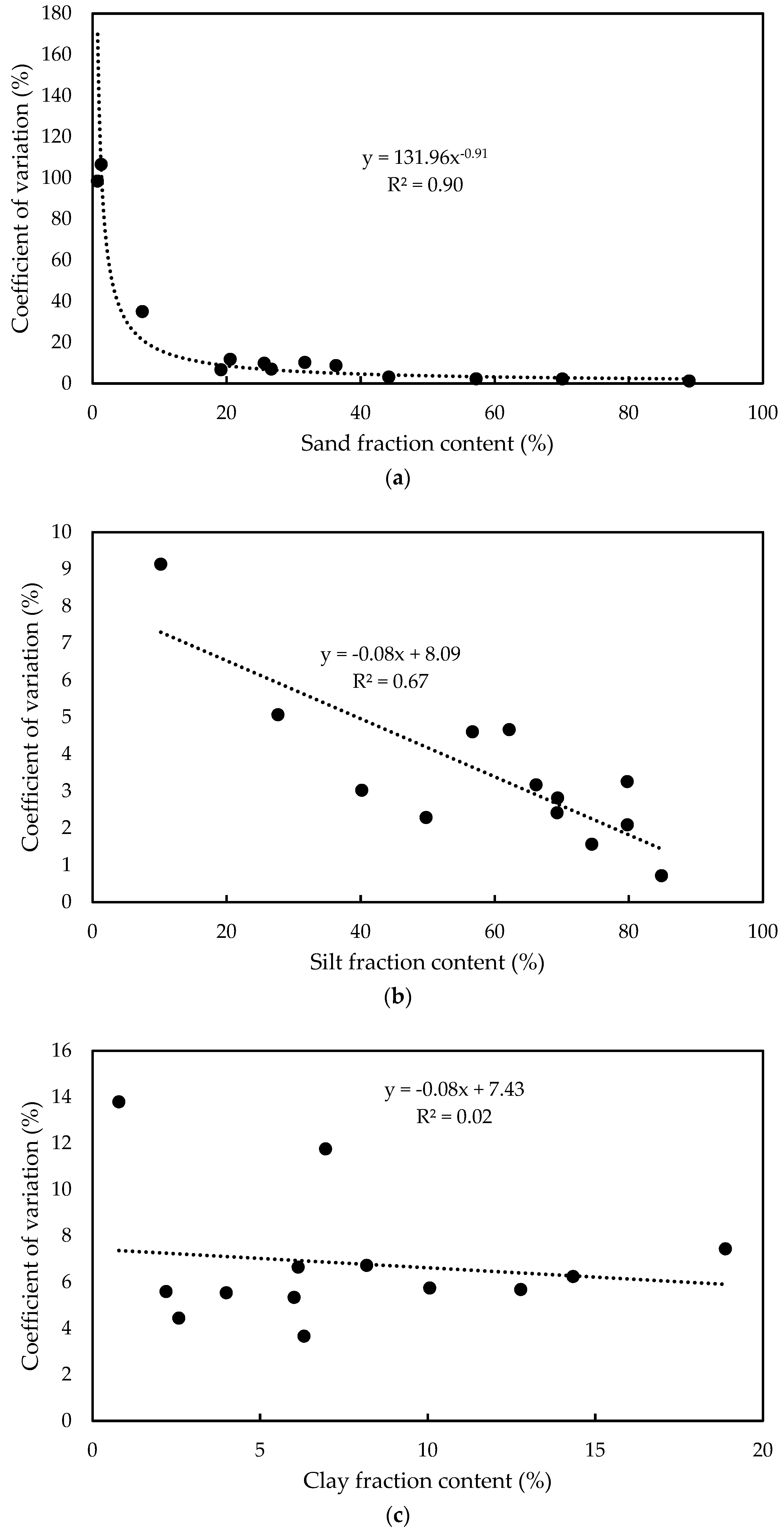
| Soil No. | GPS Coordinates | Soil Horizon (cm) | Soil Unit According to WRB * | PSD (%) | IC (%) | TOC (%) | ||
|---|---|---|---|---|---|---|---|---|
| Sand (0.05–2.00 mm) | Silt (0.002–0.05 mm) | Clay (<0.002 mm) | ||||||
| 1 | 54°6′ N 15°29′ E | A 15–20 | Brunic Arenosol | 91 | 8 | 1 | 0.00 | 1.72 |
| 2 | 54°13′ N 21°13′ E | A 15–20 | Haplic Phaeozem | 44 | 40 | 16 | 0.00 | 3.43 |
| 3 | 50°44′ N 23°49′ E | A 0–25 | Haplic Chernozem | 24 | 70 | 6 | 0.04 | 3.11 |
| 4 | 51°04′ N 21°49′ E | A 0–25 | Rendzic Leptosol | 62 | 22 | 16 | 0.04 | 1.92 |
| 5 | 51°01′ N 18°03′ E | A 0–25 | Haplic Luvisol | 71 | 27 | 2 | 0.00 | 1.14 |
| 6 | 50°10′ N 17°50′ E | A 0–35 | Mollic Gleysol | 9 | 83 | 8 | 0.00 | 1.70 |
| 7 | 52°55′ N 14°16′ E | A 20–30 | Cambic Phaeozem | 51 | 18 | 31 | 0.00 | 0.82 |
| 8 | 54°16′ N 20°55′ E | C 100–105 | Haplic Vertisol | 7 | 20 | 73 | 1.16 | 0.54 |
| 9 | 54° 18′ N 20° 20′ E | A 15–20 | Haplic Vertisol | 16 | 49 | 35 | 0.00 | 3.19 |
| 10 | 54°19′ N 20°21′ E | C 125–130 | Haplic Vertisol | 5 | 46 | 49 | 1.89 | 0.92 |
| 11 | 52°54′ N 18°1′ E | B 40–50 | Vertic Cambisol | 16 | 34 | 50 | 0.00 | 0.55 |
| 12 | 52°50′ N 20°51′ E | A 0–20 | Pellic Vertisol | 37 | 31 | 32 | 0.00 | 1.81 |
| 13 | 50°30′ N 19°52′ E | B 30–40 | Eutric Cambisol | 40 | 16 | 44 | 1.04 | 0.70 |
| Soil No. | Sand (0.05–2.00 mm) | Silt (0.002–0.05 mm) | Clay (<0.002 mm) | |||
|---|---|---|---|---|---|---|
| Content (%) | CV (%) | Content (%) | CV (%) | Content (%) | CV (%) | |
| 1 | 89.02 | 1.16 | 10.19 | 9.13 | 0.79 | 13.79 |
| 2 | 25.63 | 9.81 | 66.19 | 3.17 | 8.18 | 6.72 |
| 3 | 26.68 | 7.01 | 69.33 | 2.42 | 3.99 | 5.53 |
| 4 | 57.25 | 2.25 | 40.18 | 3.02 | 2.58 | 4.44 |
| 5 | 70.11 | 2.16 | 27.69 | 5.06 | 2.20 | 5.58 |
| 6 | 19.19 | 6.64 | 74.5 | 1.56 | 6.31 | 3.66 |
| 7 | 44.21 | 3.10 | 49.77 | 2.29 | 6.02 | 5.33 |
| 8 | 1.32 | 106.50 | 79.80 | 2.09 | 18.88 | 7.43 |
| 9 | 20.55 | 11.83 | 69.39 | 2.84 | 10.06 | 5.72 |
| 10 | 0.76 | 98.44 | 84.9 | 0.71 | 14.34 | 6.24 |
| 11 | 7.44 | 34.92 | 79.78 | 3.26 | 12.78 | 5.67 |
| 12 | 36.35 | 8.67 | 56.70 | 4.60 | 6.95 | 11.75 |
| 13 | 31.69 | 10.22 | 62.18 | 4.66 | 6.14 | 6.64 |
| Average | - | 23.28 | - | 3.44 | - | 6.81 |
| Soil No. | Sand | Silt | Clay |
|---|---|---|---|
| 1 | 0.652 | 0.434 | 0.938 |
| 2 | 0.137 | 0.085 | 0.823 |
| 3 | 0.429 | 0.361 | 0.840 |
| 4 | 0.052 | 0.048 | 0.149 |
| 5 | 0.799 | 0.886 | 0.027 |
| 6 | 0.654 | 0.477 | 0.074 |
| 7 | 0.372 | 0.386 | 0.578 |
| 8 | 0.000 | 0.443 | 0.007 |
| 9 | 0.017 | 0.022 | 0.788 |
| 10 | 0.000 | 0.587 | 0.052 |
| 11 | 0.019 | 0.020 | 0.148 |
| 12 | 0.002 | 0.001 | 0.217 |
| 13 | 0.015 | 0.026 | 0.692 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polakowski, C.; Ryżak, M.; Sochan, A.; Beczek, M.; Mazur, R.; Bieganowski, A. Particle Size Distribution of Various Soil Materials Measured by Laser Diffraction—The Problem of Reproducibility. Minerals 2021, 11, 465. https://doi.org/10.3390/min11050465
Polakowski C, Ryżak M, Sochan A, Beczek M, Mazur R, Bieganowski A. Particle Size Distribution of Various Soil Materials Measured by Laser Diffraction—The Problem of Reproducibility. Minerals. 2021; 11(5):465. https://doi.org/10.3390/min11050465
Chicago/Turabian StylePolakowski, Cezary, Magdalena Ryżak, Agata Sochan, Michał Beczek, Rafał Mazur, and Andrzej Bieganowski. 2021. "Particle Size Distribution of Various Soil Materials Measured by Laser Diffraction—The Problem of Reproducibility" Minerals 11, no. 5: 465. https://doi.org/10.3390/min11050465
APA StylePolakowski, C., Ryżak, M., Sochan, A., Beczek, M., Mazur, R., & Bieganowski, A. (2021). Particle Size Distribution of Various Soil Materials Measured by Laser Diffraction—The Problem of Reproducibility. Minerals, 11(5), 465. https://doi.org/10.3390/min11050465







