1. Introduction
Solid-liquid separation is an important part of the process chains in many industry sectors, such as the mining industry. For the high throughputs typically expected in such applications, continuously operating decanter centrifuges are a reasonable option. They are frequently used for dewatering and classification of mineral products, such as calcium carbonate water slurries. In general, the scale-up of a decanter centrifuge from pilot to industrial-scale is a major challenge.
Stahl [
1] has demonstrated that changing operating parameters often has a contrary effect on the performance of solid-bowl centrifuges. For example, the same separation result can be obtained by various parameter combinations of the process behaviour. This causes the geometry and process conditions to be unable to be simply scaled up linearly. As a result, for a successful scale-up to industrial-scale, experiments on a pilot-scale are required to determine the correct transfer function and hence map the non-linearity of the system. This has the disadvantage that often a significant number of experiments are necessary, which implies a high energy demand, personnel, and cost expenditure.
Research on scale-up for solid-bowl centrifuges has relied primarily on analytical models [
2]. Ambler [
3,
4,
5] introduced the so-called Σ-theory, which is based on the residence time of a particle in the centrifuge assuming a plug-flow, which is related to Stokes’ settling velocity. Wakeman and Tarleton [
2] presented a very similar approach compared to the Σ-theory. Leung [
6] developed a scale-up method considering the flow pattern in a rotating bowl. All three mentioned analytical methods are introduced in more detail in the next section, and their pros and cons are outlined. At this point, it should be noted that none of the methods mentioned above consider the loading of the centrifuge and its dynamic behaviour during operation, which often leads to significant deviations compared to experimental data.
An increased interest in numerical models has emerged in recent years. On the one hand, there are more detailed, but also computationally time-consuming, computational fluid dynamics (CFD) and discrete element method (DEM) simulations. On the other hand, in dynamic real-time simulations, the computational effort is reduced introducing more assumptions. Therefore, these models require material functions which characterise the real material behaviour in the simulation to compensate the model reduction.
Zhu et al. [
7] presented a CFD model for a three-phase decanter centrifuge, which is typically used in oil industry for water/oil/sand separation. The phases were modelled with a Eulerian multiphase approach (so-called particle pseudo-fluid model) in Fluent. Only monodisperse distributed particles are simulated. Sediment build-up, consolidation and transport are not considered. Therefore, the proposed simulation method is not applicable to a decanter centrifuge used for dewatering, or the classification of mineral slurries, where the sediment behaviour plays a major role and polydisperse particle size distributions typically occur. Fernandez and Nirschl [
8] proposed a coupled CFD-DEM method for simulating a solid-bowl centrifuge. Firstly, the flow of water and air is calculated with CFD as continuous phases. Secondly, particle movement is modelled with DEM. The method is not directly adaptable to the decanter centrifuge, where additionally a screw rotates with a differential speed and thus induces shear forces to the sediment influencing sediment transport and flow behaviour. Furthermore, Fernandez and Nirschl [
8] use particles with a diameter of 125 μm up to 200 μm. Here in this work, finely dispersed products are considered, which means that the particles are typically smaller than 20 µm and the local solids content in a decanter centrifuge often varies between nearly clarified liquid and a densely packed sediment. This would require an extremely high number of very small particles in DEM to map sediment consolidation and transport, which increases the computational effort of the DEM calculation enormously. For this reason, Hammerich et al. [
9] developed a multiphase CFD model for application on a tubular centrifuge, which takes sediment consolidation and rheological behaviour into account. The suspension and sediment phase are described using an Euler approach. However, the model is not transferable to the decanter centrifuge in this form, because solver internal algorithms and equations are not adapted to the screw geometry and thus additional shear forces in the sediment caused by the screw are not considered. As previously mentioned, the discussed simulation approaches allow one to predict the physical behaviour of very detailed solid-bowl centrifuges, but are time-consuming and computationally intensive.
For the application in flowsheet and process simulations or model-predictive control algorithms, a significant reduction of the computing time towards real-time simulation is essential. Stiborsky [
10] introduced a numerical model to calculate the dewatering of granular products (particles greater 50 μm) in decanter centrifuges. However, the dewatering behaviour of granular products differs substantially from finely dispersed products, meaning that the centrifugal forces are typically no longer sufficient to exceed the capillary forces within the finely dispersed sediment and it remains completely saturated.
Stickland [
11] described numerical models for the simulation of batch centrifuges, tubular centrifuges, and the cylindrical part of decanter centrifuges. The author divided the centrifuge into specific sections to calculate settling, sediment consolidation and sediment transport. Stickland [
11] obtained the conservation equations of momentum and mass as well as the boundary conditions for the cylindrical part. However, the conical part was neglected, and no equations were formulated for this part. Gleiss et al. [
12] provided a dynamic process model considering sediment build-up and classification in the cylindrical part of a counter-current decanter centrifuge, but neglects the cone as well. This conical part of the decanter centrifuge, through which the sediment is transported out of the pool to the cake discharge, plays indeed a decisive role in the dewatering and transport of the sediment. Therefore, Menesklou et al. [
13] extended the numerical model of Gleiss et al. [
12] by integrating the conical part of the decanter centrifuge in the model. The work of Menesklou et al. [
13] has focused on modelling the conical part, and the results presented in this work are promising but demand further investigations regarding scale-up capability and transferability. So far, the extended material characterisation and validation of this comprehensive approach have only been performed for one finely dispersed mineral product and for one scale.
The aim of this study is to evaluate, in a detailed way, the effectiveness of the simulation method, which includes the transferability of the material characterisation and the scale-up capability. In the present article, the authors highlight and discuss key differences between analytical and numerical scale-up for decanter centrifuges. Simulations are compared to experimental data for a lab-, pilot- and industrial-scale decanter centrifuge based on two different finely dispersed calcium carbonate water slurries (CC1 and CC2) to prove the scale-up capability and transferability of this numerical approach. It is necessary to investigate whether this works with a new calcium carbonate product which behaves differently. This would have the benefit that the simulation method is flexible, particularly in industrial applications, regarding changes in the used product, especially with respect to the transport efficiency of the consolidated sediment, which is calibrated on a lab-scale decanter centrifuge and used for industrial-scale simulations. This leads to the question if this calibration is also valid and sufficient for intermediate scales and therefore an up and down scaling is possible when the transport efficiency is calibrated at one scale, because the residence time behaviour and the centrifugal acceleration can vary significantly between the different sizes.
The next section outlines the analytical scale-up approaches, which are commonly used for the dimensioning of decanter centrifuges. Background information about the material characterisation of the products is provided and limitations of the numerical approach are explained. Next, the calcium carbonate products, centrifuges and experimental procedure are presented. Finally, both scale-up methods are compared and the results are discussed.
3. Numerical Model and Material Characterisation
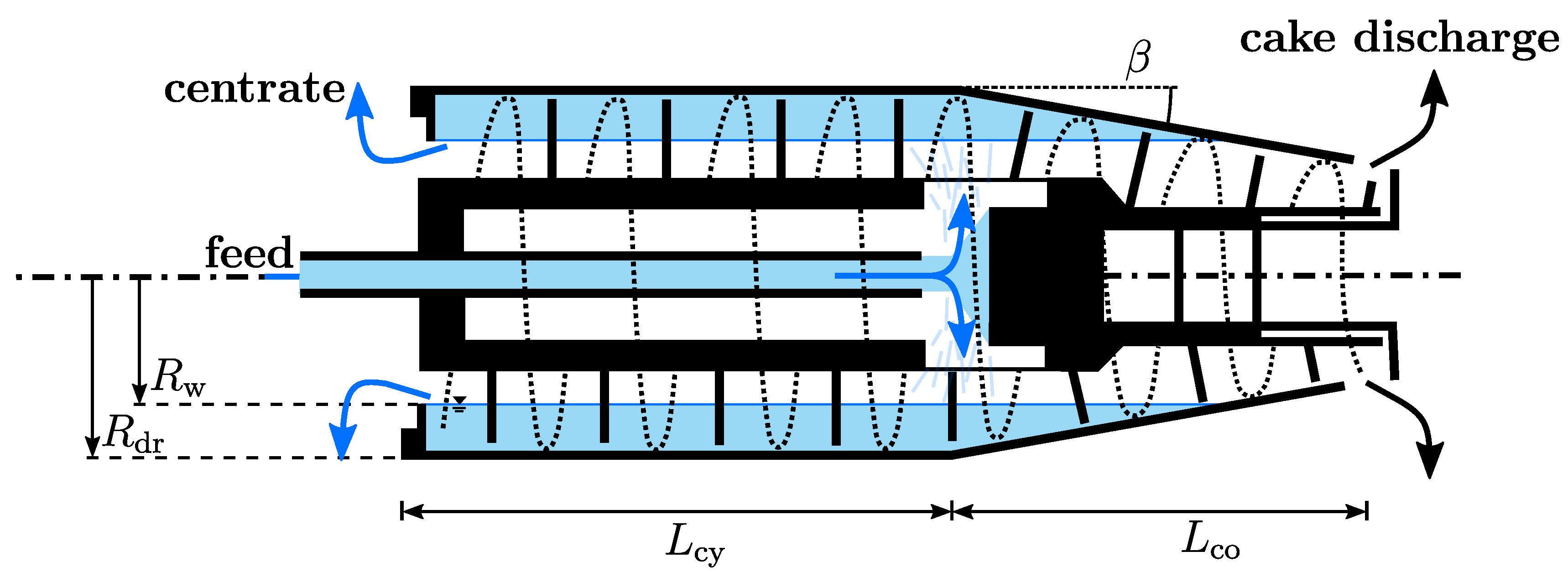
This section provides an overview of the used numerical model and the required input parameters. It is intended for use as a stand-alone simulation tool as well as parts of optimisation algorithms and model-predictive control. Therefore, this numerical approach has the ability to perform simulations in real time, which means that it runs at the same rate or faster than the actual physical process. This advantage is coupled with additional assumptions in the model and a special material characterisation, which is discussed below. These assumptions mean that due to the additionally required computational effort, no detailed flow simulations (like CFD methods) are possible with this approach, which is a limitation. However, flow simulations are not the intention of this simulation tool, but the use as a real time model. Generally, the discretisation in this approach is done along the helical screw channel into compartments, which are linked by mass balances. The settling in each compartment is determined with the separation efficiency, which is obtained by combining the residence time and settling time for each particle class. A uniformly distributed flow in each compartment of the pool is assumed for the residence time behaviour of a particle with specific size. The settling velocity is based on Stokes’ settling, which is adapted to the centrifugal field and enhanced by a hindered settling factor. This factor reflects the real settling behaviour at increased solids content compared to Stokes’ settling velocity, which is only valid for single particles. It is determined experimentally as a function of the solids volume fraction and explained in more detail below. By solving a differential equation for the compression, the consolidation of the sediment is calculated in each compartment. The properties of the individual compartments can change over time due to sediment build-up or a change in the process parameter and thus reflect the dynamic behaviour of the centrifuge. Further information about the modelling, such as discretisation, numerical algorithms, and governing equations, are explained and discussed in detail in Menesklou et al. [
13].
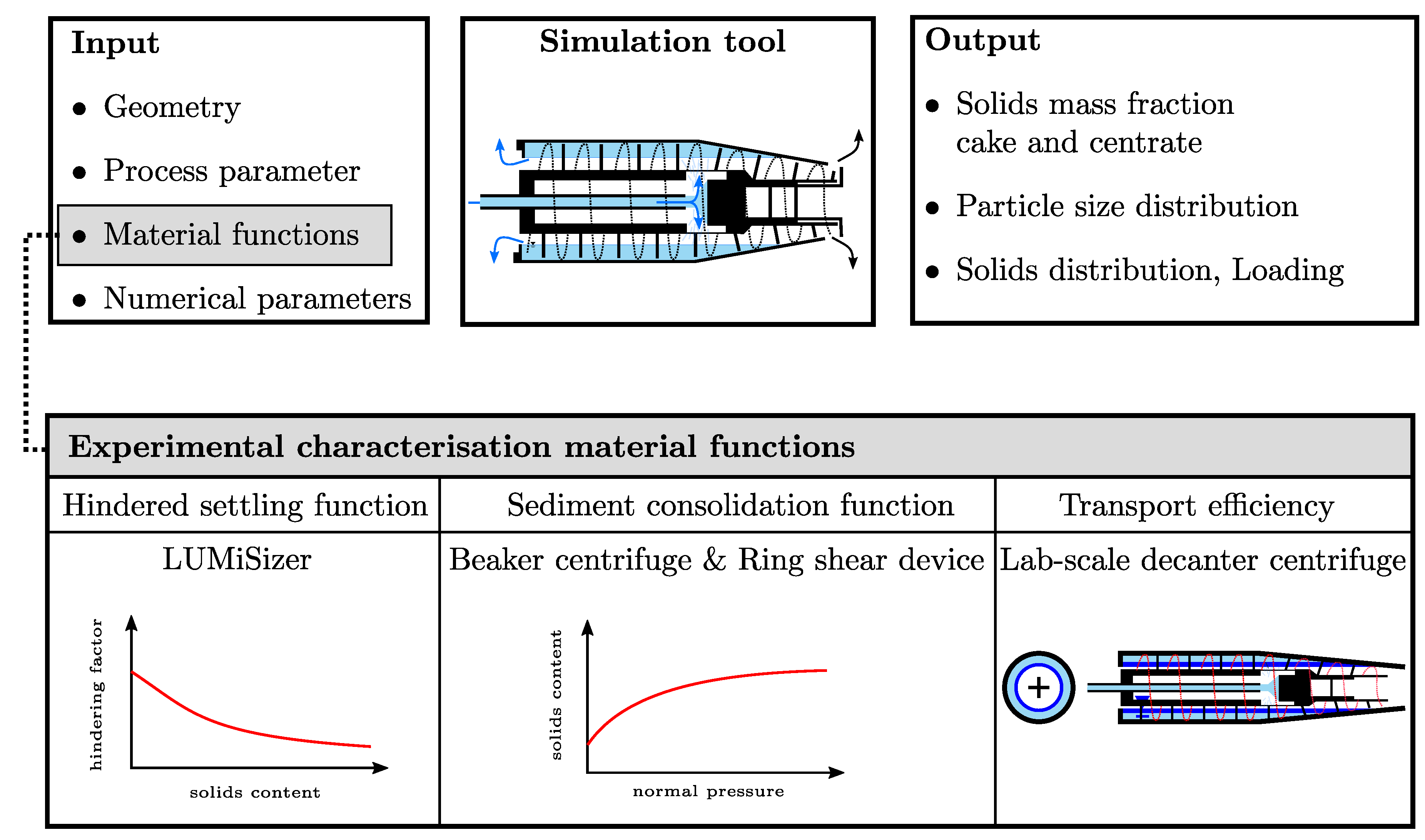
Figure 2 is a graphic summary of the input and output parameters with focus on the material functions.
The input parameters can be split into four different categories, as shown in
Figure 2. The geometry and process parameters are either given by the centrifuge or set by the operator and are generally available. The numerical parameters are determined by the required spatial and temporal discretisation to ensure a stable simulation. There are numerous mathematical criterions for an appropriate selection. Alternatively, these can be determined by preliminary studies on the influence of discretisation. This means to choose a sufficiently small time-step and a sufficiently fine spatial discretisation. The material functions specify the real separation behaviour of the processed slurry and thus couple it with shortcut models within the simulation approach. The material functions contain the hindered settling, sediment consolidation, and a transport efficiency of the screw conveyor system. All parameters are determined experimentally using well-established laboratory equipment.
The hindered settling function considers the influence of the solids volume fraction on the settling velocity. Increasing solids’ content causes swarm or zone sedimentation, which can accelerate settling compared to Stokes due to cluster formation or can hinder settling due to increased momentum exchange between particles. The settling velocity
depends on solids volume fraction and is measured with the analytical centrifuge LUMiSizer supplied by LUM GmbH and related to the theoretically expected settling velocity by Stokes
[
21]. Thus, the real settling behaviour is considered in the simulation.
For the hindered settling function
, a power law approach as used in Michaels and Bolger [
22] in the form of
was chosen. The fit parameters are
,
, and
, and are adapted to experimental data. Menesklou et al. [
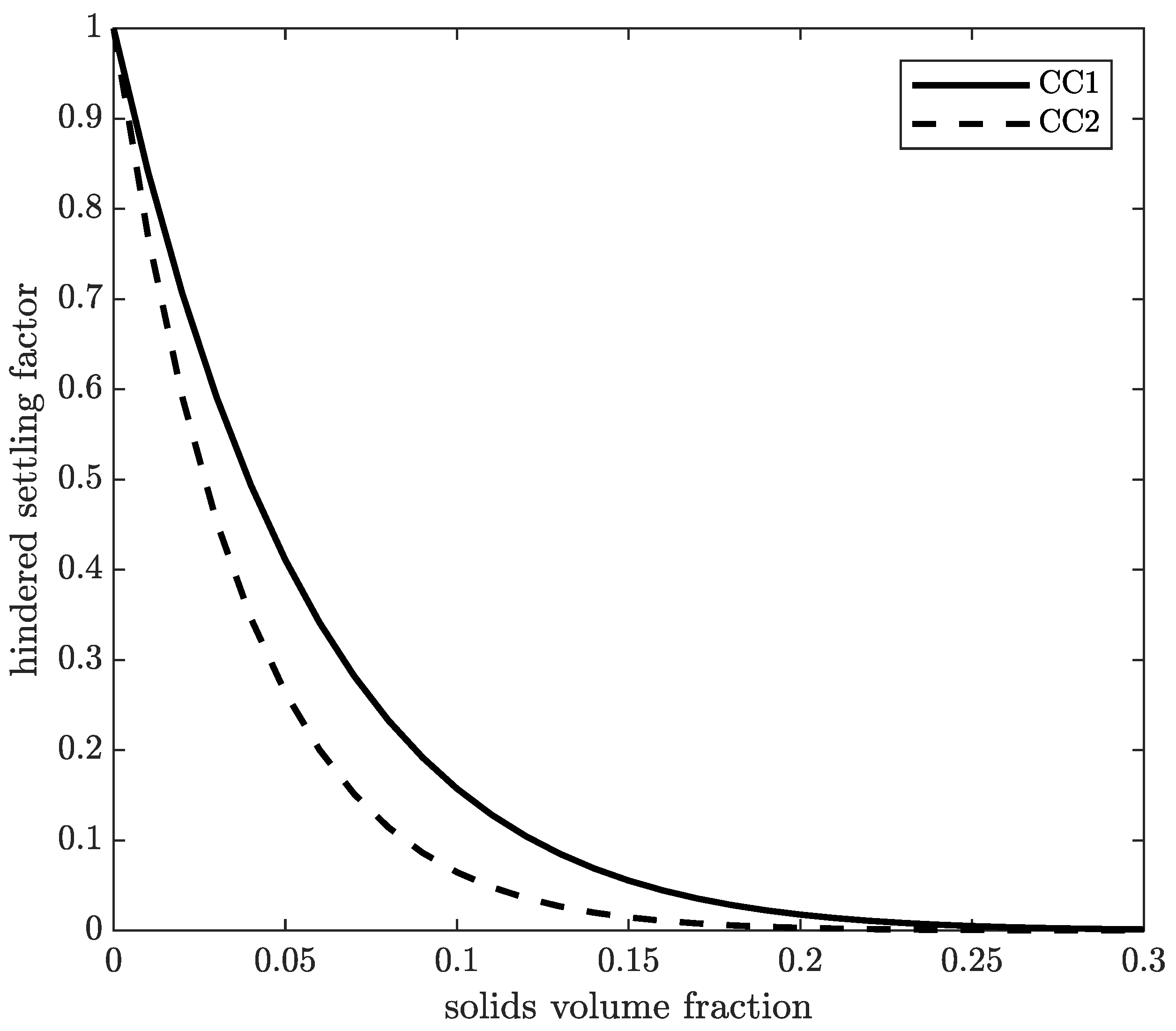
13] show that this function is able to describe the experimentally determined settling behaviour. In
Figure 3, the resulting hindered settling functions of the two used calcium carbonate products are plotted against the solids volume fraction.
The hindered settling function is for a solids volume fraction of , where single particle sedimentation according to Stokes can be assumed. The hindered settling factor decreases with increasing solids volume fraction, because of the increasing momentum exchange between the particles.
The sediment of finely dispersed calcium carbonate suspensions, as used in these investigations, shows compressible behaviour. This results in the fact that the solids volume fraction of the sediment is a function of normal stress and varies typically along the height of the sediment. The compression function introduced by Green et al. [
23] with two fit parameters
, and
,
describes the correlation between the normal stress
and the corresponding solids volume fraction
of finely dispersed, compressible sediments. The gel-point
is an experimentally determined value which describes the transition between particle settling and sediment consolidation. When shear stress occurs, as caused by the screw of the decanter centrifuge, the sediment can compact additionally [
24,
25]. Therefore, the uniaxial compression function by Green et al. [
23] is adapted and leads to the sediment consolidation function,
for the solids volume fraction with additional shear stress
. The parameters
,
, are empirical parameters which are fitted on the experimental data. If
and
, Equation (
12) decreases to uniaxial compression. A detailed description of the measuring procedure can be found in Menesklou et al. [
13]. Hammerich et al. [
26] present an overview of a modified ring shear cell to measure the yield point of liquid-saturated, compressible sediments. In contrast to Menesklou et al. [
13], the consolidation function was extended by the parameter
to better represent the consolidation function for the complete range. Especially in the region of relatively low normal stress, i.e., in lab-scale, pilot-scale, or even in some industrial-scale decanter centrifuge applications, where centrifugal acceleration is low, the relationship between the sheared and unsheared curve is no longer proportional. Therefore, the parameter
is introduced to adapt the uniaxial compression curve to the experimental data over the complete range of normal stress.
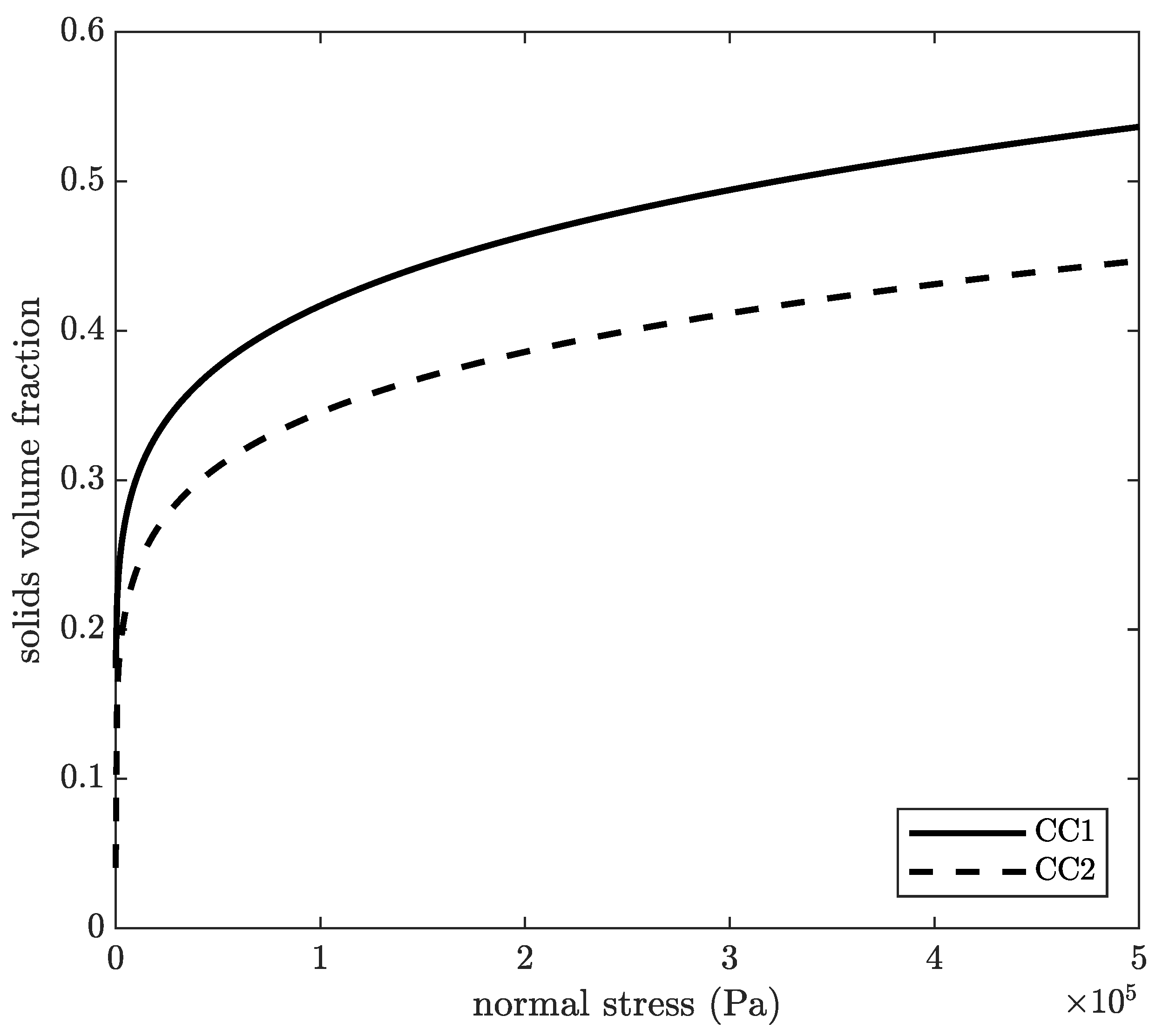
Figure 4 presents the experimentally determined and fitted sediment consolidation function for the two calcium carbonate-water slurries. The solids volume fraction with shear stress
is plotted over the normal stress
.
The two calcium carbonate products differ in their compression behaviour. The coarser mineral CC1 shows a higher compaction than CC2 at the same normal pressure. This matches with investigations on the compression by Alles and Anlauf [
27].
The transport efficiency T is an integral parameter describing the efficiency of the real sediment transport behaviour from the screw towards the cake discharge. The value varies between and . A transport efficiency of means that the sediment is not transported along the screw channel. This happens if the sediment is not sufficiently compacted and the shear forces of the screw are not high enough to convey the sediment. A transport efficiency of corresponds to an ideal sediment transport in axial direction. Experiments have shown that the value for sediments of calcium carbonate water is normally between and , due to friction in the sediment and sliding effects between screw and sediment. The transport efficiency is determined experimentally from tests with a lab-scale decanter centrifuge. This leads to the question of whether this transfer is also valid and sufficient for all scales, because the residence time behaviour can vary significantly between the different sizes.
Based on the characterisation of these three material functions for hindered settling, sediment consolidation, and sediment transport, it is possible to perform valid simulations up to the industrial scale. For this purpose, no scaling criteria or further adaptation parameters are necessary, which would be a great advantage and would enable a broad spectrum of simulating and comparing different decanter centrifuges.
4. Experimental Setup
Experimental trials were performed for the two presented mineral products on three decanter centrifuges of different sizes. The comparison between experimental data and simulations will be shown in the next section. The intension is to illustrate the accuracy, the scale-up capability, and the transferability of the simulation approach also for other calcium carbonate products.
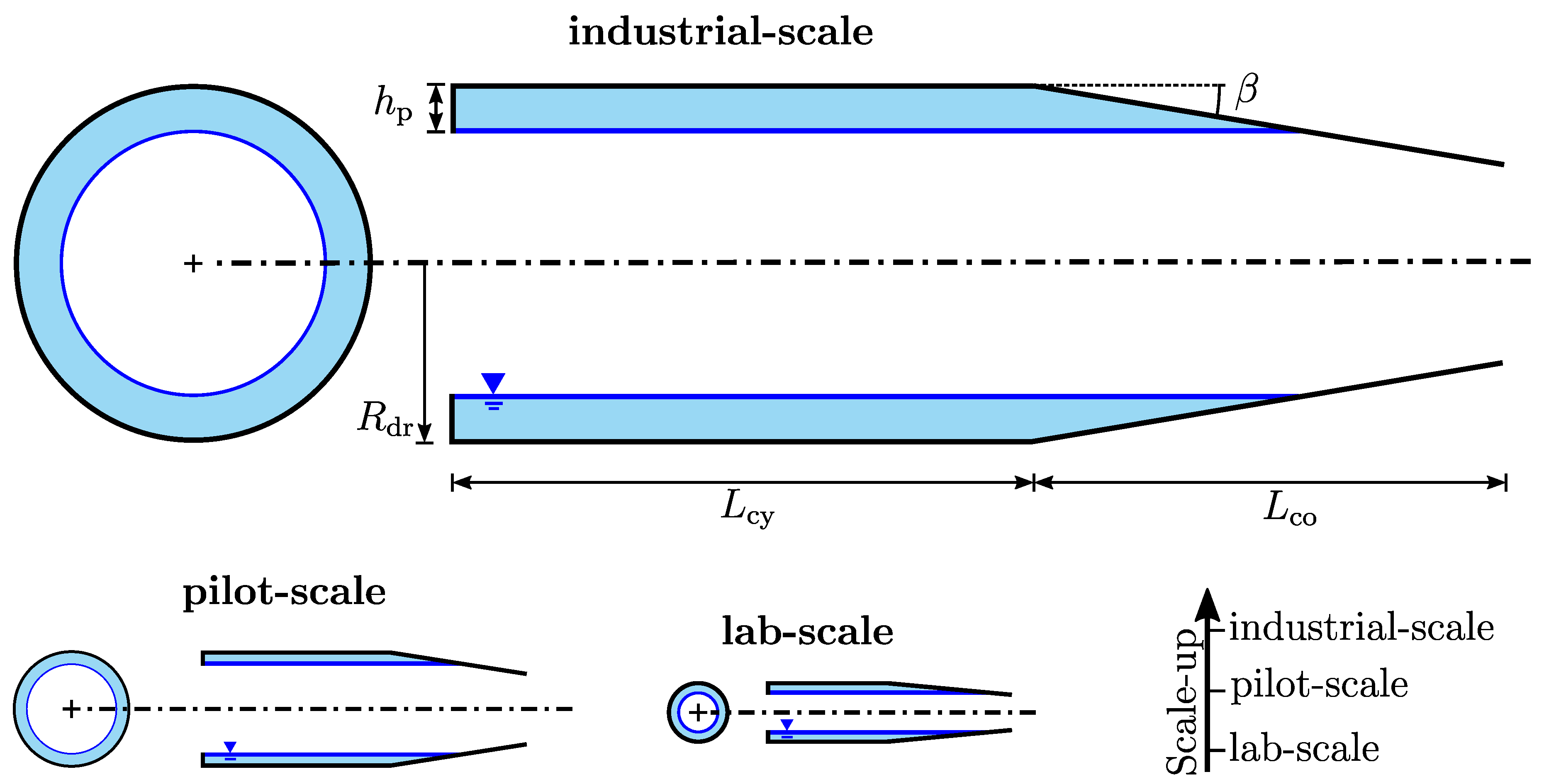
Figure 5 visualises the geometric properties of the apparatuses true to scale.
The three selected decanter centrifuges represent typical sizes. The lab-scale centrifuge is conceived for use in research and high-quality products that are only available in small quantities. The pilot-scale decanter centrifuge is also frequently used in pilot plants of production sites to check scale-up criteria as an intermediate scale and to carry out basic tests on usability in production. At this point, it should be mentioned that the centrifuges are not exactly geometrically similar in terms of the Buckingham
theorem. Furthermore, the volumetric flow rates and the solids mass fraction at the inlet are selected to be within the typical application range. The parameters for all three different scales are listed in
Table 2.
To investigate the transferability of the simulation method within the product category of finely dispersed calcium carbonate water suspensions, experiments were carried out on each scale with two different suspensions (CC1 and CC2). Both products show totally different settling (see
Figure 3), compression (see
Figure 4), and transport behaviour. The particle size was analysed by laser diffraction (Helos/Quixel, Sympatec GmbH, Germany). The logistic function,
serves as model function for the distribution function. The parameters
and
were fitted to the measurement results so that the particle size distribution is available as a continuous function and can be discretised initially prior to a simulation. They are specified in
Table 3.
During a series of measurements, the centrifuge was started up, all process parameters set, and then various rotational speeds adjusted. After each variation of rotational speed, the centrifuge was flushed with water to remove deposited sediment. This ensures that previous tests do not influence the current test series. Solids mass fraction of the discharged cake and the centrate was determined gravimetrically. Samples were taken after the machine had reached steady state. Preliminary tests were carried out for each centrifuge to determine how long it takes to reach steady state and thus to determine when samples can be collected after changing the parameters. A time interval of 5 was determined for the lab- and pilot-scale and 10 for the industrial-scale. The gravimetric determination of the solids mass fraction of the samples was measured by weighing and drying. Comparing both masses, the average solids mass fraction can be calculated. The sample was weighed in the wet state and again after drying in a drying chamber. To ensure that the sample was completely dry, a minimum drying time was obtained in preliminary tests using the most wet state.
The centrate is released continuously and homogeneously distributed from the centrifuge via a pipeline under the investigated operating conditions. For this purpose, centrate sample was taken directly from this pipe immediately behind the centrate exit. This allows a reliable and representative sampling at this point. The measured value for the solids mass fraction of the cake represents a mean value for the entire discharged sediment layer. Finely dispersed compressible sediments show a distribution of porosity over the sediment height. Typically, the compressed sediment is viscous and pasty, which leads to the fact that the sediment is discharged, rather spread, into an ejection channel. For this reason, a sufficiently large amount of the ejected sediment in the channel is collected at different points to obtain a representative sample. This means that the composition of the collected sample corresponds to the composition of the cake as it would be found immediately before ejection in the centrifuge. Thus, the evaluation of the solids mass fraction of the cake tends to have a higher statistical uncertainty than the centrate due to the sampling. In the diagrams in the following section, no error bars are plotted. The measurements are single measurements and are intended to validate the simulations.
5. Results and Discussion
In this section, simulations are compared to experimental data to discuss the scale-up capability and transferability of this numerical approach. Advantages and disadvantages of both scale-up methods are highlighted and discussed.
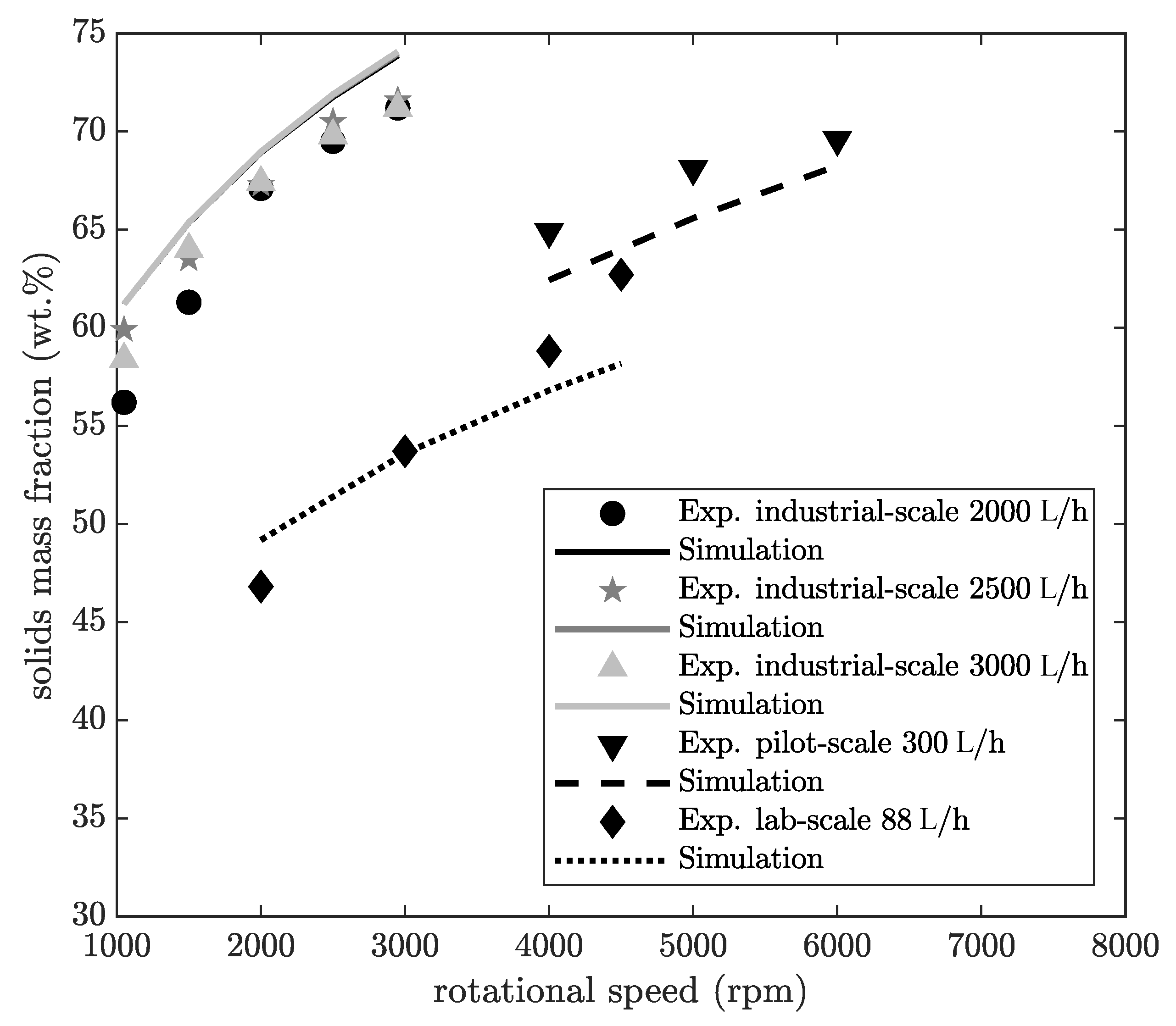
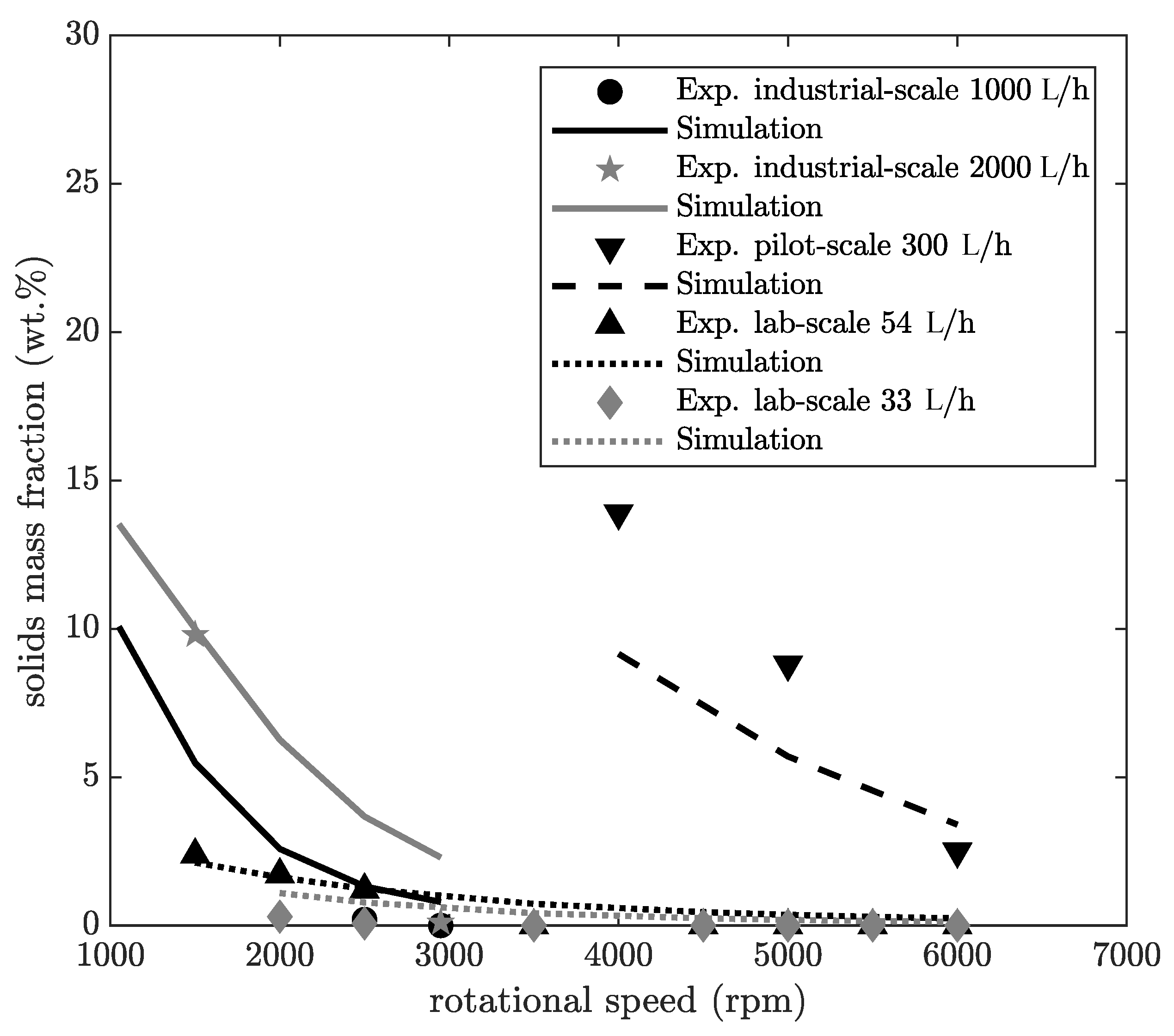
Figure 6 shows the solids mass fraction of the cake as a function of the rotational speed. Simulations were done for all three scales for CC1 and were compared to experimental values.
For both simulation and experimental data, the solids mass fraction increases to higher rotational speeds for each scale, which is explainable by the rising centrifugal acceleration. The relative deviation between simulation and experiment is always smaller than 10
. This is within the range of the expected accuracy of such a process model. Furthermore, it should be mentioned here that the transport of solids requires a three-dimensional description, but the model uses a simplified two-dimensional description, which can reduce the prediction accuracy. The solids mass fraction in the cake varies significantly for different scales for a specific rotational speed. This is because the drum radius is proportional to the centrifugal acceleration and the height of the sediment has an influence on the compression. The drum radius for the lab-scale machine is substantially smaller (see
Table 2) than that of an industrial-scale machine. Therefore, a much smaller centrifugal acceleration is reached. Additionally, the throughput of an industrial-scale centrifuge is basically much higher, and the pool is, in principle, deeper. As a result, a higher sediment builds up in the pool, which causes higher centrifugal pressure on the sediment and thus leads to a more compacted cake. The variation of the volumetric flow rate has practically no significant influence on the solids mass fraction in the cake for the simulation of the industrial-scale decanter centrifuge. The same behaviour is observed for the experimental data. This provides preliminary evidence that the simulation can predict the influence of the volumetric flow rate on the solids content of the cake.
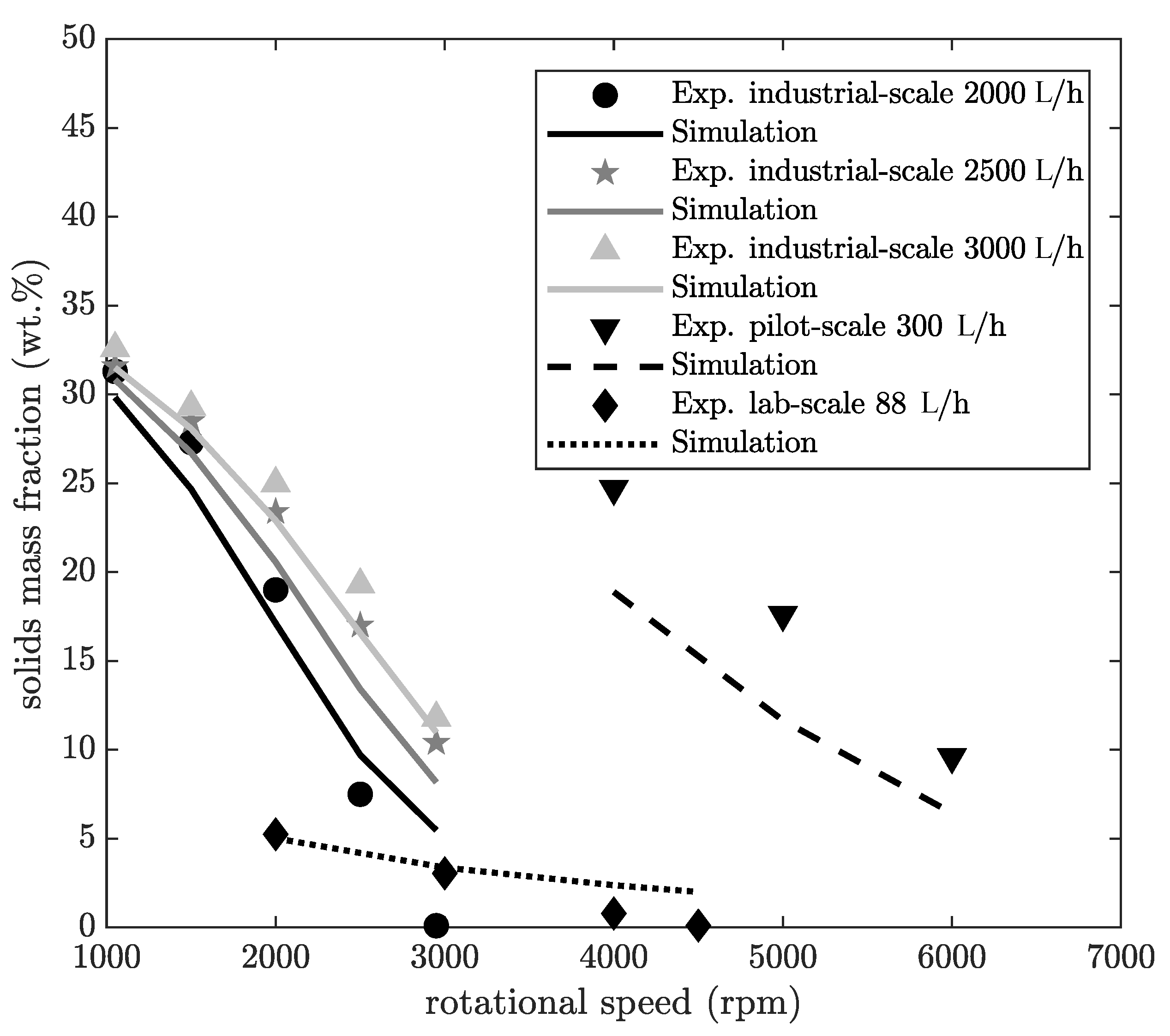
Figure 7 shows the solids mass fraction of the centrate corresponding to data from
Figure 6.
The solids mass fraction of the centrate decreases with increasing rotational speed. In general, the simulation results here also show a good agreement with experimental data. The simulation results of the pilot-scale machine are smaller than the experimental results. A possible reason for this discrepancy might be that the machine was almost fully loaded by measuring the solids content with this parameter combination during the test series. This may have resulted in a partial resuspension of already separated particles, as Stahl and Langeloh [
28] have previously shown. This effect is currently not considered in the simulation and possibly causes this difference.
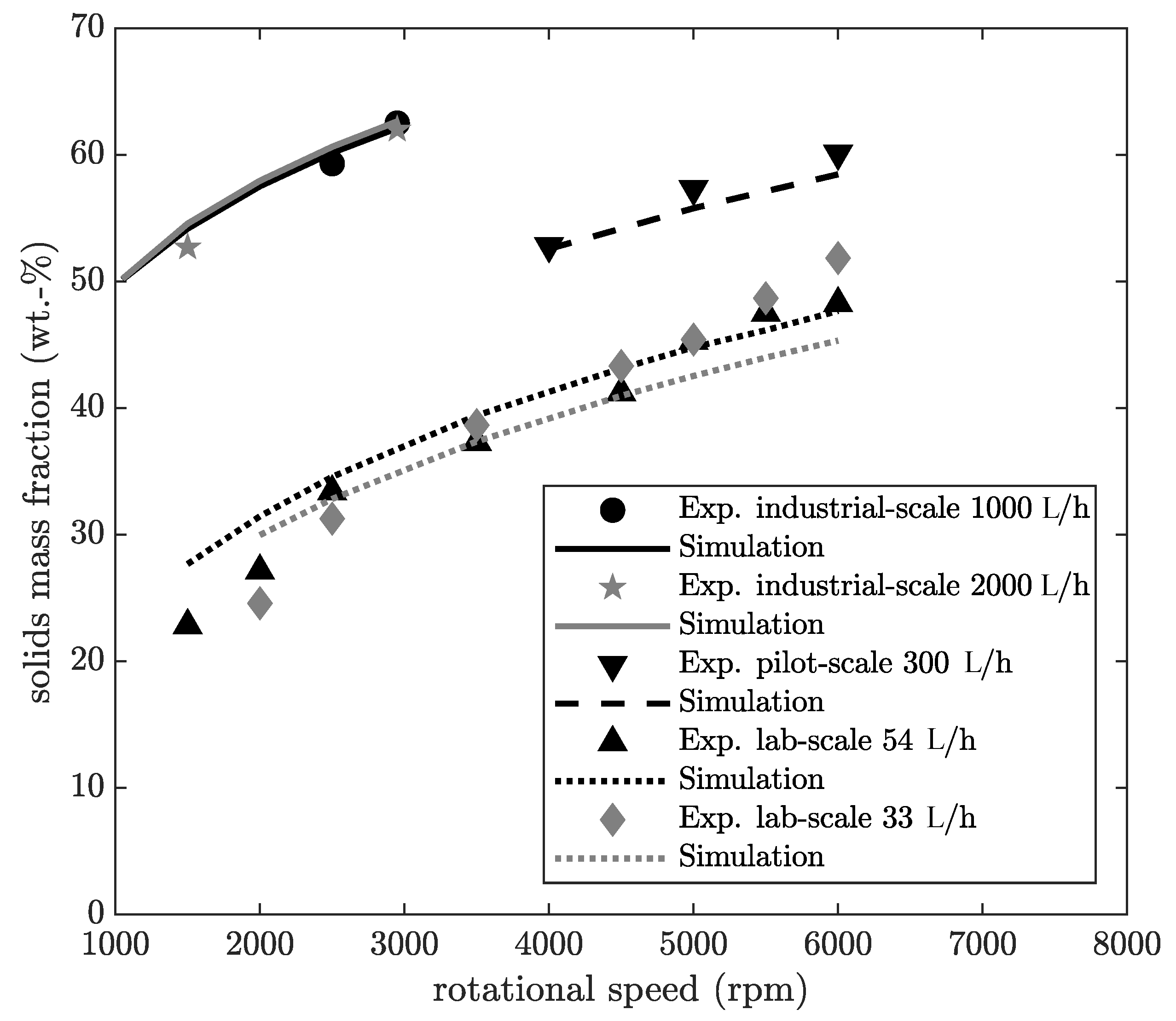
In analogy to the two previous figures, simulations are compared with experimental data for the product CC2. In
Figure 8, the solids mass fraction of the cake is plotted for material CC2 for different scales.
Similar dependencies of the solids mass fraction on the rotational speed are observed, as shown in
Figure 6. The simulation results show a relative deviation of less than 10
compared to the experimental data, except for the lab-scale data at 33 Lh
−1 for 1500
, 2000
, and 6000
. However, the absolute deviation of these points is less than 5
. This is still within the experimental measurement tolerance. Furthermore, it should be underlined that all three centrifuges, representing different scales, can be simulated with appropriate accuracy only on the basis of the material characterisation described previously.
Figure 9 illustrates that the solids mass fraction of the centrate is dependent on the rotational speed in analogy to
Figure 7 and corresponding to data from
Figure 8.
As previously discussed, the solids content in the centrifuge decreases with increasing rotational speed for both experimental data and simulation. In principle, the results agree well with each other and the absolute deviation is less than 5 . Furthermore, the physical behaviour of the simulation is reasonable. This indicates that the simulation approach can be applied to further finely dispersed mineral products.
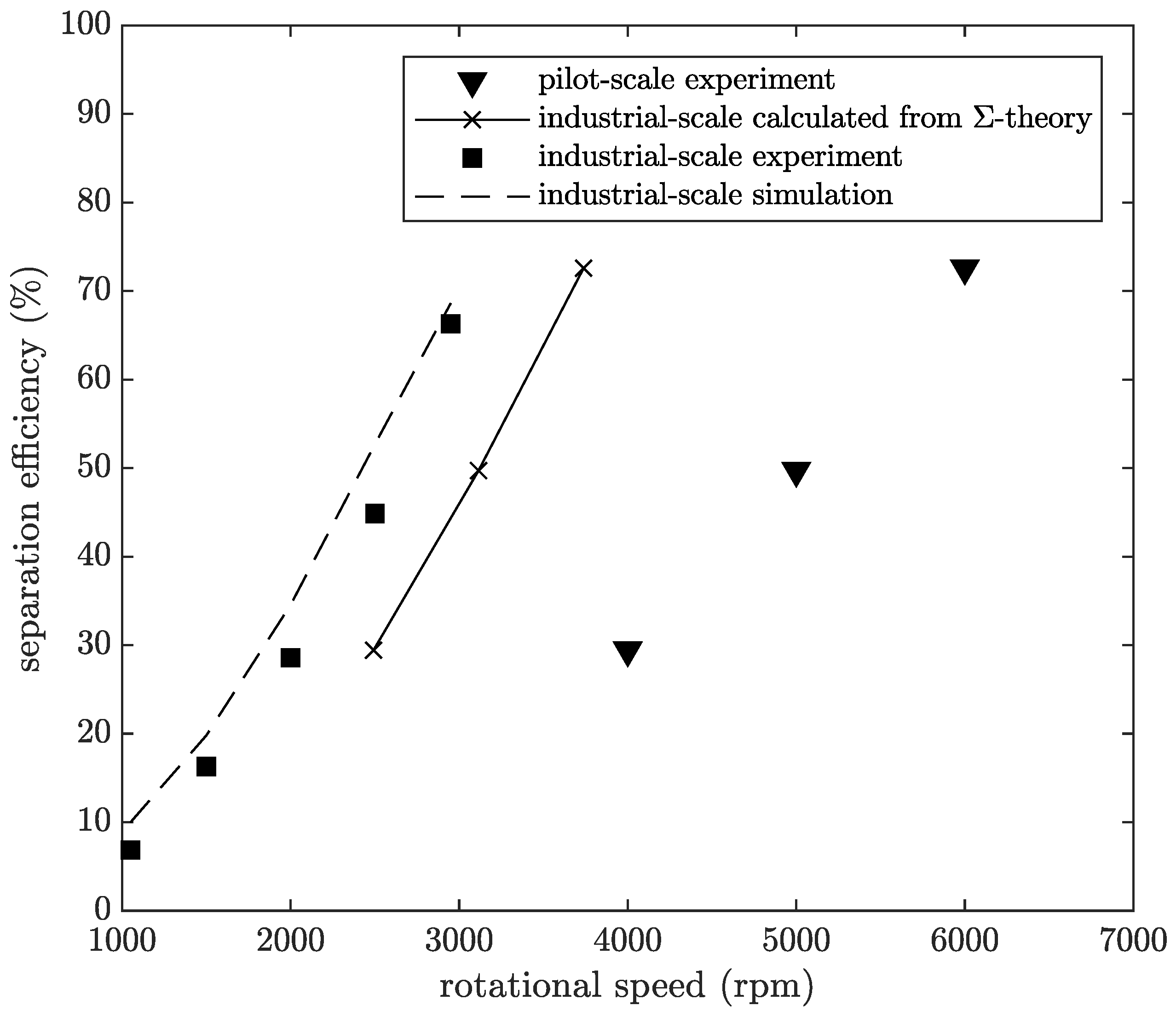
Figure 10 illustrates an exemplary scale-up with the
-theory and the numerical model. Therefore, separation efficiency is plotted over rotational speed. The separation efficiency is defined as the ratio of solids mass that has been removed from the feed stream in the centrifuge to the initial solids mass at the feed.
This example represents a typical scale-up problem. The dimensioning of an industrial-scale centrifuge is to be determined based on pilot-scale trials. Firstly, pilot-scale tests are done at a volumetric flow rate of 300 Lh
−1. The corresponding
-values are calculated from the geometry of the machine and the selected centrifugal acceleration according to Equation (
1). This allows the scaling criterion (ratio of throughput to
-value, see Equation (
5)) to be obtained for each experimentally measured parameter combination. The volumetric flow rate in this example is set to 3000 Lh
−1 for the industrial-scale decanter centrifuge. By considering the scaling criterion, the corresponding
-values of the industrial-scale decanter centrifuge can be calculated. It follows from these corresponding
-values that, on the one hand, the optimal geometry (characteristic radius and length) or, on the other hand, the optimal centrifugal acceleration and thus rotational speed can be obtained. In this case, the geometry of the industrial-scale machine is defined. Therefore, the resulting rotational speeds required for the industrial-scale apparatus are calculated. The result of the
-theory does not coincide with the experimental results of the industrial-scale decanter centrifuge.
theory leads to higher rotational speeds than observed in the experiment, which normally means higher energy consumption. The simulation method shows very good agreement with the experimental results, as already discussed previously in this section, and provides sufficient results for scale-up. As a consequence,
theory would need an empirical correction parameter to predict the correct machine behaviour in this case.
The material functions, which serve as input parameters for the simulation, are determined for a specific product with discontinuous analytical centrifuges on the laboratory scale. Only the transport efficiency, which describes the deviation from ideal transport behaviour, has to be determined by experiments on a laboratory decanter centrifuge. However, Menesklou et al. [
13] have shown that the influence of this variable has a minor influence on the result in investigated industrial-scale applications. This demonstrates that a scale-up of decanter centrifuges from a laboratory scale is possible using the presented numerical approach.
The scale-up of the solids mass fraction in the cake is not possible with the analytical methods presented. These approaches do not consider dewatering and transport models of the sediment within the centrifuge and therefore cannot provide a prediction of the solids mass fraction of the cake. Contrary to this, a model for the dewatering and transport of finely dispersed suspensions is implemented in the numerical approach. Hence, the material behaviour of the sediment within the complete centrifuge can be investigated. Furthermore, due to the discretisation of the apparatus, parameters such as particle size distribution, solids content, etc. can be determined locally and in a time-resolved manner in the centrifuge. These parameters are otherwise not measurable or only with high experimental effort in the apparatus. The analytical method only provides integral parameters of the decanter centrifuge.
To demonstrate this additional feature of the numerical approach, an example is discussed. The industrial-scale centrifuge with product CC1 at a feed rate of 3000 Lh
−1 is selected.
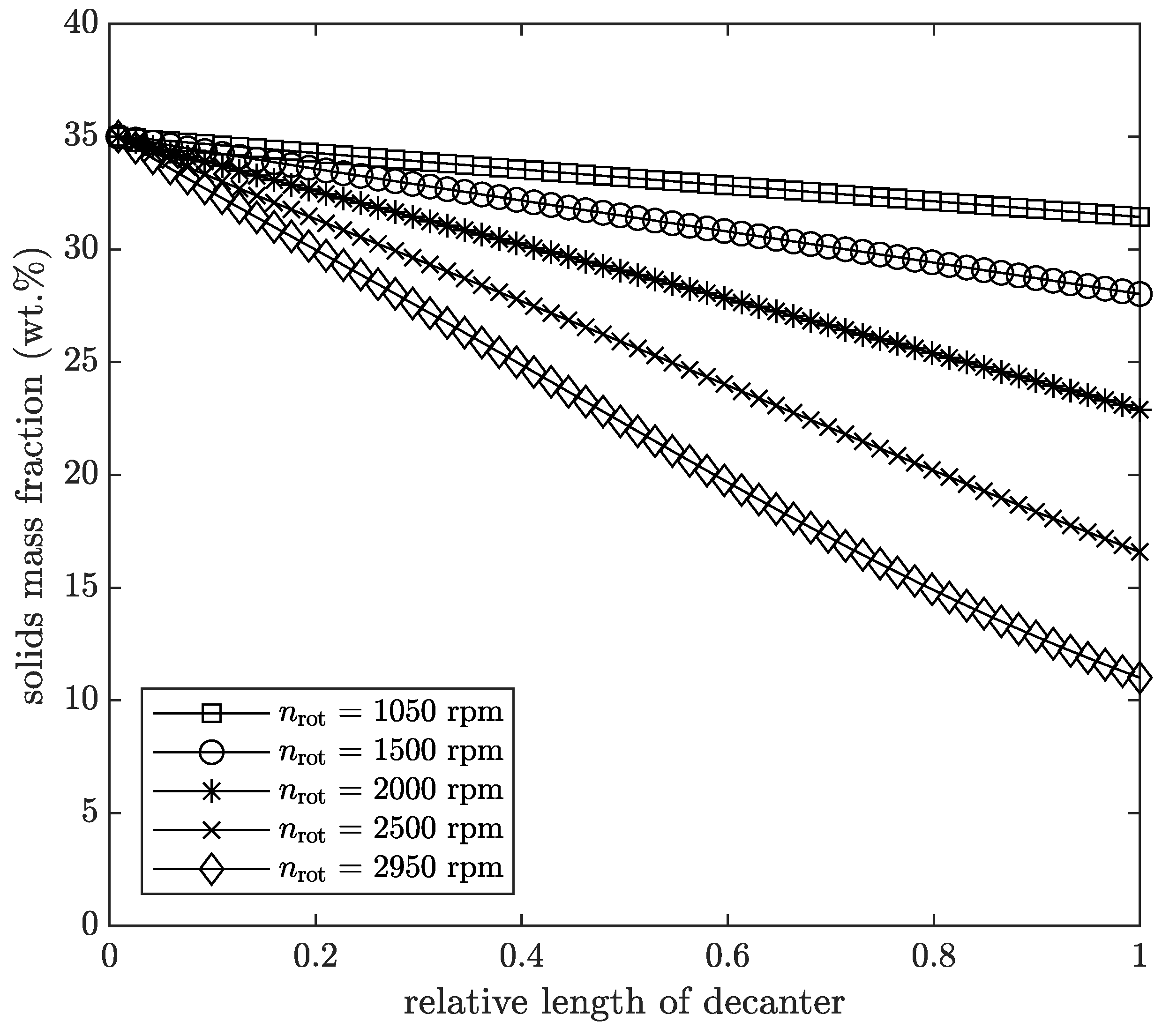
Figure 11 illustrates the solids mass fraction of the suspension along the helical screw path of the centrifuge. The relative length of the decanter
centrifuge describes the relative position in the cylindrical part of the decanter centrifuge. The feed enters the apparatus at the transition point between the conical and cylindrical parts, which corresponds to
. The centrate is drawn-off at
.
The solids mass fraction of the suspension decreases approximately linearly in the cylindrical part. This shows that the entire length of the centrifuge is used for separation and the separation is evenly distributed.
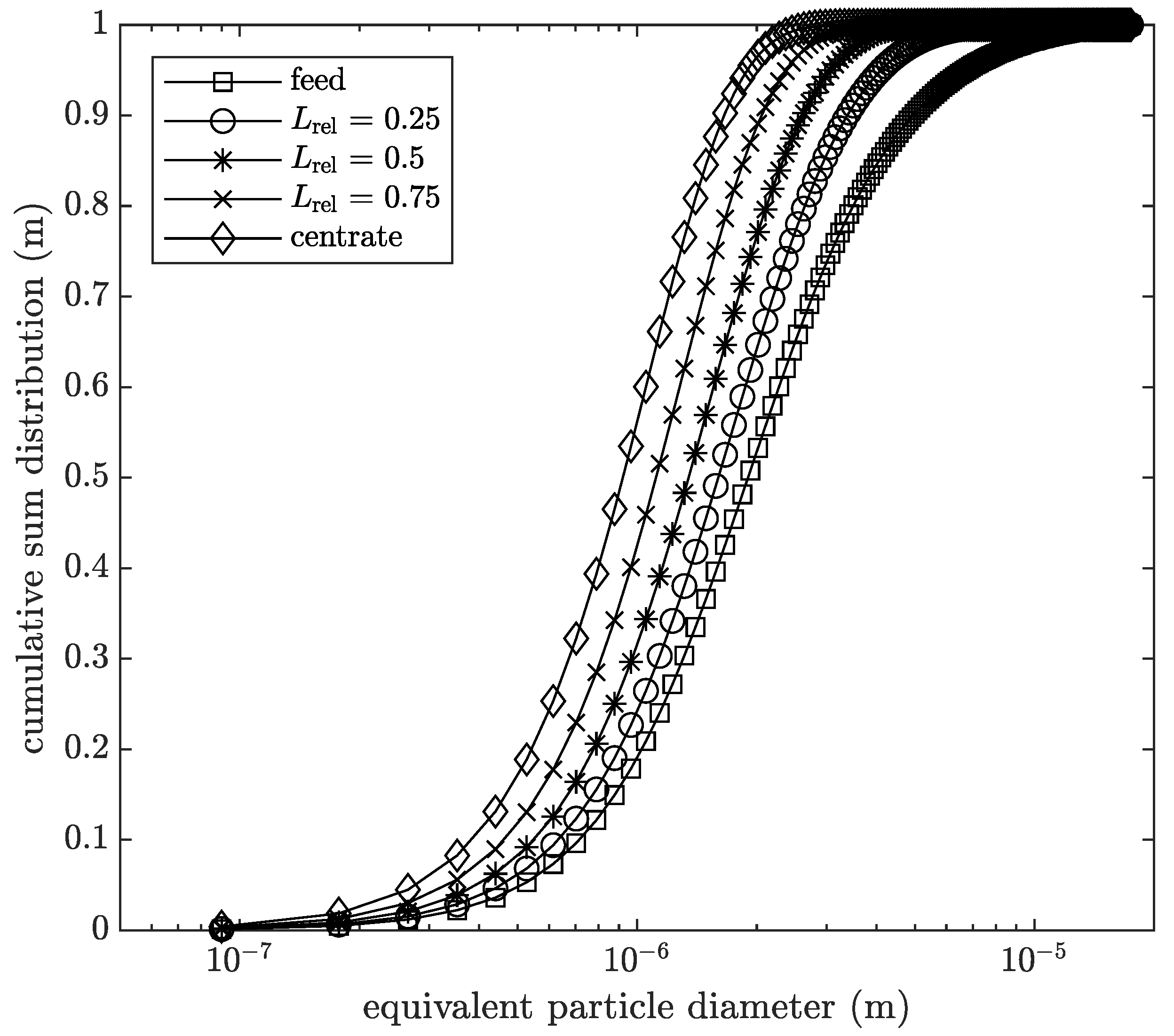
Figure 12 shows the particle size distributions of the feed and centrate and along the relative length of the centrifuge as cumulative sum distribution.
Generally, the particle size distribution changes from feed to centrate to smaller particle size classes. Furthermore, it should be mentioned that the slope of the distribution changes along the centrifuge length. On the first 25% of the length of the centrifuge, rather bigger particles are deposited. After that, smaller particle size classes are separated. This can be derived from the theory. Stokes’ settling velocity is proportional to the square of the particle diameter. It follows that if all particles have the same residence time in the apparatus, smaller particles are separated later. Especially for the classification, it is helpful to know where the separation of the individual size classes takes place. With an analytical scale-up approach, this cannot be determined at this level of detail.