1. Introduction
It is well known that experimental studies are of fundamental importance for a proper characterization of material properties, and that first-principles or ab initio theoretical calculations based on the density functional theory (DFT) are of paramount importance to predict and explain many material properties. The question is: What can we gain from combining these two types of studies?
To answer the above question, let us perform two thought experiments (Gedankenexperimente). In the first one, let us imagine that we perform experimental measurements in order to characterize the properties of an unknown material. For instance, let us assume that we carry out X-ray diffraction (XRD) or Raman scattering (RS) measurements on a material in order to study its structural or vibrational properties. Let us further assume that we perform those measurements at high pressure (HP) in order to characterize the effect of applied pressure on the change of the structural or vibrational properties of a material. In this context, we can wonder about the degree of confidence we can attribute to the obtained experimental results. In other words, can we trust the obtained experimental results? How can we be sure that the obtained experimental results are correct enough to be able to infer specific physical-chemical properties of the studied material?
To us, the answer to those questions is that results obtained only on the basis of experimental measurements with a single experimental technique can hardly have a high degree of confidence. In this regard, good experimentalists may argue that their results obtained using a single experimental technique are truly confident because of their expertise in the experimental technique and/or with the studied material (argument from authority). For instance, single-crystal HP-XRD is a very powerful technique for studying the behaviour of the crystalline structure of a single-phase unknown material at HP; however, it is difficult to have single crystals once the material has undergone a pressure-induced phase transition (PT). On the other hand, less experienced experimental researchers might even argue that the results are confident because of the nice comparison of the results they obtained for the unknown material with those previously obtained in related materials (argument from analogy). Certainly, we can agree that the two mentioned arguments increase the degree of confidence in the obtained experimental results for the unknown material. However, in any case, the degree of confidence in the obtained experimental results could not be very high when using a single experimental technique because of the limitations of the experimental technique itself.
The degree of confidence in the obtained experimental results for materials characterization can increase considerably if two experimental techniques are used to describe a single phenomenon. For instance, if HP-XRD and HP-RS measurements on a material are combined and their results are explained on a common basis, so that both experimental techniques give support to each other. We will agree that the combination of two experimental techniques is always better than one single experimental technique. Unfortunately, it is still difficult for the degree of confidence in those combined results to achieve the highest standards. The reason for this is that the limitations of the two experimental techniques prevents us from obtainin (in most cases) very accurate results, so as to provide an explanation of many material properties. For instance, many HP-XRD data are not good enough to perform Rietveld refinement to obtain accurate atomic positions and, therefore, interatomic distances or HP-RS data provide information on too many types of Raman-active modes to distinguish the different symmetries.
Let us make now a second Gedankenexperiment. Let us imagine that we perform theoretical calculations in order to predict the properties of an unknown material. For instance, let us assume that we predict the properties of an unknown material by carrying out state-of-the-art ab initio simulations based on DFT; i.e., based on Quantum Mechanics applied to condensed matter. Let us further assume that we perform those simulations at different volumes or pressures in order to characterize the effect of applied pressure on the change of the structural or vibrational properties of a material. In this context, we can again wonder about the degree of confidence we can attribute to the theoretical results. In other words, can we trust the simulated results? How can we be sure that the obtained simulated results are correct enough in order to be able to infer specific physical-chemical properties of that material?
To us, the answer to those questions is similar to that to the previous ones, i.e., results obtained only on the basis of a single theoretical simulation can hardly have a high degree of confidence. Once again, good theoreticians may argue that their results obtained from a single simulation are truly confident because of their expertise in the simulation technique and/or with the studied material. In contrast, less experienced theoreticians might argue that their results are confident because of favourable comparison of the results obtained for the unknown material with those previously obtained in related materials. Certainly, we agree that the above two considerations increase the degree of confidence in the obtained theoretical results for the unknown material. However, in any case, the degree of confidence in the obtained results could not be very high with a single simulation because of the limitations of the theoretical techniques themselves, which include several approximations for which we cannot know a priori whether they can be appropriately applied to the properties of the studied materials. In this context, we cannot forget that science laws are always based on nature, so simulations must always be validated with experimental results for them to be really trustworthy.
At this point, we can agree that the degree of confidence in simulated results for an unknown material can considerably increase if two or more different simulation techniques are used to characterize a single property. For instance, if DFT simulations on a material are performed with several functionals to describe the unknown exchange and correlation potential. In such a case, the combination of the different simulations can allow us to infer the common trends of the material; however, certain trends will be different for the different functionals, so there will be a high degree of uncertainty in certain material properties. In this context, we will agree that the combination of two or more simulation techniques is always better than one single simulation technique; however, it is difficult for the degree of confidence in those theoretical results to achieve the highest standards unless they are compared to experimental results.
The above limitation of theoretical techniques is a real pity, because theoretical simulations based on quantum mechanics can provide a large amount of information on the properties of the materials that can go beyond even the limits imposed by many experimental techniques. Moreover, thanks to quantum mechanics, we know that most material properties depend on the electron and phonon spectra of the material for given conditions of temperature and pressure. Those spectra can be obtained from the electronic charge density of the material under study, which is provided by the electronic wavefunction of the material once the Hamiltonian of the system under study is solved for a given chemical composition, spatial atomic disposition, and contour conditions. Therefore, in essence, all the information on the material properties is condensed in the electronic wavefunction of the system under study. Unfortunately, at present, the electronic wavefunction is not well known for most materials, and it is only known with a certain approximation. In conclusion, most simulated material properties can only be trusted upon comparison with experimental results due to our limited or incomplete knowledge of the electronic wavefunction of the material.
These two Gedankenexperimente lead us to a clear conclusion: experimental techniques are essential to characterize material properties, but have severe limitations that prevent us from obtaining all the material properties. In fact, one single experimental technique provides information only on a certain material property, thus avoiding obtaining an overall picture of the material properties. The characterization of material properties with a high degree of confidence would require the combined use of a lot of experimental techniques (to get a consistent picture of the material properties) that are not usually available to most experimental researchers or are not appropriate for all materials in all conditions of pressure and temperature. On the other hand, all the information of material properties is contained in the electronic wavefunction of the system, so simulations that allow us to obtain the electronic wavefunction can predict all material properties. Unfortunately, the electronic wavefunction is not well known at present, so we can only trust the predicted material properties of simulations provided that they are compared with experimental results that allow to validate the approximations used in the simulations for a given material under certain conditions of pressure and temperature.
On the basis of the above conclusion, we can address the following question: can we offer results on material properties with a high degree of confidence with a limited amount of experimental and/or theoretical resources? The answer is: yes, we can. All we have to do is combine the results of a few experimental techniques and a few theoretical simulations and explain both experimental and theoretical results on a common basis in order to get a consistent picture of the material properties.
This is the scientific philosophy that experimental and theoretical research groups in Spain have pursued by establishing the MALTA-Consolider Team, a synergetic collaboration of experimental and theoretical researchers in the HP field for over 20 years. The MALTA-Consolider Team aims to provide joint experimental and theoretical studies of material properties with special emphasis on the study of the effect of pressure on changes in structural, vibrational, electrical, and optical properties. This procedure has led to a profound understanding of the effect of pressure on chemical bonds. For simplicity, we will show here the procedure we follow in our studies by considering only a couple (the most basic) of experimental techniques. Some general details of the experimental and theoretical calculations are given in a separate section after commenting on the methodology.
2. Methodology
Usually, we proceed in the following way:
Experimental results of two experimental techniques, for instance, HP-XRD and HP-RS measurements, are obtained for a given material, thus providing a certain amount of information on the structural and vibrational properties of the material.
Theoretical results from ab initio simulations of the structural and vibrational properties of the given material, using several exchange and correlation functionals, are obtained.
A comparison of experimental and theoretical results is performed, which allows us to perform a double check of both experimental and theoretical results and check the accuracy of both our measurements and our calculations. In this regard, a good comparison of experimental and theoretical structural properties is mandatory before proceeding with the characterization of vibrational properties and other properties not accessed by experiments.
The double check proceeds as follows: on the one hand, the comparison of theoretical and experimental results on structural and vibrational properties allows us to determine which theoretical approximation better describes, in general, the experimental results. On the other hand, the theoretical results allow us to determine the limit of validity of our experimental results. In other words, accurate theoretical structural and vibrational data must be similar to experimental results obtained at room pressure (RP)—usually reported by many experimental researchers—and provide a good description of the compression of the structure and the phonon shifts in the low-pressure (LP) range (within the limit of hydrostaticity of the pressure-transmitting medium in the experiments). This allows us to check the exchange and correlation functional that best describes the system under study.
Once the exchange and correlation functional is validated at the LP range, we can reasonably trust the theoretical simulations in a larger pressure range than that allowed by our experiments. This allows us to: (i) check the limit of validity of our experimental results at HP (determine the limit of hydrostaticity of the pressure-transmitting medium) and (ii) get materials information that is beyond the limit of accuracy or capability of the experimental techniques used. In this way, a joint experimental and theoretical study can provide highly confident results with a limited amount of experimental and theoretical resources.
Unfortunately, the above strategy has several drawbacks. The first drawback is that the comparison of two or more experimental techniques with ab initio calculations and the deep understanding of the physical-chemical properties of the material under compression obtained from that comparison result in a large quantity of information, which can lead to relatively long papers if a large part of the obtained information needs to be shown. In some cases, for the sake of simplicity, many papers contain a relatively large section of additional or supplementary information. The second drawback is that, since many research groups do not follow this strategy, we commonly find that the results already published by many experimental and theoretical researchers are in disagreement with our results, likely due to the lack of sufficient information in the already-published works. In this regard, we have the obligation (for scientific integrity) to comment on these facts in our papers in order to help reach a better consensus on the properties of a given material. The comment on previous results again leads to papers of increased length.
2.1. General Details of Experiments and Calculations Performed at HP
From an experimental point of view, quality of samples is checked prior to any HP measurement. Particular attention is paid to stoichiometry, impurities, crystalline structure and the presence of more than a single phase. For HP-XRD and HP-RS measurements, the sample is loaded inside a cavity at a diamond anvil cell (DAC) together with a pressure-transmitting medium (usually a liquid or a liquified gas) and a small amount of a pressure calibrant. Typically, the pressure inside the cavity is obtained by the equation of state of reference materials, like gold or copper, or by the luminescence of ruby chips near the studied sample.
Angle-dispersive powder HP-XRD measurements are usually conducted at synchrotron sources. Integrated 2D XRD pattern profiles as a function of 2θ are analysed to extract information on the structural parameters of the sample either by Rietveld refinement (for good XRD data) or by Le Bail fitting (for not so good XRD data). On the other hand, HP-RS measurements are usually carried out with a dedicated spectrometer usually equipped with a thermoelectrically cooled multichannel charge couple device (CCD) detector. Most RS measurements are performed using the 632.8 nm line of a He:Ne laser or the 532.0 nm line of a solid-state laser. Special attention must be paid to the experimental measurements to avoid the undesired laser heating effects in samples and the sample bridging between the diamonds.
From the theoretical perspective, ab initio total-energy calculations within DFT are performed with different computer codes. The plane wave basis is extended to a high cutoff, taking into account the atomic pseudopotenctial used in the study. The exchange–correlation energy is taken in the generalized gradient approximation (GGA). To ensure a high convergence of 1–2 meV per formula-unit in the total energy and an accurate computation of the forces on the atoms, the integrations over the Brillouin zone (BZ) are performed using dense meshes of special k-points. At selected volumes, the structures are fully relaxed to the optimized configurations through the calculation of the forces on atoms and the stress tensor. In the optimized configurations, the forces on the atoms must be less than 0.002 eV·Å−1 and the deviations of the stress tensor from a diagonal hydrostatic form smaller than 1 kbar (0.1 GPa). On the other hand, lattice-dynamic calculations of the phonon modes are usually carried out at the zone centre (Γ point) of the BZ with the direct force-constant approach (or the supercell method). These calculations provide not only the frequency of the normal modes, but also their symmetry and their polarization vectors. This allows us to identify the irreducible representations and the character of the phonon modes at the Γ-point.
2.2. Examples of Combined Experimental and Theoretical Studies
As already mentioned, our research groups within the MALTA-Consolider Team have used and improved this methodology over the last 20 years. In the following, we will give some examples of the use of the proposed methodology in different areas, some of them being hot topic areas, such as phase change memories, thermoelectric and topological materials, and some being current topic areas, such as metavalent bonding or phase transitions of order higher than 2.
2.2.1. Rare-Earth Sesquioxides
One of the most recent examples of the use of our methodology is the recent characterization of Tb
2O
3, one of the more tough-to-grow rare-earth sesquioxides (RE
2O
3) [
1,
2]. It is well known that RE
2O
3 compounds may exhibit different polymorphic modifications depending on the RE ionic radius and temperature. The most common ones are the cubic (C-type, space group (s.g.) Ia-3, No. 206, Z = 16), the monoclinic (B-type, s.g. C2/m, No. 12, Z = 6), and the trigonal (A-type, P-3m1, No. 164, Z = 1) phases. Tb
2O
3 crystallizes into the C-type or bixbyite structure, which is usually a stable phase at room temperature for the heavier lanthanides and also in related sesquioxides, such as Mn
2O
3, In
2O
3, and Tl
2O
3. However, until recently, Tb
2O
3 had not been fully characterized, because of the great difficulty of growing this material, due to the coexistence of Tb
3+ and Tb
4+ states, leading to different TbO
x compounds with 1.5 < x < 2.
Since the structural properties of C-type Tb
2O
3 at RP had already been reported [
3], we carried out, in a first work, the characterization of vibrational properties of this compound at RP and at different temperatures [
1]. A good comparison of experimental and theoretical results on structural properties was provided, and a subsequent study of vibrational properties was found to be in good agreement with those provided in other C-type RE
2O
3 compounds [
4]. All Raman-active modes were predicted, up to 16 Raman-active modes were experimentally measured, and their symmetry assignments were tentatively attributed. Our work suggested performing a revision on some reported results on Eu
2O
3 and Gd
2O
3 due to the existence of some phonon anomalies that could not be justified from their structural data.
In the second work, we performed a joint experimental and theoretical study of structural and vibrational properties of Tb
2O
3 at HP up to 25 GPa [
2]. On the one hand, we found that the sequence of pressure-induced PTs in Tb
2O
3, C-B-A on upstroke and A-B on downstroke, was in agreement with related RE
2O
3 compounds. After validation of theoretical simulations with experimental data—a procedure that has not been usual in previous studies of these sesquioxides—a complete theoretical characterization of the structural properties of C, B, and A phases of Tb
2O
3 was provided. The comparison of experimental and theoretical results on mechanical properties, not only for Tb
2O
3 but also for many RE
2O
3 compounds, led to a discussion regarding the tendency of the bulk moduli of the three different phases in these compounds as a function of the ionic radii. This discussion resulted in the proposal of a revision of the experimental structural data already published for several RE
2O
3 compounds that do not show agreement with our theoretical data. In summary, that work devoted to Tb
2O
3 served to construct a reference framework to understand the behaviour of the structural and vibrational properties at HP of RE
2O
3 and isostructural compounds that we hope will stimulate further work on different sesquioxides to better constrain their bulk moduli.
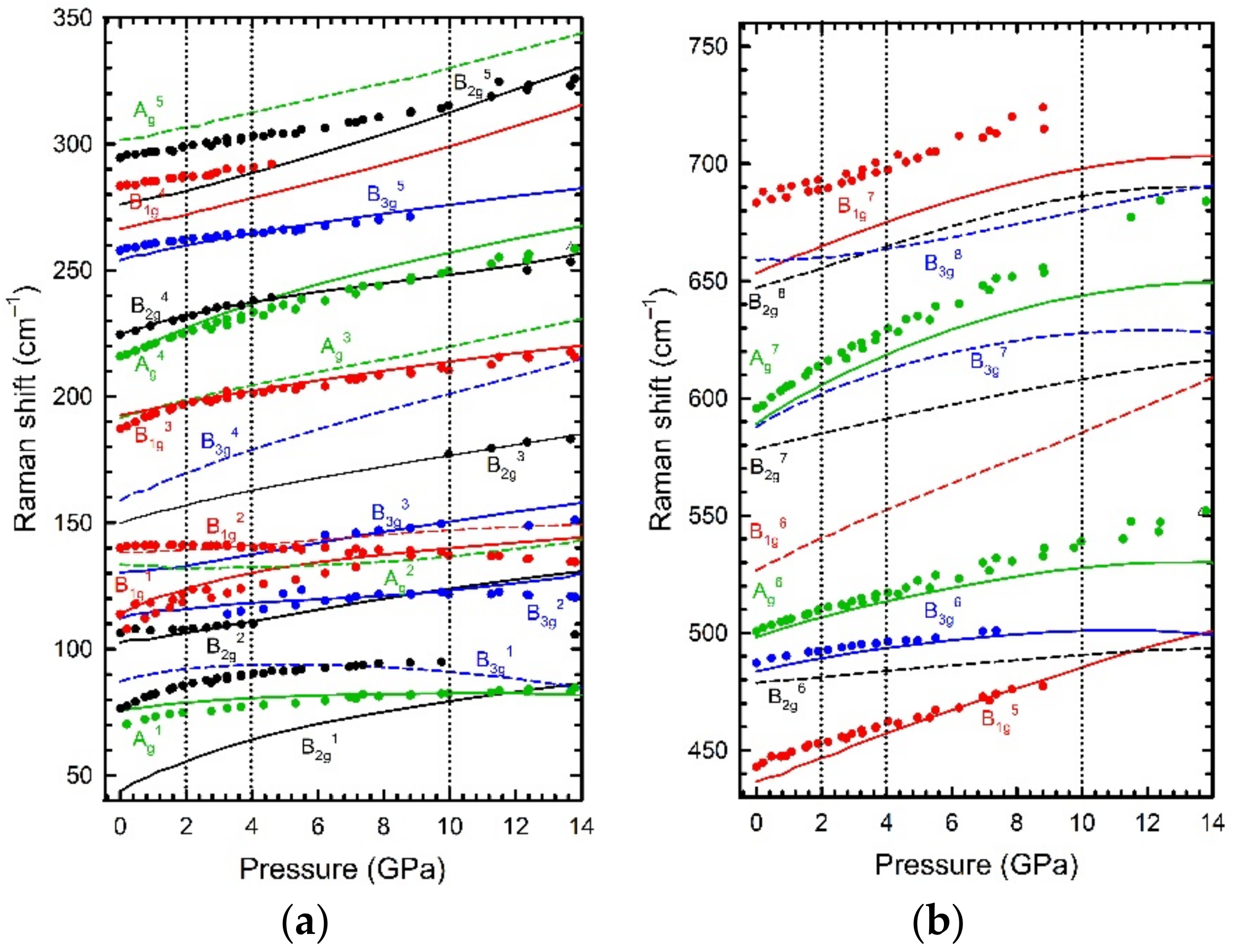
On the other hand, this second work provided a detailed study of the lattice dynamics of the three phases found in Tb
2O
3 (see
Figure 1). In particular, the Raman spectrum of B-type Tb
2O
3 was reported for the first time at RP to help to identify this metastable phase under room conditions not only from its characteristic XRD pattern, but also from its (easier to take) Raman spectrum. The pressure coefficients of the three phases were reported and compared for the first time with those of isostructural RE
2O
3 in order to obtain the systematics in this subject. We found that modes below (above) ~200 cm
−1 correspond mainly to RE (O) vibrations. Additionally, the four Raman-active modes of the A-type phase were thoroughly discussed. It was found that there was not a linear relation between the high-frequency modes of this phase and the structural
c/a ratio, as previously suggested [
5].
2.2.2. Ordered-Vacancy Compounds
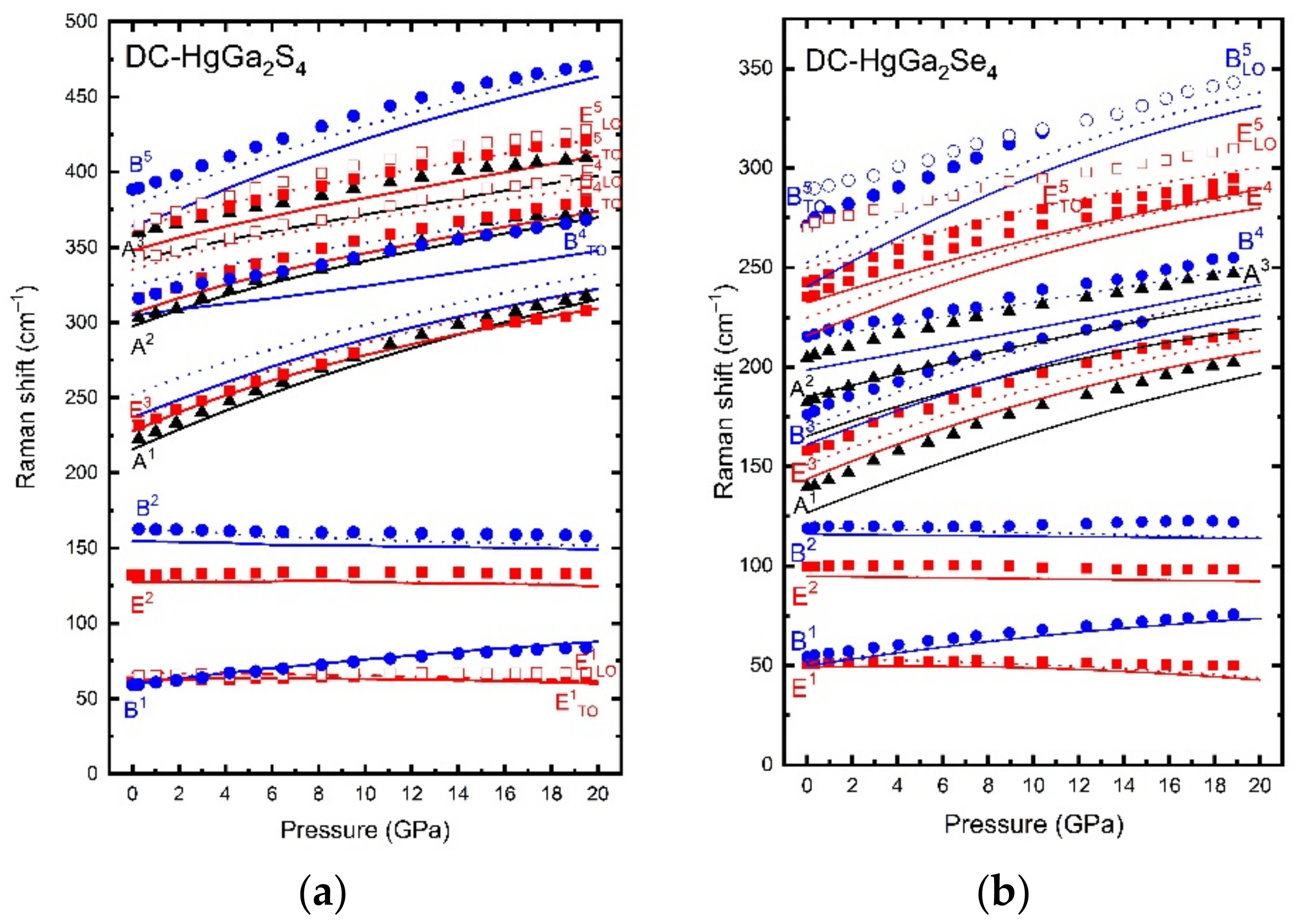
Adamantine ordered-vacancy compounds (OVCs) are a class of tetrahedrally coordinated semiconductors that derive from the cubic diamond and zincblende (s.g. F43m, No. 216, Z = 4) structures. They include binary A2X3 compounds, like sesquisulfides and sesquiselenides (Ga2S3, Ga2Se3), and ternary AB2X4 compounds, like sulfides, selenides, and tellurides (CdAl2S4, HgGa2S4, ZnGa2Se4, CdGa2Se4, HgGa2Se4, CdIn2Se4). The common characteristic of adamantine OVCs is that they have a different number of anions and cations in the unit cell, so there is a cation site occupied by a vacancy in an ordered and stoichiometric fashion, i.e., each anion is surrounded by three cations and a vacancy. Therefore, there is a lone electron pair (LEP) of the anion pointing to the vacancy. Binary adamantine OVCs, like Ga2S3 and Ga2Se3, usually crystallize in a monoclinic structure (s.g. Cc, No. 9, Z=4), while ternary adamantine OVCs, like HgGa2S4 and HgGa2Se4, usually crystallize in one of three tetragonal structures. They are: (i) the ordered pseudocubic (PC) structure (s.g. P42m, No. 111, Z = 1), (ii) the ordered defect stannite (DS) structure, also known as defect famatinite structure (s.g. I42m, No. 121, Z = 2), and (iii) the ordered defect chalcopyrite (DC) or thiogallate structure (s.g. I4, No. 82, Z = 2).
Despite their different structures, adamantine OVCs have in common their relation to the zincblende or sphalerite structure and presence of ordered cation vacancies in their crystalline structures. Please note that when cations and vacancies get fully mixed, these materials tend to crystallize in the zincblende structure. The different structural possibilities of ternary OVCs upon cation disorder have already been discussed [
6].
We have published some joint experimental and theoretical studies on structural, vibrational, and optical properties of adamantine OVCs under compression [
7,
8,
9,
10,
11,
12,
13,
14]. In general, there is a good agreement between the experimental and theoretical results on structural, vibrational, and optical properties as far as pressure-induced disorder is not crucial in the LP range. The excellent agreement of experimental and theoretical results allowed us to discuss the lattice dynamical properties of these semiconductors [
8,
9,
10,
12,
13] in analogy with zincblende-type semiconductors (see
Figure 2). The lack of agreement between the experimental and theoretical pressure dependence of the direct bandgap energy above certain pressure has allowed us to discuss the ranges of the pressure-induced disorder process that OVCs undergo prior to their transformation to the disorder rocksalt structure at HP (in analogy with zincblende-type semiconductors). However, the most striking results were the strong pressure dependence of the topmost valence band and the strong nonlinear pressure dependence of the direct bandgap [
7,
11,
13,
14], which is caused by the anticrossing between the two smallest conduction bands at HP at the Γ point. The first effect is a consequence of the strong compression of the anion LEP, which mainly contributes to the topmost valence band. On the other hand, the second effect is caused by the completely different pressure coefficients of the two lowermost conduction bands caused by the preferential distribution of ordered vacancies in the crystalline structure. All the details of these effects were evidenced by the close comparison of experimental and theoretical results and the deep understanding allowed by the knowledge of the contribution of each atom to the total wavefunction.
2.2.3. Topological Insulators
Topological insulators (TIs) are recently discovered new states of quantum matter that have attracted a great deal attention in condensed-matter physics [
15]. Tis in two or three dimensions have insulating energy gaps in the bulk and gapless edge or surface states on the sample boundary that are protected by time-reversal symmetry. Therefore, they allow electrical conductivity at edges or surfaces, but not in the bulk. These properties make them useful for applications in spintronics and quantum computation. TIs have been theoretically predicted and experimentally observed in a variety of compounds. In particular, layered A
2X
3 compounds (Bi
2Se
3, Bi
2Te
3, and Sb
2Te
3) with tetradymite [s.g. R-3m, No. 166, Z = 3] structure, which are highly efficient thermoelectric materials, have been demonstrated to behave as 3D TIs [
16,
17].
We studied the structural, vibrational, and even transport properties of the Bi
2Se
3 family of TIs at HP in several works combining experiments and simulations [
18,
19,
20,
21,
22]. After checking the good agreement of experimental and theoretical structural data, we tried to analyse other properties, like vibrational properties. Thanks to the synergetic combination of lattice dynamics experiments and simulations, we showed evidence of the observation of pressure-induced electronic topological transitions (see
Figure 3) and tentatively identified the HP phases observed in this family of compounds.
2.2.4. Phase Transitions of Second and Higher Order
The family of group-15 (As,Sb,Bi) sesquioxides show several polymorphs at RP that can be split into three different subfamilies depending on space group symmetry in which they crystallize. Highly symmetric phases (cubic polymorphs) [
23,
24,
25,
26], intermediate symmetric phases (orthorhombic and tetragonal polymorphs) [
27,
28,
29], and low-symmetry phases (monoclinic polymorphs) [
30,
31,
32]. The rich polymorphism of this family is related to the structural distortion exerted by the stereoactive cationic lone electron pairs (LEPs). The most interesting subfamily, in terms of richness of unusual behaviour at HP, is that of intermediate symmetric structures, that are represented by the beta phases of Sb
2O
3 [
29] and Bi
2O
3 [
28] together with the metastable and hard to synthesize ε phase of Bi
2O
3 (isostructural with β-Sb
2O
3) [
27]. Here, we focus on the former two structures, due to the scarce reliable information about the latter. The structures of both β-Sb
2O
3 and β-Bi
2O
3 compounds are characterized by linear empty channels in the middle of the unit cell. The empty channels are formed because the cationic LEPs are oriented towards the centre of this void.
HP studies of β-Bi
2O
3 [
28] led to very interesting results. HP-XRD measurements revealed several interesting abnormalities. First, it was impossible to fit the experimental pressure–volume data with the typical equations of state (EoS) used for inorganic compounds. It only became possible when splitting the experimental data into two main ranges: from 0 to 2 GPa and from 2 to 15 GPa. Additionally, it is noteworthy to emphasize the clear change of tendency of the
c/
a ratio under compression, changing from a positive to a negative slope at 2 GPa. All these results led us to think that we were observing a 2nd-order PT, which means, a structural transition without discontinuity in the volume, but with a discontinuity in the volume compressibility. However, the poor quality of the XRD patterns due to the use of powder sample and maybe, the distortion produced in the lattice planes by the existence of the linear empty channels, avoided us to perform a full Rietveld refinement of HP-XRD data and confirm our assumptions. On the other hand, HP-RS measurements exhibited an irregular behaviour in some of the Raman-active modes. The most striking result can be observed around 465 cm
−1, where a mode with A
1 symmetry shows a soft tendency up to 2 GPa, and changes its slope to become positive above this critical pressure. The origin of this abnormal behaviour could not be understood without the help of ab initio calculations. The good agreement of the theoretical simulations with the P-V experimental EoS helped us to validate the goodness of our calculations, allowing us to analyse the compressibility of the structure based on these simulations.
It was found that some of the theoretical coordinates of the Bi and O1 atoms tended towards fixed coordinates at 2 GPa and remained constant up to 15 GPa. This behaviour of atomic coordinates affected the interatomic distances belonging to the BiO6 polyhedral unit. These interatomic distances, which were out of the reach of the analysis of our experimental HP-XRD patterns due to their strong sensitivity with coordinates uncertainty, could be estimated by these theoretical simulations. Thus, the origin of the changes observed experimentally in the compressibility of this structure at HP could be addressed by observing the behaviour of the atomic coordinates of the Bi and O sites, the symmetrisation of the Bi-O interatomic distances belonging to the same polyhedral unit and the drastic decrease of the eccentricity of this octahedron by theoretical simulations. All these fingerprints led us to perform a theoretical analysis on the mechanical and dynamical stability of the compound, which revealed that the original structure was no longer dynamically stable above 2 GPa. A soft phonon branch in the phonon dispersion curve was observed, thus clearly identifying the 2nd-order nature of the ferroelastic isostructural PT. A PT driven by an electronic charge redistribution in the BiO6 octahedral unit.
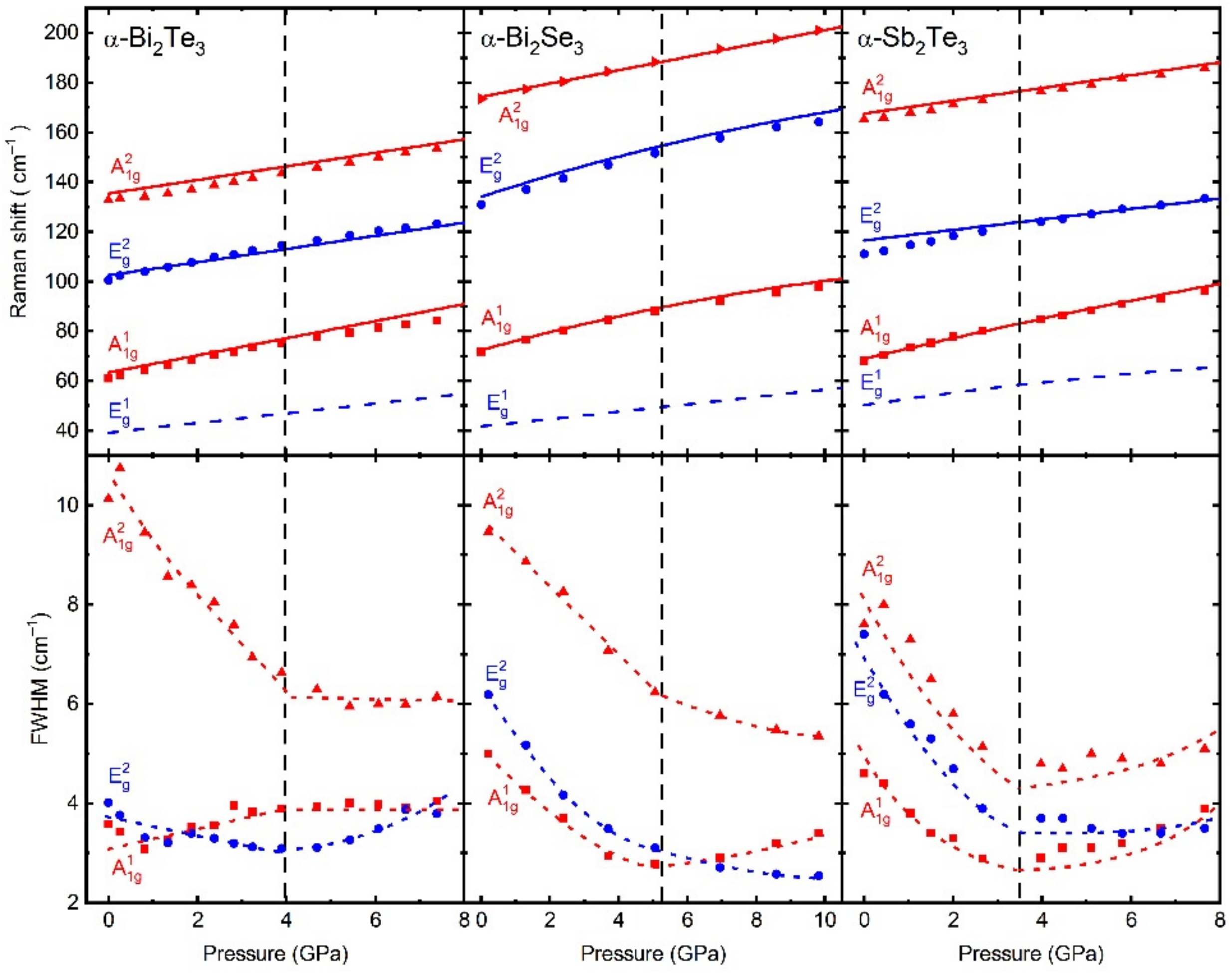
HP studies of β-Sb
2O
3 [
29] also led to very interesting results, since the strength (stereoactive interaction) of the cationic LEP is higher in this compound than in β-Bi
2O
3. As a result, the unit cell of the former contains a larger linear empty channel in the middle of the structure than the latter. With reference to β-Bi
2O
3, this channel in the crystalline structure is caused by the orientation of the cationic Sb LEPs towards the centre of the unit cell. HP-XRD measurements showed that the P-V curve and the pressure dependence of the lattice parameters exhibit a smooth and monotonous variation up to 15 GPa, where a 1st-order PT occurred. Up to 15 GPa, these results seemed to indicate the lack of PT, like those found in β-Bi
2O
3. However, HP-RS measurements again exhibited an unusual behaviour of some of the Raman-active modes, with changes at 2, 4, and 10 GPa (see
Figure 4). The most striking result was observed around 140 cm
−1, where the mode with B
1g symmetry exhibited a positive dependence of its frequency with compression up to 2 GPa, and a sudden softening above that pressure. In the search for an explanation to this behaviour, we performed ab initio theoretical calculations at HP and we could see how the real behaviour of the compressibility of the polyhedral units of this compound was hidden by the compressibility of its large structural empty channels, which dominates the bulk compression. The pressure dependence of the polyhedral unit revealed the existence of at least two ranges, up to 2 GPa and above 2 GPa, defined by the impossibility to fit the theoretically simulated volume to a typical EoS. Thanks to an analysis on the electronic density charge topology, we were able to identify the origin of this change under pressure, which was attributed to a change in the orientation of the LEPs under pressure. At ambient pressure, LEPs oriented in a determined
a–c crystallographic plane interact with the opposite (in terms of the structural empty channel) LEPs belonging to a different
a–c crystallographic plane. Above 2 GPa, these LEPs undergo a reorientation and start to interact with LEPs belonging to the same
a–
c crystallographic plane. As a result, the Sb coordination increases from 3 to 3 + 1. Noteworthy, simulations showed a saturation of the asymmetry of the LEP cloud at 4 GPa, i.e., the reaccommodation of the electronic clouds of the LEPs to cope with the volume compression ends at 4 GPa. At this pressure, the LEP cloud cannot be further distorted and it starts to seriously affect the interatomic distances in such a way that at 10 GPa, the analysis of the interatomic distances revealed an increase of the Sb coordination to a 3+1+1. To identify the nature of these subtle structural changes at 2, 4, and 10 GPa, we performed an analysis of the phonon dispersion curves at different pressures. They exhibited a lack of soft phonons, a mandatory condition to appeal for a 2nd-order isostructural PT. Thus, we concluded that the changes observed at those critical pressures belong to isostructural PTs of a degree higher than 2. In summary, we can conclude that the combination of the experimental techniques with theoretical simulations were crucial to identify subtle PTs of 2nd order or higher.
2.2.5. Metavalent Bonding
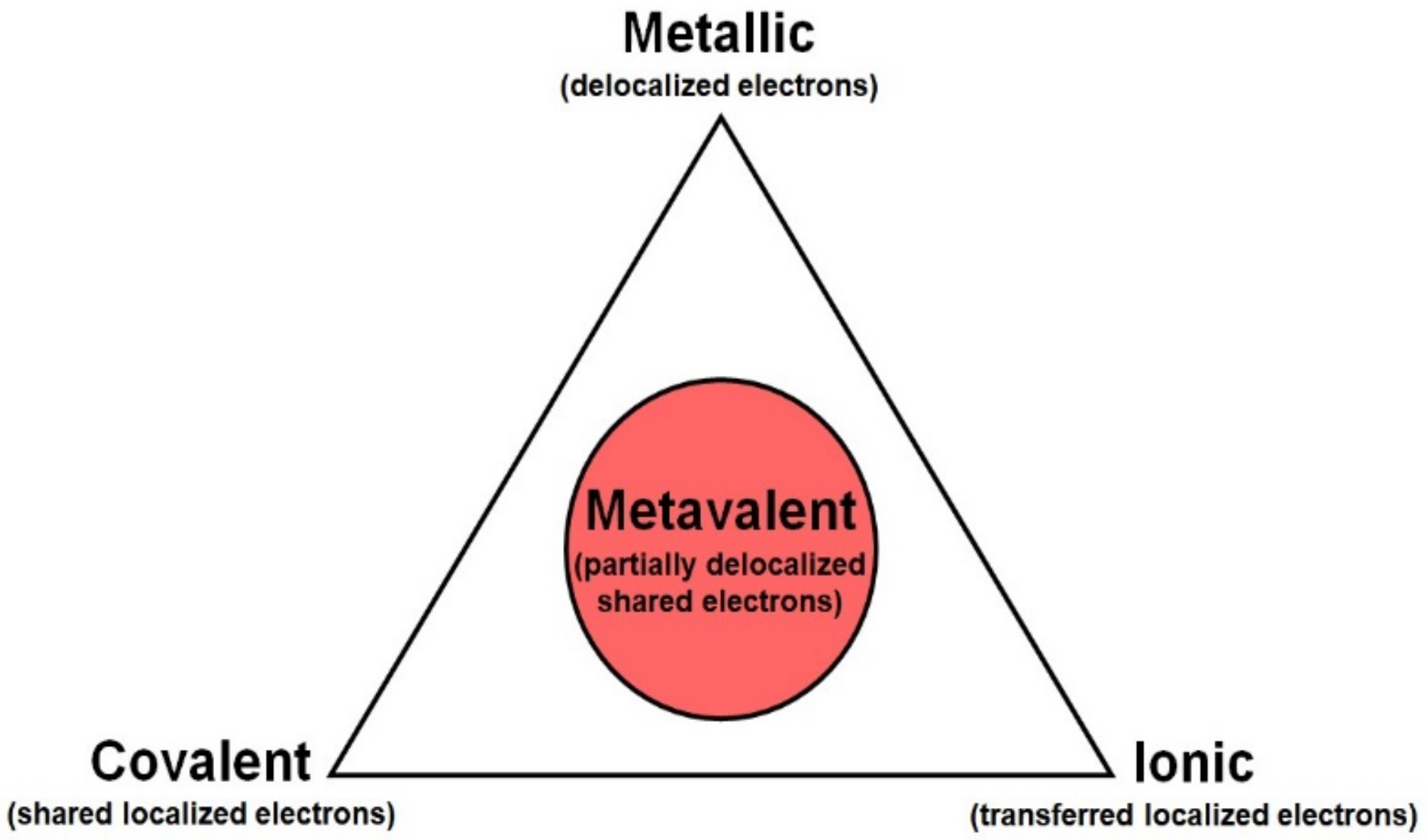
A new type of bonding, named “metavalent bonding” (MVB), was recently coined to explain the unusual properties of several families of AX (A = Ge,Sn,Pb; X = S,Se,Te), B
2X
3 (B = As,Sb,Bi; X = Se,Te), and AB
2X
4 (A = Ge,Sn,Pb; B = As,Sb,Bi; X = Se,Te) chalcogenides. These materials are of interest for phase change memories, topological insulators, and highly efficient thermolectric materials [
33,
34,
35,
36,
37]. Materials with MVB were termed as “incipient metals”, since some properties of these materials are between those of covalent materials and metals, but with a highly polarizable lattice (as in ionic bonding). Thus, MVB is considered to be a different type of bonding from conventional ionic, covalent, and metallic bondings (see
Figure 5). The unique properties of MVB are due to the partial delocalization of electrons, i.e., some electrons are shared between two atoms in a single conventional covalent or ionic bond, while some electrons are shared between different interatomic bonds (between more than two atoms). In this way, MVB is characterized by the sharing of fewer than two electrons per bond, as is usual in covalent and ionic bonds. This scenario leads to extraordinary properties for incipient metals, such as small bandgaps, leading to a moderately high electrical conductivity between 10
2–10
4 S·cm
−1; high dielectric constant, ε
∞; high Born effective charges, Z*, leading to a strong LO-TO splitting; and a high anharmonicity (characterized by high mode Grüneisen parameters, γ
i) that leads to the softening of transverse optical modes and an extraordinarily small lattice thermal conductivity [
38]. Therefore, “incipient metals” have an exciting property portfolio, which is different from conventional ionic, covalent, and metallic bonding systems, and which makes these materials interesting for highly efficient thermoelectric materials, phase change materials for digital memories, as well as for TIs with applications in spintronics and quantum computation.
Some of the above properties of incipient metals can be characterized by means of lattice dynamics experiments and simulations. In this way, we studied the structural, vibrational, and electronic properties of several compounds of these families under compression in a joint experimental and theoretical venture. In particular, we thoroughly studied the HP behaviour of SnSb
2Te
4 [
39], a van der Waals compound with tetradymite-like structure [s.g. R-3m, No. 166, Z = 3], which is a TI and shows MVB at RP, like their binary parents SnTe and Sb
2Te
3.
After proving that theoretical calculations nicely explain the pressure dependence of the structural parameters, we found a 2nd-order PT near 2 GPa and discussed the stability region of the R-3m structure in AB2X4 compounds. Additionally, we performed a complete lattice dynamics study that allowed us to identify most of the Raman-active modes of this kind of compound. Interestingly, we found a pressure-induced Fermi resonance effect above 3 GPa that is a consequence of the same effect in its binary parent SnTe (still not experimentally measured). Thanks to our confidence in theoretical simulations, we also characterized the pressure behaviour of SnSb2Te4 by means of the electron localization function (ELF), the non-covalent interaction index (NCI), and the electron density and its gradient. This characterization allowed us to distinguish the different types of bonding present in the material and to propose theoretical tools to distinguish MVB with respect to covalent, ionic, and metallic bondings. We hope these tools will guide researchers to identify this new type of bonding in future studies and help in the implementation of these interesting materials in many applications.
We also conducted a high-pressure joint experimental and theoretical work on As
2S
3, a mineral called orpiment [
40]. This material, which was known in ancient Egypt, undergoes a 2nd-order isostructural PT above 20 GPa. The PT goes from a covalent-type phase below 20 GPa to a phase with MVB above 20 GPa. Moreover, this compound undergoes a PT to a metallic phase above 40 GPa, thus completing the covalent–metavalent–metallic sequence of PTs expected at HP [
41]. In particular, we found that some cation–anion distances of the LP phase increase with pressure. In addition, cation–anion distances tend to equalize above 20 GPa in the HP phase to form a bunch of resonant bonds sharing similar electrical charges.
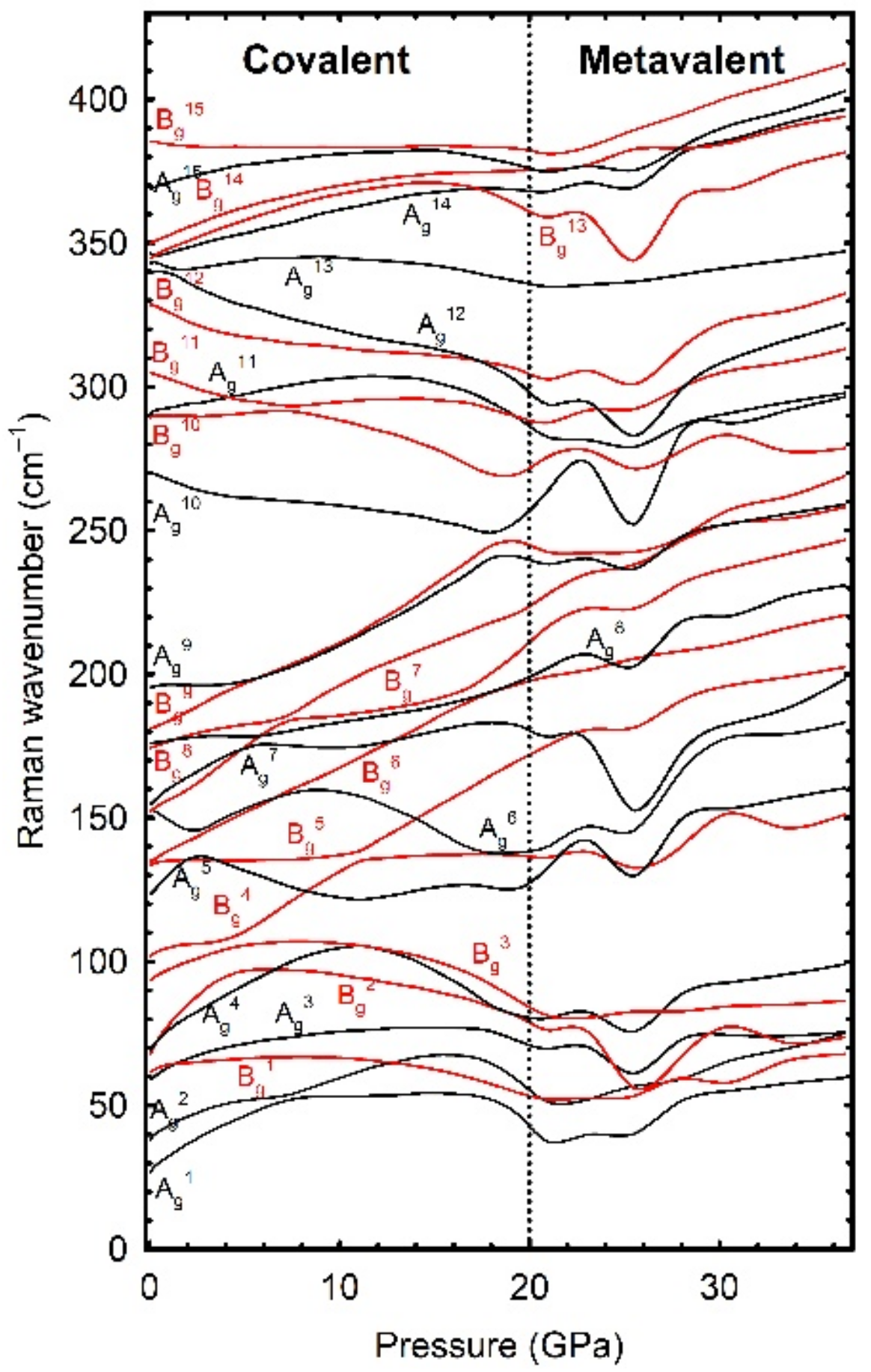
Regarding the vibrational properties, we found that high-frequency Raman-active modes in the covalent phase show negative pressure coefficients that correlate with the increase of some cation–anion distances. However, all Raman-active modes in the metavalent phase show a positive pressure coefficient (see
Figure 6), thus showing a normal behaviour of cation–anion distances and forces in that phase. Moreover, we showed that a pressure range featuring soft high-frequency modes is characteristic of the PT from the covalent to the metavalent regime. Since soft high-frequency phonons have been observed at LP in all group-15 chalcogenides that do not usually crystallize in the R-3m structure, such as As
2S
3, Sb
2S
3, Bi
2S
3, Sb
2Se
3, and As
2Te
3 [
42,
43,
44,
45], we proposed that all these sesquichalcogenides show a covalent behaviour at LP and undergo pressure-induced isostructural PTs to a metavalent phase prior to undergoing a pressure-induced PT to a metallic phase. Importantly, we can add that the appearance of soft high-frequency modes at HP must also occur with the AX (A = Ge,Sn,Pb; X = S,Se,Te) chalcogenides that show covalent bonding at RP, like GeS, GeSe, SnS and SnSe, as recently shown in SnSe [
46].
2.2.6. Anomalous Raman Modes in Tellurides
Tellurides are chalcogenide compounds that cover a vast number of compounds with many different compositions and with a great variety of applications. The comparison of experimental and theoretical lattice dynamics results in several tellurides studied at HP, like α-As
2Te
3 [
45], Sb
2Te
3 [
19], Bi
2Te
3 [
18], SnSb
2Te
4 [
39], and SnBi
2Te
4 [
47], has helped us to understand a typical problem found in Raman scattering studies of tellurides, including GaTe and GaGeTe, even under room conditions [
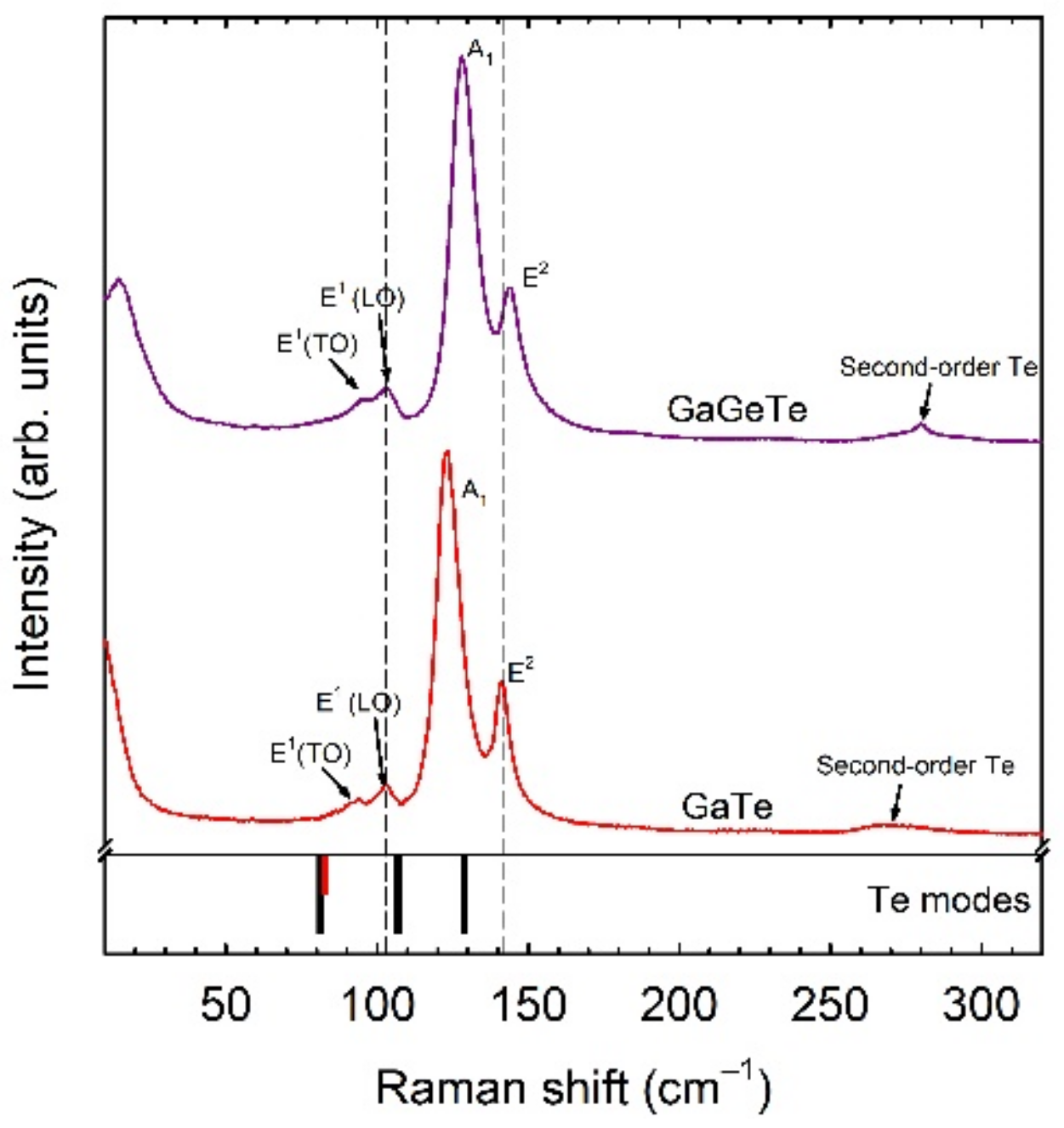
48]. Usually, tellurides are narrow-gap semiconductors or semimetals that are strongly sensitive to light, like selenides. Consequently, laser irradiation during routine Raman scattering studies can cause severe damage to these samples. In particular, laser burning can cause sample transformation or decomposition and Raman modes of trigonal Te can be observed together with those of the parent sample or even substituting them (see
Figure 7). In fact, regions with trigonal Te can be found in tellurides for other reasons, e.g., in as-grown or deteriorated samples. In many papers, where experimental data are not contrasted with theoretical data, these modes have been interpreted as coming from the sample itself (the same peaks attributed to several compounds with different compositions and stoichiometries) or have been attributed to several causes. In a recent work, we showed that several anomalous Raman modes in tellurides that are commonly observed under room conditions can be attributed to trigonal Te [
48]. This result can help researchers to better understand their samples for practical applications. In this way, we have shown that the comparison of experimental and theoretical approaches, together with the help of HP studies, is very beneficial for clarifying the origin of vibrational modes in materials, helping to solve an ongoing controversy.