Barite Scaling Potential Modelled for Fractured-Porous Geothermal Reservoirs
Abstract
:1. Introduction
2. Materials and Methods
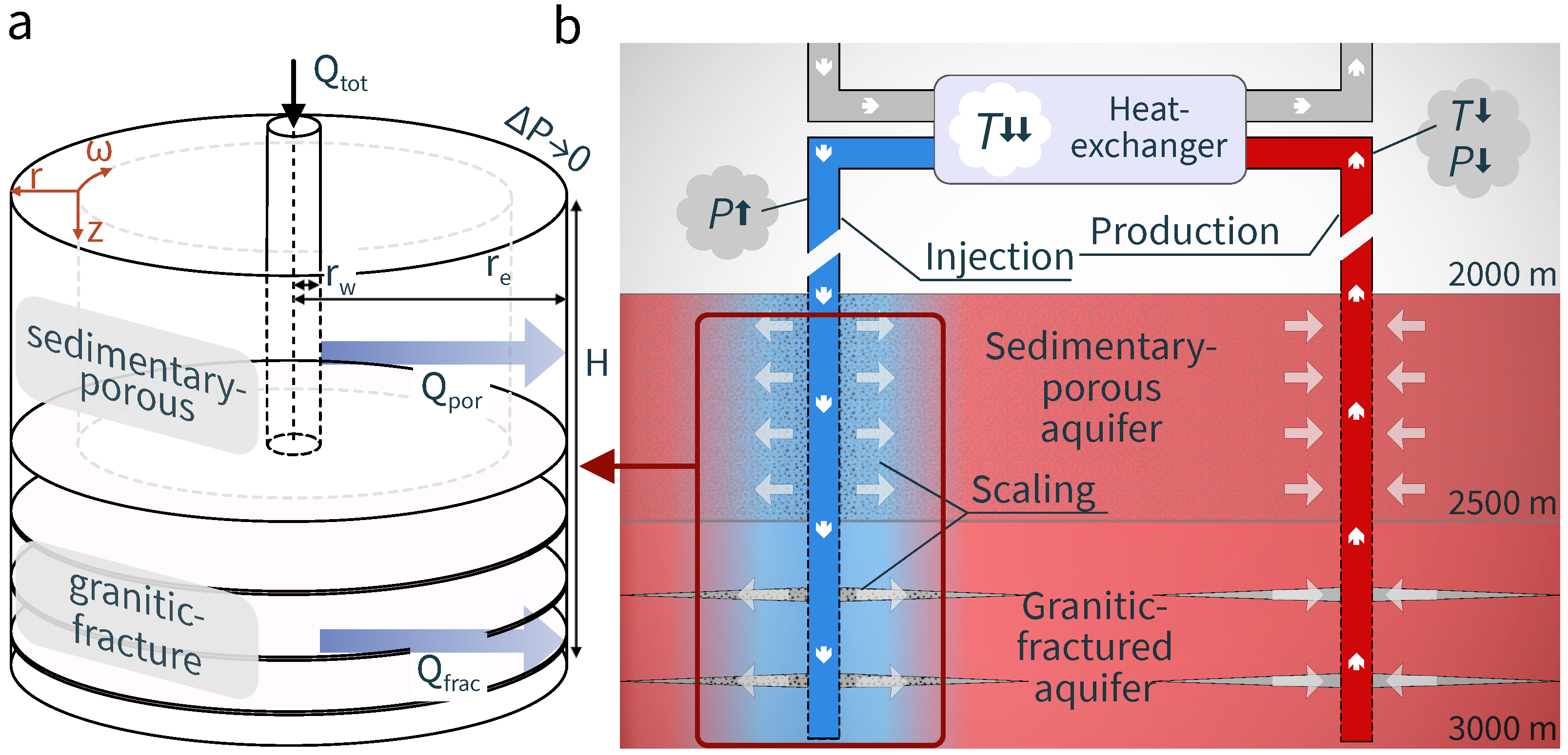
2.1. Reservoir Flow
2.2. Reactive Transport
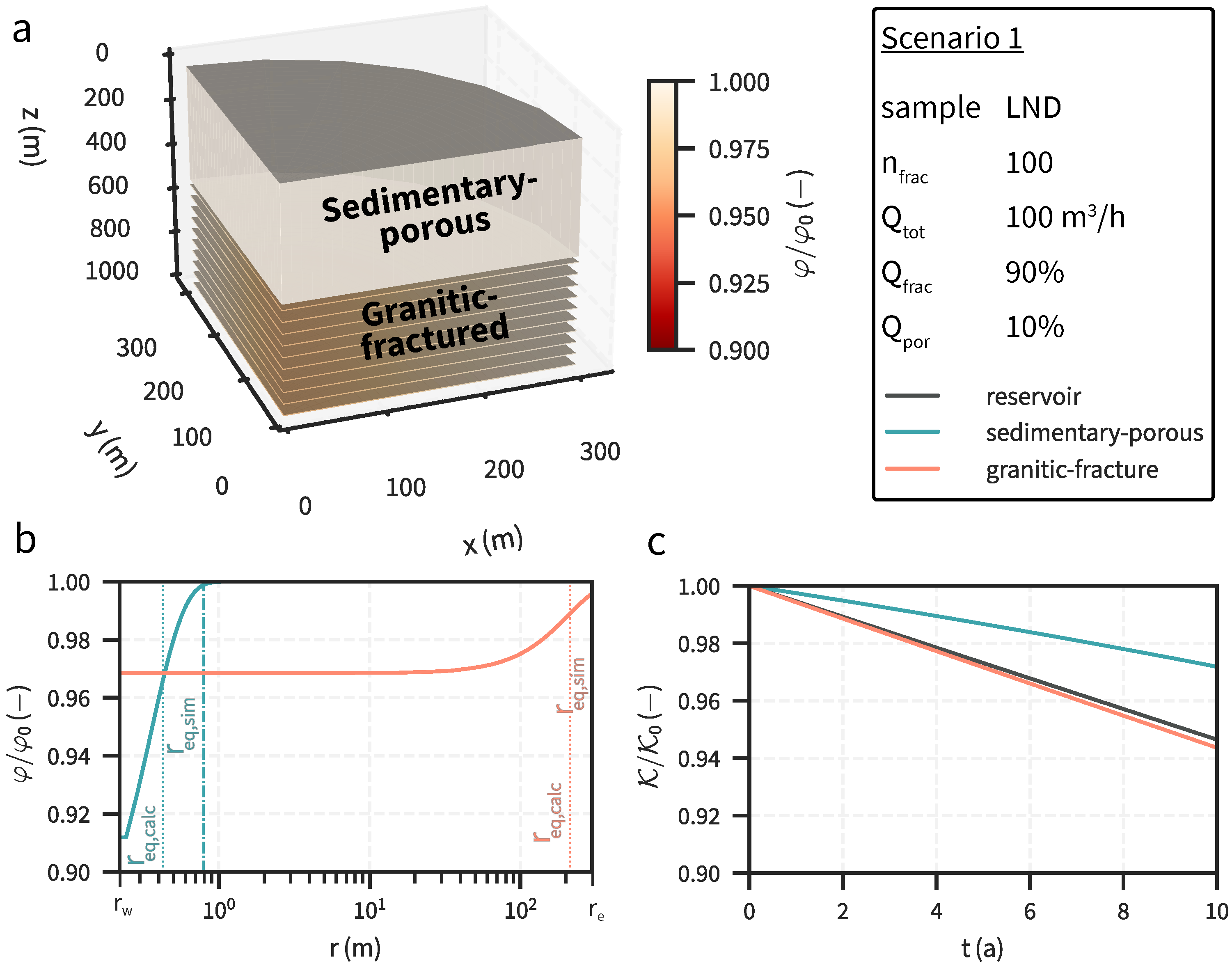
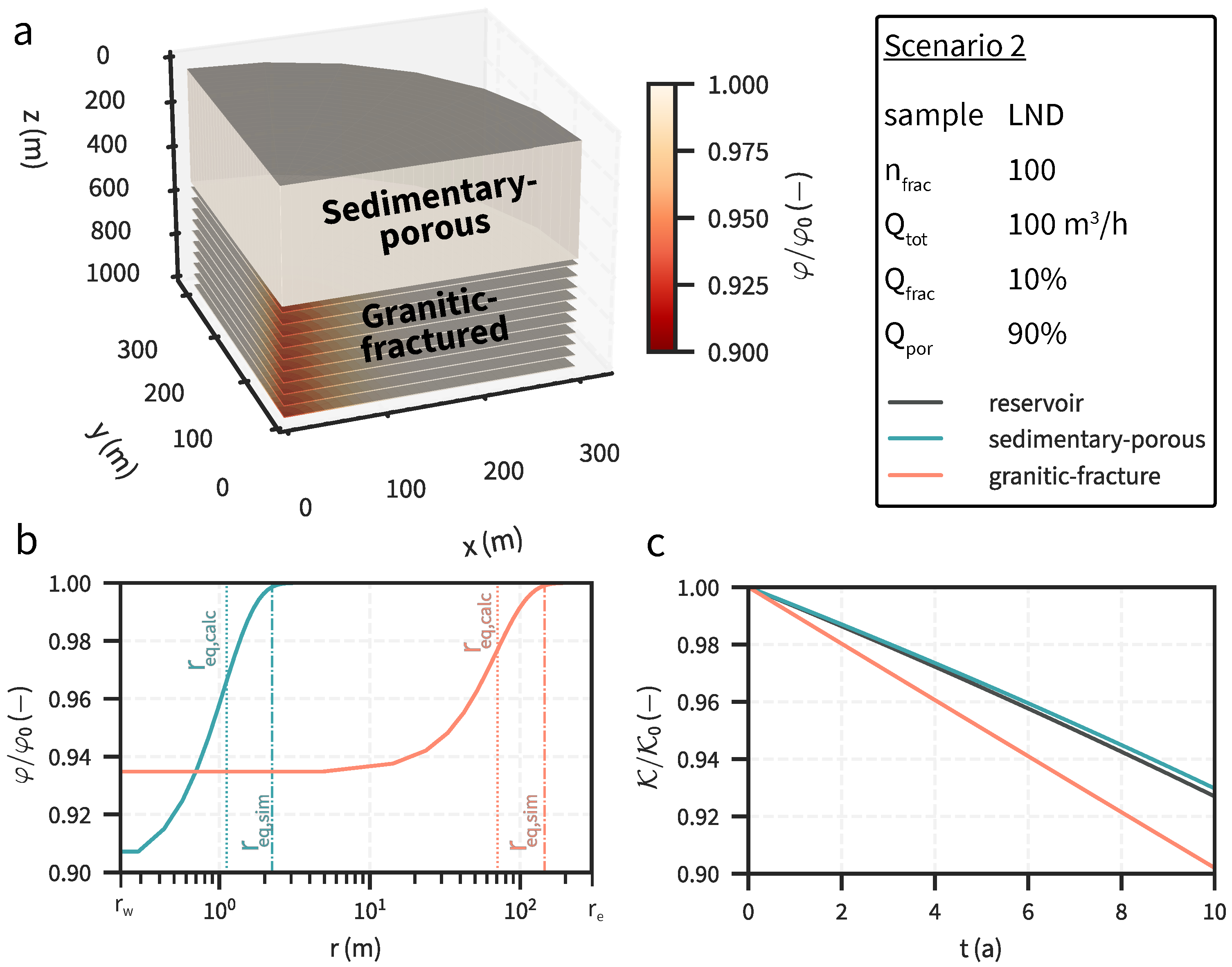
2.3. Scenarios
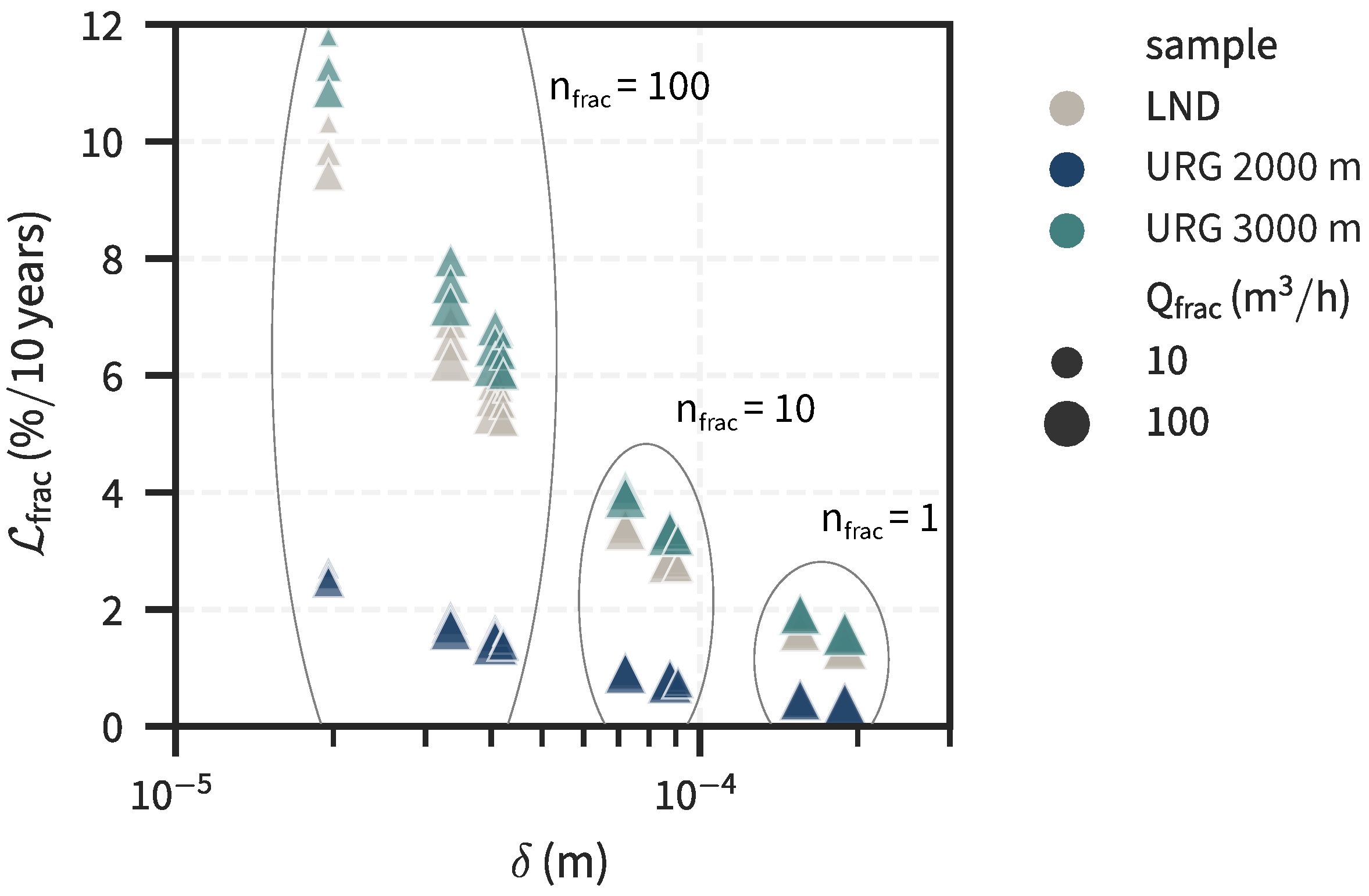
3. Results
3.1. Reservoir Simulation Scenarios
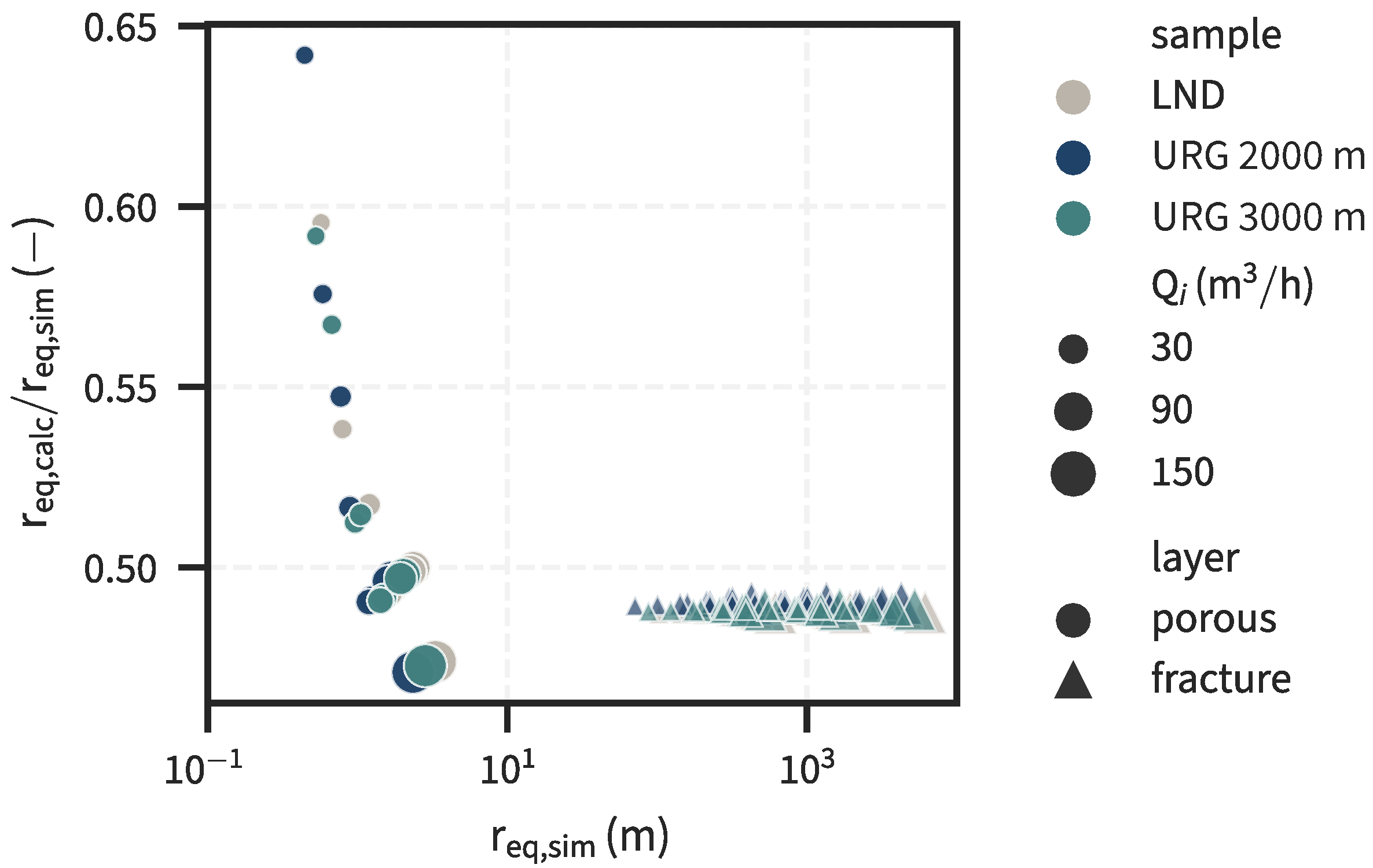
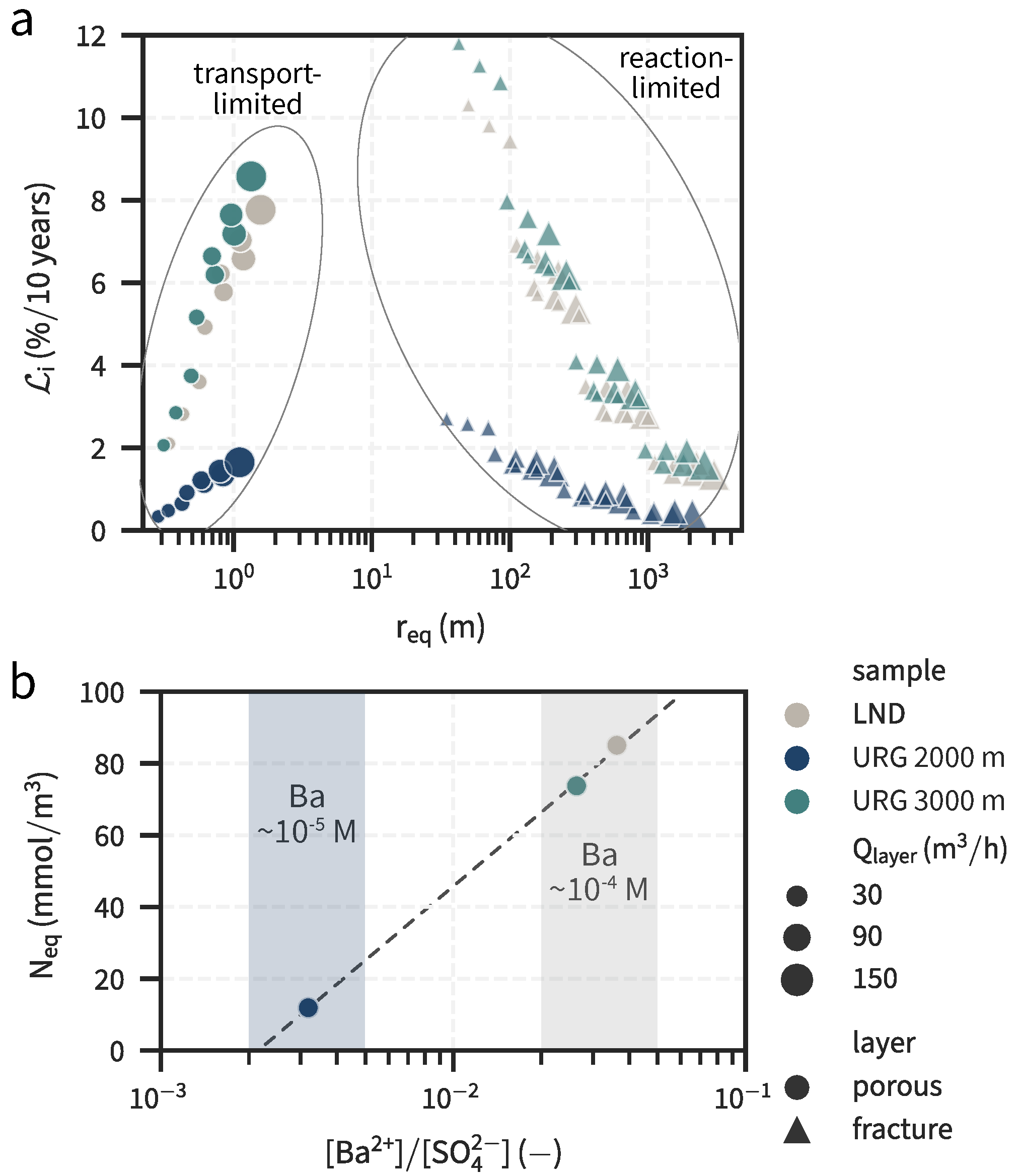
3.2. Scenario Analysis
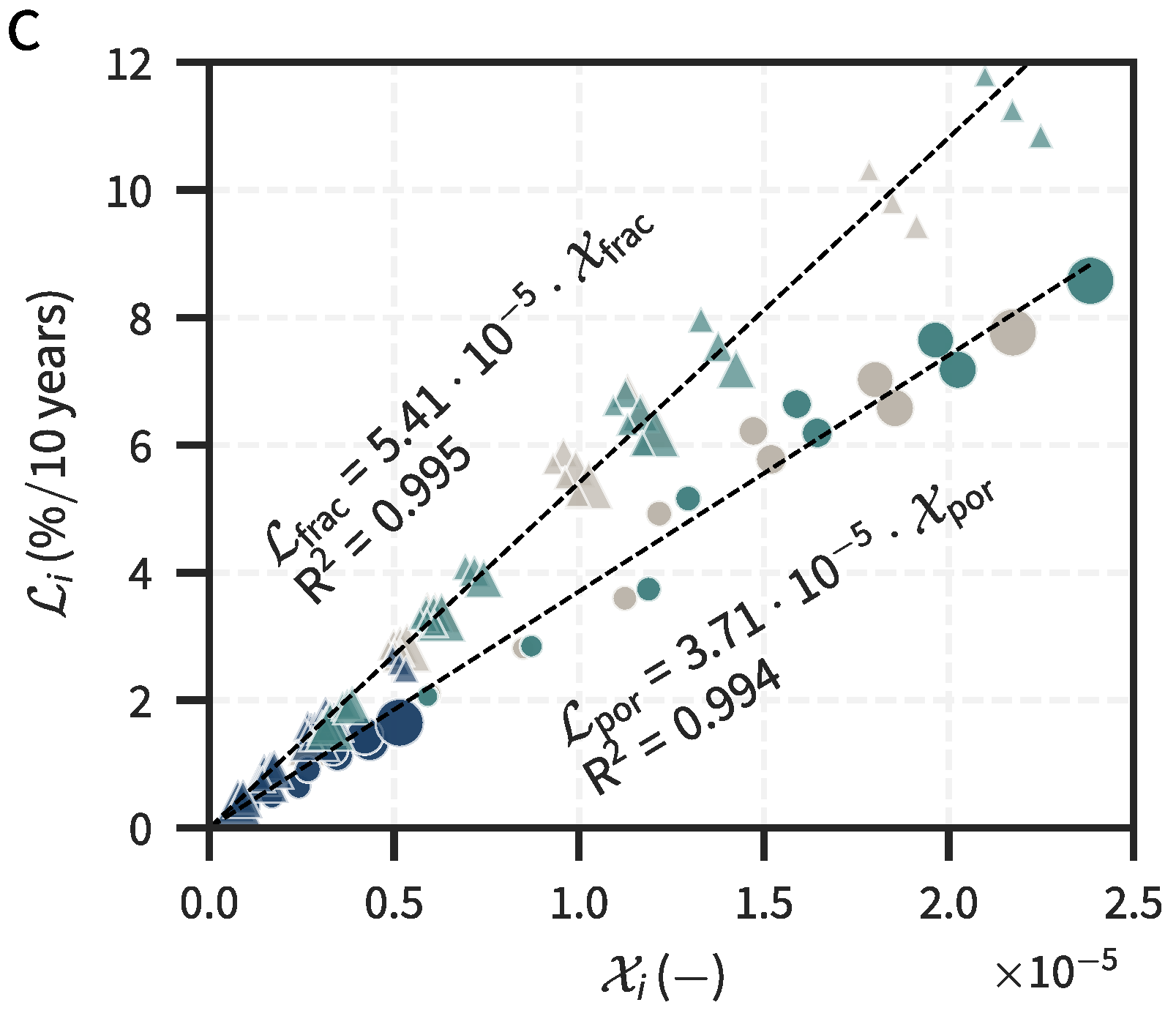
3.3. Scaling Score
4. Discussion
4.1. Simulation Results
4.2. Scenario Analysis
4.3. Scaling Score and Implications for Geothermal Systems
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Description | Unit |
| EGS | Enhanced Geothermal System | − |
| LND | Landau | − |
| NGB | North German Basin | − |
| URG | Upper Rhine Graben | − |
| A | Aquifer cross-sectional area | |
| Damköhler number | − | |
| H | Aquifer thickness | |
| I | Ionic strength | |
| Ionic activity product | − | |
| J | Injectivity | |
| Permeability | ||
| Solubility constant | − | |
| Permeability/injectivity loss | ||
| N | Precipitation potential | |
| P | Pressure | |
| Q | Flow rate | |
| R | Reaction rate | |
| S | Specific reactive surface area | |
| Scaling factor for reactive surface area | − | |
| Saturation ratio () | − | |
| Specific inner rock surface area | ||
| Transmissivity | ||
| T | Temperature | |
| V | Flow proxy () | |
| Scaling score | − | |
| Fracture aperture half-width | ||
| c | Solute concentration | |
| Gravitational acceleration | ||
| k | Rate constant | |
| Volumetric rate constant () | ||
| Dynamic viscosity | ||
| Porosity or volume fraction | − | |
| q | Darcy flow velocity | |
| Normalised Darcy flow velocity | ||
| r | Radial distance from well-centre | |
| Range of influence | ||
| Well radius | ||
| Density | ||
| s | Water column | |
| t | Simulation time | |
| Advective time | ||
| Reactive time | ||
| v | Pore velocity () | |
| x | Distance | |
| 0 | Subscript: initial value at | − |
| 1 | Subscript: value at | − |
| Subscript: characteristic | − | |
| Subscript: equilibrium | − | |
| Subscript: fluid | − | |
| Subscript: fracture layer | − | |
| i | Subscript: variable entity (solute, layer, etc.) | − |
| j | Subscript: model grid node | − |
| m | Subscript: mineral phase | − |
| Subscript: porous layer | − | |
| Subscript: radial | − | |
| Subscript: reservoir | − |
Appendix A. Numerical Implementation of the Radial Diverging Flow Field
Appendix B. Derivation of the Radial Equilibrium Length
References
- Tranter, M.; De Lucia, M.; Wolfgramm, M.; Kühn, M. Barite Scale Formation and Injectivity Loss Models for Geothermal Systems. Water 2020, 12, 3078. [Google Scholar] [CrossRef]
- Agemar, T.; Weber, J.; Schulz, R. Deep Geothermal Energy Production in Germany. Energies 2014, 7, 4397–4416. [Google Scholar] [CrossRef]
- Wolfgramm, M.; Rauppach, K.; Thorwart, K. Mineralneubildungen Und Partikeltransport Im Thermalwasserkreislauf Geothermischer Anlagen Deutschlands. Z. Für Geol. Wiss. 2011, 39, 213–239. [Google Scholar]
- Scheiber, J.; Seibt, A.; Birner, J.; Genter, A.; Moeckes, W. Application of a Scaling Inhibitor System at the Geothermal Power Plant in Soultz-Sous-Forêts: Laboratory and On-Site Studies. In Proceedings of the European Geothermal Congress, Pisa, Italy, 3–7 June 2013. [Google Scholar]
- Regenspurg, S.; Feldbusch, E.; Byrne, J.; Deon, F.; Driba, D.L.; Henninges, J.; Kappler, A.; Naumann, R.; Reinsch, T.; Schubert, C. Mineral Precipitation during Production of Geothermal Fluid from a Permian Rotliegend Reservoir. Geothermics 2015, 54, 122–135. [Google Scholar] [CrossRef]
- Vidal, J.; Genter, A. Overview of Naturally Permeable Fractured Reservoirs in the Central and Southern Upper Rhine Graben: Insights from Geothermal Wells. Geothermics 2018, 74, 57–73. [Google Scholar] [CrossRef]
- Guillou-Frottier, L.; Carrė, C.; Bourgine, B.; Bouchot, V.; Genter, A. Structure of Hydrothermal Convection in the Upper Rhine Graben as Inferred from Corrected Temperature Data and Basin-Scale Numerical Models. J. Volcanol. Geotherm. Res. 2013, 256, 29–49. [Google Scholar] [CrossRef] [Green Version]
- Bächler, D.; Kohl, T.; Rybach, L. Impact of Graben-Parallel Faults on Hydrothermal Convection––Rhine Graben Case Study. Phys. Chem. Earth Parts A/B/C 2003, 28, 431–441. [Google Scholar] [CrossRef]
- Dezayes, C.; Genter, A.; Valley, B. Structure of the Low Permeable Naturally Fractured Geothermal Reservoir at Soultz. Comptes Rendus Geosci. 2010, 342, 517–530. [Google Scholar] [CrossRef] [Green Version]
- Genter, A.; Traineau, H.; Dezayes, C.; Elsass, P.; Ledesert, B.; Meunier, A.; Villemin, T. Fracture Analysis and Reservoir Characterization of the Granitic Basement in the HDR Soultz Project (France). Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1996, 33, A69. [Google Scholar] [CrossRef]
- Baumgärtner, J.; Teza, D.; Hettkamp, T.; Hauffe, P. Stimulierung Tiefer Geothermischer Systeme. BBR Fachmagazine Fur Brunn. Und Leitungsbau 2010, 61, 14. [Google Scholar]
- Schindler, M.; Baumgärtner, J.; Gandy, T.; Hauffe, P.; Hettkamp, T.; Menzel, H.; Penzkofer, P.; Teza, D.; Tischner, T.; Wahl, G. Successful Hydraulic Stimulation Techniques for Electric Power Production in the Upper Rhine Graben, Central Europe. In Proceedings of the World Geothermal Congress, Bali, Indonesia, 25–30 April 2010; p. 7. [Google Scholar]
- Ngo, V.V.; Lucas, Y.; Clément, A.; Fritz, B. Modeling the Impact of Temperature on the Saturation State and Behavior of Minerals in the Soultz-Sous-Forêts Geothermal System. Geothermics 2016, 64, 196–208. [Google Scholar] [CrossRef]
- Griffiths, L.; Heap, M.; Wang, F.; Daval, D.; Gilg, H.; Baud, P.; Schmittbuhl, J.; Genter, A. Geothermal Implications for Fracture-Filling Hydrothermal Precipitation. Geothermics 2016, 64, 235–245. [Google Scholar] [CrossRef]
- Orywall, P.; Drüppel, K.; Kuhn, D.; Kohl, T.; Zimmermann, M.; Eiche, E. Flow-through Experiments on the Interaction of Sandstone with Ba-Rich Fluids at Geothermal Conditions. Geotherm. Energy 2017, 5, 20. [Google Scholar] [CrossRef] [Green Version]
- Tranter, M.; De Lucia, M.; Kühn, M. Numerical Investigation of Barite Scaling Kinetics in Fractures. Geothermics 2021, 91, 102027. [Google Scholar] [CrossRef]
- Wetzel, M.; Kempka, T.; Kühn, M. Diagenetic Trends of Synthetic Reservoir Sandstone Properties Assessed by Digital Rock Physics. Minerals 2021, 11, 151. [Google Scholar] [CrossRef]
- Wetzel, M.; Kempka, T.; Kühn, M. Hydraulic and Mechanical Impacts of Pore Space Alterations within a Sandstone Quantified by a Flow Velocity-Dependent Precipitation Approach. Materials 2020, 13, 3100. [Google Scholar] [CrossRef]
- Poonoosamy, J.; Klinkenberg, M.; Deissmann, G.; Brandt, F.; Bosbach, D.; Mäder, U.; Kosakowski, G. Effects of Solution Supersaturation on Barite Precipitation in Porous Media and Consequences on Permeability: Experiments and Modelling. Geochim. Cosmochim. Acta 2020, 270, 43–60. [Google Scholar] [CrossRef]
- Hommel, J.; Coltman, E.; Class, H. Porosity–Permeability Relations for Evolving Pore Space: A Review with a Focus on (Bio-)Geochemically Altered Porous Media. Transp. Porous Media 2018, 124, 589–629. [Google Scholar] [CrossRef] [Green Version]
- Pandey, S.; Chaudhuri, A.; Rajaram, H.; Kelkar, S. Fracture Transmissivity Evolution Due to Silica Dissolution/Precipitation during Geothermal Heat Extraction. Geothermics 2015, 57, 111–126. [Google Scholar] [CrossRef]
- Lucas, Y.; Ngo, V.V.; Clément, A.; Fritz, B.; Schäfer, G. Modelling Acid Stimulation in the Enhanced Geothermal System of Soultz-Sous-Forêts (Alsace, France). Geothermics 2020, 85, 101772. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Dover Books on Physics and Chemistry; Dover: New York, NY, USA, 1988. [Google Scholar]
- Renard, P.; de Marsily, G. Calculating Equivalent Permeability: A Review. Adv. Water Resour. 1997, 20, 253–278. [Google Scholar] [CrossRef] [Green Version]
- Dupuit, J. Études Théoriques et Pratiques Sur Le Mouvement Des Eaux Dans Les Canaux Découverts et à Travers Les Terrains Perméables; Technical Report; Dunod: Paris, France, 1863. [Google Scholar]
- Genske, D.D. Ingenieurgeologie: Grundlagen und Anwendung; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Tischner, T.; Pfender, M.; Teza, D. Hot Dry Rock Projekt Soultz: Erste Phase der Erstellung Einer Wissenschaftlichen Pilotanlage; Abschlussbericht 0327097; BGR: Berlin, Germany, 2006. [Google Scholar]
- Witherspoon, P.A.; Wang, J.S.Y.; Iwai, K.; Gale, J.E. Validity of Cubic Law for Fluid Flow in a Deformable Rock Fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef] [Green Version]
- Paillet, F.L.; Hess, A.E.; Cheng, C.H.; Hardin, E. Characterization of Fracture Permeability with High-Resolution Vertical Flow Measurements During Borehole Pumping. Ground Water 1987, 25, 28–40. [Google Scholar] [CrossRef]
- Wolfgramm, M.; Seibt, A. Zusammensetzung von Tiefenwässern in Deutschland und ihre Relevanz Für geothermische Anlagenteile; DGK: Los Angeles, CA, USA, 2008; pp. 503–516. [Google Scholar]
- Sanjuan, B.; Millot, R.; Innocent, C.; Dezayes, C.; Scheiber, J.; Brach, M. Major Geochemical Characteristics of Geothermal Brines from the Upper Rhine Graben Granitic Basement with Constraints on Temperature and Circulation. Chem. Geol. 2016, 428, 27–47. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C. Description of Input and Examples for PHREEQC Version 3: A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; Report 6-A43; USGS: Reston, VA, USA, 2013.
- Lasaga, A.C. Kinetic Theory in the Earth Sciences; Princeton Series in Geochemistry; Princeton University Press: Princeton, NJ, USA, 1998. [Google Scholar]
- Zhen-Wu, B.; Dideriksen, K.; Olsson, J.; Raahauge, P.; Stipp, S.; Oelkers, E. Experimental Determination of Barite Dissolution and Precipitation Rates as a Function of Temperature and Aqueous Fluid Composition. Geochim. Cosmochim. Acta 2016, 194, 193–210. [Google Scholar] [CrossRef]
- Rimstidt, J.; Barnes, H. The Kinetics of Silica-Water Reactions. Geochim. Cosmochim. Acta 1980, 44, 1683–1699. [Google Scholar] [CrossRef]
- Heberling, F.; Schild, D.; Degering, D.; Schäfer, T. How Well Suited Are Current Thermodynamic Models to Predict or Interpret the Composition of (Ba,Sr)SO4 Solid-Solutions in Geothermal Scalings? Geotherm. Energy 2017, 5, 9. [Google Scholar] [CrossRef] [Green Version]
- Vinograd, V.; Kulik, D.; Brandt, F.; Klinkenberg, M.; Weber, J.; Winkler, B.; Bosbach, D. Thermodynamics of the Solid Solution—Aqueous Solution System (Ba,Sr,Ra)SO4 + H2O: I. The Effect of Strontium Content on Radium Uptake by Barite. Appl. Geochem. 2018, 89, 59–74. [Google Scholar] [CrossRef] [Green Version]
- Beckingham, L.E. Evaluation of Macroscopic Porosity-Permeability Relationships in Heterogeneous Mineral Dissolution and Precipitation Scenarios. Water Resour. Res. 2017, 53, 10217–10230. [Google Scholar] [CrossRef] [Green Version]
- Bruss, D. Zur Herkunft der Erdöle im Mittleren Oberrheingraben und ihre Bedeutung für die Rekonstruktion der Migrationsgeschichte und der Speichergesteinsdiagenese; Number 3831 in Berichte des Forschungszentrums Jülich; Forschungszentrum Jülich GmbH Zentralbibliothek, Verlag: Jülich, Germany, 2000. [Google Scholar]
- Rabbani, A.; Jamshidi, S. Specific Surface and Porosity Relationship for Sandstones for Prediction of Permeability. Int. J. Rock Mech. Min. Sci. 2014, 71, 25–32. [Google Scholar] [CrossRef]
- Deng, H.; Spycher, N. Modeling Reactive Transport Processes in Fractures. Rev. Mineral. Geochem. 2019, 85, 49–74. [Google Scholar] [CrossRef] [Green Version]
- Seigneur, N.; Mayer, K.U.; Steefel, C.I. Reactive Transport in Evolving Porous Media. Rev. Mineral. Geochem. 2019, 85, 197–238. [Google Scholar] [CrossRef] [Green Version]
- Beckingham, L.E.; Mitnick, E.H.; Steefel, C.I.; Zhang, S.; Voltolini, M.; Swift, A.M.; Yang, L.; Cole, D.R.; Sheets, J.M.; Ajo-Franklin, J.B.; et al. Evaluation of Mineral Reactive Surface Area Estimates for Prediction of Reactivity of a Multi-Mineral Sediment. Geochim. Cosmochim. Acta 2016, 188, 310–329. [Google Scholar] [CrossRef] [Green Version]
- Deng, H.; Steefel, C.; Molins, S.; DePaolo, D. Fracture Evolution in Multimineral Systems: The Role of Mineral Composition, Flow Rate, and Fracture Aperture Heterogeneity. ACS Earth Space Chem. 2018, 2, 112–124. [Google Scholar] [CrossRef] [Green Version]
- Deng, H.; Molins, S.; Trebotich, D.; Steefel, C.; DePaolo, D. Pore-Scale Numerical Investigation of the Impacts of Surface Roughness: Upscaling of Reaction Rates in Rough Fractures. Geochim. Cosmochim. Acta 2018, 239, 374–389. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid Flow through Granular Beds. Trans. Inst. Chem. Eng. 1937, 15, 150–166. [Google Scholar] [CrossRef]
- Kozeny, J. Über Kapillare Leitung Des Wassers Im Boden. Sitzungsberichte Wien. Akad. 1927, 136, 271–306. [Google Scholar]
- King, P. The Use of Renormalization for Calculating Effective Permeability. Transp. Porous Media 1989, 4, 37–58. [Google Scholar] [CrossRef]
- Kluge, C.; Blöcher, G.; Barnhoorn, A.; Schmittbuhl, J.; Bruhn, D. Permeability Evolution During Shear Zone Initiation in Low-Porosity Rocks. Rock Mech. Rock Eng. 2021, 54, 5221–5244. [Google Scholar] [CrossRef]
- Blöcher, G.; Reinsch, T.; Henninges, J.; Milsch, H.; Regenspurg, S.; Kummerow, J.; Francke, H.; Kranz, S.; Saadat, A.; Zimmermann, G.; et al. Hydraulic History and Current State of the Deep Geothermal Reservoir Groß Schönebeck. Geothermics 2016, 63, 27–43. [Google Scholar] [CrossRef]
- Banks, J. Sulfate Mineral Scaling during the Production of Geothermal Energy from Sedimentary Basin Formation Brines: A Case Study at the Groß Schönebeck in-Situ Geothermal Laboratory, Germany. Ph.D. Thesis, Freie Universität Berlin, Berlin, Germany, 2013. [Google Scholar]
- Canic, T.; Baur, S.; Adelhelm, C.; Rauppach, K.; Wolfgramm, M. Kinetik von Barytausfällungen Aus Geothermalwasser—Einfluss Der Scherung; DGK: Los Angeles, CA, USA, 2011. [Google Scholar]
- Poonoosamy, J.; Wanner, C.; Alt Epping, P.; Águila, J.F.; Samper, J.; Montenegro, L.; Xie, M.; Su, D.; Mayer, K.U.; Mäder, U.; et al. Benchmarking of Reactive Transport Codes for 2D Simulations with Mineral Dissolution—Precipitation Reactions and Feedback on Transport Parameters. Comput. Geosci. 2021, 25, 1337–1358. [Google Scholar] [CrossRef]
- Franz, M.; Barth, G.; Zimmermann, J.; Budach, I.; Nowak, K.; Wolfgramm, M. Geothermal Resources of the North German Basin: Exploration Strategy, Development Examples and Remaining Opportunities in Mesozoic Hydrothermal Reservoirs. Geol. Soc. Lond. Spec. Publ. 2018, 469, 193–222. [Google Scholar] [CrossRef]
- Bär, K.M. Untersuchung Der Tiefengeothermischen Potenziale von Hessen. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2012. [Google Scholar]
- Lichtner, P.C. The Quasi-Stationary State Approximation to Coupled Mass Transport and Fluid-Rock Interaction in a Porous Medium. Geochim. Cosmochim. Acta 1988, 52, 143–165. [Google Scholar] [CrossRef]
- Zimmermann, G.; Moeck, I.; Blöcher, G. Cyclic Waterfrac Stimulation to Develop an Enhanced Geothermal System (EGS)—Conceptual Design and Experimental Results. Geothermics 2010, 39, 59–69. [Google Scholar] [CrossRef] [Green Version]
- Kumar, G.S.; Ghassemi, A. Numerical Modeling of Non-Isothermal Quartz Dissolution/Precipitation in a Coupled Fracture–Matrix System. Geothermics 2005, 34, 411–439. [Google Scholar] [CrossRef]
- Nitschke, F.; Scheiber, J.; Kramar, U.; Neumann, T. Formation of Alternating Layered Ba-Sr-Sulfate and Pb-Sulfide Scaling in the Geothermal Plant of Soultz-Sous-Forêts. Neues Jahrb. Für Mineral. Abh. 2014, 191, 145–156. [Google Scholar] [CrossRef]
- Wanner, C.; Eichinger, F.; Jahrfeld, T.; Diamond, L.W. Causes of Abundant Calcite Scaling in Geothermal Wells in the Bavarian Molasse Basin, Southern Germany. Geothermics 2017, 70, 324–338. [Google Scholar] [CrossRef] [Green Version]
- Forjanes, P.; Astilleros, J.M.; Fernández-Díaz, L. The Formation of Barite and Celestite through the Replacement of Gypsum. Minerals 2020, 10, 189. [Google Scholar] [CrossRef] [Green Version]
- Poonoosamy, J.; Haber-Pohlmeier, S.; Deng, H.; Deissmann, G.; Klinkenberg, M.; Gizatullin, B.; Stapf, S.; Brandt, F.; Bosbach, D.; Pohlmeier, A. Combination of MRI and SEM to Assess Changes in the Chemical Properties and Permeability of Porous Media Due to Barite Precipitation. Minerals 2020, 10, 226. [Google Scholar] [CrossRef] [Green Version]
- Blöcher, G.; Kluge, C.; Milsch, H.; Cacace, M.; Jacquey, A.B.; Schmittbuhl, J. Permeability of Matrix-Fracture Systems under Mechanical Loading – Constraints from Laboratory Experiments and 3-D Numerical Modelling. Adv. Geosci. 2019, 49, 95–104. [Google Scholar] [CrossRef] [Green Version]
- Verma, A.; Pruess, K. Thermohydrological Conditions and Silica Redistribution near High-Level Nuclear Wastes Emplaced in Saturated Geological Formations. J. Geophys. Res. 1988, 93, 1159. [Google Scholar] [CrossRef] [Green Version]
- Tranter, M.; Wetzel, M.; De Lucia, M.; Kühn, M. Reactive Transport Model of Kinetically Controlled Celestite to Barite Replacement. Adv. Geosci. 2021, 56, 57–65. [Google Scholar] [CrossRef]
- Steefel, C.I. Geochemical Kinetics and Transport. In Kinetics of Water-Rock Interaction; Brantley, S.L., Kubicki, J.D., White, A.F., Eds.; Springer: New York, NY, USA, 2008; pp. 545–589. [Google Scholar] [CrossRef]

| Sample | LND | URG 2000 m | URG 3000 m |
|---|---|---|---|
| 106 | 133 | ||
| 1270 | 894 | 1590 | |
| 196 | 104 | 177 | |
| 1790 | 1180 | 2100 | |
| I | 2010 | 1320 | 2310 |
| Variable | Range |
|---|---|
| Sample | [LND, URG 2000 m, URG 3000 m] |
| [50, 100, 200] | |
| [, , ] | |
| [1, 10, 100] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tranter, M.; De Lucia, M.; Kühn, M. Barite Scaling Potential Modelled for Fractured-Porous Geothermal Reservoirs. Minerals 2021, 11, 1198. https://doi.org/10.3390/min11111198
Tranter M, De Lucia M, Kühn M. Barite Scaling Potential Modelled for Fractured-Porous Geothermal Reservoirs. Minerals. 2021; 11(11):1198. https://doi.org/10.3390/min11111198
Chicago/Turabian StyleTranter, Morgan, Marco De Lucia, and Michael Kühn. 2021. "Barite Scaling Potential Modelled for Fractured-Porous Geothermal Reservoirs" Minerals 11, no. 11: 1198. https://doi.org/10.3390/min11111198
APA StyleTranter, M., De Lucia, M., & Kühn, M. (2021). Barite Scaling Potential Modelled for Fractured-Porous Geothermal Reservoirs. Minerals, 11(11), 1198. https://doi.org/10.3390/min11111198






