Importance of Spatial Autocorrelation in Machine Learning Modeling of Polymetallic Nodules, Model Uncertainty and Transferability at Local Scale
Abstract
:1. Introduction
2. Materials and Methods
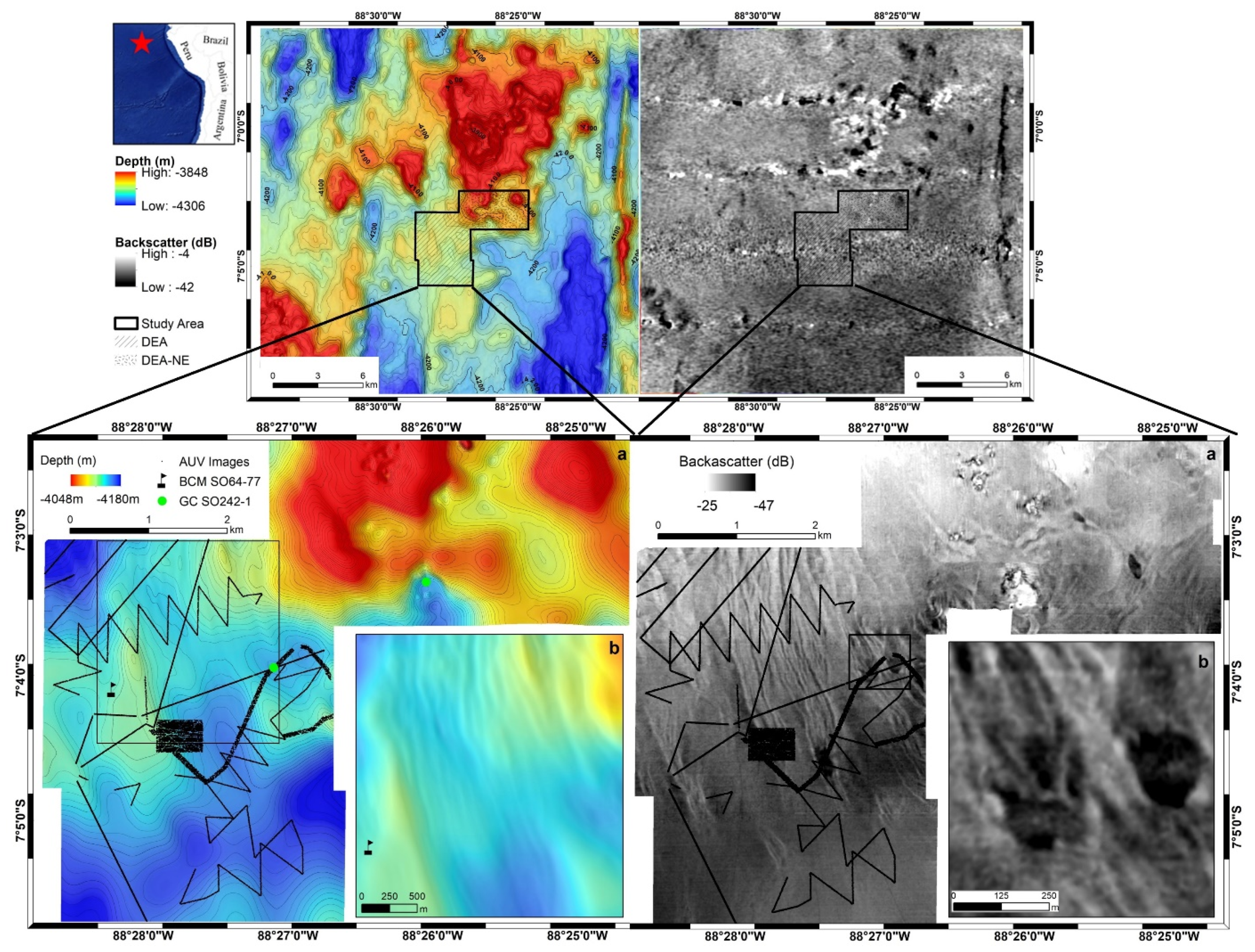
2.1. Study Area
2.2. Hydroacoustic Data
Seafloor Geomorphological Analysis
2.3. Optic Data
2.4. Spatial Data Analysis
2.5. Feature Selection
2.6. Quantile Regression Forests
2.7. Cross-Validation Techniques
2.7.1. Random k-fold Cross-Validation
2.7.2. Systematic k-fold Spatial-Blocking Cross-Validation
2.7.3. Feature Space k-fold Clustering Cross-Validation
2.8. Dissimilarity Index and Area of Applicability
3. Results
3.1. PMN Spatial Distribution and Spatial Autocorrelation
3.2. Boruta Analysis and Feature Selection
3.3. Model Training and CV Results
3.3.1. Model Training and Sample Size
3.3.2. Model Performance in Test Data
3.3.3. QRF Variable Importance
3.4. QRF Spatial Predictions and Uncertainty
3.5. Dissimilarity Analysis and Area of Applicability
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Study Area Geomorphology


Appendix B. Methodology








References
- Hein, J.R.; Koschinsky, A.; Kuhn, T. Deep-ocean polymetallic nodules as a resource for critical materials. Nat. Rev. Earth Environ. 2020, 1, 158–169. [Google Scholar] [CrossRef]
- Hein, J.R.; Mizell, K.; Koschinsky, A.; Conrad, T.A. Deep-ocean mineral deposits as a source of critical metals for high- and green-technology applications: Comparison with land-based resources. Ore Geol. Rev. 2013, 51, 1–14. [Google Scholar] [CrossRef]
- EC Communication COM, 474, F. Critical Raw Materials Resilience: Charting a Path towards Greater Security and Sustainability. 2020. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/HTML/?uri=CELEX:52020DC0474&from=EN (accessed on 30 August 2021).
- Schoening, T.; Purser, A.; Langenkämper, D.; Suck, I.; Taylor, J.; Cuvelier, D.; Lins, L.; Simon-Lledó, E.; Marcon, Y.; Jones, D.O.B.; et al. Megafauna community assessment of polymetallic-nodule fields with cameras: Platform and methodology comparison. Biogeosciences 2020, 17, 3115–3133. [Google Scholar] [CrossRef]
- Schoening, T.; Köser, K.; Greinert, J. An acquisition, curation and management workflow for sustainable, terabyte-scale marine image analysis. Sci. Data 2018, 5, 180181. [Google Scholar] [CrossRef] [PubMed]
- Simon-Lledó, E.; Bett, B.J.; Huvenne, V.A.I.; Köser, K.; Schoening, T.; Greinert, J.; Jones, D.O.B. Biological effects 26 years after simulated deep-sea mining. Sci. Rep. 2019, 9, 8040. [Google Scholar] [CrossRef] [PubMed]
- Gazis, I.Z.; Schoening, T.; Alevizos, E.; Greinert, J. Quantitative mapping and predictive modeling of Mn nodules’ distribution from hydroacoustic and optical AUV data linked by random forests machine learning. Biogeosciences 2018, 15, 7347–7377. [Google Scholar] [CrossRef] [Green Version]
- Peukert, A.; Schoening, T.; Alevizos, E.; Köser, K.; Kwasnitschka, T.; Greinert, J. Understanding Mn-nodule distribution and evaluation of related deep-sea mining impacts using AUV-based hydroacoustic and optical data. Biogeosciences 2018, 15, 2525–2549. [Google Scholar] [CrossRef] [Green Version]
- Schoening, T.; Jones, D.O.B.; Greinert, J. Compact-Morphology-based poly-metallic Nodule Delineation. Sci. Rep. 2017, 7, 13338. [Google Scholar] [CrossRef]
- Hari, V.N.; Kalyan, B.; Chitre, M.; Ganesan, V. Spatial Modeling of Deep-Sea Ferromanganese Nodules with Limited Data Using Neural Networks. IEEE J. Ocean. Eng. 2018, 43, 997–1014. [Google Scholar] [CrossRef]
- Kaikkonen, L.; Virtanen, E.A.; Kostamo, K.; Lappalainen, J.; Kotilainen, A.T. Extensive Coverage of Marine Mineral Concretions Revealed in Shallow Shelf Sea Areas. Front. Mar. Sci. 2019, 6, 541. [Google Scholar] [CrossRef]
- Wong, L.J.; Kalyan, B.; Chitre, M.; Vishnu, H. Acoustic Assessment of Polymetallic Nodule Abundance Using Sidescan Sonar and Altimeter. IEEE J. Ocean. Eng. 2021, 46, 132–142. [Google Scholar] [CrossRef]
- Dutkiewicz, A.; Judge, A.; Müller, R.D. Environmental predictors of deep-sea polymetallic nodule occurrence in the global ocean. Geology 2020, 48, 293–297. [Google Scholar] [CrossRef]
- Wasilewska-Błaszczyk, M.; Mucha, J. Application of General Linear Models (GLM) to assess nodule abundance based on a photographic survey (case study from IOM Area, Pacific Ocean). Minerals 2021, 11, 427. [Google Scholar] [CrossRef]
- Kuhn, T.; Rühlemann, C. Exploration of polymetallic nodules and resource assessment: A case study from the German contract area in the clarion-clipperton zone of the tropical northeast pacific. Minerals 2021, 11, 618. [Google Scholar] [CrossRef]
- Anselin, L. Local Indicators of Spatial Association-LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Roberts, D.R.; Bahn, V.; Ciuti, S.; Boyce, M.S.; Elith, J.; Guillera-Arroita, G.; Hauenstein, S.; Lahoz-Monfort, J.J.; Schröder, B.; Thuiller, W.; et al. Cross-validation strategies for data with temporal, spatial, hierarchical, or phylogenetic structure. Ecography 2017, 40, 913–929. [Google Scholar] [CrossRef]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.M.; Gräler, B. Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef] [Green Version]
- Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving performance of spatio-temporal machine learning models using forward feature selection and target-oriented validation. Environ. Model. Softw. 2018, 101, 1–9. [Google Scholar] [CrossRef]
- Misiuk, B.; Diesing, M.; Aitken, A.; Brown, C.J.; Edinger, E.N.; Bell, T. A Spatially Explicit Comparison of Quantitative and Categorical Modelling Approaches for Mapping Seabed Sediments Using Random Forest. Geosciences 2019, 9, 254. [Google Scholar] [CrossRef] [Green Version]
- Ploton, P.; Mortier, F.; Réjou-Méchain, M.; Barbier, N.; Picard, N.; Rossi, V.; Dormann, C.; Cornu, G.; Viennois, G.; Bayol, N.; et al. Spatial validation reveals poor predictive performance of large-scale ecological mapping models. Nat. Commun. 2020, 11, 4540. [Google Scholar] [CrossRef]
- Wenger, S.J.; Olden, J.D. Assessing transferability of ecological models: An underappreciated aspect of statistical validation. Methods Ecol. Evol. 2012, 3, 260–267. [Google Scholar] [CrossRef]
- Hao, T.; Elith, J.; Lahoz-Monfort, J.J.; Guillera-Arroita, G. Testing whether ensemble modelling is advantageous for maximising predictive performance of species distribution models. Ecography 2020, 43, 549–558. [Google Scholar] [CrossRef] [Green Version]
- Dolan, M.F.J.; Ross, R.E.; Albretsen, J.; Skarðhamar, J.; Gonzalez-Mirelis, G.; Bellec, V.K.; Buhl-Mortensen, P.; Bjarnadóttir, L.R. Using Spatial Validity and Uncertainty Metrics to Determine the Relative Suitability of Alternative Suites of Oceanographic Data for Seabed Biotope Prediction. A Case Study from the Barents Sea, Norway. Geosciences 2021, 11, 48. [Google Scholar] [CrossRef]
- Schratz, P.; Muenchow, J.; Iturritxa, E.; Richter, J.; Brenning, A. Hyperparameter tuning and performance assessment of statistical and machine-learning algorithms using spatial data. Ecol. Modell. 2019, 406, 109–120. [Google Scholar] [CrossRef] [Green Version]
- Pohjankukka, J.; Pahikkala, T.; Nevalainen, P.; Heikkonen, J. Estimating the prediction performance of spatial models via spatial k-fold cross validation. Int. J. Geogr. Inf. Sci. 2017, 31, 2001–2019. [Google Scholar] [CrossRef]
- Parmentier, I.; Harrigan, R.J.; Buermann, W.; Mitchard, E.T.A.; Saatchi, S.; Malhi, Y.; Bongers, F.; Hawthorne, W.D.; Leal, M.E.; Lewis, S.L.; et al. Predicting alpha diversity of African rain forests: Models based on climate and satellite-derived data do not perform better than a purely spatial model. J. Biogeogr. 2011, 38, 1164–1176. [Google Scholar] [CrossRef]
- Trachsel, M.; Telford, R.J. Technical note: Estimating unbiased transfer-function performances in spatially structured environments. Clim. Past 2016, 12, 1215–1223. [Google Scholar] [CrossRef] [Green Version]
- Le Rest, K.; Pinaud, D.; Monestiez, P.; Chadoeuf, J.; Bretagnolle, V. Spatial leave-one-out cross-validation for variable selection in the presence of spatial autocorrelation. Glob. Ecol. Biogeogr. 2014, 23, 811–820. [Google Scholar] [CrossRef] [Green Version]
- Ruß, G.; Brenning, A. Spatial Variable Importance Assessment for Yield Prediction in Precision Agriculture. In Advances in Intelligent Data Analysis IX; Lecture Notes in Computer Science; Cohen, P.R., Adams, N.M., Berthold, M.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6065. [Google Scholar] [CrossRef]
- Valavi, R.; Elith, J.; Lahoz-Monfort, J.J.; Guillera-Arroita, G. blockCV: An r package for generating spatially or environmentally separated folds for k-fold cross-validation of species distribution models. Methods Ecol. Evol. 2019, 10, 225–232. [Google Scholar] [CrossRef] [Green Version]
- Meyer, H.; Reudenbach, C.; Wöllauer, S.; Nauss, T. Importance of spatial predictor variable selection in machine learning applications—Moving from data reproduction to spatial prediction. Ecol. Modell. 2019, 411, 108815. [Google Scholar] [CrossRef] [Green Version]
- Randin, C.F.; Dirnböck, T.; Dullinger, S.; Zimmermann, N.E.; Zappa, M.; Guisan, A. Are niche-based species distribution models transferable in space? J. Biogeogr. 2006, 33, 1689–1703. [Google Scholar] [CrossRef]
- Yates, K.L.; Bouchet, P.J.; Caley, M.J.; Mengersen, K.; Randin, C.F.; Parnell, S.; Fielding, A.H.; Bamford, A.J.; Ban, S.; Barbosa, A.M.; et al. Outstanding Challenges in the Transferability of Ecological Models. Trends Ecol. Evol. 2018, 33, 790–802. [Google Scholar] [CrossRef] [Green Version]
- Meyer, H.; Pebesma, E. Predicting into unknown space? Estimating the area of applicability of spatial prediction models. Methods Ecol. Evol. 2021, 12, 2041–2210. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-6848-6. [Google Scholar]
- Elith, J.; Kearney, M.; Phillips, S. The art of modelling range-shifting species. Methods Ecol. Evol. 2010, 1, 330–342. [Google Scholar] [CrossRef]
- Zurell, D.; Elith, J.; Schröder, B. Predicting to new environments: Tools for visualizing model behaviour and impacts on mapped distributions. Divers. Distrib. 2012, 18, 628–634. [Google Scholar] [CrossRef]
- Owens, H.L.; Campbell, L.P.; Dornak, L.L.; Saupe, E.E.; Barve, N.; Soberón, J.; Ingenloff, K.; Lira-Noriega, A.; Hensz, C.M.; Myers, C.E.; et al. Constraints on interpretation of ecological niche models by limited environmental ranges on calibration areas. Ecol. Modell. 2013, 263, 10–18. [Google Scholar] [CrossRef]
- Mesgaran, M.B.; Cousens, R.D.; Webber, B.L. Here be dragons: A tool for quantifying novelty due to covariate range and correlation change when projecting species distribution models. Divers. Distrib. 2014, 20, 1147–1159. [Google Scholar] [CrossRef]
- Rödder, D.; Engler, J.O. Disentangling Interpolation and Extrapolation Uncertainties in Species Distribution Models: A Novel Visualization Technique for the Spatial Variation of Predictor Variable Colinearity. Biodivers. Inform. 2012, 8, 4326. [Google Scholar] [CrossRef] [Green Version]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biom. Bull. 1945, 1, 80. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Kruskal, W.H. Historical Notes on the Wilcoxon Unpaired Two-Sample Test. J. Am. Stat. Assoc. 1957, 52, 356. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 11. [Google Scholar] [CrossRef] [Green Version]
- Kursa, M.B. Robustness of Random Forest-based gene selection methods. BMC Bioinform. 2014, 15, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Degenhardt, F.; Seifert, S.; Szymczak, S. Evaluation of variable selection methods for random forests and omics data sets. Brief. Bioinform. 2019, 20, 492–503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Tran, M.; Siwabessy, J. Selecting Optimal Random Forest Predictive Models: A Case Study on Predicting the Spatial Distribution of Seabed Hardness. PLoS ONE 2016, 11, e0149089. [Google Scholar] [CrossRef]
- Li, J.; Alvarez, B.; Siwabessy, J.; Tran, M.; Huang, Z.; Przeslawski, R.; Radke, L.; Howard, F.; Nichol, S. Application of random forest, generalised linear model and their hybrid methods with geostatistical techniques to count data: Predicting sponge species richness. Environ. Model. Softw. 2017, 97, 112–129. [Google Scholar] [CrossRef]
- Li, J. A Critical Review of Spatial Predictive Modeling Process in Environmental Sciences with Reproducible Examples in R. Appl. Sci. 2019, 9, 2048. [Google Scholar] [CrossRef] [Green Version]
- Diesing, M.; Thorsnes, T. Mapping of Cold-Water Coral Carbonate Mounds Based on Geomorphometric Features: An Object-Based Approach. Geosciences 2018, 8, 34. [Google Scholar] [CrossRef] [Green Version]
- Diesing, M.; Mitchell, P.J.; O’Keeffe, E.; Gavazzi, G.O.A.M.; Bas, T. Le Limitations of Predicting Substrate Classes on a Sedimentary Complex but Morphologically Simple Seabed. Remote Sens. 2020, 12, 3398. [Google Scholar] [CrossRef]
- Diesing, M. Deep-sea sediments of the global ocean. Earth Syst. Sci. Data 2020, 12, 3367–3381. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Meinshausen, N. Quantile regression forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Kirkwood, C.; Cave, M.; Beamish, D.; Grebby, S.; Ferreira, A. A machine learning approach to geochemical mapping. J. Geochem. Explor. 2016, 167, 49–61. [Google Scholar] [CrossRef] [Green Version]
- Vaysse, K.; Lagacherie, P. Using quantile regression forest to estimate uncertainty of digital soil mapping products. Geoderma 2017, 291, 55–64. [Google Scholar] [CrossRef]
- Fouedjio, F.; Klump, J. Exploring prediction uncertainty of spatial data in geostatistical and machine learning approaches. Environ. Earth Sci. 2019, 78, 38. [Google Scholar] [CrossRef]
- Szatmári, G.; Pásztor, L. Comparison of various uncertainty modelling approaches based on geostatistics and machine learning algorithms. Geoderma 2019, 337, 1329–1340. [Google Scholar] [CrossRef]
- Diesing, M.; Kröger, S.; Parker, R.; Jenkins, C.; Mason, C.; Weston, K. Predicting the standing stock of organic carbon in surface sediments of the North–West European continental shelf. Biogeochemistry 2017, 135, 183–200. [Google Scholar] [CrossRef] [Green Version]
- Baker, E.; Beaudoin, Y. Deep Sea Minerals: A Physical, Biological, Environmental, and Technical Review; Secretariat of the Pacific Community: Suva, Fiji, 2013; ISBN 978-827-701-12-02. [Google Scholar]
- Marchig, V.; Reyss, J.L. Diagenetic mobilization of manganese in Peru Basin sediments. Geochim. Cosmochim. Acta 1984, 48, 1349–1352. [Google Scholar] [CrossRef]
- Von Stackelberg, U. Growth history of manganese nodules and crusts of the Peru Basin. Geol. Soc. Lond. Spec. Publ. 1997, 119, 153–176. [Google Scholar] [CrossRef]
- Weber, M.; von Stackelberg, U.; Marchig, V.; Wiedicke, M.; Grupe, B. Variability of surface sediments in the Peru basin: Dependence on water depth, productivity, bottom water flow, and seafloor topography. Mar. Geol. 2000, 163, 169–184. [Google Scholar] [CrossRef]
- Toro, N.; Jeldres, R.I.; Órdenes, J.A.; Robles, P.; Navarra, A. Manganese Nodules in Chile, an Alternative for the Production of Co and Mn in the Future—A Review. Minerals 2020, 10, 674. [Google Scholar] [CrossRef]
- Thiel, H.; Schriever, G.; Ahnert, A.; Bluhm, H.; Borowski, C.; Vopel, K. The large-scale environmental impact experiment DISCOL—reflection and foresight. Deep Sea Res. Part II Top. Stud. Oceanogr. 2001, 48, 3869–3882. [Google Scholar] [CrossRef]
- Gausepohl, F.; Hennke, A.; Schoening, T.; Köser, K.; Greinert, J. Scars in the abyss: Reconstructing sequence, location and temporal change of the 78 plough tracks of the 1989 DISCOL deep-sea disturbance experiment in the Peru Basin. Biogeosciences 2020, 17, 1463–1493. [Google Scholar] [CrossRef] [Green Version]
- Wiedicke, M.H.; Weber, M.E. Small-scale variability of seafloor features in the northern Peru Basin: Results from acoustic survey methods. Mar. Geophys. Res. 1996, 18, 507–526. [Google Scholar] [CrossRef]
- Paul, S.A.L.; Haeckel, M.; Bau, M.; Bajracharya, R.; Koschinsky, A. Small-scale heterogeneity of trace metals including rare earth elements and yttrium in deep-sea sediments and porewaters of the Peru Basin, southeastern equatorial Pacific. Biogeosciences 2019, 16, 4829–4849. [Google Scholar] [CrossRef] [Green Version]
- Grupe, B.; Becker, H.J.; Oebius, H.U. Geotechnical and sedimentological investigations of deep-sea sediments from a manganese nodule field of the Peru Basin. Deep Sea Res. Part II Top. Stud. Oceanogr. 2001, 48, 3593–3608. [Google Scholar] [CrossRef]
- Klein, H. Near-bottom currents in the deep Peru Basin, DISCOL experimental area. Dtsch. Hydrogr. Z. 1993, 45, 31–42. [Google Scholar] [CrossRef]
- Klein, H. Near-bottom currents and bottom boundary layer variability over manganese nodule fields in the peru basin, se-pacific. Dtsch. Hydrogr. Z. 1996, 48, 147–160. [Google Scholar] [CrossRef]
- Flood, R.D. Classification of sedimentary furrows and a model for furrow initiation and evolution. Geol. Soc. Am. Bull. 1983, 94, 630. [Google Scholar] [CrossRef]
- Lonsdale, P.; Spiess, F.N. Abyssal Bedforms Explored with a Deeply Towed Instrument Package. Dev. Sedimentol. 1977, 23, 57–75. [Google Scholar]
- Flood, R.D.; Hollister, C.D. Submersible studies of deep-sea furrows and transverse ripples in cohesive sediments. Mar. Geol. 1980, 36, M1–M9. [Google Scholar] [CrossRef]
- Haeckel, M.; König, I.; Riech, V.; Weber, M.E.; Suess, E. Pore water profiles and numerical modelling of biogeochemical processes in Peru Basin deep-sea sediments. Deep Sea Res. Part II Top. Stud. Oceanogr. 2001, 48, 3713–3736. [Google Scholar] [CrossRef]
- Greinert, J. RV Sonne Fahrtbericht/Cruise Report SO242-1 [SO242/1], JPI Oceans Ecological Aspects of Deep-Sea Mining, DISCOL Revisited, Guayaquil-Guayaquil, 28 July–25 August 2015; GEOMAR Report, N. Ser. 026; GEOMAR Helmholtz-Zentrum für Ozeanforschung: Kiel, Germany, 2015; Volume 7. [Google Scholar]
- Benites, M.; Millo, C.; Hein, J.; Nath, B.; Murton, B.; Galante, D.; Jovane, L. Integrated Geochemical and Morphological Data Provide Insights into the Genesis of Ferromanganese Nodules. Minerals 2018, 8, 488. [Google Scholar] [CrossRef] [Green Version]
- Burdige, D.J. The biogeochemistry of manganese and iron reduction in marine sediments. Earth-Sci. Rev. 1993, 35, 249–284. [Google Scholar] [CrossRef]
- Linke, P.; Lackschewitz, K. Autonomous Underwater Vehicle “ABYSS”. J. Large-Scale Res. Facil. 2016, 2, A79. [Google Scholar] [CrossRef] [Green Version]
- Klischies, M.; Rothenbeck, M.; Steinfuhrer, A.; Yeo, I.A.; dos Santos Ferreira, C.; Mohrmann, J.; Faber, C.; Schirnick, C. AUV Abyss workflow: Autonomous deep sea exploration for ocean research. In Proceedings of the 2018 IEEE/OES Autonomous Underwater Vehicle Workshop (AUV), Porto, Portugal, 6–9 November 2018; pp. 1–6. [Google Scholar]
- Caress, D.W.; Chayes, D.N. MB-System: Mapping the Seafloor. 2017. Available online: http://www.mbari.org/products/research-software/mb-system/ (accessed on 18 October 2021).
- Alevizos, E.; Schoening, T.; Koeser, K.; Snellen, M.; Greinert, J. Quantification of the fine-scale distribution of Mn-nodules: Insights from AUV multi-beam and optical imagery data fusion. Biogeosciences 2018, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Lecours, V.; Dolan, M.F.J.; Micallef, A.; Lucieer, V.L. A review of marine geomorphometry, the quantitative study of the seafloor. Hydrol. Earth Syst. Sci. 2016, 20, 3207–3244. [Google Scholar] [CrossRef] [Green Version]
- Iwahashi, J.; Pike, R.J. Automated classifications of topography from DEMs by an unsupervised nested-means algorithm and a three-part geometric signature. Geomorphology 2007, 86, 409–440. [Google Scholar] [CrossRef]
- Dolan, M.F.J.; Lucieer, V.L. Variation and Uncertainty in Bathymetric Slope Calculations Using Geographic Information Systems. Mar. Geod. 2014, 37, 187–219. [Google Scholar] [CrossRef]
- Naimi, B.; Skidmore, A.K.; Groen, T.A.; Hamm, N.A.S. Spatial autocorrelation in predictors reduces the impact of positional uncertainty in occurrence data on species distribution modelling. J. Biogeogr. 2011, 38, 1497–1509. [Google Scholar] [CrossRef]
- Stephens, D.; Diesing, M. A Comparison of Supervised Classification Methods for the Prediction of Substrate Type Using Multibeam Acoustic and Legacy Grain-Size Data. PLoS ONE 2014, 9, e93950. [Google Scholar] [CrossRef]
- Lucieer, V.; Huang, Z.; Siwabessy, J. Analyzing Uncertainty in Multibeam Bathymetric Data and the Impact on Derived Seafloor Attributes. Mar. Geod. 2016, 39, 32–52. [Google Scholar] [CrossRef]
- Lecours, V.; Devillers, R.; Edinger, E.N.; Brown, C.J.; Lucieer, V.L. Influence of artefacts in marine digital terrain models on habitat maps and species distribution models: A multiscale assessment. Remote Sens. Ecol. Conserv. 2017, 3, 232–246. [Google Scholar] [CrossRef]
- Hughes Clarke, J. The Impact of Acoustic Imaging Geometry on the Fidelity of Seabed Bathymetric Models. Geosciences 2018, 8, 109. [Google Scholar] [CrossRef] [Green Version]
- Florinsky, I.V. An illustrated introduction to general geomorphometry. Prog. Phys. Geogr. 2017, 41, 723–752. [Google Scholar] [CrossRef]
- Misiuk, B.; Lecours, V.; Bell, T. A multiscale approach to mapping seabed sediments. PLoS ONE 2018, 13, e0193647. [Google Scholar] [CrossRef] [Green Version]
- Cremers, J.; Klugkist, I. One Direction? A Tutorial for Circular Data Analysis Using R With Examples in Cognitive Psychology. Front. Psychol. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- Zevenbergen, L.W.; Thorne, C.R. Quantitative analysis of land surface topography. Earth Surf. Process. Landf. 1987, 12, 47–56. [Google Scholar] [CrossRef]
- Olaya, V. Chapter 6 Basic Land-Surface Parameters. Dev. Soil Sci. 2009, 33, 141–169. [Google Scholar]
- Sappington, J.M.; Longshore, K.M.; Thompson, D.B. Quantifying Landscape Ruggedness for Animal Habitat Analysis: A Case Study Using Bighorn Sheep in the Mojave Desert. J. Wildl. Manage. 2007, 71, 1419–1426. [Google Scholar] [CrossRef]
- Weiss, A. Topographic position and landforms analysis. Poster Present. ESRI User Conf. 2001, 64, 227–245. [Google Scholar]
- Wilson, M.F.J.; O’Connell, B.; Brown, C.; Guinan, J.C.; Grehan, A.J. Multiscale Terrain Analysis of Multibeam Bathymetry Data for Habitat Mapping on the Continental Slope. Mar. Geod. 2007, 30, 3–35. [Google Scholar] [CrossRef] [Green Version]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man. Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef] [Green Version]
- Walbridge, S.; Slocum, N.; Pobuda, M.; Wright, D. Unified Geomorphological Analysis Workflows with Benthic Terrain Modeler. Geosciences 2018, 8, 94. [Google Scholar] [CrossRef] [Green Version]
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling. R Package Version 3.4-13. 2021. Available online: https://CRAN.R-project.org/package=raster (accessed on 19 October 2021).
- Zvoleff, A. glcm: Calculate Textures from Grey-Level Co-Occurrence Matrices (GLCMs). R Package Version 1.6.5. 2020. Available online: https://CRAN.R-project.org/package=glcm (accessed on 19 October 2021).
- Kwasnitschka, T.; Köser, K.; Sticklus, J.; Rothenbeck, M.; Weiß, T.; Wenzlaff, E.; Schoening, T.; Triebe, L.; Steinführer, A.; Devey, C.; et al. DeepSurveyCam—A Deep Ocean Optical Mapping System. Sensors 2016, 16, 164. [Google Scholar] [CrossRef] [Green Version]
- Ellefmo, S.L.; Kuhn, T. Application of Soft Data in Nodule Resource Estimation. Nat. Resour. Res. 2021, 30, 1069–1091. [Google Scholar] [CrossRef]
- Wasilewska-Błaszczyk, M.; Mucha, J. Possibilities and Limitations of the Use of Seafloor Photographs for Estimating Polymetallic Nodule Resources—Case Study from IOM Area, Pacific Ocean. Minerals 2020, 10, 1123. [Google Scholar] [CrossRef]
- Yu, G.; Parianos, J. Empirical Application of Generalized Rayleigh Distribution for Mineral Resource Estimation of Seabed Polymetallic Nodules. Minerals 2021, 11, 449. [Google Scholar] [CrossRef]
- Tsune, A. Quantitative Expression of the Burial Phenomenon of Deep Seafloor Manganese Nodules. Minerals 2021, 11, 227. [Google Scholar] [CrossRef]
- Simon-Lledó, E.; Bett, B.J.; Huvenne, V.A.I.; Schoening, T.; Benoist, N.M.A.; Jones, D.O.B. Ecology of a polymetallic nodule occurrence gradient: Implications for deep-sea mining. Limnol. Oceanogr. 2019, 64, 1883–1894. [Google Scholar] [CrossRef] [Green Version]
- Caldas de Castro, M.; Singer, B.H. Controlling the False Discovery Rate: A New Application to Account for Multiple and Dependent Tests in Local Statistics of Spatial Association. Geogr. Anal. 2006, 38, 180–208. [Google Scholar] [CrossRef]
- Benjamini FDR_Benjamin_1995. Ital. J. Food Sci. 2009, 21, 89–95.
- Sullivan, G.M.; Feinn, R. Using Effect Size—or Why the p Value Is Not Enough. J. Grad. Med. Educ. 2012, 4, 279–282. [Google Scholar] [CrossRef] [Green Version]
- R, Core, T. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 19 October 2021).
- Kassambara, A. rstatix: Pipe-Friendly Framework for Basic Statistical Tests. R Package Version 0.7.0. 2021. Available online: https://CRAN.R-project.org/package=rstatix (accessed on 19 October 2021).
- Spearman, C. The proof and measurement of association between two things. Int. J. Epidemiol. 2010, 39, 1137–1150. [Google Scholar] [CrossRef] [Green Version]
- Makowski, D.; Ben-Shachar, M.; Patil, I.; Lüdecke, D. Methods and Algorithms for Correlation Analysis in R. J. Open Source Softw. 2020, 5, 2306. [Google Scholar] [CrossRef]
- Mukaka, M.M. Statistics corner: A guide to appropriate use of correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar]
- Schloerke, B.; Cook, D.; Larmarange, J.; Briatte, F.; Marbach, M.; Thoen, E.; Elberg, A.; Toomet, O.; Crowley, J.; Hofman, H.; et al. GGally: Extension to “ggplot2”. R Package Version 2.1.2. 2021. Available online: https://CRAN.R-project.org/package=GGally (accessed on 19 October 2021).
- Probst, P.; Wright, M.N.; Boulesteix, A. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, 1301. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, M. Caret: Classification and Regression Training. R package version 6.0-88. 2021. Available online: https://CRAN.R-project.org/package=caret (accessed on 19 October 2021).
- Greenwell, B.M. pdp: An R Package for Constructing Partial Dependence Plots. R J. 2017, 9, 421–436. Available online: https://journal.r-project.org/archive/2017/RJ-2017-016/index.html (accessed on 19 October 2021). [CrossRef] [Green Version]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An introduction to Statistical Learning. Curr. Med. Chem. 2000, 7, 995–1039. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Clustering Large Applications (Program CLARA). In Finding Groups in Data: An Introduction to Cluster Analysis; Wiley: Hoboken, NJ, USA, 1990; pp. 126–163. [Google Scholar]
- Kaufman, L.; Rousseeuw, P.J. Partitioning Around Medoids (Program PAM). In Finding Groups in Data: An Introduction to Cluster Analysis; Wiley: Hoboken, NJ, USA, 1990; pp. 68–125. [Google Scholar]
- Calinski, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat.—Theory Methods 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Maechler, M.; Rousseeuw, P.; Struyf, A.; Hubert, M.; Hornik, K. Cluster: Cluster Analysis Basics and Extensions. R Package Version 2.1.2. 2021. Available online: https://CRAN.R-project.org/package=cluster (accessed on 19 October 2021).
- Desgraupes, B. clusterCrit: Clustering Indices. R Package Version 1.2.8. 2018. Available online: https://CRAN.R-project.org/package=clusterCrit (accessed on 19 October 2021).
- Leutner, B.; Horning, N.; Schwalb-Willmann, J.; Hijmans, R.J. RStoolbox: Tools for Remote Sensing Data Analysis. R Package Version 0.2.6. 2019. Available online: https://CRAN.R-project.org/package=RStoolbox (accessed on 19 October 2021).
- Meyer, H.; Reudenbach, C.; Ludwig, M.; Nauss, T.; Pebesma, E. CAST: “caret” Applications for Spatial-Temporal Models. R Package Version 0.5.1. 2021. Available online: https://CRAN.R-project.org/package=CAST (accessed on 19 October 2021).
- Friedman Jerome, H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar]
- Molnar, C. Interpretable Machine Learning. A Guide for Making Black Box Models Explainable. 2019. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 19 October 2021).
- Cleveland, W.S. LOWESS: A Program for Smoothing Scatterplots by Robust Locally Weighted Regression. Am. Stat. 1981, 35, 54. [Google Scholar] [CrossRef]
- Verlaan, P.A.; Cronan, D.S. Origin and variability of resource-grade marine ferromanganese nodules and crusts in the Pacific Ocean: A review of biogeochemical and physical controls. Geochemistry 2021, 125741. [Google Scholar] [CrossRef]
- Kuhn, T.; Wegorzewski, A.; Rühlemann, C.; Vink, A. Composition, Formation, and Occurrence of Polymetallic Nodules BT—Deep-Sea Mining: Resource Potential, Technical and Environmental Considerations. In Deep-Sea Mining; Sharma, R., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 23–63. ISBN 978-3-319-52557-0. [Google Scholar]
- Skowronek, A.; Maciąg, Ł.; Zawadzki, D.; Strzelecka, A.; Baláž, P.; Mianowicz, K.; Abramowski, T.; Konečný, P.; Krawcewicz, A. Chemostratigraphic and Textural Indicators of Nucleation and Growth of Polymetallic Nodules from the Clarion-Clipperton Fracture Zone (IOM Claim Area). Minerals 2021, 11, 868. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Rossiter, D.G. About regression-kriging: From equations to case studies. Comput. Geosci. 2007, 33, 1301–1315. [Google Scholar] [CrossRef]
- Lobo, J.M. More complex distribution models or more representative data? Biodivers. Inform. 2008, 5, 40. [Google Scholar] [CrossRef] [Green Version]
- Mets, K.D.; Armenteras, D.; Dávalos, L.M. Spatial autocorrelation reduces model precision and predictive power in deforestation analyses. Ecosphere 2017, 8, e01824. [Google Scholar] [CrossRef]
- Hengl, T.; Walsh, M.G.; Sanderman, J.; Wheeler, I.; Harrison, S.P.; Prentice, I.C. Global mapping of potential natural vegetation: An assessment of machine learning algorithms for estimating land potential. PeerJ 2018, 6, e5457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Robert, K.; Jones, D.O.B.; Roberts, J.M.; Huvenne, V.A.I. Improving predictive mapping of deep-water habitats: Considering multiple model outputs and ensemble techniques. Deep Sea Res. Part I Oceanogr. Res. Pap. 2016, 113, 80–89. [Google Scholar] [CrossRef]
- Wang, J.-F.; Stein, A.; Gao, B.-B.; Ge, Y. A review of spatial sampling. Spat. Stat. 2012, 2, 1–14. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors. Ecol. Inform. 2011, 6, 228–241. [Google Scholar] [CrossRef]
- Hengl, T.; Rossiter, D.G.; Stein, A. Soil sampling strategies for spatial prediction by correlation with auxiliary maps. Soil Res. 2003, 41, 1403. [Google Scholar] [CrossRef]
- Brus, D.J. Sampling for digital soil mapping: A tutorial supported by R scripts. Geoderma 2019, 338, 464–480. [Google Scholar] [CrossRef]
- Malone, B.P.; Minansy, B.; Brungard, C. Some methods to improve the utility of conditioned Latin hypercube sampling. PeerJ 2019, 7, e6451. [Google Scholar] [CrossRef]
- Foster, S.D.; Hosack, G.R.; Hill, N.A.; Barrett, N.S.; Lucieer, V.L. Choosing between strategies for designing surveys: Autonomous underwater vehicles. Methods Ecol. Evol. 2014, 5, 287–297. [Google Scholar] [CrossRef] [Green Version]
- Yilmaz, N.K.; Evangelinos, C.; Lermusiaux, P.; Patrikalakis, N.M. Path Planning of Autonomous Underwater Vehicles for Adaptive Sampling Using Mixed Integer Linear Programming. IEEE J. Ocean. Eng. 2008, 33, 522–537. [Google Scholar] [CrossRef] [Green Version]
- Foster, S.D.; Hosack, G.R.; Monk, J.; Lawrence, E.; Barrett, N.S.; Williams, A.; Przeslawski, R. Spatially balanced designs for transect-based surveys. Methods Ecol. Evol. 2020, 11, 95–105. [Google Scholar] [CrossRef] [Green Version]
- Hughes, R.N.; Hughes, D.J.; Smith, I.P.; Dale, A.C. (Eds.) Oceanography and Marine Biology; CRC Press: Boca Raton, FL, USA, 2016; ISBN 978-131-536-8-597. [Google Scholar]
- Schmidt, K.; Behrens, T.; Daumann, J.; Ramirez-Lopez, L.; Werban, U.; Dietrich, P.; Scholten, T. A comparison of calibration sampling schemes at the field scale. Geoderma 2014, 232–234, 243–256. [Google Scholar] [CrossRef]
- Wadoux, A.M.-C.; Brus, D.J.; Heuvelink, G.B.M. Sampling design optimization for soil mapping with random forest. Geoderma 2019, 355, 113913. [Google Scholar] [CrossRef]
- Bowden, D.A.; Anderson, O.F.; Rowden, A.A.; Stephenson, F.; Clark, M.R. Assessing Habitat Suitability Models for the Deep Sea: Is Our Ability to Predict the Distributions of Seafloor Fauna Improving? Front. Mar. Sci. 2021, 8, 632389. [Google Scholar] [CrossRef]
- Fernández-Delgado, M.; Sirsat, M.S.; Cernadas, E.; Alawadi, S.; Barro, S.; Febrero-Bande, M. An extensive experimental survey of regression methods. Neural Netw. 2019, 111, 11–34. [Google Scholar] [CrossRef] [PubMed]
- Merow, C.; Smith, M.J.; Edwards, T.C.; Guisan, A.; McMahon, S.M.; Normand, S.; Thuiller, W.; Wüest, R.O.; Zimmermann, N.E.; Elith, J. What do we gain from simplicity versus complexity in species distribution models? Ecography 2014, 37, 1267–1281. [Google Scholar] [CrossRef]
- Bochare, A.; Gangopadhyay, A.; Yesha, Y.; Joshi, A.; Yesha, Y.; Brady, M.; Grasso, M.A.; Rishe, N. Integrating domain knowledge in supervised machine learning to assess the risk of breast cancer. Int. J. Med. Eng. Inform. 2014, 6, 87. [Google Scholar] [CrossRef]
- Guan, X.; Runger, G.; Liu, L. Dynamic incorporation of prior knowledge from multiple domains in biomarker discovery. BMC Bioinform. 2020, 21, 77. [Google Scholar] [CrossRef] [Green Version]
- Lauria, V.; Power, A.M.; Lordan, C.; Weetman, A.; Johnson, M.P. Spatial Transferability of Habitat Suitability Models of Nephrops norvegicus among Fished Areas in the Northeast Atlantic: Sufficiently Stable for Marine Resource Conservation? PLoS ONE 2015, 10, e0117006. [Google Scholar] [CrossRef] [PubMed]
- Shmueli, G. To Explain or to Predict? Stat. Sci. 2010, 25, 330. [Google Scholar] [CrossRef]
- Breiman, L. Statistical Modeling: The Two Cultures (with comments and a rejoinder by the author). Stat. Sci. 2001, 16, 726. [Google Scholar] [CrossRef]










| MBES Derivatives | Abbreviation | Algorithm |
|---|---|---|
| Mean Depth | MD | Focal statistics *1 |
| Deviation from Mean Depth | DFMD | Focal statistics *1 |
| Slope | S | Zevenbergen and Thorne, 1987 *1 [95] |
| Northness | N | Olaya, 2009 *2 [96] |
| Eastness | E | Olaya, 2009 *2 |
| Profile Curvature | PrC | Zevenbergen and Thorne, 1987 *1 |
| Plan Curvature | PlC | Zevenbergen and Thorne, 1987 *1 |
| Terrain Surface Convexity | TSC | Iwahashi and Pike, 2006 *1 [85] |
| Vector Ruggedness Measure | VRM | Sappington et al., 2007 *1 [97] |
| Bathymetric Position Index | BPI | Weiss, 2000 [98], Wilson et al., 2007 *1 [99] |
| Backscatter | BS | Focal statistics *1 |
| Backscatter SD | BSSD | Focal statistics *1 |
| Backscatter Local Moran | BSLM | Anselin, 1995 *3 [16] |
| Backscatter Entropy | BSE | Haralick et al. 1973 *4 [100] |
| Derivatives | Significance | Effect Size | Magnitude |
|---|---|---|---|
| Backscatter (BS) | p < 2.2 × 10−16 | 0.537 | large |
| Bathymetric Position Index (BPI100_300) | p < 2.2 × 10−16 | 0.346 | moderate |
| Northness (N) | p < 2.2 × 10−16 | 0.273 | small |
| Mean Depth (MD) | p < 2.2 × 10−16 | 0.269 | small |
| Backscatter Local Moran (BSLM) | p < 2.2 × 10−16 | 0.216 | small |
| Bathymetric Position Index (BPI30_100) | p < 2.2 × 10−16 | 0.149 | small |
| Plan Curvature (PlC) | p < 2.2 × 10−16 | 0.133 | small |
| Terrain Surface Convexity (TSC) | p < 2.2 × 10−16 | 0.117 | small |
| Eastness (E) | p < 2.2 × 10−16 | 0.077 | small |
| Vector Ruggedness Measure (VRM) | p = 8.156 × 10−16 | 0.072 | small |
| Profile Curvature (PrC) | p = 3.031 × 10−12 | 0.063 | small |
| Slope (S) | p = 1.437 × 10−6 | 0.043 | small |
| Deviation from Mean Depth (DFMD) | p = 0.00225 | 0.027 | small |
| Backscatter SD (BSSD) | p = 0.04903 | 0.018 | small |
| Bathymetric Position Index (BPI0_30) | p = 0.09455 | 0.015 | small |
| Backscatter Entropy (BSE) | p = 0.64650 | 0.004 | small |
| Training Data | OOB | Random-CV | Spatial-CV | Cluster-CV |
|---|---|---|---|---|
| H-H and L-L data (12,327) | 0.93 | 0.93 | 0.19 | 0.53 |
| All training data (19,952) | 0.87 | 0.87 | 0.14 | 0.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gazis, I.-Z.; Greinert, J. Importance of Spatial Autocorrelation in Machine Learning Modeling of Polymetallic Nodules, Model Uncertainty and Transferability at Local Scale. Minerals 2021, 11, 1172. https://doi.org/10.3390/min11111172
Gazis I-Z, Greinert J. Importance of Spatial Autocorrelation in Machine Learning Modeling of Polymetallic Nodules, Model Uncertainty and Transferability at Local Scale. Minerals. 2021; 11(11):1172. https://doi.org/10.3390/min11111172
Chicago/Turabian StyleGazis, Iason-Zois, and Jens Greinert. 2021. "Importance of Spatial Autocorrelation in Machine Learning Modeling of Polymetallic Nodules, Model Uncertainty and Transferability at Local Scale" Minerals 11, no. 11: 1172. https://doi.org/10.3390/min11111172
APA StyleGazis, I.-Z., & Greinert, J. (2021). Importance of Spatial Autocorrelation in Machine Learning Modeling of Polymetallic Nodules, Model Uncertainty and Transferability at Local Scale. Minerals, 11(11), 1172. https://doi.org/10.3390/min11111172






