A Statistical Evaluation to Compare and Analyze Estimations of the Diffusion Coefficient of Pertechnetate (99TcO4−) in Compacted Bentonite
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Bentonite Clay Sample, Radioisotopes Standards, Chemical Reagents, and the Liquid Phase
2.2. Physical Characterization of Bentonite Clay
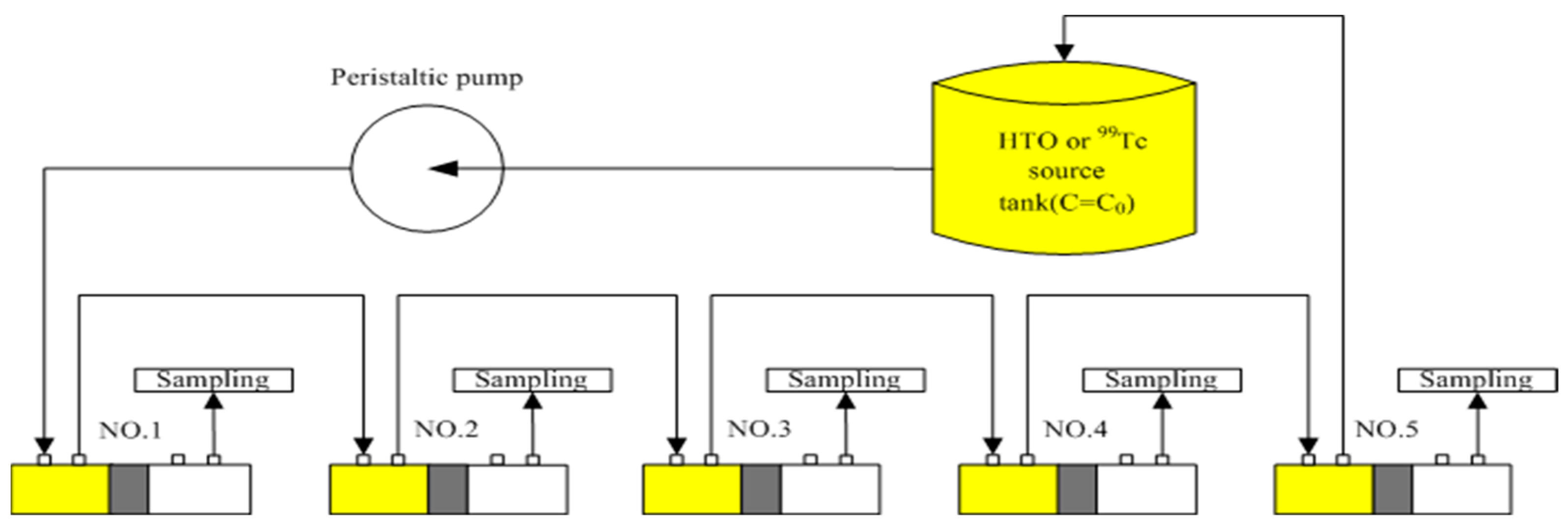
2.3. Experimental Set-Up for Through-Diffusion with a Constant Inlet Concentration–Constant Outlet Concentration
2.4. Statistical Analysis Using the Various Numerical Estimations of the Diffusion Parameter
2.4.1. Asymptote Estimation
2.4.2. Analytical Estimation Using Lsqcurvefit
2.4.3. Inverse Estimation
2.4.4. Statistical Analysis
3. Results
3.1. Characterization of the FTIR Analysis
3.2. Diffusion Behavior of HTO and 99Tc in the TD Experiments
3.3. Statistical Analysis of the Numerical Estimations of HTO and 99Tc
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- U.S. Nuclear Waste Technical Review Board. Survey of National Programs for Managing High.-Level Radioactive Waste and Spent Nuclear Fuel: Update, A Report to Congress and the Secretary of Energy; U.S. Nuclear Waste Technical Review Board: Arlington, VA, USA, 2016.
- Taiwan Power Company. Preliminary Technical Feasibility Study for Final Disposal of Spent Nuclear Fuel—2009 Progress Report (Summary); Taiwan Power Company: Taipei, Taiwan, 2009. [Google Scholar]
- Japan Nuclear Cycle Development Institute. Japan, H12: Project to Establish the Scientific and Technical Basis for HLW Disposal in Japan; Japan Nuclear Cycle Development Institute: Ibaraki, Japan, 2000. [Google Scholar]
- Svensk Kärnbränslehantering AB. Program. for Research, Development and Demonstration of Methods for the Management and Disposal of Nuclear Waste TR-16-15; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2016. [Google Scholar]
- Yang, T.; Knutsson, S.; Liu, X. Swelling properties and permeability of expandable clays of potential use for nuclear waste disposal. J. Earth Sci. Geotech. Eng. 2016, 6, 9–61. [Google Scholar]
- Yu, J.W.; Neretnieks, I. Diffusion and Sorption Properties of Radionuclides in Compacted Bentonite TR 97-12; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 1997. [Google Scholar]
- Ikäheimonen, T.K.; Vartti, V.P.; Ilus, E.; Mattila, J. Technetium-99 in Fucus and seawater samples in the Finnish coastal area of the Baltic Sea, 1999. J. Radioanal. Nucl. Chem. 2002, 252, 309–313. [Google Scholar] [CrossRef]
- Chao, J.H.; Tseng, C.L.; Lee, C.L. Sequential extraction separation for determination of technetium-99 in radwastes by ICP-MS. J. Radioanal. Nucl. Chem. 2002, 251, 105–112. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, Z.; Xu, J. 99TcO4− diffusion and sorption in compacted MX-80 bentonite studied by capillary method. J. Radioanal. Nucl. Chem. 2013, 298, 147–152. [Google Scholar] [CrossRef]
- Liu, D.J.; Fan, X.H. Adsorption behavior of 99Tc on Fe, Fe2O3 and Fe3O4. J. Radioanal. Nucl. Chem. 2005, 264, 691–698. [Google Scholar] [CrossRef]
- Wang, H.; Wu, T.; Chen, J.; Fu, B.; Juo, Y.; Zhao, Y.; He, C. Effect of humic acid on the diffusion of ReO4− in GMZ bentonite. J. Radioanal. Nucl. Chem. 2015, 303, 187–191. [Google Scholar] [CrossRef]
- Wu, T.; Wang, Z.; Li, Q.; Pan, G.; Li, J.; Van Loon, L.R. Re(VII) diffusion in bentonite: Effect of organic compounds, pH and temperature. App. Clay Sci. 2016, 127, 10–16. [Google Scholar] [CrossRef] [Green Version]
- Vinšová, H.; Večerník, P.; Jedináková-Křížová, V. Sorption characteristics of 99Tc onto bentonite material with different additives under anaerobic conditions. Radiochim. Acta 2006, 94, 435–440. [Google Scholar] [CrossRef]
- Wang, X.; Tao, Z. Diffusion of 99TcO4− in compacted bentonite: Effect of pH, concentration, density and contact time. J. Radioanal. Nucl. Chem. 2004, 260, 305–309. [Google Scholar] [CrossRef]
- Wu, T.; Wang, H.; Zheng, Q.; Zhao, Y.; Li, J. Effect of EDTA on the diffusion behavior of 99TcO4− and ReO4− in GMZ bentonite. J. Radioanal. Nucl. Chem. 2014, 299, 2037–2041. [Google Scholar] [CrossRef]
- Paul, C. Compilation of Radionuclide Sorption Coefficients for Performance Assessment TR-97-13; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 1997. [Google Scholar]
- Garcia-Gutierrez, M.; Cormenzana, J.L.; Missana, T.; Mingarro, M.; Molinero, J. Overview of laboratory methods employed for obtaining diffusion coefficients in FEBEX compacted bentonite. J. Iber. Geol. 2006, 32, 37–53. [Google Scholar]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Eriksen, T.E.; Jansson, M. Diffusion of I−, Cs+ and Sr2+ in Compacted Bentonite-Anion Exclusion and Surface Diffusion TR-96-16; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 1996. [Google Scholar]
- Eriksen, T.E.; Jansson, M.; Molera, M. Sorption effects on cation diffusion in compacted bentonite. Eng. Geol. 1999, 54, 231–236. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the Proceedings of ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 1942–1948. [Google Scholar]
- Bharat, T.V.; Das, P.; Srivastava, A. Insights into Contaminant Transport Modeling Through Compacted Bentonites. In Frontiers in Geotechnical Engineering; Latha, G.M., Ed.; Springer Nature: Singapore, 2019; pp. 101–120. [Google Scholar]
- Wu, T.; Dai, W.; Xiao, G.P.; Shu, F.J.; Yao, J.; Li, J.Y. Influence of dry density on HTO diffusion in GMZ bentonite. J. Radioanal. Nucl. Chem. 2009, 292, 853–857. [Google Scholar] [CrossRef]
- Wu, T.; Amayri, S.; Drebert, J.; Van Loon, L.R.; Reich, T. Neptunium(V) sorption and diffusion in opalinus clay. Environ. Sci. Technol. 2009, 43, 6567–6571. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.H.; Teng, S.P. A dual period diffusion model for measuring diffusion parameters. Waste Manag. 1993, 13, 15–24. [Google Scholar] [CrossRef]
- Wang, B.T.; Lee, C.P.; Wu, M.C.; Tsai, T.L.; Tsai, S.C.; Hsu, K.C. Novel Method for Analyzing Transport Parameters in Through-Diffusion Tests. J. Environ. Radioact. 2019, 196, 125–132. [Google Scholar] [CrossRef] [PubMed]
- Shih, Y.H.; Lee, I.H.; Ni, C.F.; Tsai, T.L.; Chen, L.C.; Lee, C.P.; Tsai, S.C.; Su, T.Y. Experimental and numerical investigations of 99TcO42− diffusion in compacted SPV 200 bentonite. J. Radioanal. Nucl. Chem. 2018, 316, 1081–1089. [Google Scholar] [CrossRef]
- Li, M.H.; Wang, T.H.; Teng, S.P. Experimental and numerical investigations of effect of column length on retardation factor determination: A case study of cesium transport in crushed granite. J. Hazard. Mater. 2009, 162, 530–535. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.P.; Lan, P.L.; Jan, Y.L.; Wei, Y.Y.; Teng, S.P.; Hsu, C.N. Sorption and diffusion of HTO and cesium in crushed granite compacted to different lengths. J. Radioanal. Nucl. Chem. 2008, 275, 371–378. [Google Scholar] [CrossRef]
- Lee, C.P.; Wei, Y.Y.; Tsai, S.C.; Teng, S.P.; Hsu, C.N. Diffusion of cesium and selenium in mudrock. J. Radioanal. Nucl. Chem. 2009, 275, 761–768. [Google Scholar] [CrossRef]
- Lee, C.P.; Wu, M.C.; Tsai, T.L.; Wei, H.J.; Men, L.C.; Lin, T.Y. Comparative study on retardation behavior of Cs in crushed and intact rocks: Two potential repository host rocks in the Taiwan area. J. Radioanal. Nucl. Chem. 2012, 293, 579–586. [Google Scholar] [CrossRef]
- Wildenschild, D.; Hopmans, J.W. Flow rate dependence of soil hydraulic characteristics. Soil Sci. Soc. Am. J. 2001, 65, 35–48. [Google Scholar] [CrossRef]
- Bitterlich, S.; Durner, W.; Iden, S.C.; Knabner, P. Inverse estimation of the unsaturated soil hydraulic properties from column outflow experiments using free-form parameterizations. Vadose Zone J. 2004, 3, 971–981. [Google Scholar] [CrossRef]
- Laloy, E.; Weynants, M.; Bielders, C.L.; Vanclooster, M.; Javaux, M. How efficient are one-dimensional models to reproduce the hydrodynamic behavior of structured soils subjected to multi-step outflow experiments. J. Hydrol. 2010, 393, 37–52. [Google Scholar] [CrossRef]
- Schelle, H.; Iden, S.C.; Peters, A.; Durner, W. Analysis of the agreement of soil hydraulic properties obtained from multistep-outflow and evaporation methods. Vadose Zone J. 2010, 9, 1080–1091. [Google Scholar] [CrossRef]
- Young, M.H.; Karagunduz, A.; Šimůnek, J.; Pennell, K.D. A modified upward infiltration method for characterizing soil hydraulic properties. Soil Sci. Soc. Am. J. 2002, 66, 57–64. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T. Modeling nonequilibrium flow and transport processes using HYDRUS. Vadose Zone J. 2008, 7, 782–797. [Google Scholar] [CrossRef] [Green Version]
- Van Loon, L.R.; Soler, J.M.; Bradbury, M.H. Diffusion of HTO, 36Cl− and 125I− in Opalinus Clay samples from Mont Terri: Effect of confining pressure. J. Contam. Hydrol. 2003, 61, 73–83. [Google Scholar] [CrossRef]
- Van Loon, L.R.; Soler, J.M.; Jakob, A.; Bradbury, M.H. Effect of confining pressure on the diffusion of HTO, 36Cl− and 125I− in a layered argillaceous rock (Opalinus Clay): Diffusion perpendicular to bedding. Appl. Geochem. 2003, 18, 1653–1662. [Google Scholar] [CrossRef]
- Li, J.; Dai, W.; Xiao, G.; Wang, H.; Zhang, Z.T.; Wu, T. Pertechnetate diffusion in MX-80 bentonite. J. Radioanal. Nucl. Chem. 2012, 293, 763–767. [Google Scholar] [CrossRef]
- Hedin, A. Data Report for the Safety Assessment SR-Site TR 10-52; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2010. [Google Scholar]


| Parameter | Radionuclides (RN) | Method of Estimation | Number of Samples | Bulk Density (kg/m3) | ||||
|---|---|---|---|---|---|---|---|---|
| 1200 | 1400 | 1600 | 1800 | 2000 | ||||
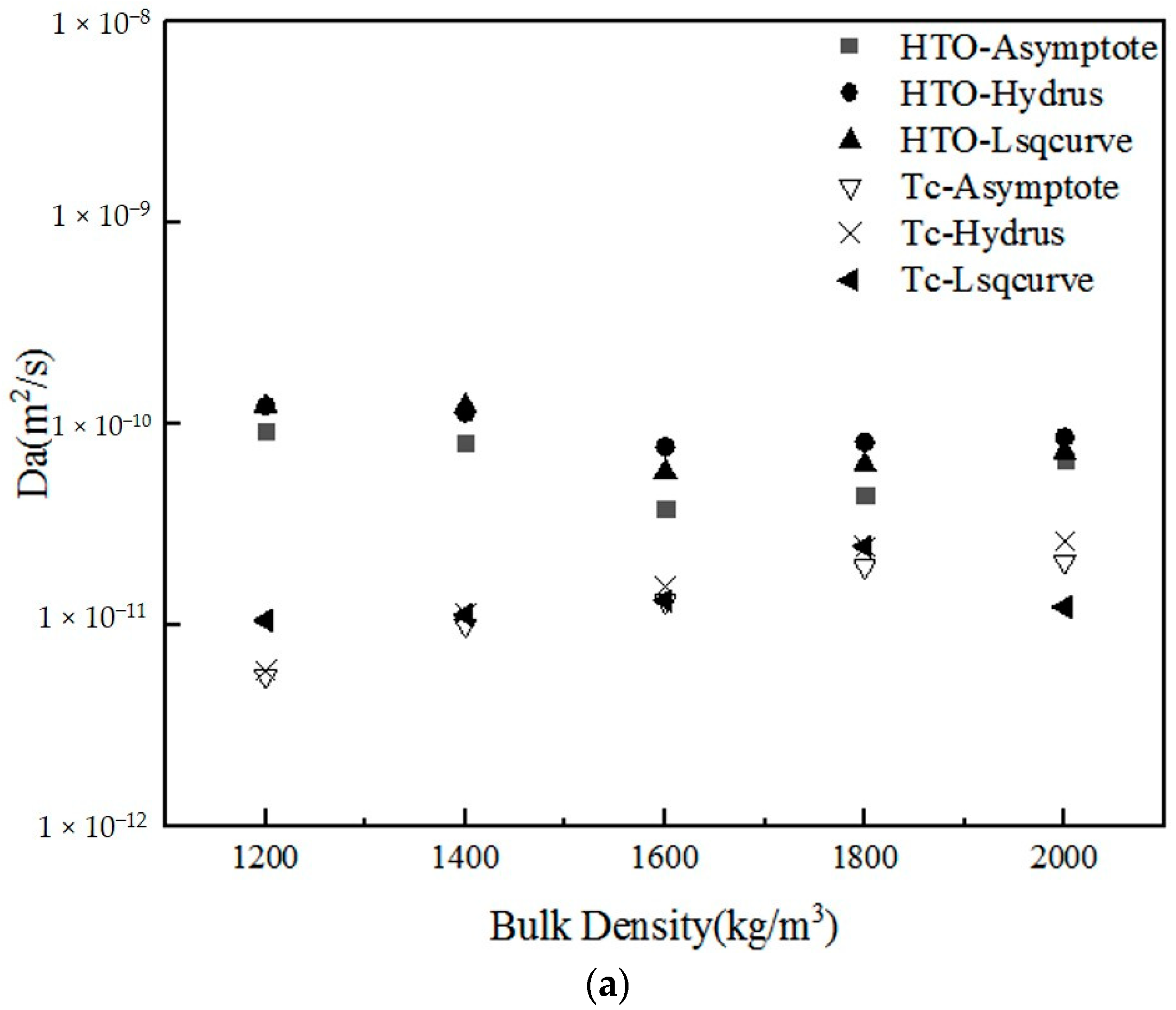
| Da (m2/s) | HTO | Asymptote | 5 | 9.18 × 10−11 | 8.01 × 10−11 | 3.79 × 10−11 | 4.41 × 10−11 | 6.60 × 10−11 |
| Hydrus-1D | 5 | 1.22 × 10−10 | 1.13 × 10−10 | 7.65 × 10−11 | 8.09 × 10−11 | 8.55 × 10−11 | ||
| Lsqcurvefit | 5 | 1.22 × 10−10 | 1.22 × 10−10 | 5.76 × 10−11 | 6.24 × 10−11 | 7.21×10−11 | ||
| Mean | 1.12 × 10−10 | 1.05 × 10−10 | 5.73 × 10−11 | 6.25 × 10−11 | 7.45 × 10−11 | |||
| Standard deviation | 1.74 × 10−11 | 2.21 × 10−11 | 1.93 × 10−11 | 1.84 × 10−11 | 9.98 × 10−12 | |||
| Tc | Asymptote | 5 | 5.54 × 10−12 | 9.94 × 10−12 | 1.30 × 10−11 | 1.94 × 10−11 | 2.05 × 10−11 | |
| Hydrus-1D | 5 | 5.90 × 10−12 | 1.13 × 10−11 | 1.56 × 10−11 | 2.43 × 10−11 | 2.60 × 10−11 | ||
| Lsqcurvefit | 5 | 1.05 × 10−11 | 1.12 × 10−11 | 1.32 × 10−11 | 2.45 × 10−11 | 1.22 × 10−11 | ||
| Mean | 7.32 × 10−12 | 1.08 × 10−11 | 1.39 × 10−11 | 2.28 × 10−11 | 1.95 × 10−11 | |||
| Standard deviation | 2.78 × 10−12 | 7.64 × 10−13 | 1.48 × 10−12 | 2.89 × 10−12 | 6.99 × 10−12 | |||
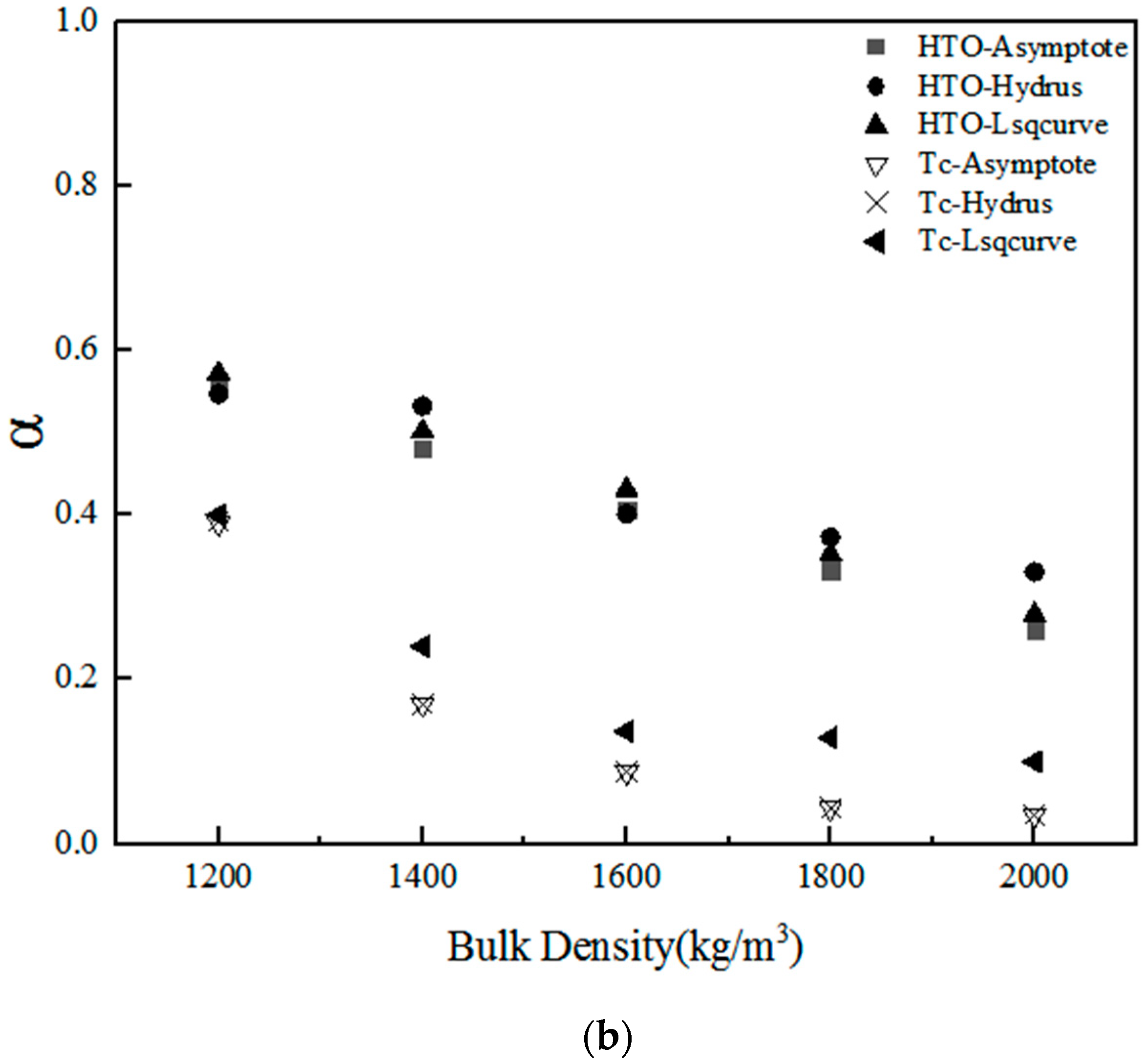
| α | HTO | Asymptote | 5 | 0.5556 | 0.4815 | 0.4074 | 0.3333 | 0.2593 |
| Hydrus-1D | 5 | 0.5475 | 0.5327 | 0.4013 | 0.3733 | 0.3310 | ||
| Lsqcurvefit | 5 | 0.5722 | 0.5019 | 0.4312 | 0.3527 | 0.2787 | ||
| Mean | 0.5584 | 0.5054 | 0.4133 | 0.3531 | 0.2897 | |||
| Standard deviation | 0.0126 | 0.0258 | 0.0158 | 0.0200 | 0.0371 | |||
| Tc | Asymptote | 5 | 0.3900 | 0.1700 | 0.0876 | 0.0433 | 0.0351 | |
| Hydrus-1D | 5 | 0.3924 | 0.1692 | 0.0876 | 0.0433 | 0.0351 | ||
| Lsqcurvefit | 5 | 0.4000 | 0.2403 | 0.1370 | 0.1290 | 0.1000 | ||
| Mean | 0.3941 | 0.1932 | 0.1041 | 0.0719 | 0.0567 | |||
| Standard deviation | 0.0052 | 0.0408 | 0.0285 | 0.0495 | 0.0375 | |||
| RN | Method of Estimation | Da | Density | α |
|---|---|---|---|---|
| HTO | Asymptote | 6.40 × 10−11 | 1200~2000 | 0.4074 |
| Hydrus-1D | 9.56 × 10−11 | 1200~2000 | 0.4372 | |
| Lsqcurvefit | 8.72 × 10−11 | 1200~2000 | 0.4273 | |
| Tc | Asymptote | 1.37 × 10−11 | 1200~2000 | 0.1452 |
| Hydrus-1D | 1.66 × 10−11 | 1200~2000 | 0.1455 | |
| Lsqcurvefit | 1.43 × 10−11 | 1200~2000 | 0.2013 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-P.; Hu, Y.; Chen, D.; Tien, N.-C.; Tsai, S.-C.; Shi, Y.; Lee, I.-H.; Ni, C.-F. A Statistical Evaluation to Compare and Analyze Estimations of the Diffusion Coefficient of Pertechnetate (99TcO4−) in Compacted Bentonite. Minerals 2021, 11, 1075. https://doi.org/10.3390/min11101075
Lee C-P, Hu Y, Chen D, Tien N-C, Tsai S-C, Shi Y, Lee I-H, Ni C-F. A Statistical Evaluation to Compare and Analyze Estimations of the Diffusion Coefficient of Pertechnetate (99TcO4−) in Compacted Bentonite. Minerals. 2021; 11(10):1075. https://doi.org/10.3390/min11101075
Chicago/Turabian StyleLee, Chuan-Pin, Yanqin Hu, Dongyang Chen, Neng-Chuan Tien, Shih-Chin Tsai, Yunfeng Shi, I-Hsien Lee, and Chuen-Fa Ni. 2021. "A Statistical Evaluation to Compare and Analyze Estimations of the Diffusion Coefficient of Pertechnetate (99TcO4−) in Compacted Bentonite" Minerals 11, no. 10: 1075. https://doi.org/10.3390/min11101075
APA StyleLee, C.-P., Hu, Y., Chen, D., Tien, N.-C., Tsai, S.-C., Shi, Y., Lee, I.-H., & Ni, C.-F. (2021). A Statistical Evaluation to Compare and Analyze Estimations of the Diffusion Coefficient of Pertechnetate (99TcO4−) in Compacted Bentonite. Minerals, 11(10), 1075. https://doi.org/10.3390/min11101075







