Computational Surface Modelling of Ices and Minerals of Interstellar Interest—Insights and Perspectives
Abstract
1. Introduction
2. Computational Chemistry Methods
2.1. Quantum Chemical (QC) Methods
2.1.1. Wave Function-Based Methods
2.1.2. Methods Based on the Density Functional Theory (DFT)
2.1.3. Semiempirical Methods
2.1.4. Basis Set
2.2. Classical Molecular Mechanic (MM) and Molecular Dynamic (MD) Simulations
3. Results
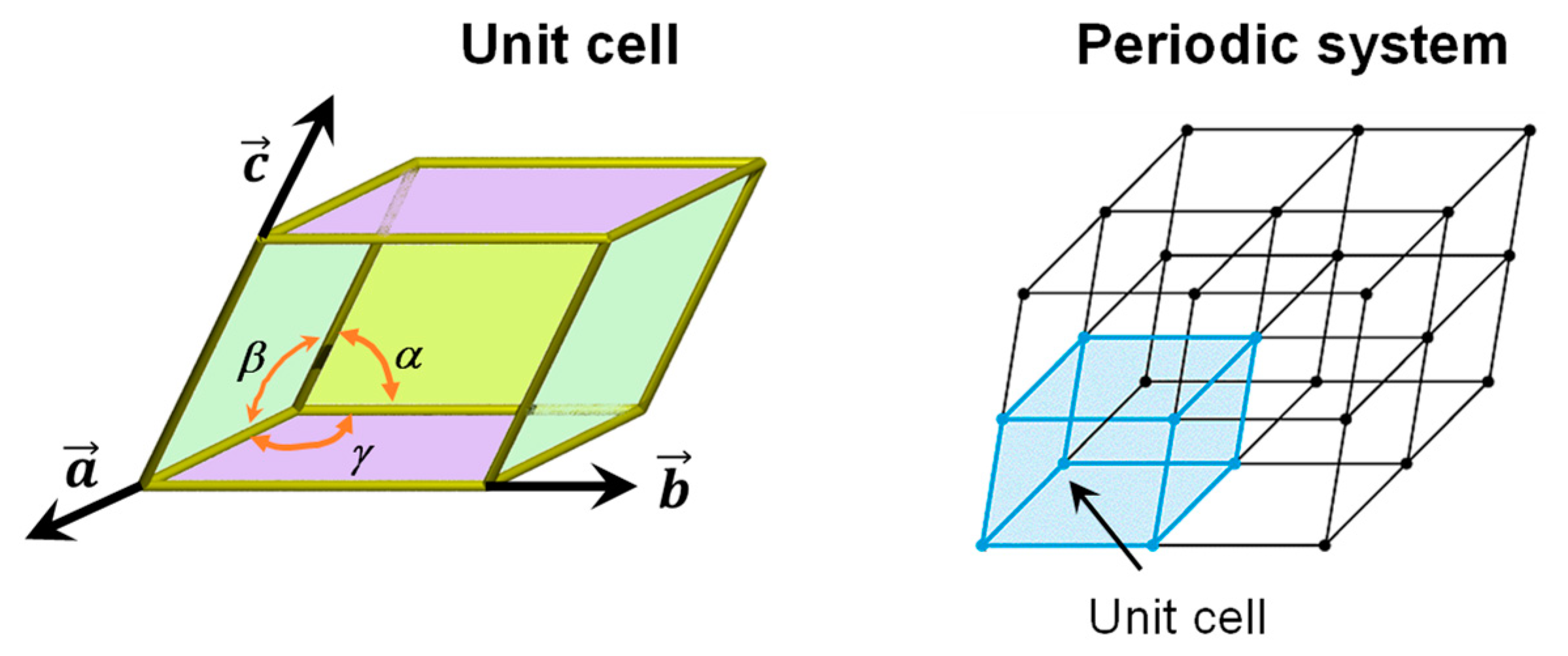
3.1. Periodic Surfaces
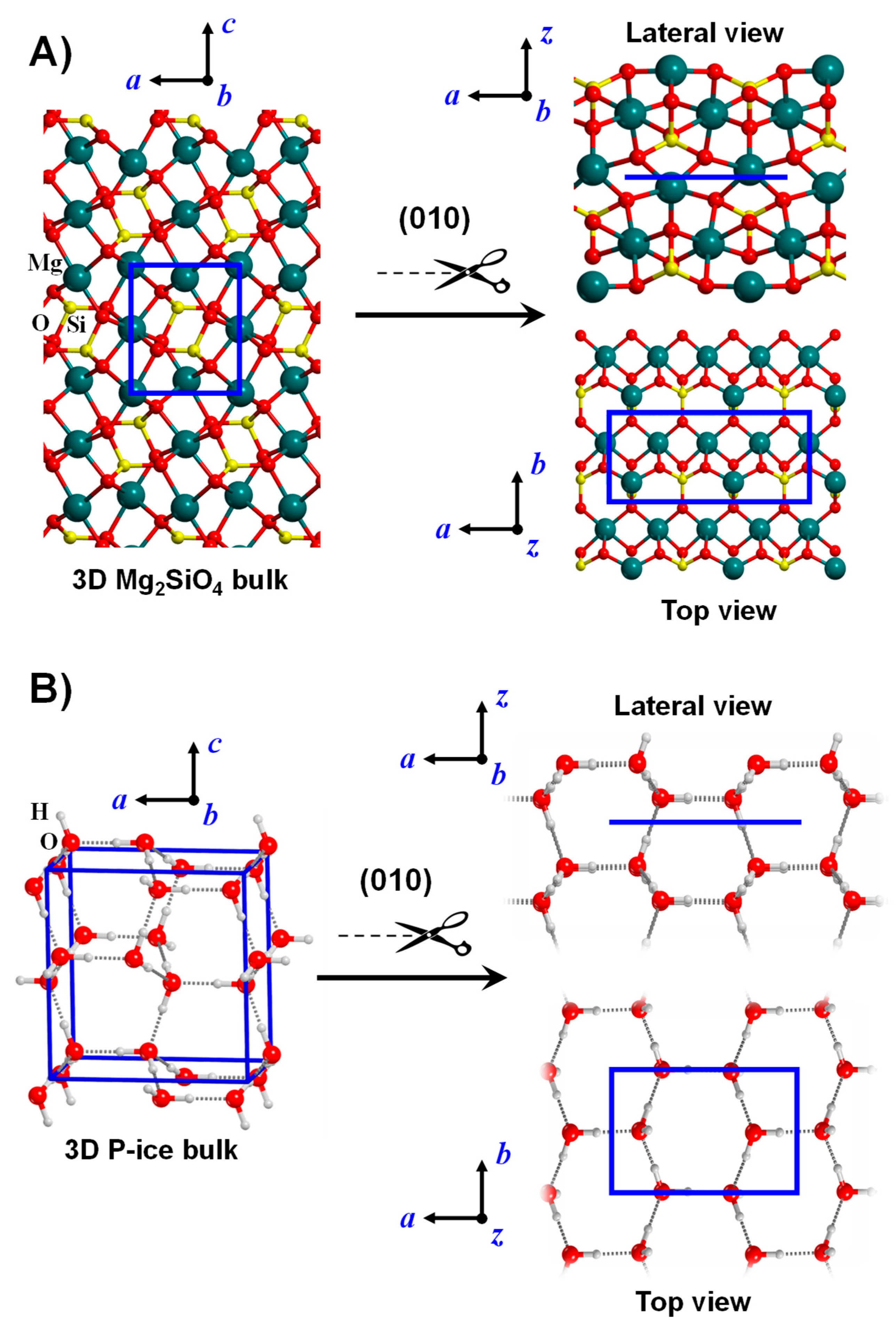
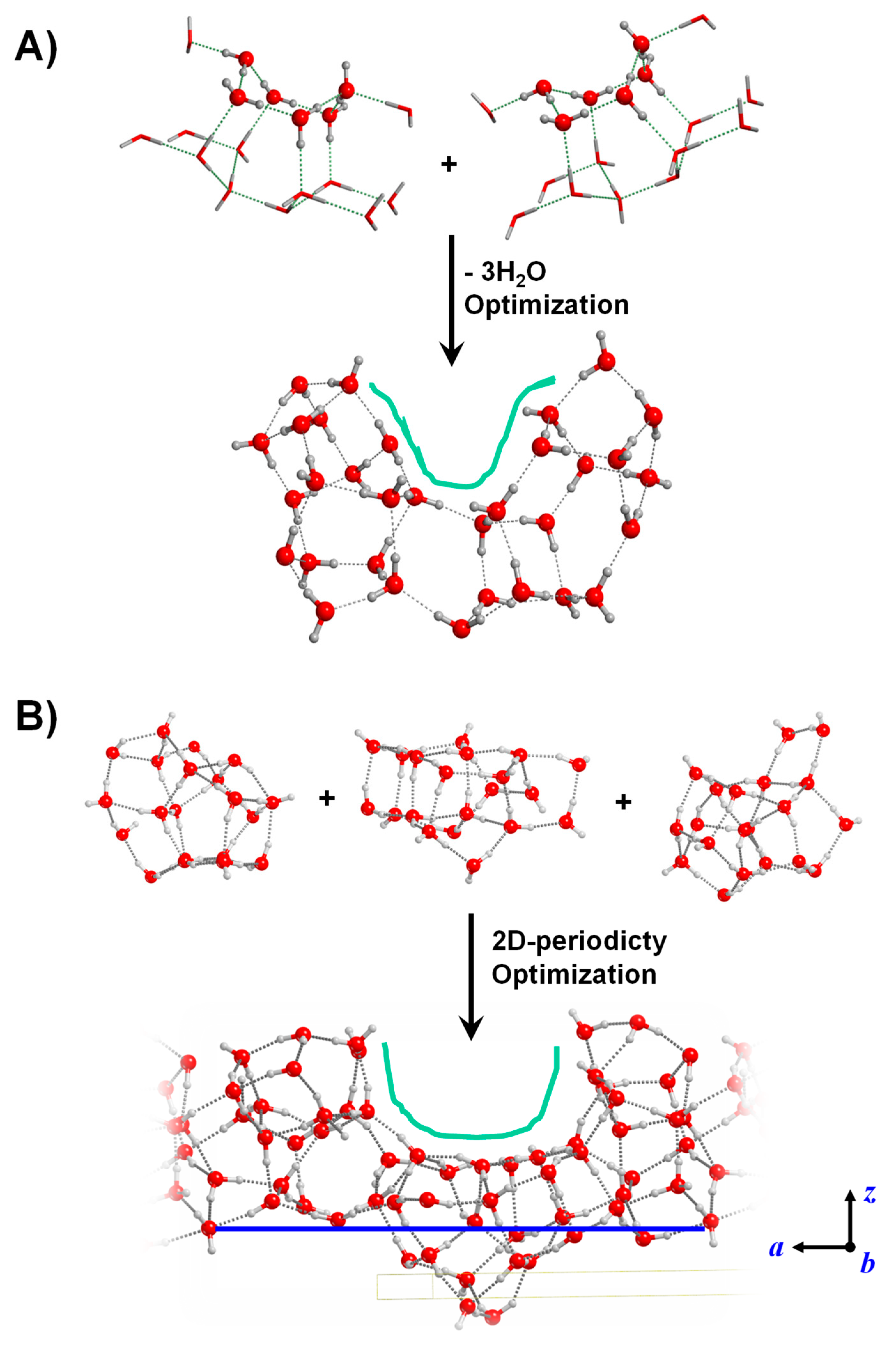
3.1.1. Crystalline Surfaces
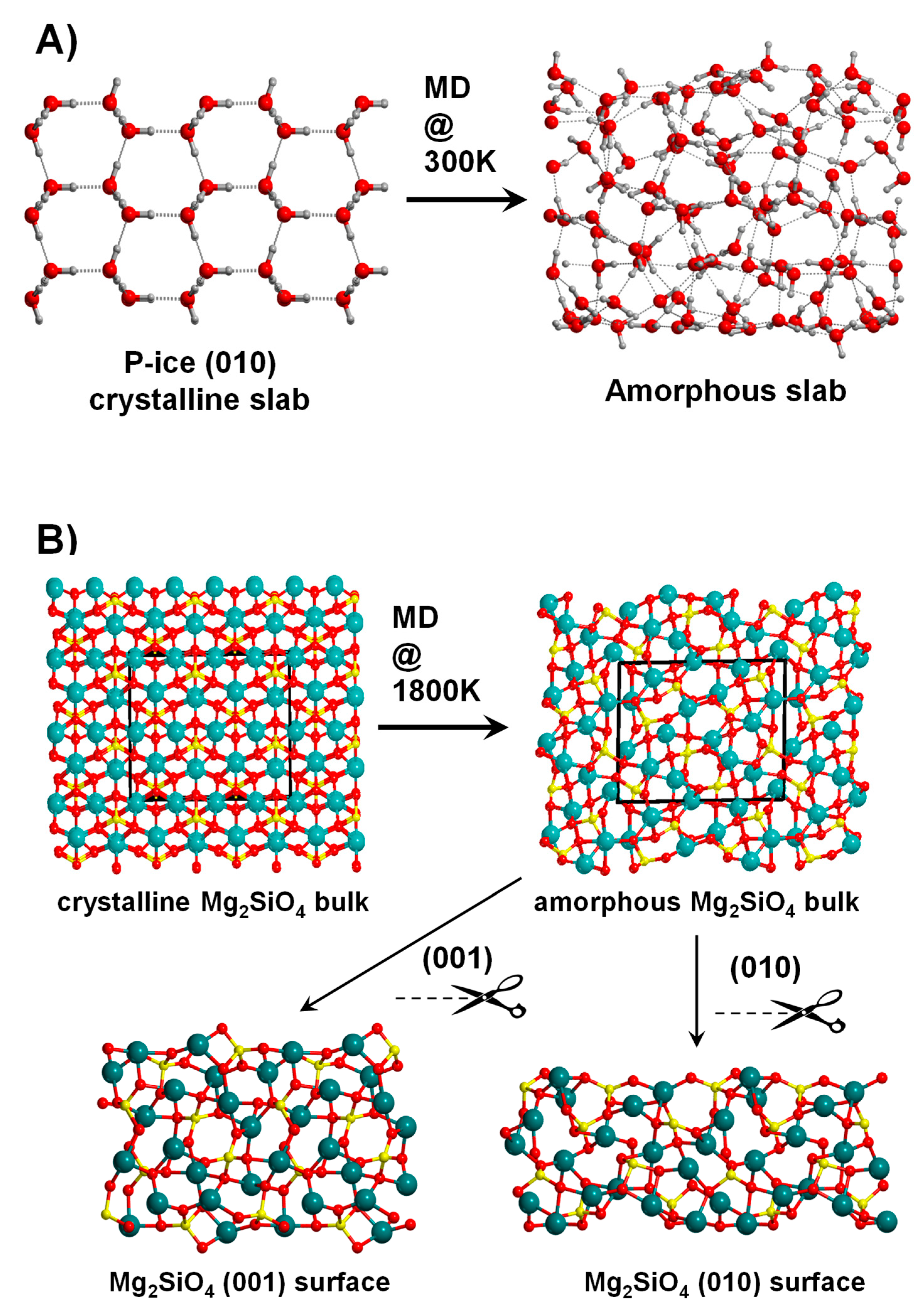
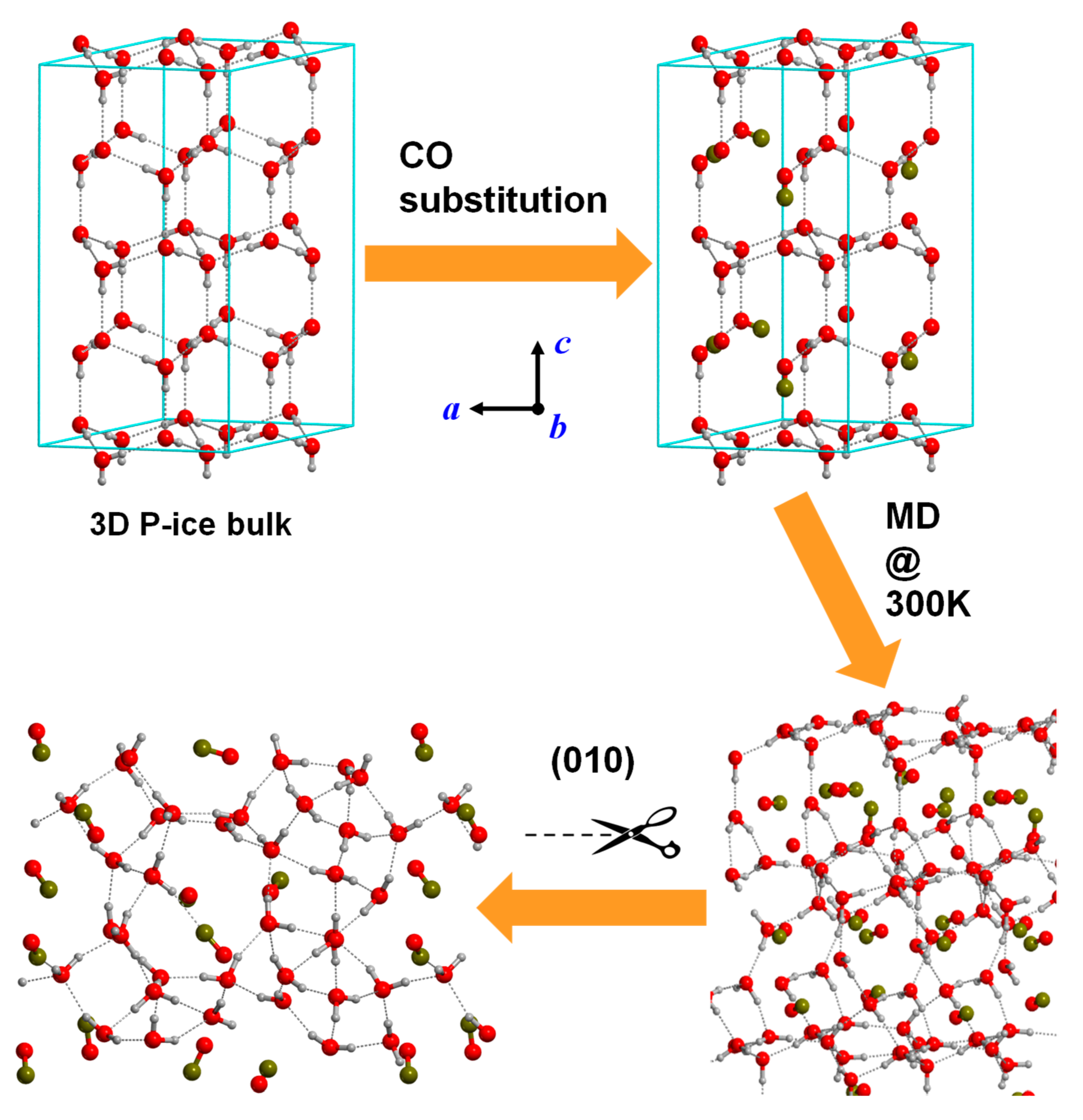
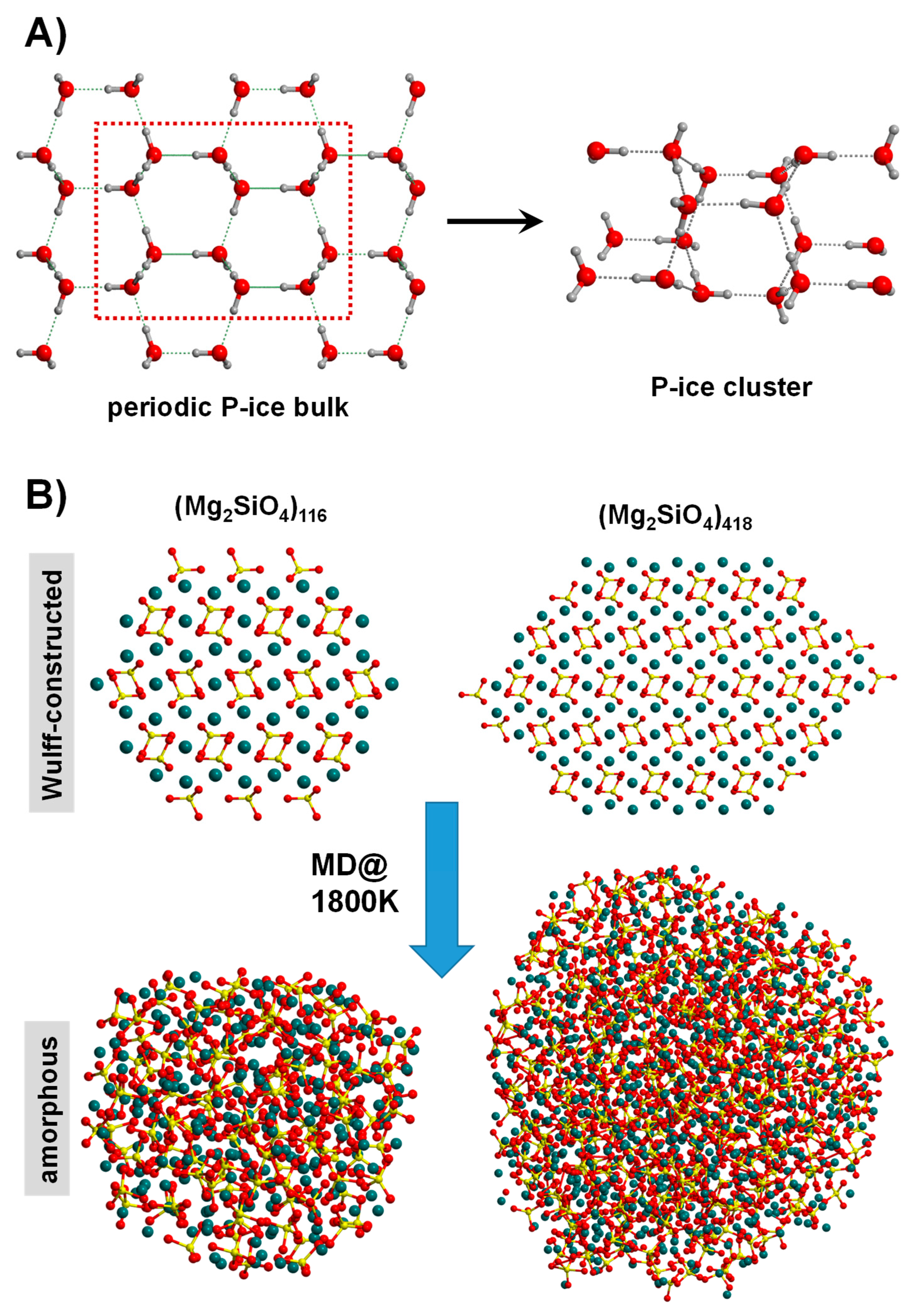
3.1.2. Amorphous Surfaces
3.2. Free and Embedded Cluster Systems
3.2.1. Top-Down Approach
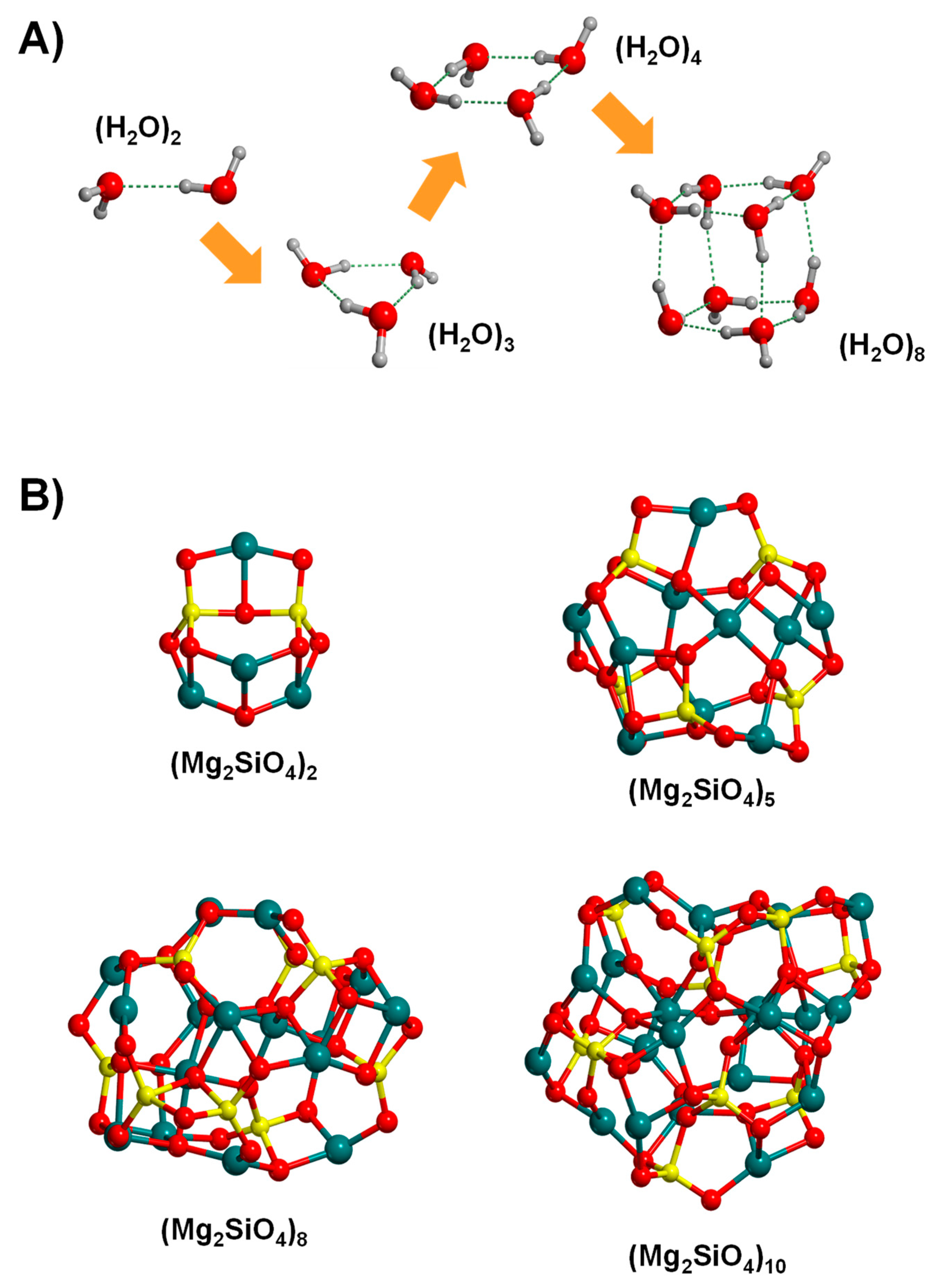
3.2.2. Bottom-up Approach
3.2.3. Embedded Clusters
3.3. Surface Models with Surface Defects
4. Summary and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Caselli, P.; Ceccarelli, C. Our astrochemical heritage. Astron. Astrophys. Rev. 2012, 20, 1–68. [Google Scholar] [CrossRef]
- Ehrenfreund, P.; Charnley, S.B. Organic molecules in the interstellar medium, comets, and meteorites: A voyage from dark clouds to the early Earth. Annu. Rev. Astron. Astrophys. 2000, 38, 427–483. [Google Scholar] [CrossRef]
- Kwok, S. Complex organics in space from Solar System to distant galaxies. Astron. Astrophys. Rev. 2016, 24, 8. [Google Scholar] [CrossRef]
- McGuire, B.A. 2018 census of interstellar, circumstellar, extragalactic, protoplanetary disk, and exoplanetary molecules. Astrophys. J. Suppl. Ser. 2018, 239, 17. [Google Scholar] [CrossRef]
- Williams, D.A.; Herbst, E. It’s a dusty Universe: Surface science in space. Surf. Sci. 2002, 500, 823–837. [Google Scholar] [CrossRef]
- Watanabe, N.; Kouchi, A. Ice surface reactions: A key to chemical evolution in space. Progress Surf. Sci. 2008, 83, 439–489. [Google Scholar] [CrossRef]
- Hama, T.; Watanabe, N. Surface processes on interstellar amorphous solid water: Adsorption, diffusion, tunneling reactions, and nuclear-spin conversion. Chem. Rev. 2013, 113, 8783–8839. [Google Scholar] [CrossRef]
- Vidali, G. H2 Formation on Interstellar Grains. Chem. Rev. 2013, 113, 8762–8782. [Google Scholar] [CrossRef]
- Herbst, E.; John, T.; Yates, J. Introduction: Astrochemistry. Chem. Rev. 2013, 113, 8707–8709. [Google Scholar] [CrossRef]
- Tielens, A.G.G.M. The molecular universe. Rev. Modern Phys. 2013, 85, 1021–1081. [Google Scholar] [CrossRef]
- Van Dishoeck, E.F. Astrochemistry of dust, ice and gas: Introduction and overview. Faraday Discuss. 2014, 168, 9–47. [Google Scholar] [CrossRef] [PubMed]
- Herbst, E. Three milieux for interstellar chemistry: Gas, dust, and ice. Phys. Chem. Chem. Phys. 2014, 16, 3344–3359. [Google Scholar] [CrossRef] [PubMed]
- Van Dishoeck, E.F.; Herbst, E.; Neufeld, D.A. Interstellar water chemistry: From laboratory to observations. Chem. Rev. 2013, 113, 9043–9085. [Google Scholar] [CrossRef] [PubMed]
- Dulieu, F.; Amiaud, L.; Congiu, E.; Fillion, J.-H.; Matar, E.; Momeni, A.; Pirronello, V.; Lemaire, J.L. Experimental evidence for water formation on interstellar dust grains by hydrogen and oxygen atoms. Astron. Astrophys. 2010, 512, A30. [Google Scholar] [CrossRef]
- Ioppolo, S.; Cuppen, H.M.; Romanzin, C.; van Dishoeck, E.F.; Linnartz, H. Laboratory Evidence for Efficient Water Formation in Interstellar Ices. Astrophys. J. 2008, 686, 1474–1479. [Google Scholar] [CrossRef]
- Oba, Y.; Watanabe, N.; Kouchi, A.; Hama, T.; Pirronello, V. Experimental studies of surface reactions among OH radicals that yield H2O and CO2 at 40-60 K. Phys. Chem. Chem. Phys. 2011, 13, 15792–15797. [Google Scholar] [CrossRef]
- Romanzin, C.; Ioppolo, S.; Cuppen, H.M.; Dishoeck, E.F.v.; Linnartz, H. Water formation by surface O3 hydrogenation. J. Chem. Phys. 2011, 134, 084504. [Google Scholar] [CrossRef]
- Watanabe, N.; Kouchi, A. Efficient Formation of Formaldehyde and Methanol by the Addition of Hydrogen Atoms to CO in H2O-CO Ice at 10 K. Astrophys. J. 2002, 571, L173–L176. [Google Scholar] [CrossRef]
- Rimola, A.; Taquet, V.; Ugliengo, P.; Balucani, N.; Ceccarelli, C. Combined quantum chemical and modeling study of CO hydrogenation on water ice. Astron. Astrophys. 2014, 572, A70. [Google Scholar] [CrossRef]
- Herbst, E.; van Dishoeck, E.F. Complex organic interstellar molecules. Annu. Rev. Astron. Astrophys. 2009, 47, 427–480. [Google Scholar] [CrossRef]
- Herbst, E. The synthesis of large interstellar molecules. Int. Rev. Phys. Chem. 2017, 36, 287–331. [Google Scholar] [CrossRef]
- Garrod, R.T.; Herbst, E. Formation of Methyl Formate and Other Organic Species in the Warm-Up Phase of Hot Molecular Cores. Astron. Astrophys. 2006, 457, 927–936. [Google Scholar] [CrossRef]
- Öberg, K.I. Photochemistry and astrochemistry: Photochemical pathways to interstellar complex organic molecules. Chem. Rev. 2016, 116, 9631–9663. [Google Scholar] [CrossRef] [PubMed]
- Zamirri, L.; Ugliengo, P.; Ceccarelli, C.; Rimola, A. Quantum Mechanical Investigations on the Formation of Complex Organic Molecules on Interstellar Ice Mantles. Review and Perspectives. ACS Earth Space Chem. 2019, 3, 1499–1523. [Google Scholar] [CrossRef]
- Garrod, R.T.; Weaver, S.L.W.; Herbst, E. Complex Chemistry in Star-forming Regions: An Expanded Gas-Grain Warm-up Chemical Model. Astrophys. J. 2008, 682, 283. [Google Scholar] [CrossRef]
- Enrique-Romero, J.; Rimola, A.; Ceccarelli, C.; Ugliengo, P.; Balucani, N.; Skouteris, D. Reactivity of HCO with CH3 and NH2 on Water Ice Surfaces. A Comprehensive Accurate Quantum Chemistry Study. ACS Earth Space Chem. 2019, 3, 2158–2170. [Google Scholar] [CrossRef]
- Öberg, K.I.; Garrod, R.T.; van Dishoeck, E.F.; Linnartz, H. Formation rates of complex organics in UV irradiated CH3OH-rich ices. Astron. Astrophys. 2009, 504, 891–913. [Google Scholar] [CrossRef]
- Enrique-Romero, J.; Rimola, A.; Ceccarelli, C.; Balucani, N. The (impossible?) formation of acetaldehyde on the grain surfaces: Insights from quantum chemical calculations. MNRAS 2016, 459, L6–L10. [Google Scholar] [CrossRef]
- Enrique-Romero, J.; Álvarez-Barcia, S.; Kolb, F.J.; Rimola, A.; Ceccarelli, C.; Balucani, N.; Meisner, J.; Ugliengo, P.; Lamberts, T.; Kästner, J. Revisiting the reactivity between HCO and CH3 on interstellar grain surfaces. Mon. Not. R. Astron. Soc. 2020, 493, 2523–2527. [Google Scholar] [CrossRef]
- Rimola, A.; Skouteris, D.; Balucani, N.; Ceccarelli, C.; Enrique-Romero, J.; Taquet, V.; Ugliengo, P. Can formamide be formed on interstellar ice? An atomistic perspective. ACS Earth Space Chem. 2018, 2, 720–734. [Google Scholar] [CrossRef]
- Williams, J.P.; Cieza, L.A. Protoplanetary Disks and Their Evolution. Annu. Rev. Astron. Astrophys. 2011, 49, 67–117. [Google Scholar] [CrossRef]
- Henning, T.; Semenov, D. Chemistry in Protoplanetary Disks. Chem. Rev. 2013, 113, 9016–9042. [Google Scholar] [CrossRef] [PubMed]
- A’Hearn, M.F. Comets as Building Blocks. Annu. Rev. Astron. Astrophys. 2011, 49, 281–299. [Google Scholar] [CrossRef]
- Mumma, M.J.; Charnley, S.B. The chemical composition of comets—Emerging taxonomies and natal heritage. Annu. Rev. Astron. Astrophys. 2011, 49, 471–524. [Google Scholar] [CrossRef]
- Trigo-Rodríguez, J.M.; Rimola, A.; Tanbakouei, S.; Soto, V.C.; Lee, M. Accretion of Water in Carbonaceous Chondrites: Current Evidence and Implications for the Delivery of Water to Early Earth. Space Sci. Rev. 2019, 215, 18. [Google Scholar] [CrossRef]
- Rotelli, L.; Trigo-Rodríguez, J.M.; Moyano-Cambero, C.E.; Carota, E.; Botta, L.; Di Mauro, E.; Saladino, R. The key role of meteorites in the formation of relevant prebiotic molecules in a formamide/water environment. Sci. Rep. 2016, 6, 38888. [Google Scholar] [CrossRef]
- Llorca, J.; Casanova, I. Formation of carbides and hydrocarbons in chondritic interplanetary dust particles: A laboratory study. Meteor. Planet. Sci. 1998, 33, 243–251. [Google Scholar] [CrossRef]
- Llorca, J.; Casanova, I. Reaction between H2, CO, and H2S over Fe, Ni metal in the solar nebula: Experimental evidence for the formation of sulfur-bearing organic molecules and sulfides. Meteor. Planet. Sci. 2000, 35, 841–848. [Google Scholar] [CrossRef]
- Le Guillou, C.; Bernard, S.; Brearley, A.J.; Remusat, L. Evolution of organic matter in Orgueil, Murchison and Renazzo during parent body aqueous alteration: In situ investigations. Geochim. Cosmochim. Acta 2014, 131, 368–392. [Google Scholar] [CrossRef]
- Vinogradoff, V.; Le Guillou, C.; Bernard, S.; Binet, L.; Cartigny, P.; Brearley, A.J.; Remusat, L. Paris vs. Murchison: Impact of hydrothermal alteration on organic matter in CM chondrites. Geochim. Cosmochim. Acta 2017, 212, 234–252. [Google Scholar] [CrossRef]
- Vinogradoff, V.; Bernard, S.; Le Guillou, C.; Remusat, L. Evolution of interstellar organic compounds under asteroidal hydrothermal conditions. Icarus 2018, 305, 358–370. [Google Scholar] [CrossRef]
- Remusat, L. Organics in primitive meteorites. In Planetary Mineralogy; Lee, M.R., Leroux, H., Eds.; European Mineralogical Union & Mineralogical Society of Great Britain and Ireland: Aberystwyth, UK, 2015; Volume 15, pp. 33–65. [Google Scholar]
- Tielens, A.G.G.M. Interstellar Polycyclic Aromatic Hydrocarbon Molecules. Annu. Rev. Astron. Astrophys. 2008, 46, 289–337. [Google Scholar] [CrossRef]
- Herrero, V.J.; Maté, B.; Molpeceres, G.; Jiménez-Redondo, M.; Tanarro, I. Spectroscopy of Interstellar Carbonaceous Dust. In Laboratory Astrophysics; Muñoz Caro, G.M., Escribano, R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 159–171. [Google Scholar]
- Molpeceres, G.; Timón, V.; Jiménez-Redondo, M.; Escribano, R.; Maté, B.; Tanarro, I.; Herrero, V.J. Structure and infrared spectra of hydrocarbon interstellar dust analogs. Phys. Chem. Chem. Phys. 2017, 19, 1352–1360. [Google Scholar] [CrossRef] [PubMed]
- Henning, T. Cosmic silicates. Annu. Rev. Astron. Astrophys. 2010, 48, 21–46. [Google Scholar] [CrossRef]
- Molster, F.; Kemper, C. Crystalline Silicates. Space Sci. Rev. 2005, 119, 3–28. [Google Scholar] [CrossRef]
- Whittet, D.C.B.; Schutte, W.A.; Tielens, A.G.G.M.; Boogert, A.C.A.; de Graauw, T.; Ehrenfreund, P.; Gerakines, P.A.; Helmich, F.P.; Prusti, T.; van Dishoeck, E.F. An ISO SWS View of Interstellar Ices: First Results. Astron. Astrophys. 1996, 360, L357–L360. [Google Scholar]
- Boogert, A.C.A.; Gerakines, P.A.; Whittet, D.C.B. Observations of the icy Universe. Annu. Rev. Astron. Astrophys. 2015, 53, 541–581. [Google Scholar] [CrossRef]
- Fraser, H.J.; Collings, M.P.; Dever, J.W.; McCoustra, M.R.S. Using laboratory studies of CO–H2O ices to understand the non-detection of a 2152 cm−1 (4.647 μm) band in the spectra of interstellar ices. Mon. Not. R. Astron. Soc. 2004, 353, 59–68. [Google Scholar] [CrossRef]
- Collings, M.P.; Anderson, M.A.; Chen, R.; Dever, J.W.; Viti, S.; Williams, D.A.; McCoustra, M.R.S. A laboratory survey of the thermal desorption of astrophysically relevant molecules. Mon. Not. R. Astron. Soc. 2004, 354, 1133–1140. [Google Scholar] [CrossRef]
- Garrod, R.T. Three-dimensional, off-lattice Monte Carlo kinetics simulations of interstellar grain chemistry and ice structure. Astrophys. J. 2013, 778, 158. [Google Scholar] [CrossRef]
- Goesmann, F.; Rosenbauer, H.; Bredehöft, J.H.; Cabane, M.; Ehrenfreund, P.; Gautier, T.; Giri, C.; Krüger, H.; Le Roy, L.; MacDermott, A.J.; et al. Organic compounds on comet 67P/Churyumov-Gerasimenko revealed by COSAC mass spectrometry. Science 2015, 349, aab0689. [Google Scholar] [CrossRef] [PubMed]
- Sandford, S.A.; Aléon, J.; Alexander, C.M.O.D.; Araki, T.; Bajt, S.; Baratta, G.A.; Borg, J.; Bradley, J.P.; Brownlee, D.E.; Brucato, J.R.; et al. Organics captured from comet 81P/Wild 2 by the Stardust spacecraft. Science 2006, 314, 1720–1724. [Google Scholar] [CrossRef] [PubMed]
- Elsila, J.E.; Glavin, D.P.; Dworkin, J.P. Cometary glycine detected in samples returned by Stardust. Meteorit. Planet. Sci. 2009, 44, 1323–1330. [Google Scholar] [CrossRef]
- Altwegg, K.; Balsiger, H.; Bar-Nun, A.; Berthelier, J.-J.; Bieler, A.; Bochsler, P.; Briois, C.; Calmonte, U.; Combi, M.R.; Cottin, H.; et al. Prebiotic chemicals-amino acid and phosphorus-in the coma of comet 67P/Churyumov-Gerasimenko. Science 2016, 2, e1600285. [Google Scholar] [CrossRef]
- Rubin, A.E. Mineralogy of meteorite groups. Meteorit. Planet. Sci. 1997, 32, 231–247. [Google Scholar] [CrossRef]
- Pizzarello, S. The Chemistry of Life’s origin: A carbonaceous meteorite perspective. Acc. Chem. Res. 2006, 39, 231–237. [Google Scholar] [CrossRef]
- Martins, Z. Organic Chemistry of Carbonaceous Meteorites. Elements 2011, 7, 35–40. [Google Scholar] [CrossRef]
- Cuppen, H.M.; Walsh, C.; Lamberts, T.; Semenov, D.; Garrod, R.T.; Penteado, E.M.; Ioppolo, S. Grain surface models and data for astrochemistry. Space Sci. Rev. 2017, 212, 1–58. [Google Scholar] [CrossRef]
- Linnartz, H.; Ioppolo, S.; Fedoseev, G. Atom addition reactions in interstellar ice analogues. Int. Rev. Phys. Chem. 2015, 34, 205–237. [Google Scholar] [CrossRef]
- Taj, S.; McCoustra, M.R.S. Thermal desorption of carbon monoxide from model interstellar ice surfaces: Revealing surface heterogeneity. Mon. Not. R. Astron. Soc. 2020, 498, 1693–1699. [Google Scholar] [CrossRef]
- Corno, M.; Ugliengo, P. Surface Modeling of Ceramic Biomaterials. In Encyclopedia of Nanotechnology; Bhushan, B., Ed.; Springer: Dordrecht, The Netherlands, 2014; pp. 1–13. [Google Scholar]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Siegbahn, P.E.M. The Configuration Interaction Method. In Lecture Notes in Quantum Chemistry: European Summer School in Quantum Chemistry; Roos, B.O., Ed.; Springer: Berlin/Heidelberg, Germany, 1992; pp. 255–293. [Google Scholar]
- Čížek, J. On the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell-Type Expansion Using Quantum-Field Theoretical Methods. J. Chem. Phys. 1966, 45, 4256–4266. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Sherrill, C.D. Frontiers in electronic structure theory. J. Chem. Phys. 2010, 132, 110902. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Sousa, S.F.; Fernandes, P.A.; Ramos, M.J. General Performance of Density Functionals. J. Phys. Chem. A 2007, 111, 10439–10452. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Hoe, W.-M.; Cohen, A.J.; Handy, N.C. Assessment of a new local exchange functional OPTX. Chem. Phys. Lett. 2001, 341, 319–328. [Google Scholar] [CrossRef]
- Handy, N.C.; Cohen, A.J. Left-right correlation energy. Mol. Phys. 2001, 99, 403–412. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Grimme, S. Density functional theory with London dispersion corrections. WIREs Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Caldeweyher, E.; Bannwarth, C.; Grimme, S. Extension of the D3 dispersion coefficient model. J. Chem. Phys. 2017, 147, 034112. [Google Scholar] [CrossRef] [PubMed]
- Pople, J.; Beveridge, D. Approximate Molecular Orbital Theory; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Pople, J.A.; Segal, G.A. Approximate Self-Consistent Molecular Orbital Theory. II. Calculations with Complete Neglect of Differential Overlap. J. Chem. Phys. 1965, 43, S136–S151. [Google Scholar] [CrossRef]
- Pople, J.A.; Segal, G.A. Approximate Self-Consistent Molecular Orbital Theory. III. CNDO Results for AB2 and AB3 Systems. J. Chem. Phys. 1966, 44, 3289–3296. [Google Scholar] [CrossRef]
- Pople, J.A.; Beveridge, D.L.; Dobosh, P.A. Approximate Self-Consistent Molecular-Orbital Theory. V. Intermediate Neglect of Differential Overlap. J. Chem. Phys. 1967, 47, 2026–2033. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Zoebisch, E.G.; Healy, E.F.; Stewart, J.J.P. Development and use of quantum mechanical molecular models. 76. AM1: A new general purpose quantum mechanical molecular model. J. Am. Chem. Soc. 1985, 107, 3902–3909. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Thiel, W. Ground states of molecules. 38. The MNDO method. Approximations and parameters. J. Am. Chem. Soc. 1977, 99, 4899–4907. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods I. Method. J. Comput. Chem. 1989, 10, 209–220. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Model. 2013, 19, 1–32. [Google Scholar] [CrossRef] [PubMed]
- Porezag, D.; Frauenheim, T.; Köhler, T.; Seifert, G.; Kaschner, R. Construction of tight-binding-like potentials on the basis of density-functional theory: Application to carbon. Phys. Rev. B 1995, 51, 12947–12957. [Google Scholar] [CrossRef]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar] [CrossRef]
- Grimme, S.; Bannwarth, C.; Shushkov, P. A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86). J. Chem. Theory Comput. 2017, 13, 1989–2009. [Google Scholar] [CrossRef]
- Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15, 1652–1671. [Google Scholar] [CrossRef]
- Pracht, P.; Caldeweyher, E.; Ehlert, S.; Grimme, S. A Robust Non-Self-Consistent Tight-Binding Quantum Chemistry Method for large Molecules. ChmRxiv 2019. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Sure, R.; Grimme, S. Corrected small basis set Hartree-Fock method for large systems. J. Comput. Chem. 2013, 34, 1672–1685. [Google Scholar] [CrossRef]
- Ceriotti, M. Unsupervised machine learning in atomistic simulations, between predictions and understanding. J. Chem. Phys. 2019, 150, 150901. [Google Scholar] [CrossRef] [PubMed]
- Jia, W.; Wang, H.; Chen, M.; Lu, D.; Lin, L.; Car, R.; E, W.; Zhang, L. Pushing the limit of molecular dynamics with ab initio accuracy to 100 million atoms with machine learning. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Atlanta, GA, USA, 9–19 November 2020; Article 5. [Google Scholar]
- Navarro-Ruiz, J.; Ugliengo, P.; Rimola, A.; Sodupe, M. B3LYP Periodic Study of the Physicochemical Properties of the Nonpolar (010) Mg-Pure and Fe-Containing Olivine Surfaces. J. Phys. Chem. A 2014, 118, 5866–5875. [Google Scholar] [CrossRef] [PubMed]
- Navarro-Ruiz, J.; Sodupe, M.; Ugliengo, P.; Rimola, A. Interstellar H adsorption and H2 formation on the crystalline (010) forsterite surface: A B3LYP-D2* periodic study. Phys. Chem. Chem. Phys. 2014, 16, 17447–17457. [Google Scholar] [CrossRef] [PubMed]
- Navarro-Ruiz, J.; Martínez-González, J.Á.; Sodupe, M.; Ugliengo, P.; Rimola, A. Relevance of silicate surface morphology in interstellar H2 formation. Insights from quantum chemical calculations. Mon. Not. R. Astron. Soc. 2015, 453, 914–924. [Google Scholar] [CrossRef]
- Molpeceres, G.; Rimola, A.; Ceccarelli, C.; Kästner, J.; Ugliengo, P.; Maté, B. Silicate-mediated interstellar water formation: A theoretical study. Mon. Not. R. Astron. Soc. 2019, 482, 5389–5400. [Google Scholar] [CrossRef] [PubMed]
- Pantaleone, S.; Enrique-Romero, J.; Ceccarelli, C.; Ugliengo, P.; Balucani, N.; Rimola, A. Chemical Desorption versus Energy Dissipation: Insights from Ab Initio Molecular Dynamics of HCO· Formation. Astrophys. J. 2020, 897, 56. [Google Scholar] [CrossRef]
- Ferrero, S.; Zamirri, L.; Ceccarelli, C.; Witzel, A.; Rimola, A.; Ugliengo, P. Binding energies of interstellar molecules on crystalline and amorphous models of water ice by ab-initio calculations. Astrophys. J. 2020, 904, 11. [Google Scholar] [CrossRef]
- Ferrero, S.; Martínez-Bachs, B.; Enrique-Romero, J.; Rimola, A. Adsorption of Atoms on a Crystalline Ice Surface Model: Results from Periodic ab Initio Simulations. In Proceedings of the Computational Science and Its Applications—ICCSA 2020; Springer: Cham, Swizterland, 2020; pp. 553–560. [Google Scholar]
- Martínez-Bachs, B.; Ferrero, S.; Rimola, A. Binding Energies of N-Bearing Astrochemically-Relevant Molecules on Water Interstellar Ice Models. A Computational Study. In Proceedings of the Computational Science and Its Applications—ICCSA 2020; Springer: Cham, Swizterland, 2020; pp. 683–692. [Google Scholar]
- Zamirri, L.; Corno, M.; Rimola, A.; Ugliengo, P. Forsterite Surfaces as Models of Interstellar Core Dust Grains: Computational Study of Carbon Monoxide Adsorption. ACS Earth Space Chem. 2017, 1, 384–398. [Google Scholar] [CrossRef]
- Bruno, M.; Massaro, F.R.; Prencipe, M.; Demichelis, R.; De La Pierre, M.; Nestola, F. Ab Initio Calculations of the Main Crystal Surfaces of Forsterite (Mg2SiO4): A Preliminary Study to Understand the Nature of Geochemical Processes at the Olivine Interface. J. Phys. Chem. C 2014, 118, 2498–2506. [Google Scholar] [CrossRef]
- Martínez-González, J.Á.; Navarro-Ruiz, J.; Rimola, A. Multiscale Computational Simulation of Amorphous Silicates’ Structural, Dielectric, and Vibrational Spectroscopic Properties. Minerals 2018, 8, 353. [Google Scholar] [CrossRef]
- Zamirri, L.; Casassa, S.; Rimola, A.; Segado-Centellas, M.; Ceccarelli, C.; Ugliengo, P. IR spectral fingerprint of carbon monoxide in interstellar water–ice models. Mon. Not. R. Astron. Soc. 2018, 480, 1427–1444. [Google Scholar] [CrossRef]
- Rimola, A.; Sodupe, M.; Ugliengo, P. Deep-space glycine formation via Strecker-type reactions activated by ice water dust mantles. A computational approach. Phys. Chem. Chem. Phys. 2010, 12, 5285–5294. [Google Scholar] [CrossRef] [PubMed]
- Ringe, E.; Van Duyne, R.P.; Marks, L.D. Wulff Construction for Alloy Nanoparticles. Nano Lett. 2011, 11, 3399–3403. [Google Scholar] [CrossRef]
- Wulff, G. Zur Frage der Geschwindigkeit des Wachstums und der Auflösung der Krystallflagen. Z. Krystallogr. Mineral. 1901, 34, 449–530. (In German) [Google Scholar]
- Zamirri, L.; Macià Escatllar, A.; Mariñoso Guiu, J.; Ugliengo, P.; Bromley, S.T. What Can Infrared Spectra Tell Us about the Crystallinity of Nanosized Interstellar Silicate Dust Grains? ACS Earth Space Chem. 2019, 3, 2323–2338. [Google Scholar] [CrossRef]
- Rahm, J.M.; Erhart, P. Beyond Magic Numbers: Atomic Scale Equilibrium Nanoparticle Shapes for Any Size. Nano Lett. 2017, 17, 5775–5781. [Google Scholar] [CrossRef] [PubMed]
- Barnard, A.S. A Thermodynamic Model for the Shape and Stability of Twinned Nanostructures. J. Phys. Chem. B 2006, 110, 24498–24504. [Google Scholar] [CrossRef]
- Lamiel-Garcia, O.; Cuko, A.; Calatayud, M.; Illas, F.; Bromley, S.T. Predicting size-dependent emergence of crystallinity in nanomaterials: Titania nanoclusters versus nanocrystals. Nanoscale 2017, 9, 1049–1058. [Google Scholar] [CrossRef]
- Lamiel-Garcia, O.; Ko, K.C.; Lee, J.Y.; Bromley, S.T.; Illas, F. When Anatase Nanoparticles Become Bulklike: Properties of Realistic TiO2 Nanoparticles in the 1–6 nm Size Range from All Electron Relativistic Density Functional Theory Based Calculations. J. Chem. Theory Comput. 2017, 13, 1785–1793. [Google Scholar] [CrossRef]
- Viñes, F.; Lamiel-Garcia, O.; Illas, F.; Bromley, S.T. Size dependent structural and polymorphic transitions in ZnO: From nanocluster to bulk. Nanoscale 2017, 9, 10067–10074. [Google Scholar] [CrossRef]
- Loschen, C.; Migani, A.; Bromley, S.T.; Illas, F.; Neyman, K.M. Density functional studies of model cerium oxide nanoparticles. Phys. Chem. Chem. Phys. 2008, 10, 5730–5738. [Google Scholar] [CrossRef] [PubMed]
- González, D.; Camino, B.; Heras-Domingo, J.; Rimola, A.; Rodríguez-Santiago, L.; Solans-Monfort, X.; Sodupe, M. BCN-M: A Free Computational Tool for Generating Wulff-like Nanoparticle Models with Controlled Stoichiometry. J. Phys. Chem. C 2020, 124, 1227–1237. [Google Scholar] [CrossRef]
- Rimola, A.; Sodupe, M.; Ugliengo, P. Computational study of interstellar glycine formation occurring at radical surfaces of water-ice dust particles. Astrophys. J. 2012, 754, 24. [Google Scholar] [CrossRef]
- Ugalde, J.M.; Alkorta, I.; Elguero, J. Water Clusters: Towards an Understanding Based on First Principles of Their Static and Dynamic Properties. Angew. Chem. Int. Ed. 2000, 39, 717–721. [Google Scholar] [CrossRef]
- Maheshwary, S.; Patel, N.; Sathyamurthy, N.; Kulkarni, A.D.; Gadre, S.R. Structure and Stability of Water Clusters (H2O)n, n = 8−20: An Ab Initio Investigation. J. Phys. Chem. A 2001, 105, 10525–10537. [Google Scholar] [CrossRef]
- Hartke, B. Global geometry optimization of clusters using genetic algorithms. J. Phys. Chem. 1993, 97, 9973–9976. [Google Scholar] [CrossRef]
- Deaven, D.M.; Ho, K.M. Molecular Geometry Optimization with a Genetic Algorithm. Phys. Rev. Lett. 1995, 75, 288–291. [Google Scholar] [CrossRef]
- Niesse, J.A.; Mayne, H.R. Global optimization of atomic and molecular clusters using the space-fixed modified genetic algorithm method. J. Comput. Chem. 1997, 18, 1233–1244. [Google Scholar] [CrossRef]
- Hartke, B. Global cluster geometry optimization by a phenotype algorithm with Niches: Location of elusive minima, and low-order scaling with cluster size. J. Comput. Chem. 1999, 20, 1752–1759. [Google Scholar] [CrossRef]
- Johnston, R.L. Evolving better nanoparticles: Genetic algorithms for optimising cluster geometries. Dalton Trans. 2003, 4193–4207. [Google Scholar] [CrossRef]
- Wales, D.J.; Doye, J.P.K. Global Optimization by Basin-Hopping and the Lowest Energy Structures of Lennard-Jones Clusters Containing up to 110 Atoms. J. Phys. Chem. A 1997, 101, 5111–5116. [Google Scholar] [CrossRef]
- Wales, D.J.; Hodges, M.P. Global minima of water clusters (H2O)n, n≤21, described by an empirical potential. Chem. Phys. Lett. 1998, 286, 65–72. [Google Scholar] [CrossRef]
- Gehrke, R.; Reuter, K. Assessing the efficiency of first-principles basin-hopping sampling. Phys. Rev. B 2009, 79, 085412. [Google Scholar] [CrossRef]
- Rondina, G.G.; Da Silva, J.L.F. Revised Basin-Hopping Monte Carlo Algorithm for Structure Optimization of Clusters and Nanoparticles. J. Chem. Inf. Model. 2013, 53, 2282–2298. [Google Scholar] [CrossRef] [PubMed]
- MaciàEscatllar, A.; Lazaukas, T.; Woodley, S.M.; Bromley, S.T. Structure and Properties of Nanosilicates with Olivine (Mg2SiO4)N and Pyroxene (MgSiO3)N Compositions. ACS Earth Space Chem. 2019, 3, 2390–2403. [Google Scholar] [CrossRef]
- Goumans, T.P.M.; Bromley, S.T. Efficient nucleation of stardust silicates via heteromolecular homogeneous condensation. Mon. Not. R. Astron. Soc. 2012, 420, 3344–3349. [Google Scholar] [CrossRef]
- Goumans, T.P.M.; Bromley, S.T. Stardust silicate nucleation kick-started by SiO+TiO2. Philos. Trans. R. Soc. A 2013, 371, 20110580. [Google Scholar] [CrossRef]
- Germain, A.; Ugliengo, P. Modeling Interstellar Amorphous Solid Water Grains by Tight-Binding Based Methods: Comparison Between GFN-XTB and CCSD(T) Results for Water Clusters. In Proceedings of the Computational Science and Its Applications—ICCSA 2020; Springer: Cham, Swizterland, 2020; pp. 745–753. [Google Scholar]
- Meldgaard, S.A.; Kolsbjerg, E.L.; Hammer, B. Machine learning enhanced global optimization by clustering local environments to enable bundled atomic energies. J. Chem. Phys. 2018, 149, 134104. [Google Scholar] [CrossRef]
- Maseras, F.; Morokuma, K. IMOMM: A new integrated ab initio + molecular mechanics geometry optimization scheme of equilibrium structures and transition states. J. Comput. Chem. 1995, 16, 1170–1179. [Google Scholar] [CrossRef]
- Dapprich, S.; Komáromi, I.; Byun, K.S.; Morokuma, K.; Frisch, M.J. A new ONIOM implementation in Gaussian98. Part I. The calculation of energies, gradients, vibrational frequencies and electric field derivatives. J. Mol. Struct. Theochem. 1999, 461-462, 1–21. [Google Scholar] [CrossRef]
- Chung, L.W.; Sameera, W.M.C.; Ramozzi, R.; Page, A.J.; Hatanaka, M.; Petrova, G.P.; Harris, T.V.; Li, X.; Ke, Z.; Liu, F.; et al. The ONIOM Method and Its Applications. Chem. Rev. 2015, 115, 5678–5796. [Google Scholar] [CrossRef] [PubMed]
- Ren, P.; Ponder, J.W. Polarizable Atomic Multipole Water Model for Molecular Mechanics Simulation. J. Phys. Chem. B 2003, 107, 5933–5947. [Google Scholar] [CrossRef]
- Sameera, W.M.C.; Maseras, F. Expanding the Range of Force Fields Available for ONIOM Calculations: The SICTWO Interface. J. Chem. Inf. Model. 2018, 58, 1828–1835. [Google Scholar] [CrossRef] [PubMed]
- Sameera, W.M.C.; Senevirathne, B.; Andersson, S.; Maseras, F.; Nyman, G. ONIOM(QM:AMOEBA09) Study on Binding Energies and Binding Preference of OH, HCO, and CH3 Radicals on Hexagonal Water Ice (Ih). J. Phys. Chem. C 2017, 121, 15223–15232. [Google Scholar] [CrossRef]
- Spicher, S.; Grimme, S. Robust Atomistic Modeling of Materials, Organometallic, and Biochemical Systems. Angew. Chem. Int. Ed. 2020, 59, 15665–15673. [Google Scholar] [CrossRef]
- Cuppen, H.M.; Garrod, R.T. Modelling of surface chemistry on an inhomogeneous interstellar grain. Astron. Astrophys. 2011, 529, A151. [Google Scholar] [CrossRef]
- Pauly, T.; Garrod, R.T. The effects of grain size and temperature distributions on the formation of interstellar ice mantles. Astrophys. J. 2016, 817, 146. [Google Scholar] [CrossRef]
- Willis, E.R.; Garrod, R.T. Kinetic Monte Carlo Simulations of the Grain-surface Back-diffusion Effect. Astrophys. J. 2017, 840, 61. [Google Scholar] [CrossRef]
- Pauly, T.; Garrod, R.T. Modeling CO, CO2, and H2O Ice Abundances in the Envelopes of Young Stellar Objects in the Magellanic Clouds. Astrophys. J. 2018, 854, 13. [Google Scholar] [CrossRef]
- Clements, A.R.; Berk, B.; Cooke, I.R.; Garrod, R.T. Kinetic Monte Carlo simulations of water ice porosity: Extrapolations of deposition parameters from the laboratory to interstellar space. Phys. Chem. Chem. Phys. 2018, 20, 5553–5568. [Google Scholar] [CrossRef]
- Signorile, M.; Zamirri, L.; Tsuchiyama, A.; Ugliengo, P.; Bonino, F.; Martra, G. On the Surface Acid–Base Properties of Amorphous and Crystalline Mg2SiO4 as Probed by Adsorbed CO, CO2, and CD3CN. ACS Earth Space Chem. 2020, 4, 345–354. [Google Scholar] [CrossRef]
- Navarro-Ruiz, J.; Ugliengo, P.; Sodupe, M.; Rimola, A. Does Fe2+ in olivine-based IS grains play any role in the formation of H2? Atomistic insights from DFT periodic simulations. Chem. Commun. 2016, 52, 6873–6876. [Google Scholar] [CrossRef] [PubMed]
- Westermayr, J.; Gastegger, M.; Menger, M.F.S.J.; Mai, S.; González, L.; Marquetand, P. Machine learning enables long time scale molecular photodynamics simulations. Chem. Sci. 2019, 10, 8100–8107. [Google Scholar] [CrossRef] [PubMed]
- Hazen, R.M.; Papineau, D.; Bleeker, W.; Downs, R.T.; Ferry, J.M.; McCoy, T.J.; Sverjensky, D.A.; Yang, H. Mineral evolution. Am. Mineral. 2008, 93, 1693–1720. [Google Scholar] [CrossRef]
- Hazen, R.M.; Bekker, A.; Bish, D.L.; Bleeker, W.; Downs, R.T.; Farquhar, J.; Ferry, J.M.; Grew, E.S.; Knoll, A.H.; Papineau, D.; et al. Needs and opportunities in mineral evolution research. Am. Mineral. 2011, 96, 953–963. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rimola, A.; Ferrero, S.; Germain, A.; Corno, M.; Ugliengo, P. Computational Surface Modelling of Ices and Minerals of Interstellar Interest—Insights and Perspectives. Minerals 2021, 11, 26. https://doi.org/10.3390/min11010026
Rimola A, Ferrero S, Germain A, Corno M, Ugliengo P. Computational Surface Modelling of Ices and Minerals of Interstellar Interest—Insights and Perspectives. Minerals. 2021; 11(1):26. https://doi.org/10.3390/min11010026
Chicago/Turabian StyleRimola, Albert, Stefano Ferrero, Aurèle Germain, Marta Corno, and Piero Ugliengo. 2021. "Computational Surface Modelling of Ices and Minerals of Interstellar Interest—Insights and Perspectives" Minerals 11, no. 1: 26. https://doi.org/10.3390/min11010026
APA StyleRimola, A., Ferrero, S., Germain, A., Corno, M., & Ugliengo, P. (2021). Computational Surface Modelling of Ices and Minerals of Interstellar Interest—Insights and Perspectives. Minerals, 11(1), 26. https://doi.org/10.3390/min11010026







