3.1. Thermal Conversion
In a first experiment, the initial concentrate was thermally treated at 1323 K (1050 °C) during 30 min and analyzed by XRD. The fractions were first analyzed separately. The coarser fraction was then ground and added to the finer fraction. The mixture obtained was then also analyzed by XRD. It must be noted that the material lost its green rocky appearance and became a red dusty powder (
Figure 2). Coarse particles were also present in the sample following heat treatment and their color also changed to a red tint. Contrary to their green counterparts, these reddish coarse particles were not hard and could easily be crushed, even by simple hand pressure. A total of 665.3 g of converted spodumene were recovered (initial mass prior to heat treatment was 680 g). Some of the heat-treated material (14.7 g) stayed on the alumina sheets that closed the inconel tube; this material was not collected to avoid unnecessary contamination. After sifting, the finer fraction weighted 534.7 g while the coarser fraction weighted 130.6 g. Hence, 81 wt% of the heat-treated concentrate collected had a size distribution of less than 425 µm. After analysis, the coarser fraction was ground down to 425 µm and added to the finer fraction. The concentrate obtained is referred to as sample A. The XRD patterns of the untreated initial concentrate and of each fraction, and sample A are presented in
Figure 3a,b.
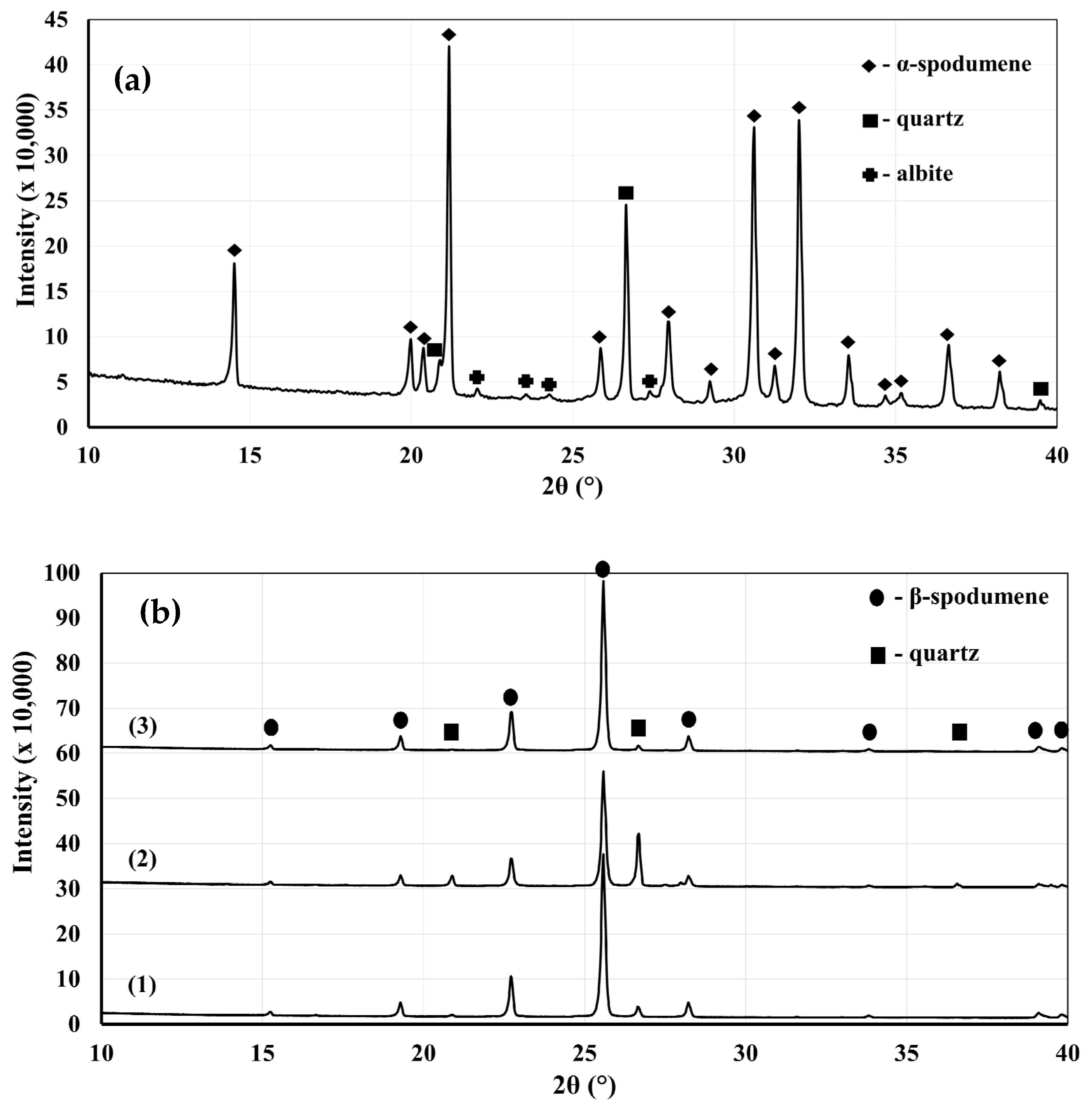
Figure 3a presents a classical α-spodumene concentrate. Many preferential orientations can be seen as the two main peaks of α-spodumene are supposed to be the two peaks at 30.6° and 32.0°, while our XRD shows the main peak at 21.2°. This is not uncommon for spodumene concentrates. According to
Figure 3b, the XRD patterns show the presence of neither α- nor γ-spodumene after the thermal treatment at 1323 K (1050 °C) during 30 min for the fine and coarse fractions, as well as sample A. We thus concluded with a full α-to-β conversion since the XRD patterns only showed the presence of β-spodumene. Aside from this major phase, the XRD identified the presence of quartz impurities that remained in the heat-treated concentrates. Albite and muscovite were not detected and are suspected to have undergone transitions or decompositions into phases that were not detectable by our XRD methodology. The Rietveld analyses show that quartz was concentrated in the coarser fraction (
Table 2).
It was thus found that a controlled temperature of 1323 K (1050 °C) inside the reactor completely converted α-spodumene into β-spodumene in our samples. However, this result was achieved under carefully controlled conditions in a batch reactor. As industrial processes do not rely on batch processes to convert spodumene for economic reasons, further work is required to assess if the same result would be obtained under continuous large-scale thermal treatment.
3.3. γ-Spodumene Formation at Lower Temperatures
The thermal conversion of the initial concentrate at 1323 K (1050 °C) showed complete transformation to β-spodumene, which is in agreement with the available literature [
11]. However, this result is not expected to readily occur at the industrial scale where incomplete conversion to β-spodumene is likely to occur for various reasons (e.g., heat transfer limitations, presence of temperature gradients, effective residence time in the reactor). As stated in the introduction, an elusive phase called γ-spodumene is known to form at lower temperatures (1073–1273 K (800–1000 °C)) [
6,
16,
17], which may strongly impact industrial performance. Under industrial conditions, the γ-spodumene phase is known to be concomitant with β-spodumene. This work attempts to quantify if the presence of γ-spodumene negatively impacts the leaching process, leading to lower lithium extraction efficiencies. In order to evaluate this effect, an attempt was made to maximize the formation of the γ-spodumene in our initial untreated concentrate through three maximum heat treatment temperatures, which are as follows: (1) 1073 K (800 °C), (2) 1148 K (875 °C), and (3) 1223 K (950 °C), respectively, samples B, C, and D. All samples were heat treated under atmospheric pressure for one hour. These conditions were expected to generate γ-spodumene based on our literature assessment [
6]. A heat treatment of one hour was used in an attempt to maximize the amount of γ-spodumene formed.
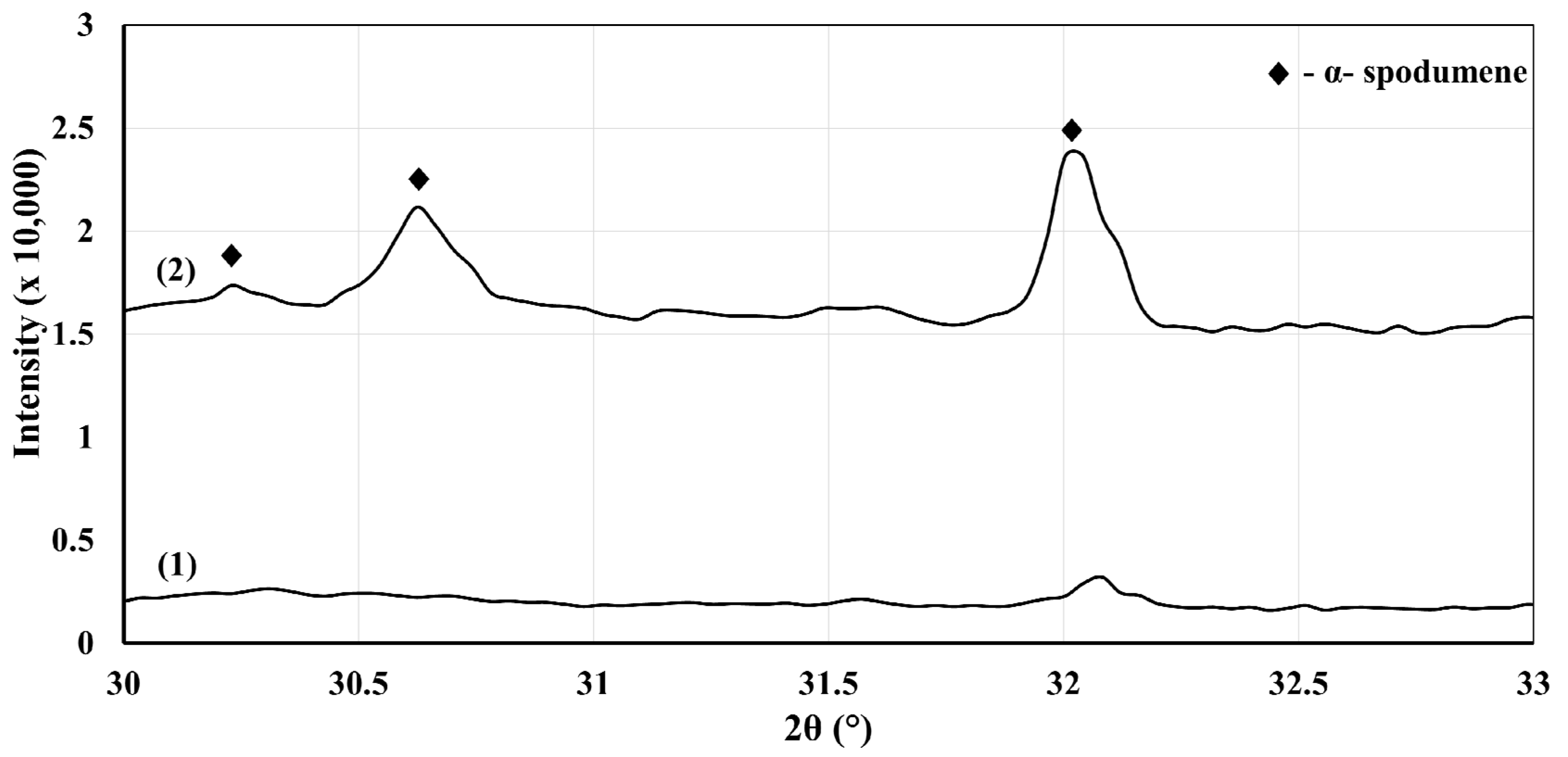
XRD analysis of samples B, C, and D did not show any sign of decrepitation; the particles remained hard. No dusty material was present in the samples. In fact, the only visible effect of these thermal treatments was a change of color, the materials becoming more reddish. The color change is difficult to explain at this point, but some hypotheses can be made. Augite ((Si,Al)
2O
6)(Ca,Mg,Fe,Ti,Al)
2 contains Fe
2+, and the change of oxidation degree of its iron into Fe
3+ could be the reason behind the reddish color. The reddish color could also be the actual color of β-spodumene. Because of that, we decided to extend the heat treatment performed at 1123 K (850 °C) (sample E) for 6 h under air (1 atm) to give even more time to the α-to-γ conversion to occur (
Figure 4).
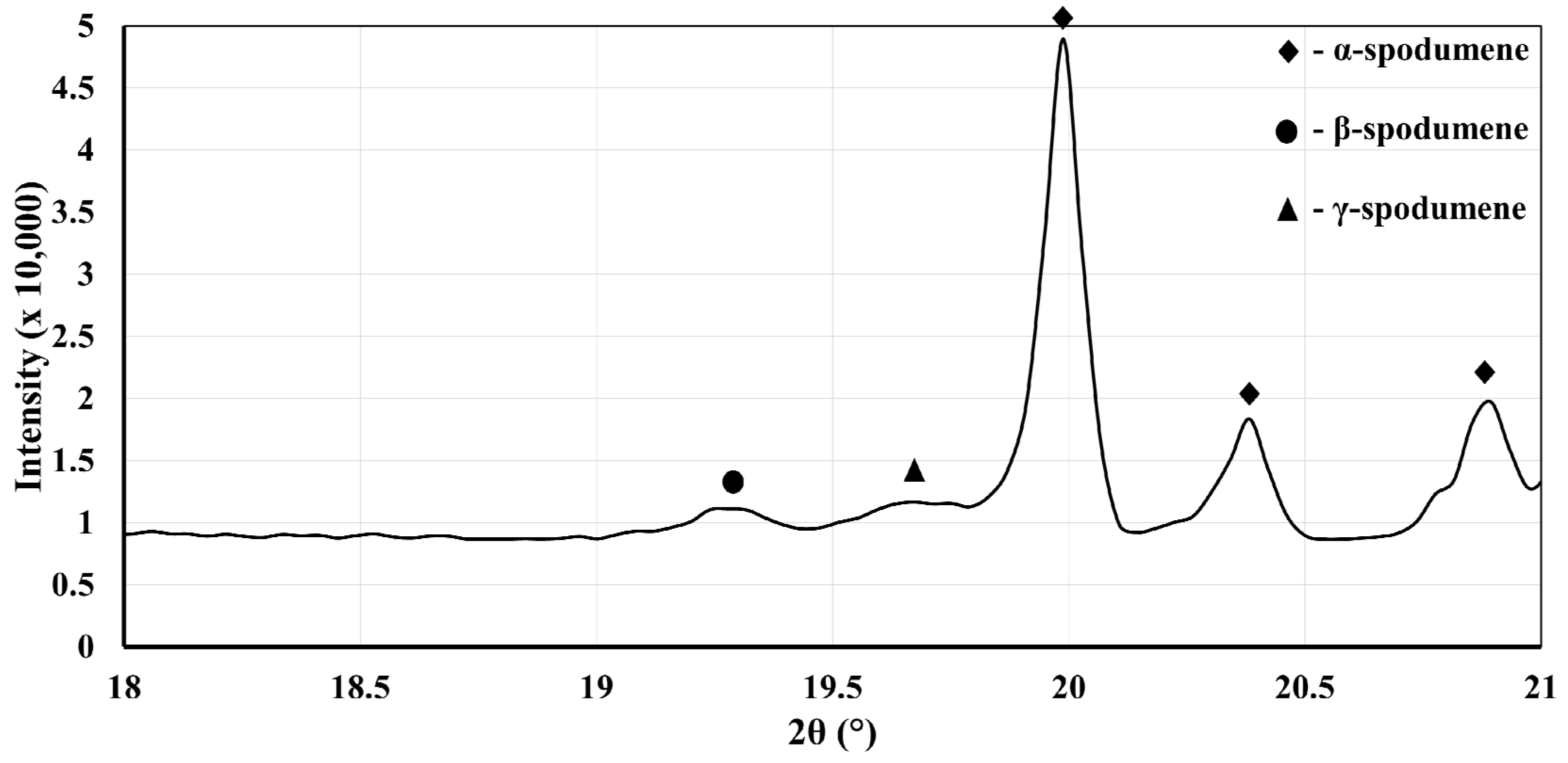
Overall, all the XRD patterns of these heat-treated samples show for the most part only the presence of α-spodumene, which confirms that phase transitions are slow in this specific temperature range. When exclusively focusing on the diffraction peaks for β-spodumene and γ-spodumene, we could confirm about 3 wt% (β + γ) conversion (results presented in
Table 3). A typical XRD pattern for one heat-treated sample (sample D) is presented in
Figure 5.
Rietveld analyses on the entire peak spectra were performed and revealed mainly the presence of α-spodumene and quartz. The respective quantity of β-spodumene and γ-spodumene was low. In fact, the error margin did not allow us to conclude whether one is formed preferentially over the other (
Table 3).
As reported in previous studies [
6,
12], γ-spodumene is metastable and thus does not form under equilibrium conditions. It could be that γ-spodumene could act as a lower energy transition state for the formation of stable β-spodumene since the formation of γ-spodumene from α-spodumene is stated as exothermic while the α-spodumene to β-spodumene transition is endothermic [
12]. The metastable character of γ-spodumene is further demonstrated here by the fact that even long heat treatment periods of up to 6 h below 1223 K (950 °C) did not produce a significant conversion of α-spodumene in the initial concentrate. Based on the kinetic studies of Botto et al. [
24], the mechanism for β-spodumene formation is limited by nucleation at lower temperatures and limited by nucleation and growth at higher temperatures. They also derived that the nucleation mechanism has a high activation energy (750 kJ mol
−1) and is effective up to approximately 1203 K (930 °C). At higher temperatures, the nucleation and growth mechanisms are dominant with a much lower activation energy (290 kJ mol
−1). Overall, this could imply that the formation of metastable γ-spodumene acts as a kinetic shortcut to α-spodumene conversion, hence the high activation energy and the observed low conversions of the concentrate at low temperatures. However, at higher temperatures, once sufficient nucleation sites are created, the γ-spodumene to β-spodumene reaction mechanism (which may be the nucleation and growth phenomenology suggested by Botto) can readily proceed with a much lower activation energy, hence the higher conversion of α-spodumene for a given heat treatment time. This analysis would be consistent with the suggestion of Gassala et al. [
20] that grinding spodumene concentrates favors the formation of γ-spodumene at lower heat treatment temperatures through the formation of favorable nucleation sites for this allotrope.
This also explains why γ-spodumene is often detected even when the conversion temperature is high, as it was in our previous work [
22]. Because of its lower kinetic barrier, the system favors the formation of β-spodumene from γ-spodumene, but some γ-spodumene may still remain in the material due to limiting experimental factors. For example, if the heat treatment time is not long enough, then γ-spodumene does not have the time to fully transition into β-spodumene. To conclude, no matter the exact reaction mechanism for spodumene conversion, these observations justify the need to reach higher conversion temperatures as reported in this study and others [
7] to maximize formation of β-spodumene from α-spodumene.
3.4. γ-Spodumene Influence on Lithium Extraction Efficiency
Section 2.3 presented some evidence that highlighted the metastable nature of γ-spodumene. It is therefore viewed here as an energetically favorable transition state (with a high activation energy for its formation) to eventually reach the equilibrium crystal structure of the β-spodumene at high temperatures. As stated, the impact of the presence of γ-spodumene on the lithium leaching extraction has yet to be reported. This is attempted here.
To investigate the impact of γ-spodumene on the leaching efficiency, several heat-treated concentrates were obtained from the initial concentrate (same initial material discussed in
Section 2.1) and were tested for lithium extraction efficiency. Heat treatment conditions and particle sizes were carefully selected to obtain different γ-spodumene proportions in each decrepitated sample. The metastable character of γ-spodumene made it difficult to precisely control its proportion in the final product, which explains the uneven distribution of final γ-spodumene contents. This difficulty also explains why our sample only reached a maximum γ-spodumene content of about 37 wt%. Converted samples were characterized by XRD to determine their phase proportions with the Rietveld method. A total of six converted concentrates (procedures and details in
Table 4) were selected, each having a different proportion of γ-spodumene (ranging from 0 wt% for sample A up to 37.4 wt% for samples I1 and I2). Each converted sample underwent the leaching extraction process detailed in
Section 2.2. The resulting lithium extraction efficiency is presented in
Table 4 and
Figure 6.
Sample A is the one featured in
Section 2.1 and
Section 2.2 for which a holding time of 30 min at 1323 K (1050 °C) was used. Samples F and H were obtained in a similar way to samples A and G, but with a higher rate of heating (~200 K min
−1 vs. ~30 K min
−1 for samples A and G). As the temperature showed no sign of stabilization, the heating was voluntarily stopped as soon as the targeted temperature of 1323 K (1050 °C) was reached in an attempt to obtain the presence of γ-spodumene (hence why the holding time is null). Sample G is the sample featured in our previous study [
22]. The base material for samples I1 and I2 was a flotation spodumene concentrate sifted between 212 μm and 425 μm. Sample I1 is the one originally obtained after heat treatment in a direct contact heating reactor, after an exploratory test of a new reactor configuration. Its γ-spodumene content reached a value of 37.4 wt%, which was the highest of all. Despite not originating from the same concentrate as the other samples presented in this study, we included it since we could not reproduce such a high γ-spodumene content in a rotary kiln. However, it aggregated during the thermal treatment and resulted in a particle size distribution of over 1000 µm in diameter. This particle size change is obviously expected to reduce lithium extraction efficiency relative to our other samples (A, F, G, H). To eliminate as much as possible the influence of the size of the particle on lithium extraction efficiency and thus isolate the effect of γ-spodumene, a portion of sample I1 was ground down to 100 µm to obtain sample I2. In this way, we believe it is reasonable to compare sample I2 to the furnace produced samples to better assess the impact of γ-spodumene content.
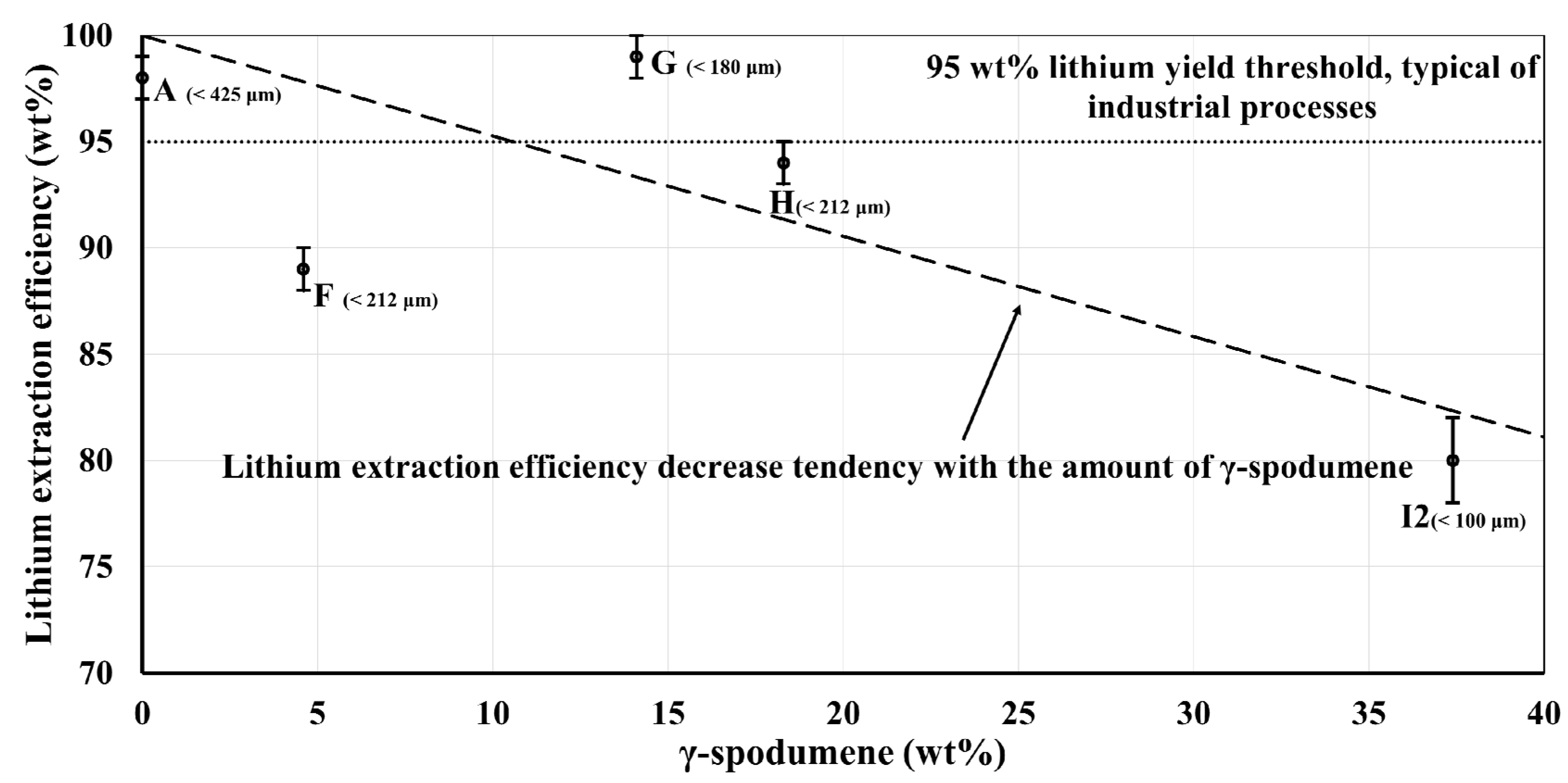
According to our results presented in
Figure 6, it seems like the amount of γ-spodumene in a sample does not have a major influence on the acid leaching lithium extraction process when its proportion is under 10 wt%. The samples with low γ-spodumene contents presents a relatively high lithium extraction efficiency while the higher content samples show a decrease, culminating with sample I2. This shows that γ-spodumene cannot be ignored when industrially converting spodumene since ignoring its formation could lead to a lower overall process efficiency.
Sample I2 clearly shows the effect of high γ-spodumene on the acid leaching process. The even lower lithium extraction efficiency of sample I1 (51 wt%) is attributed to the combined effect of higher γ-spodumene content and greater average particle size (more than 1000 µm), a consequence of the direct contact heating treatment. As stated, to isolate the contribution of γ-spodumene, the heat-treated concentrate was ground following heat treatment. This allowed an effective comparison between I2 (which has a much higher γ-spodumene content than what could readily be achieved in a furnace) and the furnace-treated samples. Overall, the present results show that a γ-spodumene content of up to about 10 wt% should not have a strong impact on the efficiency of the leaching process.
3.5. Assessing the Irreversibility of the Allotropic Transformations in Spodumene
To further extend the comprehension of the different phase transitions that may occur in the spodumene system upon heating concentrates, the irreversibility of the α-spodumene to β-spodumene transformation was studied by aging the heat-treated samples (J to Q) under controlled conditions (storage in air-tight containers in a temperature, pressure, humidity controlled room). Those heat-treated samples were obtained long before the other heat-treated samples presented in this study and during exploratory tests and equipment testing. During the decrepitation process, the conversion to the β-spodumene allotropic led to a more open crystal structure that was more suitable for the subsequent leaching and solvent extraction [
4]. At the macroscopic level, this spodumene allotropic transformation converts the coarse and hard α particles (over 2 mm) into soft, dusty, and micrometric β particles [
22]. According to the literature, this allotropic transformation is linked to irreversible volumetric changes [
40]. In addition, the β-spodumene formation is reported as irreversible [
7,
40], while the α-to-γ allotropic transition is stated as reversible [
19,
20,
40]. The nature of the γ-to-β transition is unknown.
To quantify the reversible/irreversible nature of the α-to-β allotropic transformation, several converted samples were stored in airtight containers and kept at room temperature for two years and reanalyzed by XRD. The selected samples (J to Q) all presented an initial high β-spodumene content. The typical XRD pattern of some freshly converted concentrate (sample M) and its aged counterpart are presented in
Figure 7. Rietveld quantifications were performed again on the aged thermally converted concentrates to confirm whether the crystallography of the samples had changed over the years (
Table 5). Only the diffraction peaks of the three spodumene allotropes are presented in the Rietveld quantifications. As seen in
Table 5, a total of eight samples were aged for over two years.
The XRD patterns of sample M indicate that the intensities of the peaks associated to α-spodumene increased over the years. This observation suggests that the commonly reported irreversibility of the α-to-β allotropic transformation may require a more extensive study in order to assess its validity. To study the irreversibility of the α-to-β process, we define a reversibility factor Ω as follows (Equation (3)):
If the β-spodumene and the γ-spodumene formations are indeed respectively irreversible and reversible, no change in Ω should be measured over the aging period:
- 1)
any increase in %wtα would be compensated by a corresponding decrease in %wtγ through the reversible α-to-γ phase transition;
- 2)
the variable %wtβ would not vary over time.
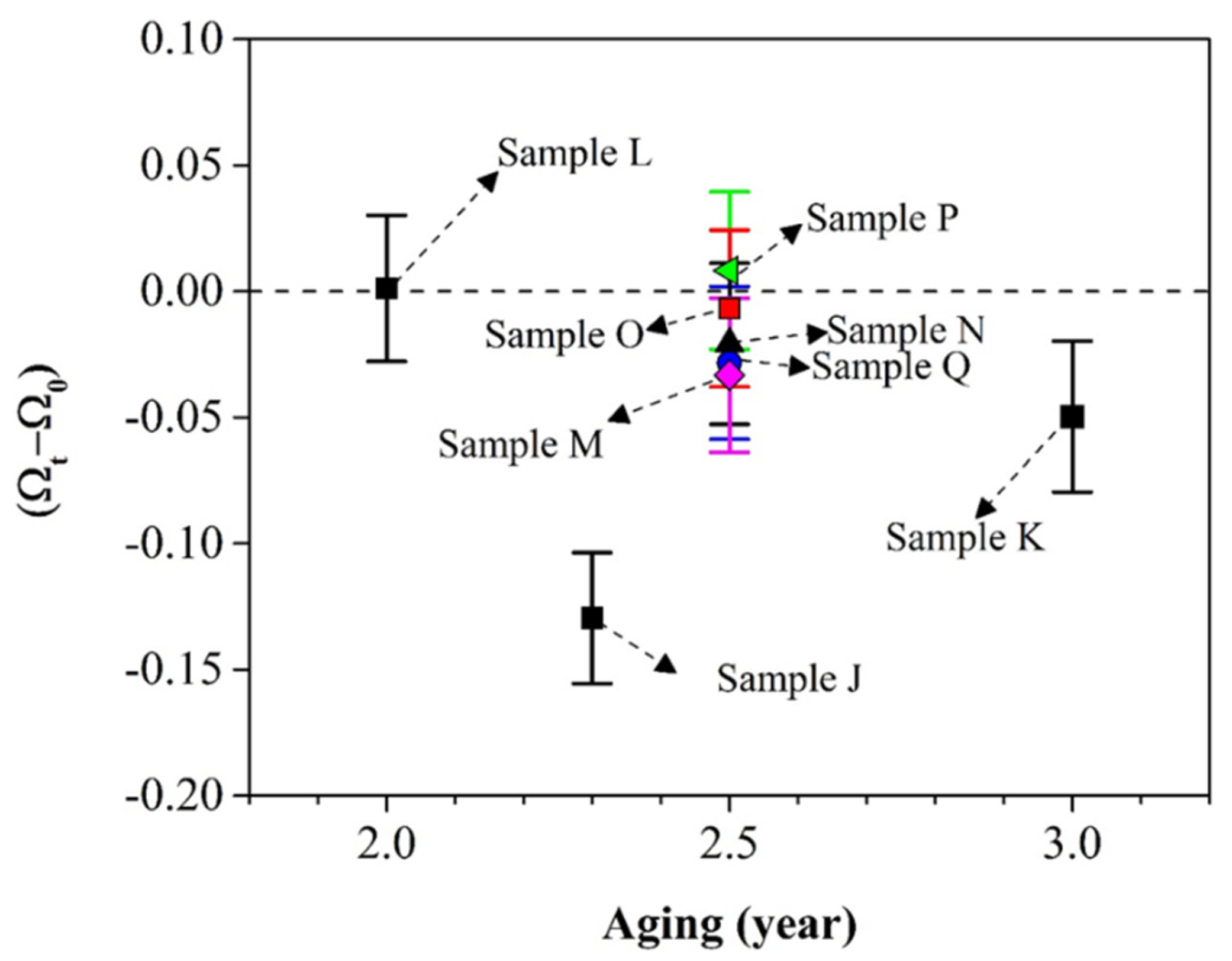
Figure 8 presents the change of Ω as a function of aging time
t. Each sample is identified by its name (from J to Q). The x-axis represents the aging time while the y-axis represents the value of (Ω
t–Ω
0). Ω
t is the value of Ω after the storage while Ω
0 is the initial value of Ω right after the first XRD analysis.
It is noted from
Figure 8 that Ω is not static as a function of time for most of our samples. Only samples L and P (respectively aged for 2 and 2.5 years) did not exhibit a decrease of Ω. All other samples (J, K, M, O, N, Q) with aging periods greater than 2 years exhibit a decrease of Ω. However, it should be noted that only samples J, K, and M exhibit a statistically significant decrease in Ω due to the error of the Rietveld method. Thus, the common statement that the conversion to β-spodumene is irreversible is challenged by our results. More fundamental work is required to validate the mechanism.
Nonetheless, the results presented in this section show that a high thermal conversion to β-spodumene is required if the concentrates are to be stored for long periods before the lithium leaching step of the process. Indeed, β-spodumene being more susceptible to lithium extraction means that its reverse conversion over time implies this will result in a reduction of the lithium extraction efficiency when performing the acid leaching. Complementary thermal treatment may be performed to these stored samples to counter this effect to ensure maximal recovery. It is expected that the degradation of β-spodumene in an industrial environment may lead to significant energy and economic inefficiencies.
3.6. Thermodynamic Analysis of the Spodumene System
Equilibrium calculations performed using the FactSage software are presented in this section to study the thermodynamic behavior of the spodumene system upon heat treatments at atmospheric pressure.
The mass balances representing the chemical composition of pure spodumene (LiAlSi
2O
6) was first imposed by constraining the molar amount of Li, Al, Si, and O
2 in the thermodynamic system. This leads to 20 gaseous species (SiO
2, SiO, Si
3, Si
2, Si, O
3, O
2, O, LiO, Li
2O
2, Li
2O, Li
2, Li, AlO
2, AlO, Al
2O
3, Al
2O
2, Al
2O, Al
2, Al), 11 pure liquid compounds (SiO
2, Si, LiAlO
2, Li
2SiO
3, Li
2Si
2O
5, Li
2O
2, Li
2O, Li, Al
2O
3, Al; (Li
2O)
2(SiO
2)), and 34 stoichiometric compounds (SiO
2: stishovite, coesite, cristobalite (h), cristobalite (l), tridymite (h), tridymite (l), quartz (h), quartz (l); Si; eucryptite LiAlSiO
4: α, β; petalite LiAlSi
4O
10; spodumene LiAlSi
2O
6: α, β; LiAlO
2; LiAl; Li
2SiO
3; Li
2Si
2O
5: I, II; Li
2O
2; Li
2O; mullite Al
6Si
2O
13; Al
2SiO
5: kyanite, sillimanite, andalusite; Al
2O
3: γ, δ, κ, corundum; Al; (Li
2O)
2(SiO
2); (Al
2O
3)(SiO
2)
2)) considered for this four-element system. Konar et al. [
15] also did thermodynamic assessments for petalite, α-eucryptite, and β-eucryptite.
Figure 9 presents the phase diagram obtained using Konar’s data for the four-element system.
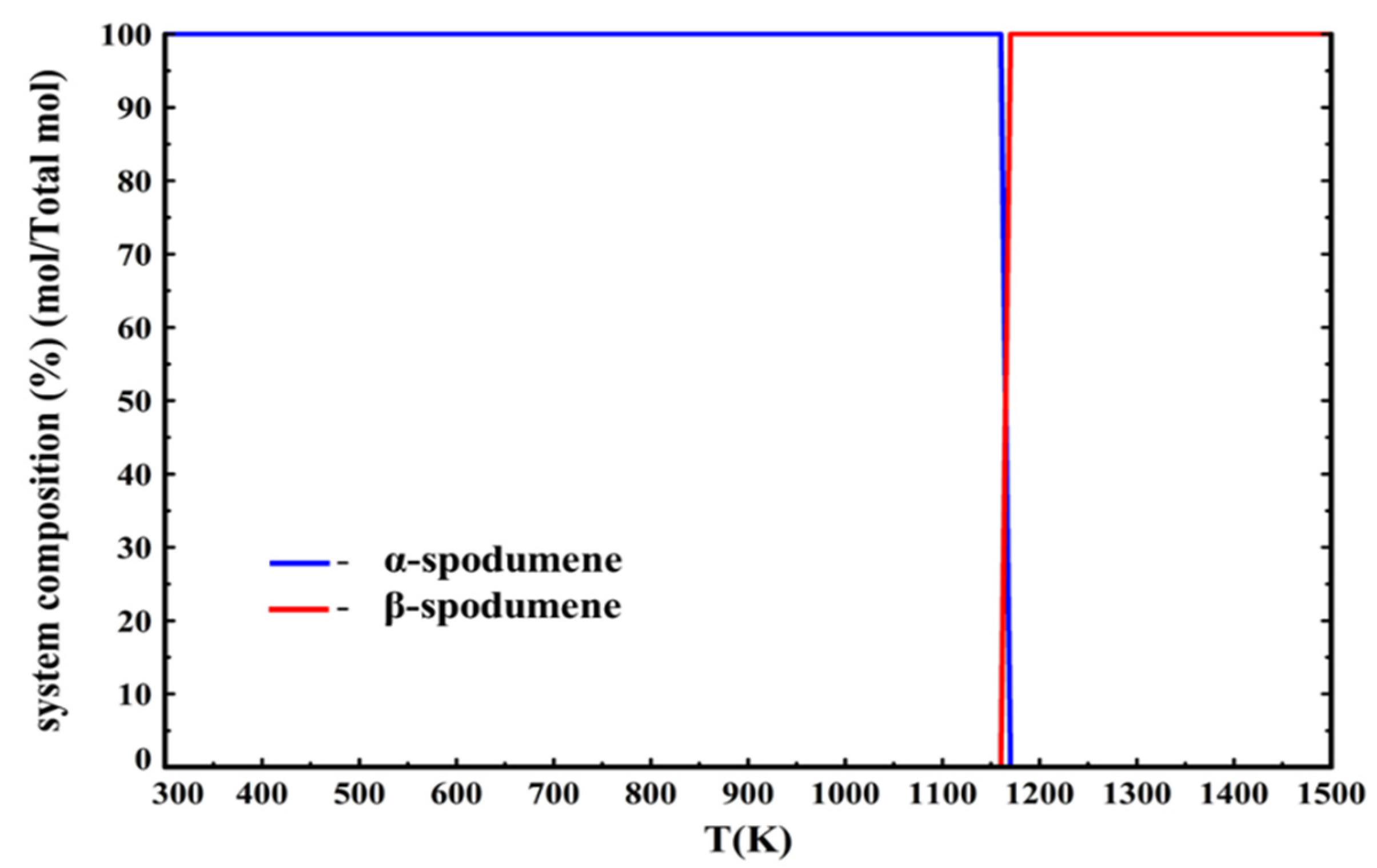
Implementing Konar’s data [
15] into the calculations results in an allotropic phase transition from α-spodumene to β-spodumene at 1162 K (889 °C). This is in agreement with our experimental results since it validates that β-spodumene is the only stable allotrope at 1323 K (1050 °C). Moreover, the beginning of this allotropic transition temperature of 1162 K (889 °C) is higher than the previous calculations presented by Roy [
8], who predicts a transition at 1023 ± 50 K (750 ± 50 °C), while being in agreement with the work of Moore [
21], who calculates a transition at 1073 ± 80 K (800 ± 80 °C).
In an effort to compare Konar’s [
15] and Barin’s [
33] data, calculations were performed using Konar’s data for α-spodumene and β-spodumene, and Barin’s data for the rest of the species.
Figure 10 presents the phase diagram.
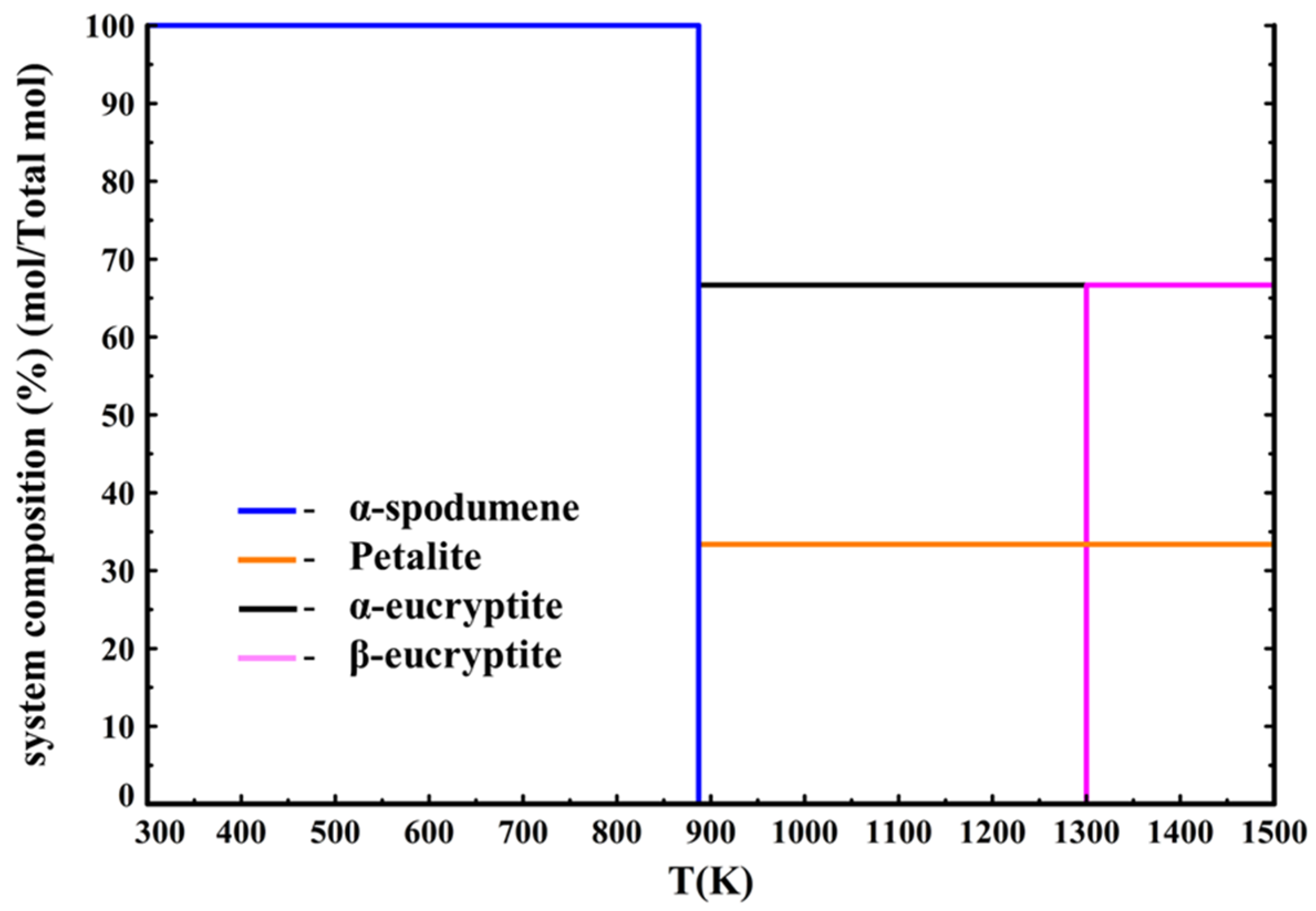
According to
Figure 10, α-spodumene dissociates into eucryptite LiAlSiO
4 and petalite LiAlSi
4O
10 (data from Barin [
33]) at 880 K (607 °C), with eucryptite transitioning into β-eucryptite at 1300 K (1027 °C). Moreover, β-spodumene (data from Konar [
15]) is also not a thermodynamically stable phase as it never forms under these equilibrium conditions. However, as β-spodumene is indeed a stable phase it should appear in the thermodynamic calculations. It is to be noted that there exist phase equilibrium data in literature [
41] involving the simultaneous presence of spodumene, eucryptite, and petalite. However, the reactions between the three minerals occur when quartz is present in excess (at least 50 wt%). As the industrial samples are cleaned from their quartz content (less than 10 wt%), it is unlikely that these reactions will occur. The CALPHAD (CALculation of PHAse Diagrams) work of Konar et al. on the Li
2O–SiO
2–Al
2O
3 system [
15] shows that the LiAlSi
2O
6 stoichiometric composition leads to the formation of an eutectic liquid in the LiAlO
2/SiO
2 pseudobinary system. Their work confirms the thermodynamic stability of spodumene at high temperature.
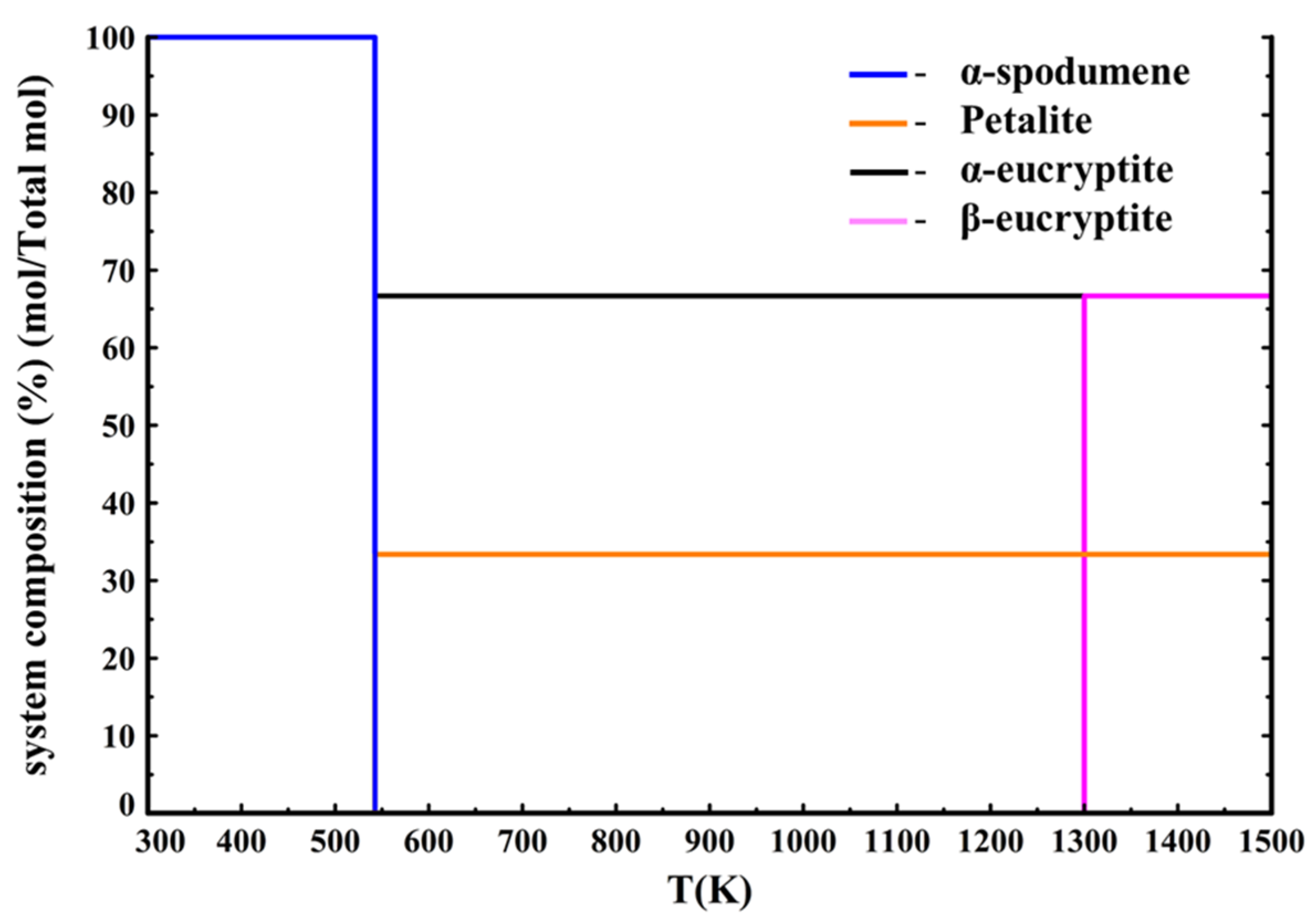
Finally, calculations using only Barin’s data were performed. The phase diagram is presented in
Figure 11.
Figure 11 shows that using only Barin’s data [
33] leads to the same kind of diagram as in
Figure 10, where Konar’s data were only used for α-spodumene and β-spodumene except that α-spodumene now decomposes into eucryptite and petalite at 540 K (267 °C) instead of 880 K (607 °C), making this diagram even further away from the experimental results. This means that using Barin’s data to perform calculations on the spodumene system leads to results that are far from the experimental results. Therefore, we recommend using Konar’s data when performing calculations on the spodumene system.
However, these thermodynamic calculations do not include the potential formation of the γ-spodumene metastable phase. Literature data on the energetic behavior of γ-spodumene are scarce. Fasshauer et al. [
42] assumed, for example, that virgilite (the natural form of γ-spodumene) has the same heat capacity function as β-spodumene, which was taken from the work of Robie et al [
43]. Their data are presented in
Table 6. In the absence of experimental data, the same assumption is used in our work.
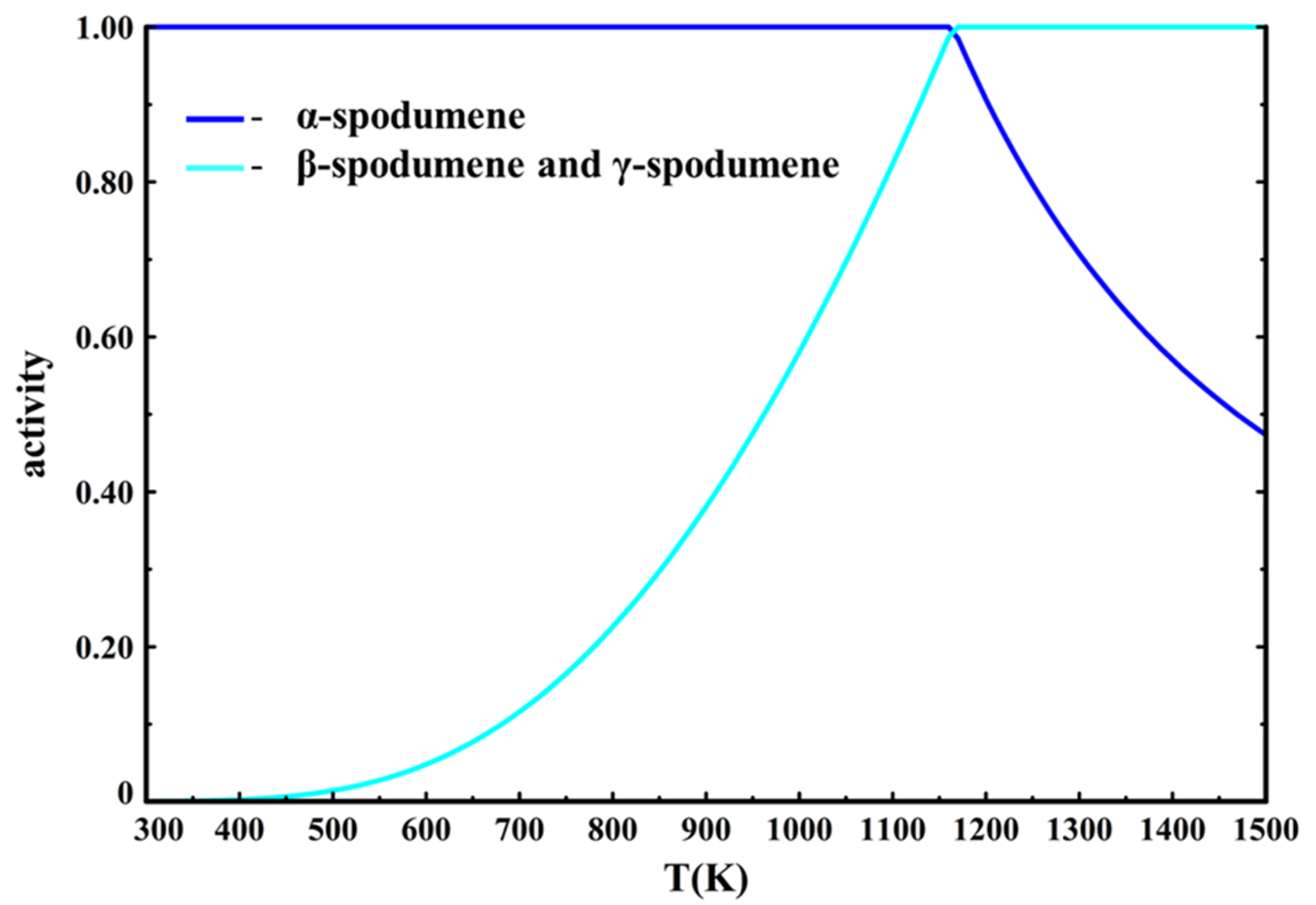
When adding γ-spodumene into the phase selection, our equilibrium calculations still predict that β-spodumene is the only stable phase above 1162 K (889 °C). However, it also calculates that the activity of both β-spodumene and γ-spodumene are always equal and equal to one above 1162 K (
Figure 12).
This is logical since the thermodynamic data of the two phases are the same, FactSage does not differentiate them. However, it was proven that while β-spodumene is the stable phase at higher temperature, γ-spodumene presents a metastable character and is not present in concentrates thermally treated at high temperature. This means that γ-spodumene’s activity should never be equal to one and that the calculations should show β-spodumene being the favored allotrope at higher temperatures. To assess the sensitivity of this issue, data for γ-spodumene’s thermodynamic properties were changed to better fit the experimental behavior according to these assumptions:
the higher the temperature, the lesser γ-spodumene is thermodynamically favored compared to β-spodumene;
the γ-to-β transition is an endothermic reaction;
γ-spodumene and β-spodumene are concomitant in a wide range of temperature (at least in the 1073–1223 K or 800–950 °C range).
From hypothesis (1), it can be deduced that γ-spodumene’s entropy must be smaller than β-spodumene’s, as entropy dominates the stability of compounds at high temperature. From hypothesis (2), it can be deduced that β-spodumene’s enthalpy must be less negative than γ-spodumene’s. Finally, from hypothesis (3), it can be deduced that the thermodynamic properties of the two allotropes must remain reasonably close to each other.
Following this reasoning, γ-spodumene’s entropy was set to 150 J K
−1 mol
−1 (the reported [
15] entropy of β-spodumene was 154.2 J K
−1 mol
−1)
. The enthalpy was changed to –3035 kJ mol
−1 (the reported [
15] enthalpy of β-spodumene was –3030.517 kJ mol
−1).
Table 7 and
Table 8 present a summary of spodumene’s data.
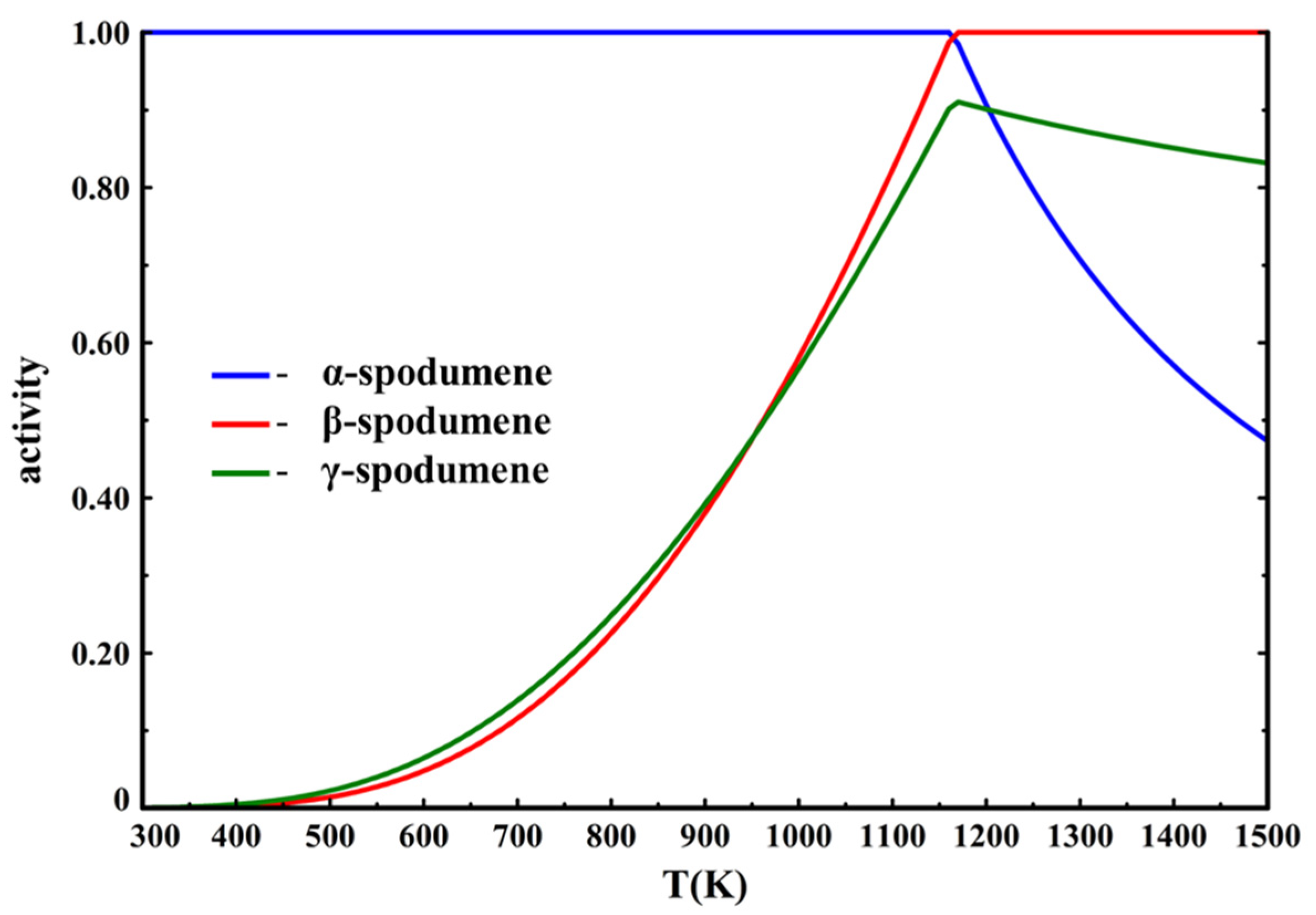
The calculations show that only β-spodumene is stable above 1162 K (889 °C). However, this time the activity of γ-spodumene shows it to be favored compared to β-spodumene at lower temperature, before becoming increasingly less favored with the temperature increase, while never being a thermodynamically stable phase (
Figure 13).
These results show the sensitivity of the spodumene system. With these minor changes to γ-spodumene’s data, its metastable character is immediately observed. It also shows how it is less favored at increasingly higher temperatures. This means that γ-spodumene could indeed function as an intermediate metastable phase and could act as barrier to β-spodumene formation if the thermodynamic conditions for metastability for hexagonal spodumene are met (e.g., the proposed greater availability of nucleation sites [
20]).
3.7. DSC Analysis
Section 2.6 presented thermodynamic calculations to evaluate the allotropic phase transition temperature in the spodumene system. These phase transitions are highly sensitive to the thermodynamic description of each allotrope used in the calculations. Because of that, DSC experiments were performed to ensure that the energetic behavior of our concentrate is compatible with these thermodynamic calculations.
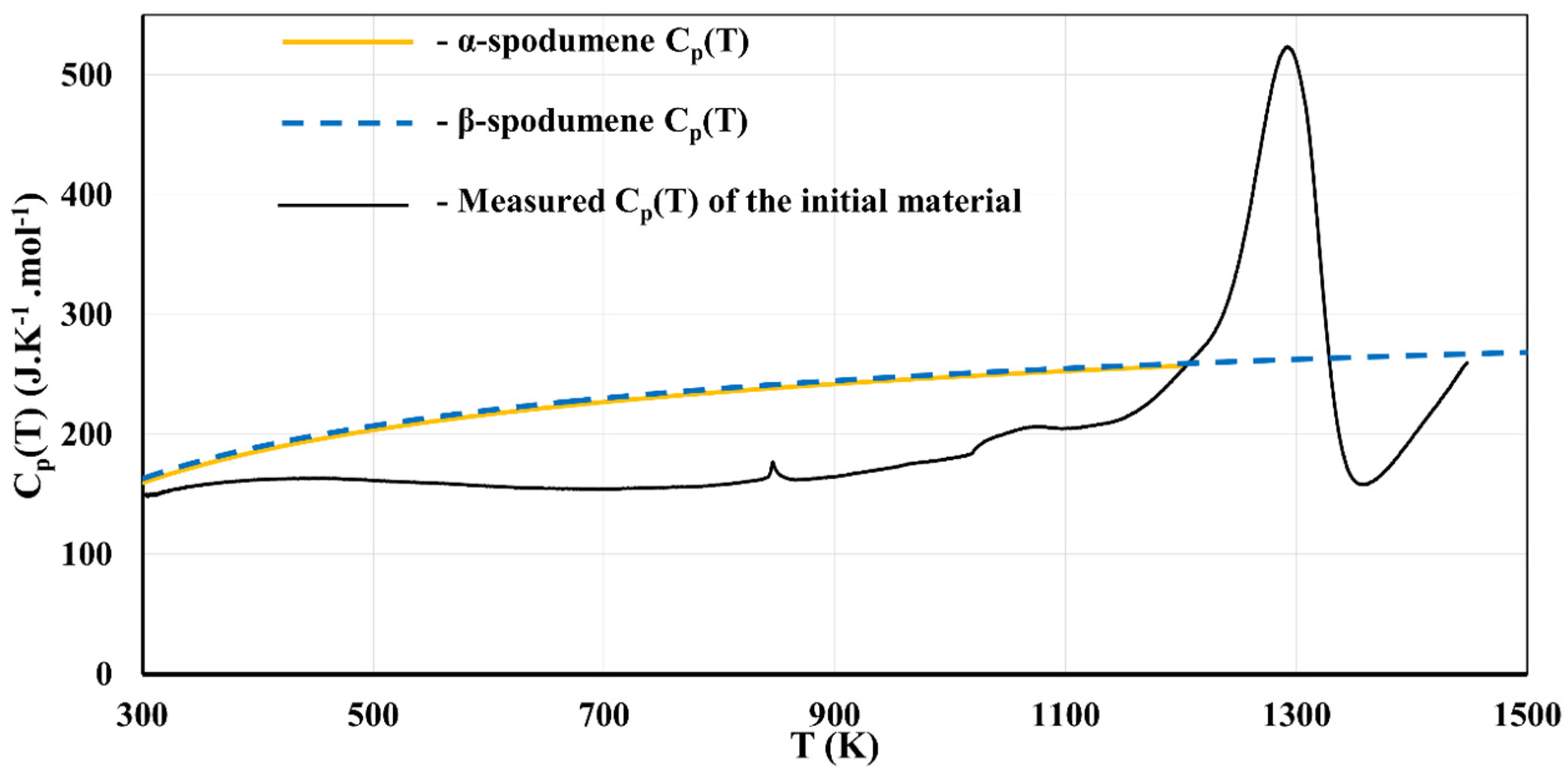
The DSC samples consist of the initial concentrate material (which was not heat treated) that was ground to obtain a fine powder suitable for the DSC capsules (<10 µm). The samples were composed of 1 wt% muscovite, 2 wt% albite, 5–10 wt% quartz, 1 wt% of other impurities (including augite, anorthite, diopside), with the rest being spodumene (exclusively composed of monoclinic α-spodumene). DSC experiments were performed to assess the isobaric heat capacity C
p as a function of temperature. The apparent C
p(T) expression of the material was then derived from this heat flow vs T measurement and compared to the fitted C
p(T) of the α-spodumene and β-spodumene phases from Konar [
15] (
Figure 14).
Four phase transitions can be identified. The first transition occurs at 850 K (577 °C) and corresponds to the α-to-β quartz allotropic transition, which starts at 845 K (572 °C) at 1 bar [
44]. The second transition occurs at 1050 K (777 °C) and corresponds to the dehydration of muscovite [
45]. The third transition starts at around 1100 K (827 °C) and is found to be dominated by an endothermic process up to around 1300 K (1027 °C). This is attributed to the β-spodumene formation, which is an endothermic process. Finally, after 1300 K (1027 °C) an exothermic reaction dominates. This is attributed to impurities and the appearance of vitreous phases. This reaction is not a concern for the samples presented in this study since the heat treatments were never significantly above this temperature. Contrary to Salakjani et al. [
12], we do not report an exothermic reaction before the β-spodumene formation. Our DSC measurements do not allow for pointing out the formation of γ-spodumene. However, our XRD results show that γ-spodumene is present in concentrates heat treated at temperatures below 1300 K (1027 °C). This means that γ-spodumene would be a mandatory step in the formation of β-spodumene, making the α–γ–β route the only possible one. The other proposed route, the α–β route, originated in older studies, which only considered α-spodumene and β-spodumene. For example, White and McVay [
46] report that α-spodumene is fully converted into β-spodumene at 1323 K (1050 °C). The first two peaks of β-spodumene they report show a
d(
hkl) of 3.48 Å and 3.91 Å, (2θ angles of 25.6° and 22.7°), respectively.
Figure 3b shows the first two peaks of β-spodumene also at 25.6° and 22.7°. However, they report two other peaks with a
d(
hkl) of 4.51 Å and 4.68 Å, (2θ angles of 19.6° and 18.9°), while
Figure 3b only shows one peak at 19.3°. In a previous study [
22], it was reported that if γ-spodumene shares its main peak’s angle with β-spodumene’s main peak, it can be identified through its second peak, which was reported at 19.7°. The closeness of the two peaks reported by White and McVay may be linked to the presence of γ-spodumene in their sample. This would mean that even in older studies, spodumene conversion took the α–γ–β route and that the α–β route was reported due to the lack of data about γ-spodumene.