Structure and Behavior of the Ni End-Member Schreibersite Ni3P under Compression to 50 GPa
Abstract
1. Introduction
2. Materials and Methods
2.1. Single Crystal X-Ray Diffraction at Ambient Conditions
2.2. High-Pressure X-Ray Diffraction
3. Results
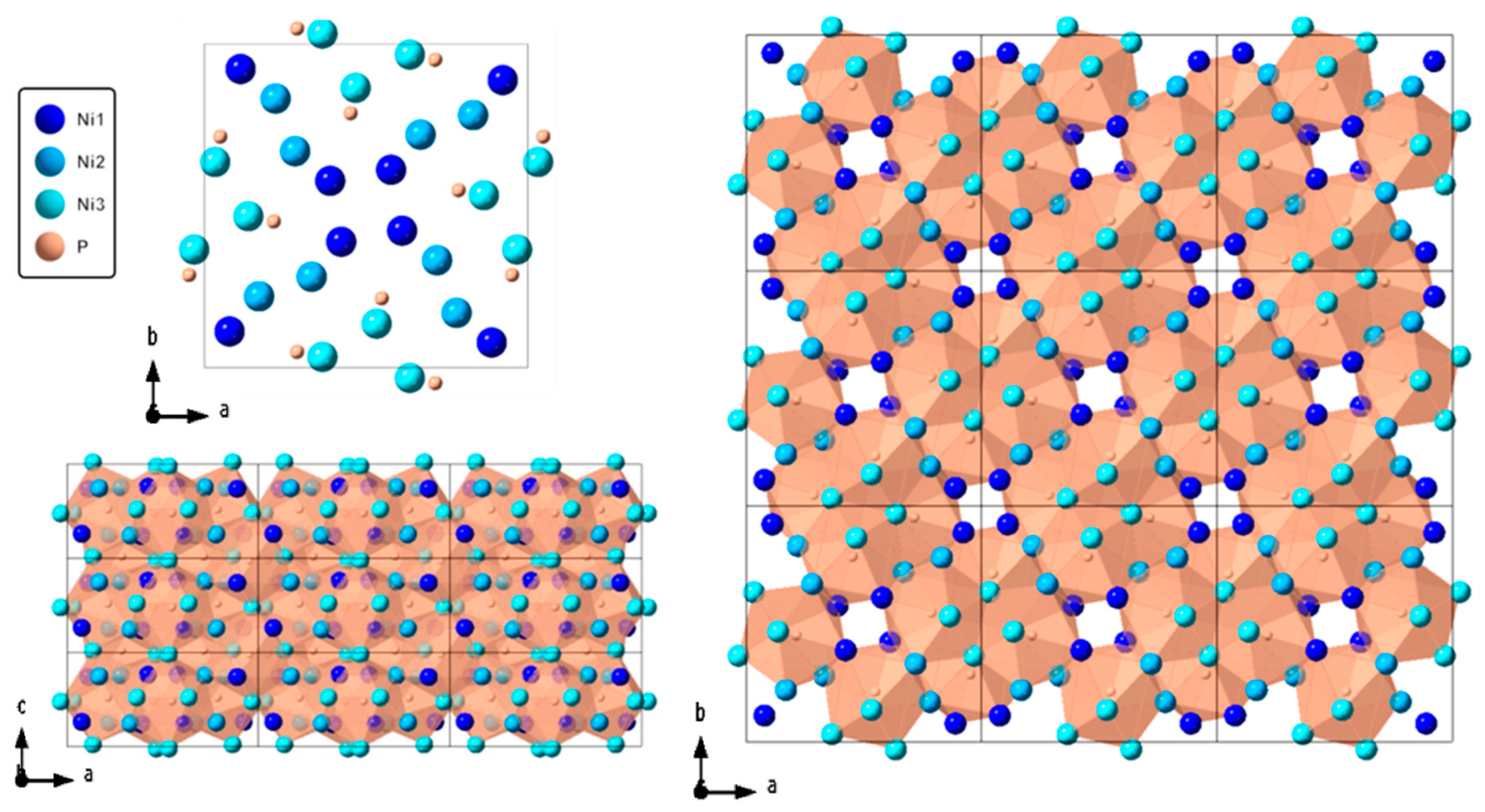
3.1. Single Crystal X-Ray Diffraction at Ambient Conditions
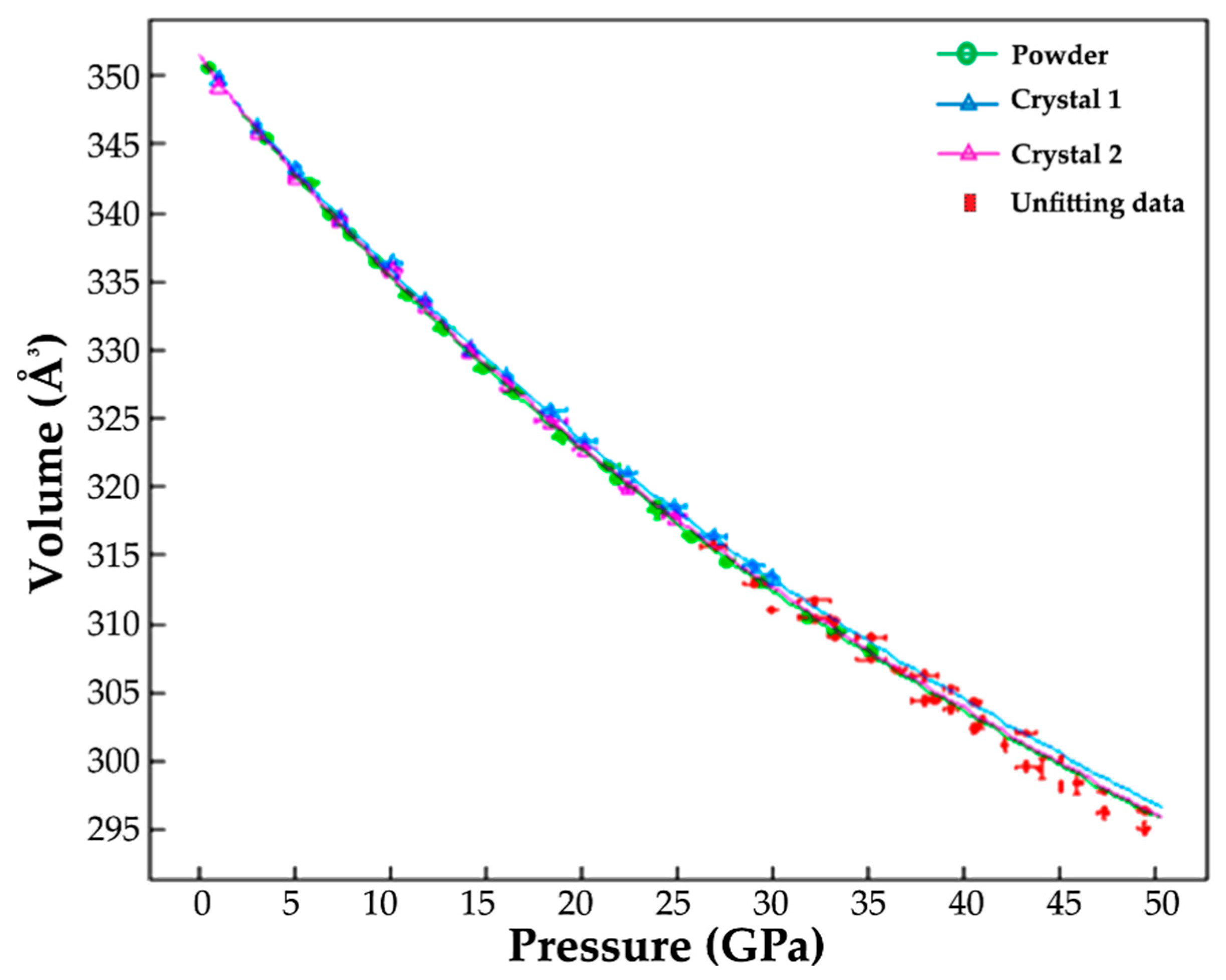
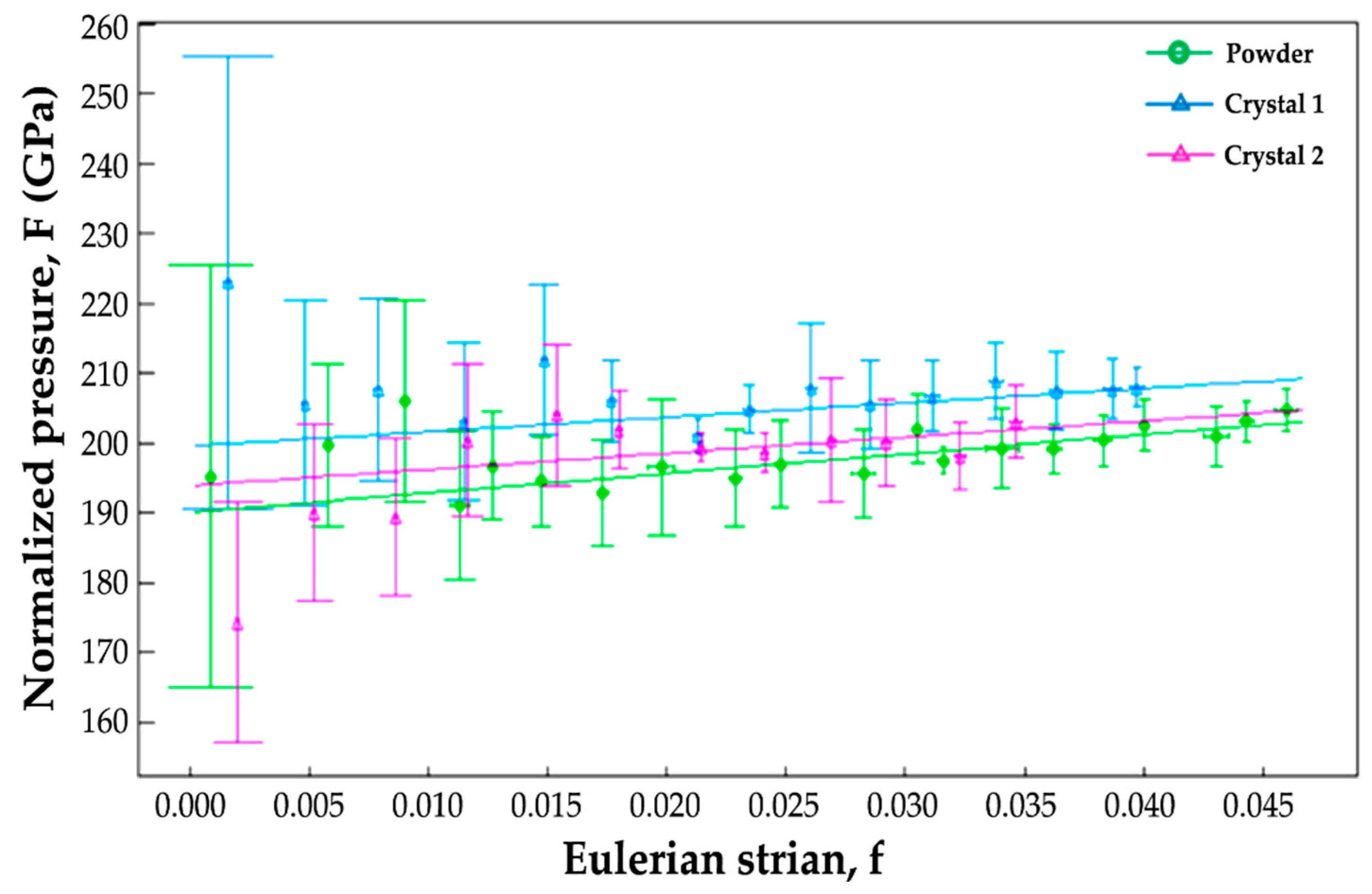
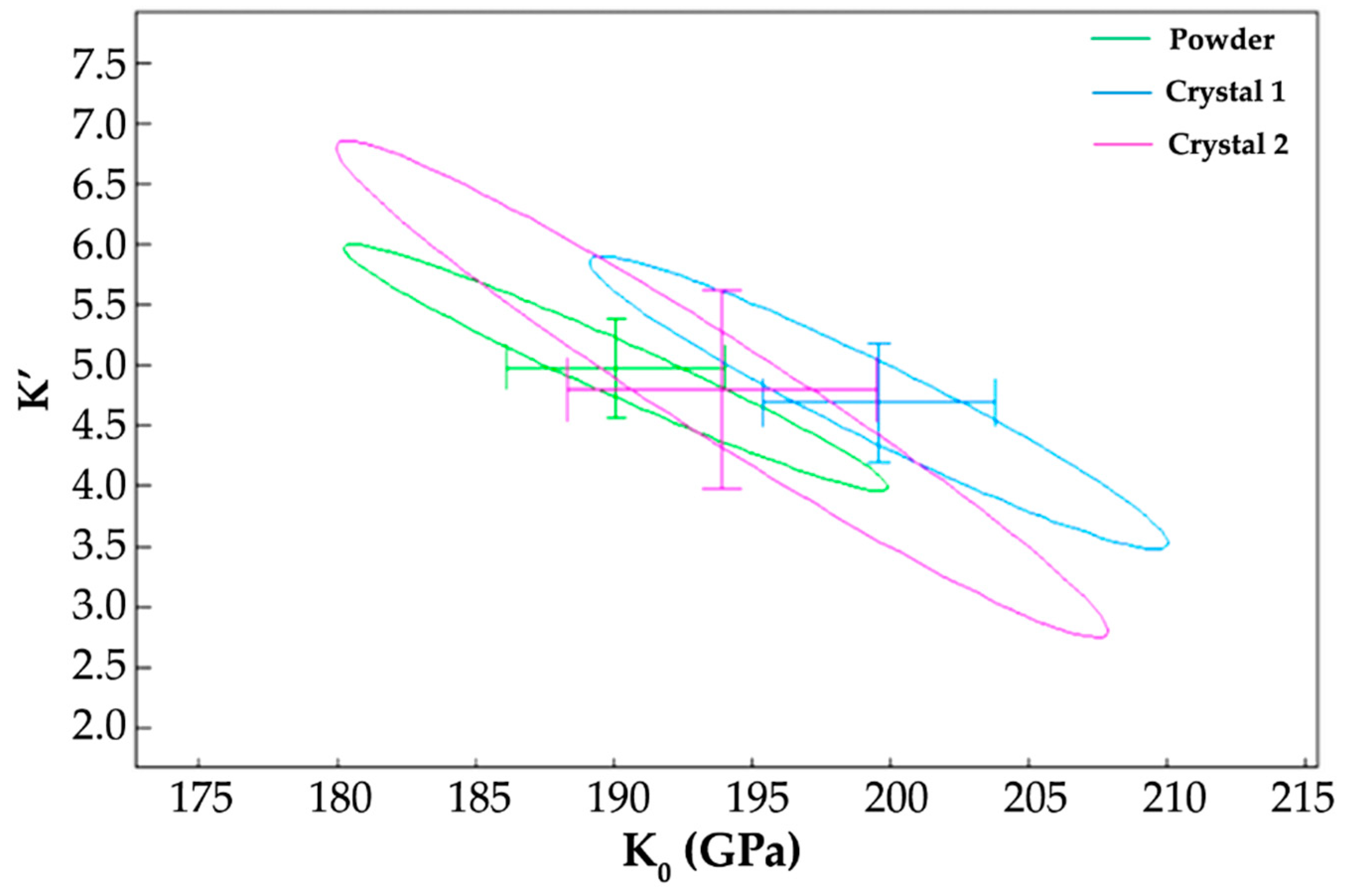
3.2. High-Pressure X-Ray Diffraction
4. Discussion
4.1. Crystal Structure at Ambient Condition.
4.2. Crystal Structure Evolution on Compression to 50 GPa
4.3. Implications for Planetary Cores
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McDonough, W.F.; Sun, S.S. The composition of the Earth. Chem. Geol. 1995, 120, 223–253. [Google Scholar] [CrossRef]
- Allègre, C.J.; Poirier, J.P.; Humler, E.; Hofmann, A.W. The chemical composition of the Earth. Earth Planet. Sci. Lett. 1995, 134, 515–526. [Google Scholar] [CrossRef]
- Litasov, K.D.; Shatskiy, A.F. Composition of the Earth’s core. Russ. Geol. Geophys. 2016, 57, 22–46. [Google Scholar] [CrossRef]
- Kozlovsky, Y.A. The world’s deepest well. Sci. Am. 1984, 251, 98–105. [Google Scholar] [CrossRef]
- Birch, F. Elasticity and constitution of the Earth’s interior. J. Geophys. Res. 1952, 57, 227–286. [Google Scholar] [CrossRef]
- Li, J.; Fei, Y. Experimental constraints on core composition. Treatise Geochem. 2003, 2, 568. [Google Scholar]
- Poirier, J.P. Light elements in the Earth’s outer core: A critical review. Phys. Earth Planet. Inter. 1994, 85, 319–337. [Google Scholar] [CrossRef]
- Lin, J.F.; Struzhkin, V.V.; Sturhahn, W.; Huang, E.; Zhao, J.; Hu, M.Y.; Alp, E.E.; Mao, H.K.; Boctor, N.; Hemley, R.J. Sound velocities of iron-nickel and iron-silicon alloys at high pressures. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Maciá, E.; Hernández, M.V.; Oró, J. Primary sources of phosphorus and phosphates in chemical evolution. Orig. Life Evol. Biosph. 1997, 27, 459–480. [Google Scholar] [CrossRef]
- Bryant, D.E.; Greenfield, D.; Walshaw, R.D.; Johnson, B.R.; Herschy, B.; Smith, C.; Pasek, M.A.; Telford, R.; Scowen, I.; Munshi, T.; et al. Hydrothermal modification of the Sikhote-Alin iron meteorite under low pH geothermal environments. A plausibly prebiotic route to activated phosphorus on the early Earth. Geochim. Cosmochim. Acta 2013, 109, 90–112. [Google Scholar] [CrossRef]
- McDonough, W.F. 3.16–Compositional model for the Earth’s core. Treatise Geochem (2nd edition). 2014, 3, 559–577. [Google Scholar]
- Gu, T.; Wu, X.; Qin, S.; Dubrovinsky, L. In situ high-pressure study of FeP: Implications for planetary cores. Phys. Earth Planet. Inter. 2011, 184, 154–159. [Google Scholar] [CrossRef]
- Stewart, A.J.; Schmidt, M.W. Sulfur and phosphorus in the Earth’s core: The Fe-P-S system at 23 GPa. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Dera, P.; Lazarz, J.D.; Lavina, B. Pressure-induced development of bonding in NiAs type compounds and polymorphism of NiP. J. Solid State Chem. 2011, 184, 1997–2003. [Google Scholar] [CrossRef]
- Britvin, S.N.; Rudashevsky, N.S.; Krivovichev, S.V.; Burns, P.C.; Polekhovsky, Y.S. Allabogdanite, (Fe, Ni)2P, a new mineral from the Onello meteorite: The occurrence and crystal structure. Am. Mineral. 2002, 87, 1245–1249. [Google Scholar] [CrossRef]
- Brandstätter, F.; Koeberl, C.; Kurat, G. The discovery of iron barringerite in lunar meteorite Y-793274. Geochim. Cosmochim. Acta 1991, 55, 1173–1174. [Google Scholar] [CrossRef]
- Buseck, P.R. Phosphide from meteorites: Barringerite, a new iron-nickel mineral. Science 1969, 165, 169–171. [Google Scholar] [CrossRef]
- Dera, P.; Lavina, B.; Borkowski, L.A.; Prakapenka, V.B.; Sutton, S.R.; Rivers, M.L.; Downs, R.T.; Prewitt, C.T. Structure and behavior of the barringerite Ni end-member, Ni2P, at deep Earth conditions and implications for natural Fe-Ni phosphides in planetary cores. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Geist, V.; Wagner, G.; Nolze, G.; Moretzki, O. Investigations of the meteoritic mineral (Fe, Ni)3P. Cryst. Res. Technol. J. Exp. Ind. Crystallogr. 2005, 40, 52–64. [Google Scholar] [CrossRef]
- Scott, H.P.; Huggins, S.; Frank, M.R.; Maglio, S.J.; Martin, C.D.; Meng, Y.; Santillán, J.; Williams, Q. Equation of state and high-pressure stability of Fe3P -schreibersite: Implications for phosphorus storage in planetary cores. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- He, X.J.; Guo, J.Z.; Wu, X.; Huang, S.X.; Qin, F.; Gu, X.P.; Qin, S. Compressibility of natural schreibersite up to 50 GPa. Phys. Chem. Miner. 2019, 46, 91–99. [Google Scholar] [CrossRef]
- Britvin, S.N.; Kolomenskii, V.D.; Boldyreva, M.M.; Bogdanova, A.N.; Kretser, Y.L.; Boldyreva, O.N.; Rudashevskii, N.S. Nickelphosphide (Ni, Fe)3P, the nickel analog of schreibersite. 3AПИCKИ POCCИЙCKOГO MИHEPAЛOГИЧECKOГO OБЩECTBA 1999, 128, 64–72. [Google Scholar]
- Skála, R.; Drábek, M. Nickelphosphide from the Vicenice octahedrite: Rietveld crystal structure refinement of synthetic analogue. Mineral. Mag. 2003, 67, 783–792. [Google Scholar] [CrossRef]
- Pratesi, G.; Bindi, L.; Moggi-Cecchi, V. Icosahedral coordination of phosphorus in the crystal structure of melliniite, a new phosphide mineral from the Northwest Africa 1054 acapulcoite. Am. Mineral. 2006, 91, 451–454. [Google Scholar] [CrossRef]
- Skála, R.; Císařová, I. Crystal structure of meteoritic schreibersite: Determination of absolute structure. Phys. Chem. Miner. 2005, 31, 721–732. [Google Scholar] [CrossRef]
- Pritekel, C. The crystal structure of meteoritic schreibersite: Refinement of the absolute crystal structure. Bachelor’s Thesis, University of Colorado Boulder, Boulder, CO, USA, January 2015. [Google Scholar]
- Pasek, M.A.; Lauretta, D.S. Aqueous corrosion of phosphide minerals from iron meteorites: A highly reactive source of prebiotic phosphorus on the surface of the early Earth. Astrobiology 2005, 5, 515–535. [Google Scholar] [CrossRef]
- Gull, M.; Mojica, M.A.; Fernández, F.M.; Gaul, D.A.; Orlando, T.M.; Liotta, C.L.; Pasek, M.A. Nucleoside phosphorylation by the mineral schreibersite. Sci. Rep. 2015, 5, 17198. [Google Scholar] [CrossRef]
- Hemley, R.J.; Mao, H.K. In situ studies of iron under pressure: New windows on the Earth’s core. Int. Geol. Rev. 2001, 43, 1–30. [Google Scholar]
- Kuwayama, Y.; Hirose, K.; Sata, N.; Ohishi, Y. Phase relations of iron and iron–nickel alloys up to 300 GPa: Implications for composition and structure of the Earth’s inner core. Earth Planet. Sci. Lett. 2008, 273, 379–385. [Google Scholar] [CrossRef]
- Huang, E.; Bassett, W.A.; Weathers, M.S. Phase relationships in Fe-Ni alloys at high pressures and temperatures. J. Geophys. Res. Solid Earth 1988, 93, 7741–7746. [Google Scholar] [CrossRef]
- Lin, J.F.; Heinz, D.L.; Campbell, A.J.; Devine, J.M.; Shen, G. Iron-silicon alloy in Earth’s core? Science 2002, 295, 313–315. [Google Scholar] [CrossRef] [PubMed]
- Mao, W.L.; Campbell, A.J.; Heinz, D.L.; Shen, G. Phase relations of Fe–Ni alloys at high pressure and temperature. Phys. Earth Planet. Inter. 2006, 155, 146–151. [Google Scholar] [CrossRef]
- Steinle-Neumann, G.; Stixrude, L.; Cohen, R.E.; Gülseren, O. Elasticity of iron at the temperature of the Earth’s inner core. Nature 2001, 413, 57. [Google Scholar] [CrossRef] [PubMed]
- Gu, T.; Fei, Y.; Wu, X.; Qin, S. High-pressure behavior of Fe3P and the role of phosphorus in planetary cores. Earth Planet. Sci. Lett. 2014, 390, 296–303. [Google Scholar] [CrossRef]
- Fei, Y.; Li, J.; Bertka, C.M.; Prewitt, C.T. Structure type and bulk modulus of Fe3S, a new iron-sulfur compound. Am. Mineral. 2000, 85, 1830–1833. [Google Scholar] [CrossRef]
- Lin, J.F.; Fei, Y.; Sturhahn, W.; Zhao, J.; Mao, H.K.; Hemley, R.J. Magnetic transition and sound velocities of Fe3S at high pressure: Implications for Earth and planetary cores. Earth Planet. Sci. Lett. 2004, 226, 33–40. [Google Scholar] [CrossRef]
- Seagle, C.T.; Campbell, A.J.; Heinz, D.L.; Shen, G.; Prakapenka, V.B. Thermal equation of state of Fe3S and implications for sulfur in Earth’s core. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Kamada, S.; Terasaki, H.; Ohtani, E.; Sakai, T.; Kikegawa, T.; Ohishi, Y.; Hirao, N.; Sata, N.; Kondo, T. Phase relationships of the Fe-FeS system in conditions up to the Earth’s outer core. Earth Planet. Sci. Lett. 2010, 294, 94–100. [Google Scholar] [CrossRef]
- Bruker. APEX3 Crystallography Software Suite; Bruker AXS Inc.: Madison, WI, USA, 2016. [Google Scholar]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A Found. Crystallogr. 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Heinz, D.L.; Jeanloz, R. The equation of state of the gold calibration standard. J. Appl. Phys. 1984, 55, 885–893. [Google Scholar] [CrossRef]
- Mao, H.K.; Bell, P.M.; Shaner, J.T.; Steinberg, D.J. Specific volume measurements of Cu, Mo, Pd, and Ag and calibration of the ruby R1 fluorescence pressure gauge from 0.06 to 1 Mbar. J. Appl. Phys. 1978, 49, 3276–3283. [Google Scholar] [CrossRef]
- Mao, H.K.; Xu, J.A.; Bell, P.M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. Solid Earth 1986, 91, 4673–4676. [Google Scholar] [CrossRef]
- Rivers, M.; Prakapenka, V.B.; Kubo, A.; Pullins, C.; Holl, C.M.; Jacobsen, S.D. The COMPRES/GSECARS gas-loading system for diamond anvil cells at the Advanced Photon Source. High Press. Res. 2008, 28, 273–292. [Google Scholar] [CrossRef]
- Prescher, C.; Prakapenka, V.B. DIOPTAS: A program for reduction of two-dimensional X-ray diffraction data and data exploration. High Press. Res. 2015, 35, 223–230. [Google Scholar] [CrossRef]
- Dera, P.; Zhuravlev, K.; Prakapenka, V.; Rivers, M.L.; Finkelstein, G.J.; Grubor-Urosevic, O.; Tschauner, O.; Clark, S.M.; Downs, R.T. High pressure single-crystal micro X-ray diffraction analysis with GSE_ADA/RSV software. High Press. Res. 2013, 33, 466–484. [Google Scholar] [CrossRef]
- Aronsson, B. The crystal structure of Ni3P.(Fe3P-Type). Acta Chem. Scand. 1955, 9, 137–140. [Google Scholar] [CrossRef][Green Version]
- Rundqvist, S.; Hassler, E.; Lundvik, L. Refinement of Ni3P Structure. Acta Chem. Scand. 1962, 16, 242. [Google Scholar]
- Jun, R.E.N.; Wang, J.G.; Li, J.F.; Li, Y.W. Density functional theory study on crystal nickel phosphides. J. Fuel Chem. Technol. 2007, 35, 458–464. [Google Scholar]
- Gonzalez-Platas, J.; Alvaro, M.; Nestola, F.; Angel, R. EosFit7-GUI: A new graphical user interface for equation of state calculations, analyses and teaching. J. Appl. Crystallogr. 2016, 49, 1377–1382. [Google Scholar] [CrossRef]
- Birch, F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300 K. J. Geophys. Res. Solid Earth 1978, 83, 1257–1268. [Google Scholar] [CrossRef]
- Flack, H.D. Chiral and achiral crystal structures. Helv. Chim. Acta 2003, 86, 905–921. [Google Scholar] [CrossRef]
- Howard, J.W. Finite strain studies of single crystal Fe3P under high pressures. Master’s Thesis, University of Nevada Las Vegas, Las Vegas, NV, USA, 2010. [Google Scholar]
- Greenwood, N.N.; Earnshaw, A. Chemistry of the Elements; Elsevier: Oxford, UK, 2012. [Google Scholar]
- Badro, J.; Teter, D.M.; Downs, R.T.; Gillet, P.; Hemley, R.J.; Barrat, J.L. Theoretical study of a five-coordinated silica polymorph. Phys. Rev. B 1997, 56, 5797. [Google Scholar] [CrossRef]
- Dove, M.T.; Craig, M.S.; Keen, D.A.; Marshall, W.G.; Redfern, S.A.T.; Trachenko, K.O.; Tucker, M.G. Crystal structure of the high-pressure monoclinic phase-II of cristobalite, SiO2. Min. Mag. 2000, 64, 569–576. [Google Scholar] [CrossRef]
- Dera, P.; Lazarz, J.D.; Prakapenka, V.B.; Barkley, M.; Downs, R.T. New insights into the high-pressure polymorphism of SiO2 cristobalite. Phys. Chem. Miner. 2011, 38, 517–529. [Google Scholar] [CrossRef]
- Dera, P.; Jayaraman, A.; Prewitt, C.T.; Gramsch, S.A. Structural basis for high-pressure polymorphism in CuGeO3. Phys. Rev. B 2002, 65, 134105. [Google Scholar] [CrossRef]
- Klotz, S.; Chervin, J.C.; Munsch, P.; Le Marchand, G. Hydrostatic limits of 11 pressure transmitting media. J. Phys. D Appl. Phys. 2009, 42, 075413. [Google Scholar] [CrossRef]
- Dera, P.; Lavina, B.; Meng, Y.; Prakapenka, V.B. Structural and electronic evolution of Cr2O3 on compression to 55 GPa. J. Solid State Chem. 2011, 184, 3040–3049. [Google Scholar] [CrossRef]
- Golosova, N.O.; Kozlenko, D.P.; Kichanov, S.E.; Lukin, E.V.; Liermann, H.P.; Glazyrin, K.V.; Savenko, B.N. Structural and magnetic properties of Cr2O3 at high pressure. J. Alloy. Compd. 2017, 722, 593–598. [Google Scholar] [CrossRef]
- Zhao, D.; Zhou, L.; Du, Y.; Wang, A.; Peng, Y.; Kong, Y.; Sha, C.; Ouyang, Y.; Zhang, W. Structure, elastic and thermodynamic properties of the Ni–P system from first-principles calculations. Calphad 2011, 35, 284–291. [Google Scholar] [CrossRef]
- Urakawa, S.; Matsubara, R.; Katsura, T.; Watanabe, T.; Kikegawa, T. Stability and bulk modulus of Ni3S, a new nickel sulfur compound, and the melting relations of the system Ni-NiS up to 10 GPa. Am. Mineral. 2011, 96, 558–565. [Google Scholar] [CrossRef]
- Lyman, T. Metallography, Structures and Phase Diagrams, Metal Handbook; American Society for Metals: Metals Park, OH, USA, 1973. [Google Scholar]
- Okamoto, H. Fe-P (Iron-Phosphorus). J. Phase Equilibria Diffus. 2007, 28, 588. [Google Scholar] [CrossRef]
- Kim, T.Y.; Son, H.J.; Lim, S.K.; Song, Y.I.; Park, H.S.; Suh, S.J. Electroless Nickel Alloy Deposition on SiO2 for Application as a Diffusion Barrier and Seed Layer in 3D Copper Interconnect Technology. J. Nanosci. Nanotechnol. 2014, 14, 9515–9524. [Google Scholar] [CrossRef] [PubMed]
- Gambino, R.J.; McGuire, T.R.; Nakamura, Y. Magnetic Properties of the Iron-Group Metal Phosphides. J. Appl. Phys. 1967, 38, 1253–1255. [Google Scholar] [CrossRef]
- Goto, M.; Tange, H.; Tokunaga, T.; Fujii, H.; Okamoto, T. Magnetic properties of the (Fe1−xMx)3P compounds. Jpn. J. Appl. Phys. 1977, 16, 2175. [Google Scholar] [CrossRef]
- Li, L.H.; Wang, W.L.; Hu, L.; Wei, B.B. First-principle calculations of structural, elastic and thermodynamic properties of Fe–B compounds. Intermetallics 2014, 46, 211–221. [Google Scholar] [CrossRef]
- Wu, J.; Chong, X.; Zhou, R.; Jiang, Y.; Feng, J. Structure, stability, mechanical and electronic properties of Fe–P binary compounds by first-principles calculations. RSC Adv. 2015, 5, 81943–81956. [Google Scholar] [CrossRef]

| Element | x | y | z |
|---|---|---|---|
| Ni | 0.9228(1) | 0.8887(1) | 0.7608(1) |
| Ni | 0.6353(1) | 0.9675(1) | 0.0219(1) |
| Ni | 0.8313(1) | 0.7802(1) | 0.2458(1) |
| P | 0.7139(1) | 0.9517(1) | 0.5192(2) |
| Atom pair | Interatomic Distance (Å) |
|---|---|
| NiI–NiI | 2.425(1), 2.710(1) × 2, 2.859(1) |
| NiI–NiII | 2.649(1) |
| NiI–NiIII | 2.478(1), 2.592(1), 2.708(1), 2.732(1), 2.813(1) |
| NiII–NiII | 2.491(1), 2.669(1), 2.669(1) |
| NiII–NiIII | 2.511(1), 2.544(1), 2.618(1) |
| NiIII–NiIII | 2.687(1), 2.687(1) |
| NiI–P | 2.222(1), 2.284(1) |
| NiII–P | 2.296(1), 2.317(1), 2.318(1), 2.345(1) |
| NiIII–P | 2.214(1), 2.278(1), 2.337 (1) |
| Pressure (GPa) | a [Å] | c [Å] | Volume [A3] |
|---|---|---|---|
| 0.50(1) | 8.945(1) | 4.381(1) | 350.5(1) |
| 3.6(2) | 8.901(1) | 4.360(1) | 345.5(1) |
| 5.8(4) | 8.874(1) | 4.345(1) | 342.2(1) |
| 6.9(3) | 8.853(4) | 4.336(2) | 339.9(4) |
| 8.0(3) | 8.842(1) | 4.330(1) | 338.5(1) |
| 9.3(3) | 8.824(1) | 4.321(1) | 336.5(1) |
| 10.9 (4) | 8.801(2) | 4.311(2) | 334.0(2) |
| 12.9(5) | 8.781(4) | 4.301(4) | 331.6(5) |
| 15.0(5) | 8.755(2) | 4.288(2) | 328.6(3) |
| 16.5(5) | 8.739(2) | 4.280(1) | 326.9(2) |
| 19.0(5) | 8.709(4) | 4.267(3) | 323.6(4) |
| 21.5(5) | 8.692(1) | 4.257(1) | 321.6(2) |
| 21.8(1) | 8.683(2) | 4.253(1) | 320.6(2) |
| 24.0(4) | 8.663(6) | 4.242(3) | 318.4(6) |
| 25.8(4) | 8.646(2) | 4.233(2) | 316.4(2) |
| 27.7(4) | 8.629(3) | 4.225(2) | 314.6(3) |
| 29.5(5) | 8.616(2) | 4.218(1) | 313.1(2) |
| 31.9(5) | 8.592(4) | 4.207(3) | 310.5(4) |
| 33.4(4) | 8.581(3) | 4.200(1) | 309.4(3) |
| 35.2(3) | 8.569(4) | 4.194(2) | 308.0(4) |
| 36.6(4) | 8.556(2) | 4.189(2) | 306.7(2) |
| 38.5(4) | 8.536(3) | 4.180(1) | 304.6(3) |
| 41.0(2) | 8.518(4) | 4.174(3) | 302.9(4) |
| 42.2(2) | 8.499(5) | 4.170(3) | 301.2(5) |
| 44.1(1) | 8.480(7) | 4.165(5) | 299.5(7) |
| 46.0(2) | 8.467(7) | 4.163(7) | 298.4(8) |
| Pressure (GPa) | Crystal | a [Å] | c [Å] | Volume [A3] |
|---|---|---|---|---|
| 1.1(1) | C1 | 8.939(1) | 4.378(2) | 349.8(2) |
| C2 | 8.936(1) | 4.375(1) | 349.4(1) | |
| 3.1(2) | C1 | 8.911(1) | 4.363(1) | 346.4(1) |
| C2 | 8.906(1) | 4.362(1) | 346.0(1) | |
| 5.1(3) | C1 | 8.883(1) | 4.350(2) | 343.3(2) |
| C2 | 8.876(1) | 4.348(1) | 342.6(1) | |
| 7.4(4) | C1 | 8.853(1) | 4.334(2) | 339.7(1) |
| C2 | 8.851(1) | 4.334(1) | 339.5(1) | |
| 10.2(5) | C1 | 8.823(1) | 4.321(1) | 336.4(1) |
| C2 | 8.819(1) | 4.318(1) | 335.8(1) | |
| 11.9(3) | C1 | 8.799(1) | 4.309(2) | 333.6(2) |
| C2 | 8.797(1) | 4.307(2) | 333.3(2) | |
| 14.3(1) | C1 | 8.768(1) | 4.294(2) | 330.1(2) |
| C2 | 8.767(1) | 4.293(2) | 330.0(1) | |
| 16.2(2) | C1 | 8.749(1) | 4.286(3) | 328.1(2) |
| C2 | 8.745(1) | 4.282(2) | 327.5(2) | |
| 18.5(8) | C1 | 8.727(1) | 4.276(2) | 325.7(2) |
| C2 | 8.721(1) | 4.271(2) | 324.9(2) | |
| 20.2(6) | C1 | 8.706(1) | 4.266(2) | 323.4(2) |
| C2 | 8.702(1) | 4.262(3) | 322.8(2) | |
| 22.5(5) | C1 | 8.685(1) | 4.256(3) | 321.0(2) |
| C2 | 8.677(1) | 4.250(3) | 319.9(2) | |
| 25.0(6) | C1 | 8.664(1) | 4.244(3) | 318.6(3) |
| C2 | 8.655(1) | 4.243(3) | 317.8(3) | |
| 27.0(7) | C1 | 8.643(1) | 4.235(3) | 316.3(2) |
| C2 | 8.634(2) | 4.234(4) | 315.7(3) | |
| 29.1(5) | C1 | 8.623(1) | 4.226(4) | 314.3(3) |
| C2 | 8.608(2) | 4.223(4) | 312.9(3) | |
| 30.0(3) | C1 | 8.613(1) | 4.224(3) | 313.4(3) |
| C2 | 8.599(2) | 4.223(1) | 311.0(1) | |
| 32.3(8) | C1 | 8.594(1) | 4.220(4) | 311.7(3) |
| C2 | 8.581(2) | 4.216(4) | 310.4(3) | |
| 33.3(3) | C1 | 8.579(1) | 4.215(4) | 310.2(3) |
| C2 | 8.568(2) | 4.211(4) | 309.1(3) | |
| 35.2(8) | C1 | 8.565(1) | 4.212(4) | 309.0(3) |
| C2 | 8.551(2) | 4.204(5) | 307.5(3) | |
| 38.0(7) | C1 | 8.539(2) | 4.200(5) | 306.2(3) |
| C2 | 8.521(2) | 4.193(5) | 304.5(4) | |
| 39.4(4) | C1 | 8.529(1) | 4.197(4) | 305.3(3) |
| C2 | 8.514(2) | 4.191(5) | 303.8(4) | |
| 40.6(3) | C1 | 8.519(1) | 4.193(3) | 304.3(3) |
| C2 | 8.501(2) | 4.184(5) | 302.4(4) | |
| 43.3(5) | C1 | 8.497(1) | 4.184(3) | 302.1(2) |
| C2 | 8.473(2) | 4.173(5) | 299.6(4) | |
| 45.2(1) | C1 | 8.479(1) | 4.174(3) | 300.1(2) |
| C2 | 8.460(2) | 4.166(5) | 298.2(4) | |
| 47.4(3) | C1 | 8.457(1) | 4.164(3) | 297.8(3) |
| C2 | 8.440(2) | 4.159(6) | 296.3(4) | |
| 49.5(3) | C1 | 8.441(1) | 4.160(4) | 296.4(3) |
| C2 | 8.427(3) | 4.156(6) | 295.1(4) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chornkrathok, S.; Zhang, D.; Dera, P. Structure and Behavior of the Ni End-Member Schreibersite Ni3P under Compression to 50 GPa. Minerals 2020, 10, 306. https://doi.org/10.3390/min10040306
Chornkrathok S, Zhang D, Dera P. Structure and Behavior of the Ni End-Member Schreibersite Ni3P under Compression to 50 GPa. Minerals. 2020; 10(4):306. https://doi.org/10.3390/min10040306
Chicago/Turabian StyleChornkrathok, Sasithorn, Dongzhou Zhang, and Przemyslaw Dera. 2020. "Structure and Behavior of the Ni End-Member Schreibersite Ni3P under Compression to 50 GPa" Minerals 10, no. 4: 306. https://doi.org/10.3390/min10040306
APA StyleChornkrathok, S., Zhang, D., & Dera, P. (2020). Structure and Behavior of the Ni End-Member Schreibersite Ni3P under Compression to 50 GPa. Minerals, 10(4), 306. https://doi.org/10.3390/min10040306





