Incorporation of Incompatible Strontium and Barium Ions into Calcite (CaCO3) through Amorphous Calcium Carbonate
Abstract
1. Introduction
2. Experimental Procedures
2.1. Synthesis of Sr-Doped Calcite and Ba-Doped Calcite
2.2. Sample Analysis
3. Molecular Dynamics (MD) Simulations of Ba-Doped Calcite
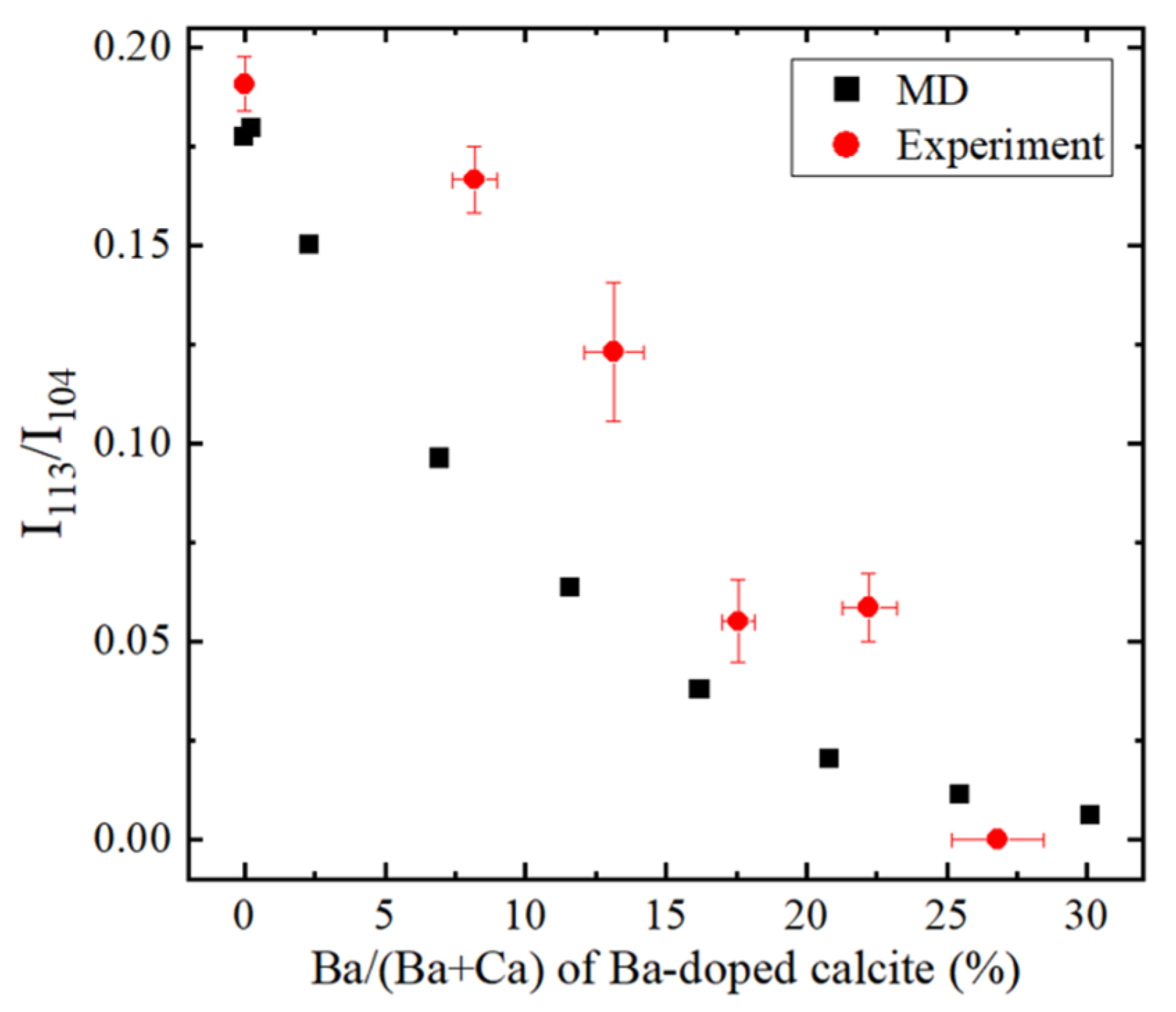
4. Results and Discussion
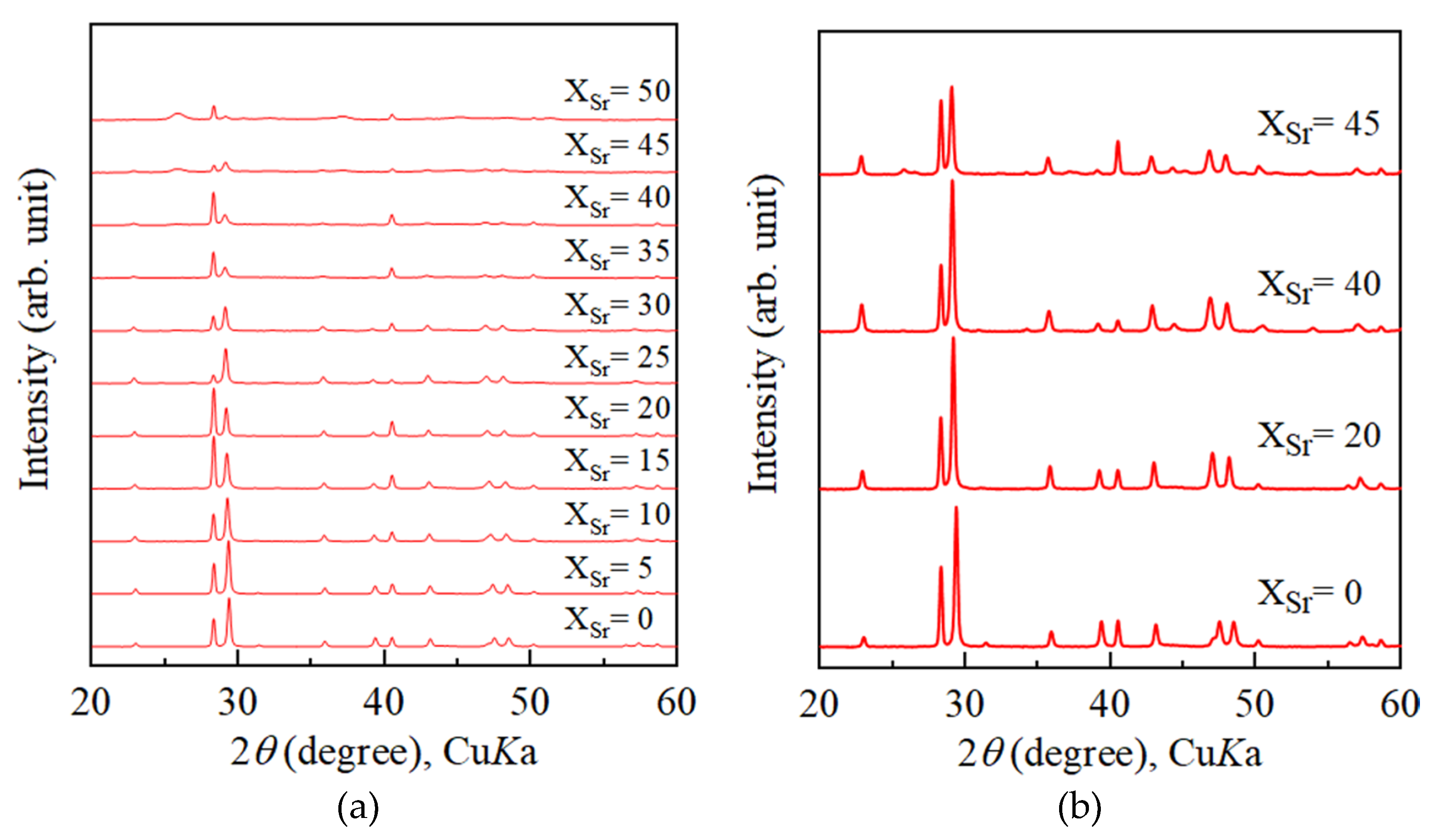
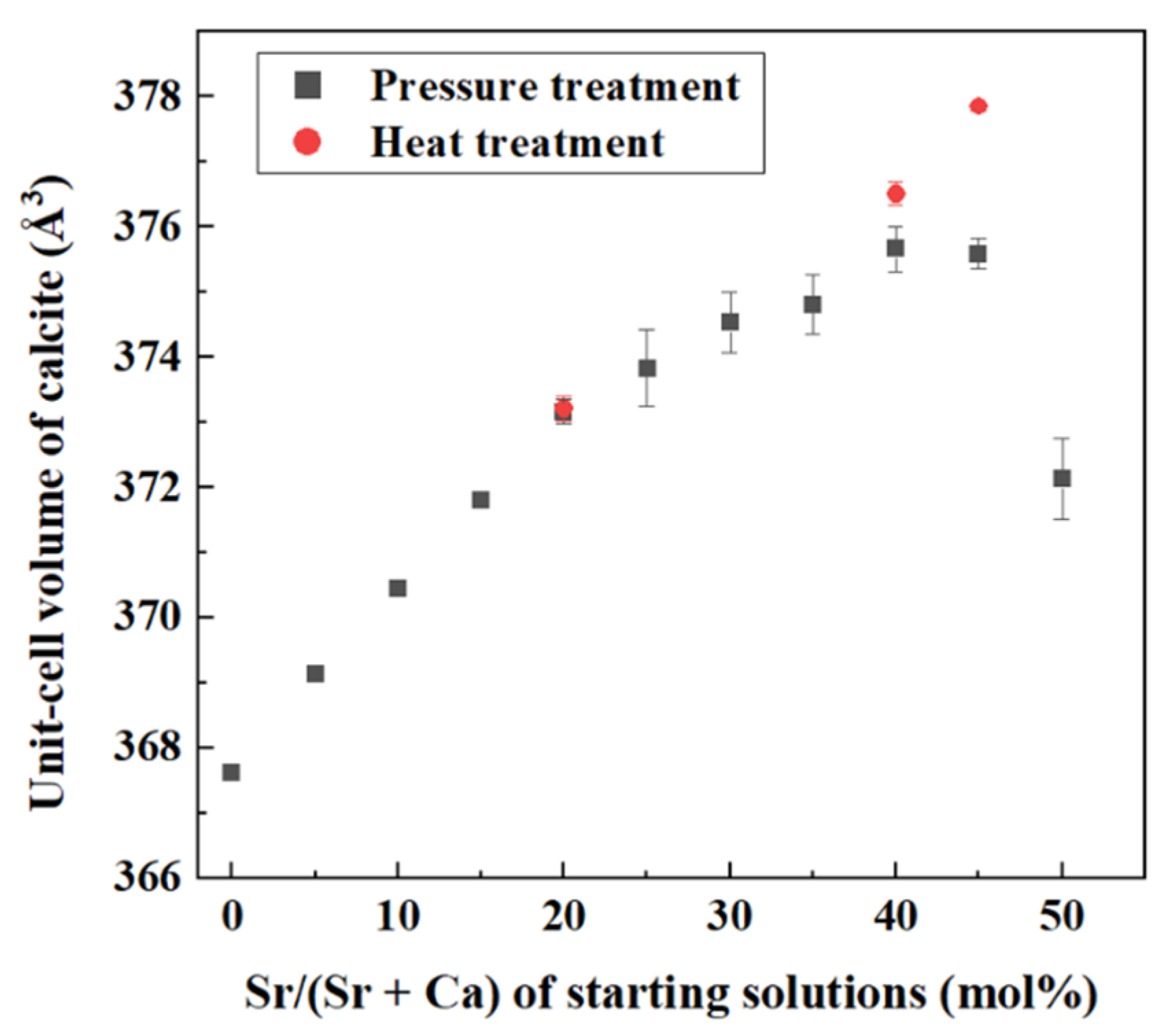
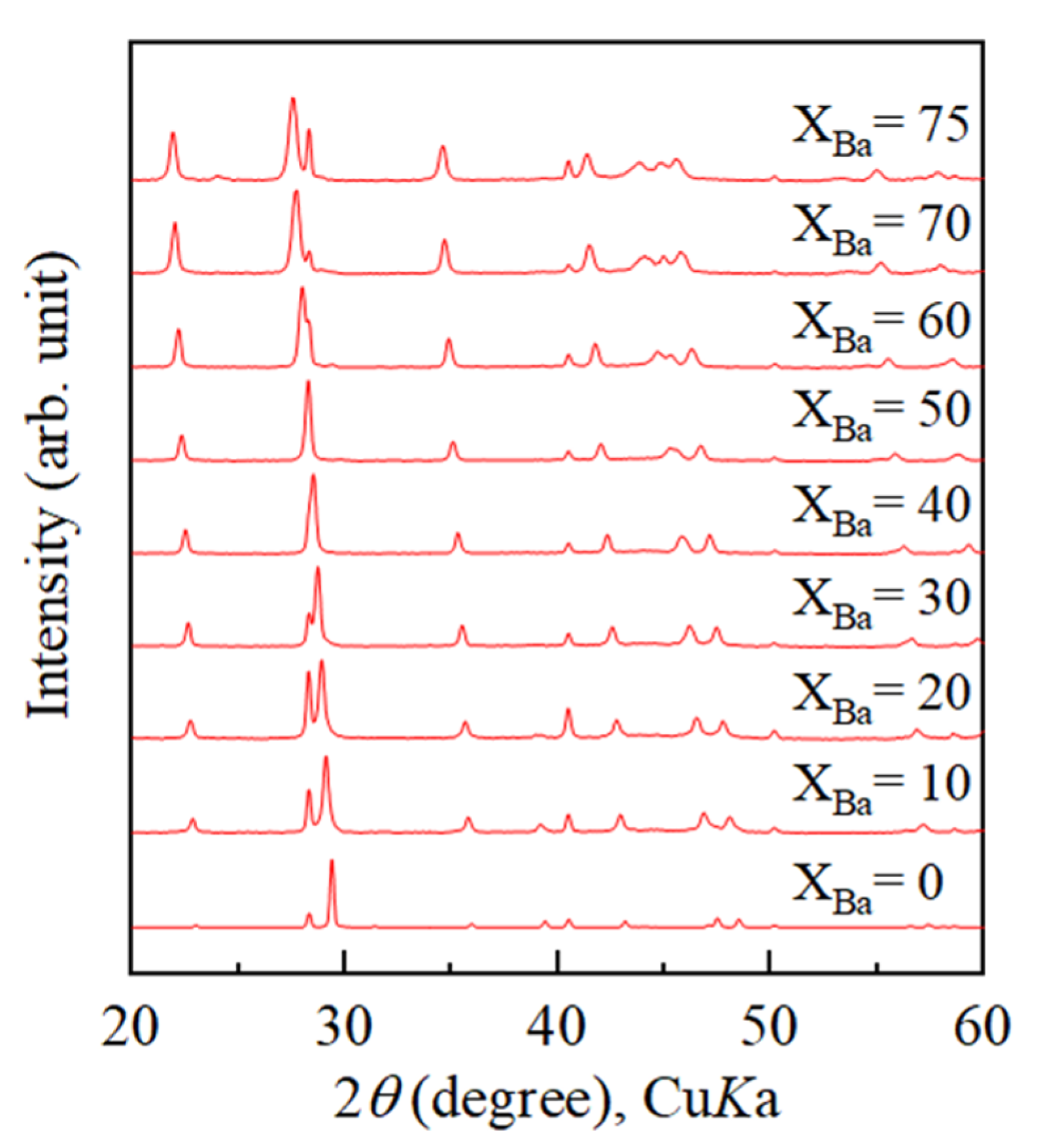
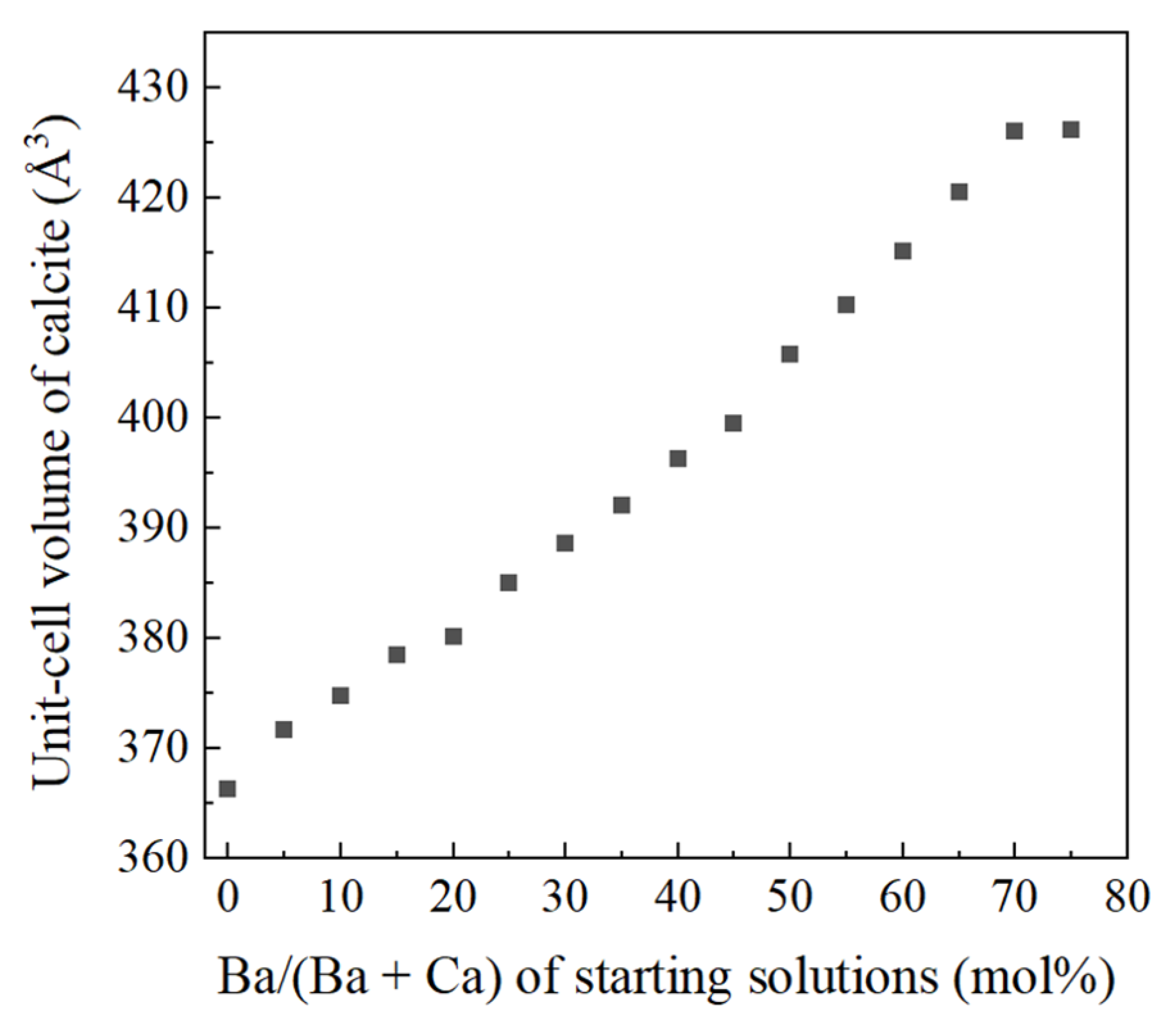
4.1. Increase of Lattice Parameters of Calcite Induced by Incorporation of Sr and Ba
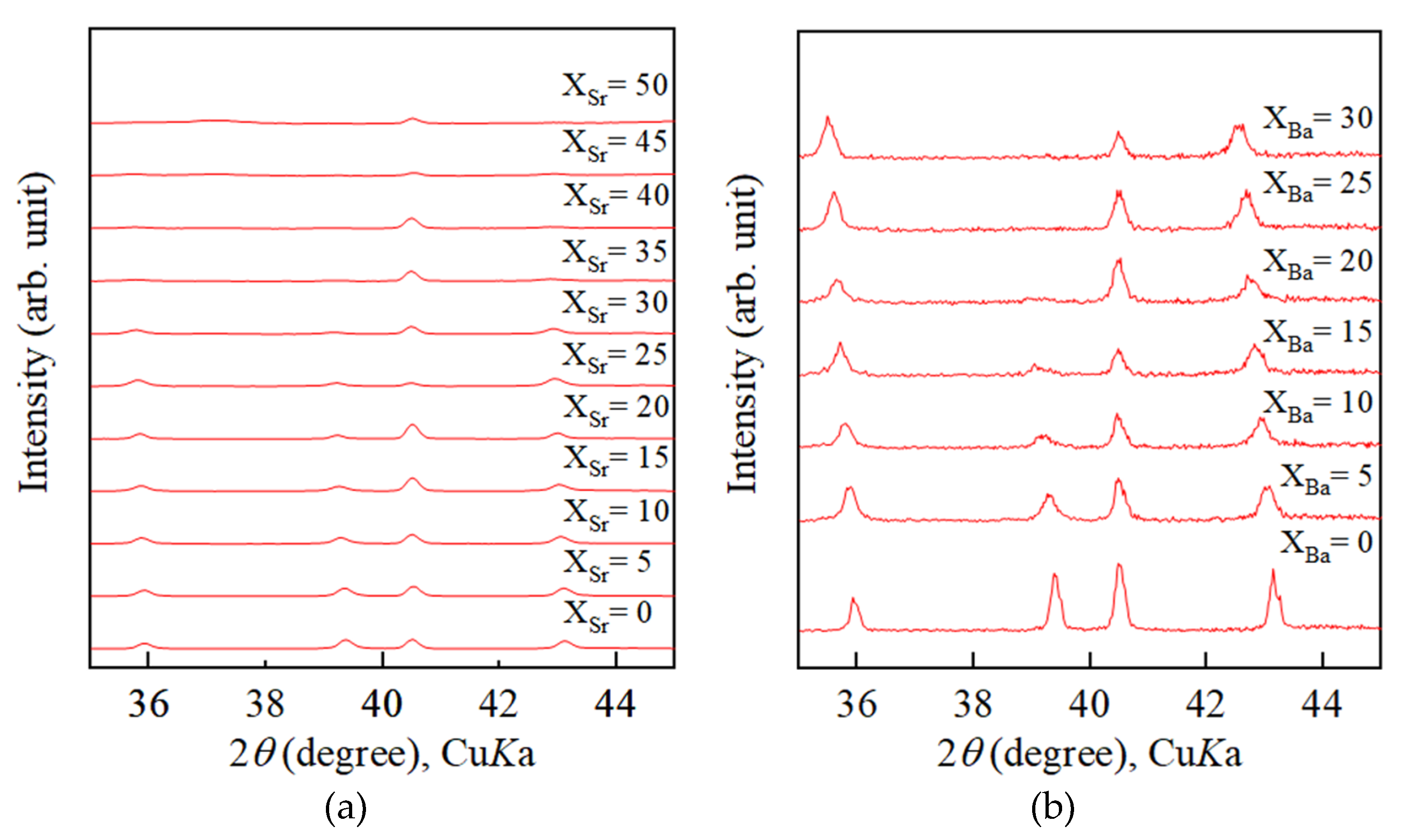
4.2. Growth Texture of Sr-Doped Calcite and Ba-Doped Calcite
4.3. Incorporation of Sr and Ba into Calcite Lattice
4.4. Impurity-Induced Order–Disorder Phase Transition
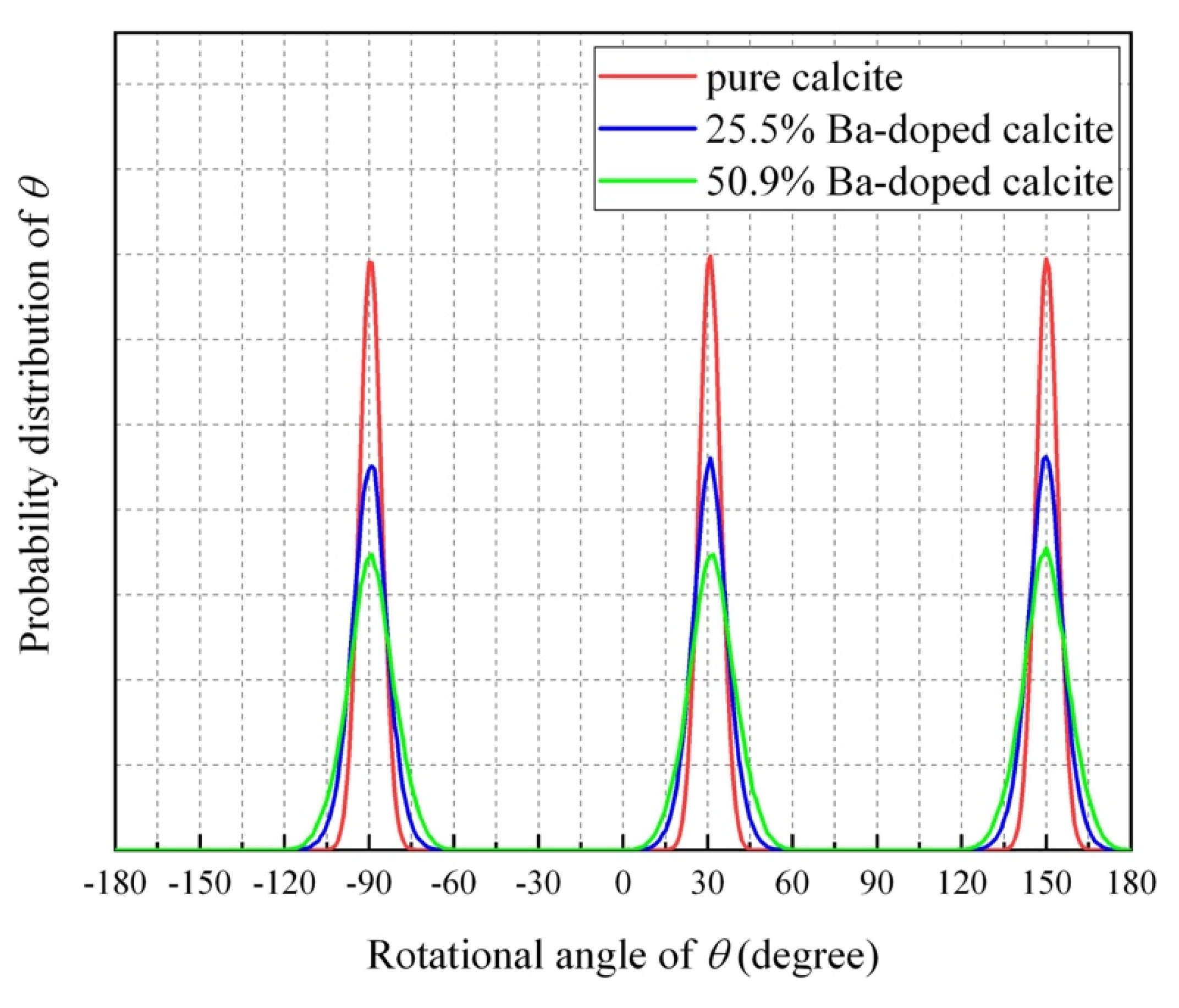
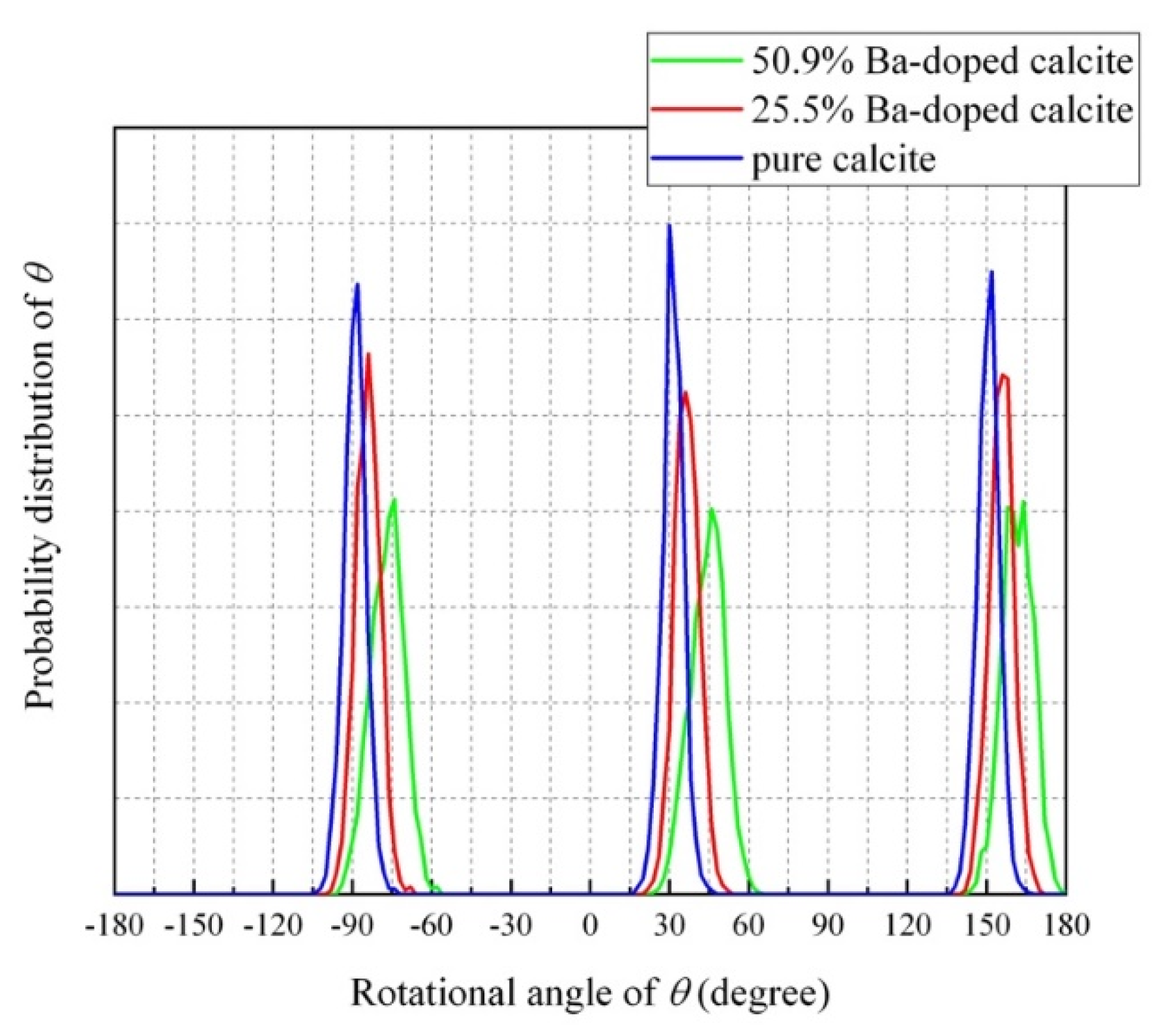
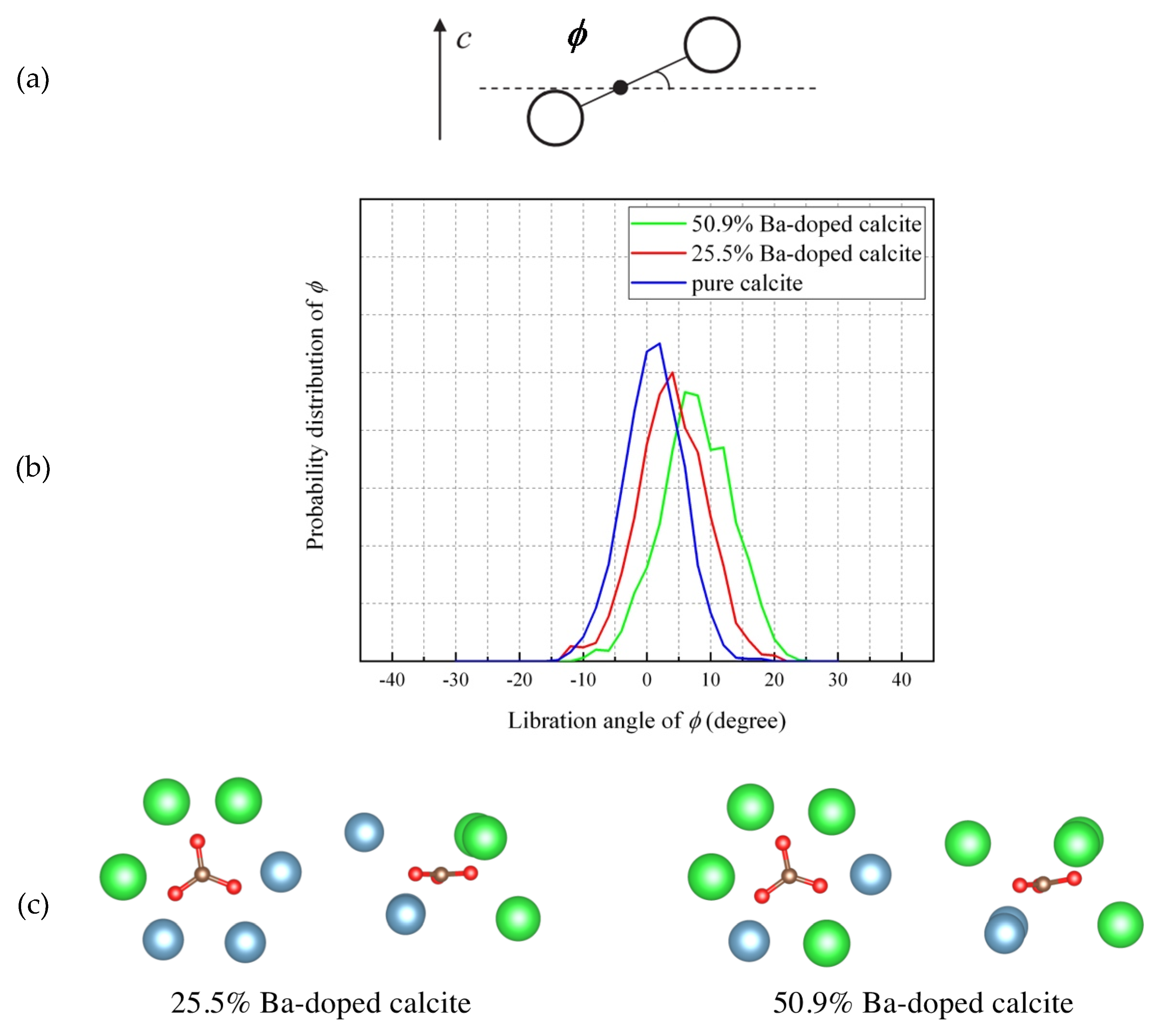
4.5. Molecular Dynamics (MD) Simulations of Ba-Doped Calcite
5. Conclusions
- (1)
- Crystallization from Sr-doped amorphous calcium carbonate and Ba-doped amorphous calcium carbonate resulted in the formation of calcite containing notably high concentrations of Sr and Ba. The maximum Ba concentration corresponded to the chemical formula of Ba0.7Ca0.3CO3.
- (2)
- With increasing Sr and Ba concentrations, the intensity of the 113 reflection of calcite decreased. The 113 reflection vanished at room temperature when Ba concentration was higher than 25 mol% (Ca0.75Ba0.25CO3).
- (3)
- The MD simulation indicated that the CO32− ions in Ba-doped calcites are not in the rotational (dynamical) disorder but in the static disorder at room temperature. The CO32− ions are tilted and angularly displaced from the equilibrium position of pure calcite.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Addadi, B.L.; Raz, S.; Weiner, S. Taking Advantage of Disorder: Amorphous Calcium Carbonate and Its Roles in Biomineralization. Adv. Mater. 2003, 15, 959–970. [Google Scholar] [CrossRef]
- Cantaert, B.; Kuo, D.; Matsumura, S.; Nishimura, T.; Sakamoto, T.; Kato, T. Use of amorphous calcium carbonate for the design of new materials. ChemPlusChem 2017, 82, 107–120. [Google Scholar] [CrossRef] [PubMed]
- Cartwright, J.H.E.; Checa, A.G.; Gale, J.D.; Gebauer, D.; Sainz-Díaz, C.I. Calcium carbonate polyamorphism and its role in biomineralization: How many amorphous calcium carbonates are there? Angew. Chem. Int. Ed. 2012, 51, 11960–11970. [Google Scholar] [CrossRef] [PubMed]
- Koga, N.; Nakagoe, Y.; Tanaka, H. Crystallization of amorphous calcium carbonate. Thermochim. Acta 1998, 318, 239–244. [Google Scholar] [CrossRef]
- Yoshino, T.; Maruyama, K.; Kagi, H.; Nara, M.; Kim, J.C. Pressure-Induced Crystallization from Amorphous Calcium Carbonate. Cryst. Growth Des. 2012, 12, 3357–3361. [Google Scholar] [CrossRef]
- Veizer, J. Trace elements and isotopes in sedimentary carbonates. In Carbonates: Mineralogy and Chemistry; Reviews in Mineralogy; Reeder, R.J., Ed.; Mineralogical Society of America: Washington, DC, USA, 1983; Volume 11, pp. 265–299. [Google Scholar]
- Pingitore, N.E.; Eastman, M.P. The experimental partitioning of Ba2+ into calcite. Chem. Geol. 1984, 45, 113–120. [Google Scholar] [CrossRef]
- Matsunuma, S.; Kagi, H.; Komatsu, K.; Maruyama, K.; Yoshino, T. Doping incompatible elements into calcite through amorphous calcium carbonate. Cryst. Growth Des. 2014, 14, 5344–5348. [Google Scholar] [CrossRef]
- Larson, A.C.; Von Dreele, R.B. General Structure Analysis System (GSAS); Los Alamos National Laboratory: Los Alamos, NM, USA, 2000; pp. 86–748. [Google Scholar]
- Toby, B.H. EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 2001, 34, 210–213. [Google Scholar] [CrossRef]
- Kawamura, K. MXDTRICL. Japan Chemical Program Exchange, #77, 1997.
- Kawano, J.; Miyake, A.; Shimobayashi, N.; Kitamura, M.J. Molecular dynamics simulation of the rotational order–disorder phase transition in calcite. Phys. Condens. Matter 2009, 21, 95406. [Google Scholar] [CrossRef] [PubMed]
- Miyake, A.; Hasegawa, H.; Kawamura, K.; Kitamura, M. Symmetry and its change in a reciprocal space of a quartz crystal simulated by molecular dynamics. Acta Cryst. 1998, A54, 330–337. [Google Scholar] [CrossRef]
- Mackenzie, F.T.; Bischoff, W.D.; Bishop, F.C.; Loijens, M.; Schoonmaker, J.; Wollast, R. Magnesian calcites: Low temperature occurrence, solubility and solid-solution behavior. In Carbonates: Mineralogy and Chemistry; Reviews in Mineralogy; Reeder, R.J., Ed.; Mineralogical Society of America: Washington, DC, USA, 1983; Volume 11, pp. 97–144. [Google Scholar]
- Maruyama, K.; Kagi, H.; Inoue, T.; Ohfuji, H.; Yoshino, T. In situ observation of pressure-induced crystallization from amorphous calcium carbonate by time-resolved X-ray diffraction. Chem. Lett. 2015, 44, 434–436. [Google Scholar] [CrossRef]
- Pingitore, N.E.; Lytle, F.W.; Davies, B.M.; Eastman, M.P.; Eller, P.G.; Larson, E.M. Mode of incorporation of Sr2+ in calcite: Determination by X-ray absorption spectroscopy. Geochim. Cosmochim. Acta 1992, 56, 1531–1538. [Google Scholar] [CrossRef]
- Allison, N.; Austin, W.E.N. The potential of ion microprobe analysis in detecting geochemical variations across individual foraminifera tests. Geochem. Geophys. Geosystems 2003, 4, 1–9. [Google Scholar] [CrossRef]
- Dove, M.T.; Powell, B.M. Neutron diffraction study of the tricritical orientational order/disorder phase transition in calcite at 1260 K. Phys. Chem. Miner. 1989, 16, 503–507. [Google Scholar] [CrossRef]
- Ferrario, M.; Lynden-Bell, R.M.; McDonald, I.R. Structural fluctuations and the order–disorder phase transition in calcite. J. Phys. Condens. Matter 1994, 6, 1345–1358. [Google Scholar] [CrossRef]
- Liu, J.; Duan, C.G.; Ossowski, M.M.; Mei, W.N.; Smith, R.W.; Hardy, J.R. Simulation of structural phase transition in NaNO3 and CaCO3. Phys. Chem. Miner. 2001, 28, 586–590. [Google Scholar] [CrossRef]
- Dove, M.T.; Swainson, I.P.; Powell, B.M.; Tennant, D.C. Neutron powder diffraction study of the orientational order–disorder phase transition in calcite, CaCO3. Phys. Chem. Miner. 2005, 32, 493–503. [Google Scholar] [CrossRef]
- Ishizawa, N.; Setoguchi, H.; Yanagisawa, K. Structural evolution of calcite at high temperatures: Phase V unveiled. Sci. Rep. 2013, 3, 2832. [Google Scholar] [CrossRef] [PubMed]

| Atoms | Z (e) | A (Å) | B (Å) | C (kcal1/2 Å3 mol−1/2) |
|---|---|---|---|---|
| O | −0.915 | 1.8836 | 0.1658 | 23.351 |
| C | 1.045 | 0.4638 | 0.0784 | 0 |
| Ca | 1.7 | 1.4466 | 0.1042 | 10.086 |
| Ba | 1.7 | 1.65 | 0.102 | 13 |
| Atomic Pair | D1 (kJ mol−1) | β1 (Å−1) | D2 (kJ mol−1) | β2 (Å−1) |
| O–C | 45735 | 5.14 | −4936.066 | 2.57 |
| Sr/(Sr + Ca) in Starting Solutions (mol%) | Sr/(Sr + Ca) in Calcite Determined from EDS Measurements (mol%) | |
|---|---|---|
| Pressure Treatment | Heat Treatment | |
| 5 | 5.1 ± 0.1 | |
| 10 | 9.5 ± 0.2 | |
| 15 | 14.2 ± 0.2 | |
| 20 | 19.4 ± 0.2 | 19.3 ± 0.7 |
| 40 | 30.7 ± 0.6 | |
| Ba/(Ba + Ca) in Starting Solutions (mol%) | Ba/(Ba + Ca) in Calcite Determined from EDS Measurements (mol%) |
|---|---|
| 5 | 8.2 ± 0.8 |
| 10 | 13.1 ± 1.1 |
| 15 | 17.6 ± 0.6 |
| 20 | 22.2 ± 1.0 |
| 25 | 26.8 ± 1.6 |
| 30 | 31.7 ± 1.4 |
| 35 | 36.5 ± 1.2 |
| 40 | 39.6 ± 1.7 |
| 45 | 43.0 ± 1.6 |
| 50 | 50.2 ± 1.6 |
| 55 | 53.2 ± 1.2 |
| 60 | 57.6 ± 1.3 |
| 65 | 63.3 ± 1.7 |
| 70 | 68.6 ± 1.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saito, A.; Kagi, H.; Marugata, S.; Komatsu, K.; Enomoto, D.; Maruyama, K.; Kawano, J. Incorporation of Incompatible Strontium and Barium Ions into Calcite (CaCO3) through Amorphous Calcium Carbonate. Minerals 2020, 10, 270. https://doi.org/10.3390/min10030270
Saito A, Kagi H, Marugata S, Komatsu K, Enomoto D, Maruyama K, Kawano J. Incorporation of Incompatible Strontium and Barium Ions into Calcite (CaCO3) through Amorphous Calcium Carbonate. Minerals. 2020; 10(3):270. https://doi.org/10.3390/min10030270
Chicago/Turabian StyleSaito, Ayaka, Hiroyuki Kagi, Shiho Marugata, Kazuki Komatsu, Daisuke Enomoto, Koji Maruyama, and Jun Kawano. 2020. "Incorporation of Incompatible Strontium and Barium Ions into Calcite (CaCO3) through Amorphous Calcium Carbonate" Minerals 10, no. 3: 270. https://doi.org/10.3390/min10030270
APA StyleSaito, A., Kagi, H., Marugata, S., Komatsu, K., Enomoto, D., Maruyama, K., & Kawano, J. (2020). Incorporation of Incompatible Strontium and Barium Ions into Calcite (CaCO3) through Amorphous Calcium Carbonate. Minerals, 10(3), 270. https://doi.org/10.3390/min10030270




