1. Introduction
Mining is a business that bases its productive parameters and those of an economic–financial nature on the basis of fragmentary information, which must be used to limit the various existing uncertainties about the mineral resource, guaranteeing profitability [
1]. Accurate evaluation of viable mineral resources is crucial in optimal sustainable development and mine planning procedures [
2]. In mineral resource estimation, it is crucial the identification of the geological domains to be used for modeling [
3]. Several types of variables, such as regionalized variables or spatial variables, are relevant [
2,
4,
5] and they must be taken into account for business profitability maximization. Often, it is difficult to get reliable information of this type.
According to the Pan European Reserves and Resources Reporting Committee (PERC) Reporting Standard [
6], a mineral resource is a concentration or occurrence of material of intrinsic economic interest in or on the earth’s crust in the form and quantity in which there are reasonable probabilities of eventual economic extraction. These resources are studied through variables that by nature have spatial structure. This means that they are not randomly arranged, but rather have a certain order. This feature is distinctive of data from the field of geology, and they are called regionalized variables in geostatistics [
7].
For Isaaks and Srivastava [
8], geostatistics offers a way to describe spatial continuity, an essential feature of many natural phenomena that takes advantage from the classical regression techniques. When the limits of spatial dependence of the variable of interest are known, a linear, unbiased and optimal estimation technique called kriging is used [
8,
9]. This is a generic term applied to a variety of estimation methods that depend on minimizing the estimation error by a least squares procedure [
10]. The name of the technique was introduced by Matheron [
11], in honor of the pioneering works of D. G. Krige when estimating gold concentrations in South Africa [
12]. When this technique is used in the mining industry, in most of the cases, the process only depends on a primary variable, and auxiliary variables (such as sub-elements, pollutants or others) are not considered. Pan et al. [
13] state that cokriging is theoretically more attractive than univariate kriging when estimating simultaneously a set of correlated variables. Wackernagel [
14] defines cokriging as the extension of kriging, where an auxiliary variable is used to improve the accuracy of the estimate. Due to its complexity when modeling joint spatial continuity, this coestimation technique has not received sufficient credit. Almeida and Journel [
15] emphasize the use of more easily applicable but still precise techniques, and they introduce a simplified cokriging method called collocated ordinary cokriging.
The Sequential Gaussian Simulation (SGS) algorithm is also widely used because it is fast and efficient when building conditional cumulative distribution functions [
16]. Techniques like fractal and multifractal modeling are also used along with SGS to separate various geological processes [
17,
18].
In this study, the collocated ordinary cokriging and the SGS are applied. When mapping spatial variables two important stages must be taken into account: the way in which sampling is done, and the techniques used in prediction. Both processes determine the accuracy of the results. Sampling aspects are analyzed in diverse works. It is known that purposive sampling is in general more efficient for model-based mapping [
19]. In [
20] the universal kriging variance is used as a quality measure to design samples. In [
21] the size of the sample is studied, and they conclude that it is an important factor to obtain accurate empirical variograms, resulting crucial to sample sufficiently and without bias.
However, costs associated with obtaining information from the earth’s crust are high, especially in the sector of hard rock mining in which the only way to extract samples is through mechanized methods. This is the reason this study analyzes the influence of the sampling density on the coestimation error in an area defined by the target population. The aim of this work is to calculate an approximation of the appropriate sampling size to obtain good results when applying the collocated ordinary cokriging technique.
2. Theoretical Framework
The nature of geological data allows examination of some characteristics of the whole population only in some specific cases. This is the reason in most of the cases part of the population is analyzed, from which inferences about the total population are made [
22]. The objective is to estimate a parameter of the whole population using information of a sample.
Geostatistics is an applied science that focuses on modeling the spatial continuity of natural phenomena. This information is used to estimate values in not sampled locations using an unbiased optimal linear method. This rigorous mathematical formulation was born in France in the 1960s [
11]. An essential aspect of geostatistical modeling is the establishment of quantitative measures of spatial variability or continuity, which are subsequently used as input data in the estimation. Modeling the spatial variability is a standard process of mineral resource analysts, where for the past 25 years, the experimental semivariogram has been the most applied tool in mining [
23].
Geostatistics studies regionalized phenomena, i.e., phenomena that in the geographical space follow a certain structure. Sinclair and Blackwell [
10] define regionalized variables as variables distributed in a partially structured manner in the space, such that there is some degree of spatial self-correlation. These variables can be interpreted as a natural extension of random variables when they depend on the position. A regionalized variable, at each point
x belonging to a domain
in space, being
d the dimension of the space (
for 2D and
for 3D), makes it correspond a variable
that depends on the position of the point
x in space. The regionalized variable is stationary if its joint distribution function is invariant by translation in space.
The semivariogram is the basic geostatistical tool to measure the spatial self-correlation of a regionalized variable [
24]. It is used in different directions of the space to study the continuity of the variable. In almost all cases of reservoir modeling, there is a need to model the joint distribution of multiple variables [
25]. In this context, cross semivariograms are defined.
Interpolation algorithms are used to map a primary variable (variable of interest). Some interpolation algorithms are based on regression of the unknown value on the sample data. Kriging is one of these regression algorithms. It is a geostatistical estimation technique that gives the best unbiased linear estimator of a variable. Known certain values of a variable of interest
,
,
, …,
, the unknown value at point
,
, is estimated by a linear combination:
being
the estimation weights calculated in a way that they minimize the variance.
Sometimes, the sampling of the primary variable is poor but there are other variables (auxiliary variables) more densely sampled. Assume that
and
are two regionalized variables. Variable
will be the primary variable and
will work as the auxiliary one. Known certain values of the first variable
,
, …,
, and the auxiliary variable
,
, …,
, ordinary cokriging consists of calculating
as a linear combination of data from both variables located at sample points in the vicinity of the point:
Each variable is defined in different number of samples. Cokriging is the extension of kriging to the multivariate case, i.e., it considers not only the variable to be estimated in space, but also the information of one or several additional variables in nearby sites [
26]. Although cokriging has the same characteristics as kriging, considering additional variables improves the precision of the estimation in some cases, obtaining also more consistent results than when each variable is estimated independently using kriging in a multivariate study. However, it should be noted that it makes estimation more difficult.
Cokriging has several variants and collocated ordinary cokriging is one of them [
27]. It can be used when primary data are available in sparsely distributed points while secondary data are present in all points of the mesh. According to Xu et al. [
28] a full cokriging approach may cause matrix instabilities due to high autocorrelation between closer secondary data, as opposed to large separation and low autocorrelation in primary data. This problem can be overcome by retaining at each location to be estimated the collocated secondary data. The collocated ordinary cokriging estimator is given by [
28]:
being
and
the means of the primary and secondary variables,
is the secondary variable sampled at the same location in which the primary variable will be estimated. The weights
for
and
are calculated from the system:
where
and
are the covariances of the primary and secondary variables, respectively; and
and
are the cross-covariances (being
). These can be obtained by calculating the variograms and cross-variograms. Because of the complexity of this process, Markov-type screening hypothesis are considered [
29]. In Markov’s model the influence of any primary data
on the secondary collocated variable
is screened by the primary data
. In this context, the cross-covariance can be calculated using:
or equivalently:
being
the correlogram function of the primary variable and
the cross-correlogram function between primary and secondary variables.
Under the Markov model, the collocated cokriging Equations (
3) and (
4) can be written as:
and:
where
and
are the two stationary standard deviations of the variables
and
respectively.
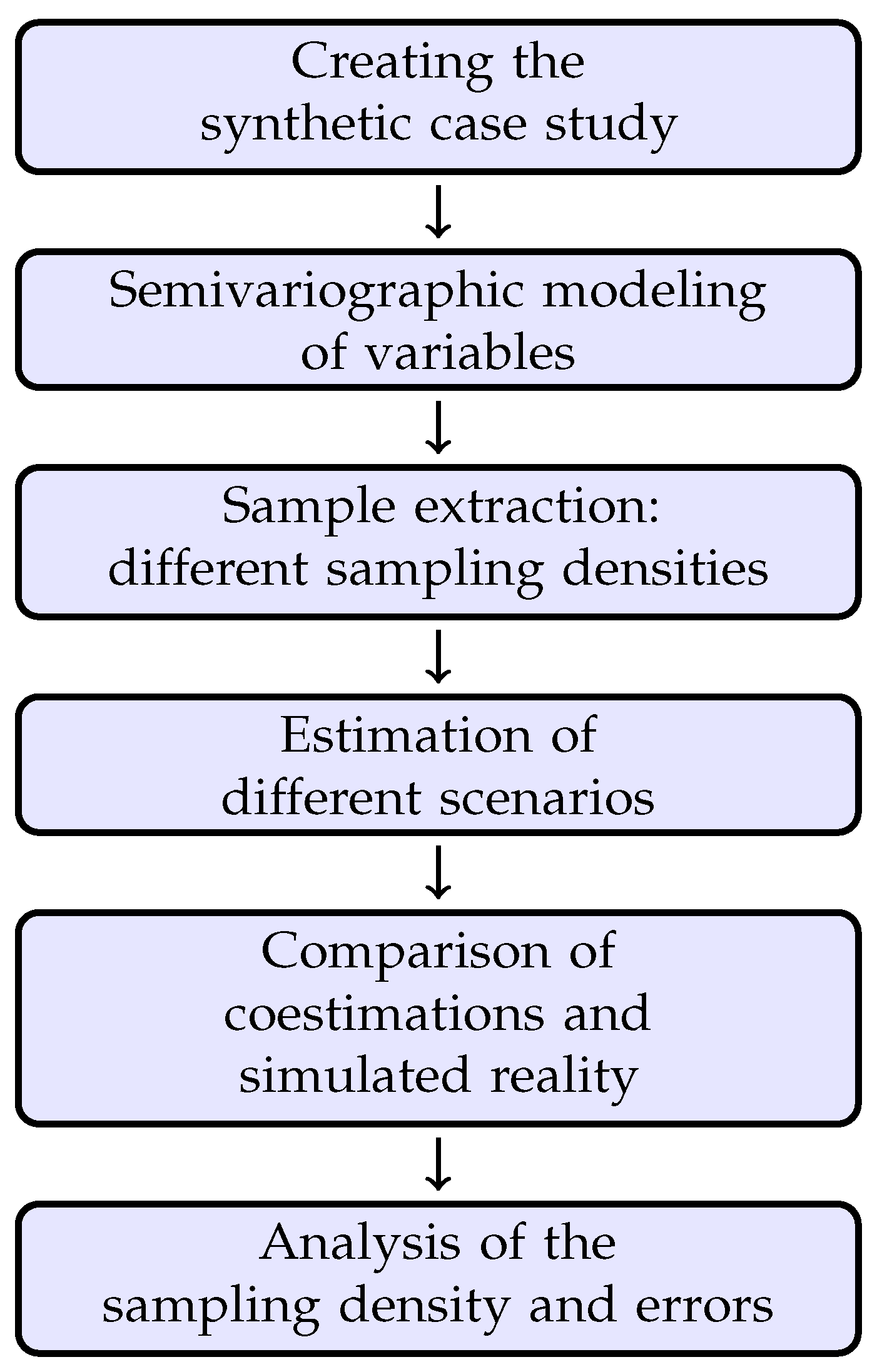
3. Methodology
This section summarizes the most relevant stages of the study, which are implemented using the GSLIB algorithms, acronym for “Geostatistical Software Library”, developed in the Petroleum Engineering Department of Stanford University. It is considered one of the most relevant computer developments in the history of geostatistics by some researchers [
30]. The whole process is computed in Python by the authors. The sequence of the main stages of this study is represented in
Figure 1.
3.1. Synthetic Case Study Creation
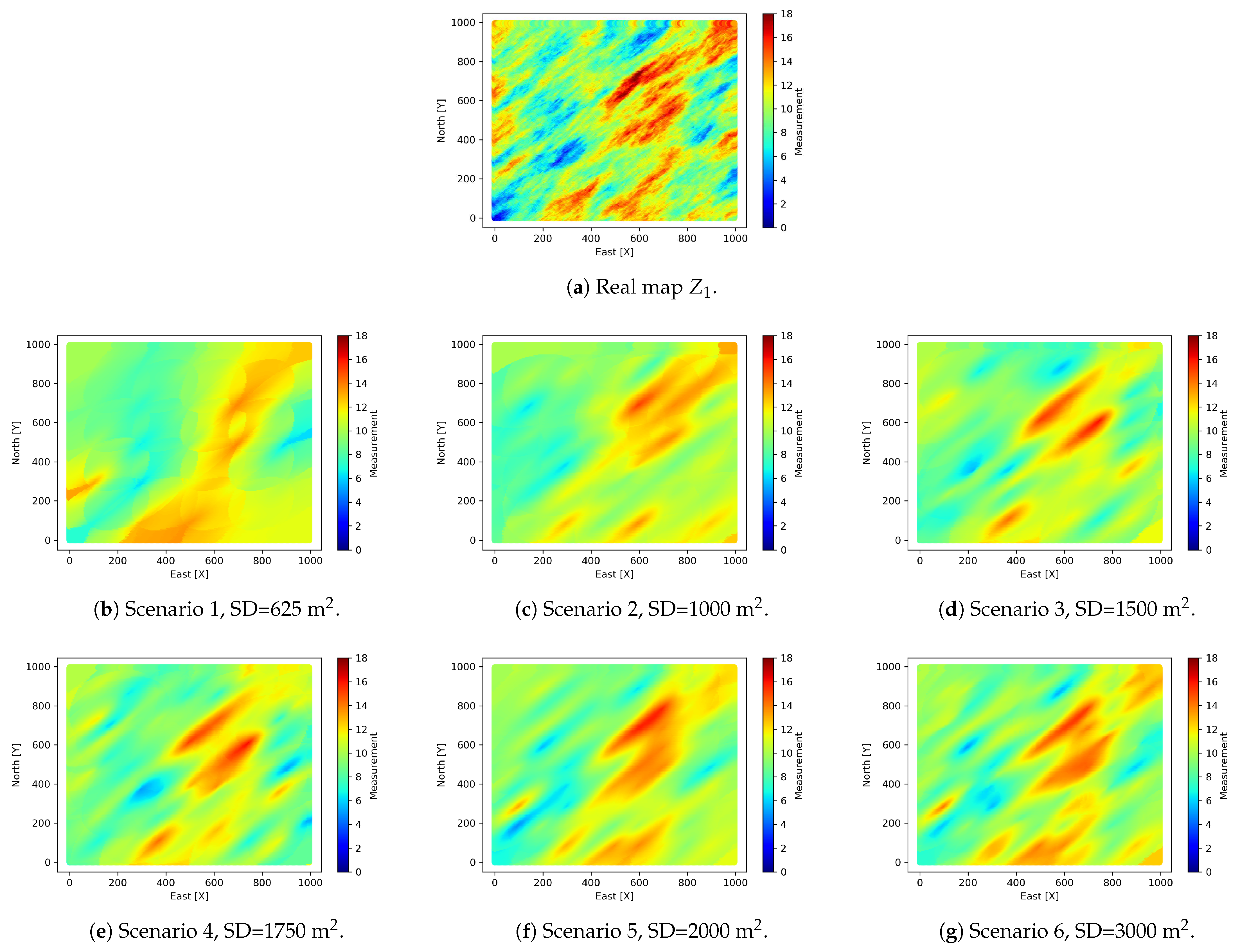
First, a synthetic case study has been created. This option has been chosen because it enables having data at the population level (universe), making possible to compare this reality with estimations that depend on different sampling densities. In this way, the real error can be calculated, and the influence of the sampling density can be measured. Thus, an area of 1 km2 is defined as spatial domain with coordinates ranging from the origin to 1 km in the East (X) and in the North (Y). A squared geometry is considered, thus, 40,000 cells of 25 m2 are considered to be target population.
In each cell a primary variable () and an auxiliary one () are created following the Sequential Gaussian Simulation, and using a random number generator (random seed) and spatial structure parameters. In this first stage, both variables are measured in the whole population and they are spatially correlated. Hence, conditions required by the collocated ordinary cokriging technique are satisfied. On the other hand, real values of are also known, making possible the comparison with the estimations obtained for different sampling densities.
3.2. Semivariographic Modeling of Variables
The spatial structure of and is described using the experimental semivariogram. The spatial continuity is modeled and parameters such as the anisotropy direction, features of the ellipse and plateau (maximum semivariance) are obtained. These parameters are required in the next stage.
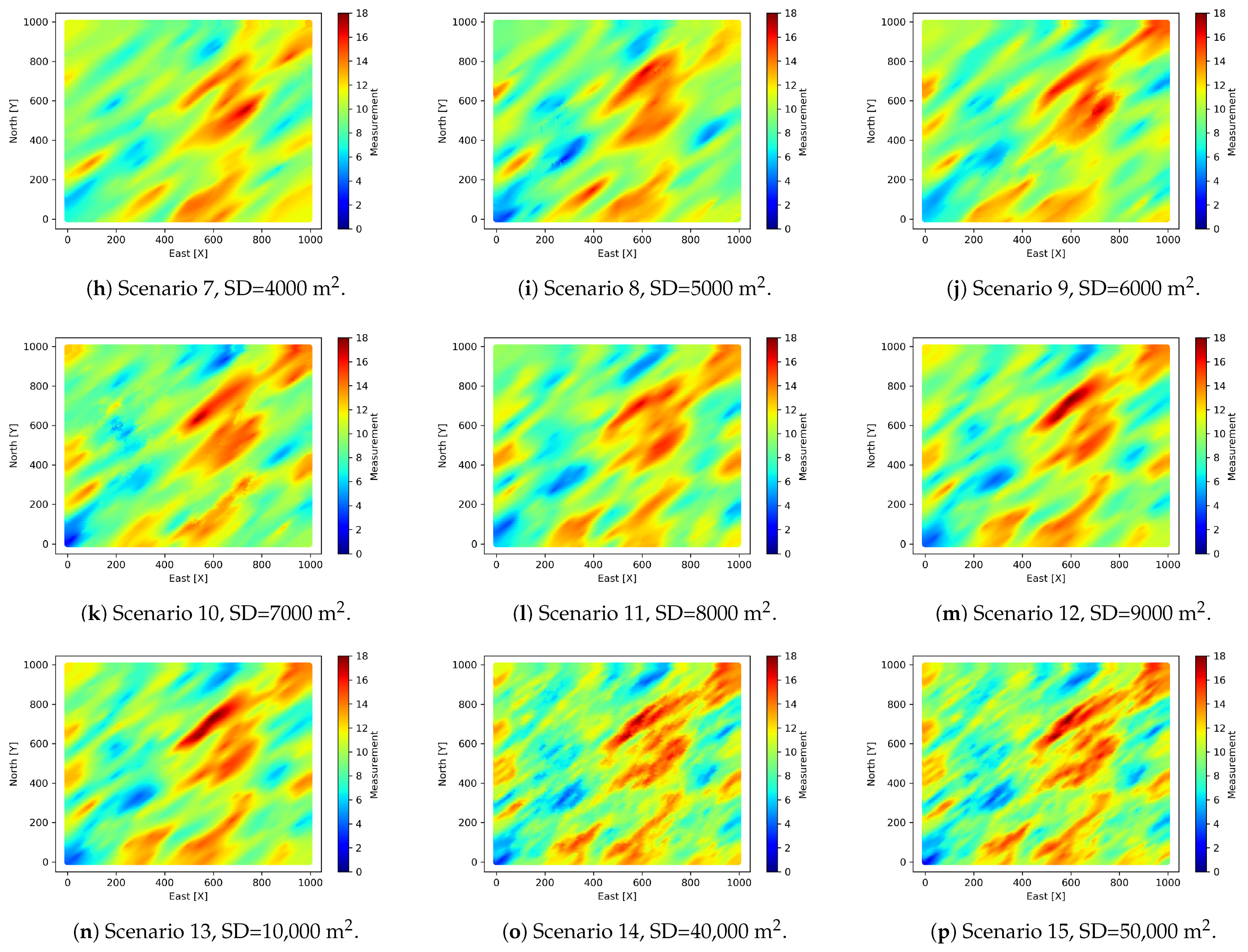
3.3. Sample Extraction at Different Densities
From the exhaustive variable , 15 different sampling densities are extracted. The minimum is equivalent to 0.06% of the population and the maximum is the 5% of the population. These scenarios have been used to develop the study. The spatial arrangement of the samplings is regular, it does not have clusters.
3.4. Estimation of Different Scenarios
Results of 15 scenarios are estimated using the collocated ordinary cokriging method. The technique uses parameters that have been calculated in the structural modeling, the spatial correlation between the variables and the scopes defined for sample search.
3.5. Comparison of Estimations and Simulated Reality
With the purpose of evaluating the representativeness of the sample and the accuracy of the technique, the estimated results are compared with the simulated reality of the variable , using the mean squared error (MSE).
3.6. Analysis of the Sampling Density and Errors
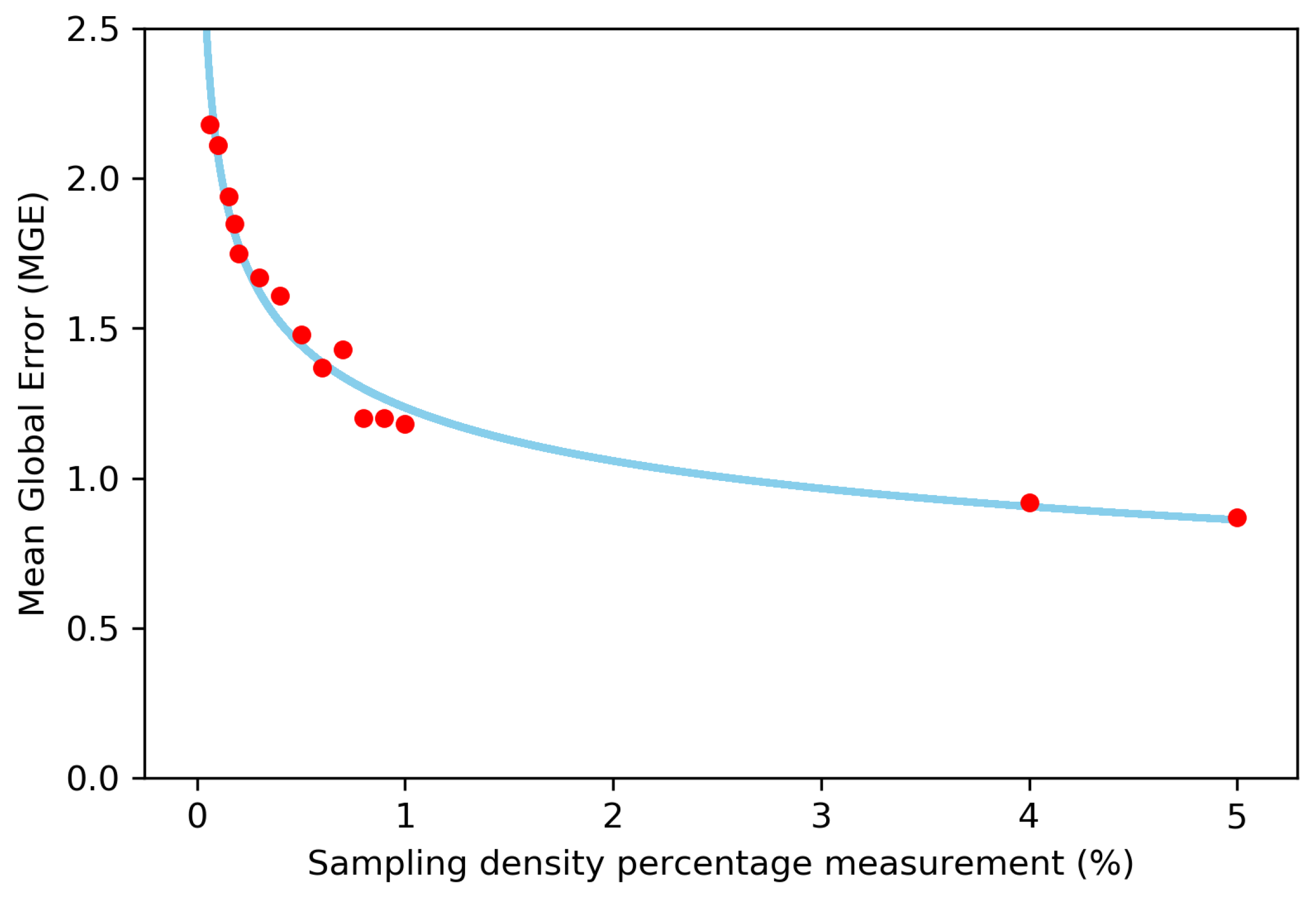
At this stage, the relationship between sampling density and the coestimation errors is analyzed. They result inversely proportional, and it can be expressed by a potential function restricted to a maximum sample size equivalent to 5% of the target population. It must be taken into account that it is difficult to have bigger samples than the indicated above in the evaluation of metallic mineral deposits.
4. Application
The first stage is the creation of the synthetic case study. Two regionalized and spatially correlated variables in a two-dimensional space are created. Both variables, the primary
and auxiliary
have a location in the georeferenced space in East (
X) and North (
Y). The unconditional SGS method has been used, taking into account a spatial structure and a random seed. This process is developed using the SGSIM algorithm (Sequential Gaussian simulation program) of GSLIB reimplemented in Python code, with data presented in
Table 1 and
Table 2.
Table 2 contains the structural anisotropic-type parameters for both variables. The contribution refers to the plateau of the semivariogram (the value at which the semivariogram stops changing).
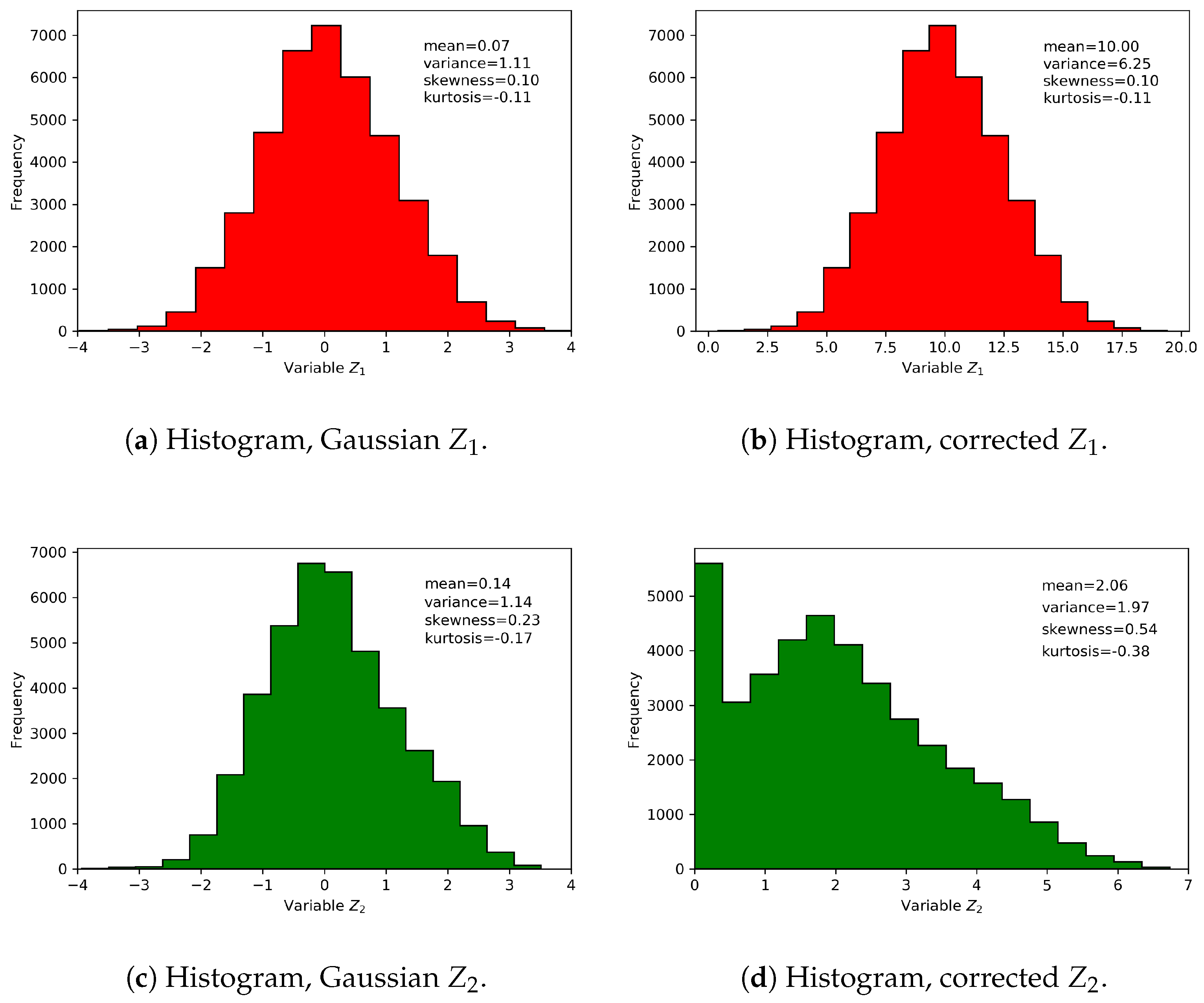
Subsequently, a corrective affine transformation is applied to the distribution of the variable correcting the mean and the standard deviation.
Table 3 contains the statistics of form and dispersion applied in the correction of the Gaussian distributions of the simulation.
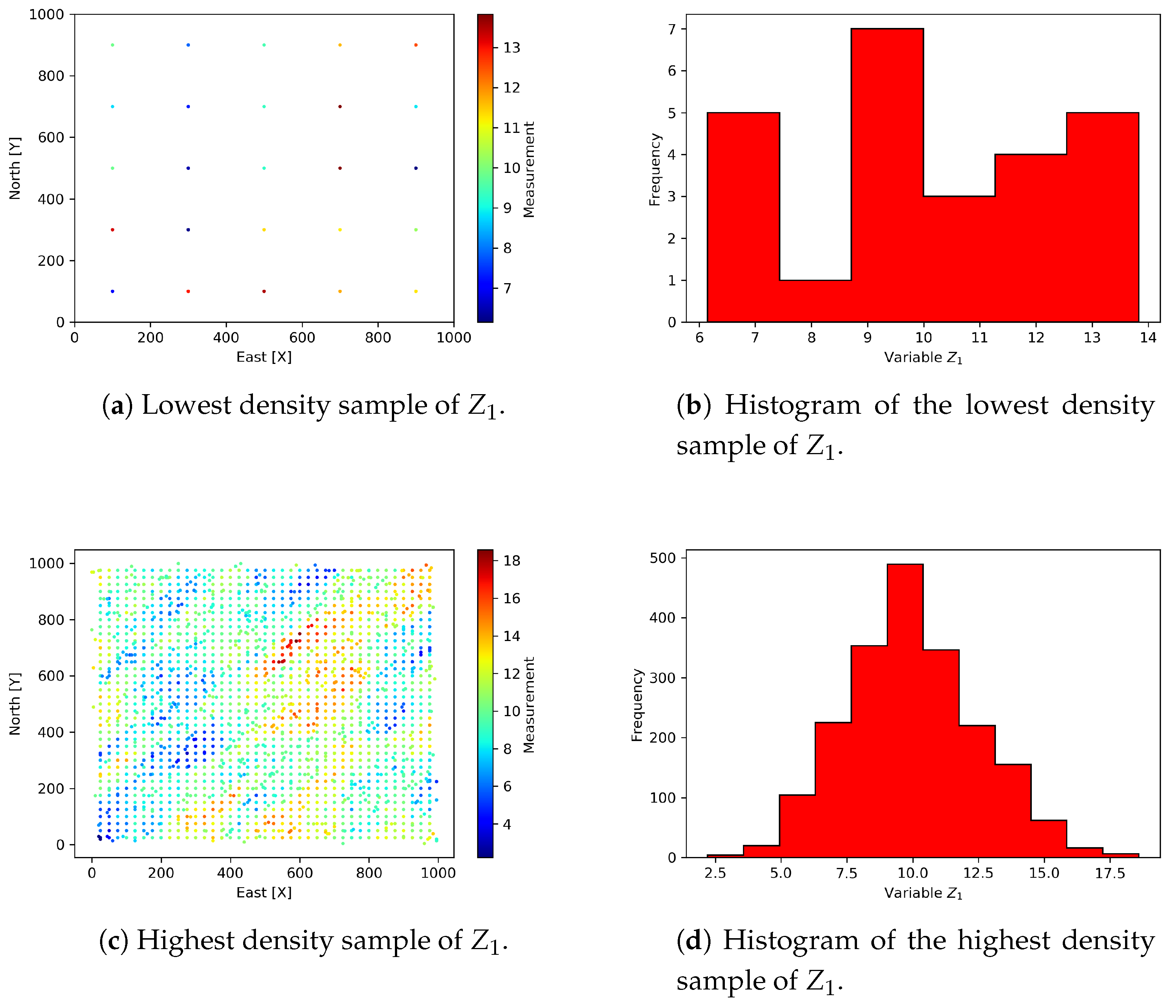
For
, the 47% of the corrected data were negative and they were replaced by a positive small value. Thus, the histogram has a positive asymmetric form, see
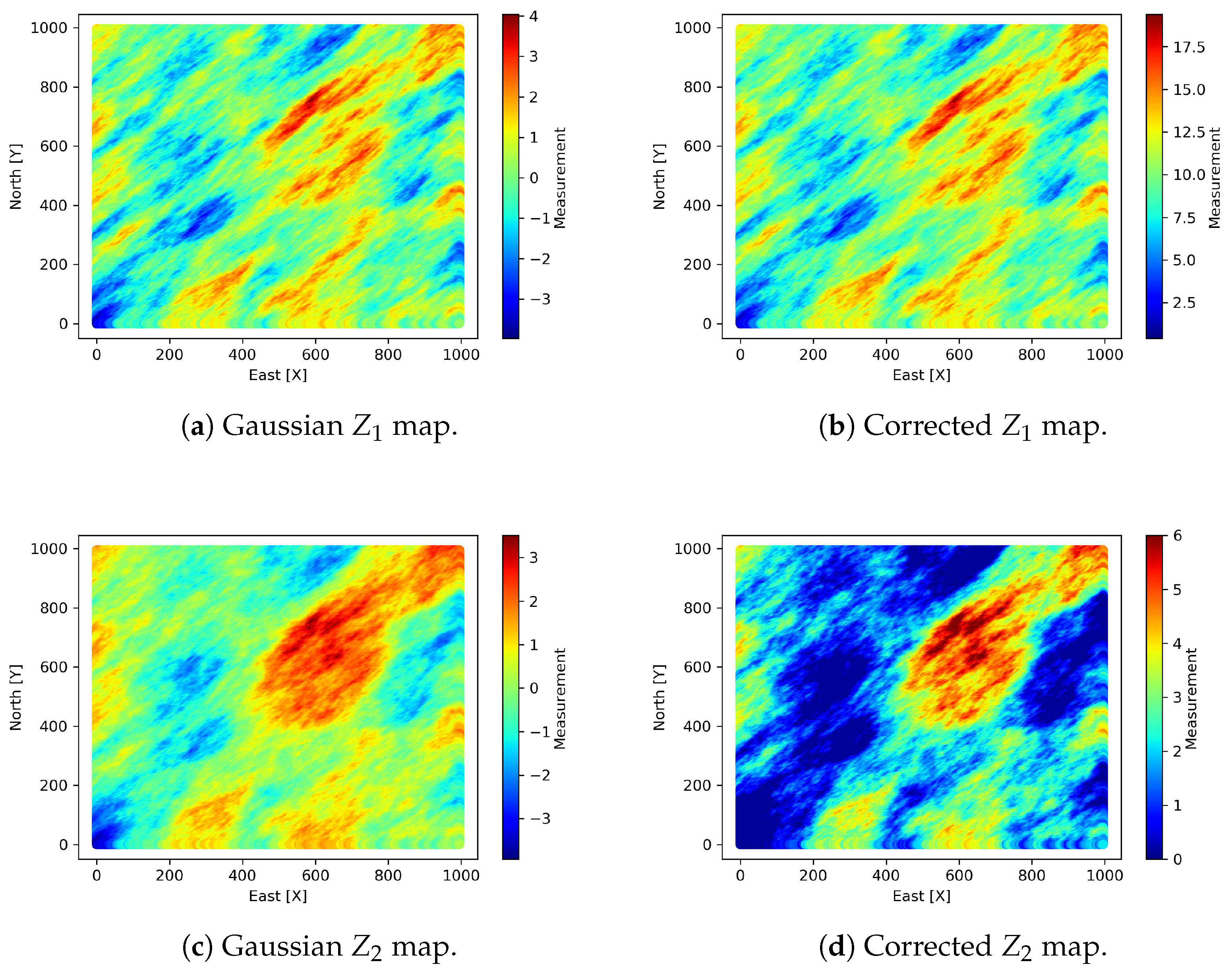
Figure 2. The simulations for both variables are shown in
Figure 3.
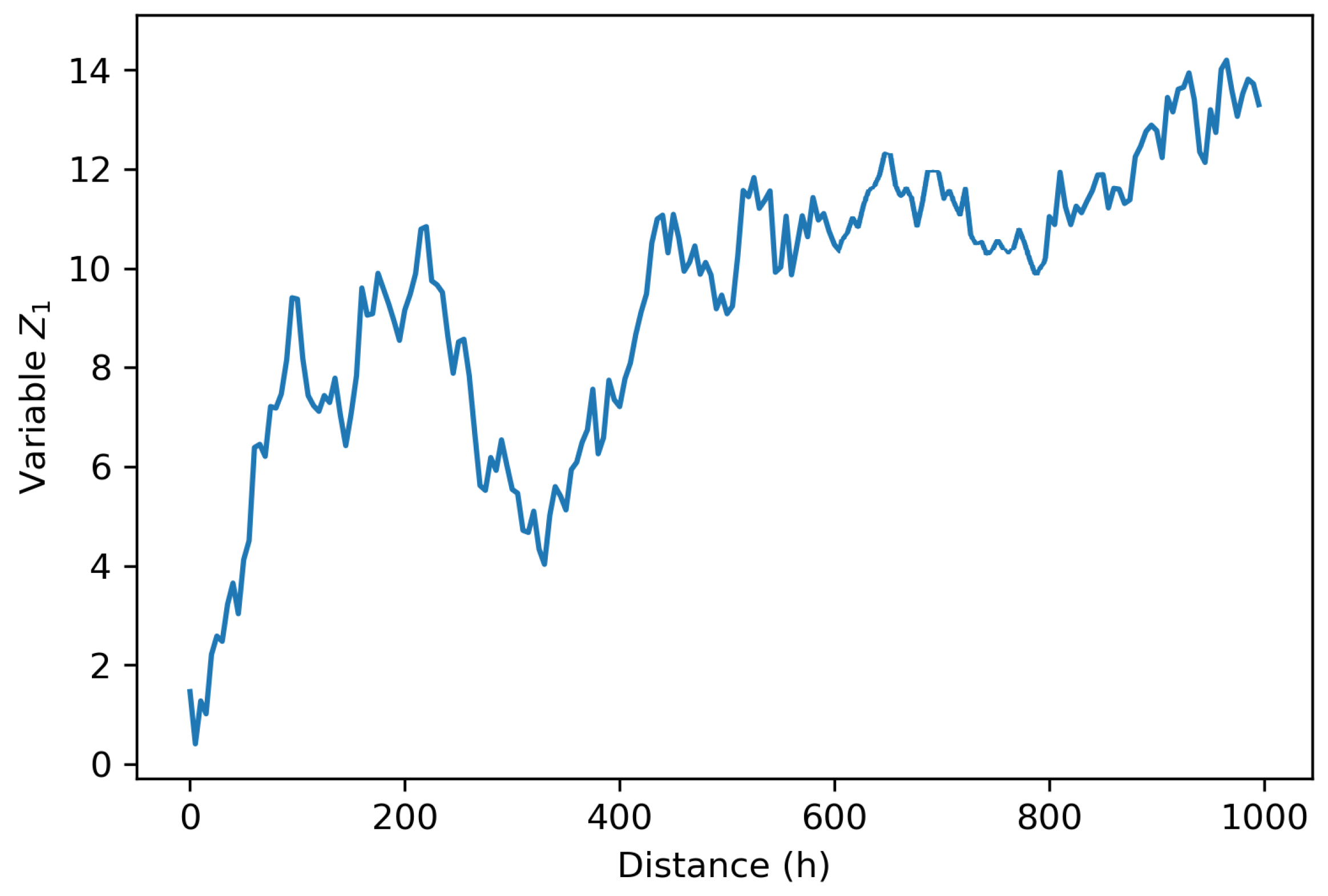
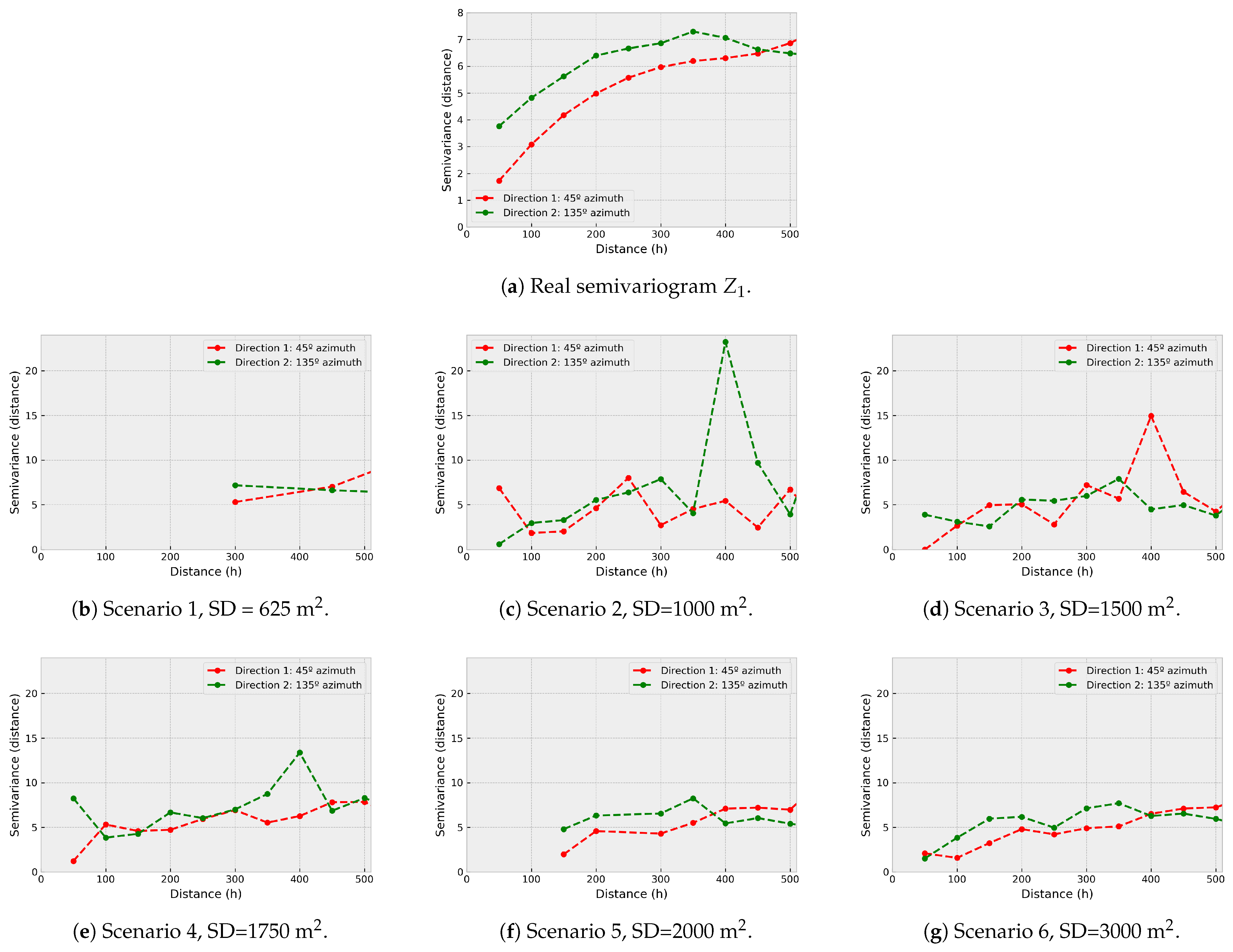
With the aim of analyzing the behavior of the primary variable, a diagonal cut is performed from southwest to northeast on the map of this variable (45° azimuth), coinciding with the direction of anisotropy. We observe the existence of local stationarity between 500 and 900 meters approximately, see
Figure 4. Armstrong [
31] states that this assumption of quasi-stationarity is essential between the homogeneity scale of the phenomenon and the sampling density.
In the second stage, the data required for the estimation processes is prepared. The collocated ordinary cokriging method with a Markov model is used. The required data are the following:
Semivariographic fitting model for the primary variable ().
Semivariographic fitting model for the exhaustive auxiliary variable ().
Linear correlation coefficient between and .
At this point both
and
are exhaustive. The auxiliary variable that contributes in the estimation process of the primary variable is static. The semivariographic fitting models are described according to the target population of each variable and they will remain constant during the estimation processes. In
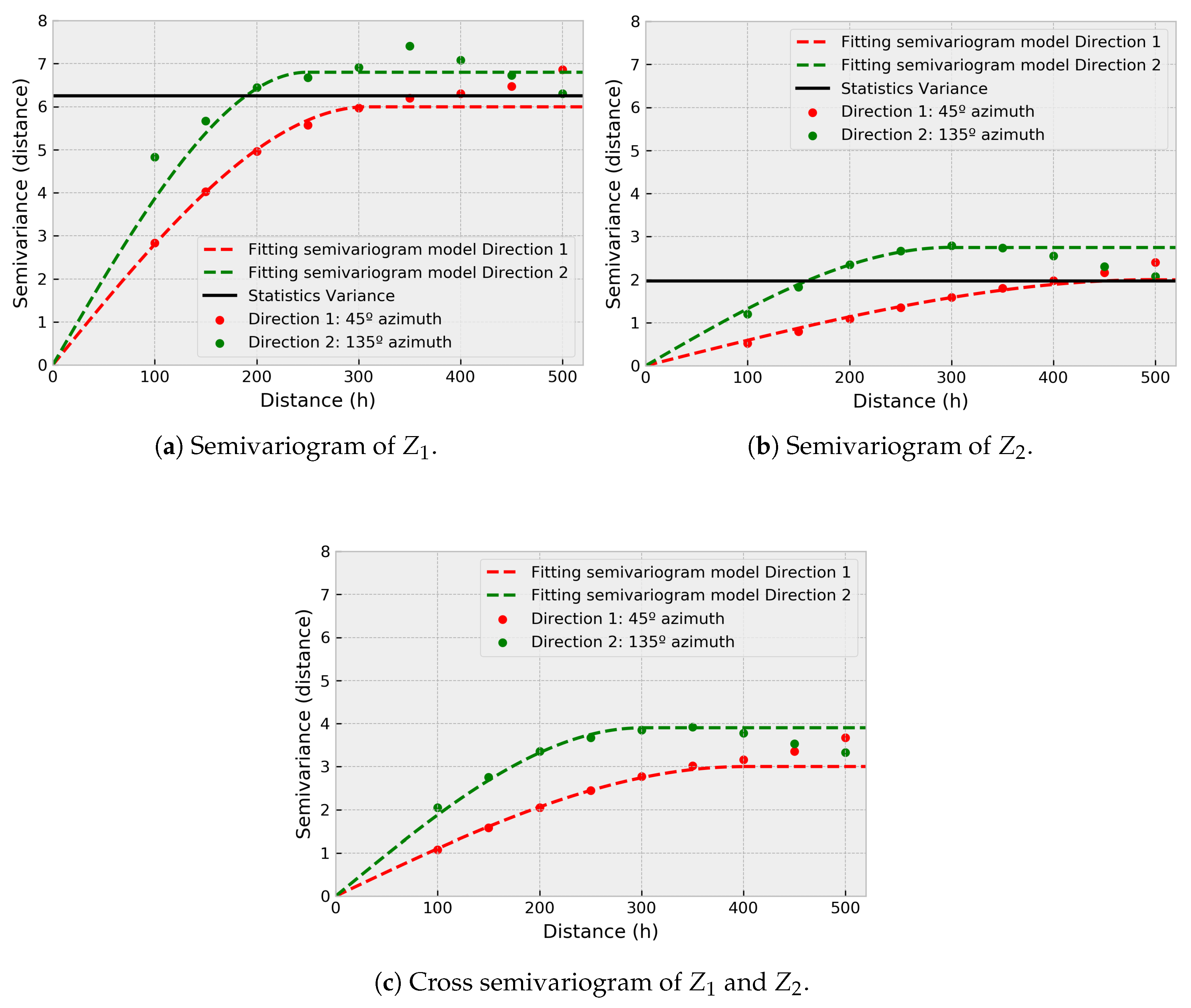
Figure 5 the semivariograms of the variables are presented.
From
Figure 5, a zonal anisotropy is concluded in 45° azimuth direction as the main axis, for both variables
and
. In both variables, there is a slower variability in the direction of 45° azimuth than in its orthogonal direction (135° azimuth), where the variables present a faster variability. The experimental data of
and
fit two nested spherical structures:
for
; and
for
. The linear correlation coefficient between
and
will vary depending on the sampling density.
The third stage consists of extracting 15 different sampling densities (SD) from the exhaustive variable
. These values will be combined with the values of
to create the scenarios of estimation.
Table 4 shows the sampling densities for
. It can be observed that at higher sampling densities the error in statistical characterization is lower. The sampling density is constant for
, i.e., all the spatial area of 1 km
2 is considered for
. A maximum sample size of 5% of the population has been considered, associated with high costs when retrieving information of metallic elements from the earth’s crust. It is typical to have case studies with smaller sample size than the 1% of the target population [
17,
32]. The limit scenarios (lowest and highest sampling densities) are presented in
Figure 6.
In the fourth stage, the collocated ordinary cokriging process for each scenario is developed (
Table 5), varying the linear correlation coefficient depending on the sampling density. Before performing the coestimation process, it is necessary to define the search neighborhood, determining the spatial limits that restrict the number of observations that interact in the coestimation. In a study about the kriging method, Rivoirard [
33] points out that the higher the search limits, the greater the accuracy in the estimation process. However, the latter is limited to the number of existing observations and their distances over the estimation grid. For example, it would not be adequate to estimate at point
for the lowest density sample of
(in an univariate assumption) in the mesh of samples in
Figure 6 using the existing 25 observations, given that the influence of those farther observations will hardly describe the reality at that point, unless there exists a complete stationarity in the study area. In this case, the information obtained from the semivariogram is used to define the search limits, reducing the size of the ellipse given the increase of the sampling density. The anisotropy direction for the searched ellipse is 45° azimuth and it varies based on the amount of information available in each scenario. The number of samples used for estimating
varies also based on the amount of information available. In
Table 5 the minimum and the maximum number of samples for coestimation are presented. The ellipse will be larger in lower sampling density scenarios because of the absence of samples close to the sites to be estimated.
5. Results
The estimation scenarios are compared with the simulated real map from which the samples of
are extracted. It can be observed that smoothing is more noticeable in those scenarios with lower sampling density, see
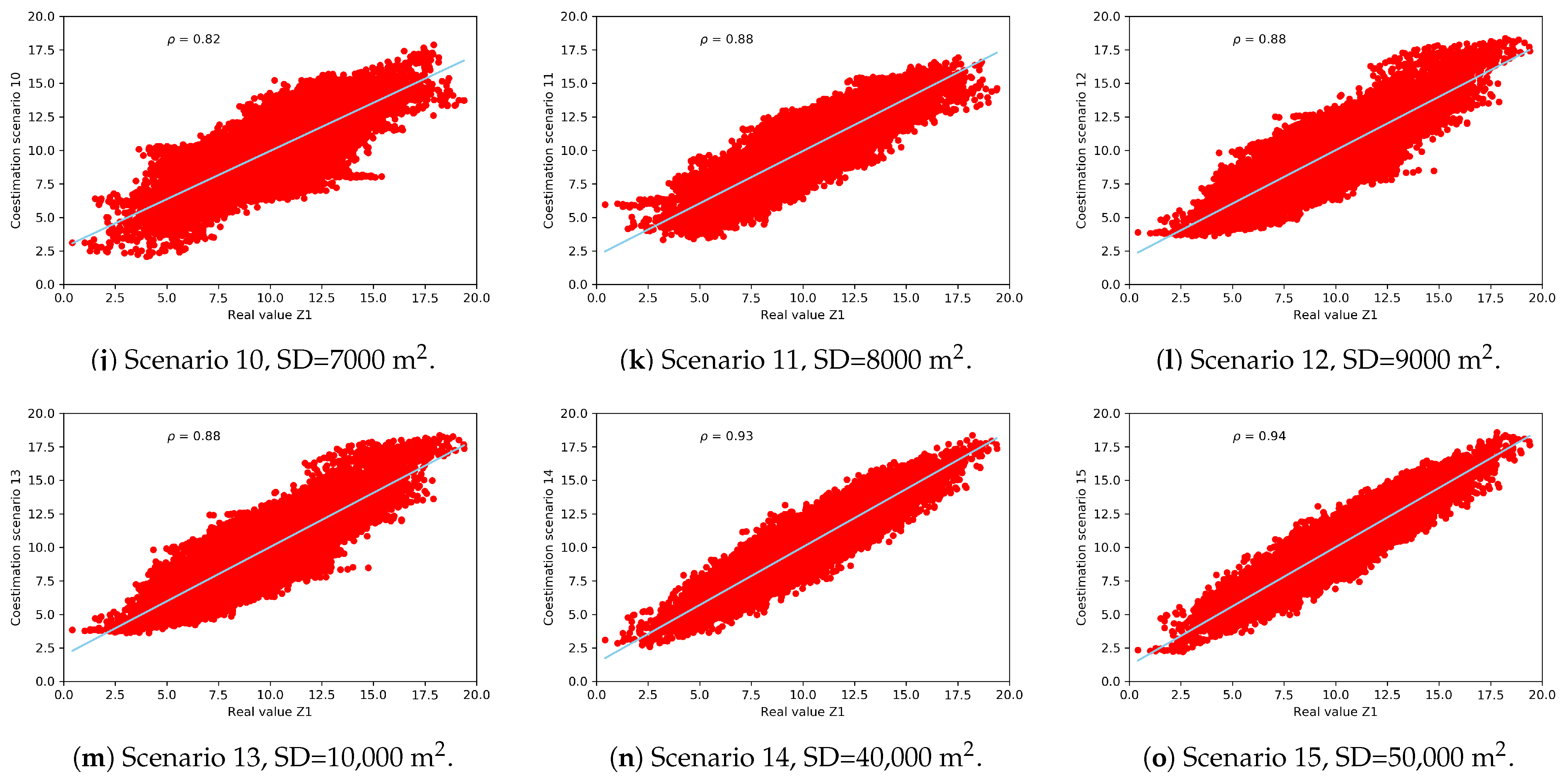
Figure 7. The coestimation is perfect when the linear correlation coefficient between the real scenario and the estimated scenario is 1. The linear correlation coefficient will depend on the number of observations and the semivariographic model that can be fitted according to these observations. Not very dense scenarios will poorly describe the spatial correlation, obtaining less accurate results. In
Figure 8 the dispersion diagrams between the real variable
and the 15 scenarios are represented, indicating the linear correlation coefficient. The linear correlation coefficient of scenario 11 (320 observations) is 0.88 and the map of the variable
respects the real spatial structure. Scenarios with higher sampling density present also good features.
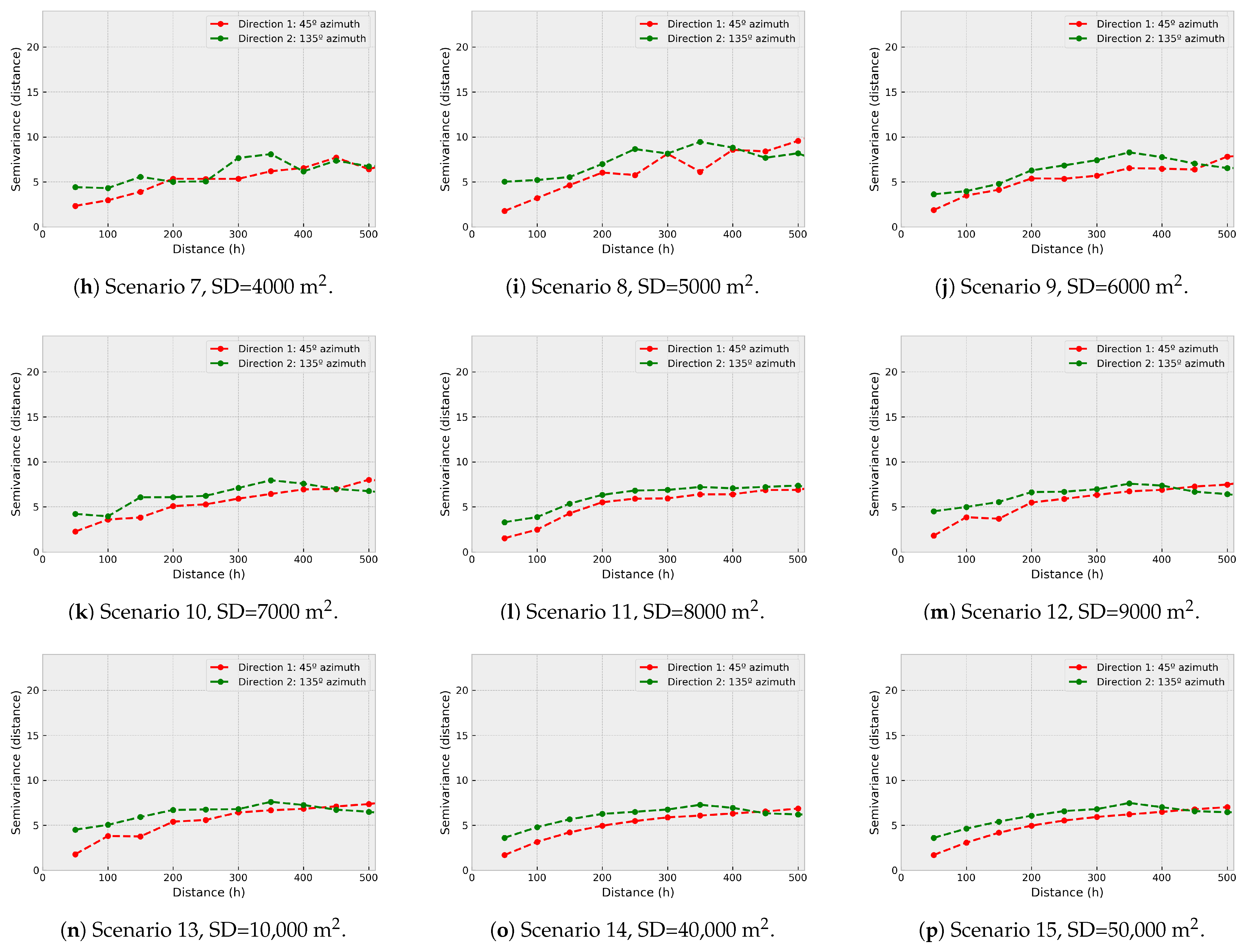
In
Figure 9 the direct semivariograms of
are shown. It can be observed that they are similar to the real one for densities equivalent to 0.8% or greater, which is associated with the fact that in these cases the mathematical adjustment should also be similar to the real with independence of the modelization technique. When the sampling density decreases, the direct semivariogram of
becomes more erratic, decreasing its spatial correlation.
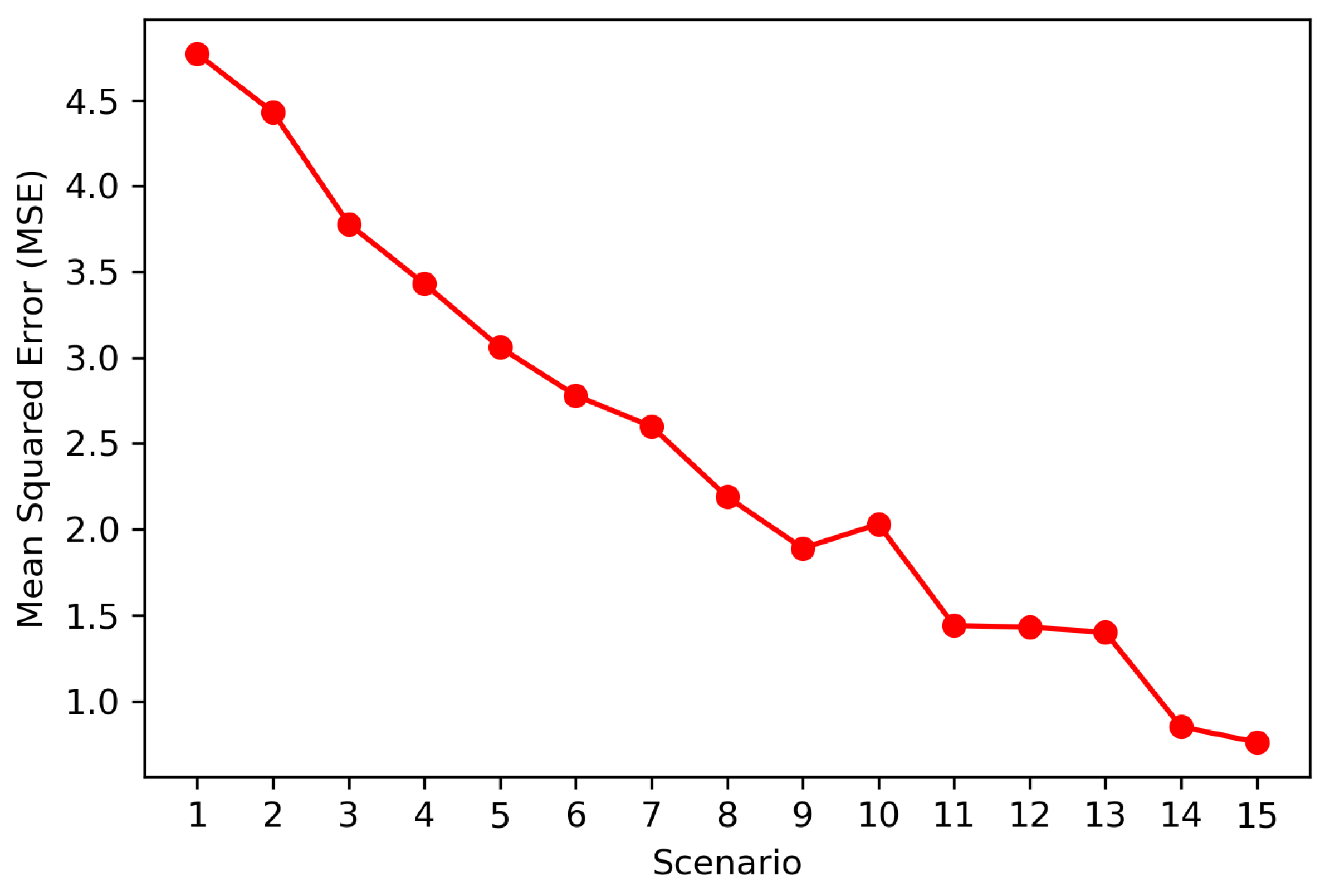
As expected at higher sampling densities, the mean squared error is smaller (MSE), see
Figure 10. The relationship between the sampling density in percentage measure (SDP) and the mean global error (MGE) can be expressed using this potential function:
In
Figure 11 the mean global error versus the equivalent sampling density is shown.
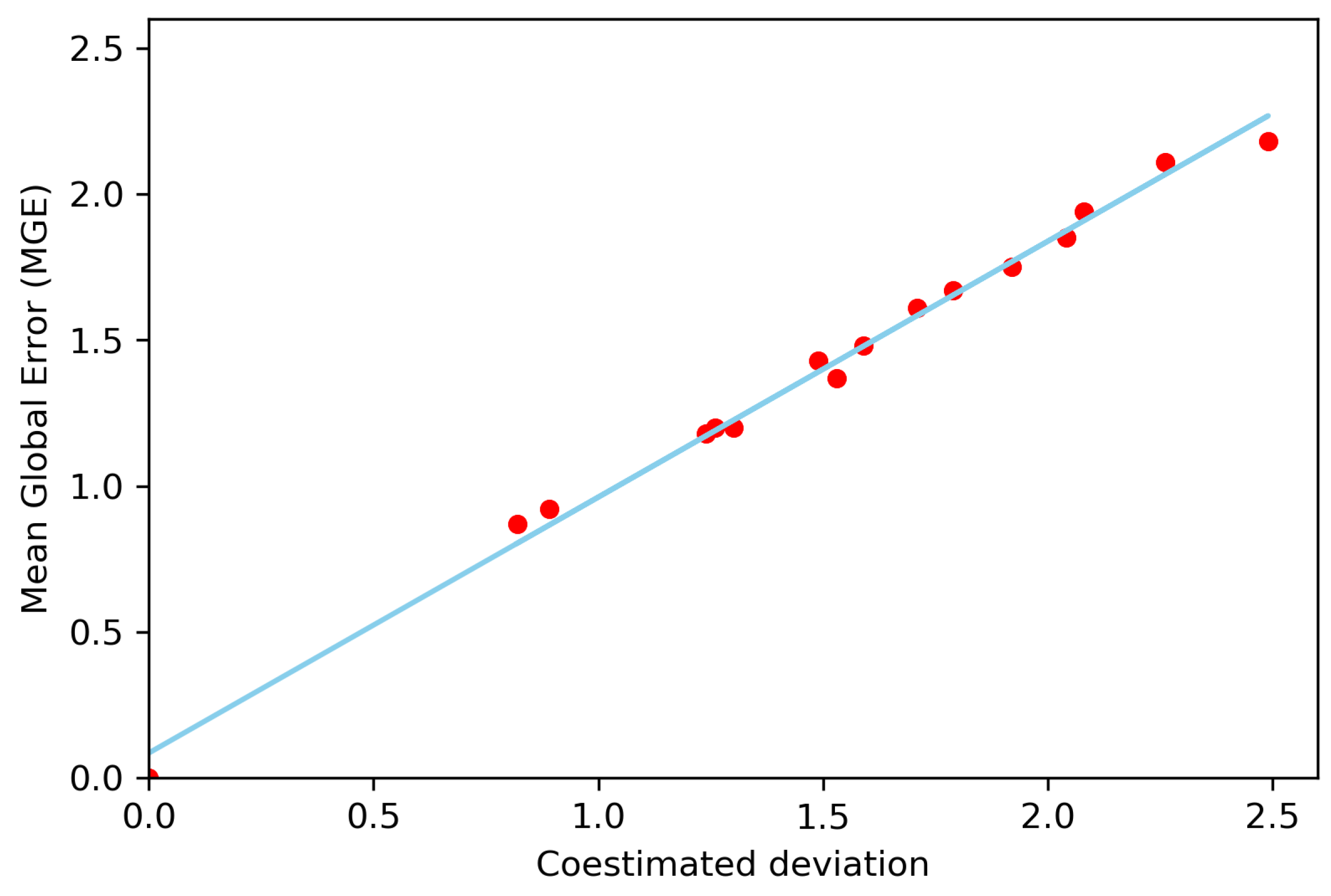
The deviation of the coestimation is directly proportional to the mean global error. The correlation coefficient is 0.99, which indicates that the application of the collocated ordinary cokriging method was consistent and reliable, see
Figure 12. Applying linear regression to find the relationship between the mean global error and the coestimated deviation, the corrected coestimated deviation
is obtained:
There is no optimal scenario, since the overall process depends on factors such as the sensitivity of the variable of interest, the amount of resources to invest to obtain the sample, the error tolerance, and so on. For example, in the 13th scenario with a sampling density equivalent to 1% of the target population, the estimated mean is 10.02 and the deviation 1.24:
. This means that the estimated value could vary between 8.78 and 11.26. A similar value
is obtained after correcting the deviation with the proposed function (
10). Different parameters of the 15 scenarios are presented in
Table 6.
6. Conclusions
Collocated ordinary cokriging is reliable and easier to implement than other multivariable geostatistical methods when an auxiliary variable is spatially correlated with the primary one, and when the auxiliary data is much more extensive than the primary data. In advance, the primary variable must be estimated in some domains checking delimitations where homogeneity by translation exists.
The sampling density is inversely proportional to the coestimation error; the larger the sampling density the lower the uncertainty of the estimated population. However, there is not a quantification of the sampling density that guarantees obtaining perfect results, since the coestimation error is subject to an intrinsic error. It is crucial to manage the degree of sparsity of the primary data. This must be related to the sensitivity of the coestimation error in commercial terms. It is assumed that an error of 1 unit of measure will affect a variable with a low level of sparsity, which has a greater variability. For decision-making, the global mean deviation of the coestimation is a relevant parameter, since it determines the mean global error with a very high correlation coefficient. This parameter defines the worst and best of the cases, deriving in the choice of a sample size with an assumed and controlled risk.
Scenario 11 (320 observations) is presented as one of the best options balancing the number of samples versus results. It has a linear correlation coefficient of 0.88, a mean squared error of 1.44 and its linear correlation coefficient is similar to higher density sampling scenarios.