Abstract
Hydrothermal venting is an important transfer process of energy and elements between the Earth’s solid material and the oceans. Compared to mid-ocean-ridge hydrothermal vent fields, those at intra-oceanic island arcs are typically in shallower water depth and have a more variable geochemical fluid composition. Biologically essential trace elements (such as Fe and Mn) are generally elevated in fluids of both deep and shallow hydrothermal vent fields, while vents at shallower water depth influence the photic zone more directly and thus are potentially more relevant for marine primary productivity. However, fluid flux estimations of island arc hydrothermal systems into the surrounding water column are scarce. This study (I) presents a method based on short-lived radium isotopes to estimate submarine hydrothermal discharge (SHD), (II) applies this method at Brothers volcano in the southern Kermadec arc, located northeast of New Zealand, and (III) gives dissolved Fe, Mn and He isotope flux estimates for the Earth´s longest intra-oceanic island arc, the Kermadec arc. The comparison between measured inert He isotope concentrations in the plume with calculated concentrations based on Ra isotopes matched reasonably well, which supports the use of a Ra-based discharge model. Overall, this study represents a novel approach to assess fluid and thus trace element fluxes from one hydrothermal vent field, which can be applied in future studies on various hydrothermal systems to improve geochemical models of element cycling in the ocean.
Keywords:
hydrothermal flux; radium isotopes; Kermadec island arc; helium; iron flux; manganese flux; 224Ra; 223Ra 1. Introduction
Volcanic arcs result from continuous magma generation caused by the subduction of oceanic crust, a process, which has been present for a long time in Earth´s history [1,2,3]. Associated submarine hydrothermal systems are instrumental in transferring heat into the global ocean [4]. Further, convection-driven fluid circulation in hydrothermal systems plays an important role for element and gas fluxes into the ocean, as hydrothermal fluids are generally enriched in several gases and elements relative to ambient seawater e.g., [5,6], for overviews. However, only a fraction of the hydrothermally derived dissolved metals can escape from the near field precipitation process, staying in solution owing to organic ligand complexation [7]. These dissolved metals can then be transported on ocean basin scales, as shown for dissolved Fe in the South Pacific Ocean [7,8,9,10] and in the South Atlantic [11]. This far-field effect of hydrothermal discharge can also be seen in the basin-wide distribution of primordial helium in the Pacific e.g., [12] and the Atlantic e.g., [13].
Global hydrothermal input is dominated by deep mid-ocean-ridge (MOR) hosted systems, whereas submarine island arc systems are thought to account only for ~9% of hydrothermal fluxes [1]. Submarine island arc systems are typically shallower (<1800 m) compared to MOR settings and commonly discharge highly acidic, metal-rich (e.g., Fe) fluids [14,15,16,17]. Considering the shallow water depth, bioactive elements from submarine island arc hydrothermal systems may be relevant to the overlying photic zone and likely influence primary production [16,18]. For instance, it was shown that Fe introduced by volcanic ash stimulates phytoplankton growth [19,20], and just recently Ardyna et al. [21] provided the first observation of upwelled deep water with hydrothermal signature causing phytoplankton blooms. They observed two dense phytoplankton blooms in the Southern Ocean, which were likely triggered by upwelled hydrothermal Fe, introduced into the deep ocean at the Southwest Indian Ridge [21].
In order to assess the importance of submarine hydrothermal arc volcanism for the surrounding water column, including the photic zone, it is essential to quantify trace metal and element fluxes from these systems. A few different flux estimation approaches have been reported, but most of them provide snapshots of the dispersing hydrothermal fluid within a hydrothermal plume, but not time-integrated information. Often, fluxes are based on oceanographic estimations by measuring heat anomalies [22,23], tracer release experiments [24], elemental concentration gradients [25,26,27], or current meter studies [23,28]. However, to date, published elemental fluxes of hydrothermal systems are mostly limited to MOR settings [4,26,29,30] and data for island arc hydrothermal systems remain scarce [18]. The current study aims to address this knowledge gap for island arc hydrothermal systems by using naturally occurring radium (Ra) isotopes as new tracers for hydrothermal fluxes, which also provide temporal plume information. Previous work showed the suitability of Ra as a hydrothermal and crustal residence time tracer [31,32,33].
Radium isotopes are enriched in hydrothermal fluids due to the decay of naturally present U and Th in subsurface rocks and sediments. Desorption of Ra from minerals is controlled by the ionic strength of the adjacent water, rather than temperature [34,35,36,37]. Hence, once separated from the oceanic floor, there is no other source for excess Ra in the open ocean than a hydrothermal one, and thus Ra isotopes above background levels can serve as plume tracers [38,39]. Radium has four naturally occurring isotopes with half-lives ranging from days to centuries (T1/2 223Ra 11.4 d, 224Ra 3.66 d, 226Ra 1600 yrs., 228Ra 5.7 yrs.). Short-lived isotopes 224Ra and 223Ra are suitable to investigate near-field (<10 km) plume dynamics and dispersion and transport processes [39], whereas longer-lived isotopes can be used to trace plumes hundreds of kilometers and to calculate their transport velocity [38]. Therefore, Ra isotopes are considered suitable tools for flux estimations in hydrothermal settings, similar to the wide application of Ra in coastal submarine groundwater discharge (SGD) research e.g., [40,41,42]. Despite the successful application of Ra isotopes in coastal zones and their identification as a potential useful natural tracer of venting in hydrothermal research [43], only a few studies so far focused on Ra isotopes or their precursors at sites of hydrothermal venting: e.g., at the Puna Ridge, Hawaii [44], and the TAG vent field at the Mid-Atlantic-Ridge [45,46].
Consequently, in this study, we used the short-lived Ra isotopes to estimate submarine hydrothermal discharge (SHD) from a vent field at the Brothers volcano, located at the Kermadec intraoceanic arc, northeast of New Zealand (Figure 1) to contribute to a better understanding of hydrothermal discharges and fluxes to the ocean and the influence on global biogeochemical cycles. We hypothesize that the well-established modeling approach for coastal SGD using Ra isotopes is also applicable for the estimation of SHD. We then used the estimated fluid discharge to calculate associated elemental fluxes for Fe, Mn, 3He, and 4He. The metals are transported within the hydrothermal plume where a fraction can be transported far field [8,9]. Iron and Mn were selected, as they are closely linked to marine bioproductivity and are commonly enriched in hydrothermal fluids, while helium was used as it is a prominent hydrothermal tracer. We also calculated fluxes for Pb to discuss the limitations of the SHD approach. Based on the trace element fluxes for Brothers NW caldera we further provide an estimate of the relative importance of the shallow southern and mid-Kermadec arc hydrothermal vents in the context of global hydrothermal element input into the oceans.
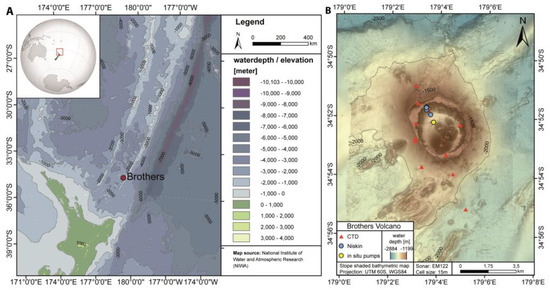
Figure 1.
(A) Overview map of the southern Kermadec intraoceanic arc near the Northern Island of New Zealand. The map source is provided by the National Institute of Water and Atmospheric Research, New Zealand (NIWA) [52]. The scale is 1:12,000,000 and the map uses the UTM Zone 60S projection. The map and figure captions were taken from Neuholz et al. [39]. (B) Local bathymetry map of Brothers volcano with marked sample locations based on multibeam data from SO253 cruise [53]. Note that due to the map section the 083_TMR station (Appendix A.2 Table A1) NW of Brothers is not displayed here.
2. Materials
2.1. Study Area
This study is part of the “HYDROTHERMADEC” project with its related cruise SO253 on the German RV Sonne from December 2016 to January 2017 [47]. Seawater and fluid samples were taken from the submarine Brothers volcano (34° S, 179° E; Figure 1), located within the southern Kermadec intraoceanic arc, which is one of the best-studied submarine island arc caldera volcanoes in our oceans [15,48,49]. The Brothers volcano is characterized by a near circular caldera with a diameter of approximately three kilometers. Situated at about 1540 m depth, the caldera rim completely surrounds the caldera. Active venting is located at the northwest (NW) caldera (1600 m depth) and at the dual cone structure, which outcrops at the southeastern half of the caldera (as shallow as 1200 m depth) [50,51]. For a more detailed description of the location, the reader is referred to [39]. The current study focuses on the black smoker dominated vent field at the NW caldera of Brothers volcano (1580–1680 m depth). The venting at the main cone and side cone were not considered due to fluid discharges at shallower depth, 1195 m and 1335 m depth, respectively, and thus a different plume depth [15].
2.2. Sampling and Analysis
2.2.1. Radium
A comprehensive description of sampling techniques and subsequent sample processing for Ra analysis on board the vessel and in the laboratory can be found in Neuholz et al. [39]. In short, the remotely operated vehicle (ROV) “Quest 4000” (MARUM, University of Bremen, Germany) collected fluid samples within the direct vicinity of the hydrothermal vents of interest. The ROV was equipped with titanium syringe samplers (major samplers) [54], an all-Teflon fluid sampling system (Kiel pumping system KIPS) [55,56], and three Teflon-coated 5 L Niskin bottles (General Oceanics). Water column samples including large volume samples (up to 580 L) from the hydrothermal plume were obtained by a CTD rosette sampler system or in-situ pumps (McLane WTS-LV 4). The CTD rosette sampler consisted of an SBE 32 carousel equipped with a mounted SBE 9plus underwater unit and two TRDI 300 kHz Workhorse Monitor Acoustic Doppler Current Profiler (ADCP) for direct current measurements. For plume depth identification, the CTD was equipped with two custom-built optical backscatter sensors (Seapoint Turbidity Meters; 5x normal gain) and an oxidation-reduction potential (ORP) sensor (Pacific Marine Environmental Laboratory). Dissolved Ra in discrete water samples was adsorbed by gravity filtration (~1 L/min) onto MnO2 coated acrylic fiber (Mn fiber) filled columns [57] after checking the pH and for fluid samples, if necessary, adjusting it to around neutral with NaOH. For Ra sampling using in-situ pumps, the columns filled with Mn fiber were directly attached to the pump´s outlet and thus Ra was adsorbed in-situ at the desired depth. The pumps operated at a speed of 1.9 ± 0.8 L/min, which is still slow enough to enable quantitative adsorption [58]. All Mn fibers were subsequently measured on board with Radium Delayed Coincidence Counters (RaDeCC) [59,60], following the procedure by Garcia-Solsona et al. [61] for the calculation of 224Ra and 223Ra activities. To obtain excess 224Ra activity (ex224Ra) and excess 223Ra activity (ex223Ra), the measured activities were corrected for the supported proportion coming from 228Th and 227Ac, respectively. Both 228Th and 227Ac were also adsorbed on the Mn fiber. The 228Ra activity was later calculated based on the measured 228Th ingrowth after more than six months according to Moore [62] with the corrected equation given in Charette et al. [46]. The system efficiency for 224Ra was monitored regularly with a standard sample prepared from an aged 232Th solution, similar to procedures described in [61,63]. The trueness for 224Ra was <6% and the method precision was <9%. The efficiency for 223Ra was calculated according to Moore and Cai [64]. The efficiency was initially cross-checked with other standards by repeated measurements on the same RaDeCC systems (standards kindly provided by M. Rutgers v.d. Loeff, AWI Bremerhaven, and J. Scholten, University of Kiel).
2.2.2. Iron and Manganese
Near-field plume samples were obtained by the CTD rosette sampler (SBE 9plus with SBE 32 carousel water sampler), while far field plume samples and background seawater samples were collected using 12 acid-cleaned Teflon-coated polyvinylchloride (PVC) 12L GO-FLO bottles (General Oceanics Inc., Miami, FL, USA) mounted on a trace-metal-clean rosette system (TMR) and deployed on a Dyneema rope.
Directly after recovery of the CTD rosette, hydrothermal plume samples were pressure-filtered (99.99% N2) through 0.2 μm Nuclepore polycarbonate (PC) membrane filters in a Sartorius filtration unit installed in a laminar flow bench, acidified with suprapure conc. HCl (30%) to pH ~1.7 and stored in acid cleaned low-density polyethylene (LDPE) bottles in the dark at 4 °C until further analysis. Directly upon recovery of the GO-FLO bottles, sample bottles were transported into a class-100 clean container fitted with a HEPA (high efficiency particulate air) filter system. Samples were subsequently pressure-filtered (0.5 bar of 0.1 μm filtered N2) through 0.2 μm cartridge-filters (AcroPak Supor, Pall Corporation, New York, NY, USA), acidified on-board with quartz distilled HCl to a final concentration of 0.024 mol/L hydrochloric acid, which results in a pH of 1.7 to 1.8 and stored in acid-cleaned LDPE bottles at ambient temperature in the dark until analysis in a land-based laboratory. In the home-laboratory, all water column samples were pre-concentrated with an offline seaFAST system (Elemental Scientific, Omaha, NE, USA) prior to analysis with high-resolution sector field inductively coupled plasma-mass spectrometry (HR-SF-ICP-MS, Thermo Fisher Element 2, Walsham, MA, USA) at the Royal Netherlands Institute for Sea Research (NIOZ). The recovery of this method was 100%. The trueness (we follow the trueness definition by JCGM [65], Menditto et al. [66], and Staats [67]) was monitored with different GEOTRACES seawater reference standards (D1 and GS) and values for Mn and Fe were within the consensus values range [68]. The overall reproducibility, which was better than 5%, was checked using a seawater in-house standard.
2.2.3. Helium
Samples for helium analysis were directly transferred, avoiding gas bubbles, from either Niskin bottles attached to the ROV or to the CTD carousel sampler, into pinched-off copper tubes (approx. 40 mL volume). The analysis of 3He and 4He was done at the University of Bremen mass spectrometric facility with a high-resolution sector field mass spectrometer (MAP 215-50, Mass Analyser Products, Manchester, UK). Additional Ne and He analysis was done in the same run with a quadrupole mass spectrometer (Balzers QMG 112a). The method is described in detail in Sültenfuss et al. [69]. Total errors based on the instrument performance and standard reference samples for 3He, 4He, and Ne concentrations were below 2%, 1%, and 1%, respectively. The excess 3He from the hydrothermal sources is here reported as δ3He in percent, defined by the isotopic ratio (R) between 3He and 4He compared to the atmospheric ratio (RA) of 3He to 4He, with RA = 1.39 × 10−6 (Equation (1)).
2.3. Submarine Hydrothermal Discharge (SHD) Calculation
The SHD calculation is deduced from its pendant in coastal research. Radium is enriched in groundwater relative to the coastal ocean and therefore, groundwater input can be measured by means of Ra isotopes [34,35,36,37]. Due to the different half-lives of the Ra isotopes, the ratio of 224Ra to 223Ra activity can be used to calculate water mass ages, when the system is advection dominated and conservative behavior of Ra is assumed [70]. Depending on the dimensions in time and space of the studied system, the longer-lived isotopes, i.e., 228Ra and 226Ra, may be used to normalize the short-lived Ra activity and correct for mixing effects. In any case, the ratio of two isotopes is preferably used, to rule out dilution effects.
Advantageous settings for using Ra based calculation approaches are SGD influenced coastal embayments since they have a well-defined water body volume (Vbay in m3). Considering the average residence time of water within the bay (τbay in days), the Ra activities of the groundwater end member (RaGW in dpm/100 L), the bay water (Rabay in dpm/100 L), the open ocean (Raoce in dpm/100 L) and the radioactive decay constant (λ in 1/d) when using short-lived Ra isotopes, respectively, it is possible to calculate the SGD input flux into the bay in m3/day as follows (Equation (2); [71]). Note that this study uses the terms “flux” and “discharge” in an interchangeable meaning.
We transferred Equation (2) to the submarine hydrothermal setting at Brothers volcano and re-named the indices accordingly (Equation (3); modified after Null et al. [71]).
The average Ra activity of end member hydrothermal fluid is written as Ravent and has the unit dpm/100 L. Raplume (dpm/100 L) is the mean Ra activity within the hydrothermal plume based on multiple samples. The Ra background activity is defined as Raoce (dpm/100 L) and was determined from samples with the greatest distance to the active vent sites located upstream with regards to the main current direction to avoid any hydrothermal fluid signal interference. The water volume of the hydrothermal plume is written as Vplume with the unit m3 (respective values given in Section 3). And Tplume denotes the average calculated apparent water age of the plume in days (Table 1 and average age given in Table 2), see Neuholz et al. [39] for a detailed discussion. Briefly, the calculation for Tplume (Equation (4)) followed the approach of Moore [70], which calculates the apparent age (T) using the difference between activity ratios of samples (a shorter- to a longer-lived Ra isotope, in Equation (4)) and the end member activity ratio () divided by the respective isotope decay constants ( and ). The end member activity ratio for ex223Ra to ex224Ra () is 50.2 ± 22.8, calculated by Neuholz et al. [39] for hot (>150 °C; black smokers) end member fluids. The apparent water age for each sample (Table 1) was calculated according to this ratio, using ex223Ra and ex224Ra activities of the sample. The term Tplume represents an average value obtained from all the ages of samples with excess 224Ra activity.

Table 1.
Radium isotope activities for 223Ra, 224Ra, and 228Ra of all used plume samples at Brothers volcano. Actinium (Ac) and thorium (Th) activities were used to calculate excess 223Ra and excess 224Ra, respectively. All activities are given in dpm/100 L. The presented ages were calculated according to the hot hydrothermal end member ratio from Neuholz et al. [39] and represent apparent ages in days (d).

Table 2.
The parameterization and results for Ra isotopes used in the submarine hydrothermal discharge (SHD) calculation, Equation (3). The uncertainties assigned to each parameter are discussed in Section 4.2. The SHD flux range according to the propagated uncertainty is given in parentheses. The average residence time of the plume, Tplume, was calculated using the hot hydrothermal end member activity ratio from Neuholz et al. [39] and sample ex223Ra and ex224Ra activity ratios.
The term “apparent age” was used, as plume ages were calculated based on the assumption of advective transport and exponential decay laws and may underestimate fluid ages due to linear mixing processes or diffusive transport [35,70].
At Brothers, the discharge of hydrothermal fluids through hot focused vents, i.e., black smokers, and diffuse discharge fields occurs in a limited spatial area and thus can be simplified as a well-defined source with high-end member Ra activities. We used an average activity (Table 2) from 25 different samples of fluids taken directly out of the hot vents (170–311 °C) and samples collected at fractures above mussel beds or bacterial mats (diffuse venting) for Ravent, as these fluids contribute to the Ra enrichment inside the caldera. Water column samples from the CTD and in-situ pumps were selected for excess 224Ra and excess 223Ra activity above background levels; the average of those was defined as Raplume (Table 2). The sample locations were then used to model the shape and volume of the hydrothermal plume, as Ra activity above the background level is a result of hydrothermal discharge and thus is indicative of the plume location and dimensions. As the water volume of a plume is not enclosed by bathymetric boundaries, as it is the case for bay volumes or coastal ocean volumes (tidal prism), the plume dimensions have to be defined in a different way. Most plume simulations show an axisymmetric dome shape of the plume when no currents are present [72,73]. This dome structure is bent in one direction if the influence of currents is simulated, which results in an ellipsoidal shape [73,74]. Thus, we used an ellipsoid as a geometric analog to describe the natural hydrothermal plume for our plume volume calculations, as we assume the plume dispersion is influenced by prevailing currents [75]. In this study, an ellipsoid shape was mathematically fitted to the sample locations for excess 224Ra and excess 223Ra activity above background levels, using the “rgl” package in statistic software “R” [76,77,78]. The two resulting fitted ellipsoids mark the one sigma standard deviation around the mean of the total dataset in x, y, and z direction and reflect the most likely plume dimension and location relative to the local caldera topography (Figure 2 and Figure 3 and Appendix A.1 Figure A1). Both fitted ellipsoids are widely identical in shape and geographic position (Table 3). We did not use 228Ra and 226Ra activity for plume volume calculations, due to the long half-live of the isotopes and the potential of far field input from other volcanoes.

Figure 2.
Local bathymetry of Brothers volcano (2-fold exaggeration) with the calculated plume ellipsoid for ex224Ra marked in yellow. Red dots indicate sample locations with excess 224Ra activity above background level, which were used for the ellipsoid calculation. The black triangle marks the mean x and y location of plume samples (depth not representative for display reasons), which was used as ellipsoid center. The direction of view in the upper panel is westwards, and northeastwards in the lower panel. Local bathymetry from Koschinsky et al. [53].
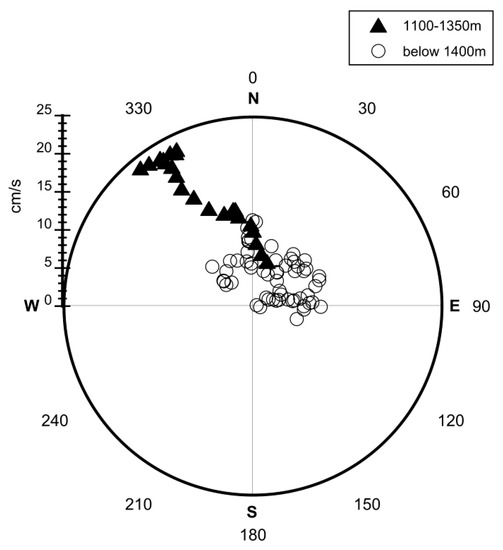
Figure 3.
Mean-lowered Acoustic Doppler Current Profiler (LADCP) data obtained from multiple vertical CTD casts at Brothers volcano. The displayed data is separated in the two depth intervals 1100 m–1350 m and deeper than 1400 m.

Table 3.
Comparison of calculated plume ellipsoids dimensions and volumes based on excess 224Ra and excess 223Ra activity above background levels. The volume is corrected for any overlap of the plume ellipsoid with local topography (i.e., caldera rim).
The overlapping local bathymetry of the caldera rim was subtracted from the calculated ellipsoid volumes to obtain the correct hydrothermal plume volumes. The main current direction, based on the lowered Acoustic Doppler Current Profiler (LADCP) data, was northward with a variable East/West component (Figure 3). To account for the main current direction, the section of the ellipsoids expanding beyond the southern end of the caldera wall was neglected and consequently subtracted from the volume, as intense plume dispersion against the main current direction is considered unlikely. The arithmetic mean of the two corrected ellipsoid volumes was then further used in the calculation (Vplume) to obtain SHD (Equation (3)).
2.3.1. SHD of Associated Trace Elements and Isotopes
The calculated discharge of the submarine hydrothermal fluid can be used to calculate the discharge for trace elements and isotopes associated with the hydrothermal fluid. Here, we calculated fluxes for Fe, Mn, He isotopes, and Pb (). Obtained Pb fluxes may not be robust due to strong precipitation effects of the metal e.g., [79,80]. Nonetheless, we use Pb to evaluate the application limits of the SHD calculation for highly particle reactive elements (see discussion in Section 4.4) but these fluxes were not considered for further interpretation. For elemental flux calculations of Mn, Fe, and He isotopes (Equations (5) and (6)) we used the mean SHD based on ex223Ra and ex224Ra activity (, respectively) and either the average element concentration (C) of the end member fluid or the average concentrations of the water samples from the Niskin bottles sampled above hot focused vents (). These hydrothermal fluid samples are identical to those samples used for Ravent. As metal precipitation (e.g., Fe-rich sulfide or (hydr)oxide minerals) is a dominant process when hot hydrothermal fluids mix with cold seawater, the Niskin samples may provide more realistic estimates on the metal load that reaches the buoyant plume in the dissolved form.
3. Results
The radium isotope activities of all plume samples and their age based on 224Ra/223Ra isotope ratios can be found in Table 1. The calculation of SHD using Equation (3) was applied two times with a different parameterization (Table 2), each calculation used a separate Ra isotope (223Ra and 224Ra) with the mean plume volume calculated via the ellipsoid fitting procedure (Table 3). The mean prevailing currents at Brothers volcano achieved from multiple vertical ADCP profiles during cruise SO253 point northward with a variable East/West component (Figure 3). The helium flux calculations were based on He plume data (Table 4).

Table 4.
Helium isotope data at Brothers volcano acquired during cruise SO253. R/RA reports the 3He/4He isotope ratio of the sample divided by 3He/4He isotope ratio of the atmosphere e.g., [81].
Three vertical CTD casts were carried out within the Brothers caldera (053 CTD, 054 CTD, and 058 CTD, Figure 4 and Appendix A.2 Table A1). Dissolved metal concentrations, turbidity signals, and He data indicate three plume depths within the caldera. Diffuse and clear to white fluid venting at the two cones in the SE of the caldera, located at 1196 m (main cone) and 1300 m (side cone) water depth probably results in the shallowest plume found between 1200 m and 1250 m [15]. The two deeper plumes below 1350 m likely result from black smoker venting at the NW caldera wall. With increasing distance to the NW (outside the caldera), the two deeper plumes within the predominant current direction (Figure 3) remain clearly detectable based on 3He concentration. The metal concentrations decreased from max. concentrations of 250 nmol/L Fe at the vents to 12 nmol/L 6 km NW and 15 nmol/L at 12 km NW of the caldera (Figure 4), thereby still being enriched compared to ambient background Fe concentration (around 1 nmol/L). Manganese concentrations, however, showed a consistent decrease with increasing distance from the caldera. Inside the caldera, max. concentrations of around 150 nmol/L Mn were found and decreased subsequently to 11 nmol/L and 3–5 nmol/L at 6 km NW and 12 km NW of the caldera, respectively.
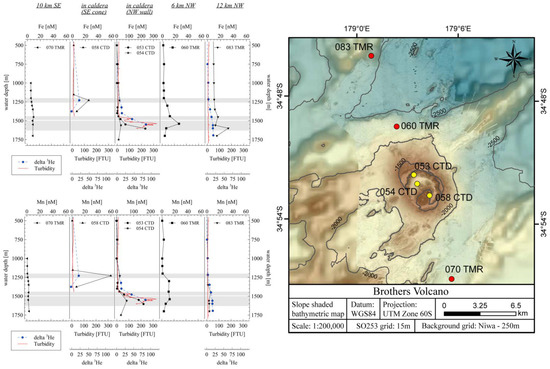
Figure 4.
Dissolved metal concentrations of Fe and Mn for different CTD casts over the Brothers volcano together with delta 3He and turbidity data. No helium and turbidity data are available for TMR casts (070 TMR and 060 TMR). Turbidity and helium data shown for 083 TMR were taken from an equivalent CTD cast (082 CTD) at the same position. The grey areas indicate plume depths.
Both deep plumes are indistinguishable using Ra isotopes and thus considered as one deep plume. Within the deep plume, positive correlations for ex224Ra and ex223Ra activities (228Ra and 226Ra were neglected because of their long half-lives) with dissolved Mn and Fe concentrations are evident (Figure 5). The linear correlation coefficient is high for ex224Ra and decreases when using ex223Ra with a longer half-life.
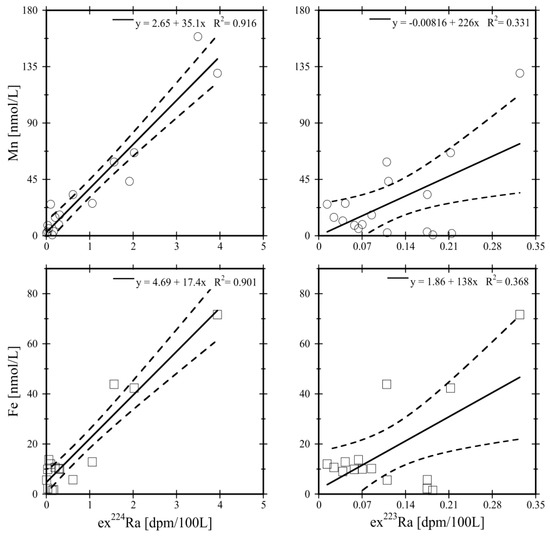
Figure 5.
Linear correlations of ex224Ra and ex223Ra activities with dissolved Mn and Fe within the plume of Brothers volcano. The dashed lines indicate the 95-percent confidence interval.
On average, 30% of the measured 223Ra activity was assigned to 227Ac, which is corrected for, in the reported excess 223Ra activities (Table 1). The excess 223Ra activity ranged between 0.01 dpm/100 L and 0.33 dpm/100 L in the plume samples of Brothers volcano. For the 224Ra activity, on average a proportion of 13% 228Th activity was corrected to result for the given excess 224Ra activities. Excess 224Ra activity was found to be between 0.07 dpm/100 L and 7.1 dpm/100 L for all plume samples. As explained in detail in Section 2.3, the average of all excess Ra activities above background was used as Raplume in Equation (3) and are listed in Table 2. Using both short-lived Ra isotopes, two independent SHD estimations are calculated: ex223Ra 8.2 m3/s (range 0–25.5 m3/s), ex224Ra 14.5 m3/s (range 0–29.6 m3/s) (Table 2) with an average of 11.4 m3/s (range 0–27.6 m3/s). The difference in the two SHD estimations is considered acceptable in the view of the given error range (Table 2). We note that given errors for SHD estimations are large due to the propagation of errors of used parameters, which is discussed in more detail in Section 4.2.
Based on the average calculated SHD the associated trace element and isotope fluxes () for dissolved Fe, Mn, Pb, 3He, and 4He were calculated using Equation (5) (Section 2.3.1 and Section 4.4 and Table 5). The metal concentrations of hot hydrothermal end-member fluids and Niskin bottle concentrations were taken from Kleint et al. [82]. As we did not sample hot end-member fluids for He and Ne analysis (due to volume limitations) we extrapolated the most likely prevailing end-member concentration for 3He and 4He at Brothers volcano. For this, we used the linear trends of R/RA (3He/4He of the sample divided by atmospheric 3He/4He, a common measure for 3He enrichments e.g., [81]) and total He concentration plotted against the total Ne to total He ratio (Figure 6 and Table 4). As Ne has only minor contributions from magma degassing or mantle material and is almost entirely atmospherically derived, the undiluted hydrothermal fluid is supposed to show negligible Ne concentrations [83,84]. By extrapolating the two linear trends to Ne/He = 0 (linear regression of R/RA versus Ne/He gives an R2 of 0.997, linear regression of He concentration versus Ne/He gives an R2 of 0.981), we calculate the estimated end-member concentrations of both He isotopes based on the prevailing total He concentration and the ratio of 3He to 4He. The extrapolated concentrations can be found in Table 5 marked with diamonds.

Table 5.
Submarine hydrothermal discharge of dissolved Fe, Mn, and Pb, as well as He isotopes at Brothers volcano. Flux estimates are based on mean discharge and calculated from Ra isotopes. “conc. Vent” represents the average of all samples from hot fluids and diffuse vents. “conc. plume” is the average concentration of all Niskin samples (n = 10) directly above hot focused vents. The concentration of Pb is marked with * as this is the concentration of one Niskin sample instead of an average of n = 10 and therefore a conservative estimate of 100% uncertainty was assumed. Data for vent fluids were taken from Kleint et al. [82]. The presented flux range in round parentheses is based on the propagated uncertainty of the calculation. Helium concentrations marked with a diamond (◇) were extrapolated based on the Ne/He ratio. Note that fluxes for Pb are presented in square parentheses, as they are no robust results and are only used to demonstrate limitations of the Ra-based calculation (discussion in Section 4.4).
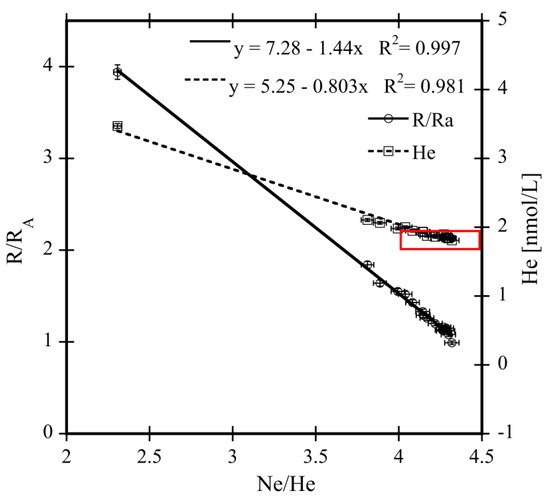
Figure 6.
He isotope ratio to atmospheric He isotope ratio (R/RA) and total helium concentrations of hydrothermal plume samples from Brothers volcano plotted against the Ne/He ratio. The linear trends were extrapolated to calculate the 3He and 4He concentration in the end member fluid at Ne/He = 0. The average Pacific deep water He concentration and Ne/He ratio is marked with a red frame; averages were taken from Ozima and Podosek [81]. Please note that errors are within the range of the symbol size.
According to Equation (6) in Section 2.3.1 a second element and isotope flux () estimation was done based on average concentrations of the water samples from the Niskin bottles above hot focused vents for Fe, Mn, Pb, and the He concentrations without extrapolation (‘conc. plume and below listed flux in Table 5). Niskin bottle-based flux estimates for Fe, Mn, and Pb are only 0.2, 0.6, and 6.4% of the end member-based flux estimates, respectively. For 3He and 4He fluxes, the proportions are 36 and 66%, respectively (Table 5). Note that Table 5 includes fluxes for Pb in parentheses, which are no robust results but are presented to show Ra-based calculation application limits, as discussed in Section 4.4.
4. Discussion
4.1. Dissolved Metals in the Plume
Iron-sulfide particles form rapidly in hydrothermal plumes and can be transported several kilometers from the source before they either settle to the seafloor or dissolve in the water column. Additionally, a certain fraction of the hydrothermally released Fe will be oxidized to hydroxides, while another fraction may be stabilized in its dissolved form by organic ligands [7,9,85,86]. These processes may be responsible for the observed variable Fe decrease with distance from the vent source at Brothers. The increase in dissolved Fe at 12 km distance might either be due to a contribution of a different vent source or due to dissolution of small sulfide particles, releasing colloidal Fe (belonging to the operationally defined dissolved fraction) [87,88]. Manganese does not form sulfide particles and is also not known to be stabilized by organic ligands in the open ocean [8,89], which would explain the constant decrease of Mn concentration with time and distance from the vent source.
As in the southern part of the caldera, the shallow plume is most pronounced around 1200 m and the location of 058 CTD coincides with the Brothers cone site [15], the plume signal is assumed to originate from hydrothermal vents at the cone. Similar to the deeper plume signal, the prevailing NW current direction during sampling prevents plume dispersion towards SE of the caldera (Figure 4). The shallow plume around 1200 m is situated above the caldera rim depth, which likely favors a fast dilution by ambient seawater, which may be the reason for the rapid down-current decrease of dissolved Fe and Mn concentrations within the plume.
4.2. Uncertainty of Ra-Based Hydrothermal Flux Estimations
As Ra is present in low concentrations in open-ocean seawater (e.g., <0.03 dpm/100 L 223Ra and <0.3 dpm/100 L 224Ra in the North Atlantic [90]), sample volume has to be high (100–1000 L) to obtain precise measurements. However, volume is often a limiting factor and thus, measured activities of open ocean seawater can have uncertainties as high as ~40% [61]. Nonetheless, a recent study by Le Roy et al. [91] showed that real measurement uncertainty might be lower than calculated from Garcia-Solsona et al. [61]. When this error is propagated within the complete SHD calculation, including all additional uncertainties of the input parameters, the resulting discharge flux likely has an uncertainty exceeding 100%.
Further, flux estimations based on excess 223Ra and 224Ra can be affected by additional Ra input from particulate 227Ac and 228Th. As Mn fiber shows a similar adsorption efficiency for Ra, Ac, and Th [92], it is straight forward to correct the measured Ra activity for adsorbed dissolved Ac and Th (see Section 2.2.1). However, additional Ra from particulate Ac and Th may further alter excess 223Ra and 224Ra activities, which cannot be quantified by Mn fiber analysis. As Ac and Th adsorb onto Mn and Fe(hydr)oxides [45,93,94,95,96], these Fe particles can be used as a proxy for particulate Ac. At station 16 on GEOTRACES North Atlantic transect at the TAG vent field Kipp et al. [45] analyzed the distribution of particulate and dissolved 227Ac and additionally, Lam et al. [97] studied size-fractionated SPM distribution. At plume depth of 3300 m, they found the maximum Fe(OH)3 particle concentration of 4.9 µg/L, which accounts for 52% of the total 1–51 µm size fraction SPM [97]. This corresponds to 45.8 nmol/L particulate Fe, which scavenged 5–11% of the total 227Ac in the plume [45]. At Brothers, Baker et al. [98] found concentrations of 214 ± 244 nmol/L particulate Fe, which is in agreement with a total of approx. 180 µg/L SPM based on turbidity data. Following the scavenging activity of particulate Fe for 227Ac from [45], a maximum of 20–40% of the total 227Ac would be present in particulate phase. Due to the known adsorption of Th onto Fe(hydr)oxides [45,93,94,95,96] and the scarce data basis for particulate radio isotopes in hydrothermal plumes, we assume 228Th to be comparable with 227Ac in terms of particle dynamics. Nevertheless, the uncertainty aspects are not disqualifying Ra isotopes as a tracer for hydrothermal flux estimates. As it is important to mention that this estimate is only reasonable inside the caldera, as turbidity and particle density rapidly decrease outside of the caldera [50,51,98]. Therefore, Ra input from particulate 227Ac and 228Th is considered to add minor uncertainty and does not affect the distribution of excess 223Ra and 224Ra. Various other methods show similar levels of uncertainty, e.g., heat flux estimates—100%; numerical heat flux model—400%; 3He-based flux estimate—100%; Mg-based flux estimate—600% [22]. In the following, we discuss two aspects of our discharge calculation and the associated uncertainty.
4.2.1. Uncertainty Caused by Estimations of the Plume Dimension
The presented Ra approach used to assess the hydrothermal discharge has some assumptions and sources of uncertainty, which have to be kept in mind, when using and interpreting the data. Since the plume is not bordered by seafloor topography the volume is difficult to estimate but represents a key parameter in the SHD approach. As described in Section 2.3, we used an ellipsoid as a geometric analog of the plume because plume simulations generally show an ellipsoidal shape of the plume when ocean currents are present [73,74], which is the case at Brothers. The quality of the simplified ellipsoidal model used here is strongly dependent on the sample location spacing when calculating the dimensions of the ellipsoid. The model assumes that the samples cover the full extent of the plume, which is difficult to ensure, but a sufficiently large sample set can minimize this problem. The sample locations in our study did cover the full extent of the plume; however, we assigned a rather conservative estimate of 100% uncertainty to the calculated plume volume. We note further that, the displayed heights of the ellipsoids might not be fully exact and add additional uncertainty. In addition, the ellipsoid is constructed fully symmetrical along its main axes for mathematical reasons, which may not reflect the true nature of the plume e.g., [99]. The orientation of the ellipsoid is solely depending on the discrete point sample locations. Ocean currents, as an important influencing factor, were not considered during the mathematical fitting of the ellipsoid. Nevertheless, currents influenced the distribution of the excess Ra activity and were thus taken into account indirectly, as only samples showing excess Ra activity above background were considered. We also calculated the plume volume based on a two-sigma ellipsoid, which increased the volume itself and also increased the resulting SHD fluxes by a factor of 2.7 (Table 2, data for 2s ellipsoid not shown). Regarding the propagated errors of calculated SHD fluxes, results and respective errors based on the two-sigma plume volume were within the error range of SHD fluxes presented in Table 2. In addition to 224Ra, the calculated plume ellipsoid using samples with excess 223Ra activity above background level in a separate calculation was very similar in shape and geographic position. The similarity provides justification to use the average of both Ra isotopes and the available water samples as plume volume estimate (Table 3 and Appendix A.1 Figure A1).
4.2.2. Uncertainty of Extrapolated 3He and 4He End Member
The extrapolated 3He and 4He end-member concentrations need to be critically discussed, as they could not be measured directly. Generally, plume samples allow only a vague conclusion on prevailing end-member concentrations due to the high dilution factor with seawater. Consequently, the Ne/He ratio of such samples is usually not significantly different from that of seawater (average Pacific deep water marked in Figure 6, red box). However, samples from Brothers volcano taken during the SO253 cruise do show significant deviations from the average Pacific deep water He concentration, Ne/He ratio, and R/RA ratio and, therefore, allow an extrapolation to undiluted end-member fluid. Hereby the obtained R/RA of 7.28 in undiluted end-member fluid agrees well with the previously reported R/RA of NW caldera hot fluids from 2005 of 7.16 (Figure 7 and [15]), corroborating the correctness of the conducted extrapolation.
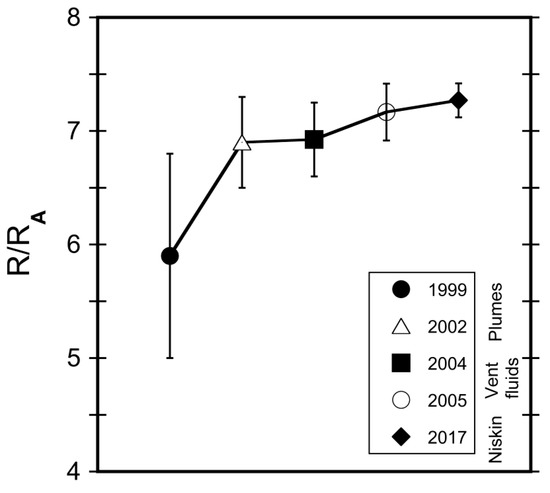
Figure 7.
Brothers NW caldera end member fluid He isotope composition expressed as a factor of the atmospheric 3He/4He ratio (R/RA). The figure is modified from de Ronde et al. [15]. Data for 1999 and 2002 were estimated based on plume samples, 2004 and 2005 ratios were directly measured in end member samples and the 2017 ratio is extrapolated from Niskin bottle samples (see Section 3).
4.2.3. Uncertainty of Trace Element End Member and Niskin Bottle Concentrations
In Table 5, average trace element concentrations for hot hydrothermal end-member fluids and the plume (Niskin bottles) are listed. A closer inspection revealed that the dilution factor between the end member concentration and the plume concentration of the trace elements is not identical for presented elements and isotopes, as would be expected if only dilution was at play. Differing factors can also be found for ex224Ra and ex223Ra activities (data not shown). The deviating factors can have multiple reasons. As discussed above, the extrapolated He isotope end-member concentrations can have an influence on the factors between end member and plume concentrations. Additionally, as mean values are presented Table 5), a sufficiently large number of individual samples is necessary to calculate consistent means, which cannot always be ensured due to limited data density and availability. Further, the deviating factors are potentially also due to the different physicochemical properties of the elements of interest, such as precipitation rate or bioavailability of the trace elements (i.e., the inert gas He versus the bio-essential Fe and Mn). We note that the deviating factors may limit the significance of the here presented calculated fluxes. Nonetheless, with the dataset density presently available, this uncertainty cannot be excluded completely.
4.3. Additional Near-Bottom Input of 227Ac and 223Ra
Kipp et al. [45] found elevated 223Ra/224Ra ratios in the bottom water of the TAG vent field as a result of 227Ac enrichment in the metalliferous surface sediments, demonstrating that 227Ac enrichments are an important aspect to consider when using 223Ra or 227Ac as a tracer in the near-bottom water column. At Brothers volcano, however, large sediment accumulation is hampered by currents and winnowing effects [100]. In contrast to Kipp et al. [45] (223Ra/224Ra = 12.4), our data showed 223Ra/224Ra ratios below one in bottom water samples (Table 1), but a small increase within the error range of the 227Ac activity with depth. The minor 227Ac enrichment in the bottom water does not considerably alter the 223Ra activity of the plume during potential mixing processes with adjacent bottom water. Therefore, 227Ac enrichments are expected to have a small effect on the usage of Ra isotopes as tracers at Brothers volcano to calculate discharge. The apparent absence of elevated 223Ra/224Ra ratios at Brothers volcano might also be explained by the different magma composition compared to the MOR settings, as magmas below island arc volcanic systems also receive material from the subducting slab with high Th/U. Consequently, fresh dacitic rocks from Brothers volcano have higher Th/U ratios compared to MORB (2.72–3.87 versus 2.15–2.25, respectively) [101,102,103].
4.4. Comparison of Measured and Calculated Trace Element Plume Concentrations at Brothers Volcano
The SHD calculation was used to reproduce concentrations of dissolved trace elements within the plume based on calculated trace element inventories and the quantified plume volume. Following the Ra approach, it is possible to gain information about the behavior, the persistence and the precipitation effects of trace elements in the hydrothermal plume. The positive correlations of Ra activity with dissolved Fe and Mn concentrations in the plume (Figure 5) indicate that both short-lived Ra isotopes show a similar behavior and it emphasizes the connection between hydrothermally derived dissolved Fe, Mn, and Ra, presuming they all originate from the same vent source. The correlation coefficient between the Ra isotopes and Fe or Mn concentration decreased with increasing half-life of the Ra isotope. The decrease was expected, as the longer-lived isotopes might also show signals from other nearby submarine volcanoes (nearest active submarine volcano is Kibblewhite volcano located 37 km away in north-western direction) [104] and precipitation of Fe and Mn would increase the decoupling with Ra.
To calculate average concentrations of dissolved Fe, Mn and He isotopes in the plume, we first multiplied the average apparent Ra age (Tplume in seconds, Table 2) with the specific calculated trace element flux (JSHD in mol/s, Table 5) based on the SHD calculation, see Equation (7). We calculated two scenarios (“Scenario 1 and 2” in Table 6), each with a different parameterization, which is discussed in the following.

Table 6.
Mean calculated and measured concentrations of dissolved Fe, Mn, Pb, 3He, and 4He of two hydrothermal plume scenarios at Brothers volcano with propagated uncertainty, which is indicated by the range given in round parentheses. The median of measured concentrations is given with 1s standard deviation of representative plume samples (range presented in round parentheses). For Fe and Mn, we used the flux (JSHD) based on concentrations in the plume (Niskin bottles) for a comparison with average measured data and for 3He and 4He the fluxes based on end-member concentrations were used. Local background concentrations were already added to the respective mean calculated concentration to enable a comparison. Background concentrations are measured concentrations between 1000 and 1700 m depth at the TMR background station of the cruise SO 253 (−35.25837° S, 178.7771° E). Scenario 1 uses the plume volume of the total plume extending beyond the caldera rim and Scenario 2 uses the plume volume of the inner caldera plume section. Note that calculated concentrations and factors for Pb are presented in square parentheses, as those are no robust results, which is further detailed in Section 4.4. For an exemplary step-by-step calculation, the reader is referred to the Appendix A.3.
This calculation results in the total inventory for each specific trace element within the plume (Qplume) assuming conservative behavior. Equation (7), however, excludes precipitation, even though formation of solid phases is an important process for some elements when hot, reducing fluids mix with cold, oxic seawater e.g., [5] and references therein. We therefore calculated the inventory Qplume) and the resulting trace metal fluxes (JSHD) in two different ways: (a) based on the hot hydrothermal end-member concentrations, using Equation (5); and (b) based on the element concentrations in the Niskin bottles, which sampled fluid <3 m above the vent outflow, using Equation (6) (Table 5). The Niskin sampling technique mainly sampled dissolved elements since most elements precipitate immediately after venting of the hot fluids [105]. The element concentrations in the Niskin samplers are thus assumed to represent more realistic element export concentrations of the dissolved fraction to the buoyant plume. For Fe and Mn as reactive compounds, which are known to form precipitates, we used the flux (JSHD) based on concentrations in the Niskin bottles for the comparison with average measured data, while the fluxes based on end-member concentrations were used for 3He and 4He as non-reactive noble gas isotopes. In a second step, the calculated inventory for each trace element (Qplume) was divided by the plume volume (Vplume) for calculation of the average concentration of the trace elements in the hydrothermal plume (Cplume), see Equation (8). In “Scenario 1” the volume of the whole extended plume is used for Equation (8), while in “Scenario 2” the plume volume was segmented into an inner and an outer caldera plume, and solely the volume of the inner caldera plume segment was considered for Equation (8).
Results of both scenarios, the full plume “Scenario 1” and the inner caldera plume “Scenario 2”, are compared to the average measured concentrations of selected dissolved trace elements in plume samples (n = 32) and local background concentrations of the Brothers volcano (Table 6) (trace metal data are presented in Figure 4 and Appendix A.2 Table A1). The median of the plume samples was used for comparison, as it is more robust towards extreme values. Note that the average measured concentrations were only used to assess the accuracy of the Ra-based calculation results. The averages neglect the increasing plume dilution with distance to the vent source and thus, are a strong simplification of the natural trace metal distribution.
The calculated concentrations of “Scenario 1” (Table 6) for Fe and Mn are higher than the mean measured concentration in the plume by a factor of 2.9 and 1.7, respectively. However, mean calculated concentrations for 3He and 4He match the mean measured concentrations. In “Scenario 2” (Table 6), we used the volume of the inner caldera plume segment. Using this procedure, we can check whether the Ra-based calculated trace element concentrations correspond better to average concentrations of trace elements within the well-defined plume, compared to the total plume in “Scenario 1”. The inner caldera plume segment is surrounded by the caldera rim and is therefore more separated from the rest of the water column with respect to topography and consists of generally younger hydrothermal fluid. This is demonstrated by the mean apparent age of the caldera plume, which is younger (16 days–used in Scenario 2) compared to the mean age of the total plume volume (17.7 days—used in Scenario 1) [39]. Using the volume of the inner caldera plume segment, the element inventory was converted into a mean concentration using Equation (8). The output of Scenario 2 showed larger deviations compared to Scenario 1 with a factor of 7.3 and 2.3 between the measured and the calculated concentration for Fe and Mn, respectively, indicating different drivers of dissolved Fe and Mn concentrations compared to Ra activities. Nevertheless, similar to “Scenario 1,” calculated and measured results for 3He and 4He in “Scenario 2” agreed well with ≤5% deviation.
A closer inspection of the data (Table 6) revealed that the Ra model was able to predict correct concentrations for the inert 3He and 4He isotopes in the plume, while average concentrations for the reactive metals Fe and Mn in the plume were overestimated with a greater difference for Fe than for Mn. The overestimation was to be expected, as neither Fe nor Mn show conservative mixing behavior in the buoyant and neutrally buoyant hydrothermal plume. In contrast, Fe and Mn are subject to precipitation processes removing these elements from the dissolved pool, while removal of Fe is generally thought to be faster compared to Mn removal [5,9,106,107]. The different behavior of Fe and Mn in hydrothermal plumes has been documented by numerous studies at a variety of widespread hydrothermal vent sites e.g., [5,8] and references therein. The studies of Boyle et al. [108] and Massoth et al. [109] investigated dissolved and particulate Fe and Mn concentrations in hydrothermal plumes off Hawaii and the Cleft segment of the Juan de Fuca Ridge, respectively. They consistently found that particulate Fe makes up a larger fraction of total Fe compared to the proportion of particulate Mn. More recently, decoupling of Fe and Mn from the largest hydrothermal plume extending from the Southern East Pacific Rise was detailed by Resing et al. [9] and Fitzsimmons et al. [8]. These studies indicate that Fe tends to form particulates faster than Mn [110]. Further, it is well known that Mn shows rather slow oxidation kinetics [111,112,113] and thus, Mn does not immediately precipitate within the first meters of the buoyant plume as it would, if being fully oxidized according to its thermodynamically predicted behavior. Therefore, Mn remains longer in solution and consequently the calculated concentrations correspond better to the mean measured concentrations of Mn.
The faster precipitation of Fe led to a considerable proportion of Fe being removed from the dissolved phase in the buoyant plume due to precipitation, adsorption, and biological uptake processes. Fitzsimmons et al. [8] and Lough et al. [107] showed that there is an exchange of Fe between the dissolved and the particulate phase in both directions during plume aging. Further, Fe is strongly coupled to hydrothermal biomass production. Li et al. [114] could show that Fe-related genes are the most abundant genes in the metatranscriptome of the Guaymas Basin deep-sea hydrothermal plume. The authors conclude that Fe uptake by microbes, even from the particulate phase, is a very active microbial mechanism in vent settings. A study performed during this cruise (SO253) on parameters governing the microbial community structure and element turnover in hydrothermal fluids from the Brothers volcano, showed that the highest autotrophic CO2 fixation was observed for fluid cultures supplemented with iron(II) or hydrogen. This demonstrates the close coupling of iron with hydrothermal microbes in these fluids [115]. Therefore, it may well be possible that the microbial Fe uptake also diminishes the dissolved Fe pool at Brothers, which may be an additional cause for the deviating measured and calculated concentrations of Fe. Similarly, microbial uptake of hydrothermal Mn was also documented for the Guaymas Basin; however, this uptake was found to be less significant in open ocean hydrothermal plumes compared to the Guaymas Basin [116]. Up to now, this Mn removal process was not documented at Brothers volcano.
In this work, we cannot discriminate which process (precipitation versus biological uptake) is more important for the depletion of dissolved Fe and Mn within the caldera environment. Both processes are able to cause a locally distorted relation between trace metals and Ra isotopes and therefore hamper the use of Ra isotopes to calculate average dissolved trace metal concentrations inside the inner caldera hydrothermal plume. However, an in-depth discussion of the dissolved trace metal behavior in the plume and processes affecting precipitation or complexation will be the subject of another complementary publication.
The calculations of “Scenario 1 and 2” were also used to calculate the hydrothermal plume concentrations of Pb, a highly particle reactive element, which is known to intensely interact with the particulate phase in hydrothermal environments e.g., [79,80]. The calculation can evaluate the necessary preconditions and physicochemical properties of elements of interest to apply the Ra-based calculation. “Scenario 1” calculated an average of 3.73 pmol/L (range 0–10.4 pmol/L) Pb in the plume and “Scenario 2” an average of 9.73 pmol/L (range 0–27.3 pmol/L), while the average measured concentration was merely 26.1 pmol/L. The simulation greatly underestimated the average plume concentration potentially due to interactions of the particulate and the dissolved phase of Pb on shorter time scales than Ra decay or unrepresentative end-member concentrations. However, interaction mechanisms could not be resolved within the work of this study. Therefore, the Ra-based calculation may not be suitable for Pb.
In summary, dissolved Fe and Mn concentrations are overestimated, likely because of potential precipitation effects and/or microbial uptake. These processes occur on time scales shorter than investigated by the short-lived Ra isotopes and thus are more intense during the early stage of the hydrothermal plume, i.e., inside the caldera, causing a larger difference between calculated and measured results (larger deviation for “Scenario 2” inside the caldera compared to “Scenario 1” referring to the total plume). In contrast, plume concentrations of the inert He isotopes were successfully modeled based on Ra isotopes.
4.5. Importance of Hydrothermal Fluxes at Brothers Compared to Other Hydrothermal Vent Sites
To gain an insight into the relative importance of island arc hydrothermal circulation for oceanic element budgets, the calculated volume and trace element fluxes for Brothers NW caldera are compared to other hydrothermal systems (Table 7). Published estimates of discharging fluid volume are mostly available for MOR settings, such as the Juan de Fuca Ridge, the Rainbow vent field, and the Logatchev vents [29,30,117]. The fluid fluxes estimated for the Rainbow vent field and the Logatchev vent field are smaller compared to Brothers NW caldera, although the 3He discharge significantly exceeds that at Brothers. Fluxes from the Endeavour vent field, a part of the Juan de Fuca Ridge located in the NE-Pacific, exceed the fluid fluxes at Brothers NW caldera by orders of magnitude. However, these fluxes also include entrained seawater and are thus different from the flux calculations presented here, making comparison difficult. The Ra based flux estimations give information on the amount of hydrothermal fluid that gets expelled either in hot focused vents or as shimmering diffuse discharge. Such an approach does not include surrounding seawater that is mixed into the buoyant or neutrally buoyant plume due to turbulent entrainment. It is also important to note that the fluid fluxes presented for Brothers NW caldera represent fluxes from only one vent field at Brothers volcano. The main cone and side cone are also sites of known hydrothermal activity at shallower depth with different fluid chemistry [15,82] (see also Figure 4). We therefore focus on the comparison of trace element fluxes rather than discharge volume.

Table 7.
Comparison between hydrothermal discharge estimates published in the literature and results from Brothers volcano (end member and Niskin estimates taken from Table 5). If ranges were given in the references, min and max values are included in the table. JDFR: Juan de Fuca Ridge, MOR: mid ocean ridge. The data from Okinawa Trough is originally published as sum of 15 vents, we here list 1/15 of the sum as the individual vent contribution for a better comparability. Data: 1 data from present study; 2 Rosenberg et al. [117]; 3 Massoth et al. [109]; 4 German et al. [29]; 5 Schmale et al. [30]; 6 Buck et al. [18]; 7 Staudigel et al. [4]; 8 Zeng et al. [118].
The Fe discharge at the Ahyi seamount, Northern Mariana Island, was found to be comparable to Brothers volcano, using the flux estimates derived from the Niskin bottle plume sampling [18]. The similarity between Fe fluxes was expected, as the Ahyi seamount is also located on an island arc. The 3He flux at Ahyi seamount, however, is much larger compared to Brothers, but this may be attributed to a recent eruption of the Ahyi seamount. In contrast, the reported Mn flux at Ahyi seamount is lower compared to Brothers, despite the fact that this flux was based on total dissolvable Mn (TDMn) instead of dissolved Mn and the TDMn flux is expected to exceed the dissolved Mn flux [18].
The plume-based (Niskin samples) Mn flux of Brothers is similar to those of the intra-plate volcano Vailulu’u seamount [4] and to the minimum estimate for vents of the back-arc basin Okinawa Trough, considering the contribution of an individual vent as 1/15 of the field total reported by Zeng et al. [118]. The Mn flux range for Okinawa Trough hydrothermal vents estimated by Zeng et al. [118] is also comparable with the range calculated for Brothers based on the plume and hot fluid calculation (Table 7).
Fluxes of Fe, Mn, and 3He reported for the MOR-based Endeavour vent field, Cleft segment, Rainbow vent field, and Logatchev vent field [29,30,109,117] exceed the plume-based (Niskin samples) fluxes at Brothers and therefore highlight the global dominance of MOR-based hydrothermalism compared to island arc systems. The elevated 3He fluxes at MOR-based vent fields can be attributed to the higher magmatic influence compared to oceanic island arc hydrothermal systems [119]. Nonetheless, the discharge volume at the Endeavour vent site exceeds that at Brothers NW caldera by a factor of 103, while associated Mn fluxes differ by factor ~10 This confirms the overall higher concentrations of dissolved metals in hydrothermal end-member fluids at the island arc volcano Brothers and therefore underlines the importance of island arc vents for global ocean element budgets [16].
In addition, our cruise can add data to the previously published He isotope time series at Brothers NW caldera by de Ronde et al. [15]. The R/RA in 2017 was very similar compared to those of 2005, a further increase of this ratio as reported from 1999 to 2005 could thus not be shown (Figure 7). We therefore can assume steady magmatic conditions over the past twelve years below the Brothers NW caldera.
If we consider Brothers volcano as representative for island arc volcanism and if we combine our results with those from the “New Zealand American Plume Mapping Expedition” (NZAPLUME I and II) [104,120] we can estimate an annual trace element discharge of the southern and mid Kermadec arc. The average molar Fe/Mn ratio of hydrothermal plumes is found to be 4.5 ± 4.6 along the Kermadec arc [104,120]. The ratio at Brothers was 8.3 based on end-member fluids and 2.5 when Niskin samples were used. Thus, to provide a first general estimate, the fluid composition at Brothers is considered to represent the range of Fe/Mn ratios found along the Kermadec arc based on the data available. NZAPLUME I and II identified a total of 21 hydrothermal plumes. Taking into account the number of plumes and Brothers trace element fluxes, an annual discharge of 9.8 × 107–4.7 × 1010 mol/yr Fe, 3.9 × 107–5.7 × 109 mol/yr Mn, 0.1–0.4 mol/yr 3He and 2.6 × 104–3.9 × 104 mol/yr 4He was calculated. The range is based on Niskin bottle concentrations and hot fluid concentrations, although maximum estimates based on hot fluid concentrations are not solely exported in dissolved form. This is a simplified minimum estimate, as the number of 21 hydrothermal plumes is given without any claim of completeness. Additionally, this estimate also disregards the known variety of vent fluids found along the Kermadec arc e.g., [82,104], since element and volume fluxes for them are currently unavailable. The large range of estimated trace element fluxes is due to the maximum estimate including the fraction that precipitates immediately after venting. According to Lough et al. [107] the global input of dissolved Fe from hydrothermal vents is estimated to be on average 2 × 109 mol/yr to the deep ocean based on available flux estimations. Further, the gross global hydrothermal Fe flux (dissolved + fast precipitates) is estimated at 11.3 × 109 mol/yr [121]. Consequently, the Kermadec arc would provide ~5% of the global dissolved hydrothermal input, based on the minimum flux estimate and neglecting the shallow nature of the Kermadec arc hydrothermal vents (all vents shallower than 2000 m depth). Considering the maximum Fe estimate from the Kermadec arc, including the fast precipitating fraction, the Kermadec arc flux equals >100% of the gross global hydrothermal Fe input, and therefore proves itself as an overestimation. Mn fluxes due to hydrothermal venting are estimated for the global ocean and on a basin scale by van Hulten et al. [122] with 60 × 109 mol/yr for the Pacific Ocean and 102 × 109 mol/yr for the global flux. The Kermadec arc would then account for 0.06–9% of the annual dissolved Mn input to the Pacific Ocean, based on the minimum and maximum Kermadec arc estimate, respectively. These calculations show that there is a need for more data to improve estimates of the discharge of metals from both shallow and deep hydrothermal vents into the global ocean.
5. Conclusions
The present work demonstrates the use of Ra isotopes, with a focus on short-lived Ra isotopes for hydrothermal element flux estimates. We adapted a submarine groundwater discharge calculation from coastal environments to the hydrothermal system of Brothers volcano within the southern Kermadec Arc. The calculation used the Ra activity of end-member hydrothermal fluids, the average Ra activity within the plume, and its volume to calculate the discharging flux of hydrothermal fluid and of He isotopes as well as Fe and Mn. Hereby, the Ra-derived SHD calculation could accurately reproduce the concentrations of 3He and 4He present in the hydrothermal plume. The calculated SHD refers to pure hot fluid at focused vents or diffuse discharge at sites with shimmering water. It only indirectly includes surrounding seawater that gets entrained during the buoyant ascent of the plume. This method is completely independent from heat flux measurements or artificial tracer release experiments, as naturally occurring Ra isotopes were used. To obtain correct dissolved element fluxes, it is important to consider the precipitation behavior in hydrothermal systems for each element, when specifying the end-member concentration. The dissolved Fe flux estimate from Brothers NW caldera was found to be comparable to a previously reported flux estimate from the island arc-based Ahyi seamount. The estimated dissolved Mn flux is in the same range as fluxes reported for the Vailulu´u seamount and the vents in the Okinawa Trough. Fluid flux reports for MOR hydrothermal settings span over a large range, which includes the calculated fluxes at Brothers NW Caldera.
Overall, this study introduces a new method to estimate fluid discharge and associated trace element fluxes from a single hydrothermal source by applying a Ra isotope-based (SHD) calculation. With this study presenting the first trace element fluxes from Brothers volcano and the Kermadec Arc, it contributes to the understanding of the global ocean trace element cycles, as these fluxes help to decipher the global importance of hydrothermal trace element discharge. Minimum estimates of hydrothermal dissolved Fe and Mn discharge for the southern and mid Kermadec arc revealed a relative contribution of ~5% to the global Fe discharge and 0.06% to the Pacific Ocean hydrothermal Mn discharge. These flux estimates are subject to significant uncertainty and underline the necessity for a number of other similar studies to reduce the overall uncertainty. In addition, the simultaneous sampling of Ra isotopes and dissolved trace elements can be the basis for interpretations on the physicochemical behavior of dissolved trace elements within the hydrothermal plume (e.g., the split between precipitation versus ligand complexation), which can help to evaluate the economic potential of hydrothermal systems and the adjacent seafloor.
Author Contributions
Conceptualization, R.N., C.K. and B.S.; methodology, R.N., C.K., B.S., M.W., A.T., R.Z., S.S., A.K., P.L., R.M., H.-J.B.; validation, R.N., C.K., B.S., M.W., A.T., R.Z., S.S., A.K., P.L., R.M., H.-J.B.; investigation, R.N., C.K., B.S., M.W., A.T., J.T., R.Z., S.S., A.K., P.L., R.M.; data curation, R.N. and C.K.; writing—original draft preparation, R.N., C.K. and B.S.; writing—review and editing, R.N., C.K., B.S., M.W., A.T., J.T., R.Z., S.S., A.K., P.L., R.M., H.-J.B.; visualization, R.N., C.K. and J.T.; supervision, A.K., B.S. and H.-J.B.; project administration, R.N. and C.K.; funding acquisition, A.K. and H.-J.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Federal Ministry of Education and Research of Germany, grant number 03G0253 and a University of Otago grant as part of the HYDROTHERMADEC project.
Acknowledgments
C. Lehners is highly acknowledged for her help in preparing the cruise, on board work and lab based analysis. Captain L. Mallon and the crew of RV Sonne (SO253) as well as the team of MARUM ROV Quest are thanked for enabling sampling with high professionalism. The National Institute of Water and Atmospheric Research (NIWA), Wellington is acknowledged for provided in-situ pumps for the cruise. As part of the HYDROTHERMADEC project, the Federal Ministry of Education and Research of Germany funded this work [project grant number 03G0253]. Support was also provided from the University of Otago Grant. The IAEA is grateful to the Government of the Principality of Monaco for the support provided to its Environment Laboratories. The working permit for the Kermadec Intraoceanic Arc by the New Zealand authorities is acknowledged. We thank the editor and two anonymous reviewers whose constructive comments helped to strengthen the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Calculated Plume Ellipsoids at Brothers Volcano

Figure A1.
Local bathymetry of Brothers volcano (2-fold exaggeration) with the calculated plume ellipsoid. The two panels mark in orange color the ellipsoid based on excess 223Ra activity above background. The red dots indicate sample locations with Ra activity above background, which were used for the ellipsoid calculation. The black triangle in each panel marks the mean latitude and longitude location of plume samples (depth not representative for display reasons), which was used as ellipsoid center. The direction of view in the first panel is westward, and northeastward in the second panel. Local bathymetry from Koschinsky et al. [53].
Appendix A.2. Dissolved Trace Metal Concentrations in the Plume

Table A1.
Dissolved trace metal concentrations for Fe and Mn of hydrothermal plume samples in the depth range 1350–1700 m at Brothers volcano which were used in Section 4.4 for the calculations. The prefix (•) indicates samples taken outside of the caldera. The overall error of analysis was 5 percent.
Table A1.
Dissolved trace metal concentrations for Fe and Mn of hydrothermal plume samples in the depth range 1350–1700 m at Brothers volcano which were used in Section 4.4 for the calculations. The prefix (•) indicates samples taken outside of the caldera. The overall error of analysis was 5 percent.
| Sample ID | Lat (°N) | Long (°E) | Depth (m) | Mn (nmol/L) | Fe (nmol/L) |
|---|---|---|---|---|---|
| 46_CTD_4 | −34.86228333 | 179.0593333 | 1576 | 101.6 | 49.0 |
| 46_CTD_6 | −34.86938333 | 179.0626833 | 1584 | 30.9 | 12.0 |
| • 46_CTD_14 | −34.89270000 | 179.0736833 | 1530 | 8.9 | 6.4 |
| 49_CTD_3 | −34.86228333 | 179.0593333 | 1576 | 8.8 | 9.6 |
| 49_CTD_5 | −34.86938333 | 179.0626833 | 1584 | 51.1 | 20.6 |
| 49_CTD_17 | −34.89525000 | 179.0550833 | 1557 | 0.7 | 1.7 |
| 53_CTD_2 | −34.86230000 | 179.0593667 | 1604 | 158.0 | 233.4 |
| 53_CTD_4 | −34.86230000 | 179.0593667 | 1549 | 129.6 | 71.3 |
| 53_CTD_10 | −34.86230000 | 179.0593667 | 1478 | 43.1 | 30.7 |
| 53_CTD_12 | −34.86230000 | 179.0593667 | 1400 | 2.1 | 3.8 |
| 54_CTD_6 | −34.86943333 | 179.0626500 | 1560 | 58.8 | 34.6 |
| 54_CTD_10 | −34.86943333 | 179.0626500 | 1440 | 16.6 | 12.7 |
| • 57_CTD_6 | −34.86155000 | 179.0387000 | 1515 | 10.6 | 14.3 |
| 57_CTD_8 | −34.86701667 | 179.0500667 | 1441 | 4.8 | 6.0 |
| 57_CTD_14 | −34.86903333 | 179.0542667 | 1556 | 95.3 | 57.3 |
| 57_CTD_18 | −34.88135000 | 179.0799167 | 1518 | 30.9 | 13.2 |
| • 57_CTD_20 | −34.88788333 | 179.0935333 | 1495 | 5.4 | 6.1 |
| 58_CTD_2 | −34.87895000 | 179.0750500 | 1376 | 7.0 | 6.8 |
| • 60_TMR_1 | −34.82296667 | 179.0411167 | 1700 | 3.0 | 3.6 |
| • 60_TMR_2 | −34.82296667 | 179.0411167 | 1600 | 5.8 | 5.8 |
| • 60_TMR_3 | −34.82296667 | 179.0411167 | 1540 | 11.9 | 3.4 |
| • 60_TMR_4 | −34.82296667 | 179.0411167 | 1440 | 10.3 | 11.4 |
| • 62_CTD_2 | −34.84910000 | 179.0501667 | 1607 | 8.3 | 8.3 |
| 62_CTD_4 | −34.84913333 | 179.0501667 | 1486 | 25.9 | 19.0 |
| 62_CTD_8 | −34.87051667 | 179.0503667 | 1462 | 14.7 | 16.7 |
| • 62_CTD_10 | −34.87416667 | 179.0503833 | 1441 | 15.7 | 14.5 |
| • 62_CTD_14 | −34.87911667 | 179.0504167 | 1524 | 11.9 | 10.9 |
| • 62_CTD_19 | −34.88058333 | 179.0504167 | 1404 | 2.4 | 5.6 |
| • 83_TMR_1 | −34.76591667 | 179.0144833 | 1700 | 3.8 | 14.5 |
| • 83_TMR_2 | −34.76591667 | 179.0144833 | 1600 | 3.4 | 32.0 |
| • 83_TMR_3 | −34.76591667 | 179.0144833 | 1560 | 3.1 | 12.2 |
| • 83_TMR_4 | −34.76591667 | 179.0144833 | 1450 | 5.7 | 16.2 |
Appendix A.3. Calculation Example for Calculated Mean Metal Concentration in the Plume (Section 4.4)
For transparency, we exemplarily document for Fe each calculation step made to obtain the calculated average metal concentration within the plume.
- Calculation of JSHD with average SHD for 223Ra and 224Ra from Equation (3) and average Fe concentration in plume samples (Niskin bottles) (Table 5). See also Section 2.3.1.
References
- Baker, E.T.; Embley, R.W.; Walker, S.L.; Resing, J.A.; Lupton, J.E.; Nakamura, K.-I.; de Ronde, C.E.J.; Massoth, G.J. Hydrothermal activity and volcano distribution along the Mariana arc. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Hekinian, R. Subduction Zones. In Sea Floor Exploration: Scientific Adventures Diving into the Abyss; Springer International Publishing: Cham, Switzerland, 2014; pp. 347–363. [Google Scholar]
- Sigurdsson, H. Introduction. In The Encyclopedia of Volcanoes, 2nd ed.; Sigurdsson, H., Ed.; Academic Press: Amsterdam, The Netherlands, 2015; pp. 1–12. [Google Scholar]
- Staudigel, H.; Hart, S.R.; Koppers, A.A.P.; Constable, C.; Workman, R.; Kurz, M.; Baker, E.T. Hydrothermal venting at Vailulu’u Seamount: The smoking end of the Samoan chain. Geochem. Geophys. Geosyst. 2004, 5. [Google Scholar] [CrossRef]
- German, C.R.; Seyfried, W.E., Jr. 8.7—Hydrothermal Processes. In Treatise on Geochemistry, 2nd ed.; Holland, H.D., Turekian, K.K., Eds.; Elsevier: Oxford, UK, 2014; Volume 8, pp. 191–233. [Google Scholar]
- Herzig, P.M.; Hannington, M.D. Input from the Deep: Hot Vents and Cold Seeps. In Marine Geochemistry; Schulz, H.D., Zabel, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 457–479. [Google Scholar]
- Sander, S.G.; Koschinsky, A. Metal flux from hydrothermal vents increased by organic complexation. Nat. Geosci. 2011, 4, 145–150. [Google Scholar] [CrossRef]
- Fitzsimmons, J.N.; John, S.G.; Marsay, C.M.; Hoffman, C.L.; Nicholas, S.L.; Toner, B.M.; German, C.R.; Sherrell, R.M. Iron persistence in a distal hydrothermal plume supported by dissolved-particulate exchange. Nat. Geosci. 2017, 10, 195–201. [Google Scholar] [CrossRef]
- Resing, J.A.; Sedwick, P.N.; German, C.R.; Jenkins, W.J.; Moffett, J.W.; Sohst, B.M.; Tagliabue, A. Basin-scale transport of hydrothermal dissolved metals across the South Pacific Ocean. Nature 2015, 523, 200–203. [Google Scholar] [CrossRef]
- Tagliabue, A.; Bopp, L.; Dutay, J.-C.; Bowie, A.R.; Chever, F.; Jean-Baptiste, P.; Bucciarelli, E.; Lannuzel, D.; Remenyi, T.; Sarthou, G.; et al. Hydrothermal contribution to the oceanic dissolved iron inventory. Nat. Geosci. 2010, 3, 252–256. [Google Scholar] [CrossRef]
- Saito, M.A.; Noble, A.E.; Tagliabue, A.; Goepfert, T.J.; Lamborg, C.H.; Jenkins, W.J. Slow-spreading submarine ridges in the South Atlantic as a significant oceanic iron source. Nat. Geosci. 2013, 6, 775–779. [Google Scholar] [CrossRef]
- Lupton, J. Hydrothermal helium plumes in the Pacific Ocean. J. Geophys. Res.-Ocean. 1998, 103, 15853–15868. [Google Scholar] [CrossRef]
- Rüth, C.; Well, R.; Roether, W. Primordial He-3 in South Atlantic deep waters from sources on the Mid-Atlantic Ridge. Deep-Sea Res. Part I-Oceanogr. Res. Pap. 2000, 47, 1059–1075. [Google Scholar] [CrossRef]
- de Ronde, C.E.J.; Massoth, G.J.; Baker, E.T.; Lupton, J.E. Submarine Hydrothermal Venting Related to Volcanic Arcs Volcanic, Geothermal, and Ore-Forming Fluids: Rulers and Witnesses of Processes within the Earth; Simmons, S.F., Graham, I., Eds.; Society of Economic Geologists: Littleton, CO, USA, 2005; Volume 10. [Google Scholar]
- de Ronde, C.E.J.; Massoth, G.J.; Butterfield, D.A.; Christenson, B.W.; Ishibashi, J.; Ditchburn, R.G.; Hannington, M.D.; Brathwaite, R.L.; Lupton, J.E.; Kamenetsky, V.S.; et al. Submarine hydrothermal activity and gold-rich mineralization at Brothers Volcano, Kermadec Arc, New Zealand. Miner. Depos. 2011, 46, 541–584. [Google Scholar] [CrossRef]
- Hawkes, J.A.; Connelly, D.P.; Rijkenberg, M.J.A.; Achterberg, E.P. The importance of shallow hydrothermal island arc systems in ocean biogeochemistry. Geophys. Res. Lett. 2014, 41, 942–947. [Google Scholar] [CrossRef]
- Resing, J.A.; Lebon, G.; Baker, E.T.; Lupton, J.E.; Embley, R.W.; Massoth, G.J.; Chadwick, W.W.; de Ronde, C.E.J. Venting of Acid-Sulfate Fluids in a High-Sulfidation Setting at NW Rota-1 Submarine Volcano on the Mariana Arc. Econ. Geol. 2007, 102, 1047–1061. [Google Scholar] [CrossRef]
- Buck, N.J.; Resing, J.A.; Baker, E.T.; Lupton, J.E. Chemical Fluxes From a Recently Erupted Shallow Submarine Volcano on the Mariana Arc. Geochem. Geophys. Geosyst. 2018, 19, 1660–1673. [Google Scholar] [CrossRef]
- Achterberg, E.P.; Moore, C.M.; Henson, S.A.; Steigenberger, S.; Stohl, A.; Eckhardt, S.; Avendano, L.C.; Cassidy, M.; Hembury, D.; Klar, J.K.; et al. Natural iron fertilization by the Eyjafjallajökull volcanic eruption. Geophys. Res. Lett. 2013, 40, 921–926. [Google Scholar] [CrossRef]
- Baker, E.T. Exploring the ocean for hydrothermal venting: New techniques, new discoveries, new insights. Ore Geol. Rev. 2017, 86, 55–69. [Google Scholar] [CrossRef]
- Ardyna, M.; Lacour, L.; Sergi, S.; d’Ovidio, F.; Sallee, J.B.; Rembauville, M.; Blain, S.; Tagliabue, A.; Schlitzer, R.; Jeandel, C.; et al. Hydrothermal vents trigger massive phytoplankton blooms in the Southern Ocean. Nat. Commun. 2019, 10, 2451. [Google Scholar] [CrossRef]
- Elderfield, H.; Schultz, A. Mid-Ocean Ridge Hydrothermal Fluxes and the Chemical Composition of the Ocean. Annu. Rev. Earth Planet. Sci. 1996, 24, 191–224. [Google Scholar] [CrossRef]
- Murton, B.J.; Redbourn, L.J.; German, C.R.; Baker, E.T. Sources and fluxes of hydrothermal heat, chemicals and biology within a segment of the Mid-Atlantic Ridge. Earth Planet. Sci. Lett. 1999, 171, 301–317. [Google Scholar] [CrossRef]
- Hart, S.R.; Staudigel, H.; Workman, R.; Koppers, A.A.P.; Girard, A.P. A fluorescein tracer release experiment in the hydrothermally active crater of Vailulu’u volcano, Samoa. J. Geophys. Res.-Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Jenkins, W.J.; Edmond, J.M.; Corliss, J.B. Excess He-3 and He-4 in Galapagos Submarine Hydrothermal Waters. Nature 1978, 272, 156–158. [Google Scholar] [CrossRef]
- Nielsen, S.G.; Rehkämper, M.; Teagle, D.A.H.; Butterfield, D.A.; Alt, J.C.; Halliday, A.N. Hydrothermal fluid fluxes calculated from the isotopic mass balance of thallium in the ocean crust. Earth Planet. Sci. Lett. 2006, 251, 120–133. [Google Scholar] [CrossRef]
- Wheat, C.G.; Mottl, M.J. Composition of pore and spring waters from Baby Bare: Global implications of geochemical fluxes from a ridge flank hydrothermal system. Geochim. Cosmochim. Acta 2000, 64, 629–642. [Google Scholar] [CrossRef]
- Thurnherr, A.M.; Richards, K.J. Hydrography and high-temperature heat flux of the Rainbow hydrothermal site (36 degrees 14′N, Mid-Atlantic Ridge). J. Geophys. Res.-Ocean. 2001, 106, 9411–9426. [Google Scholar] [CrossRef]
- German, C.R.; Thurnherr, A.M.; Knoery, J.; Charlou, J.L.; Jean-Baptiste, P.; Edmonds, H.N. Heat, volume and chemical fluxes from submarine venting: A synthesis of results from the Rainbow hydrothermal field, 36 degrees N MAR. Deep-Sea Res. Part I—Oceanogr. Res. Pap. 2010, 57, 518–527. [Google Scholar] [CrossRef]
- Schmale, O.; Walter, M.; Schneider von Deimling, J.; Sültenfuß, J.; Walker, S.; Rehder, G.; Keir, R. Fluid and gas fluxes from the Logatchev hydrothermal vent area. Geochem. Geophys. Geosyst. 2012, 13. [Google Scholar] [CrossRef]
- Kadko, D.; Butterfield, D.A. The relationship of hydrothermal fluid composition and crustal residence time to maturity of vent fields on the Juan de Fuca Ridge. Geochim. Cosmochim. Acta 1998, 62, 1521–1533. [Google Scholar] [CrossRef]
- Kadko, D.; Gronvold, K.; Butterfield, D. Application of radium isotopes to determine crustal residence times of hydrothermal fluids from two sites on the Reykjanes Peninsula, Iceland. Geochim. Cosmochim. Acta 2007, 71, 6019–6029. [Google Scholar] [CrossRef]
- Kadko, D.; Moore, W. Radiochemical Constraints on the crustal residence time of submarine hydrothermal fluids—Endeavor ridge. Geochim. Cosmochim. Acta 1988, 52, 659–668. [Google Scholar] [CrossRef]
- Elsinger, R.J.; Moore, W.S. Ra-224,Ra-228, and Ra-226 in Winyah Bay and Delaware Bay. Earth Planet. Sci. Lett. 1983, 64, 430–436. [Google Scholar] [CrossRef]
- Moore, W.S.; Krest, J. Distribution of Ra-223 and Ra-224 in the plumes of the Mississippi and Atchafalaya Rivers and the Gulf of Mexico. Mar. Chem. 2004, 86, 105–119. [Google Scholar] [CrossRef]
- Webster, I.T.; Hancock, G.J.; Murray, A.S. Use of Radium Isotopes to Examine Pore-Water Exchange in an Estuary. Limnol. Oceanogr. 1994, 39, 1917–1927. [Google Scholar] [CrossRef]
- Yang, H.-S.; Hwang, D.-W.; Kim, G. Factors controlling excess radium in the Nakdong River estuary, Korea: Submarine groundwater discharge versus desorption from riverine particles. Mar. Chem. 2002, 78, 1–8. [Google Scholar] [CrossRef]
- Kipp, L.E.; Sanial, V.; Henderson, P.B.; van Beek, P.; Reyss, J.-L.; Hammond, D.E.; Moore, W.S.; Charette, M.A. Radium isotopes as tracers of hydrothermal inputs and neutrally buoyant plume dynamics in the deep ocean. Mar. Chem. 2018, 201, 51–65. [Google Scholar] [CrossRef]
- Neuholz, R.; Schnetger, B.; Kleint, C.; Koschinsky, A.; Lettmann, K.; Sander, S.; Türke, A.; Walter, M.; Zitoun, R.; Brumsack, H.-J. Near-field hydrothermal plume dynamics at Brothers Volcano (Kermadec Arc): A short-lived radium isotope study. Chem. Geol. 2020, 533, 119379. [Google Scholar] [CrossRef]
- Cho, H.M.; Kim, G.; Kwon, E.Y.; Moosdorf, N.; Garcia-Orellana, J.; Santos, I.R. Radium tracing nutrient inputs through submarine groundwater discharge in the global ocean. Sci. Rep. 2018, 8, 2439. [Google Scholar] [CrossRef] [PubMed]
- Moore, W.S. Sources and fluxes of submarine groundwater discharge delineated by radium isotopes. Biogeochemistry 2003, 66, 75–93. [Google Scholar] [CrossRef]
- Taniguchi, M.; Dulai, H.; Burnett, K.M.; Santos, I.R.; Sugimoto, R.; Stieglitz, T.; Kim, G.; Moosdorf, N.; Burnett, W.C. Submarine Groundwater Discharge: Updates on Its Measurement Techniques, Geophysical Drivers, Magnitudes, and Effects. Front. Environ. Sci. 2019, 7. [Google Scholar] [CrossRef]
- Lupton, J.E.; Weiss, R.F.; Craig, H. Mantle Helium in Hydrothermal Plumes in the Galapagos Rift. Nature 1977, 267, 603–604. [Google Scholar] [CrossRef]
- Moore, W.S.; Ussler, W.; Paull, C.K. Short-lived radium isotopes in the Hawaiian margin: Evidence for large fluid fluxes through the Puna Ridge. Mar. Chem. 2008, 109, 421–430. [Google Scholar] [CrossRef]
- Kipp, L.E.; Charette, M.A.; Hammond, D.E.; Moore, W.S. Hydrothermal vents: A previously unrecognized source of actinium-227 to the deep ocean. Mar. Chem. 2015, 177, 583–590. [Google Scholar] [CrossRef]
- Charette, M.A.; Morris, P.J.; Henderson, P.B.; Moore, W.S. Radium isotope distributions during the US GEOTRACES North Atlantic cruises. Mar. Chem. 2015, 177, 184–195. [Google Scholar] [CrossRef]
- Koschinsky, A. RV Sonne 253 Cruise Report/Fahrtbericht, Nouméa (New Caledonia) 22.12.2016—Auckland (New Zealand) 21.01.2017, SO253—HYDROTHERMADEC; Jacobs University Bremen: Bremen, Germany, 2017; p. 183. [Google Scholar]
- De Ronde, C.E.J.; Humphris, S.E.; Höfig, T.W. Expedition 376 Scietific Prospectus: Brothers Arc Flux; International Ocean Discovery Program: Bremen, Germany, 2017. [Google Scholar] [CrossRef]
- De Ronde, C.E.J.; Humphris, S.E.; Höfig, T.W.; The Expedition 376 Scientists. Expedition 376 Preliminary Report: Brothers Arc Flux; International Ocean Discovery Program: Bremen, Germany, 2019. [Google Scholar]
- Baker, E.T.; Walker, S.L.; Embley, R.W.; de Ronde, C.E.J. High-Resolution Hydrothermal Mapping of Brothers Caldera, Kermadec Arc. Econ. Geol. 2012, 107, 1583–1593. [Google Scholar] [CrossRef]
- de Ronde, C.E.J.; Hannington, M.D.; Stoffers, P.; Wright, I.C.; Ditchburn, R.G.; Reyes, A.G.; Baker, E.T.; Massoth, G.J.; Lupton, J.E.; Walker, S.L.; et al. Evolution of a Submarine Magmatic-Hydrothermal System: Brothers Volcano, Southern Kermadec Arc, New Zealand. Econ. Geol. 2005, 100, 1097–1133. [Google Scholar] [CrossRef]
- Mitchell, J.; Mackay, K.; Neil, H.; Mackay, E.; Pallentin, A.; Notman, P. Undersea New Zealand, 1: 5,000,000; NIWA chart, miscellaneous series; NIWA: Auckland, New Zealand, 2012. [Google Scholar]
- Koschinsky, A.; Thal, J.; Wölfl, A.-C. Raw Multibeam EM122 Data: Transits of SONNE Cruise SO253 (South Pacific); PANGAEA: Bremen, Germany, 2018. [Google Scholar] [CrossRef]
- Von Damm, K.L.; Edmond, J.M.; Grant, B.; Measures, C.I.; Walden, B.; Weiss, R.F. Chemistry of submarine hydrothermal solutions at 21 °N, East Pacific Rise. Geochim. Cosmochim. Acta 1985, 49, 2197–2220. [Google Scholar] [CrossRef]
- Garbe-Schönberg, D.; Koschinsky, A.; Ratmeyer, V.; Westernströer, U.; Jähmlich, H. KIPS -A new Multiport Valve-based all-Teflon Fluid Sampling System for ROVs. In EGU Meeting; Geophysical Research Abstracts: Vienna, Austria, 2006; Volume 8. [Google Scholar]
- Petrick, G.; Schulz-Bull, D.E.; Martens, V.; Scholz, K.; Duinker, J.C. An in-situ filtration/extraction system for the recovery of trace organics in solution and on particles tested in deep ocean water. Mar. Chem. 1996, 54, 97–105. [Google Scholar] [CrossRef]
- Moore, W.S. Sampling Ra-228 in Deep Ocean. Deep-Sea Res. 1976, 23, 647–651. [Google Scholar] [CrossRef]
- Henderson, P.B.; Morris, P.J.; Moore, W.S.; Charette, M.A. Methodological advances for measuring low-level radium isotopes in seawater. J. Radioanal Nucl. Chem. 2013, 296, 357–362. [Google Scholar] [CrossRef]
- Giffin, C.; Kaufman, A.; Broecker, W. Delayed coincidence counter for the assay of actinon and thoron. J. Geophys. Res. 1963, 68, 1749–1757. [Google Scholar] [CrossRef]
- Moore, W.S.; Arnold, R. Measurement of Ra-223 and Ra-224 in coastal waters using a delayed coincidence counter. J. Geophys. Res.-Ocean. 1996, 101, 1321–1329. [Google Scholar] [CrossRef]
- Garcia-Solsona, E.; Garcia-Orellana, J.; Masqué, P.; Dulaiova, H. Uncertainties associated with Ra-223 and Ra-224 measurements in water via a Delayed Coincidence Counter (RaDeCC). Mar. Chem. 2008, 109, 198–219. [Google Scholar] [CrossRef]
- Moore, W.S. Fifteen years experience in measuring Ra-224 and Ra-223 by delayed-coincidence counting. Mar. Chem. 2008, 109, 188–197. [Google Scholar] [CrossRef]
- Scholten, J.C.; Pham, M.K.; Blinova, O.; Charette, M.A.; Dulaiova, H.; Eriksson, M. Preparation of Mn-fiber standards for the efficiency calibration of the delayed coincidence counting system (RaDeCC). Mar. Chem. 2010, 121, 206–214. [Google Scholar] [CrossRef]
- Moore, W.S.; Cai, P. Calibration of RaDeCC systems for 223Ra measurements. Mar. Chem. 2013, 156, 130–137. [Google Scholar] [CrossRef]
- JCGM. International Vocabulary of Metrology—Basic and General Concepts and Associated Terms (VIM). Joint Committee for Guides in Metrology. 2008. Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_200_2012.pdf (accessed on 28 August 2020).
- Menditto, A.; Patriarca, M.; Magnusson, B. Understanding the meaning of accuracy, trueness and precision. Accredit. Qual. Assur. 2007, 12, 45–47. [Google Scholar] [CrossRef]
- Staats, G. The Semantic and Technical Concept of True Values and of Trueness of Values in Inorganic Bulk and Trace Analysis. Fresenius J. Anal. Chem. 1995, 352, 413–419. [Google Scholar] [CrossRef]
- GEOTRACES Standards and Reference Materials. Available online: http://www.geotraces.org/sic/intercalibrate-a-lab/standards-and-reference-materials (accessed on 28 August 2020).
- Sültenfuss, J.; Roether, W.; Rhein, M. The Bremen mass spectrometric facility for the measurement of helium isotopes, neon, and tritium in water. Isot. Environ. Health Stud. 2009, 45, 83–95. [Google Scholar] [CrossRef] [PubMed]
- Moore, W.S. Ages of continental shelf waters determined from Ra-223 and Ra-224. J. Geophys. Res. Ocean 2000, 105, 22117–22122. [Google Scholar] [CrossRef]
- Null, K.A.; Reide Corbett, D.; Crenshaw, J.; Peterson, R.N.; Peterson, L.E.; Lyons, W.B. Groundwater discharge to the western Antarctic coastal ocean. Polar Res. 2019, 38, 11. [Google Scholar] [CrossRef]
- Dissanayake, A.L.; Yapa, P.D.; Nakata, K. Modelling of hydrothermal vent plumes to assess the mineral particle distribution. J. Hydraul. Res. 2014, 52, 49–66. [Google Scholar] [CrossRef]
- Tao, Y.; Rosswog, S.; Brüggen, M. A simulation modeling approach to hydrothermal plumes and its comparison to analytical models. Ocean Model. 2013, 61, 68–80. [Google Scholar] [CrossRef]
- Tao, C.; Chen, S.; Baker, E.T.; Li, H.; Liang, J.; Liao, S.; Chen, Y.J.; Deng, X.; Zhang, G.; Gu, C.; et al. Hydrothermal plume mapping as a prospecting tool for seafloor sulfide deposits: A case study at the Zouyu-1 and Zouyu-2 hydrothermal fields in the southern Mid-Atlantic Ridge. Mar. Geophys. Res. 2017, 38, 3–16. [Google Scholar] [CrossRef]
- Lavelle, J.W.; Massoth, G.J.; Baker, E.T.; de Ronde, C.E.J. Ocean current and temperature time series at Brothers volcano. J. Geophys. Res. Ocean 2008, 113. [Google Scholar] [CrossRef]
- Adler, D.; Murdoch, D.; Nenadic, O.; Urbanek, S.; Chen, M.; Gebhardt, A.; Bolker, B.; Csardi, G.; Strzelecki, A.; Senger, A.; et al. rgl: 3D Visualization Using OpenGL, 0.99.16. CRAN R-Project. 2018. Available online: https://CRAN.R-project.org/package=rgl (accessed on 28 August 2020).
- R Foundation for Statistical Computing. R: A Language and Environment for Statistical Computing, 3.6.1; R Foundation for Statistical Computing: Vienna, Australia, 2019. [Google Scholar]
- RStudio. RStudio: Integrated Development Environment for R, 1.2.5001; RStudio: Boston, MA, USA, 2019. [Google Scholar]
- Angel, B.M.; Apte, S.C.; Batley, G.E.; Raven, M.D. Lead solubility in seawater: An experimental study. Environ. Chem. 2016, 13, 489–495. [Google Scholar] [CrossRef]
- Fergusson, J.E. The heavy elements in water and sediments. In The Heavy Elements: Chemistry, Environmental Impact and Health Effects, 1st ed.; Fergusson, J.E., Ed.; Pergamon Press: Oxford, UK, 1990. [Google Scholar]
- Ozima, M.; Podosek, F.A. Chapter 4—Water. In Nobel Gas Geochemistry; Cambridge University Press: Cambridge, UK, 2001; Volume 2, pp. 98–122. [Google Scholar]
- Kleint, C.; Bach, W.; Diehl, A.; Fröhberg, N.; Garbe-Schönberg, D.; Hartmann, J.F.; de Ronde, C.E.J.; Sander, S.G.; Strauss, H.; Stucker, V.K.; et al. Geochemical characterization of highly diverse hydrothermal fluids from volcanic vent systems of the Kermadec intraoceanic arc. Chem. Geol. 2019, 528, 119289. [Google Scholar] [CrossRef]
- Sano, Y.; Fischer, T.P. The Analysis and Interpretation of Noble Gases in Modern Hydrothermal Systems. In The Noble Gases as Geochemical Tracers; Burnard, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 249–317. [Google Scholar]
- Shimizu, A.; Sumino, H.; Nagao, K.; Notsu, K.; Mitropoulos, P. Variation in noble gas isotopic composition of gas samples from the Aegean arc, Greece. J. Volcanol. Geotherm. Res. 2005, 140, 321–339. [Google Scholar] [CrossRef]
- Gerringa, L.J.A.; Slagter, H.A.; Bown, J.; van Haren, H.; Laan, P.; de Baar, H.J.W.; Rijkenberg, M.J.A. Dissolved Fe and Fe-binding organic ligands in the Mediterranean Sea—GEOTRACES G04. Mar. Chem. 2017, 194, 100–113. [Google Scholar] [CrossRef]
- Kleint, C.; Hawkes, J.A.; Sander, S.G.; Koschinsky, A. Voltammetric Investigation of Hydrothermal Iron Speciation. Front. Mar. Sci. 2016, 3. [Google Scholar] [CrossRef]
- Feely, R.A.; Trefry, J.H.; Massoth, G.J.; Metz, S. A Comparison of the Scavenging of Phosphorus and Arsenic from Seawater by Hydrothermal Iron Oxyhydroxides in the Atlantic and Pacific Oceans. Deep-Sea Res. Part A 1991, 38, 617–623. [Google Scholar] [CrossRef]
- Rudnicki, M.D.; Elderfield, H. A Chemical-Model of the Buoyant and Neutrally Buoyant Plume above the Tag Vent Field, 26 Degrees-N, Mid-Atlantic Ridge. Geochim. Cosmochim. Acta 1993, 57, 2939–2957. [Google Scholar] [CrossRef]
- Millero, F.; Woosley, R.; DiTrolio, B.; Waters, J. Effect of Ocean Acidification on the Speciation of Metals in Seawater. Oceanography 2009, 22, 72–85. [Google Scholar] [CrossRef]
- Schlitzer, R.; Anderson, R.F.; Dodas, E.M.; Lohan, M.; Geibere, W.; Tagliabue, A.; Bowie, A.; Jeandel, C.; Maldonado, M.T.; Landing, W.M.; et al. The GEOTRACES Intermediate Data Product 2017. Chem. Geol. 2018, 493, 210–223. [Google Scholar] [CrossRef]
- Le Roy, E.; Sanial, V.; Lacan, F.; van Beek, P.; Souhaut, M.; Charette, M.A.; Henderson, P.B. Insight into the measurement of dissolved 227-Ac in seawater using radium delayed coincidence counter. Mar. Chem. 2019, 212, 64–73. [Google Scholar] [CrossRef]
- Reid, D.F.; Key, R.M.; Schink, D.R. Radium, thorium, and actinium extraction from seawater using an improved manganese-oxide-coated fiber. Earth Planet. Sci. Lett. 1979, 43, 223–226. [Google Scholar] [CrossRef]
- German, C.R.; Klinkhammer, G.P.; Edmond, J.M.; Mitra, A.; Elderfield, H. Hydrothermal scavenging of rare-earth elements in the ocean. Nature 1990, 345, 516–518. [Google Scholar] [CrossRef]
- German, C.R.; Fleer, A.P.; Bacon, M.P.; Edmond, J.M. Hydrothermal scavenging at the Mid-Atlantic Ridge: Radionuclide distributions. Earth Planet. Sci. Lett. 1991, 105, 170–181. [Google Scholar] [CrossRef]
- Sherrell, R.M.; Field, M.P.; Ravizza, G. Uptake and fractionation of rare earth elements on hydrothermal plume particles at 9 degrees 45′N, East Pacific Rise. Geochim. Cosmochim. Acta 1999, 63, 1709–1722. [Google Scholar] [CrossRef]
- Edmonds, H.N.; German, C.R. Particle geochemistry in the Rainbow hydrothermal plume, Mid-Atlantic Ridge. Geochim. Cosmochim. Acta 2004, 68, 759–772. [Google Scholar] [CrossRef]
- Lam, P.J.; Ohnemus, D.C.; Auro, M.E. Size-fractionated major particle composition and concentrations from the US GEOTRACES North Atlantic Zonal Transect. Deep-Sea Res. Part II-Top. Stud. Oceanogr. 2015, 116, 303–320. [Google Scholar] [CrossRef]
- Baker, E.T.; Feely, R.A.; De Ronde, C.E.J.; Massoth, G.J.; Wright, I.C. Submarine hydrothermal venting on the southern Kermadec volcanic arc front (offshore New Zealand): Location and extent of particle plume signatures. Geol. Soc. Lond. Spec. Publ. 2003, 219, 141–161. [Google Scholar] [CrossRef]
- Di Iorio, D.; Lavelle, J.W.; Rona, P.; Bemis, K.; Xu, G.; Germanovich, L.; Lowell, R.; Genc, G. Measurements and Models of Heat Flux and Plumes from Hydrothermal Discharges Near the Deep Seafloor. Oceanography 2012, 25, 168–179. [Google Scholar] [CrossRef]
- Wright, I.C. In situ modification of modern submarine hyaloclastic/pyroclastic deposits by oceanic currents: An example from the Southern Kermadec arc (SW Pacific). Mar. Geol. 2001, 172, 287–307. [Google Scholar] [CrossRef]
- Haase, K.M.; Stroncik, N.; Garbe-Schönberg, D.; Stoffers, P. Formation of island arc dacite magmas by extreme crystal fractionation: An example from Brothers Seamount, Kermadec island arc (SW Pacific). J. Volcanol. Geotherm. Res. 2006, 152, 316–330. [Google Scholar] [CrossRef]
- Haase, K.M.; Worthington, T.J.; Stoffers, P.; Garbe-Schönberg, D.; Wright, I. Mantle dynamics, element recycling, and magma genesis beneath the Kermadec Arc-Havre Trough. Geochem. Geophys. Geosyst. 2002, 3, 1–22. [Google Scholar] [CrossRef]
- Timm, C.; de Ronde, C.E.J.; Leybourne, M.I.; Layton-Matthews, D.; Graham, I.J. Sources of Chalcophile and Siderophile Elements in Kermadec Arc Lavas. Econ. Geol. 2012, 107, 1527–1538. [Google Scholar] [CrossRef]
- de Ronde, C.E.J.; Baker, E.T.; Massoth, G.J.; Lupton, J.E.; Wright, I.C.; Sparks, R.J.; Bannister, S.C.; Reyners, M.E.; Walker, S.L.; Greene, R.R.; et al. Submarine hydrothermal activity along the mid-Kermadec Arc, New Zealand: Large-scale effects on venting. Geochem. Geophys. Geosyst. 2007, 8. [Google Scholar] [CrossRef]
- Findlay, A.J.; Gartman, A.; Shaw, T.J.; Luther, G.W. Trace metal concentration and partitioning in the first 1.5 m of hydrothermal vent plumes along the Mid-Atlantic Ridge: TAG, Snakepit, and Rainbow. Chem. Geol. 2015, 412, 117–131. [Google Scholar] [CrossRef]
- Feely, R.A.; Baker, E.T.; Marumo, K.; Urabe, T.; Ishibashi, J.; Gendron, J.; Lebon, G.T.; Okamura, K. Hydrothermal plume particles and dissolved phosphate over the superfast-spreading southern East Pacific Rise. Geochim. Cosmochim. Acta 1996, 60, 2297–2323. [Google Scholar] [CrossRef]
- Lough, A.J.M.; Homoky, W.B.; Connelly, D.P.; Comer-Warner, S.A.; Nakamura, K.; Abyaneh, M.K.; Kaulich, B.; Mills, R.A. Soluble iron conservation and colloidal iron dynamics in a hydrothermal plume. Chem. Geol. 2019, 511, 225–237. [Google Scholar] [CrossRef]
- Boyle, E.A.; Bergquist, B.A.; Kayser, R.A.; Mahowald, N. Iron, manganese, and lead at Hawaii Ocean Time-series station ALOHA: Temporal variability and an intermediate water hydrothermal plume. Geochim. Cosmochim. Acta 2005, 69, 933–952. [Google Scholar] [CrossRef]
- Massoth, G.J.; Baker, E.T.; Lupton, J.E.; Feely, R.A.; Butterfield, D.A.; Von Damm, K.L.; Roe, K.K.; Lebon, G.T. Temporal and Spatial Variability of Hydrothermal Manganese and Iron at Cleft Segment, Juan-De-Fuca Ridge. J. Geophys. Res. Solid Earth 1994, 99, 4905–4923. [Google Scholar] [CrossRef]
- Morgan, J.J. Kinetics of reaction between O-2 and Mn(II) species in aqueous solutions. Geochim. Cosmochim. Acta 2005, 69, 35–48. [Google Scholar] [CrossRef]
- Cowen, J.P.; Bertram, M.A.; Baker, E.T.; Feely, R.A.; Massoth, G.J.; Summit, M. Geomicrobial transformation of manganese in Gorda Ridge event plumes. Deep Sea Res. Part II 1998, 45, 2713–2737. [Google Scholar] [CrossRef]
- Cowen, J.P.; Massoth, G.J.; Feely, R.A. Scavenging Rates of Dissolved Manganese in a Hydrothermal Vent Plume. Deep-Sea Res. Part A-Oceanogr. Res. Pap. 1990, 37, 1619–1637. [Google Scholar] [CrossRef]
- Mandernack, K.W.; Tebo, B.M. Manganese Scavenging and Oxidation at Hydrothermal Vents and in Vent Plumes. Geochim. Cosmochim. Acta 1993, 57, 3907–3923. [Google Scholar] [CrossRef]
- Li, M.; Toner, B.M.; Baker, B.J.; Breier, J.A.; Sheik, C.S.; Dick, G.J. Microbial iron uptake as a mechanism for dispersing iron from deep-sea hydrothermal vents. Nat. Commun. 2014, 5, 3192. [Google Scholar] [CrossRef] [PubMed]
- Böhnke, S.; Sass, K.; Gonnella, G.; Diehl, A.; Kleint, C.; Bach, W.; Zitoun, R.; Koschinsky, A.; Indenbirken, D.; Sander, S.G.; et al. Parameters Governing the Community Structure and Element Turnover in Kermadec Volcanic Ash and Hydrothermal Fluids as Monitored by Inorganic Electron Donor Consumption, Autotrophic CO2 Fixation and 16S Tags of the Transcriptome in Incubation Experiments. Front. Microbiol. 2019, 10. [Google Scholar] [CrossRef] [PubMed]
- Campbell, A.C.; Gieskes, J.M.; Lupton, J.E.; Lonsdale, P.F. Manganese geochemistry in the Guaymas Basin, Gulf of California. Geochim. Cosmochim. Acta 1988, 52, 345–357. [Google Scholar] [CrossRef]
- Rosenberg, N.D.; Lupton, J.E.; Kadko, D.; Collier, R.; Lilley, M.D.; Pak, H. Estimation of heat and chemical fluxes from a seafloor hydrothermal vent field using radon measurements. Nature 1988, 334, 604–607. [Google Scholar] [CrossRef]
- Zeng, Z.; Wang, X.; Chen, C.-T.A.; Qi, H. Understanding the Compositional Variability of the Major Components of Hydrothermal Plumes in the Okinawa Trough. Geofluids 2018, 2018, 1536352. [Google Scholar] [CrossRef]
- Ozima, M.; Podosek, F.A. Chapter 6—Mantle. In Nobel Gas Geochemistry; Cambridge University Press: Cambridge, UK, 2001; Volume 2, pp. 160–216. [Google Scholar]
- de Ronde, C.E.J.; Baker, E.T.; Massoth, G.J.; Lupton, J.E.; Wright, I.C.; Feely, R.A.; Greene, R.R. Intra-oceanic subduction-related hydrothermal venting, Kermadec volcanic arc, New Zealand. Earth Planet. Sci. Lett. 2001, 193, 359–369. [Google Scholar] [CrossRef]
- Tagliabue, A.; Resing, J. Impact of hydrothermalism on the ocean iron cycle. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2016, 374. [Google Scholar] [CrossRef] [PubMed]
- Van Hulten, M.; Middag, R.; Dutay, J.-C.; de Baar, H.; Roy-Barman, M.; Gehlen, M.; Tagliabue, A.; Sterl, A. Manganese in the west Atlantic Ocean in the context of the first global ocean circulation model of manganese. Biogeosciences 2017, 14, 1123–1152. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).