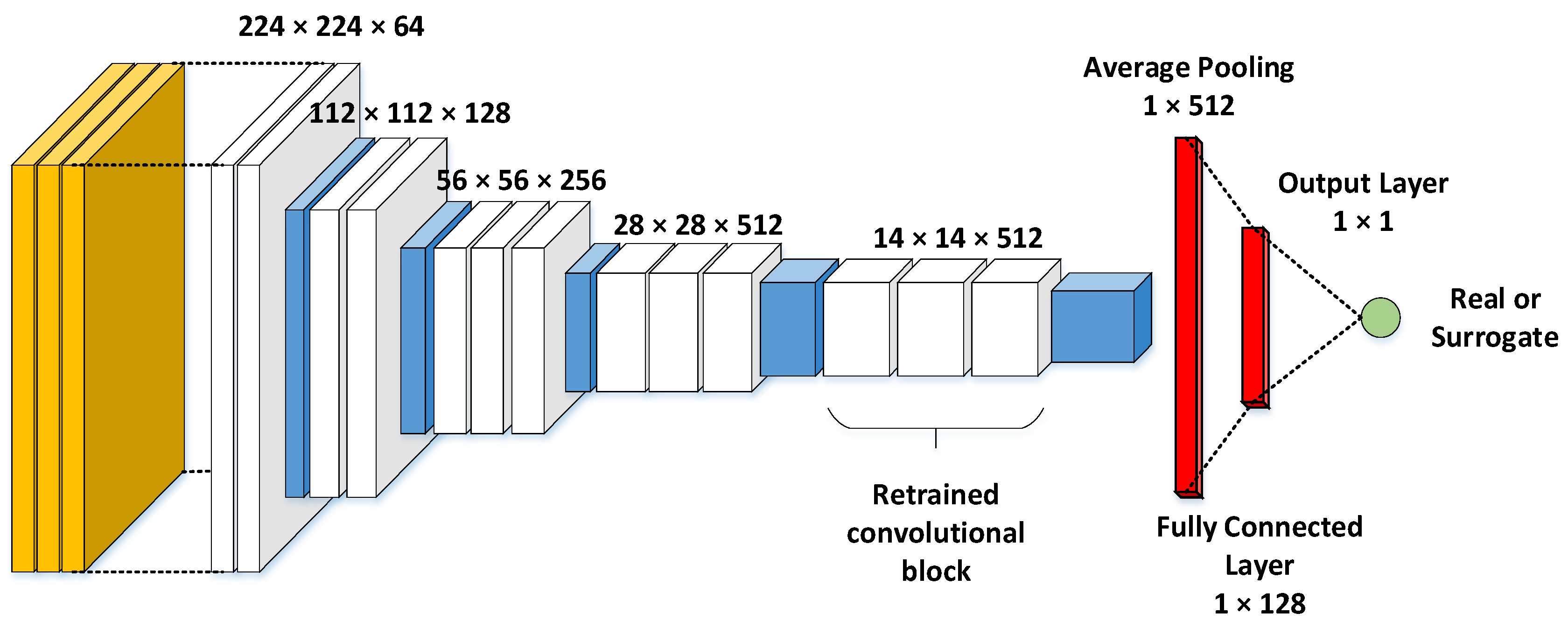
Figure 1.
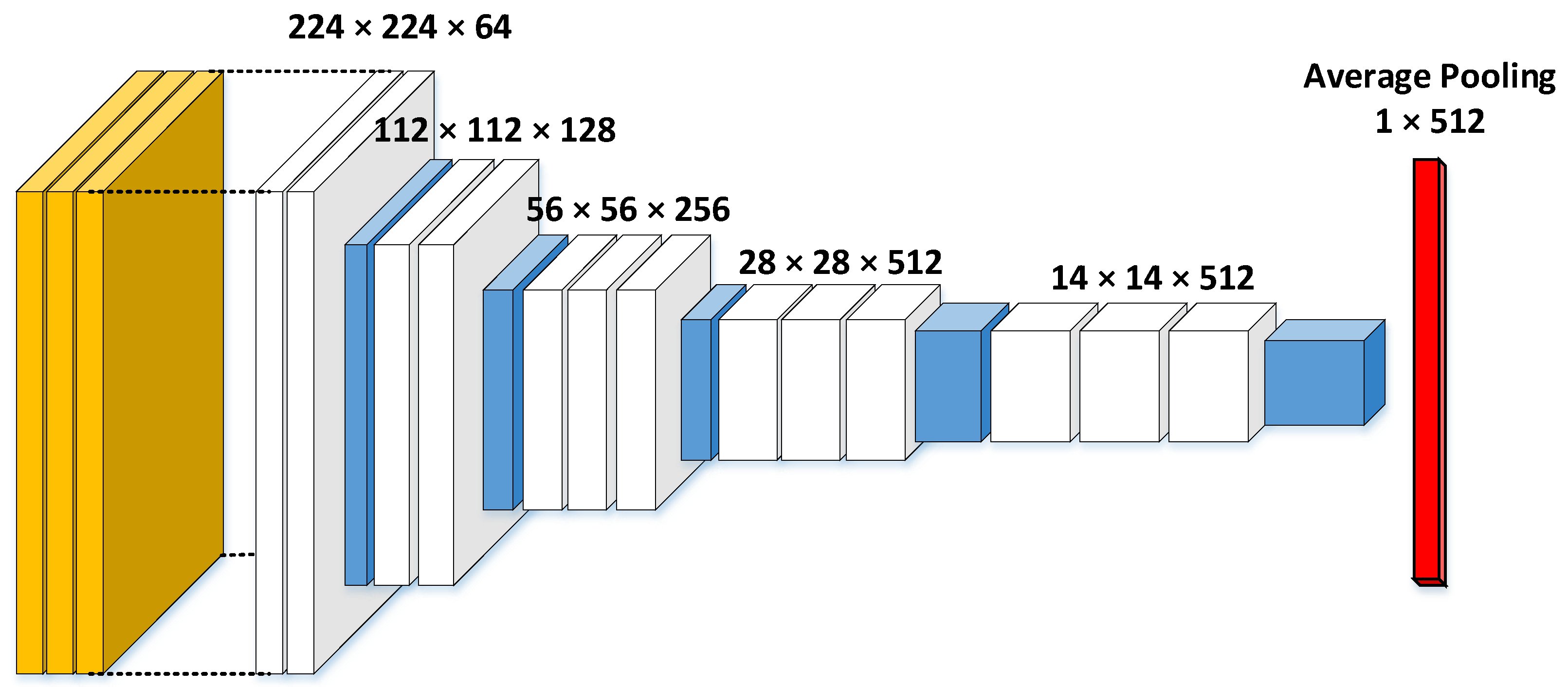
VGG19 network architecture adapted for transfer learning. Layers include convolutional (white), pooling (blue) and an average pooling layer (red). Classification layers were replaced with an average pooling layer to output a flat vector of extracted features.
Figure 1.
VGG19 network architecture adapted for transfer learning. Layers include convolutional (white), pooling (blue) and an average pooling layer (red). Classification layers were replaced with an average pooling layer to output a flat vector of extracted features.
Figure 2.
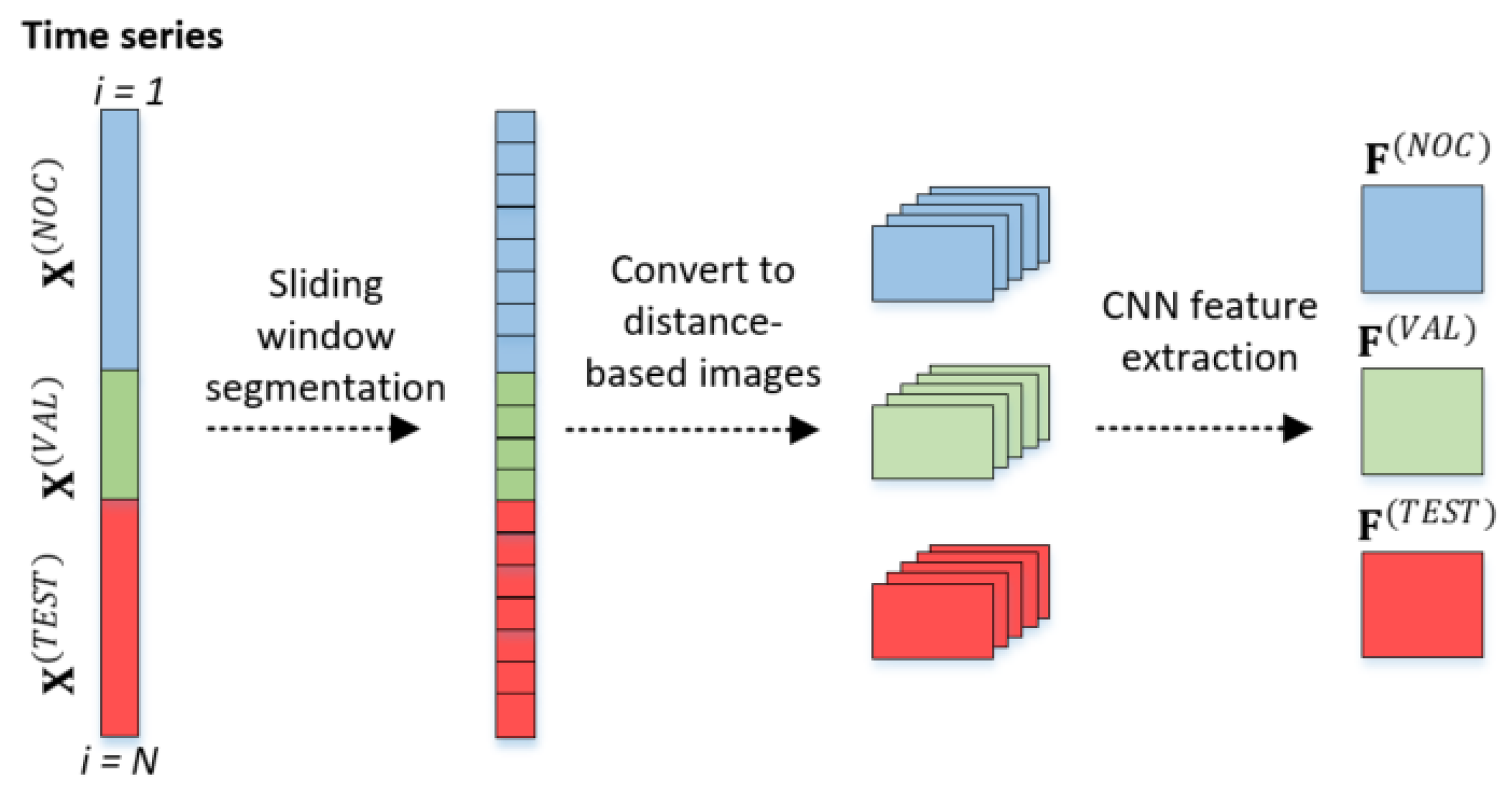
General approach to feature extraction from time series data with CNNs, showing normal operating condition (NOC) and validation (VAL) data used for training, as well as independent test data (TEST) not used in the construction of the model.
Figure 2.
General approach to feature extraction from time series data with CNNs, showing normal operating condition (NOC) and validation (VAL) data used for training, as well as independent test data (TEST) not used in the construction of the model.
Figure 3.
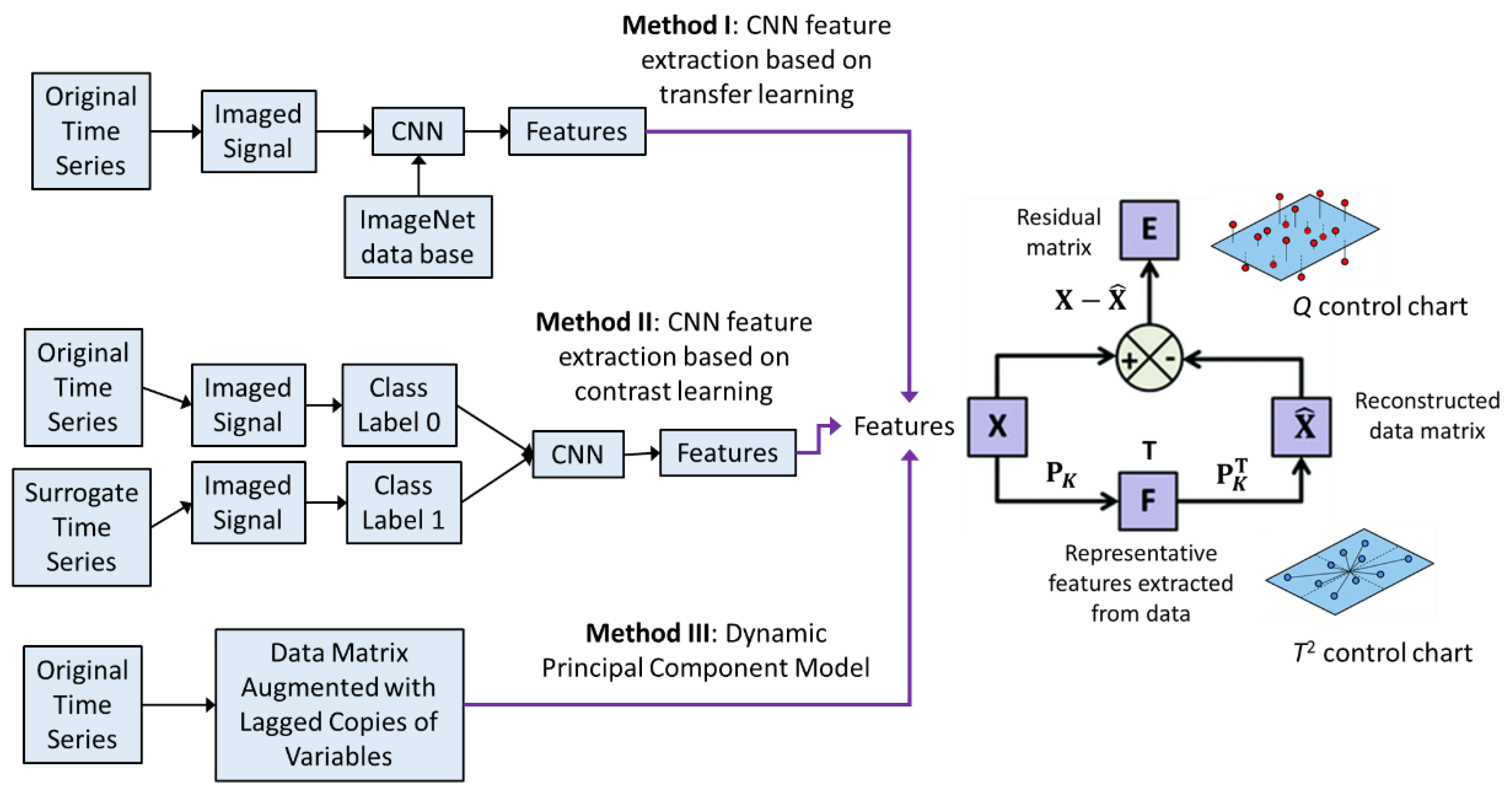
Three approaches to dynamic process monitoring: Method I is based on the use of a principal component model derived from the features extracted from the time series with convolutional neural networks and transfer learning; Method II is the same as Method I, except for extraction of enhanced features; and Method III is based on dynamic principal component analysis.
Figure 3.
Three approaches to dynamic process monitoring: Method I is based on the use of a principal component model derived from the features extracted from the time series with convolutional neural networks and transfer learning; Method II is the same as Method I, except for extraction of enhanced features; and Method III is based on dynamic principal component analysis.
Figure 4.
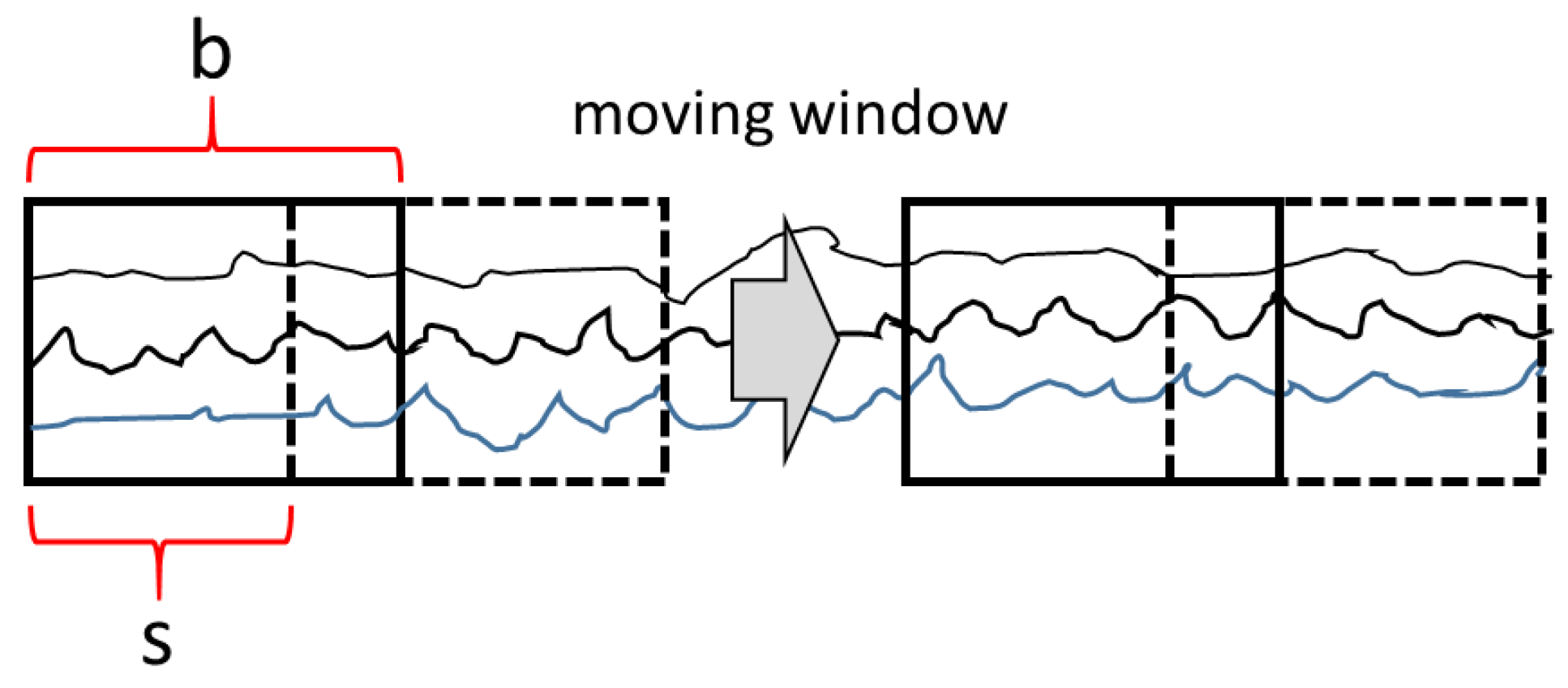
Time series segmentation using a sliding window algorithm.
Figure 4.
Time series segmentation using a sliding window algorithm.
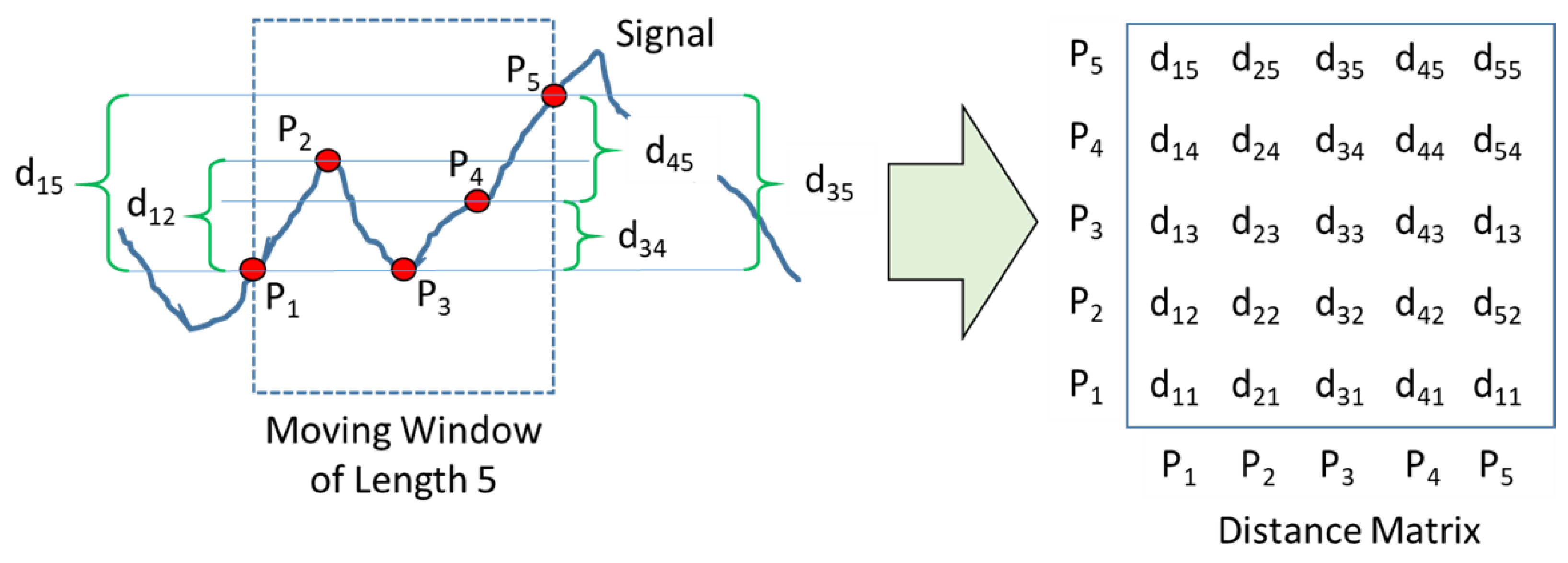
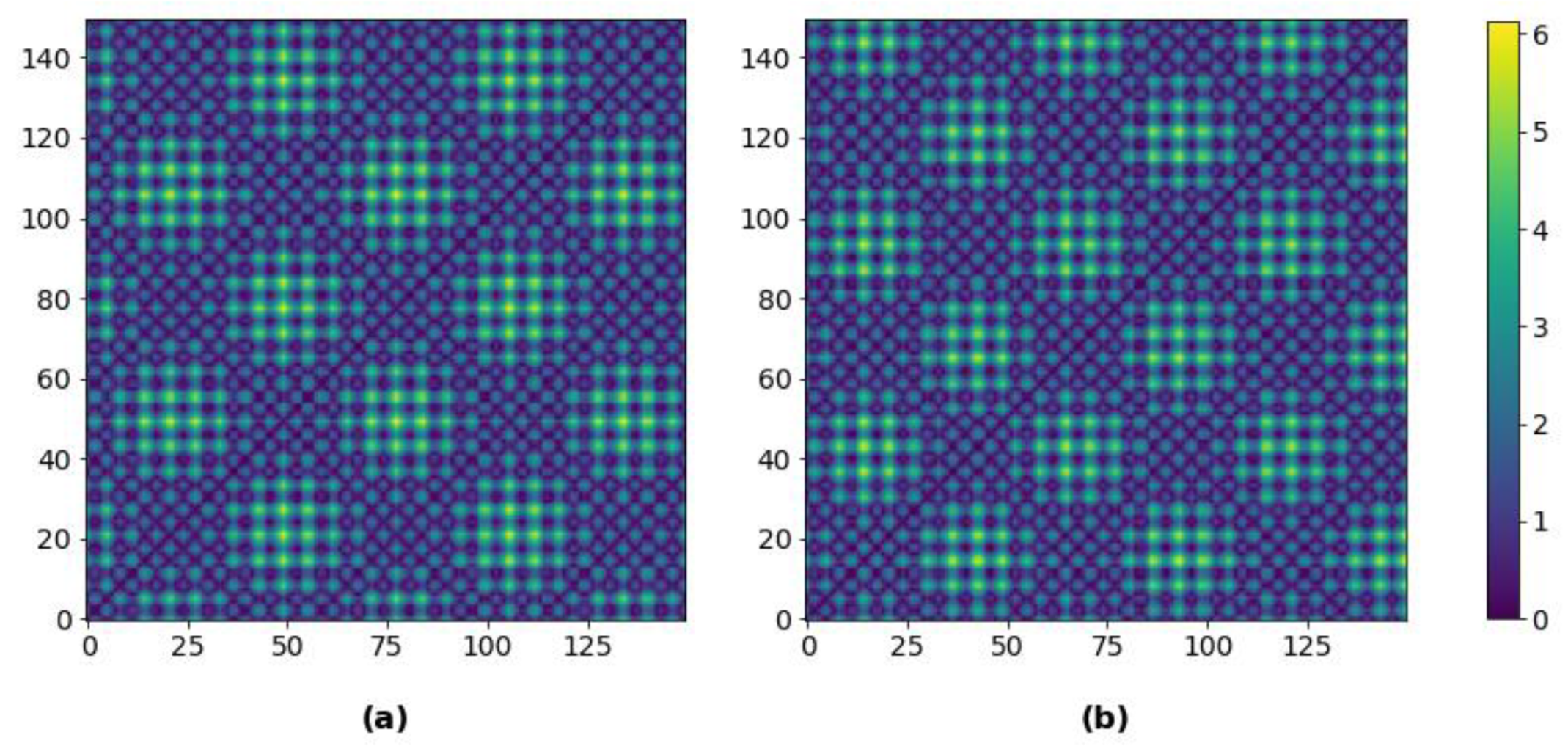
Figure 5.
Generation of a distance matrix associated with a window sliding across a univariate process signal.
Figure 5.
Generation of a distance matrix associated with a window sliding across a univariate process signal.
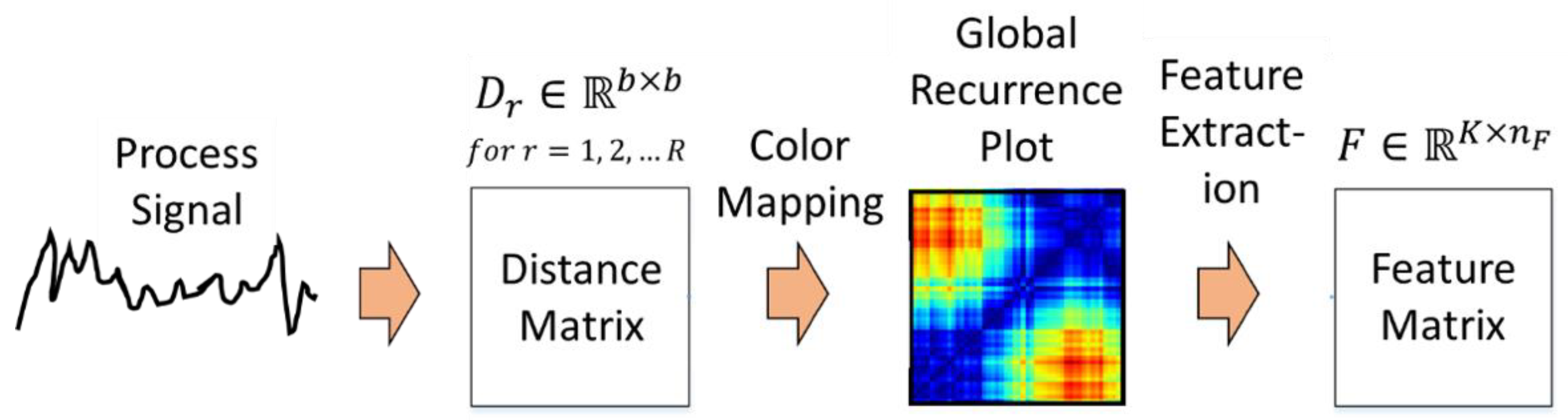
Figure 6.
CNN feature extraction from global recurrence plots.
Figure 6.
CNN feature extraction from global recurrence plots.
Figure 7.
VGG19 CNN modified for contrast-based learning.
Figure 7.
VGG19 CNN modified for contrast-based learning.
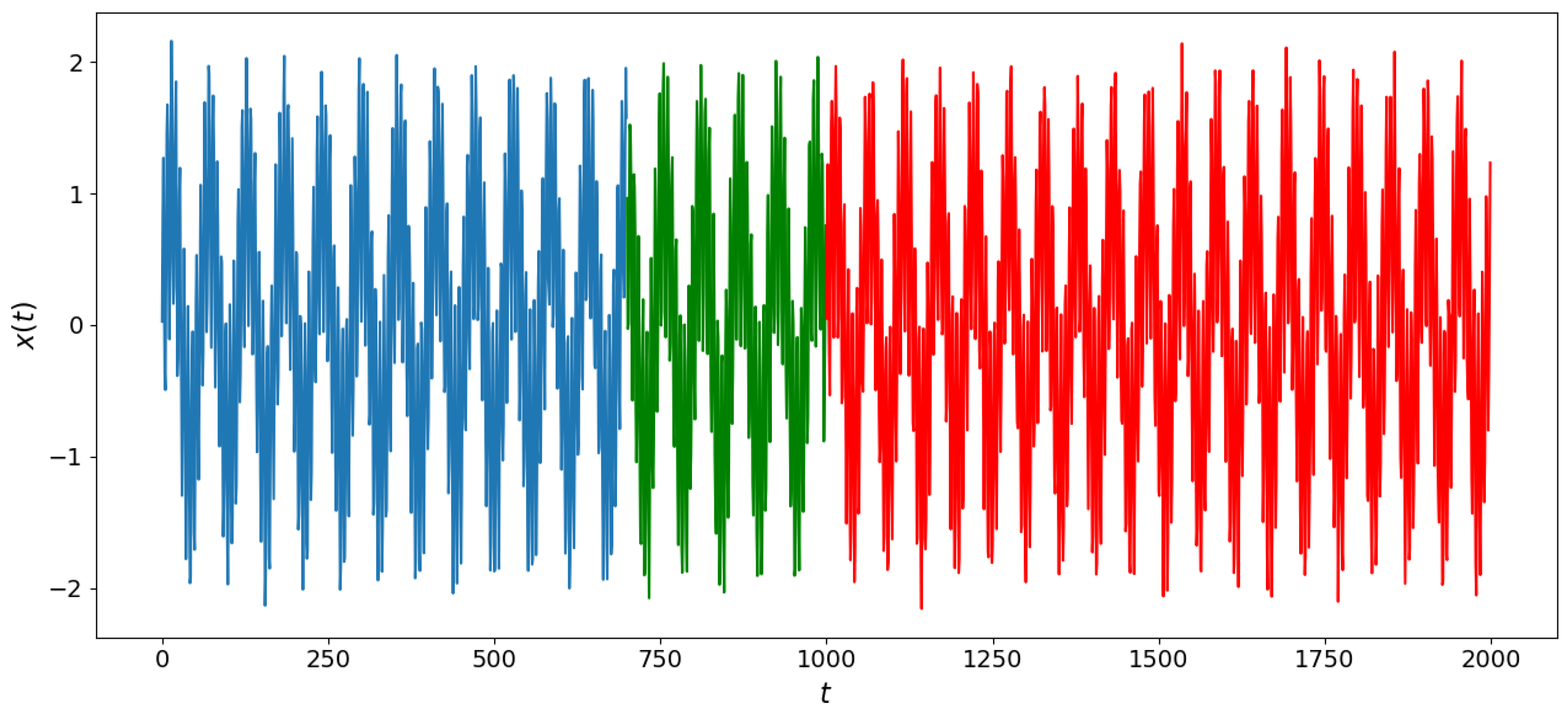
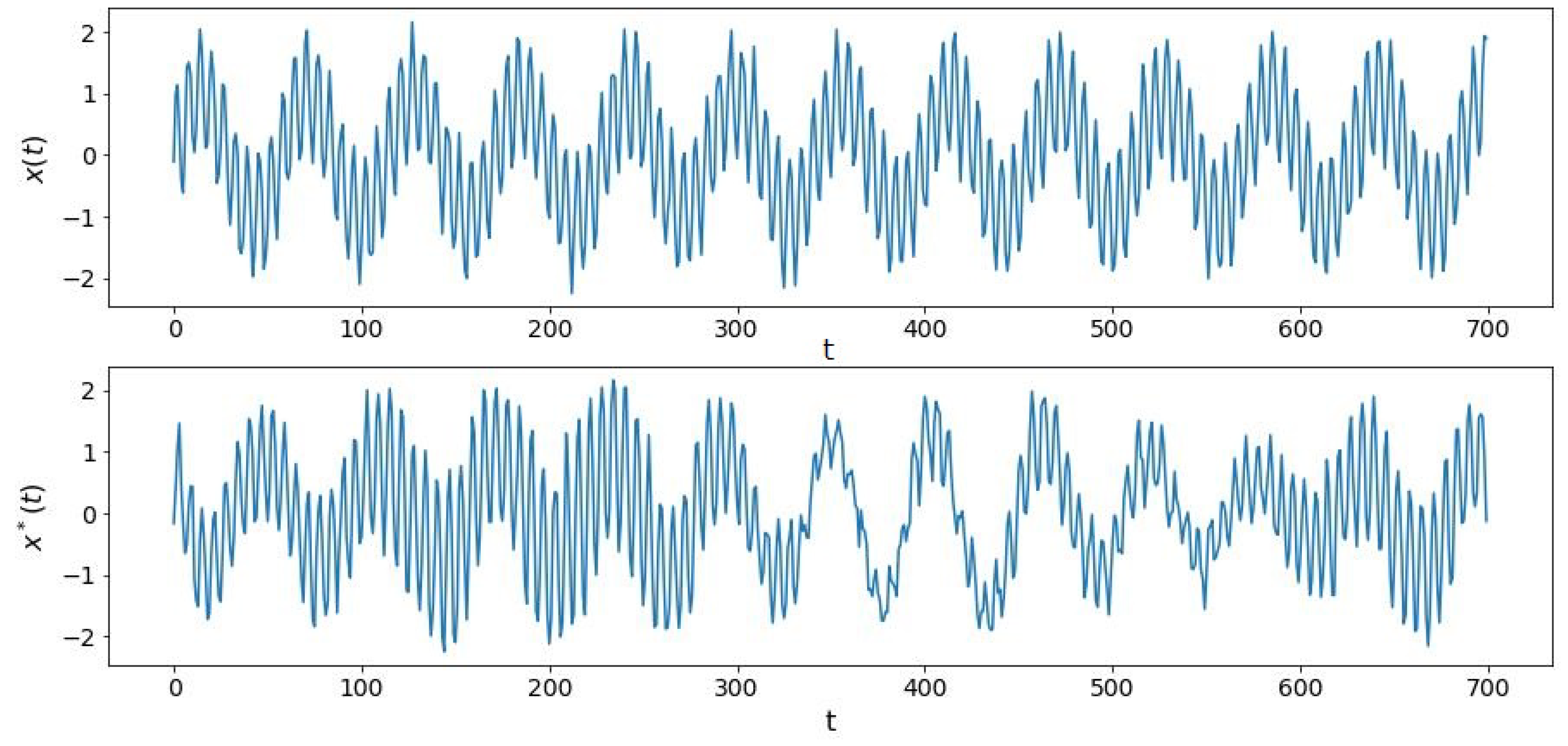
Figure 8.
Simulated sinusoidal signal with parameter change occurring in the red region.
Figure 8.
Simulated sinusoidal signal with parameter change occurring in the red region.
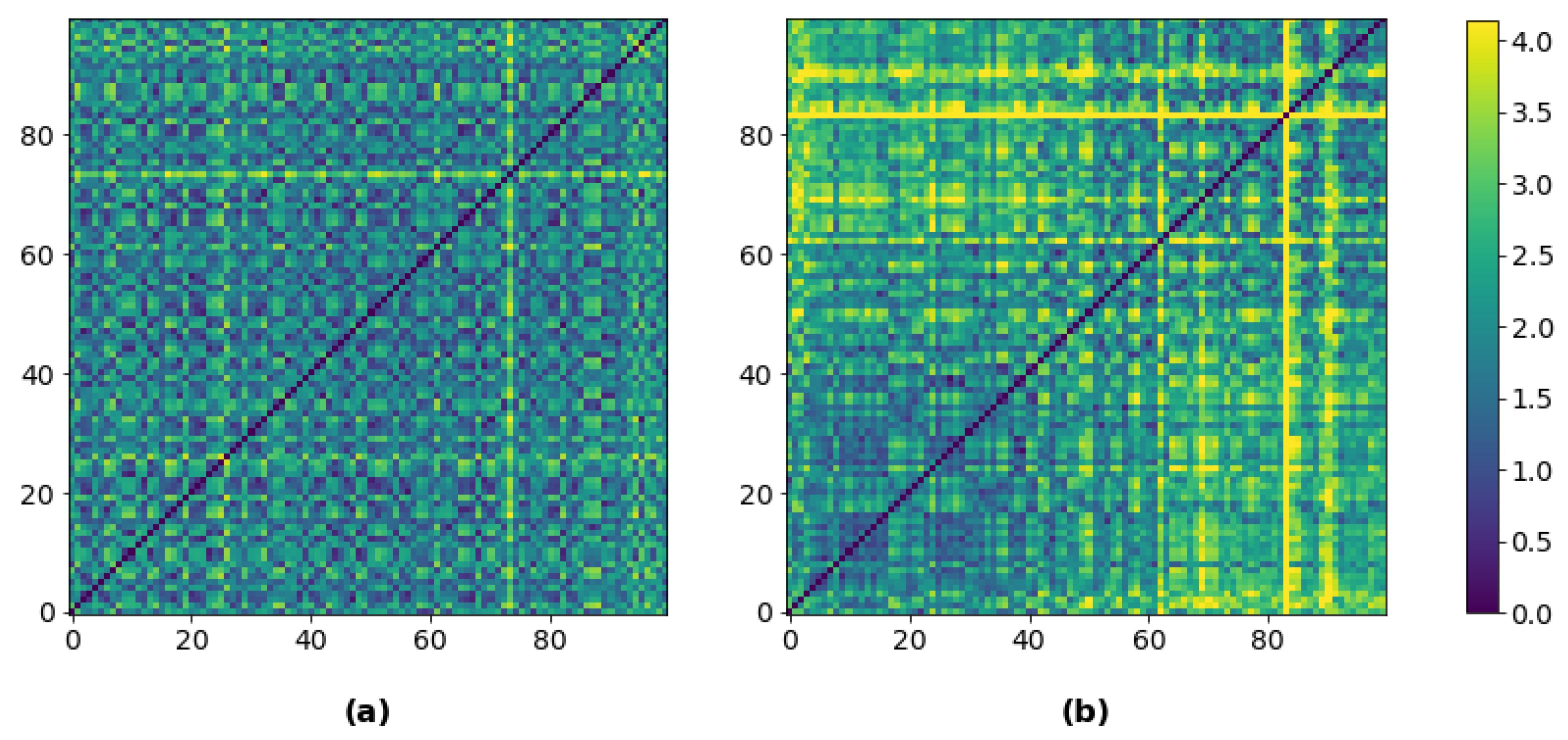
Figure 9.
GRPs for CNN feature extraction through transfer learning: (
a) NOC data (occurring before
t = 1000); and (
b) fault data (occurring after
t = 1000 in
Figure 8). The color scale defines the Euclidean distances represented by different RGB pixel values.
Figure 9.
GRPs for CNN feature extraction through transfer learning: (
a) NOC data (occurring before
t = 1000); and (
b) fault data (occurring after
t = 1000 in
Figure 8). The color scale defines the Euclidean distances represented by different RGB pixel values.
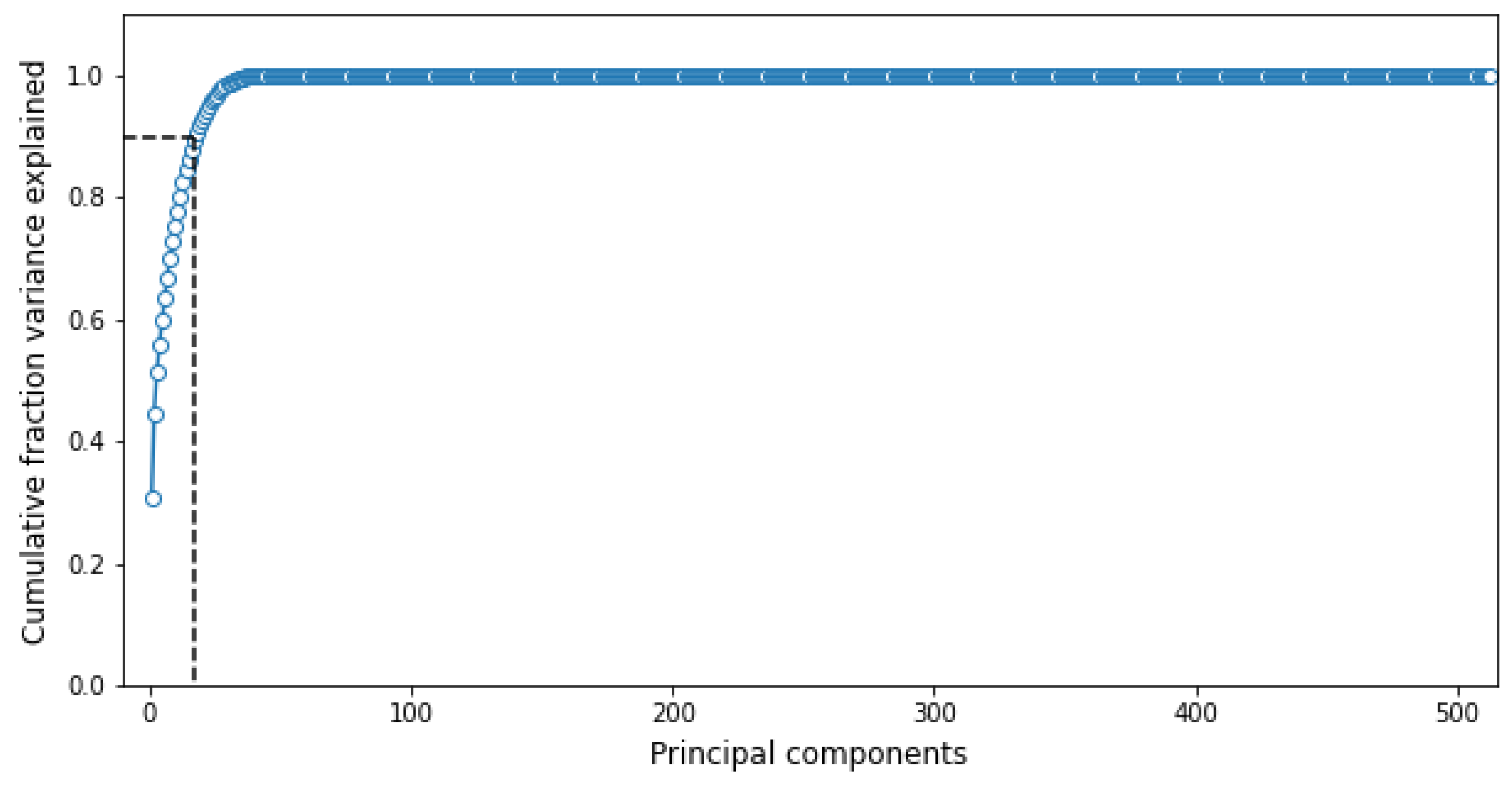
Figure 10.
Cumulative fraction variance explained by each principal component from CNN feature extraction with transfer learning, for a window length of 150 time steps.
Figure 10.
Cumulative fraction variance explained by each principal component from CNN feature extraction with transfer learning, for a window length of 150 time steps.
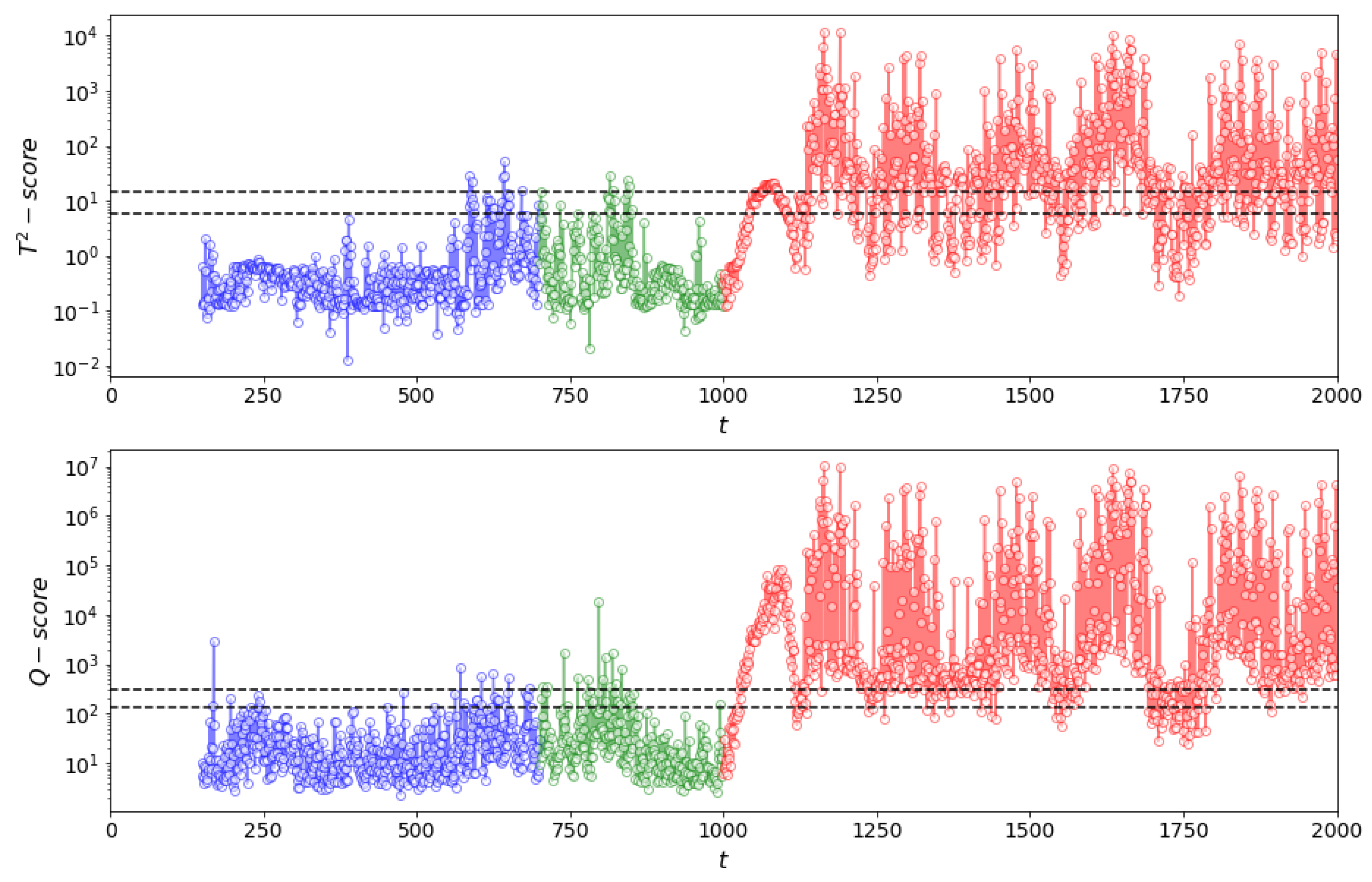
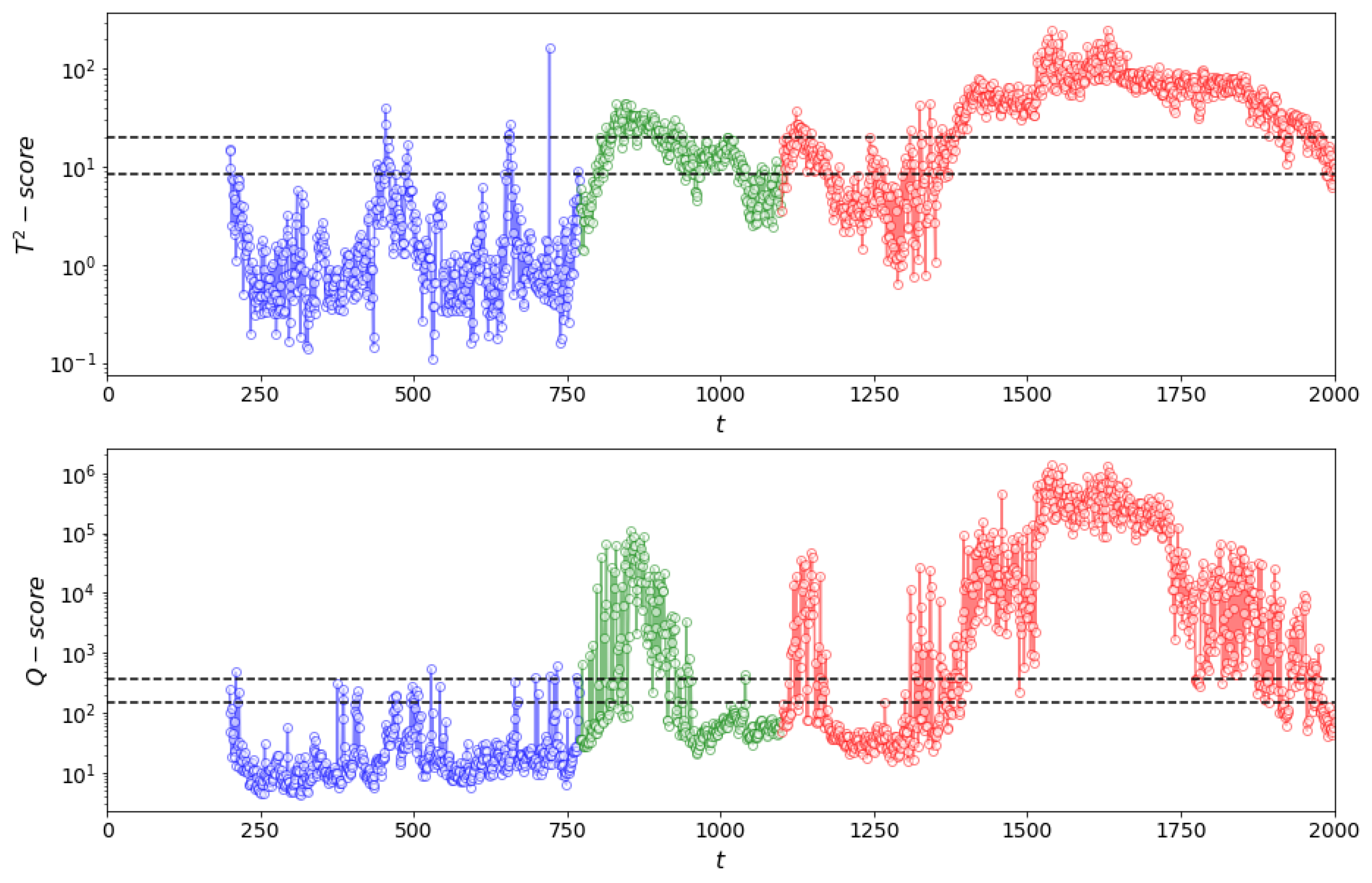
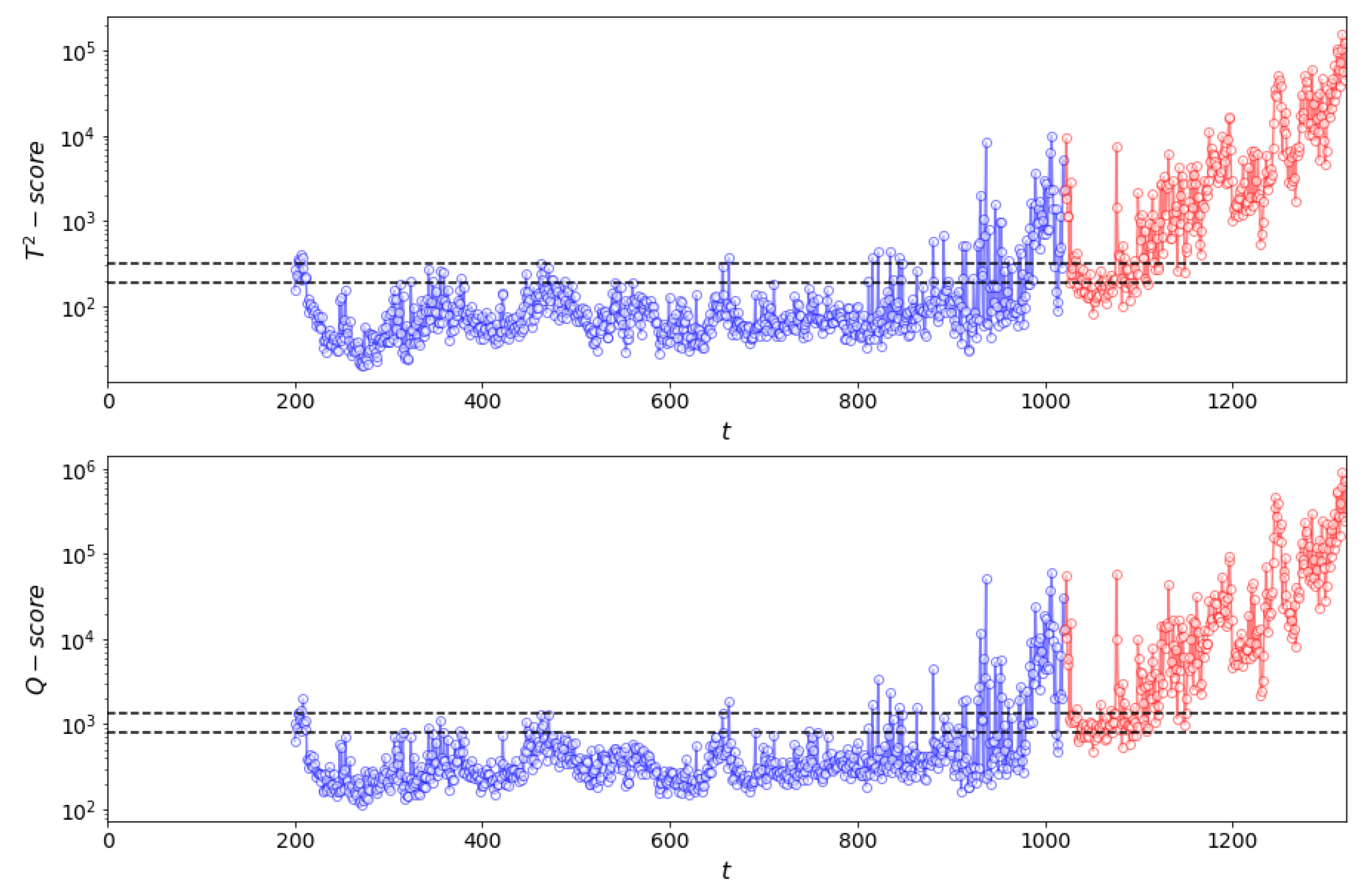
Figure 11.
(top) and Q (bottom) process monitoring charts of simulated dataset for a window length of 150 time steps using Method I. NOC data are shown in blue (up to index 749), validation data in green (indices 750–999) and test (fault) data in red (indices 1000–2000).
Figure 11.
(top) and Q (bottom) process monitoring charts of simulated dataset for a window length of 150 time steps using Method I. NOC data are shown in blue (up to index 749), validation data in green (indices 750–999) and test (fault) data in red (indices 1000–2000).
Figure 12.
Simulated data (top) and IAAFT surrogate of the simulated data (bottom).
Figure 12.
Simulated data (top) and IAAFT surrogate of the simulated data (bottom).
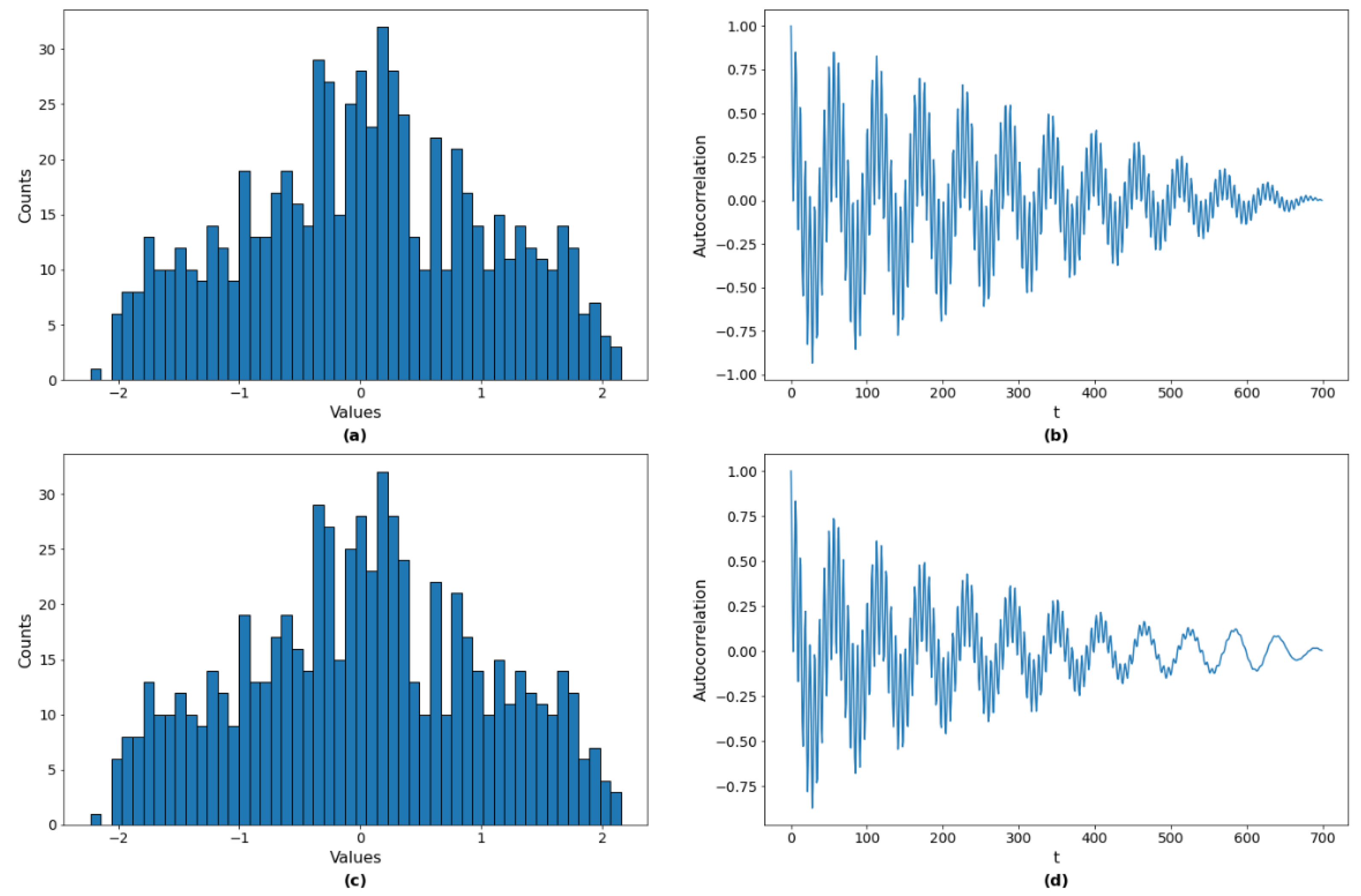
Figure 13.
Distribution (a) and autocorrelation function (b) of the simulated data and the distribution (c) and autocorrelation function (d) of the IAAFT surrogate data.
Figure 13.
Distribution (a) and autocorrelation function (b) of the simulated data and the distribution (c) and autocorrelation function (d) of the IAAFT surrogate data.
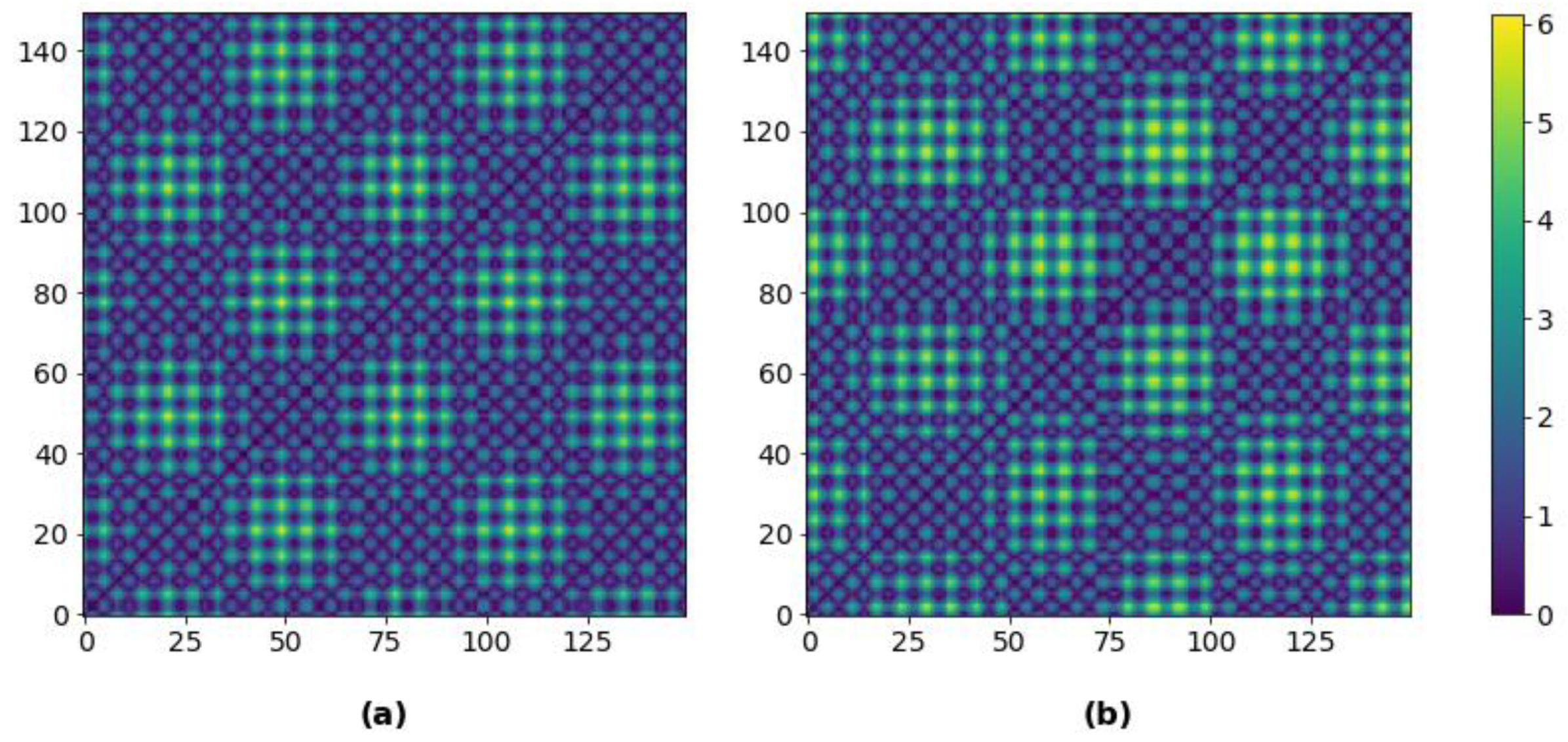
Figure 14.
Distance plots for training the CNN in Method II, with a window length of 150 time steps: (a) original time series; and (b) surrogate time series.
Figure 14.
Distance plots for training the CNN in Method II, with a window length of 150 time steps: (a) original time series; and (b) surrogate time series.
Figure 15.
Cumulative fraction variance explained by each principal component from CNN feature extraction with contrast-based learning (Method II), for a window length of 150 time steps.
Figure 15.
Cumulative fraction variance explained by each principal component from CNN feature extraction with contrast-based learning (Method II), for a window length of 150 time steps.
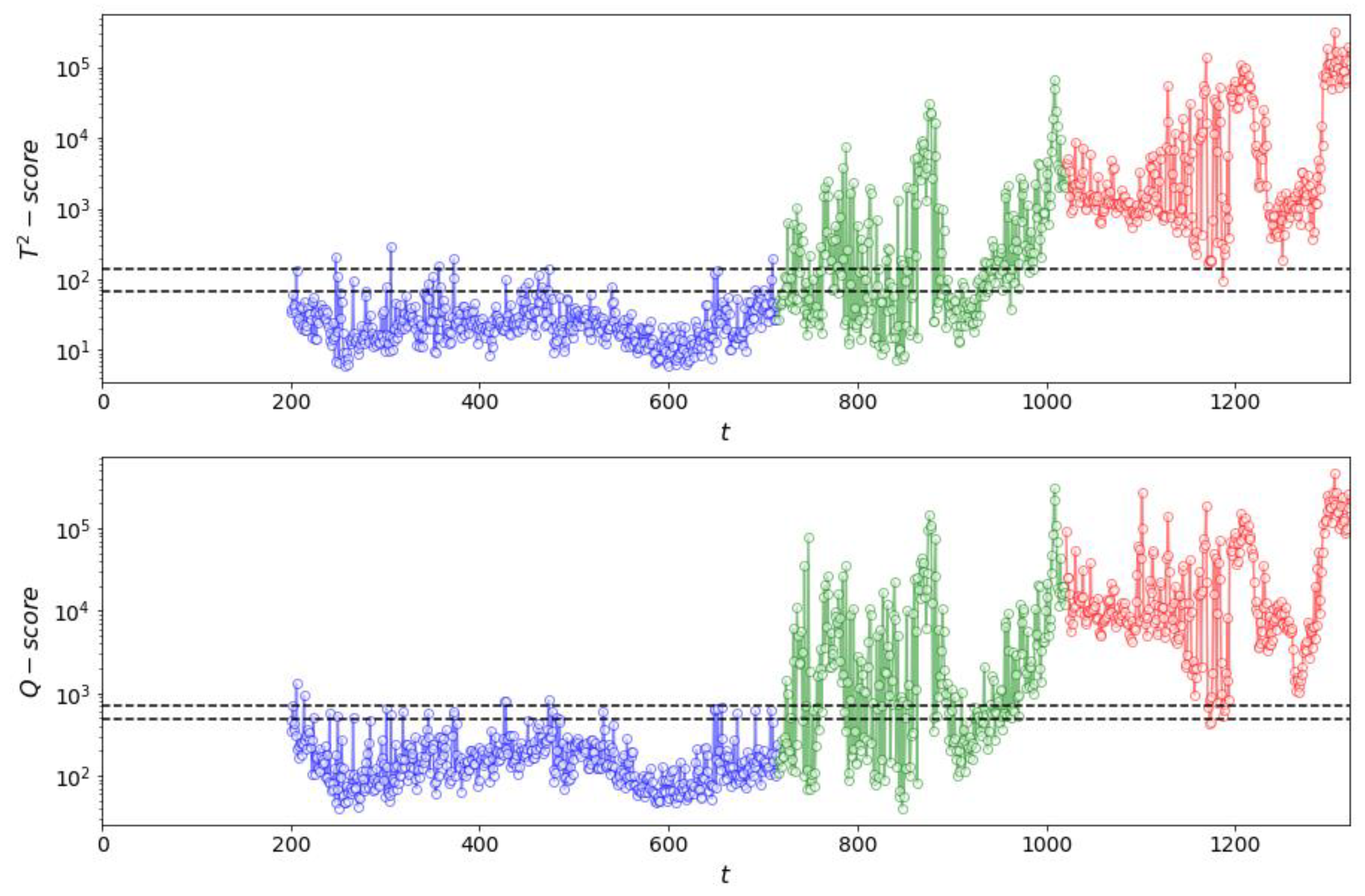
Figure 16.
(top) and Q (bottom) process monitoring charts of simulated dataset for a window length of 150 time steps using Method II. NOC data are shown in blue (up to index 749), validation data in green (indices 750–999) and test (fault) data in red (indices 1000–2000).
Figure 16.
(top) and Q (bottom) process monitoring charts of simulated dataset for a window length of 150 time steps using Method II. NOC data are shown in blue (up to index 749), validation data in green (indices 750–999) and test (fault) data in red (indices 1000–2000).
Figure 17.
(top) and Q (bottom) process monitoring charts of simulated dataset using Method III, with an embedding dimension of four and an embedding lag of 30. NOC data are shown in blue (indices 0–600), validation data in green (indices 601–800) and test (fault) data in red (indices 800–1720).
Figure 17.
(top) and Q (bottom) process monitoring charts of simulated dataset using Method III, with an embedding dimension of four and an embedding lag of 30. NOC data are shown in blue (indices 0–600), validation data in green (indices 601–800) and test (fault) data in red (indices 800–1720).
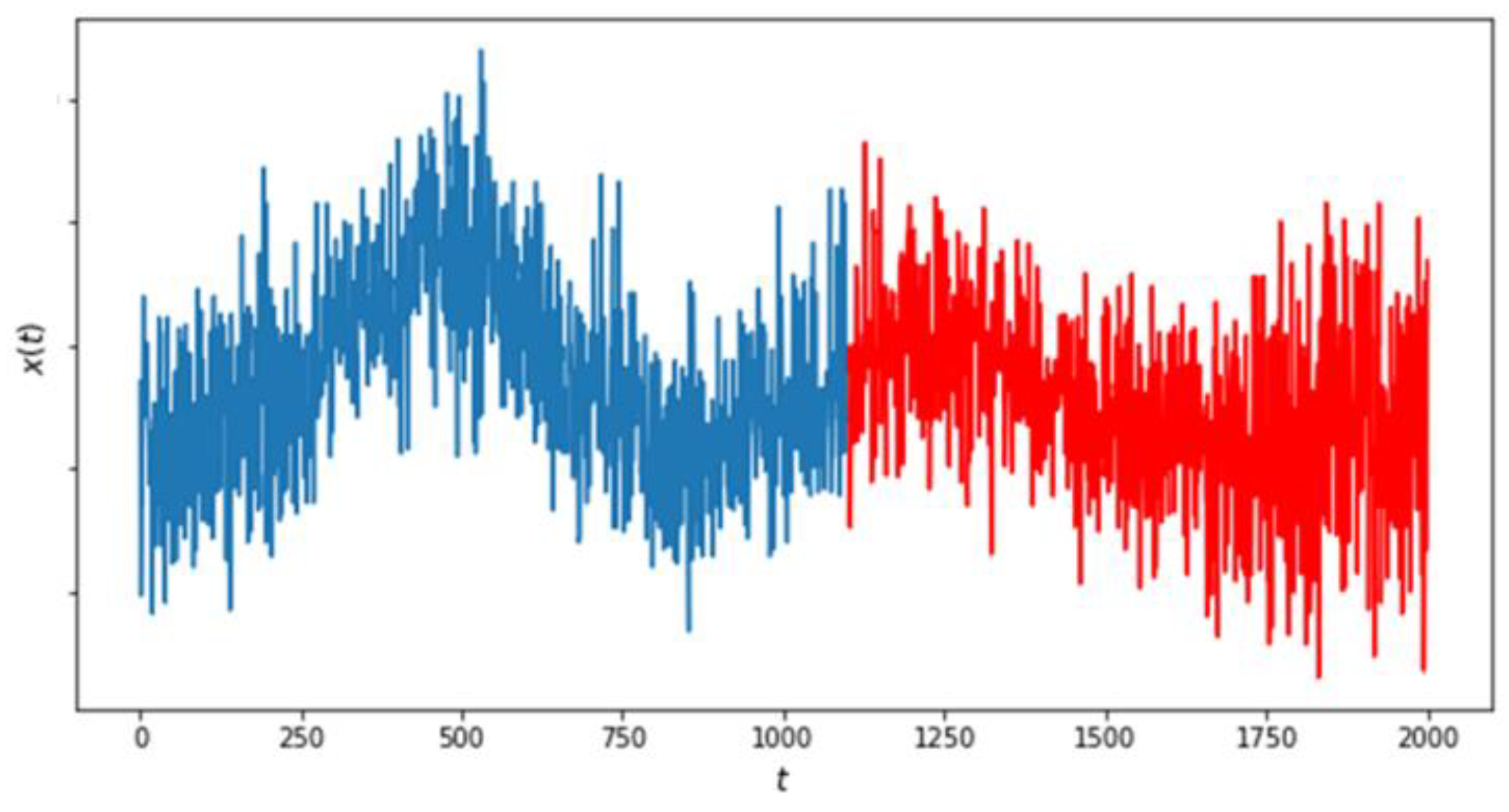
Figure 18.
AG mill power draw gradually transforming from non-fault data (blue) into white noise through the fault region (red).
Figure 18.
AG mill power draw gradually transforming from non-fault data (blue) into white noise through the fault region (red).
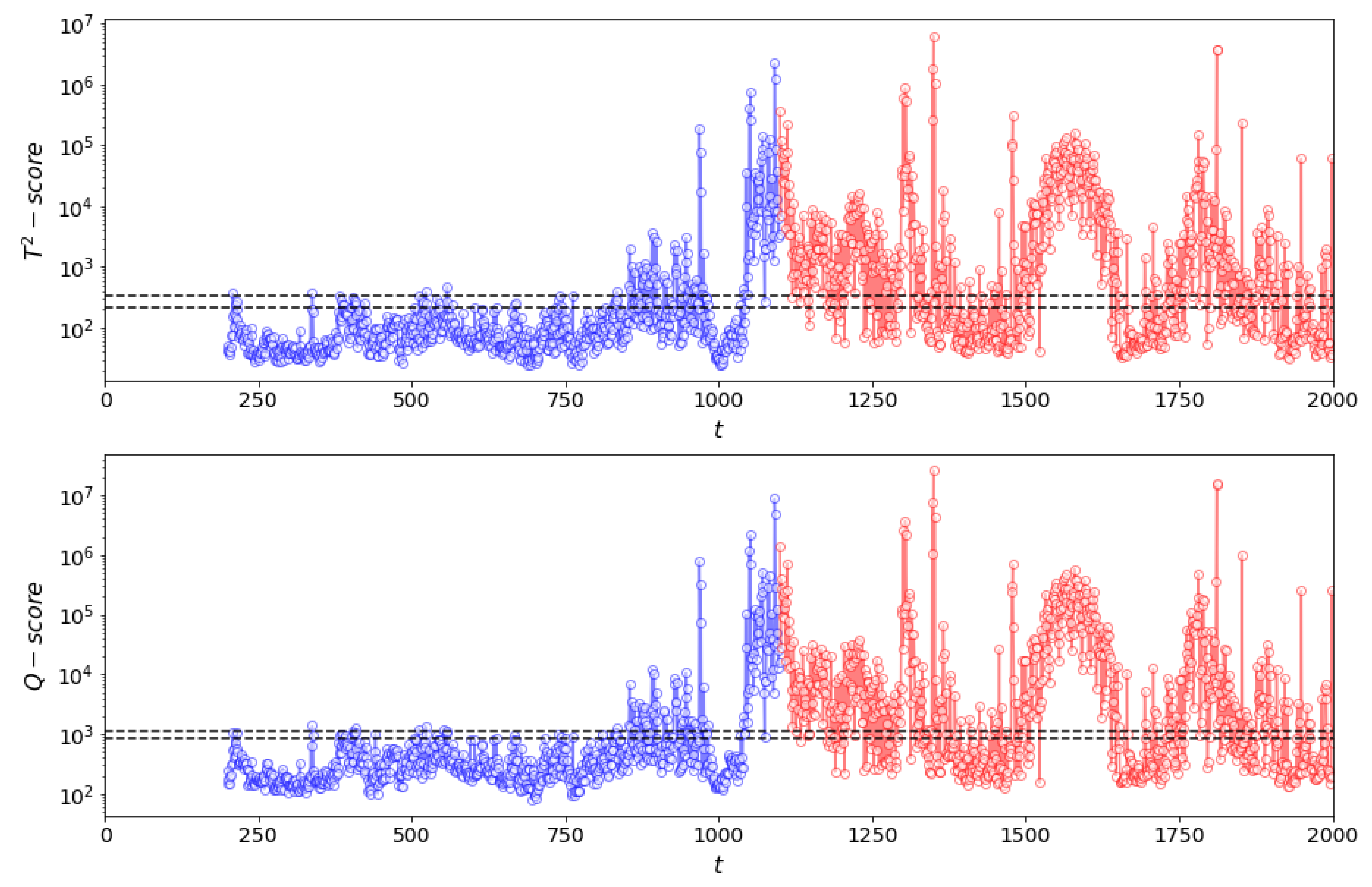
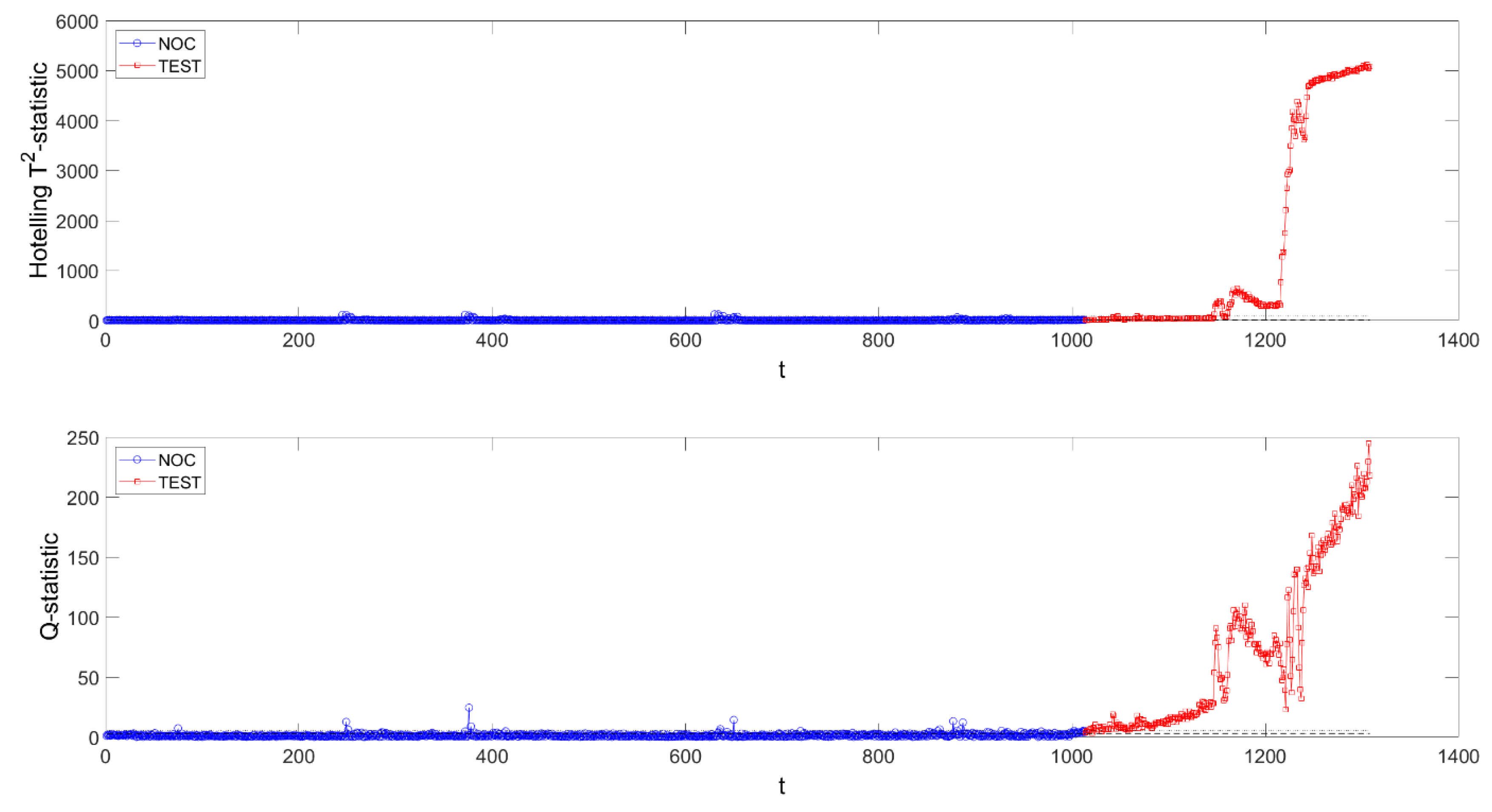
Figure 19.
(top) and Q (bottom) process monitoring charts of AG mill power draw for a window length of 200 time steps using Method I. NOC data are shown in blue and test (fault) data in red.
Figure 19.
(top) and Q (bottom) process monitoring charts of AG mill power draw for a window length of 200 time steps using Method I. NOC data are shown in blue and test (fault) data in red.
Figure 20.
(top) and Q (bottom) process monitoring charts of AG mill power draw for a window length of 200 time steps using Method II. Training non-fault data are shown in blue, untrained non-fault data in green and test (fault) data in red.
Figure 20.
(top) and Q (bottom) process monitoring charts of AG mill power draw for a window length of 200 time steps using Method II. Training non-fault data are shown in blue, untrained non-fault data in green and test (fault) data in red.
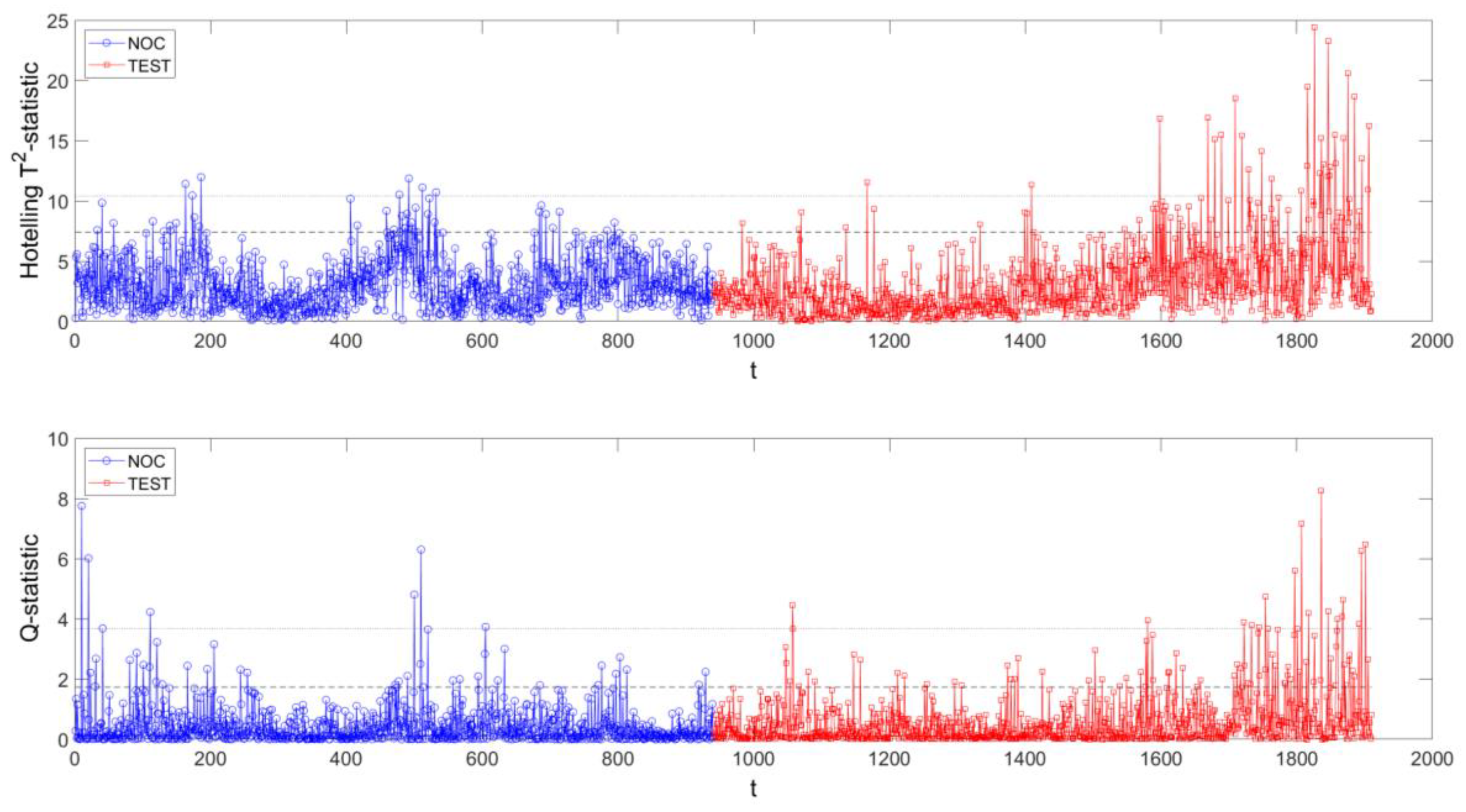
Figure 21.
(top) and Q (bottom) process monitoring charts of simulated dataset using Method III, with embedding dimension of four and embedding lag of 10. NOC data are shown in blue and test (fault) data in red.
Figure 21.
(top) and Q (bottom) process monitoring charts of simulated dataset using Method III, with embedding dimension of four and embedding lag of 10. NOC data are shown in blue and test (fault) data in red.
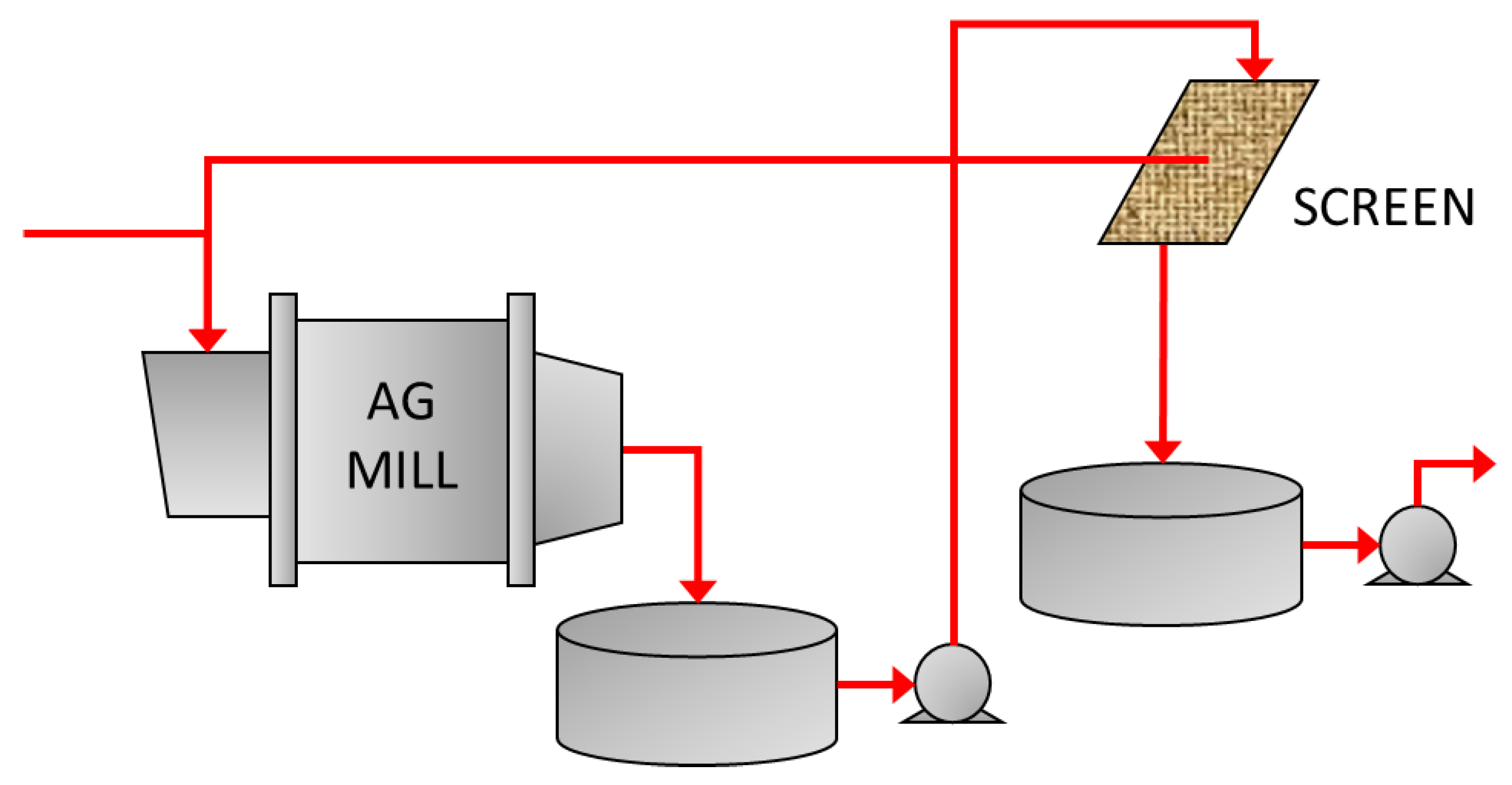
Figure 22.
Fully autogenous grinding circuit flow diagram.
Figure 22.
Fully autogenous grinding circuit flow diagram.
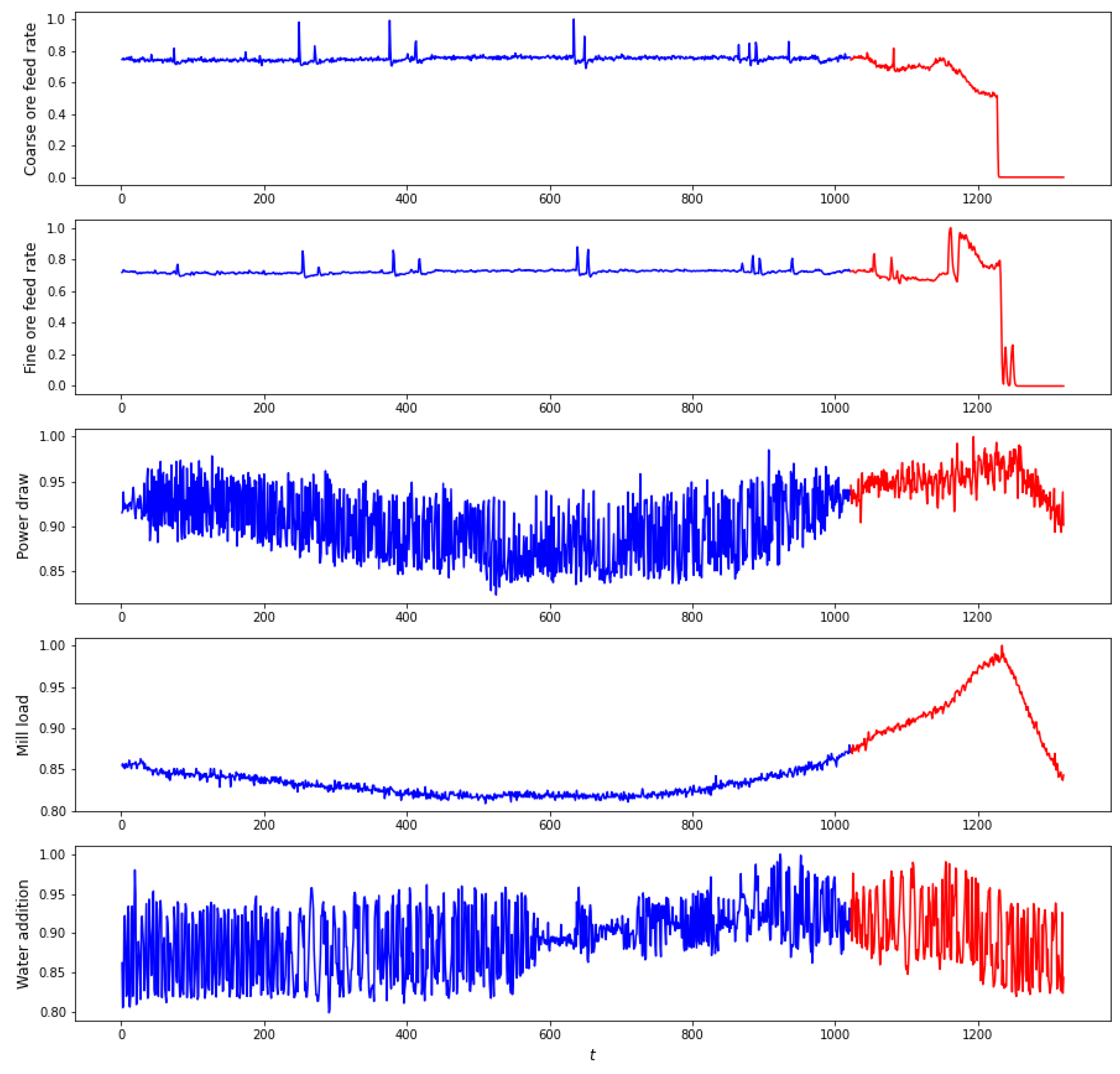
Figure 23.
Scaled multivariate grinding circuit data. Circuit operational state changes from NOC (blue) to overloaded mill (red), as logged by the expert mill controller.
Figure 23.
Scaled multivariate grinding circuit data. Circuit operational state changes from NOC (blue) to overloaded mill (red), as logged by the expert mill controller.
Figure 24.
Distance plots for CNN feature extraction, with a window length of 100 time steps: (a) NOC state; and (b) overloaded mill state.
Figure 24.
Distance plots for CNN feature extraction, with a window length of 100 time steps: (a) NOC state; and (b) overloaded mill state.
Figure 25.
(top) and Q (bottom) process monitoring charts of multivariate grinding circuit data for a window length of 200 time steps using Method I. NOC (trained) data are shown in blue and test (fault) data in red.
Figure 25.
(top) and Q (bottom) process monitoring charts of multivariate grinding circuit data for a window length of 200 time steps using Method I. NOC (trained) data are shown in blue and test (fault) data in red.
Figure 26.
(top) and Q (bottom) process monitoring charts of multivariate grinding circuit data for a window length of 100 time steps using Method II. Training non-fault data are shown in blue, untrained non-fault data in green and test (fault) data in red.
Figure 26.
(top) and Q (bottom) process monitoring charts of multivariate grinding circuit data for a window length of 100 time steps using Method II. Training non-fault data are shown in blue, untrained non-fault data in green and test (fault) data in red.
Figure 27.
(top) and Q (bottom) process monitoring charts of multivariate grinding circuit data using Method III. NOC data are shown in blue and test (fault) data in red.
Figure 27.
(top) and Q (bottom) process monitoring charts of multivariate grinding circuit data using Method III. NOC data are shown in blue and test (fault) data in red.
Table 1.
Modified CNN architecture for contrast-based learning (Method II).
Table 1.
Modified CNN architecture for contrast-based learning (Method II).
| Layers | Output Shape | Description |
|---|
| VGG 19 pretrained feature extraction layers | | Feature map dimensions, , dependent on window length |
| Global Average Pooling | | Calculates average value over feature map |
| Fully connected | | 128 nodes with Rectified Linear Units (ReLU) nonlinearity |
| Output node | | Single output node with sigmoidal nonlinearity |
Table 2.
Monitoring results on simulated dataset using Method I.
Table 2.
Monitoring results on simulated dataset using Method I.
| Window Length | FAR | TAR | DD |
|---|
| Q (SPE) | | Q (SPE) | | Q (SPE) |
|---|
| 50 | 0.063 | 0.035 | 0.062 | 0.076 | 15 | 16 |
| 100 | 0.044 | 0.052 | 0.288 | 0.280 | 10 | 10 |
| 150 | 0.047 | 0.031 | 0.481 | 0.487 | 24 | 24 |
| 200 | 0.033 | 0.042 | 0.537 | 0.623 | 23 | 20 |
Table 3.
CNN training parameters during contrast-based learning for Method II.
Table 3.
CNN training parameters during contrast-based learning for Method II.
| Parameter | Details |
|---|
| Pretrain Newly-Added Classification Section | Fine-Tune Classification and Feature Extraction Sections |
|---|
| Loss function | Binary cross-entropy | Binary cross-entropy |
| Optimizer | Adam [51] | Adam [51] |
| Learning rate | 0.01 | 0.0001 |
| Training epochs | 20 | 100 |
Table 4.
Monitoring results on simulated dataset using Method II.
Table 4.
Monitoring results on simulated dataset using Method II.
| Window Length | FAR | TAR | DD |
|---|
| Q (SPE) | | Q (SPE) | | Q (SPE) |
|---|
| 50 | 0.050 | 0.050 | 0.109 | 0.142 | 13 | 13 |
| 100 | 0.010 | 0.003 | 0.322 | 0.392 | 15 | 14 |
| 150 | 0.013 | 0.040 | 0.849 | 0.880 | 41 | 31 |
| 200 | 0.113 | 0.123 | 0.415 | 0.341 | 3 | 9 |
Table 5.
Monitoring results on simulated dataset using Method III with embedding dimension of four.
Table 5.
Monitoring results on simulated dataset using Method III with embedding dimension of four.
| Embedding Lag | FAR | TAR | DD |
|---|
| Q (SPE) | | Q (SPE) | | Q (SPE) |
|---|
| 1 | 0.081 | 0.040 | 0.052 | 0.040 | 172 | - |
| 5 | 0.063 | 0.053 | 0.061 | 0.039 | 407 | - |
| 10 | 0.070 | 0.067 | 0.107 | 0.009 | 407 | - |
| 30 | 0.033 | 0.076 | 0.154 | 0.580 | 292 | 3 |
| 50 | 0.133 | 0.047 | 0.104 | 0.004 | 292 | - |
Table 6.
Monitoring results on AG mill power draw using Method I.
Table 6.
Monitoring results on AG mill power draw using Method I.
| Window Length | TAR | DD |
|---|
| Q (SPE) | | Q (SPE) |
|---|
| 50 | 0.061 | 0.067 | 78 | 79 |
| 100 | 0.163 | 0.173 | 20 | 20 |
| 150 | 0.350 | 0.392 | 50 | 50 |
| 200 | 0.758 | 0.777 | 3 | 3 |
Table 7.
Monitoring results on AG mill power draw using Method II.
Table 7.
Monitoring results on AG mill power draw using Method II.
| Window Length | TAR | DD |
|---|
| Q (SPE) | | Q (SPE) |
|---|
| 50 | 0.026 | 0.050 | 431 | 41 |
| 100 | 0.737 | 0.760 | 3 | 3 |
| 150 | 0.515 | 0.801 | 170 | 3 |
| 200 | 1.000 | 0.996 | 3 | 3 |
Table 8.
Monitoring results on AG mill power draw using Method III with embedding dimension of four.
Table 8.
Monitoring results on AG mill power draw using Method III with embedding dimension of four.
| Embedding Lag | TAR | DD |
|---|
| Q (SPE) | | Q (SPE) |
|---|
| 2 | 0.0573 | 0.07645 | - | 776 |
| 5 | 0.0822 | 0.0792 | 797 | - |
| 10 | 0.0856 | 0.0907 | 791 | 805 |
| 30 | 0.0626 | 0.0484 | - | 819 |
| 50 | 0.0718 | 0.0588 | 803 | - |
Table 9.
Monitoring AG mill operational state using Method I.
Table 9.
Monitoring AG mill operational state using Method I.
| Window Length | TAR | DD |
|---|
| Q (SPE) | | Q (SPE) |
|---|
| 50 | 0.723 | 0.753 | 3 | 3 |
| 100 | 0.965 | 0.975 | 3 | 3 |
| 150 | 0.820 | 0.870 | 62 | 34 |
| 200 | 0.900 | 0.937 | 3 | 3 |
Table 10.
Monitoring AG mill operational state using Method II.
Table 10.
Monitoring AG mill operational state using Method II.
|
Window Length
|
TAR
|
DD
|
|---|
| Q (SPE) | | Q (SPE) |
|---|
| 50 | 0.610 | 0.797 | 3 | 3 |
| 100 | 1.000 | 0.990 | 3 | 3 |
| 150 | 0.553 | 0.497 | 3 | 3 |
| 200 | 1.000 | 1.000 | 3 | 3 |
Table 11.
Monitoring AG mill operational state using Method III.
Table 11.
Monitoring AG mill operational state using Method III.
| Embedding Dimension/Lag | TAR | DD |
|---|
| Q (SPE) | | Q (SPE) |
|---|
| 2/4 | 0.993 | 1.000 | 6 | 3 |