An Automated Method to Generate and Evaluate Geochemical Tectonic Discrimination Diagrams Based on Topological Theory
Abstract
1. Introduction
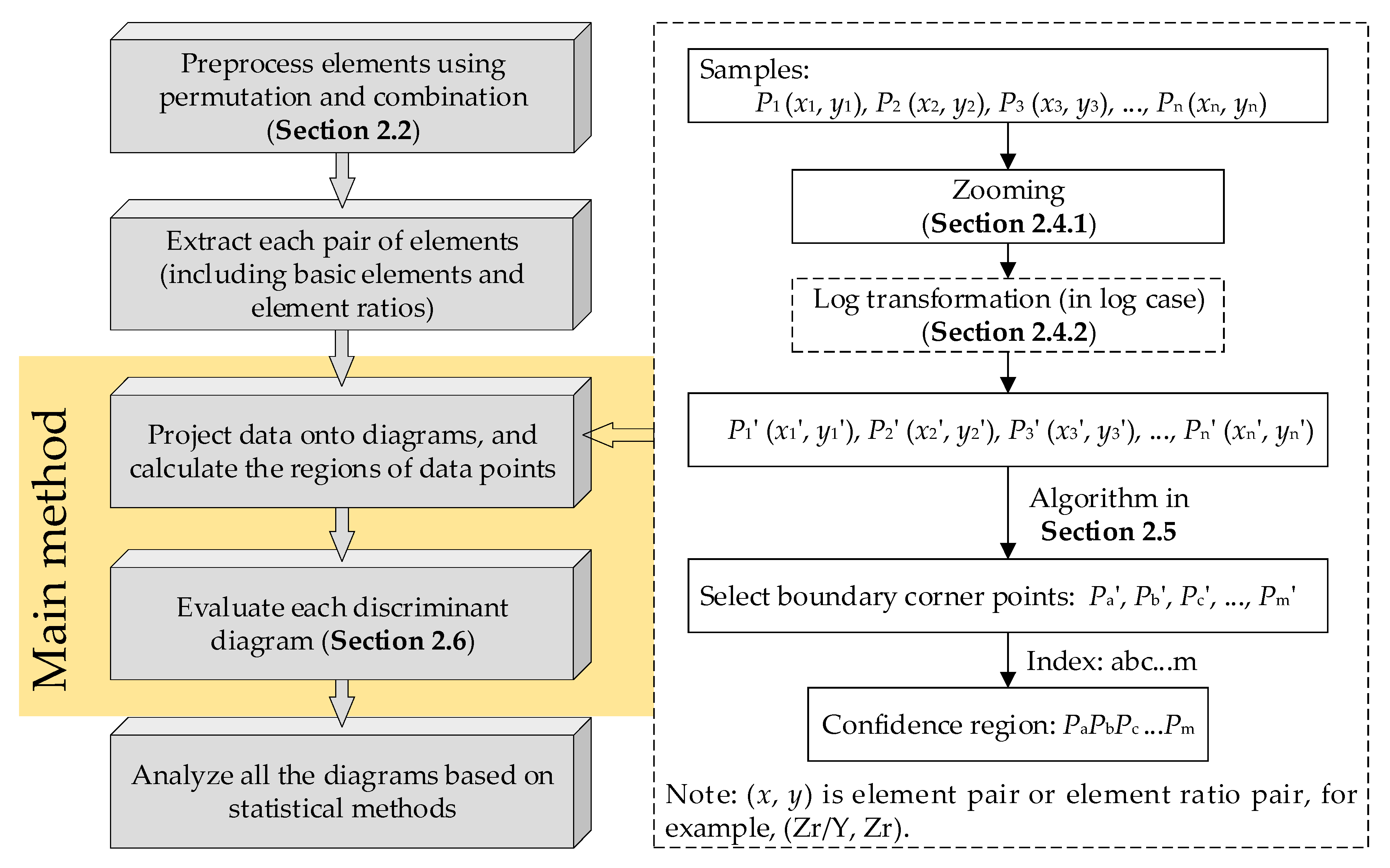
2. Methodology
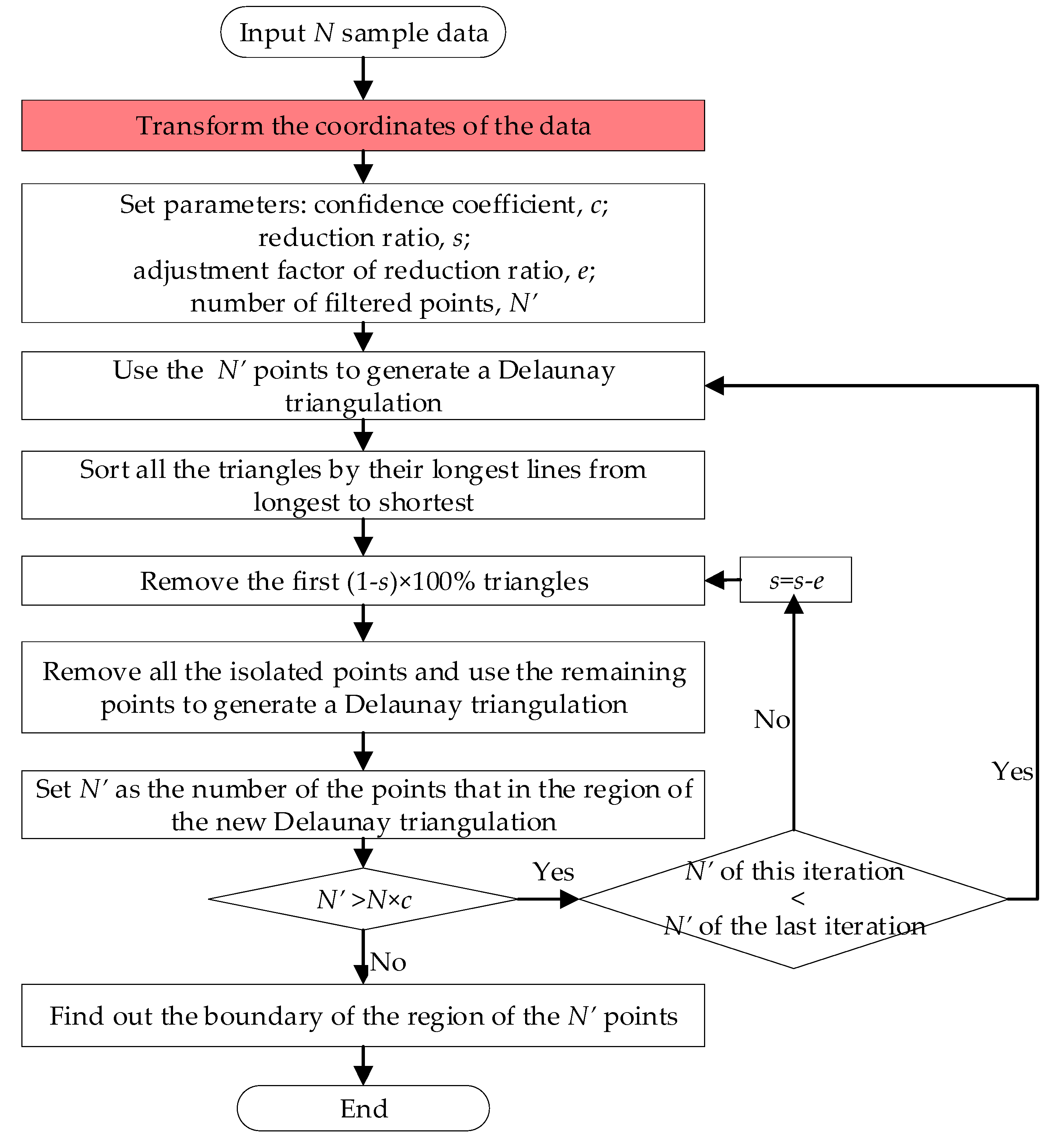
2.1. Overall Framework
2.2. Element (or Element Ratio) Pairs
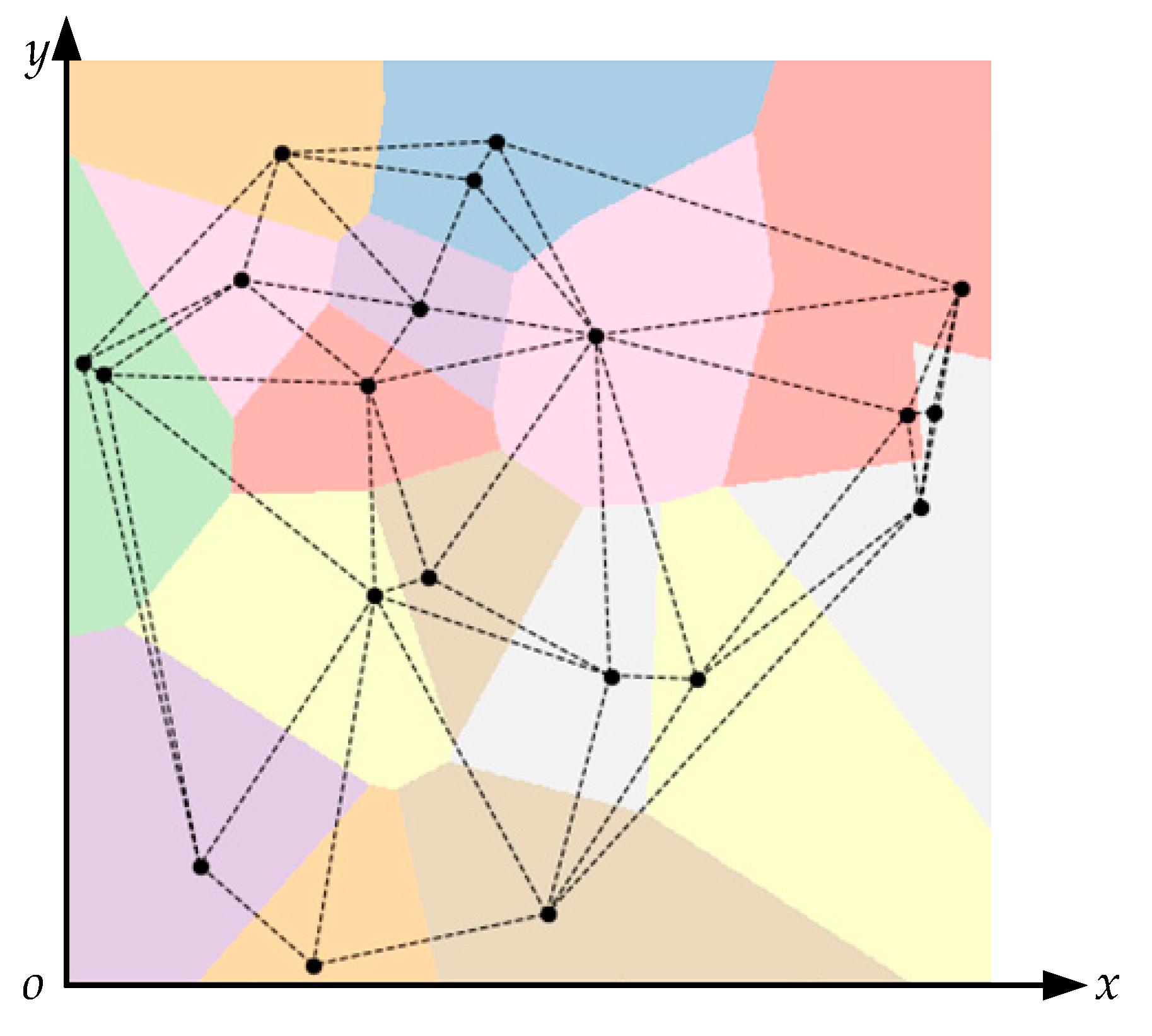
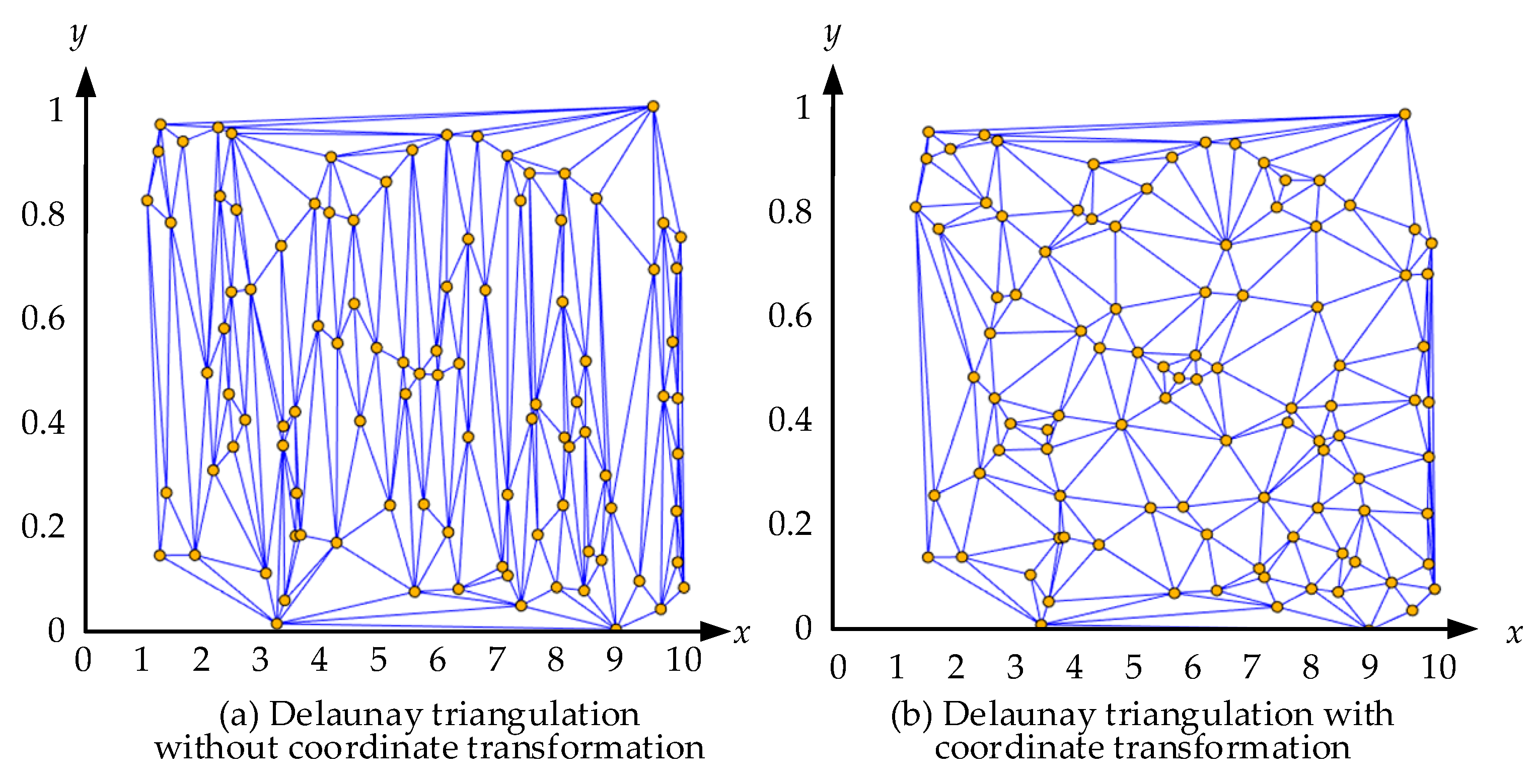
2.3. Delaunay Triangulation
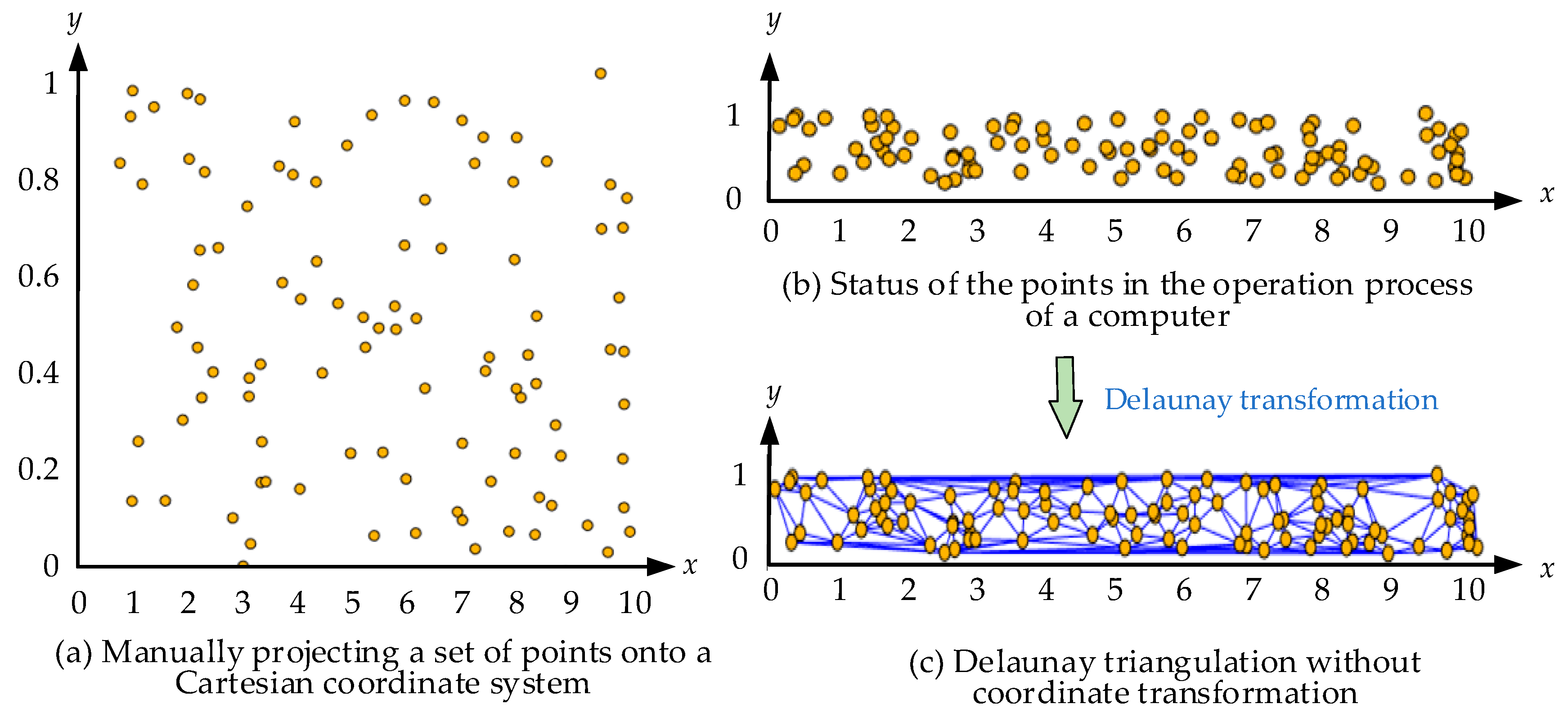
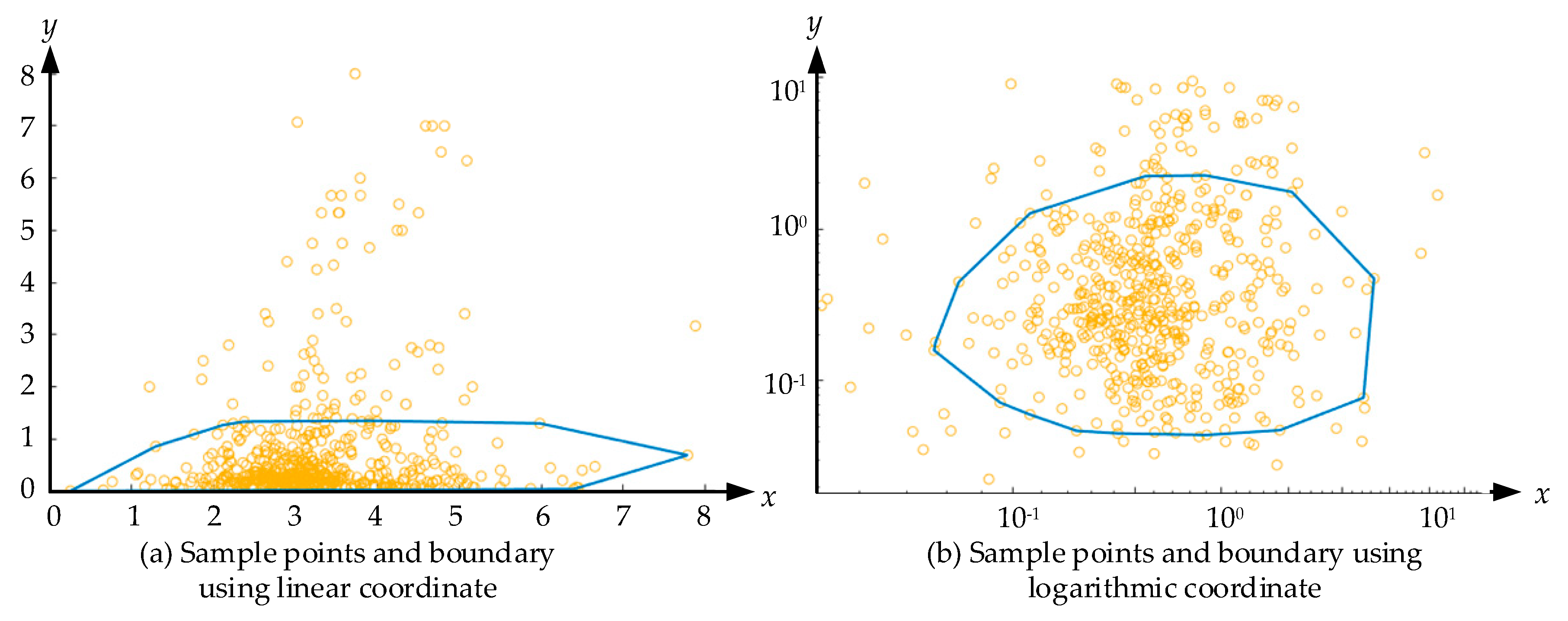
2.4. Coordinate Transformation of Samples
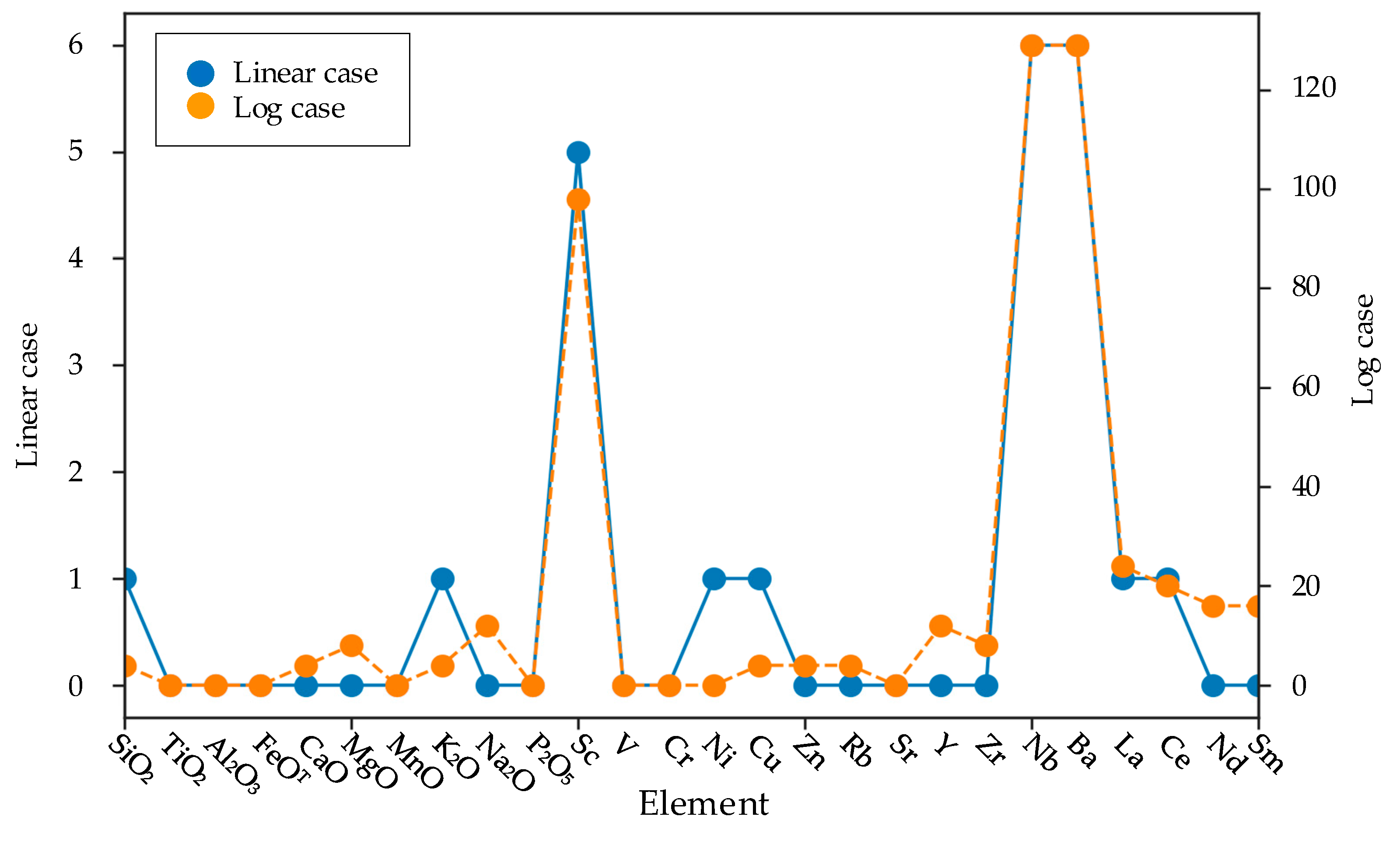
2.4.1. Coordinate Transformation under Multiscale Coordinates
2.4.2. Coordinate Transformation under Linear and Logarithmic Coordinates
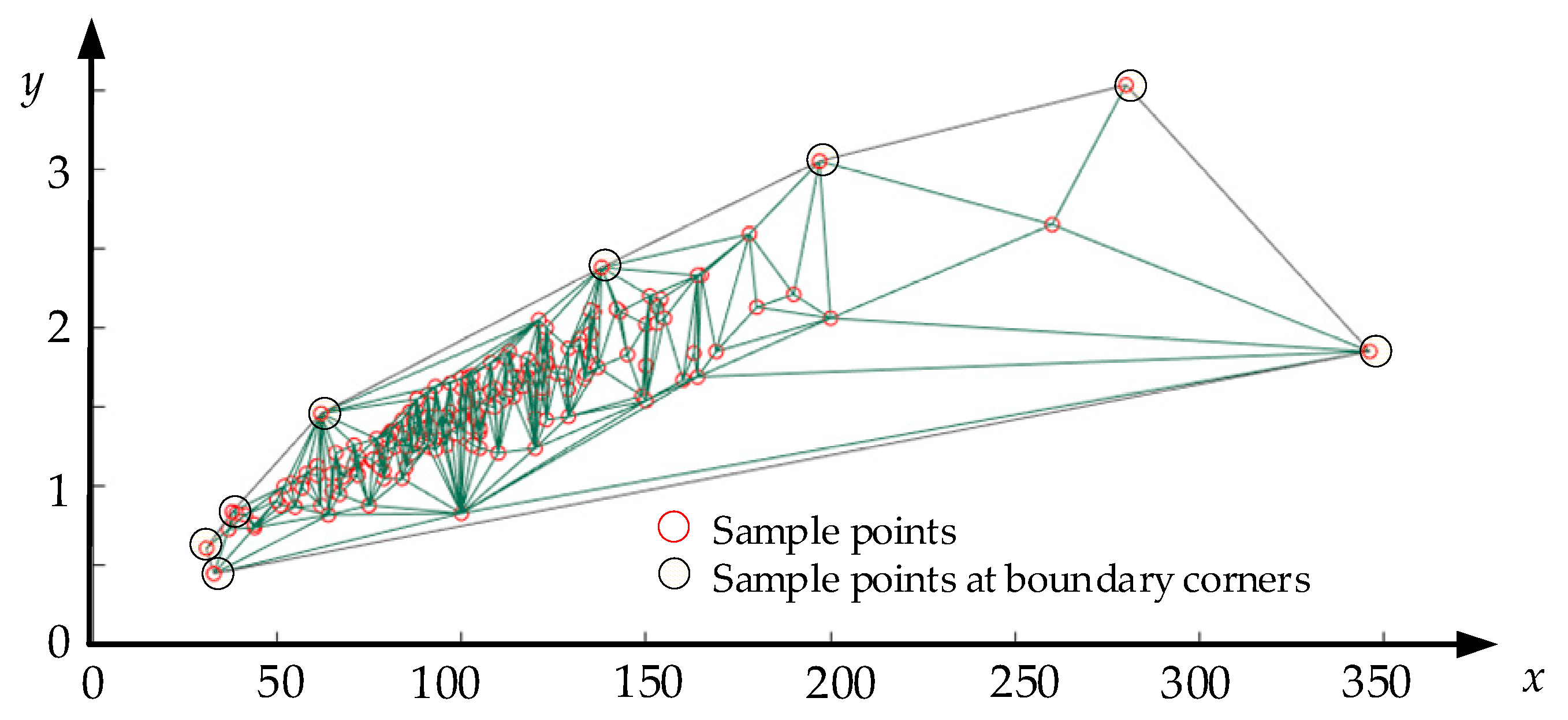
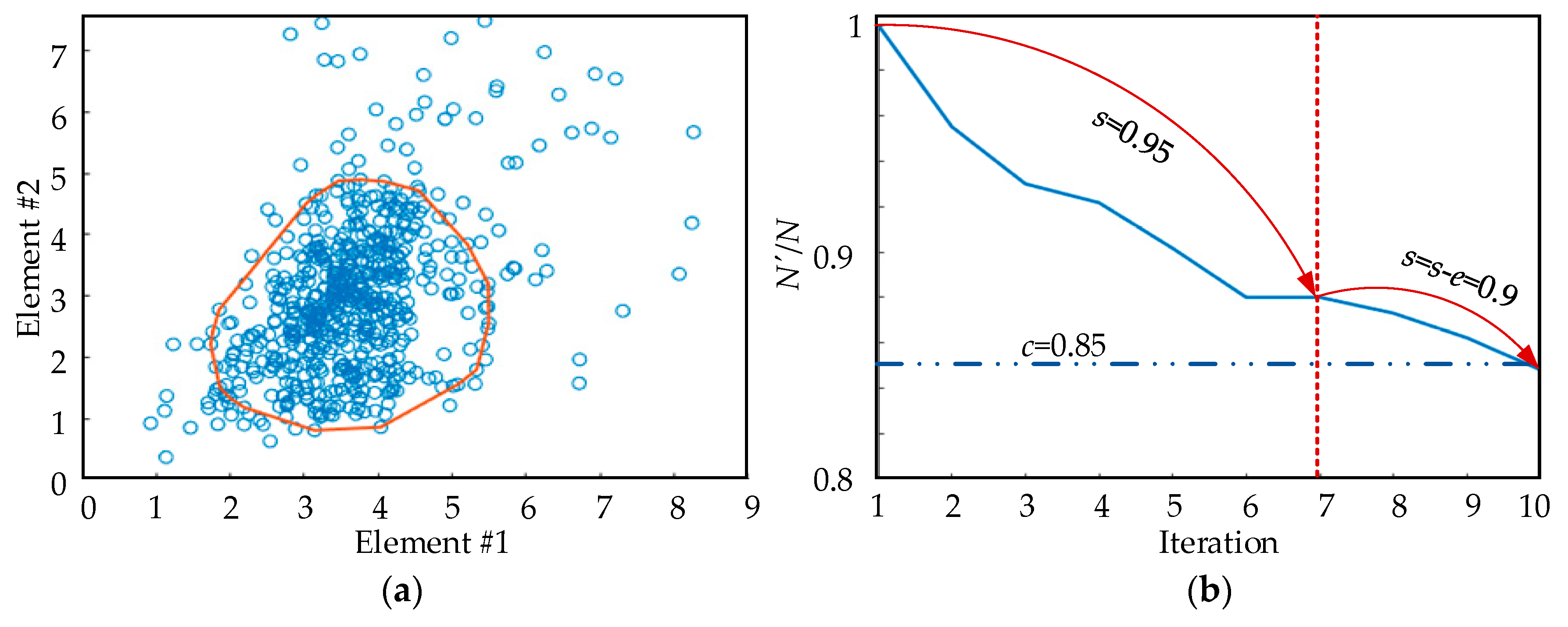
2.5. Confidence Region
2.6. Evaluation of Discrimination Diagrams
3. Experiment and Analysis
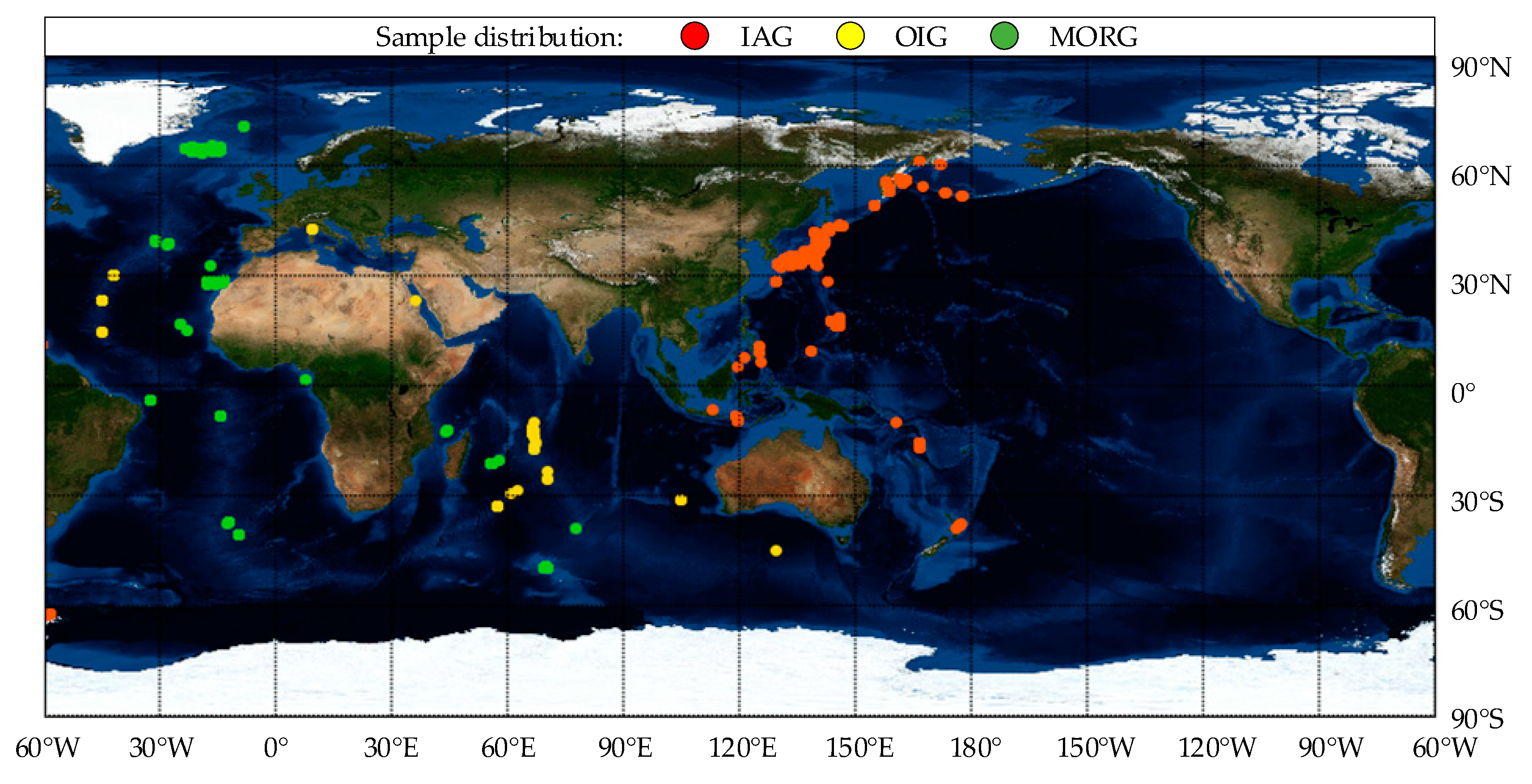
3.1. Data Collection and Preprocessing
3.2. Designation and Evaluation of Discrimination Diagrams
3.2.1. Discrimination Diagrams for IAG and Non-IAG
3.2.2. Discrimination Diagrams for OIG and Non-OIG
3.2.3. Discrimination Diagrams for MORG and Non-MORG
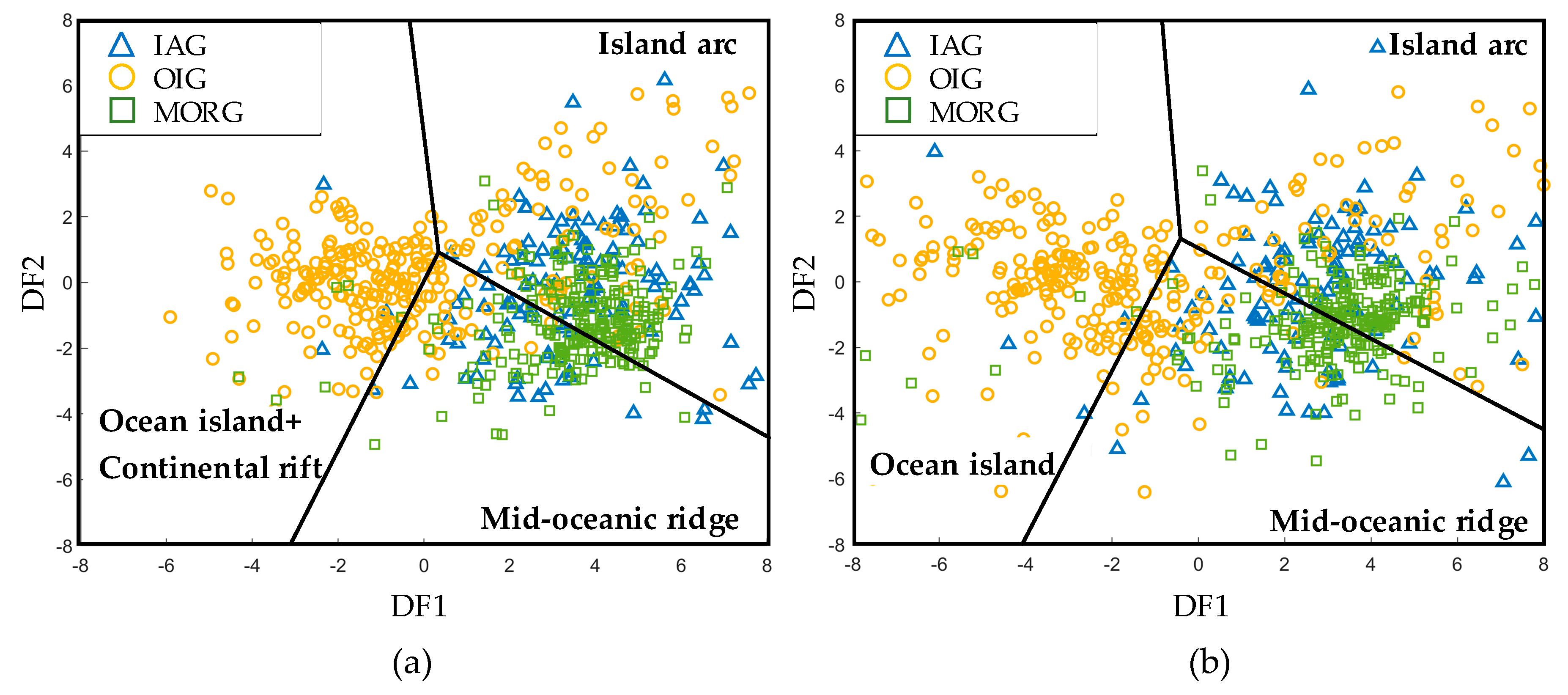
3.2.4. Discrimination Diagrams for IAG–OIG–MORG
4. Discussion
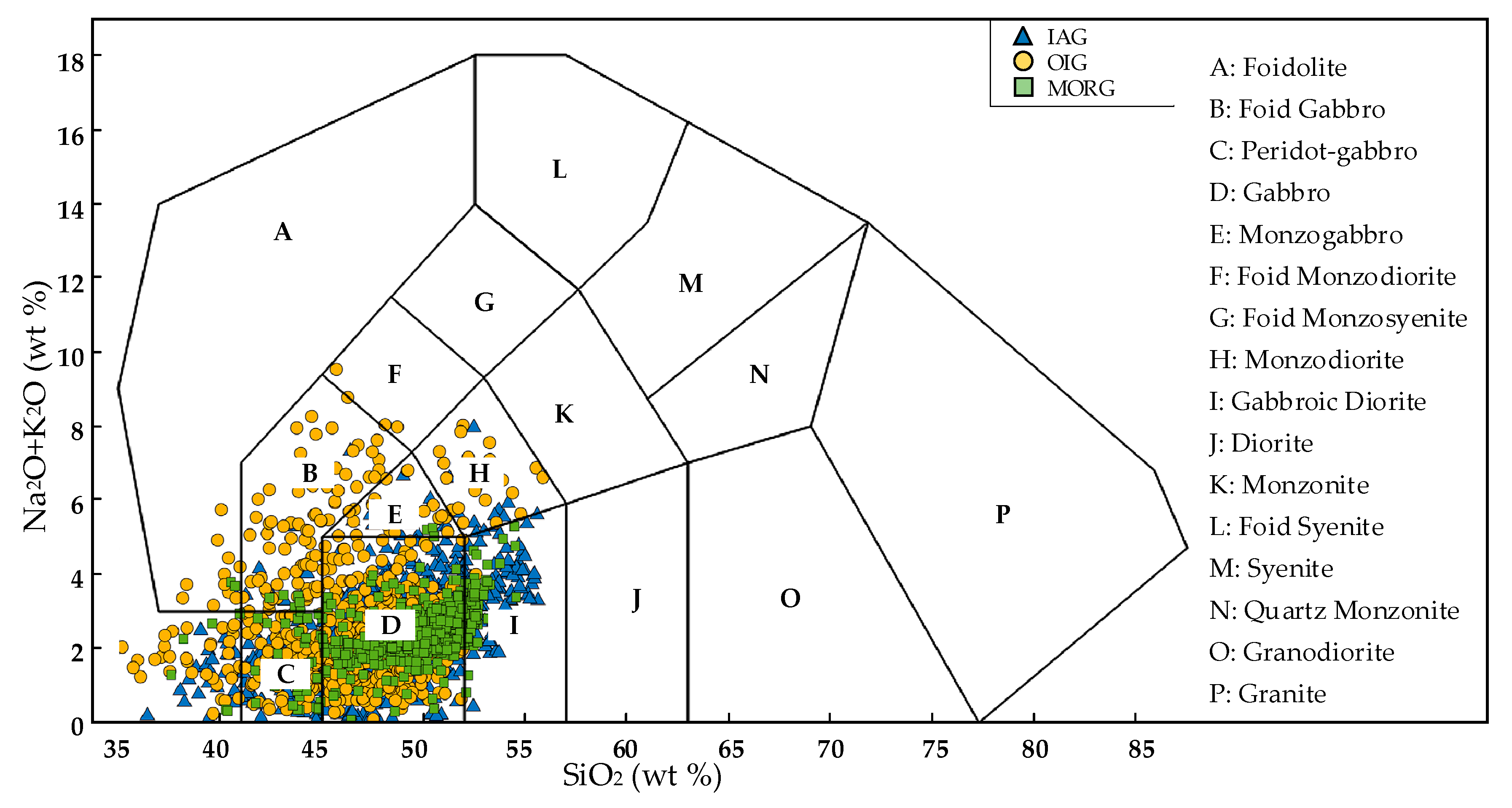
4.1. The Use of Basalt in Discriminating among Different Tectonic Settings
4.2. Using Gabbroic Rocks in Discrimination Tasks?
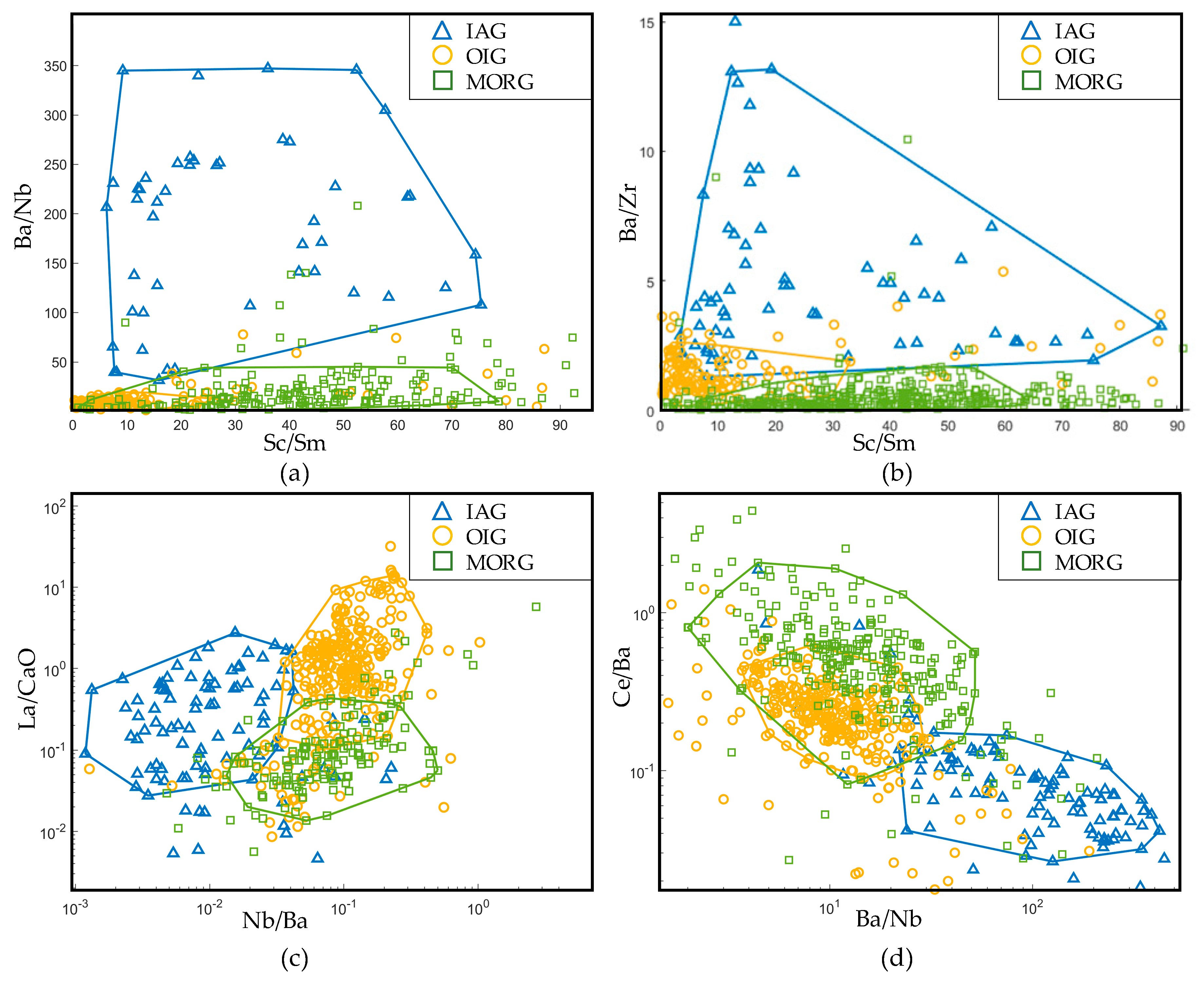
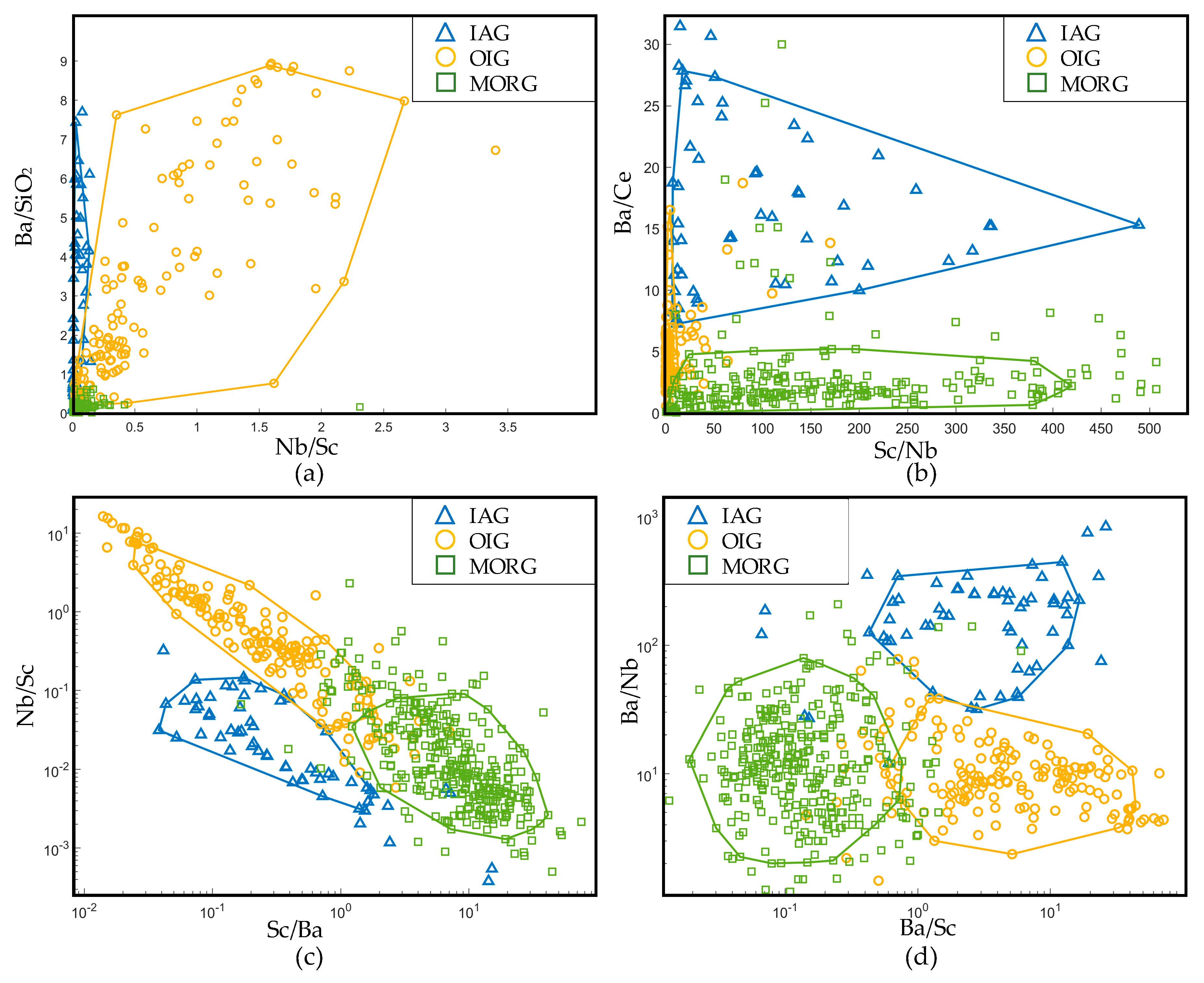
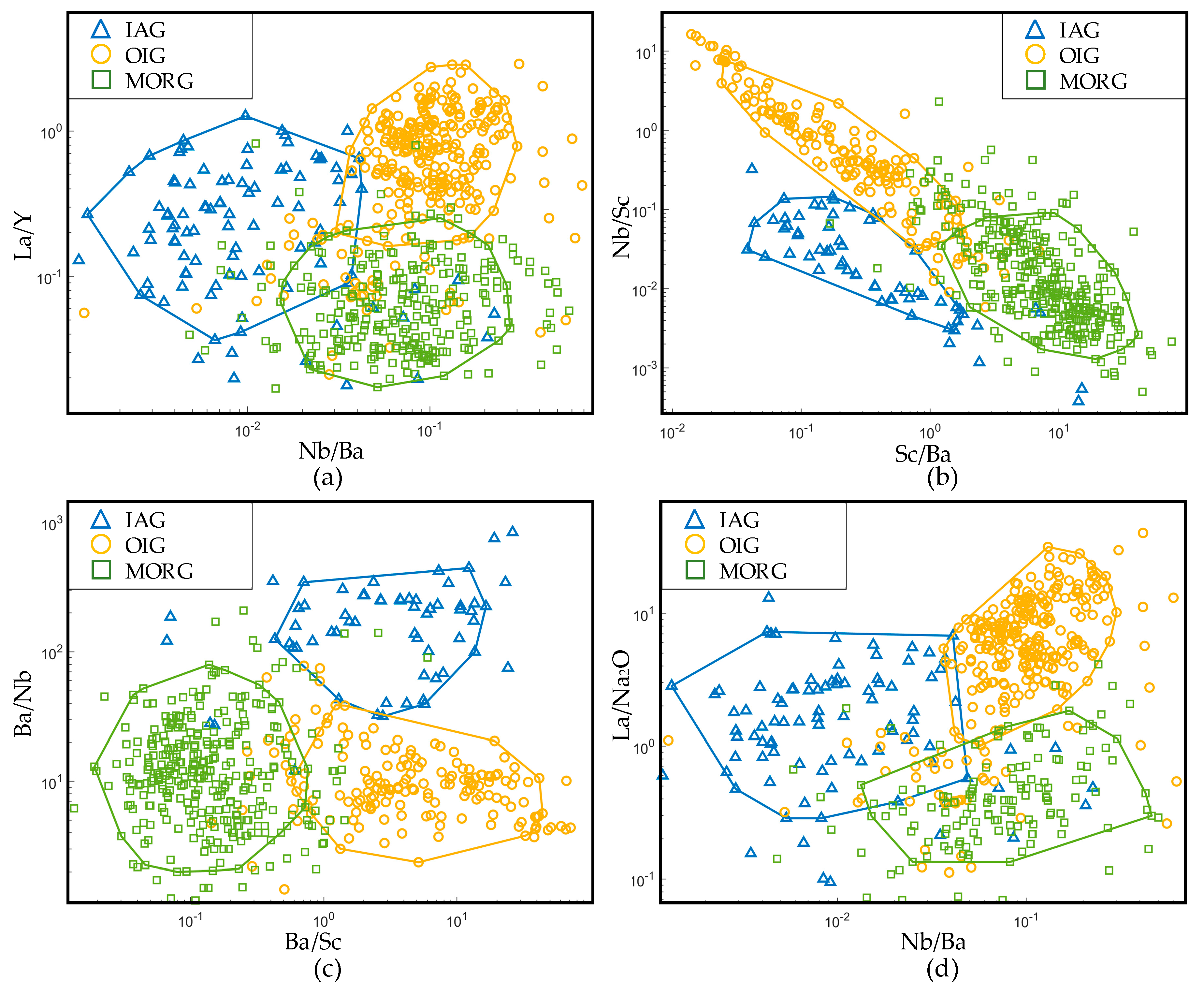
4.3. New Gabbroic Rock Discrimination Diagrams
4.3.1. La/Y–Nb/Ba Diagram
4.3.2. Nb/Sc–Sc/Ba Diagram
4.3.3. Ba/Nb–Ba/Sc Diagram
4.3.4. La/Na2O–Nb/Ba Diagram
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, P.; Glover, L., III. A tectonics test of the most commonly used geochemical discriminant diagrams and patterns. Earth-Sci. Rev. 1992, 33, 111–131. [Google Scholar] [CrossRef]
- Song, S.; Niu, Y.; Su, L.; Xia, X. Tectonics of the north Qilian orogen, NW China. Gondwana Res. 2013, 23, 1378–1401. [Google Scholar] [CrossRef]
- Wilson, M. Igneous Petrogenesis; Springer: Dordrecht, The Netherlands, 1989; 466p. [Google Scholar]
- Xia, L.; Li, X.M. Basalt geochemistry as a diagnostic indicator of tectonic setting. Gondwana Res. 2019, 65, 43–67. [Google Scholar] [CrossRef]
- Pearce, J.A.; Cann, J.R. Ophiolite origin investigated by discriminant analysis using Ti, Zr and Y. Earth Planet. Sci. Lett. 1971, 12, 339–349. [Google Scholar] [CrossRef]
- Pearce, J.A.; Cann, J.R. Tectonic setting of basic volcanic rocks determined using trace element analyses. Earth Planet. Sci. Lett. 1973, 19, 290–300. [Google Scholar] [CrossRef]
- Pearce, J.A.; Norry, M.J. Petrogenetic implications of Ti, Zr, Y, and Nb variations in volcanic rocks. Contrib. Mineral. Petrol. 1979, 69, 33–47. [Google Scholar] [CrossRef]
- Roser, B.P.; Korsch, R.J. Determination of Tectonic Setting of Sandstone-Mudstone Suites Using SiO2 Content and K2O/Na2O Ratio. J. Geol. 1986, 94, 635–650. [Google Scholar] [CrossRef]
- Pearce, J.A.; Peate, D.W. Tectonic implications of the composition of volcanic arc magmas. Annu. Rev. Earth Planet. Sci. 1995, 23, 251–286. [Google Scholar] [CrossRef]
- Vermeesch, P. Tectonic discrimination diagrams revisited. Geochem. Geophys. Geosystems 2013, 7, 1–55. [Google Scholar] [CrossRef]
- Jankovics, M.É.; Taracsák, Z.; Dobosi, G.; Embey-Isztin, A.; Batki, A.; Harangi, S.; Hauzenberger, C.A. Clinopyroxene with diverse origins in alkaline basalts from the western Pannonian Basin: Implications from trace element characteristics. Lithos 2016, 262, 120–134. [Google Scholar] [CrossRef]
- Sánchez-Muñoz, L.; Müller, A.; Andrés, S.L.; Martin, R.F.; Modreski, P.J.; Moura, O.J.M.D. The P–Fe diagram for K-feldspars: A preliminary approach in the discrimination of pegmatites. Lithos 2016, 272, 116–127. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, G.; Eizenhöfer, P.R.; Sun, M.; Han, Y.; Hou, W.; Xu, B. Varying contents of sources affect tectonic-setting discrimination of sediments: A case study from permian sandstones in the eastern tianshan, Northwestern China. J. Geol. 2017, 125, 299–316. [Google Scholar] [CrossRef][Green Version]
- Verma, S.P.; Pandarinath, K.; Verma, S.K.; Agrawal, S. Fifteen new discriminant-function-based multi-dimensional robust diagrams for acid rocks and their application to Precambrian rocks. Lithos 2013, 168, 113–123. [Google Scholar] [CrossRef]
- Verma, S.P.; Rivera-Gómez, M.A.; Díaz-González, L.; Pandarinath, K.; Amezcua-Valdez, A.; Rosales-Rivera, M.; Verma, S.K.; Quiroz-Ruiz, A.; Armstrong-Altrin, J.S. Multidimensional classification of magma types for altered igneous rocks and application to their tectonomagmatic discrimination and igneous provenance of siliciclastic sediments. Lithos 2017, 278, 321–330. [Google Scholar] [CrossRef]
- Stepanova, A.V.; Stepanov, V.S.; Larionov, A.N.; Azimov, P.Y.; Egorova, S.V.; Larionova, Y.O. 2.5 Ga gabbro–anorthosites in the Belomorian Province, Fennoscandian Shield: Petrology and tectonic setting. Petrology 2017, 25, 566–591. [Google Scholar] [CrossRef]
- Yamasaki, T.; Nanayama, F. Enriched mid–ocean ridge basalt–type geochemistry of basalts and gabbros from the Nikoro Group, Tokoro Belt, Hokkaido, Japan. J. Mineral. Petrol. Sci. 2017, 112, 311–323. [Google Scholar] [CrossRef]
- Gavryushkina, O.A.; Kruk, N.N.; Semenov, I.V.; Vladimirov, A.G.; Kuibida, Y.V.; Serov, P.A. Petrogenesis of Permian-Triassic intraplate gabbro–granitic rocks in the Russian Altai. Lithos 2018, 326, 71–89. [Google Scholar] [CrossRef]
- Liu, X.L.; Zhang, Q.; Li, W.C.; Yang, F.C.; Zhao, Y.; Li, Z.; Chen, W.F. Applicability of large-ion lithophile and high field strength element basalt discrimination diagrams. Int. J. Digit. Earth 2018, 11, 752–760. [Google Scholar] [CrossRef]
- Jiao, S.; Zhang, Q.; Zhou, Y.; Chen, W.; Liu, X.; Gopalakrishnan, G. Progress and challenges of big data research on petrology and geochemistry. Solid Earth Sci. 2018, 3, 105–114. [Google Scholar] [CrossRef]
- Di, P.F.; Chen, W.F.; Zhang, Q.; Wang, J.R.; Tang, Q.Y.; Jiao, S.T. Comparison of global N-MORB and E-MORB classification schemes. Acta Petrol. Sin. 2018, 34, 264–274. [Google Scholar]
- Snow, C.A. A reevaluation of tectonic discrimination diagrams and a new probabilistic approach using large geochemical databases: Moving beyond binary and ternary plots. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Delaunay, B. Sur la sphère vide. Izv. Akad. Nauk SSSR Otd. Mat. Estestv. Nauk 1934, 7, 1–2. [Google Scholar]
- Lee, D.T.; Schachter, B.J. Two algorithms for constructing a Delaunay triangulation. Int. J. Comput. Inf. Sci. 1980, 9, 219–242. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Tan, T.S.; Waupotitsch, R. An O (n2 log n) time algorithm for the minmax angle triangulation. SIAM J. Sci. Stat. Comput. 1992, 13, 994–1008. [Google Scholar] [CrossRef]
- Cao, T.T.; Edelsbrunner, H.; Tan, T.S. Proof of correctness of the digital Delaunay triangulation algorithm. Comput. Geom. Theory Appl. 2015, 48, 507–519. [Google Scholar] [CrossRef]
- Su, T.; Wang, W.; Lv, Z.; Wu, W.; Li, X. Rapid Delaunay triangulation for randomly distributed point cloud data using adaptive Hilbert curve. Comput. Graph. 2016, 54, 65–74. [Google Scholar] [CrossRef]
- Buccianti, A.; Mateu-Figueras, G.; Pawlowsky-Glahn, V. Frequency distributions and natural laws in geochemistry. Geol. Soc. Lond. Spec. Publ. 2006, 264, 175–189. [Google Scholar] [CrossRef]
- PetDB Search: Find & Select Samples & Data. Available online: https://search.earthchem.org/ (accessed on 8 January 2020).
- Geochemistry of Rocks of the Oceans and Continents. Available online: http://georoc.mpch-mainz.gwdg.de/georoc/ (accessed on 8 January 2020).
- Middlemost, E.A.K. Naming materials in the magma/igneous rock system. Earth Sci. Rev. 1994, 37, 215–224. [Google Scholar] [CrossRef]
- Bowen, N.L. The Evolution of Igneous Rocks; Princeton University Press: New York, NY, USA, 1928; 334p. [Google Scholar]
- Best, M.G.; Christiansen, E.H. Igneous Petrology; Blackwell Science: Oxford, UK, 2001; 458p. [Google Scholar]
- Wager, L.R.; Brown, G.M. Layered Igneous Rocks; Oliver and Boyd: Edinburgh, UK; Oliver and Boyd: London, UK, 1968; 588p. [Google Scholar]
- Rollison, H.R. Using Geochemical Data: Evaluation, Presentation, Interpretation; Routledge: London, UK, 1993; 384p. [Google Scholar]
- Irvine, T.N.; Baragar, W.R.A. A guide to the chemical classification of the common volcanic rocks. Can. J. Earth Sci. 1971, 8, 523–548. [Google Scholar] [CrossRef]
- Miyashiro, A. The Troodos ophiolitic complex was probably formed in an island arc. Earth Planet. Sci. Lett. 1973, 19, 218–224. [Google Scholar] [CrossRef]
- Glassley, W. Geochemistry and tectonics of the Crescent volcanic rocks, Olympic Peninsula, Washington. Geol. Soc. Am. Bull. 1974, 85, 785–794. [Google Scholar] [CrossRef]
- Pearce, J.A. Basalt geochemistry used to investigate past tectonic environments on Cyprus. Tectonophysics 1975, 25, 41–67. [Google Scholar] [CrossRef]
- Pearce, J.A. Statistical analysis of major element patterns in basalts. J. Pet. 1976, 17, 15–43. [Google Scholar] [CrossRef]
- Pearce, J.A. Trace element characteristics of lavas from destructive plate boundaries. Andesites 1982, 8, 525–548. [Google Scholar]
- Pearce, J.A. Role of the Subcontinental Lithosphere in Magma Genesis at Active Continental Margins. In Continental Basalt and Mantle Xenoliths, Nantwich, England; Hawkesworth, C.J., Norry, M.J., Eds.; Shiva Publications: Chandigarh, India, 1983; pp. 230–249. [Google Scholar]
- Pearce, J.A. Supra-Subduction Zone Ophiolites: The Search for Modern Analogues. In Ophiolite Concept and the Evolution of Geological Thought: Geological Society of America Special Paper; Dilek, Y., Newcomb, S., Eds.; Geological Society of America: Boulder, CO, USA, 2003; Volume 373, pp. 269–293. [Google Scholar]
- Pearce, T.H.; Gorman, B.E.; Birkett, T.C. The relationship between major element chemistry and tectonic environment of basic and intermediate volcanic rocks. Earth Planet. Sci. Lett. 1977, 36, 121–132. [Google Scholar] [CrossRef]
- Wood, D.A.; Joron, J.L.; Treuil, M. A re-appraisal of the use of trace elements to classify and discriminate between magma series erupted in different tectonic settings. Earth Planet. Sci. Lett. 1979, 45, 326–336. [Google Scholar] [CrossRef]
- Wood, D.A. The application of a Th–Hf–Ta diagram to problems of tectonomagmatic classification and to establishing the nature of crustal contamination of basaltic lavas of the British Tertiary Volcanic Province. Earth Planet Sci. Lett. 1980, 50, 11–30. [Google Scholar] [CrossRef]
- Capedri, S.; Venturelli, G.; Bocchi, G.; Dostal, J.; Garuti, G.; Rossi, A. The geochemistry and petrogenesis of an ophiolitic sequence from Pindos, Greece. Contrib. Mineral. Petrol. 1980, 74, 189–200. [Google Scholar] [CrossRef]
- Mullen, E.D. MnO–TiO2–P2O5: A minor element discriminant for basaltic rocks of oceanic environments and its implications for petrogenesis. Earth Planet. Sci. Lett. 1983, 62, 53–62. [Google Scholar] [CrossRef]
- Pearce, J.A.; Lippard, S.J.; Roberts, S. Characteristics and tectonic significance of supra-subduction zone ophiolites. Geol. Soc. Lond. Spec. Publ. 1984, 16, 77–94. [Google Scholar] [CrossRef]
- Harris, N.B.W.; Pearce, J.A.; Tindle, A.G. Geochemical characteristics of collision-zone magmatism. Geol. Soc. Lond. Spec. Publ. 1986, 19, 67–81. [Google Scholar] [CrossRef]
- Meschede, M. A method of discriminating between different types of mid-ocean ridge basalts and continental tholeiites with the Nb, Zr, Y diagram. Chem. Geol. 1986, 56, 207–218. [Google Scholar] [CrossRef]
- Workman, R.K.; Hart, S.R. Major and trace element composition of the depleted MORB mantle (DMM). Earth Planet. Sci. Lett. 2005, 231, 53–72. [Google Scholar] [CrossRef]
- Galoyan, G.; Rolland, Y.; Sosson, M.; Corsini, M.; Melkonyan, R. Evidence for superposed MORB, oceanic plateau and volcanic arc series in the Lesser Caucasus (Stepanavan, Armenia). C. R. Geosci. 2007, 339, 482–492. [Google Scholar] [CrossRef]
- Zhao, Z.H. How to use the trace element diagrams to discriminate tectonic settings. Geotecton. Metallog. 2007, 31, 92–103. [Google Scholar]
- Hickey, R.L.; Frey, F.A. Geochemical characteristics of boninite series volcanics: Implications for their source. Geochim. Cosmochim. Acta 1982, 46, 2099–2115. [Google Scholar] [CrossRef]
- Crawford, A.J.; Falloon, T.J.; Green, D.H. Classification, Petrogenesis and Tectonic Settings of Boninites. In Boninite; Crawford, A.J., Ed.; Unwin Hyman: London, UK, 1989; pp. 1–49. [Google Scholar]
- Kocaka, K.; Isıka, F.; Arslanb, M.; Zedef, V. Petrological and source region characteristics of ophiolitic hornblende gabbros from the Aksaray and Kayseri regions, central Anatolian crystalline complex, Turkey. J. Asian Earth Sci. 2005, 25, 883–891. [Google Scholar] [CrossRef]
- Pollock, J.C.; Hibbard, J.P. Geochemistry and tectonic significance of the Stony Mountain gabbro, North Carolina: Implications for the Early Paleozoic evolution of Carolinia. Gondwana Res. 2010, 17, 500–515. [Google Scholar] [CrossRef]
- Verma, S.P.; Guevara, M.; Agrawal, S. Discriminating four tectonic settings: Five new geochemical diagrams for basic and ultrabasic volcanic rocks based on log-ratio transformation of major-element data. J. Earth Syst. Sci. 2006, 115, 485–528. [Google Scholar] [CrossRef]
- Agrawal, S.; Guevara, M.; Verma, S.P. Tectonic discrimination of basic and ultrabasic rocks through log-transformed ratios of immobile trace elements. Int. Geol. Rev. 2008, 50, 1057–1079. [Google Scholar] [CrossRef]
- Verma, S.P.; Agrawal, S. New tectonic discrimination diagrams for basic and ultrabasic volcanic rocks through log-transformed ratios of high field strength elements and implications for petrogenetic processes. Rev. Mex. Cienc. Geológicas 2011, 28, 24–44. [Google Scholar]
- Verma, S.P.; Torres-Alvarado, I.S.; Sotelo-Rodríguez, Z.T. SINCLAS: Standard igneous norm and volcanic rock classification system. Comput. Geosci. 2002, 28, 711–715. [Google Scholar] [CrossRef]
- Egozcue, J.J.; Pawlowsky-Glahn, V.; Mateu-Figueras, G.; Barcelo-Vidal, C. Isometric logratio transformations for compositional data analysis. Math. Geol. 2003, 35, 279–300. [Google Scholar] [CrossRef]
- Pawlowsky-Glahn, V.; Egozcue, J.J. Compositional data and their analysis: An introduction. Geol. Soc. Lond. Spec. Publ. 2006, 264, 1–10. [Google Scholar] [CrossRef]
- Verma, S.P. Statistical evaluation of bivariate, ternary and discriminant function tectonomagmatic discrimination diagrams. Turk. J. Earth Sci. 2010, 19, 185–238. [Google Scholar]
- Buccianti, A. Is compositional data analysis a way to see beyond the illusion? Comput. Geosci. 2013, 50, 165–173. [Google Scholar] [CrossRef]
- Parent, S.É.; Parent, L.E.; Egozcue, J.J.; Rozane, D.E.; Hernandes, A.; Lapointe, L.; Hebert-Gentile, V.; Naess, K.; Marchand, S.; Lafond, J.; et al. The plant ionome revisited by the nutrient balance concept. Front. Plant Sci. 2013, 4, 39. [Google Scholar] [CrossRef]
- Aitchison, J. The statistical analysis of compositional data. J. R. Stat. Soc. Ser. B 1982, 44, 139–160. [Google Scholar] [CrossRef]
- Hart, S.R.; Dunn, T. Experimental cpx/melt partitioning of 24 trace elements. Contrib. Mineral. Petrol. 1993, 113, 1–8. [Google Scholar] [CrossRef]
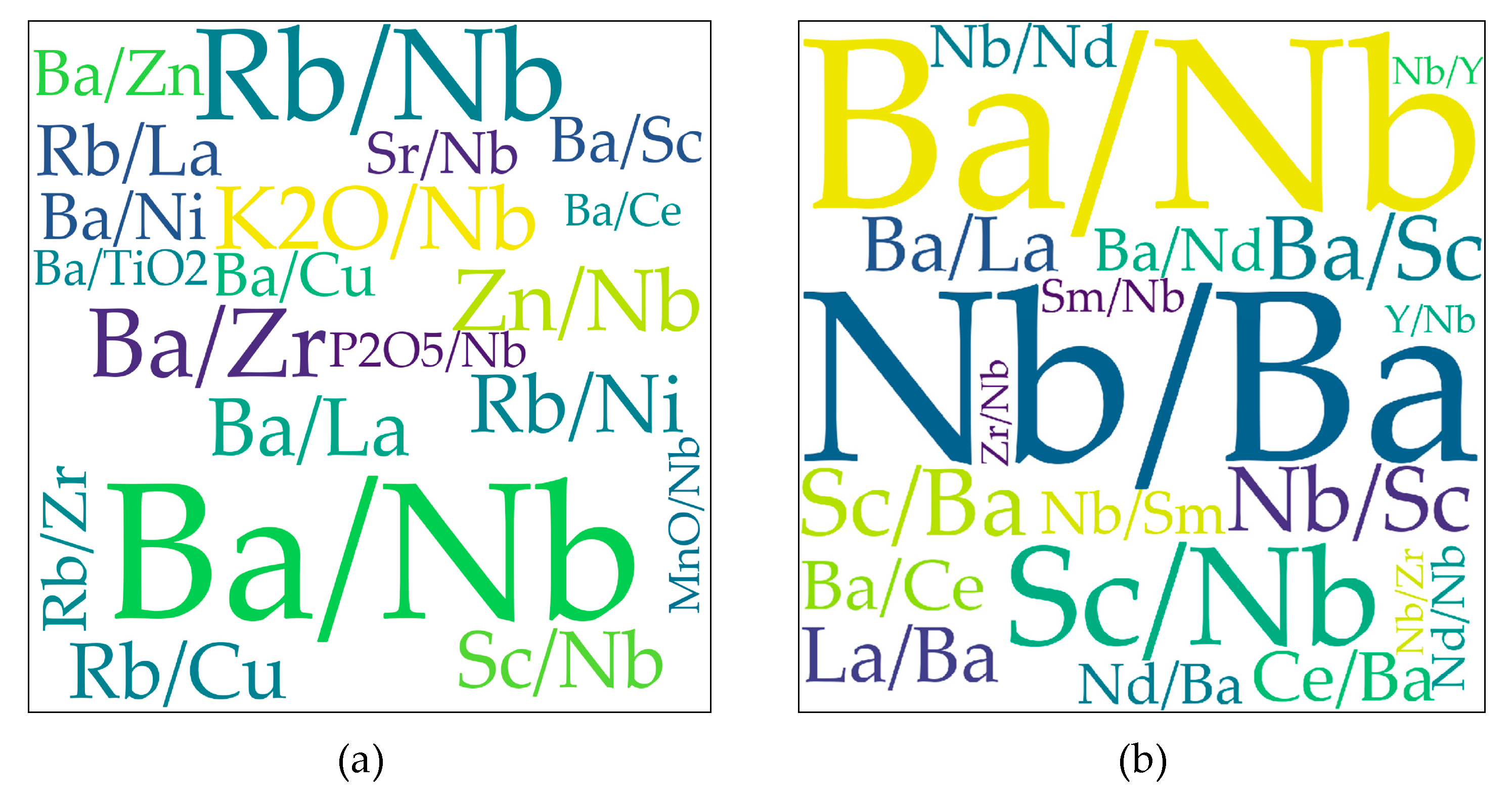
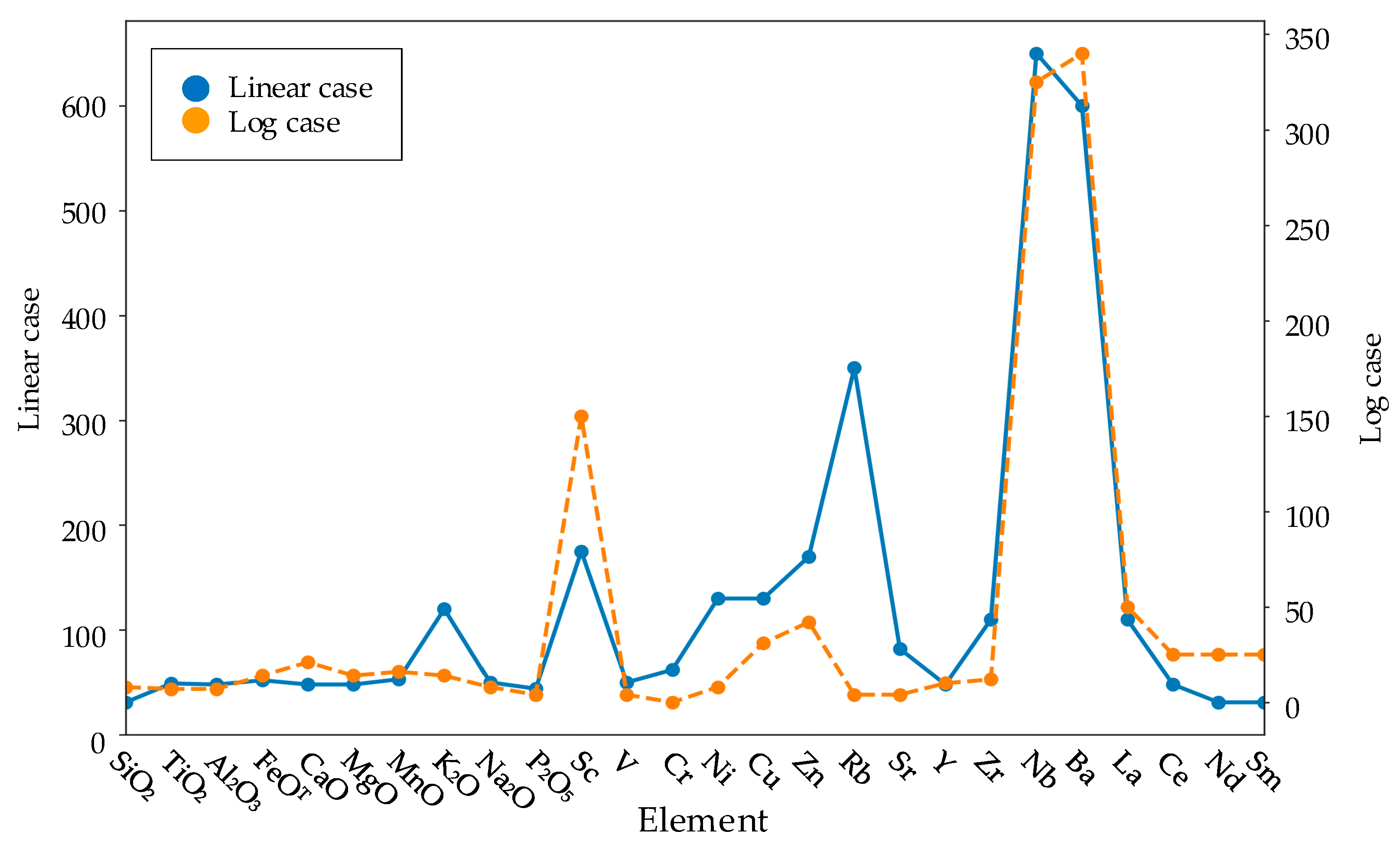
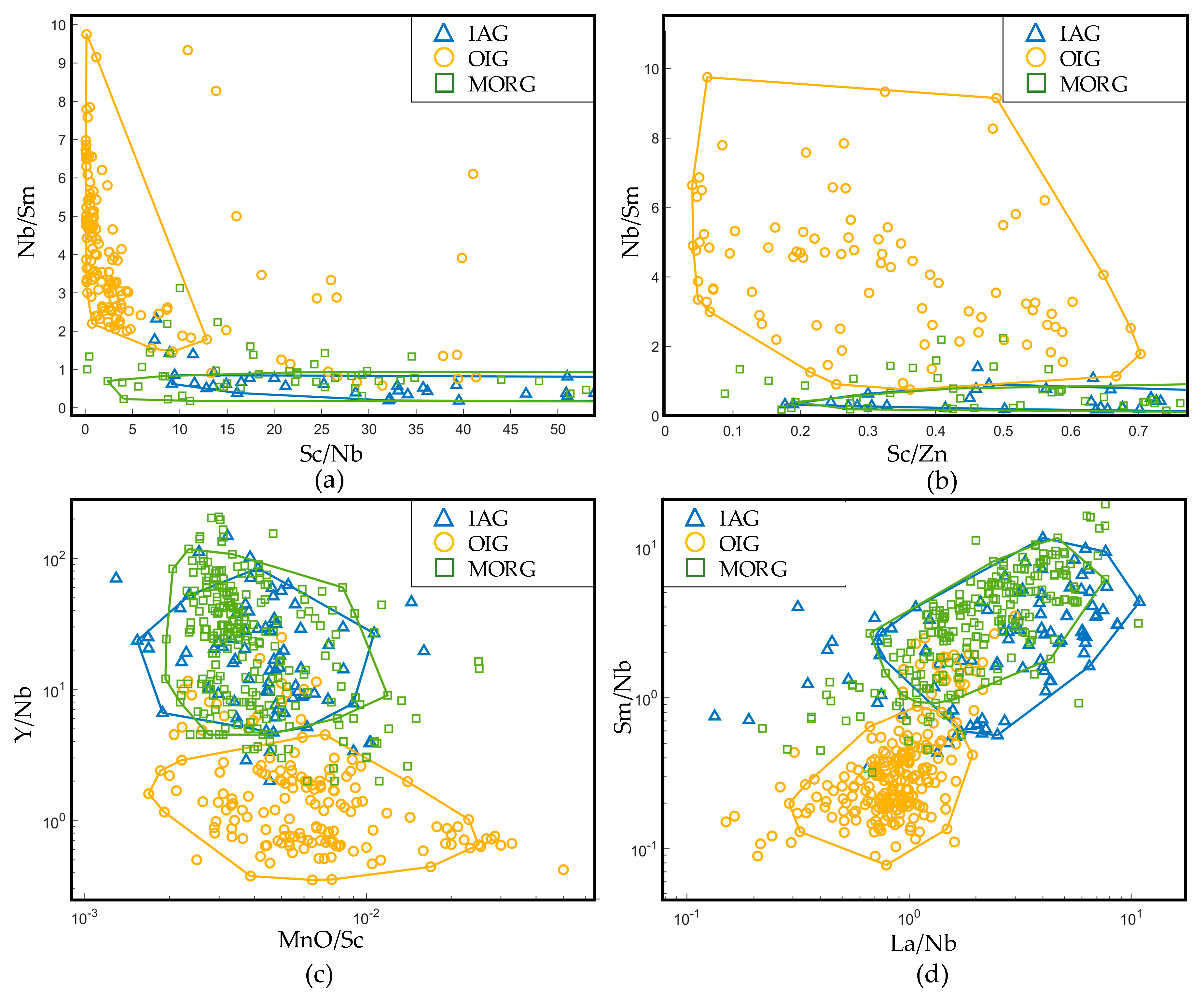
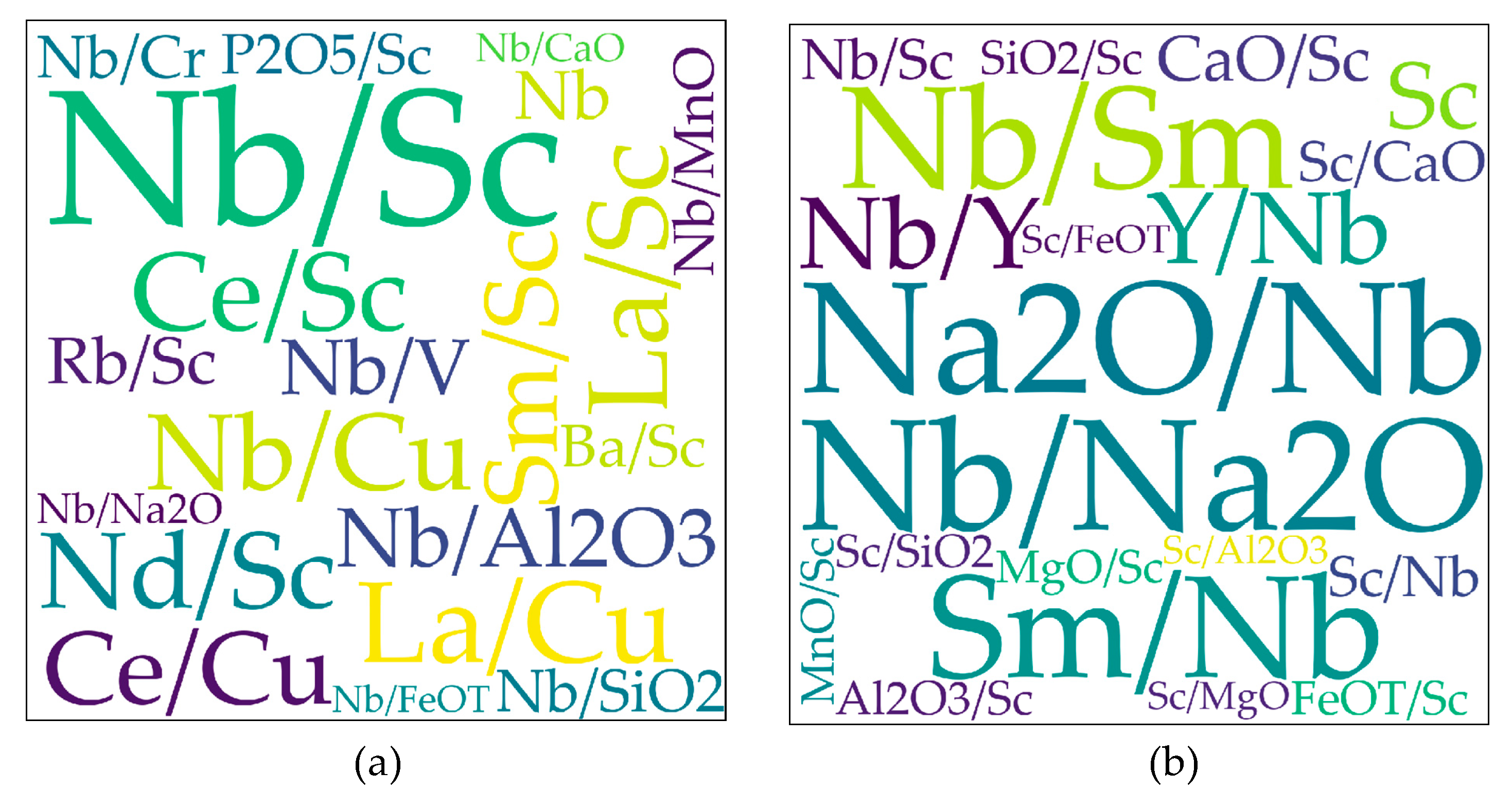
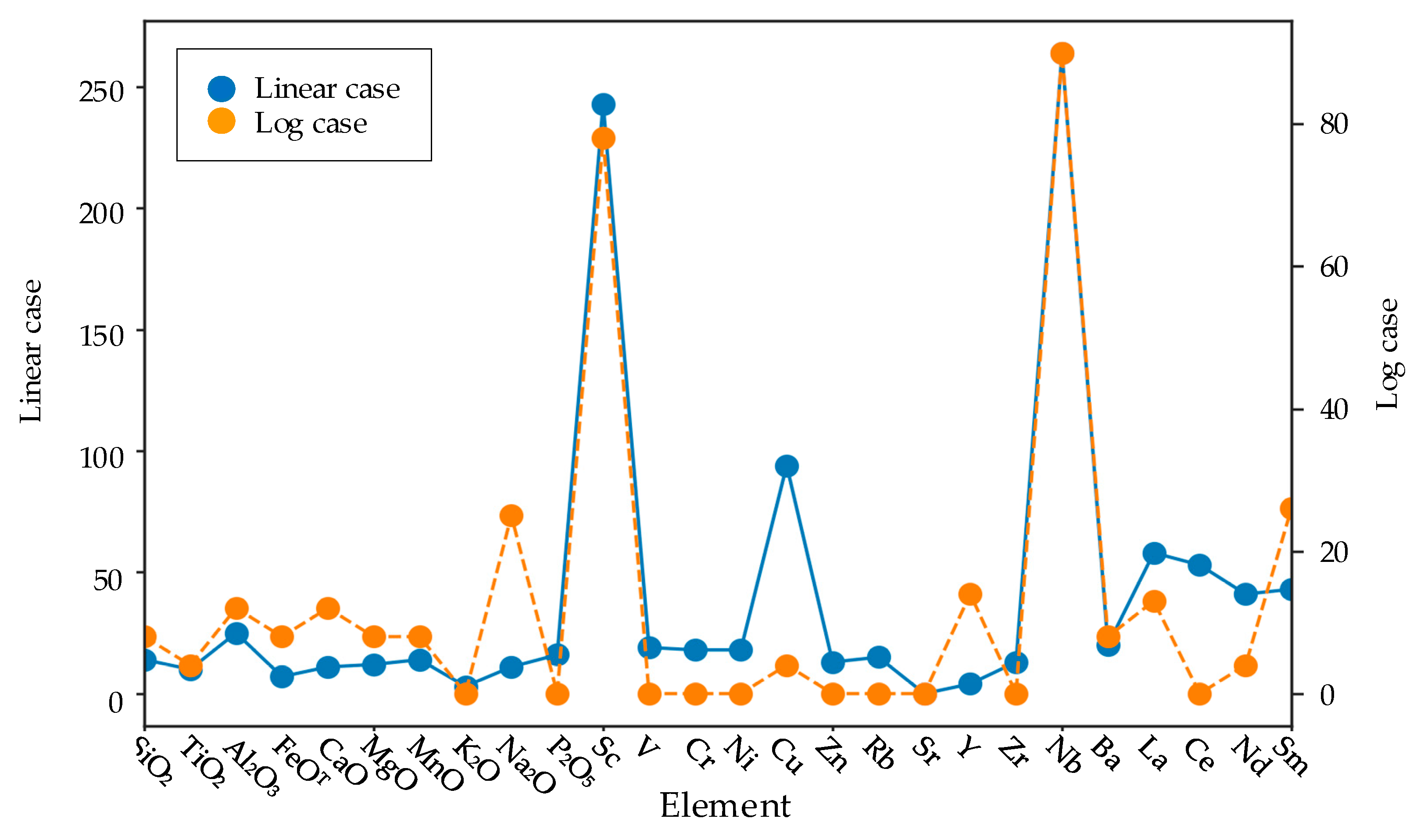
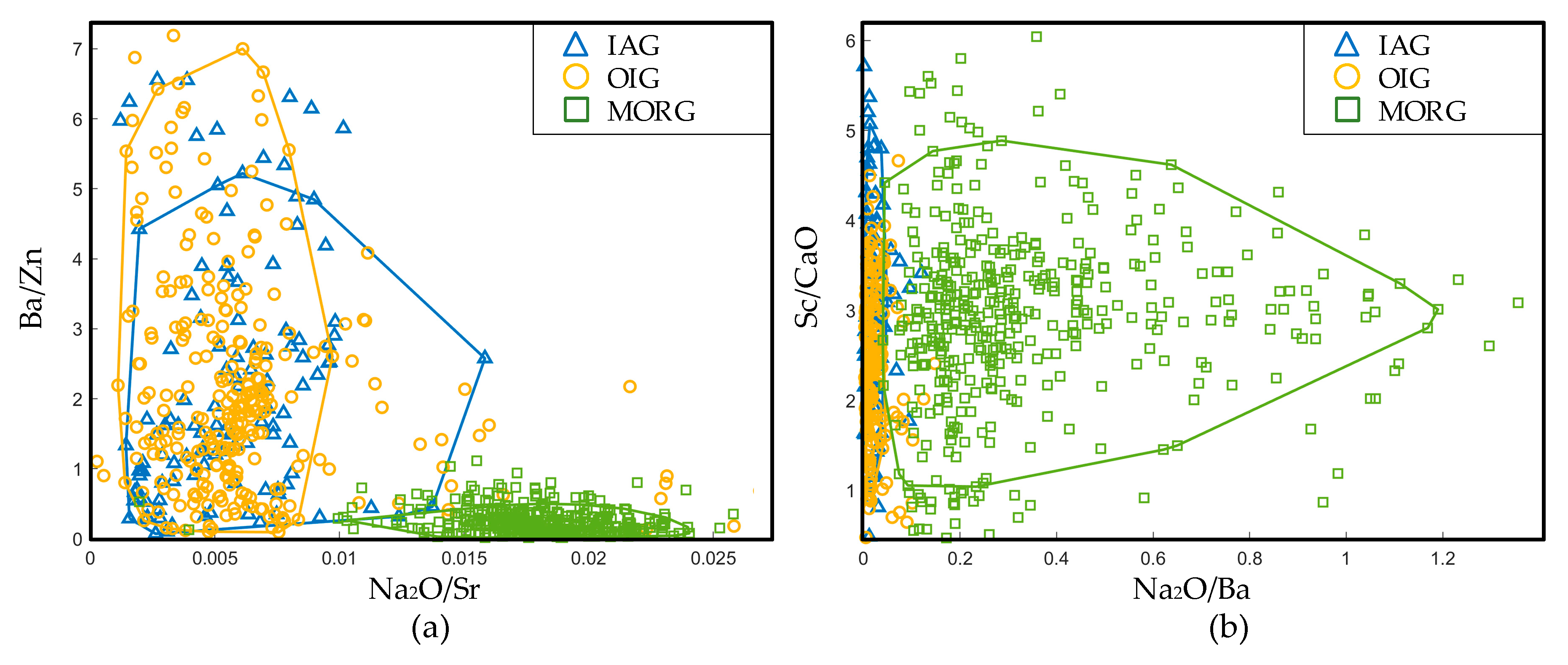
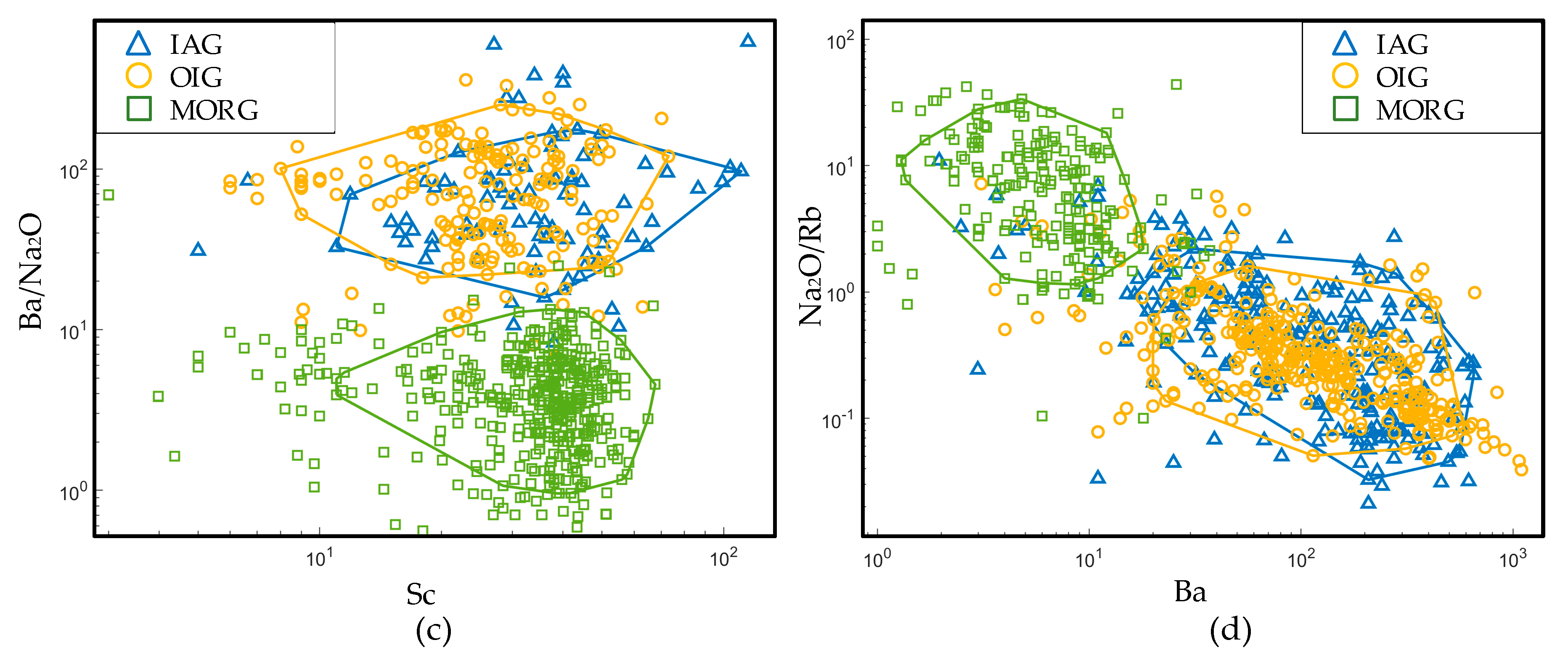
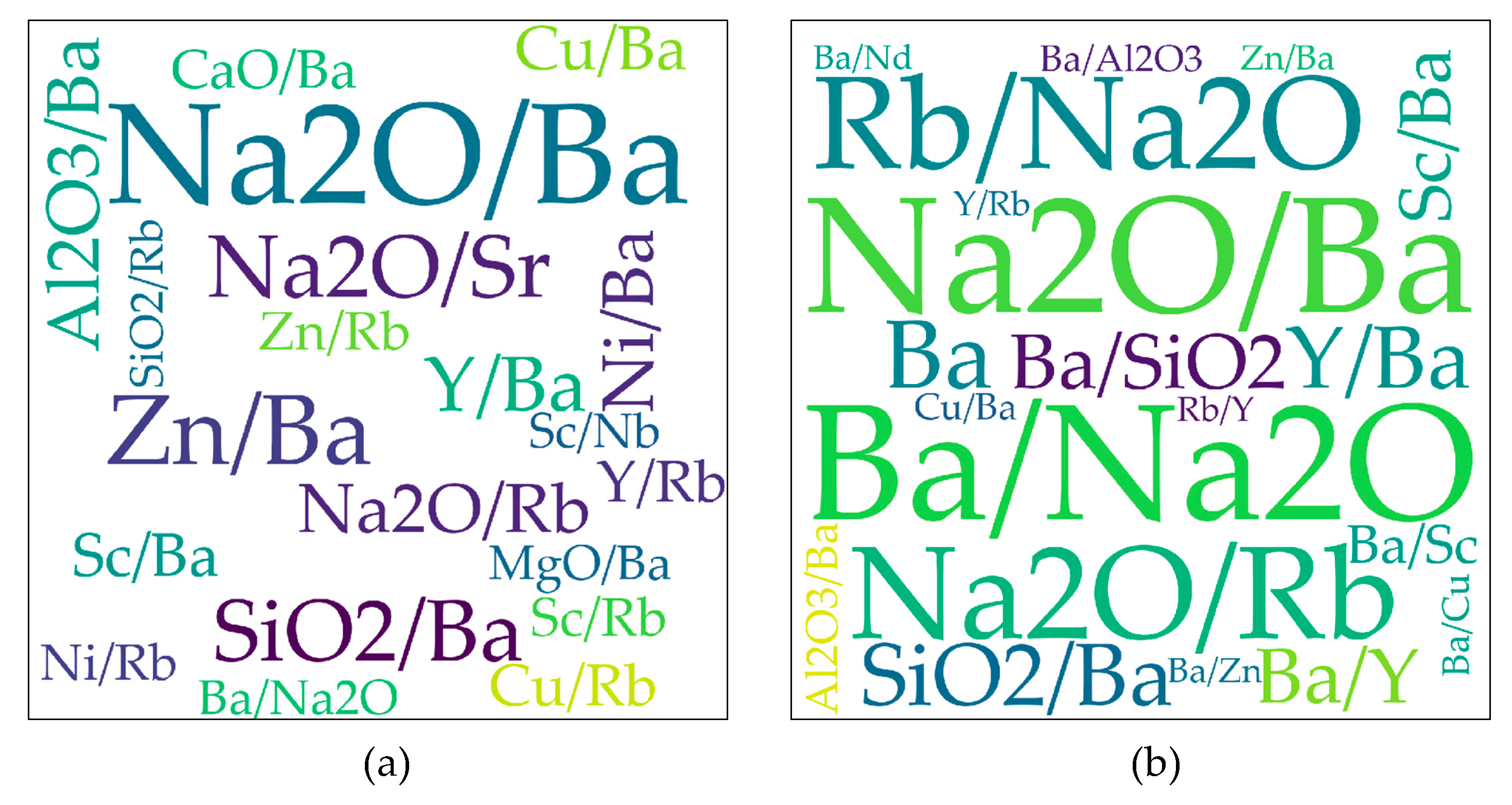
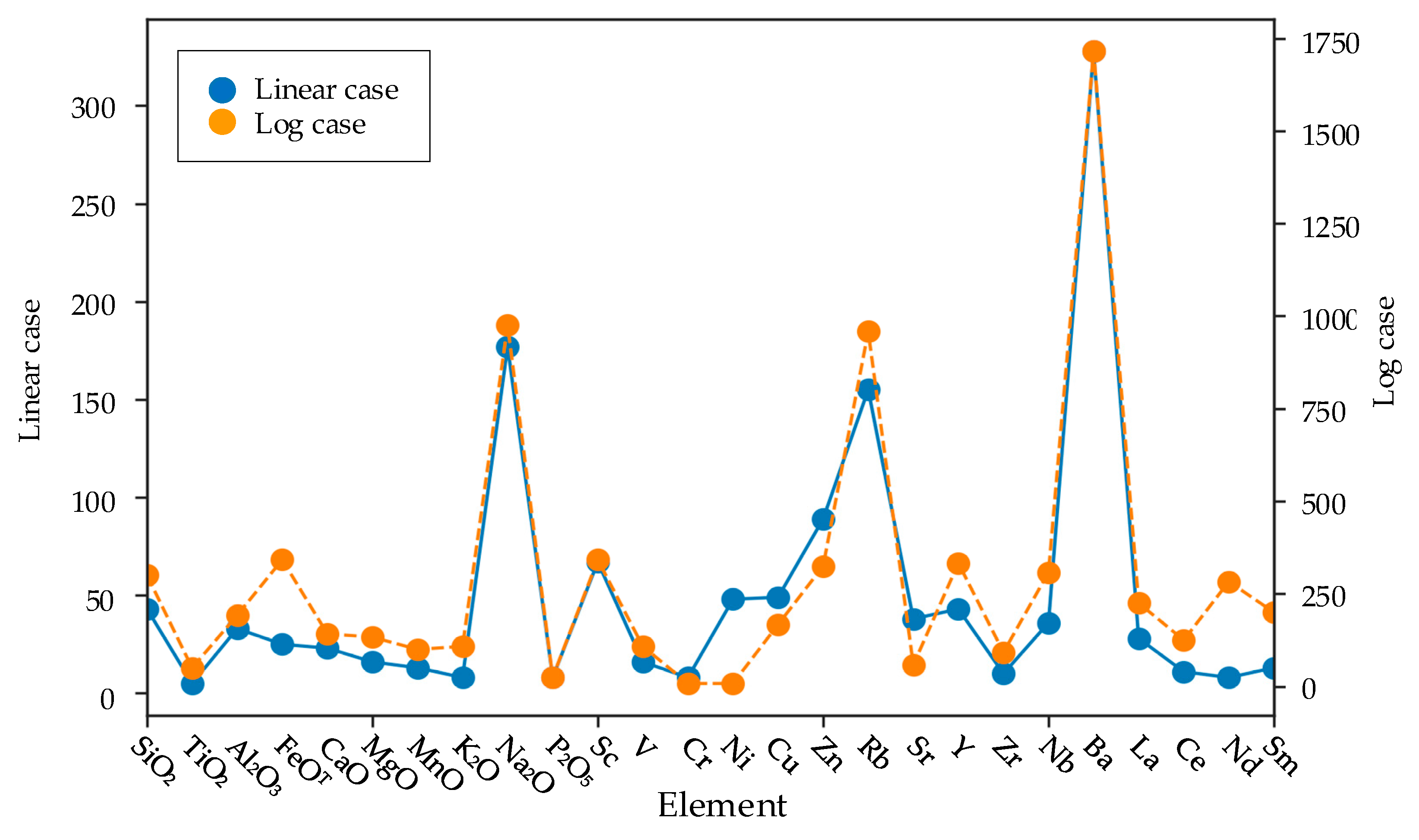
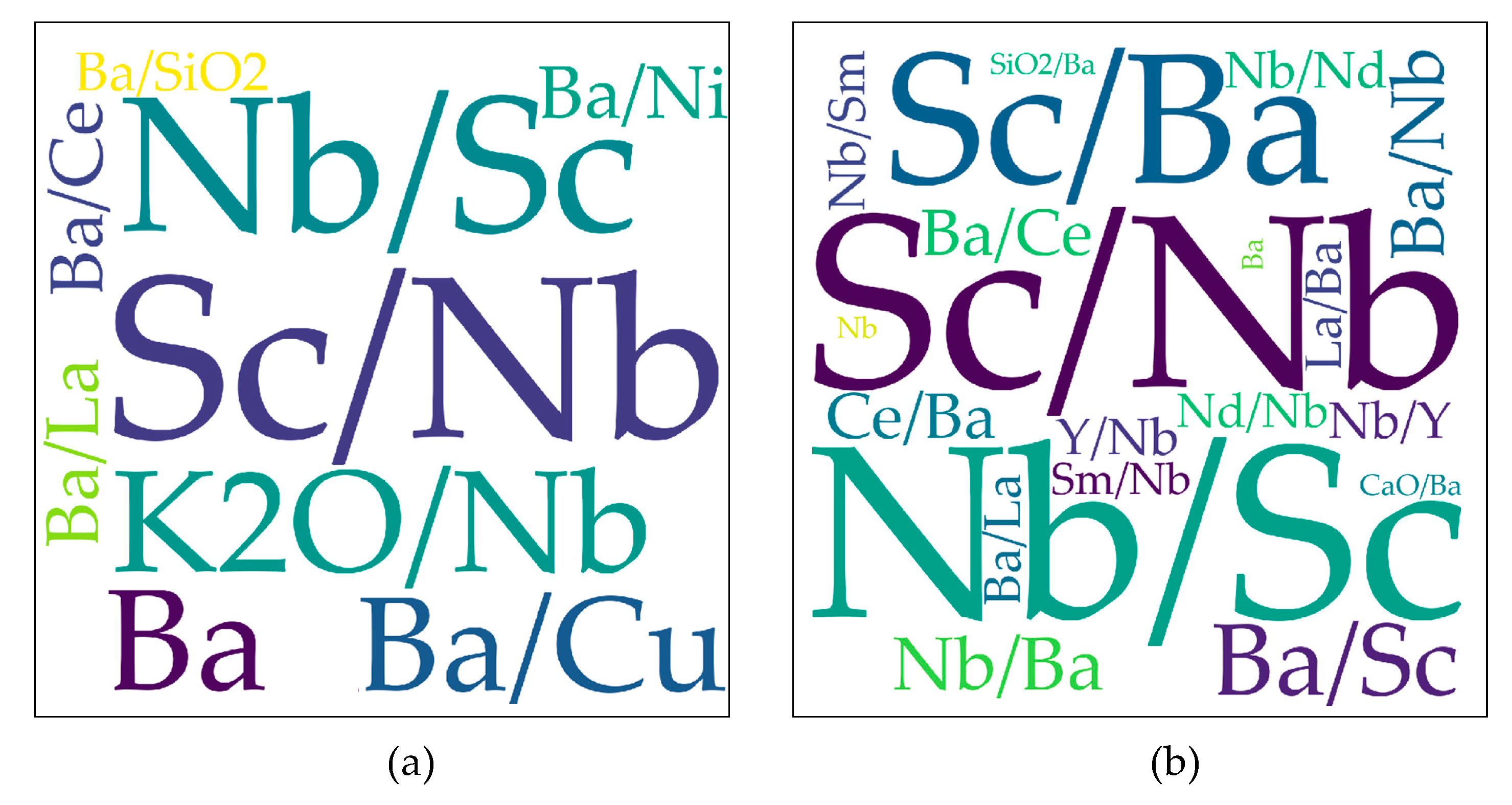
| Basic Elements | IAG | OIG | MORG | Basic Elements | IAG | OIG | MORG |
|---|---|---|---|---|---|---|---|
| SiO2 (wt%) | 47.9 | 46.5 | 49.6 | Ni (ppm) | 79.3 | 191 | 202 |
| TiO2 (wt%) | 0.933 | 2.17 | 0.812 | Cu (ppm) | 47.5 | 77.5 | 65.4 |
| Al2O3 (wt%) | 17.6 | 15.6 | 16.4 | Zn (ppm) | 77.0 | 75.0 | 52.7 |
| FeOT (wt%) | 9.10 | 9.78 | 6.81 | Rb (ppm) | 12.3 | 13.9 | 0.512 |
| CaO (wt%) | 11.4 | 12.1 | 12.0 | Sr (ppm) | 381 | 465 | 130 |
| MgO (wt%) | 8.11 | 8.70 | 9.64 | Y (ppm) | 15.3 | 19.2 | 15.7 |
| MnO (wt%) | 0.165 | 0.150 | 0.14 | Zr (ppm) | 44.4 | 111 | 31.3 |
| K2O (wt%) | 0.549 | 0.777 | 0.0762 | Nb (ppm) | 2.44 | 18.3 | 1.14 |
| Na2O (wt%) | 2.17 | 2.35 | 2.64 | Ba (ppm) | 157 | 181 | 9.59 |
| P2O5 (wt%) | 0.154 | 0.336 | 0.0890 | La (ppm) | 5.17 | 19.2 | 1.97 |
| Sc (ppm) | 39.1 | 28.1 | 33.9 | Ce (ppm) | 14.3 | 40.6 | 6.22 |
| V (ppm) | 261 | 269 | 177 | Nd (ppm) | 7.87 | 23.0 | 6.57 |
| Cr (ppm) | 272 | 468 | 300 | Sm (ppm) | 2.04 | 5.06 | 2.18 |
| Basic Elements | IAG | OIG | MORG | Basic Elements | IAG | OIG | MORG |
|---|---|---|---|---|---|---|---|
| SiO2 (wt%) | 3.67 | 3.25 | 2.63 | Ni (ppm) | 91.5 | 211 | 277 |
| TiO2 (wt%) | 0.695 | 1.50 | 1.14 | Cu (ppm) | 35.1 | 71.2 | 39.0 |
| Al2O3 (wt%) | 3.83 | 4.60 | 3.09 | Zn (ppm) | 39.2 | 39.0 | 31.7 |
| FeOT (wt%) | 2.83 | 3.55 | 2.42 | Rb (ppm) | 17.9 | 19.5 | 0.570 |
| CaO (wt%) | 2.69 | 2.97 | 1.87 | Sr (ppm) | 243 | 345 | 44.8 |
| MgO (wt%) | 4.17 | 5.20 | 3.44 | Y (ppm) | 9.06 | 13.5 | 16.0 |
| MnO (wt%) | 0.0581 | 0.05 | 0.06 | Zr (ppm) | 38.7 | 110 | 38.3 |
| K2O (wt%) | 0.666 | 0.90 | 0.13 | Nb (ppm) | 2.83 | 22.7 | 2.33 |
| Na2O (wt%) | 1.05 | 1.20 | 0.85 | Ba (ppm) | 144 | 191 | 7.78 |
| P2O5 (wt%) | 0.163 | 0.43 | 0.25 | La (ppm) | 4.93 | 21.6 | 3.58 |
| Sc (ppm) | 21.5 | 12.5 | 13.2 | Ce (ppm) | 15.0 | 46.0 | 12.1 |
| V (ppm) | 124 | 156 | 125 | Nd (ppm) | 5.99 | 25.2 | 12.8 |
| Cr (ppm) | 418 | 600 | 363 | Sm (ppm) | 1.48 | 4.85 | 3.57 |
| Type of Coordinates | Type of Important Elements | IAG vs. Non-IAG | OIG vs. Non-OIG | MORG vs. Non-MORG | IAG–OIG–MORG |
|---|---|---|---|---|---|
| Linear | Elements or element ratios | Ba/Nb, Rb/Nb | Nb/Sc | Na2O/Ba | Sc/Nb, Nb/Sc |
| Basic elements | Nb, Ba, Rb | Nb, Sc, Cu | Ba, Na2O, Rb | Nb, Ba, Sc | |
| Logarithmic | Elements or elements | Nb/Ba, Ba/Nb | Na2O/Nb, Nb/Na2O, Nb/Sm, Sm/Nb | Na2O/Ba, Ba/Na2O, Na2O/Rb, Rb/Na2O | Sc/Nb, Nb/Sc, Sc/Ba, Ba/Sc |
| Basic elements | Ba, Nb, Sc | Nb, Sc, Sm, Na2O | Ba, Na2O, Rb | Nb, Ba, Sc |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, S.; Li, M.; Zhang, Q.; Song, L. An Automated Method to Generate and Evaluate Geochemical Tectonic Discrimination Diagrams Based on Topological Theory. Minerals 2020, 10, 62. https://doi.org/10.3390/min10010062
Han S, Li M, Zhang Q, Song L. An Automated Method to Generate and Evaluate Geochemical Tectonic Discrimination Diagrams Based on Topological Theory. Minerals. 2020; 10(1):62. https://doi.org/10.3390/min10010062
Chicago/Turabian StyleHan, Shuai, Mingchao Li, Qi Zhang, and Lingguang Song. 2020. "An Automated Method to Generate and Evaluate Geochemical Tectonic Discrimination Diagrams Based on Topological Theory" Minerals 10, no. 1: 62. https://doi.org/10.3390/min10010062
APA StyleHan, S., Li, M., Zhang, Q., & Song, L. (2020). An Automated Method to Generate and Evaluate Geochemical Tectonic Discrimination Diagrams Based on Topological Theory. Minerals, 10(1), 62. https://doi.org/10.3390/min10010062







