Multivariate Statistical Analysis of Trace Elements in Pyrite: Prediction, Bias and Artefacts in Defining Mineral Signatures
Abstract
1. Introduction
2. Approach, Methods and Data Treatment
2.1. Data Acquisition
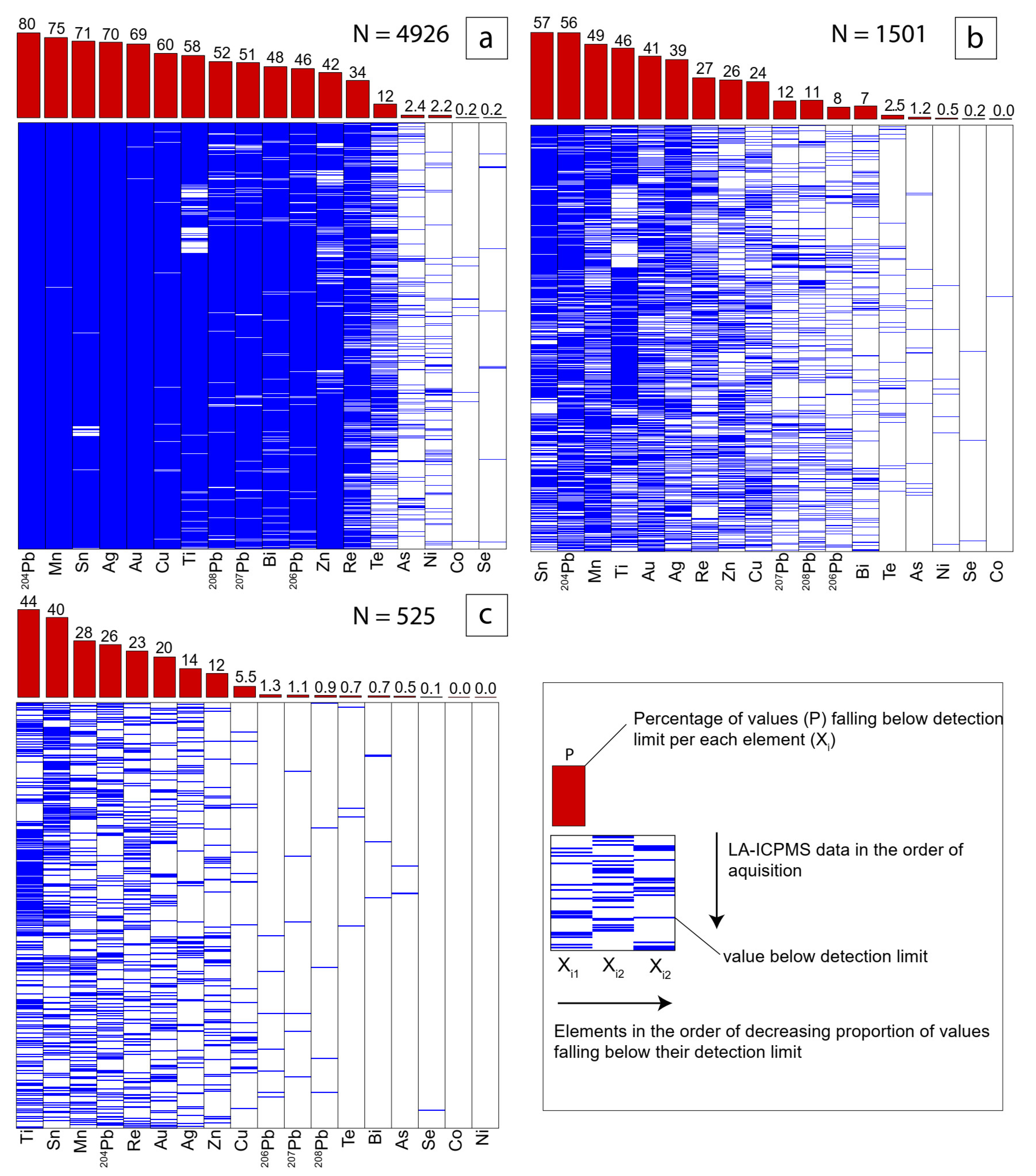
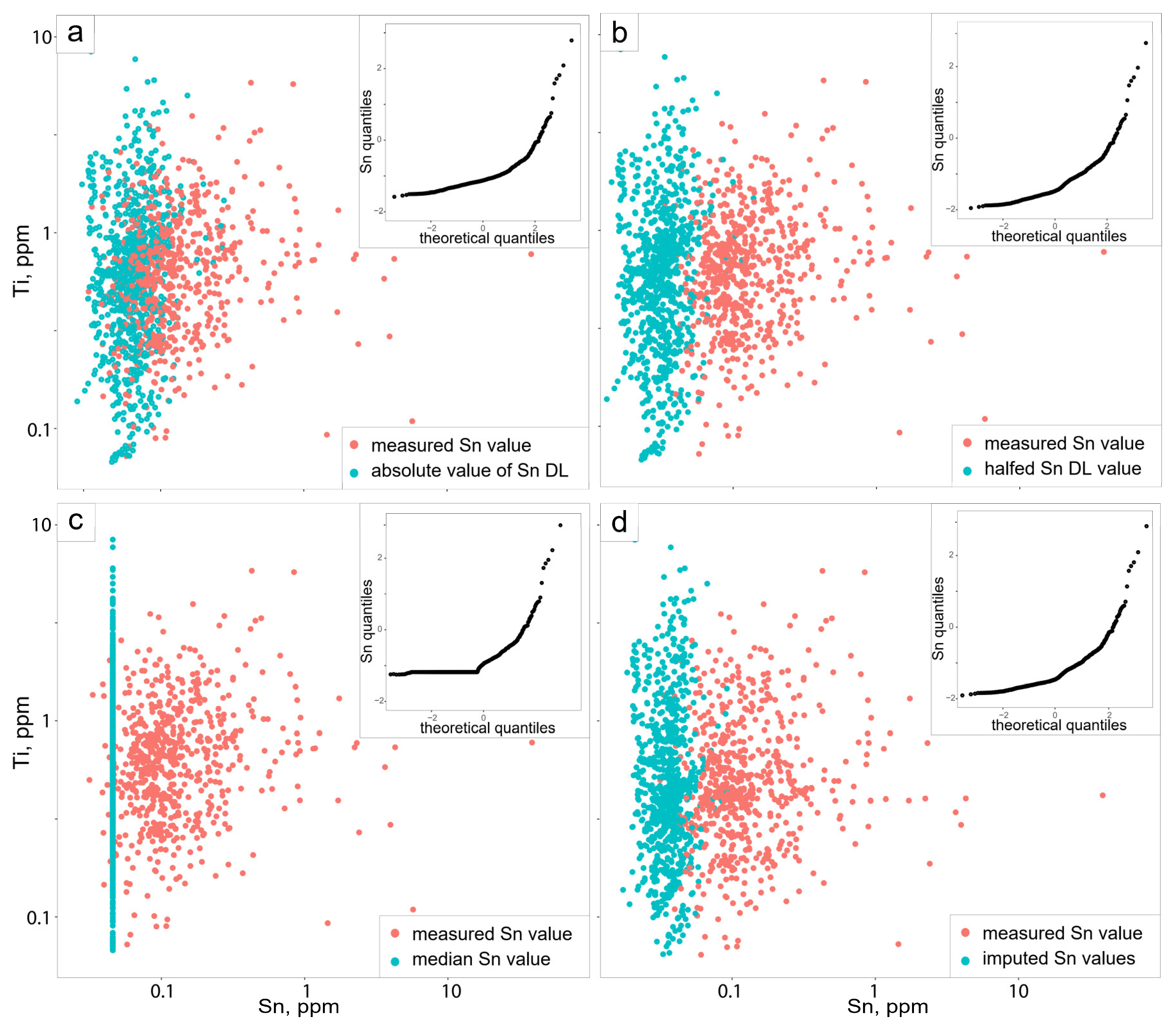
2.2. Data Quality Control, Trimming and Imputation
2.3. Multivariate Analyses
3. Results
3.1. Summary of Trace Element Signatures in Pyrite
| Co | Se | Ni | As | Te | Cu | Zn | Mn | Ti | |
| minimum | 0.28 | 4.0 | 0.015 | 0.35 | 0.009 | 0.096 | 0.12 | 0.060 | 0.049 |
| maximum | 44267 | 1075 | 4357 | 8586 | 815 | 5467 | 167 | 809 | 56 |
| median | 643 | 133 | 69 | 25 | 4.89 | 2.74 | 0.54 | 0.38 | 0.43 |
| geom. mean | 586 | 121 | 48 | 26 | 4.06 | 3.68 | 0.62 | 0.58 | 0.48 |
| 206Pb | 204Pb | 207Pb | 208Pb | Bi | Sn | Ag | Re | Au | |
| minimum | 0.001 | 0.043 | 0.001 | 0.0008 | 0.0003 | 0.017 | 0.001 | 0.0004 | 0.0003 |
| maximum | 765 | 467 | 490 | 466 | 156 | 611 | 223 | 0.72 | 14.9 |
| median | 0.29 | 0.23 | 0.12 | 0.10 | 0.12 | 0.045 | 0.022 | 0.014 | 0.005 |
| geom. mean | 0.40 | 0.36 | 0.16 | 0.14 | 0.12 | 0.064 | 0.037 | 0.011 | 0.008 |
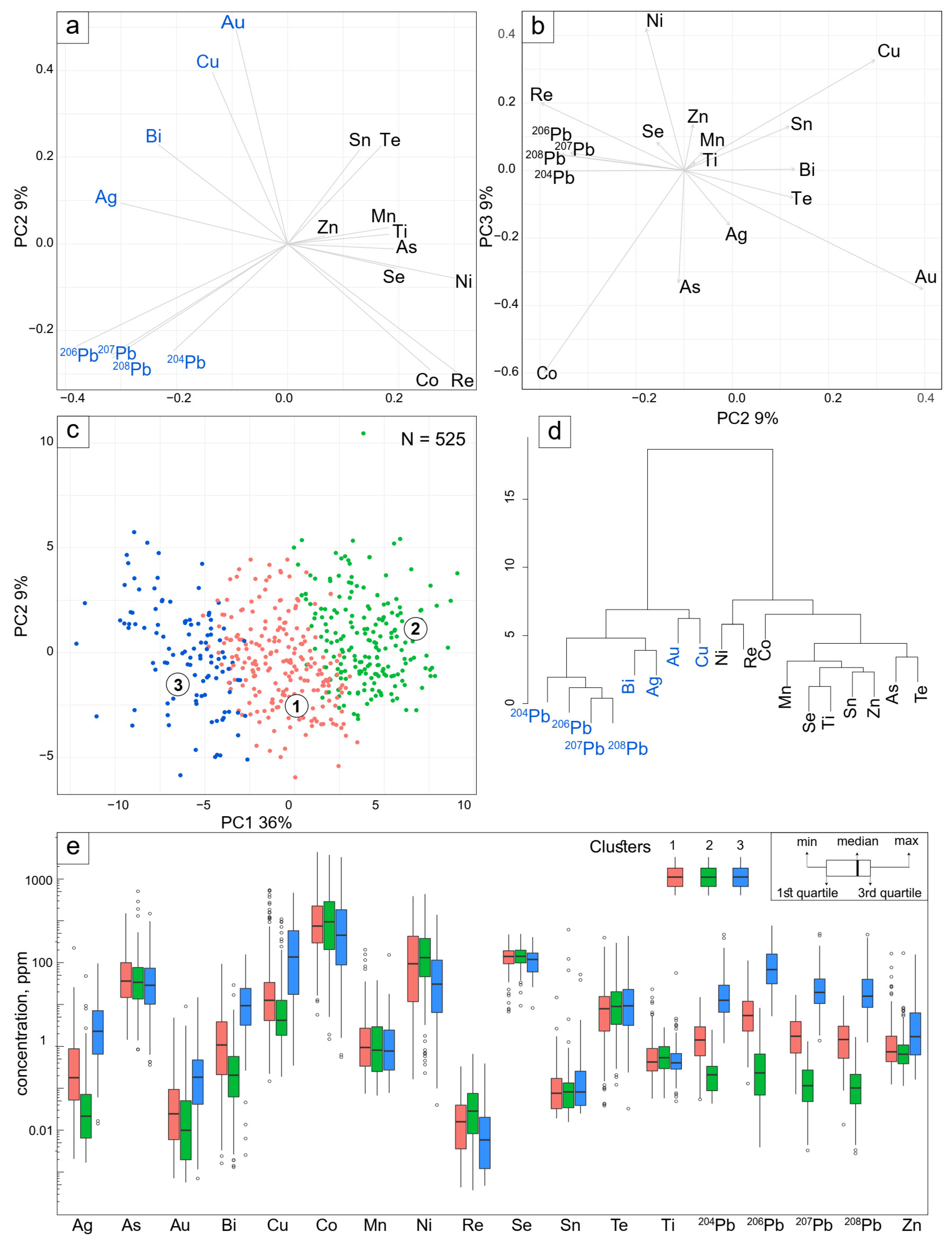
3.2. Principal Component Analysis, K-Means Clustering and Dendrogram
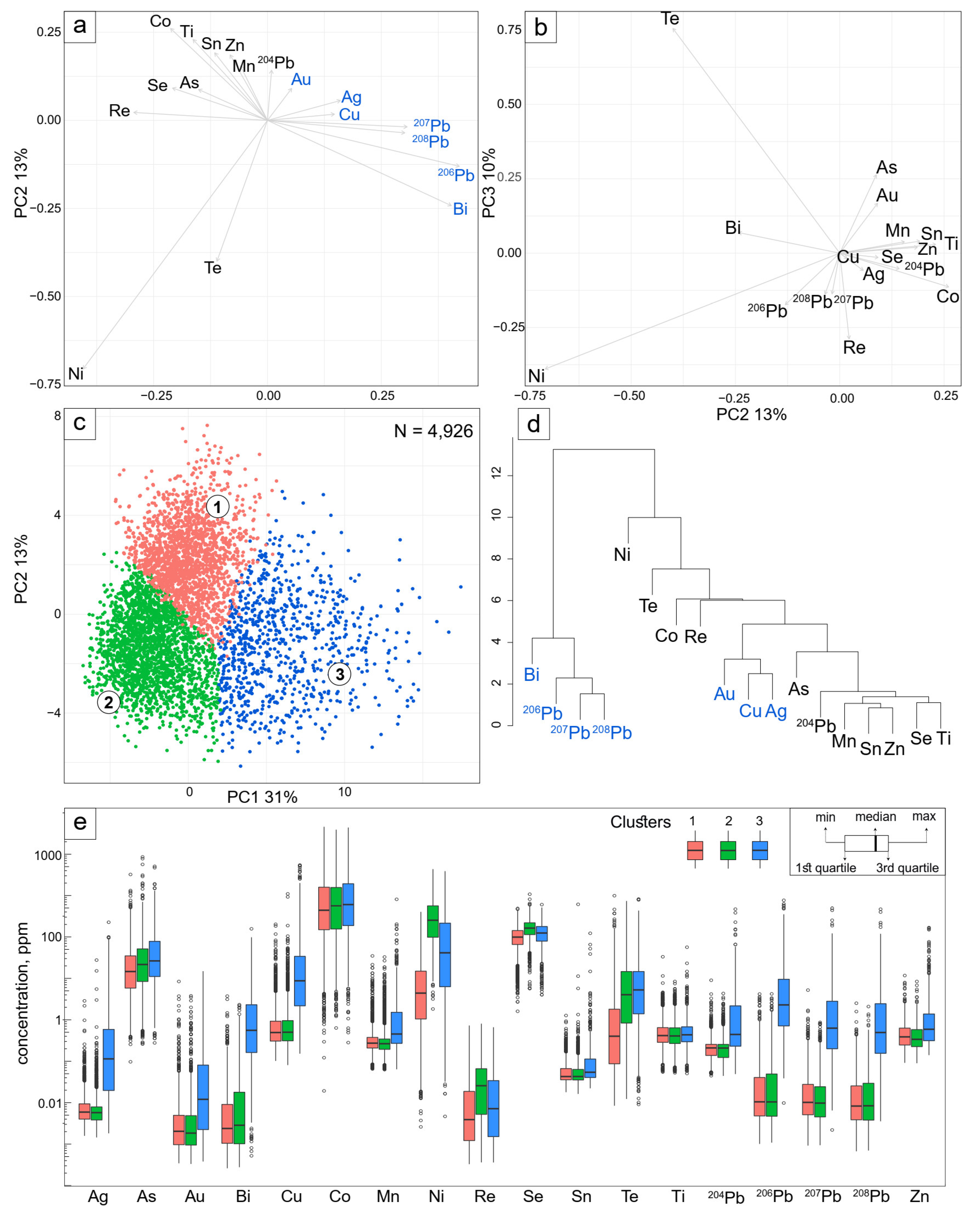
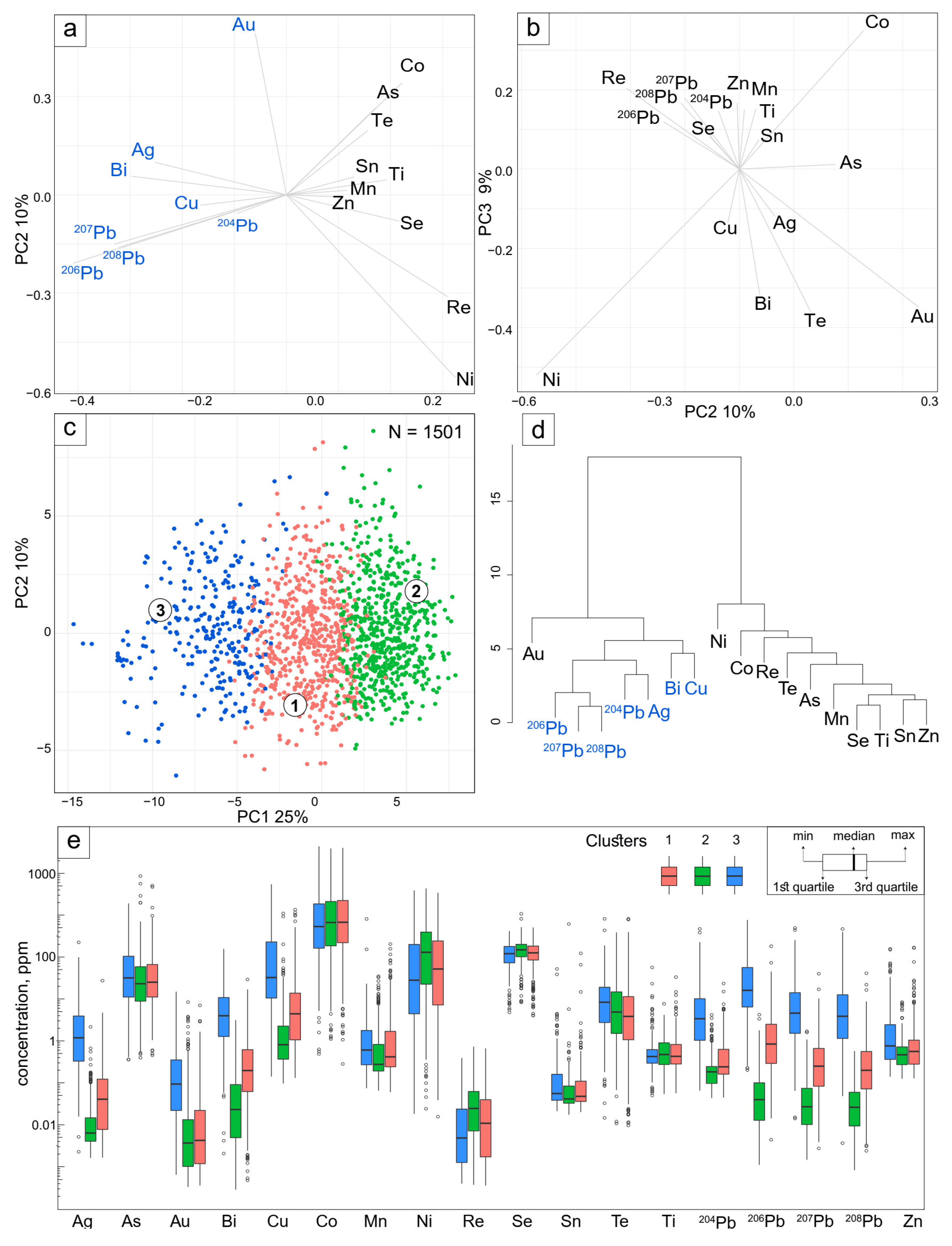
| Au | Bi | Cu | Co | Mn | Ni | Re | Se | Sn | Te | Ti | 204Pb | 206Pb | 207Pb | 208Pb | Zn | Ag | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| As | 4.1 | 7.4 | 4.6 | 4.4 | 3.0 | 7.6 | 5.9 | 2.6 | 2.7 | 5.3 | 2.8 | 3.1 | 7.4 | 5.7 | 5.8 | 2.7 | 4.5 |
| Au | 5.2 | 3.4 | 5.7 | 2.7 | 9.0 | 6.1 | 3.4 | 2.6 | 5.7 | 3.1 | 2.3 | 5.4 | 3.9 | 4.0 | 2.6 | 2.6 | |
| Bi | 4.1 | 9.6 | 5.6 | 12.3 | 10.1 | 7.4 | 6.4 | 8.0 | 7.4 | 5.3 | 3.5 | 3.7 | 3.7 | 6.1 | 4.1 | ||
| Cu | 6.2 | 2.8 | 9.1 | 6.2 | 3.5 | 2.8 | 6.3 | 3.6 | 2.6 | 3.9 | 3.0 | 3.0 | 2.7 | 2.5 | |||
| Co | 4.3 | 8.7 | 6.4 | 4.1 | 4.1 | 8.4 | 4.1 | 4.5 | 9.2 | 7.2 | 7.3 | 4.2 | 5.8 | ||||
| Mn | 7.4 | 4.0 | 1.4 | 1.1 | 5.1 | 1.3 | 1.5 | 5.2 | 3.5 | 3.5 | 0.9 | 2.8 | |||||
| Ni | 6.9 | 5.6 | 7.1 | 8.4 | 7.2 | 7.5 | 12.2 | 10.6 | 10.4 | 7.3 | 9.0 | ||||||
| Re | 2.8 | 3.6 | 7.5 | 3.8 | 4.2 | 9.4 | 7.5 | 7.4 | 3.8 | 6.1 | |||||||
| Se | 1.0 | 4.9 | 1.1 | 1.7 | 6.7 | 4.8 | 4.8 | 1.2 | 3.3 | ||||||||
| Sn | 5.1 | 1.1 | 1.4 | 5.8 | 4.1 | 4.1 | 0.9 | 2.8 | |||||||||
| Te | 5.7 | 5.5 | 8.6 | 7.3 | 7.2 | 5.2 | 6.4 | ||||||||||
| Ti | 1.7 | 6.7 | 4.8 | 4.8 | 1.2 | 3.3 | |||||||||||
| 204Pb | 4.3 | 2.6 | 2.7 | 1.1 | 1.8 | ||||||||||||
| 206Pb | 2.1 | 2.2 | 5.4 | 3.5 | |||||||||||||
| 207Pb | 1.5 | 3.6 | 2.5 | ||||||||||||||
| 208Pb | 3.6 | 2.6 | |||||||||||||||
| Zn | 2.6 |
| Au | Bi | Cu | Co | Mn | Ni | Re | Se | Sn | Te | Ti | 204Pb | 206Pb | 207Pb | 208Pb | Zn | Ag | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| As | 5.6 | 7.5 | 6.5 | 4.1 | 4.1 | 6.9 | 5.9 | 2.8 | 3.1 | 4.0 | 3.0 | 4.3 | 8.7 | 7.2 | 7.1 | 3.3 | 6.7 |
| Au | 6.0 | 6.1 | 7.4 | 5.7 | 9.9 | 8.8 | 5.5 | 4.6 | 5.3 | 5.2 | 4.3 | 7.6 | 6.1 | 6.2 | 4.8 | 4.6 | |
| Bi | 4.7 | 10.0 | 6.5 | 11.5 | 10.8 | 7.5 | 6.4 | 7.4 | 7.6 | 4.6 | 4.3 | 4.1 | 3.9 | 6.3 | 4.3 | ||
| Cu | 8.6 | 5.5 | 9.8 | 8.7 | 5.5 | 4.4 | 6.8 | 5.7 | 4.2 | 5.1 | 4.6 | 4.7 | 4.6 | 4.5 | |||
| Co | 5.4 | 8.4 | 6.5 | 4.2 | 4.8 | 6.7 | 4.4 | 5.8 | 10.8 | 8.9 | 8.9 | 5.0 | 8.3 | ||||
| Mn | 7.0 | 5.0 | 2.4 | 2.4 | 4.2 | 2.5 | 3.5 | 7.6 | 5.8 | 5.6 | 1.8 | 6.6 | |||||
| Ni | 6.3 | 4.5 | 6.1 | 6.8 | 5.9 | 7.7 | 12.9 | 11.3 | 11.1 | 6.4 | 10.6 | ||||||
| Re | 2.7 | 4.2 | 6.3 | 3.9 | 5.8 | 11.6 | 9.7 | 9.6 | 4.4 | 9.3 | |||||||
| Se | 1.5 | 3.5 | 1.2 | 3.0 | 8.2 | 6.4 | 6.3 | 1.6 | 5.9 | ||||||||
| Sn | 3.8 | 1.6 | 2.8 | 7.2 | 5.6 | 5.5 | 1.5 | 5.6 | |||||||||
| Te | 4.2 | 5.0 | 9.3 | 7.8 | 7.6 | 4.0 | 7.3 | ||||||||||
| Ti | 3.1 | 8.3 | 6.5 | 6.5 | 1.9 | 6.2 | |||||||||||
| 204Pb | 3.9 | 2.4 | 2.4 | 2.2 | 3.3 | ||||||||||||
| 206Pb | 1.8 | 1.9 | 6.5 | 4.0 | |||||||||||||
| 207Pb | 1.1 | 4.8 | 3.4 | ||||||||||||||
| 208Pb | 4.7 | 3.5 | |||||||||||||||
| Zn | 5.3 |
| Au | Bi | Cu | Co | Mn | Ni | Re | Se | Sn | Te | Ti | 204Pb | 206Pb | 207Pb | 208Pb | Zn | Ag | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| As | 5.9 | 7.0 | 7.4 | 3.8 | 4.2 | 6.3 | 5.7 | 2.6 | 4.0 | 3.4 | 3.1 | 5.7 | 8.4 | 7.0 | 7.1 | 4.1 | 7.8 |
| Au | 4.8 | 6.3 | 8.2 | 6.8 | 9.6 | 9.5 | 5.7 | 5.3 | 5.0 | 5.4 | 5.1 | 6.7 | 5.7 | 5.8 | 5.4 | 4.8 | |
| Bi | 4.7 | 9.6 | 6.9 | 9.9 | 9.5 | 6.1 | 5.9 | 6.3 | 6.2 | 3.7 | 4.2 | 3.4 | 3.5 | 5.5 | 3.9 | ||
| Cu | 10.1 | 6.7 | 9.4 | 9.3 | 5.5 | 5.0 | 6.6 | 5.8 | 5.2 | 5.6 | 5.2 | 5.4 | 4.8 | 5.7 | |||
| Co | 5.7 | 8.0 | 6.3 | 4.3 | 6.4 | 6.0 | 4.6 | 7.4 | 10.9 | 9.2 | 9.3 | 6.0 | 9.9 | ||||
| Mn | 6.7 | 5.7 | 2.6 | 3.4 | 3.5 | 2.8 | 5.5 | 8.4 | 6.7 | 6.8 | 2.4 | 8.8 | |||||
| Ni | 5.8 | 4.1 | 6.2 | 6.0 | 5.1 | 8.7 | 12.1 | 10.2 | 10.3 | 6.4 | 11.0 | ||||||
| Re | 2.8 | 5.6 | 5.5 | 4.0 | 7.6 | 11.2 | 9.5 | 9.5 | 5.2 | 10.6 | |||||||
| Se | 2.3 | 2.6 | 1.3 | 4.3 | 7.2 | 5.8 | 5.8 | 2.1 | 6.7 | ||||||||
| Sn | 3.5 | 2.2 | 4.9 | 7.5 | 6.0 | 6.1 | 2.3 | 7.5 | |||||||||
| Te | 3.2 | 5.6 | 8.4 | 7.0 | 7.0 | 3.7 | 7.6 | ||||||||||
| Ti | 4.6 | 7.5 | 6.0 | 6.1 | 2.5 | 7.0 | |||||||||||
| 204Pb | 2.4 | 1.1 | 1.1 | 3.5 | 3.6 | ||||||||||||
| 204Pb | 0.9 | 1.2 | 5.9 | 3.7 | |||||||||||||
| 204Pb | 0.4 | 4.5 | 3.4 | ||||||||||||||
| 204Pb | 4.4 | 3.4 | |||||||||||||||
| Zn | 6.4 |
3.3. Multiple Linear Regression
4. Discussion
4.1. Trace Element Signature of Pyrite: Prediction and Bias for Complex Sulphide Ores
4.2. Trapping of Trace Elements during Ore Overprinting
4.3. Impact of Left-Censored Data on the Interpretation of Statistical Analyses: Artefacts and False Interpretations
4.4. Implications and Significance
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vaughan, D.J.; Corkhill, C.L. Mineralogy of Sulphides. Elements 2017, 13, 81–87. [Google Scholar] [CrossRef]
- Craig, J.R.; Vokes, F.M.; Solberg, T.N. Pyrite: Physical and chemical textures. Miner. Depos. 1998, 34, 82–101. [Google Scholar] [CrossRef]
- Carstens, C.W. Om geokjemiske undersøkelser av malmer. Norsk Geol. Tidsskr. 1941, 21, 213–221. [Google Scholar]
- Fleischer, M. Minor Elements in Some Sulphide Minerals. In Economic Geology Fiftieth Anniversary, Volume 1905–1955; Bateman, A.M., Ed.; Economic Geology Publishing Company: Urbana, IL, USA, 1955; pp. 970–1024. [Google Scholar]
- Hawley, J.E.; Nichol, I. Trace elements in pyrite, pyrrhotite and chalcopyrite of different ores. Econ. Geol. 1961, 56, 467–487. [Google Scholar] [CrossRef]
- Gregory, D.D.; Lyons, T.W. The effects of trace element content on pyrite oxidation rates. In Proceedings of the American Geophysical Union Fall Meeting, New Orleans, LA, USA, 11–15 December 2017. 2017AGUFM.H41I1554G. [Google Scholar]
- Abraitis, P.K.; Pattrick, R.A.D.; Vaughan, D.J. Variations in the Compositional, Textural and Electrical Properties of Natural Pyrite: A Review. Int. J. Miner. Process. 2004, 74, 41–59. [Google Scholar] [CrossRef]
- Large, R.R.; Maslennikov, V.V.; Robert, V.; Danyushevsky, L.V.; Chang, Z.S. Multistage sedimentary and metamorphic origin of pyrite and gold in the giant Sukhoi Log deposit, Lena Gold Province, Russia. Econ. Geol. 2007, 102, 1233–1267. [Google Scholar] [CrossRef]
- Large, R.R.; Danyushevsky, L.D.; Hollit, C.; Maslennikov, V.V.; Meffre, S.; Gilbert, S.; Bull, S.; Scott, R.; Emsbo, P.; Thomas, H.; et al. Gold and trace element zonation in pyrite using a laser imaging technique; implications for the timing of gold in orogenic and Carlin-style sediment-hosted deposits. Econ. Geol. 2009, 104, 635–668. [Google Scholar] [CrossRef]
- Sung, Y.H.; Brugger, J.; Ciobanu, C.L.; Pring, A.; Skinner, W.; Nugus, M. Invisible gold in arsenian pyrite and arsenopyrite from a multistage Archaean gold deposit: Sunrise Dam, Eastern Goldfields Province, Western Australia. Miner. Depos. 2009, 44, 765–791. [Google Scholar] [CrossRef]
- Cook, N.J.; Ciobanu, C.L.; Mao, J. Textural control on gold distribution in As-free pyrite from the Dongping, Huangtuliang and Hougou gold deposits, North China Craton (Hebei Province, China). Chem. Geol. 2009, 264, 101–121. [Google Scholar] [CrossRef]
- Thomas, H.V.; Large, R.R.; Bull, S.W.; Maslennikov, V.; Berry, R.F.; Frazer, R.; Froud, F.; Moye, R. Pyrite and pyrrhotite textures and composition in sediments, laminated quartz veins, and reefs at Bendigo Gold Mine, Australia: Insights for ore genesis. Econ. Geol. 2011, 106, 1–31. [Google Scholar] [CrossRef]
- Cook, N.J.; Ciobanu, C.L.; Meria, D.; Silcock, D.; Wade, B.P. Arsenopyrite–Pyrite Association in an Orogenic Gold Ore: Tracing Mineralization History from Textures and Trace Elements. Econ. Geol. 2013, 108, 1273–1283. [Google Scholar] [CrossRef]
- Cook, N.J.; Chryssoulis, S.L. Concentrations of invisible gold in the common sulphides. Can. Mineral. 1990, 28, 1–16. [Google Scholar]
- Reich, M.; Kesler, S.E.; Utsunomiya, S.; Palenik, C.S.; Chryssoulis, S.L.; Ewing, R.C. Solubility of gold in arsenian pyrite. Geochim. Cosmochim. Acta 2005, 69, 2781–2796. [Google Scholar] [CrossRef]
- Deditius, A.P.; Reich, M. Constraints on the solid solubility of Hg, Tl, and Cd in arsenian pyrite. Am. Mineral. 2016, 101, 1451–1459. [Google Scholar] [CrossRef]
- George, L.L.; Biagioni, C.; D’Orazio, M.; Cook, N.J. Textural and trace element evolution of pyrite during greenschist facies metamorphic recrystallization in the southern Apuan Alps (Tuscany, Italy): Influence on the formation of Tl-rich sulfosalt melt. Ore Geol. Rev. 2018, 102, 59–105. [Google Scholar] [CrossRef]
- George, L.; Biagioni, C.; Lepore, G.O.; Lacalamita, M.; Agrosì, G.; Capitani, G.C.; Bonaccorsi, E.; D’Acapito, F. The speciation of thallium in (Tl, Sb, As)-rich pyrite. Ore Geol. Rev. 2019, 107, 364–380. [Google Scholar] [CrossRef]
- Cook, N.J.; Ciobanu, C.L.; George, L.; Zhu, Z.-Y.; Wade, B.; Ehrig, K. Trace Element Analysis of Minerals in Magmatic-Hydrothermal Ores by Laser Ablation Inductively-Coupled Plasma Mass Spectrometry: Approaches and Opportunities. Minerals 2016, 6, 111. [Google Scholar] [CrossRef]
- Ciobanu, C.L.; Verdugo-Ihl, M.R.; Slattery, A.; Cook, N.J.; Ehrig, K.; Courtney-Davies, L.; Wade, B.P. Silician magnetite: Si–Fe nanoprecipitates and other mineral inclusions in magnetite from the Olympic Dam deposit, South Australia. Minerals 2019, 9, 311. [Google Scholar] [CrossRef]
- Xu, J.; Ciobanu, C.L.; Cook, N.J.; Slattery, A.D. Crystals from the Powellite–Scheelite Series at the Nanoscale: A Case Study from the Zhibula Cu Skarn, Gangdese Belt, Tibet. Minerals 2019, 9, 340. [Google Scholar] [CrossRef]
- Keyser, W.; Ciobanu, C.L.; Cook, N.J.; Feltus, H.; Johnson, G.; Slattery, A.; Wade, B.P.; Ehrig, K. Mineralogy of Zirconium in Iron-Oxides: A Micron- to Nanoscale Study of Hematite Ore from Peculiar Knob, South Australia. Minerals 2019, 9, 244. [Google Scholar] [CrossRef]
- Van Tendeloo, G.; Bals, S.; Van Aert, S.; Verbeeck, J.; Van Dyck, D. Advanced electron microscopy for advanced materials. Adv. Mater. 2012, 24, 5655–5675. [Google Scholar] [CrossRef]
- Ciobanu, C.L.; Cook, N.J.; Utsunomiya, S.; Kogagwa, M.; Green, L.; Gilbert, S.; Wade, B. Gold-telluride nanoparticles revealed in arsenic-free pyrite. Am. Mineral. 2012, 97, 1515–1518. [Google Scholar] [CrossRef]
- Ciobanu, C.L.; Cook, N.J.; Maunders, C.; Wade, B.P.; Ehrig, K. Focused ion beam and advanced electron microscopy for minerals: Insights and outlook from bismuth sulphosalts. Minerals 2016, 6, 112. [Google Scholar] [CrossRef]
- Winderbaum, L.; Ciobanu, C.L.; Cook, N.J.; Paul, M.; Metcalfe, A.; Gilbert, S. Multivariate Analysis of an LA-ICP-MS Trace Element Dataset for Pyrite. Mathem. Geosci. 2012, 44, 823–842. [Google Scholar] [CrossRef]
- Dmitrijeva, M.; Metcalfe, A.V.; Ciobanu, C.L.; Cook, N.J.; Frenzel, M.; Keyser, W.M.; Johnson, G.; Ehrig, K. Discrimination and Variance Structure of Trace Element Signatures in Fe-Oxides: A Case Study of BIF-Mineralisation from the Middleback Ranges, South Australia. Math. Geosci. 2018, 50, 381–415. [Google Scholar] [CrossRef]
- Dmitrijeva, M.; Ehrig, K.; Ciobanu, C.L.; Cook, N.J.; Verdugo-Ihl, M.R.; Metcalfe, A. Defining IOCG signatures through compositional data analysis: A case study of lithogeochemical zoning from the Olympic Dam deposit, South Australia. Ore Geol. Rev. 2019, 105, 86–101. [Google Scholar] [CrossRef]
- Dmitrijeva, M.; Ehrig, K.; Ciobanu, C.L.; Cook, N.J.; Verdugo-Ihl, M.R.; Metcalfe, A. Mineralization-alteration footprints in the Olympic Dam IOCG district, South Australia: The Acropolis prospect. J. Geochem. Explor. 2019, 205, 106333. [Google Scholar] [CrossRef]
- Palarea-Albaladejo, J.; Martin-Fernandez, J.A. Values below detection limit in compositional chemical data. Anal. Chim. Acta 2013, 764, 32–43. [Google Scholar] [CrossRef]
- Palarea-Albaladejo, J.; Martin-Fernandez, J.A. ZCompositions—R package for multivariate imputation of left-censored data under a compositional approach. Chemom. Intell. Lab. Syst. 2015, 143, 85–96. [Google Scholar] [CrossRef]
- Hron, K.; Templ, M.; Filzmoser, P. Imputation of missing values for compositional data using classical and robust methods. Comput. Stat. Data Anal. 1986, 54, 3095–3107. [Google Scholar] [CrossRef]
- Ehrig, K.; McPhie, J.; Kamenetsky, V.S. Geology and mineralogical zonation of the Olympic Dam Iron Oxide Cu–U–Au–Ag deposit, South Australia. In Geology and Genesis of Major Copper Deposits and Districts of the World: A Tribute to Richard H. Sillitoe; Society of Economic Geologists Special Publication: Littleton, CO, USA, 2012; Volume 16, pp. 237–267. [Google Scholar]
- Foster, A.R.; Williams, P.; Ryan, C. Distribution of Gold in Hypogene Ore at the Ernest Henry Iron Oxide Copper-Gold Deposit, Cloncurry District, NW Queensland. Explor. Mining Geol. 2007, 16, 125–143. [Google Scholar] [CrossRef]
- Rusk, B.; Oliver, N.; Cleverley, J.; Blenkinsop, T.; Dexian, Z.; Patrick, P.; Habermann, P. Physical and chemical characteristics of the Ernest Henry iron oxide copper gold deposit, Australia; implications for IOGC genesis. In Hydrothermal Iron Oxide Copper-Gold & Related Deposits: A Global Perspective-Advances in the Understanding of IOCG Deposits; Porter, T.M., Ed.; Global Perspective Series 3; PGC Publishing: Linden Park, Australia, 2010; pp. 201–218. [Google Scholar]
- Reich, M.; Simon, A.C.; Deditius, A.; Barra, F.; Chryssoulis, S.; Lagas, G.; Tardani, D.; Knipping, J.; Bilenker, L.; Sánchez-Alfaro, P.; et al. Trace Element Signature of Pyrite from the Los Colorados Iron Oxide-Apatite (IOA) Deposit, Chile: A Missing Link Between Andean IOA And Iron Oxide Copper–Gold Systems? Econ. Geol. 2016, 111, 743–761. [Google Scholar] [CrossRef]
- Gregory, D.D.; Cracknell, M.J.; Large, R.R.; McGoldrick, P.; Kuhn, S.; Maslennikov, V.V.; Baker, M.J.; Fox, N.; Belousov, I.; Figueroa, M.C.; et al. Distinguishing Ore Deposit Type and Barren Sedimentary Pyrite Using Laser Ablation-Inductively Coupled Plasma-Mass Spectrometry Trace Element Data and Statistical Analysis of Large Data Sets. Econ. Geol. 2019, 114, 771–786. [Google Scholar] [CrossRef]
- Román, N.; Reich, M.; Leisen, M.; Morata, D.; Barra, F.; Deditius, A.P. Geochemical and micro-textural fingerprints of boiling in pyrite. Geochim. Cosmochim. Acta 2019, 246, 60–85. [Google Scholar] [CrossRef]
- Elghali, A.; Benzaazoua, M.; Bussière, B.; Genty, T. Spatial Mapping of Acidity and Geochemical Properties of Oxidized Tailings within the Former Eagle/Telbel Mine Site. Minerals 2019, 9, 180. [Google Scholar] [CrossRef]
- Danyushevsky, L.V.; Robinson, P.; Gilbert, S.; Norman, M.; Large, R.; McGoldrick, P.; Shelley, J.M.G. Routine quantitative multi-element analysis of sulphide minerals by laser ablation ICP-MS: Standard development and consideration of matrix effects. Geochem. Explor. Environ. Anal. 2011, 11, 51–60. [Google Scholar] [CrossRef]
- Norris, A.; Danyushevsky, L. Towards Estimating the Complete Uncertainty Budget of Quantified Results Measured by LA-ICP-MS; Goldschmidt: Boston, MA, USA, 2018. [Google Scholar]
- Schmandt, D.S. Mineralogical Distributions of Radionuclides in Copper–Uranium Ores from Olympic Dam, South Australia. Ph.D. Thesis, The University of Adelaide, Adelaide, Australia, 2019. Unpublished. [Google Scholar]
- Ciobanu, C.L.; Wade, B.P.; Cook, N.J.; Schmidt Mumm, A.; Giles, D. Uranium-bearing hematite from the Olympic Dam Cu–U–Au deposit, South Australia; a geochemical tracer and reconnaissance Pb–Pb geochronometer. Precambr. Res. 2013, 238, 129–147. [Google Scholar] [CrossRef]
- Verdugo-Ihl, M.R.; Ciobanu, C.L.; Cook, N.J.; Ehrig, K.; Courtney-Davies, L.; Gilbert, S. Textures and U–W–Sn–Mo signatures in hematite from the Cu–U–Au–Ag orebody at Olympic Dam, South Australia: Defining the archetype for IOCG deposits. Ore Geol. Rev. 2017, 91, 173–195. [Google Scholar] [CrossRef]
- Aitchison, J. The Statistical Analysis of Compositional Data. In Monographs on Statistics and Applied Probability; Chapman & Hall: London, UK, 1986; p. 416. [Google Scholar] [CrossRef]
- Pawlowsky-Glahn, V.; Egozcue, J.J.; Tolosana-Delgado, R. Modeling and Analysis of Compositional Data; Wiley: Chichester, UK, 2015; p. 272. [Google Scholar] [CrossRef]
- van den Boogart, K.G.; Tolosana-Delgado, R.; Bren, M. Compositions: Compositional Data Analysis. R Package Version 1.40-2. 2018. Available online: https://CRAN.R-project.org/package=compositions (accessed on 8 January 2020).
- Egozcue, J.J.; Pawlowsky-Glahn, V.; Mateu-Figueras, G.; Barceló-Vidal, C. Isometric logratio transformations for compositional data analysis. Math. Geol. 2003, 35, 279–300. [Google Scholar] [CrossRef]
- Egozcue, J.J.; Pawlowsky-Glahn, V. Simplicial Geometry for Compositional Data. In Compositional Data Analysis in the Geosciences: From Theory to Practice; Buccianti, A., Mateu-Figueras, G., Pawlowsky-Glahn, V., Eds.; Special Publications; Geological Society: London, UK, 2006; Volume 264, pp. 145–159. [Google Scholar] [CrossRef]
- Aitchison, J.; Barceló-Vidal, C.; Pawlowsky-Glahn, V. Some comments on compositional data analysis in archaeometry, in particular the fallacies in Tangri and Wright’s dismissal of logratio analysis. Archaeometry 2002, 44, 295–304. [Google Scholar] [CrossRef][Green Version]
- Mathieu, L. Detecting magmatic-derived fluids using pyrite chemistry: Example of the Chibougamau area, Abitibi Subprovince, Québec. Ore Geol. Rev. 2019, 114, 103127. [Google Scholar] [CrossRef]
- Caciagli, N. Multielement Geochemical Modelling for Mine Planning: Case Study from an Epithermal Gold Deposit. In Compositional Data Analysis; Martín-Fernández, J.A., Thió-Henestrosa, S., Eds.; Springer: Berlin, Germany, 2016; Volume 187, pp. 45–61. [Google Scholar] [CrossRef]
- Gabriel, K.R. The biplot graphical display of matrices with application to principal component analysis. Biometrika 1971, 58, 453–467. [Google Scholar] [CrossRef]
- Templ, M.; Hron, K.; Filzmoser, P. robCompositions: An R-Package for Robust Statistical Analysis of Compositional Data. In Compositional Data Analysis. Theory and Applications; Pawlowsky-Glahn, V., Buccianti, A., Eds.; John Wiley & Sons: Chichester, UK, 2018; pp. 341–355. [Google Scholar] [CrossRef]
- Filsmozer, P.; Hron, K.; Templ, M. Applied Compositional Data Analysis with Worked Examples in R; Springer: New York, NY, USA, 2018; p. 280. [Google Scholar] [CrossRef]
- Bowles, J.F.W.; Howie, R.A.; Vaughan, D.J.; Zussman, J. Non-silicates: Volume 5A. In Rock-Forming Minerals; Deer, W.A., Howie, R.A., Zussman, J., Eds.; Geological Society: London, UK, 2011; p. 920. [Google Scholar]
- Barton, M.D. Iron oxide (–Cu–Au–REE–P–Ag–U–Co) systems. In Treatise on Geochemistry, 2nd ed.; Holland, H.D., Turekian, K.K., Eds.; Elsevier: Oxford, UK, 2014; pp. 515–541. [Google Scholar] [CrossRef]
- Li, R.; Chen, H.; Xia, X.; Yang, Q.; Danyushevsky, L.D.; Lai, C. Using integrated in-situ sulphide trace element geochemistry and sulfur isotopes to trace ore-forming fluids: Example from the Mina Justa IOCG deposit (southern Perú). Ore Geol. Rev. 2018, 101, 165–179. [Google Scholar] [CrossRef]
- Macmillan, E.; Cook, N.J.; Ehrig, K.; Ciobanu, C.L.; Pring, A. Uraninite from the Olympic Dam IOCG–U–Ag deposit: Linking textural and compositional variation to temporal evolution. Am. Mineral. 2016, 101, 1295–1320. [Google Scholar] [CrossRef]
- Macmillan, E.; Ehrig, K.; Ciobanu, C.L.; Cook, N.J.; Pring, A. Replacement of uraninite by bornite via coupled dissolution-reprecipitation: Evidence from texture and microstructure. Can. Mineral. 2016, 54, 1369–1383. [Google Scholar] [CrossRef]
- Macmillan, E.; Cook, N.J.; Ehrig, K.; Pring, A. Chemical and textural interpretation of late-stage coffinite and brannerite from the Olympic Dam IOCG–Ag–U deposit. Mineral. Mag. 2017, 81, 1323–1366. [Google Scholar] [CrossRef]
- Owen, N.D. The Mineralogical Deportment of Radionuclides in South Australian Cu–Au–(U) Ores. Ph.D. Thesis, The University of Adelaide, Adelaide, Australia, 2019. Unpublished. [Google Scholar]
- Owen, N.D.; Ciobanu, C.L.; Cook, N.J.; Slattery, A.D.; Basak, A.K. Nanoscale Study of Clausthalite-Bearing Symplectites in Cu–Au–(U) Ores: Implications for Ore Genesis. Minerals 2018, 8, 67. [Google Scholar] [CrossRef]
- Rollog, M.; Cook, N.J.; Guagliardo, P.; Ehrig, K.; Ciobanu, C.L.; Kilburn, M. Detection of Trace Elements/Isotopes in Olympic Dam Copper Concentrates by nanoSIMS. Minerals 2019, 9, 336. [Google Scholar] [CrossRef]
- Rollog, M.; Cook, N.J.; Guagliardo, P.; Ehrig, K.; Kilburn, M. Radionuclide distributions in Olympic Dam copper concentrates: The significance of minor hosts, incorporation mechanisms, and the role of mineral surfaces. Minerals Eng. 2020, 148, 106176. [Google Scholar] [CrossRef]
- Owen, N.D.; Cook, N.J.; Rollog, M.; Ehrig, K.J.; Schmandt, D.S.; Ram, R.; Brugger, J.; Ciobanu, C.L.; Wade, B.; Guagliardo, P. REE-, Sr-, Ca-aluminum-phosphate-sulfate minerals of the alunite supergroup and their role as hosts for radionuclides. Am. Mineral. 2019, 104, 1806–1819. [Google Scholar] [CrossRef]
- Ciobanu, C.L.; Cook, N.J.; Ehrig, K. Ore minerals down to the nanoscale: Cu–(Fe)-sulphides from the iron oxide copper gold deposit at Olympic Dam, South Australia. Ore Geol. Rev. 2017, 81, 1218–1235. [Google Scholar] [CrossRef]
- Cook, N.J.; Ciobanu, C.L.; Ehrig, K.; Slattery, A.; Verdugo-Ihl, M.R.; Courtney-Davies, L.; Gao, W. Advances and opportunities in ore mineralogy. Minerals 2017, 7, 233. [Google Scholar] [CrossRef]
| Intercept | Se | Ag | 204Pb | Te | Bi | 206Pb | Mn | Co | |
| Estimate | 0.11 | −0.33 | 0.18 | 0.10 | 0.07 | 0.05 | −0.05 | −0.03 | −0.02 |
| Std. Error | 0.17 | 0.02 | 0.01 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| t value | 0.67 | −13.55 | 14.63 | 5.52 | 6.61 | 4.12 | −3.07 | −2.18 | −2.01 |
| Pr(>|t|) | 0.505 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.030 | 0.045 |
| significance | *** | *** | *** | *** | *** | ** | * | * | |
| Cu | Ni | As | Sn | Re | 208Pb | 207Pb | Zn | Ti | |
| Estimate | −0.02 | 0.01 | 0.01 | 0.01 | 0.00 | −0.01 | 0.00 | 0.00 | 0.00 |
| Std. Error | 0.01 | 0.01 | 0.01 | 0.02 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 |
| t value | −1.57 | 0.75 | 0.71 | 0.36 | −0.36 | −0.28 | 0.15 | 0.04 | 0.11 |
| Pr(>|t|) | 0.117 | 0.451 | 0.481 | 0.719 | 0.719 | 0.777 | 0.879 | 0.968 | 0.911 |
| significance | - | - | - | - | - | - | - | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dmitrijeva, M.; Cook, N.J.; Ehrig, K.; Ciobanu, C.L.; Metcalfe, A.V.; Kamenetsky, M.; Kamenetsky, V.S.; Gilbert, S. Multivariate Statistical Analysis of Trace Elements in Pyrite: Prediction, Bias and Artefacts in Defining Mineral Signatures. Minerals 2020, 10, 61. https://doi.org/10.3390/min10010061
Dmitrijeva M, Cook NJ, Ehrig K, Ciobanu CL, Metcalfe AV, Kamenetsky M, Kamenetsky VS, Gilbert S. Multivariate Statistical Analysis of Trace Elements in Pyrite: Prediction, Bias and Artefacts in Defining Mineral Signatures. Minerals. 2020; 10(1):61. https://doi.org/10.3390/min10010061
Chicago/Turabian StyleDmitrijeva, Marija, Nigel J. Cook, Kathy Ehrig, Cristiana L. Ciobanu, Andrew V. Metcalfe, Maya Kamenetsky, Vadim S. Kamenetsky, and Sarah Gilbert. 2020. "Multivariate Statistical Analysis of Trace Elements in Pyrite: Prediction, Bias and Artefacts in Defining Mineral Signatures" Minerals 10, no. 1: 61. https://doi.org/10.3390/min10010061
APA StyleDmitrijeva, M., Cook, N. J., Ehrig, K., Ciobanu, C. L., Metcalfe, A. V., Kamenetsky, M., Kamenetsky, V. S., & Gilbert, S. (2020). Multivariate Statistical Analysis of Trace Elements in Pyrite: Prediction, Bias and Artefacts in Defining Mineral Signatures. Minerals, 10(1), 61. https://doi.org/10.3390/min10010061






