Parallelization of Modified Merge Sort Algorithm
Abstract
:1. Introduction
Related Works
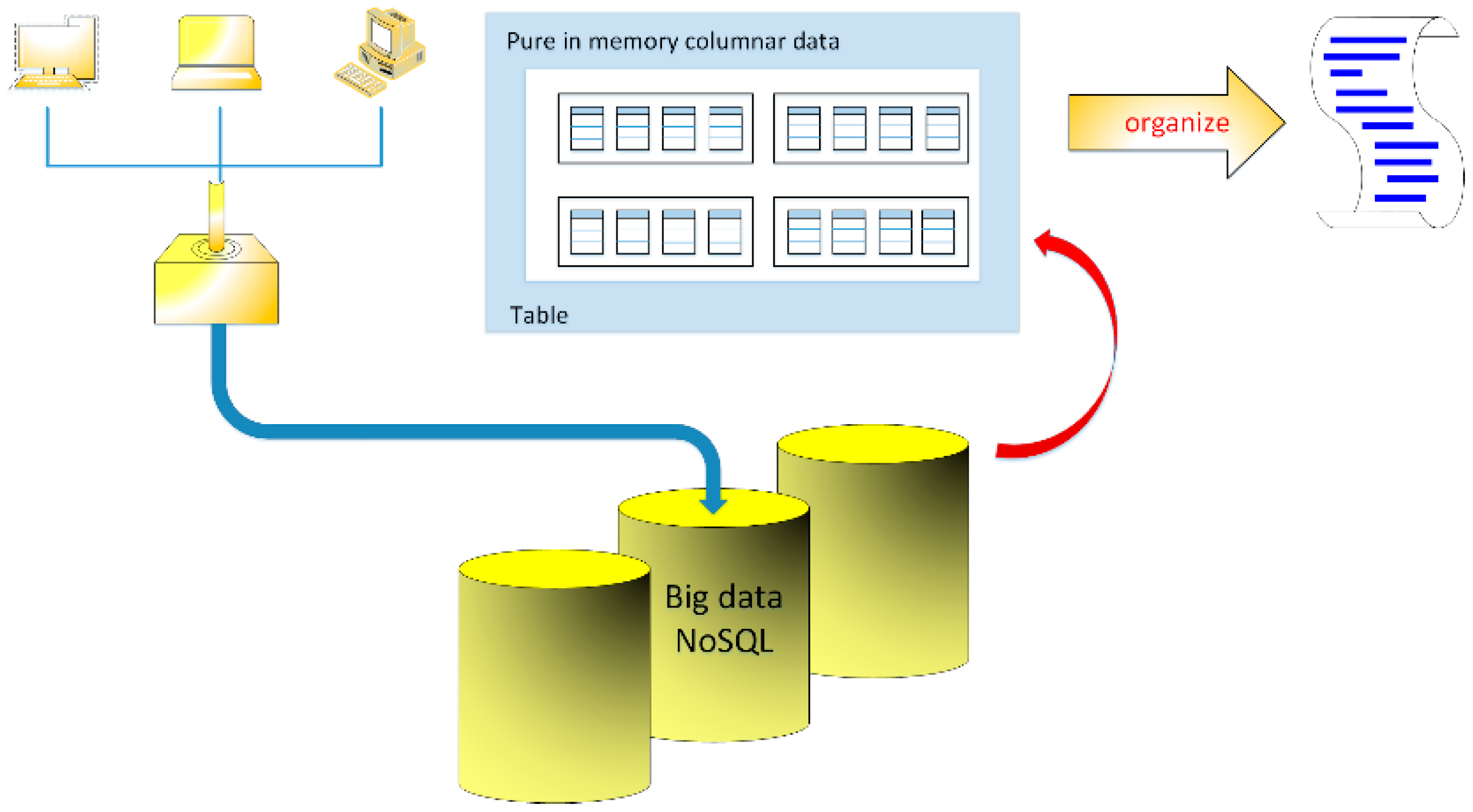
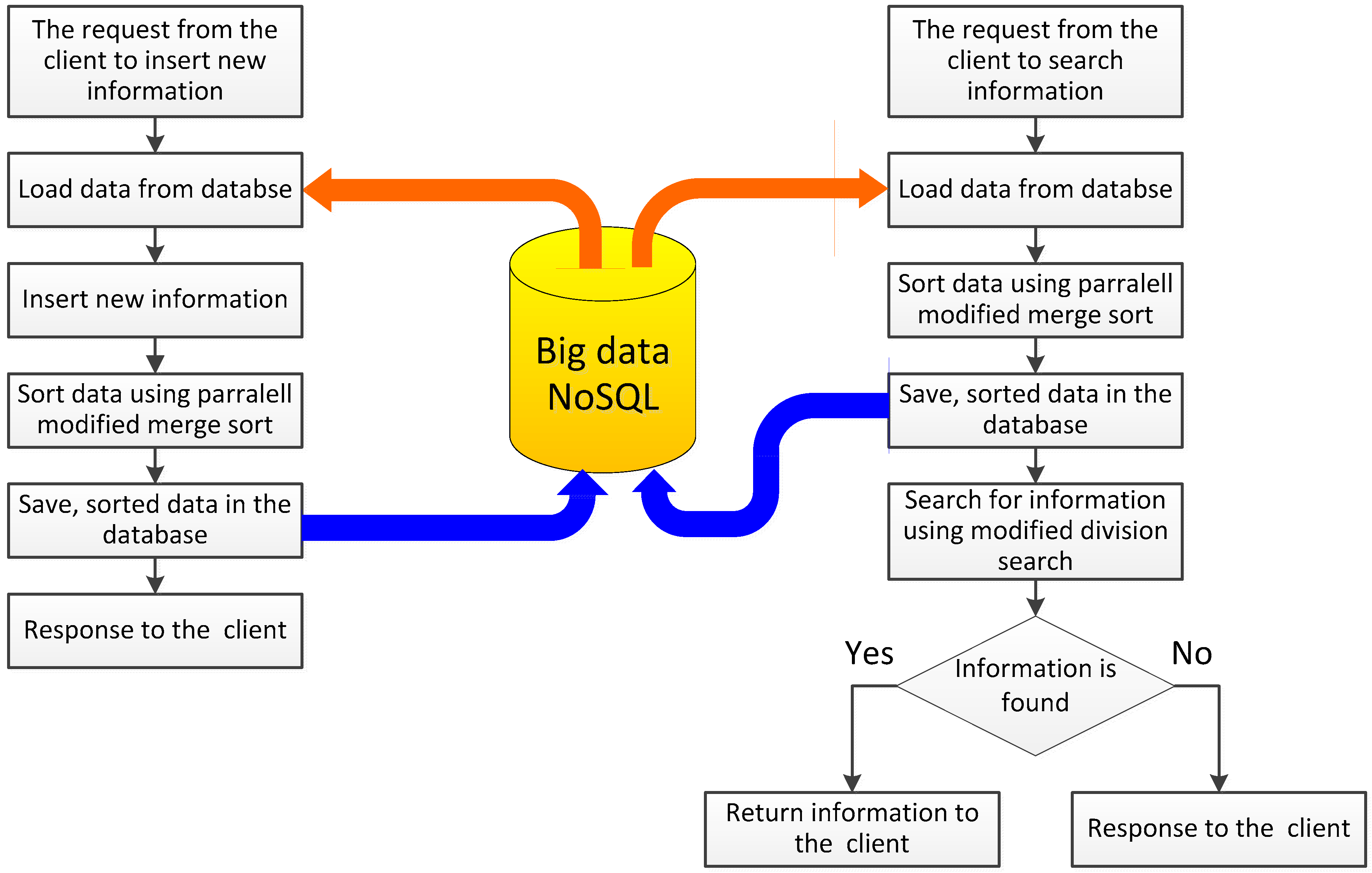
2. Data Processing in NoSQL Database and Parallel Sort Algorithms
Statistical Approach to the Research on Algorithm Performance
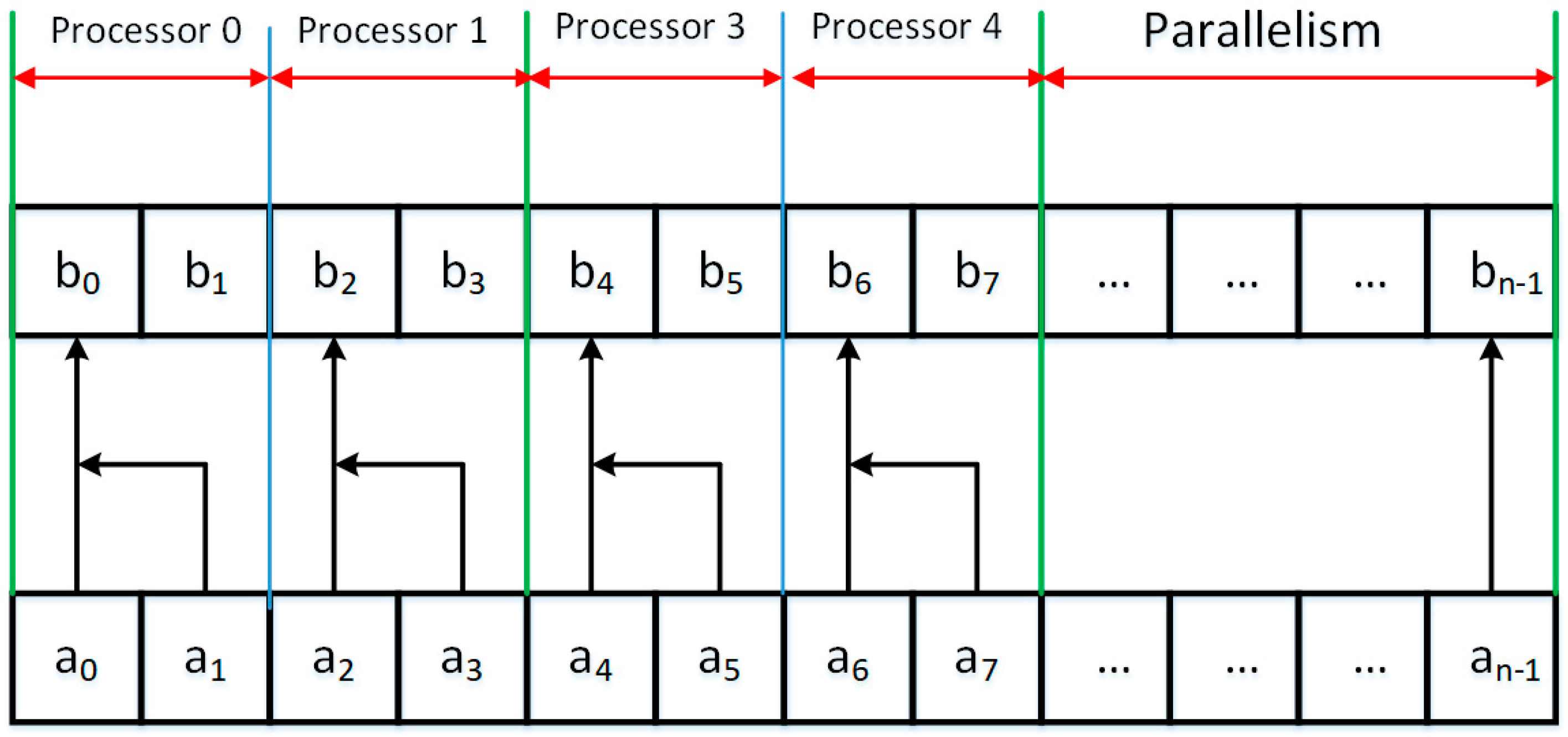
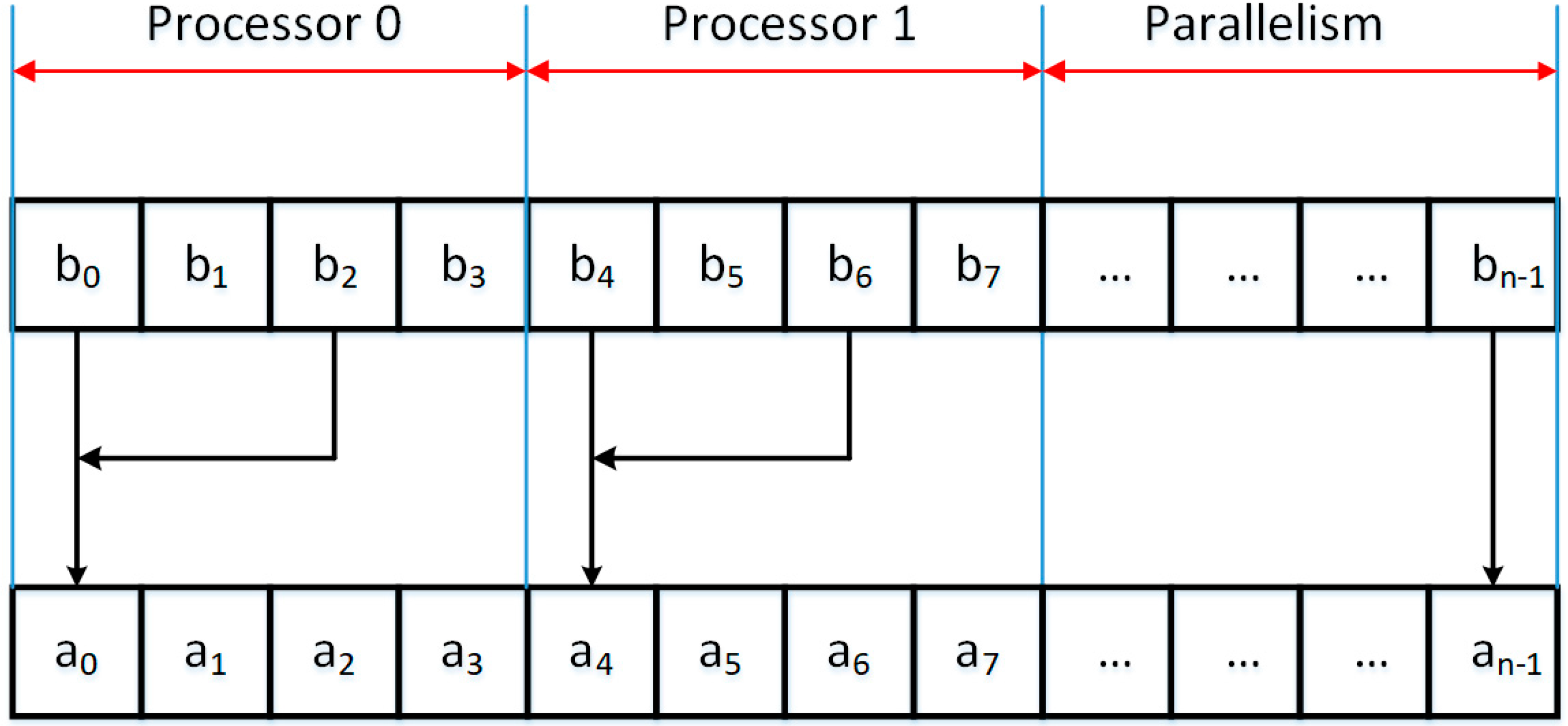
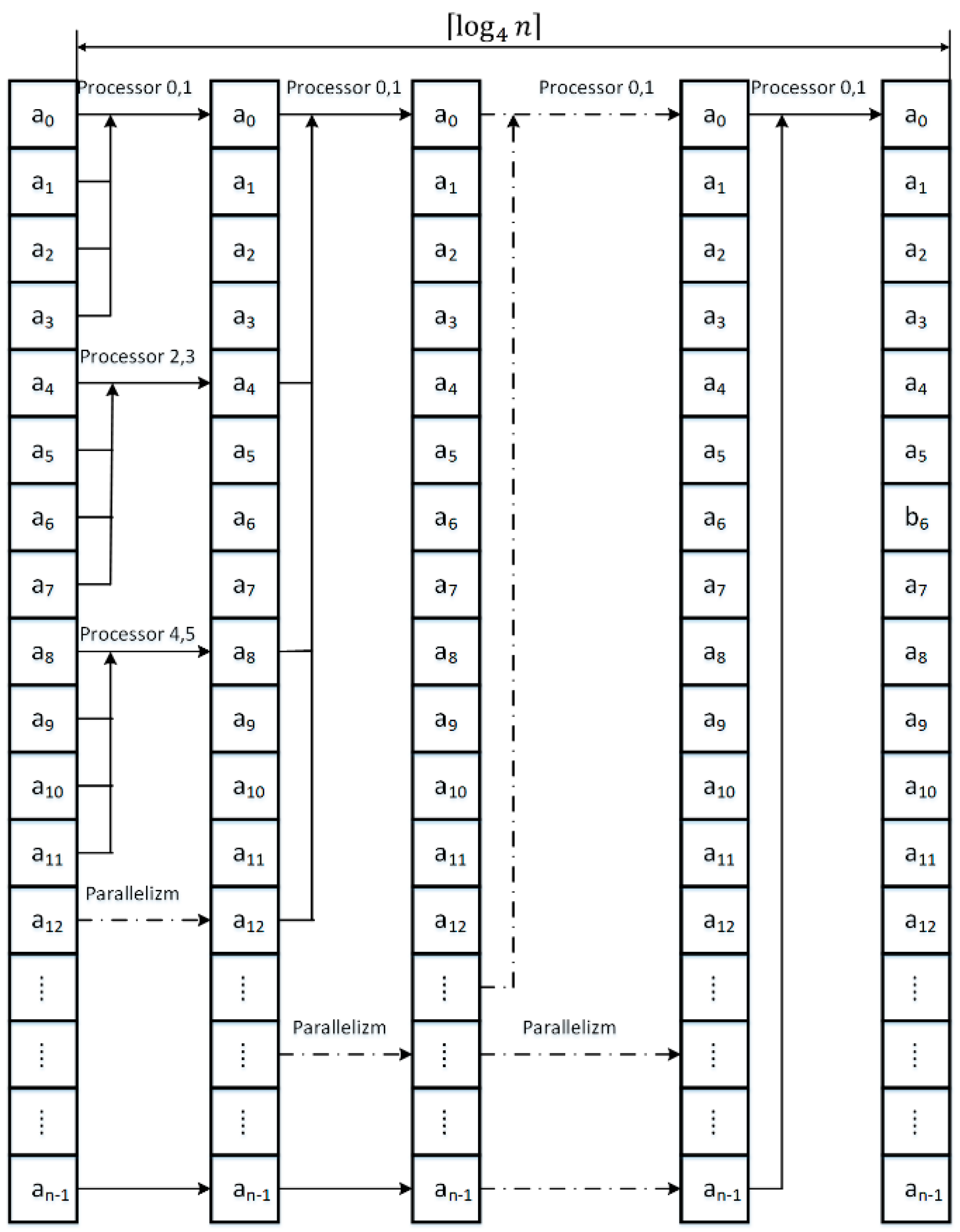
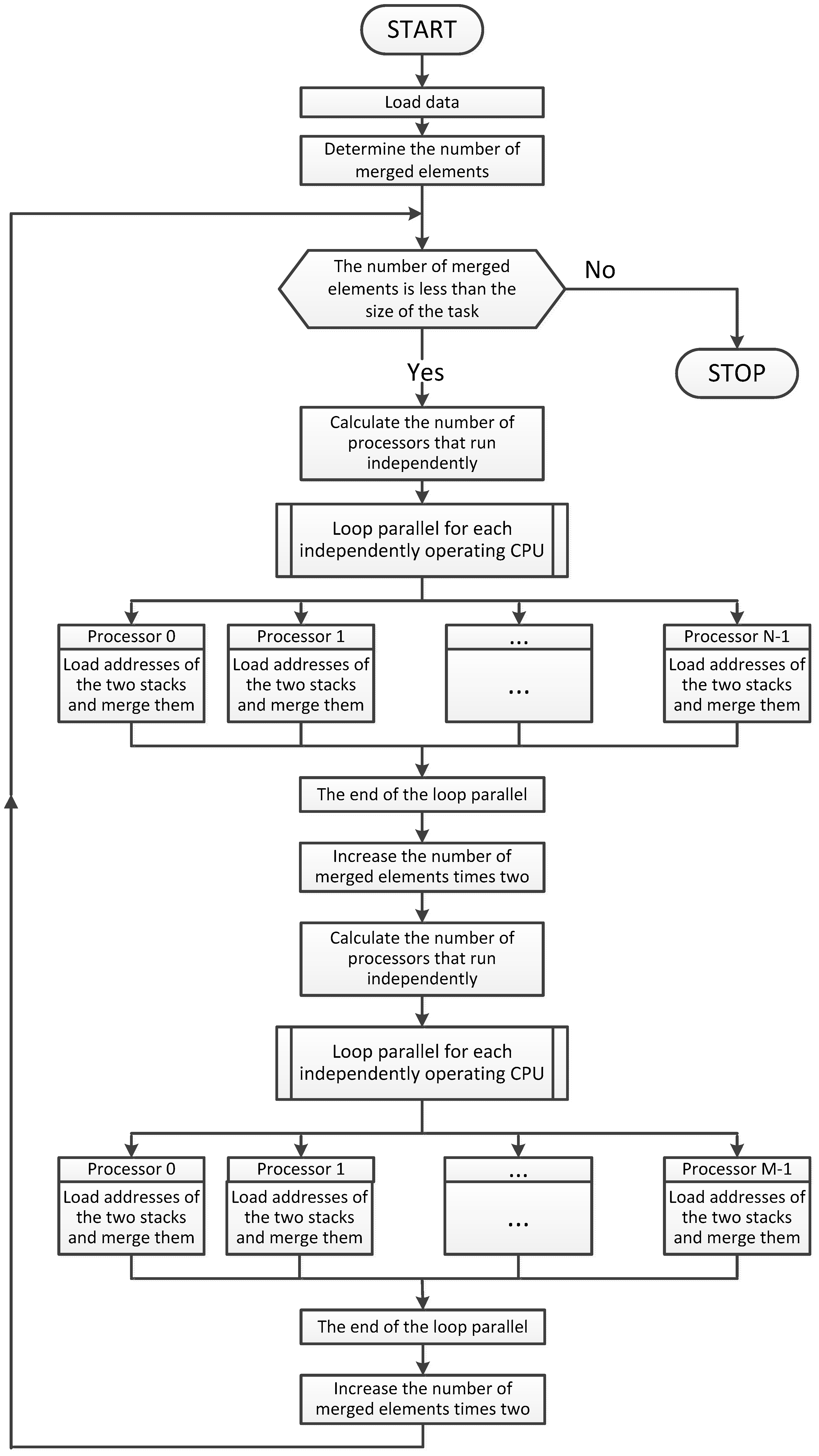
3. Parallel Modified Merge Sort Algorithm
| Algorithm 1. Parallelized Modified Merge Sort Algorithm |
| Start Load table a Load dimension of table a into n Create an array of b of dimension n Start Load table a Load dimension of table a into n Create an array of b of dimension n Set options for parallelism to use all processors of the system Remember 1 in m While m is less than n then do Begin Remember 2*m in m2 Remember 4*m in m4 Remember (n-1)/m2 in it1 Parallel for each processor at index j greater or equal 0 and less than it1 + 1 do Begin parallel for Remember j*m2 in i Remember i in p1 Remember i+m in p2 If p2 greater than n then do Begin Remember n in p2 End Remember n-p1 in c1 If c1 greater than m then do Begin Remember m in c1 End Remember n-p2 in c2 If c2 greater than m then do Begin Remember m in c2 End Proceed function the merge algorithm of two sorting string merging of array a and write in the array b End of the parallel for Remember (n-1)/m4 in it3 Parallel for each processor at index j greater or equal 0 and less than it3 + 1 do Begin parallel for Remember j*m4 in i Remember i in p1 Remember i+m2 in p2 If p2 greater than n then do Begin Remember n in p2 End Remember n-p1 in c1 If c1 greater than m2 then do Begin Remember m2 in c1 End Remember n-p2 in c2 If c2 greater than m2 then do Begin Remember m2 in c2 End Proceed function the merge algorithm of two sorting string merging of array b and write in the array a End of the parallel for Multiply variable m by four End Stop |
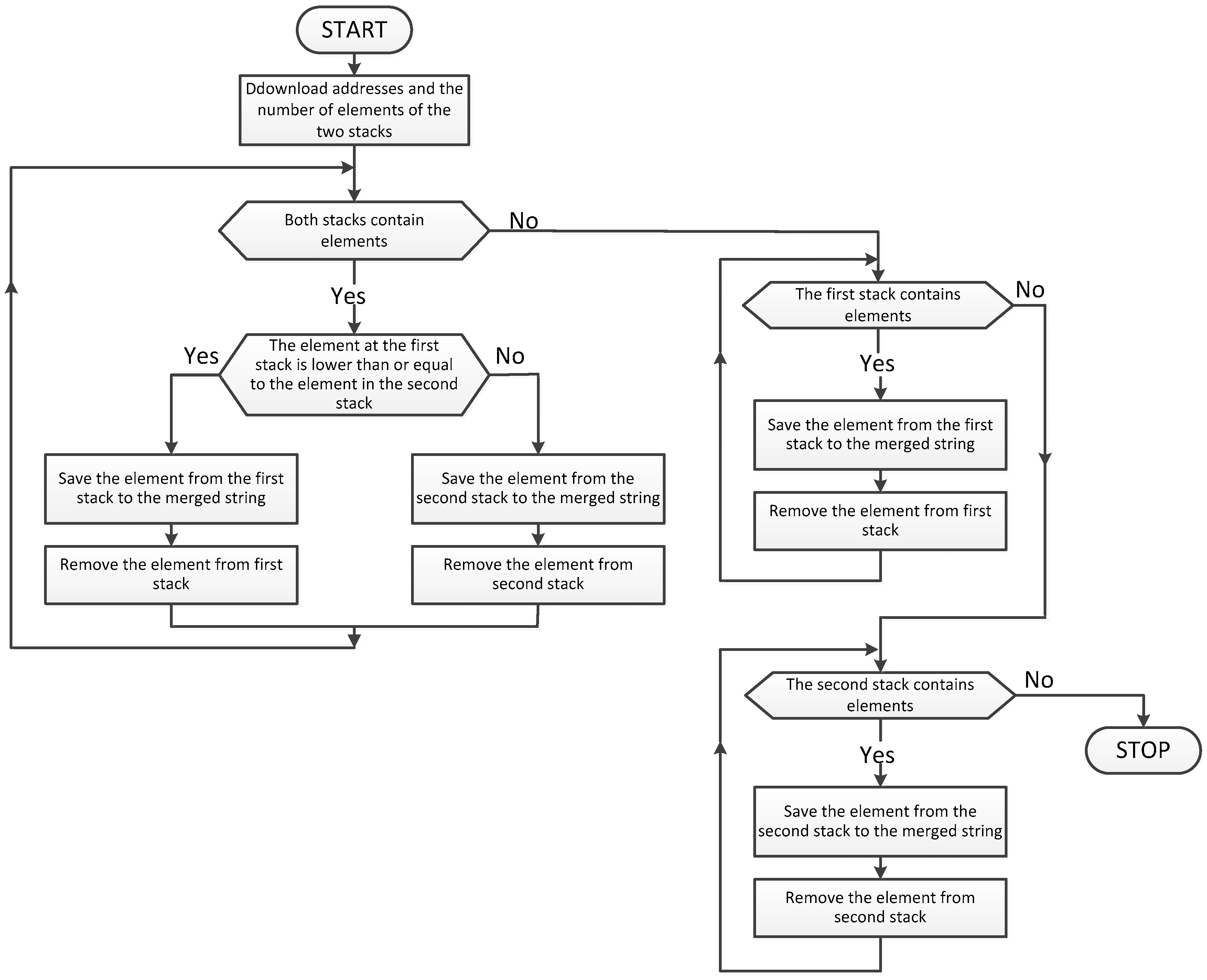
| Algorithm 2. The Merge Algorithm of Two Sorted Strings |
| Start Load table a Load table b Load index p1 Load variable c1 Load index p2 Load variable c2 Remember p1 in pb While c1 greater than 0 and c2 greater than 0 then do Begin If a[p1] less or equal a[p2] then do Begin Remember a[p1] in b[pb] Add to index p1 one Add to index pb one Subtract from variable c1 one End Else Remember a[p2] in b[pb] Add to index p2 one Add to index pb one Subtract from variable c2 one End End While c1 greater than 0 then do Begin Remember a[p1] in b[pb] Add to index p1 one Add to index pb one Subtract from variable c1 one End While c2 greater than 0 then do Begin Remember a[p2] in b[pb] Add to index p2 one Add to index pb one Subtract from variable c2 one End Stop |
4. The Study of the Parallelized Modified Merge Sort
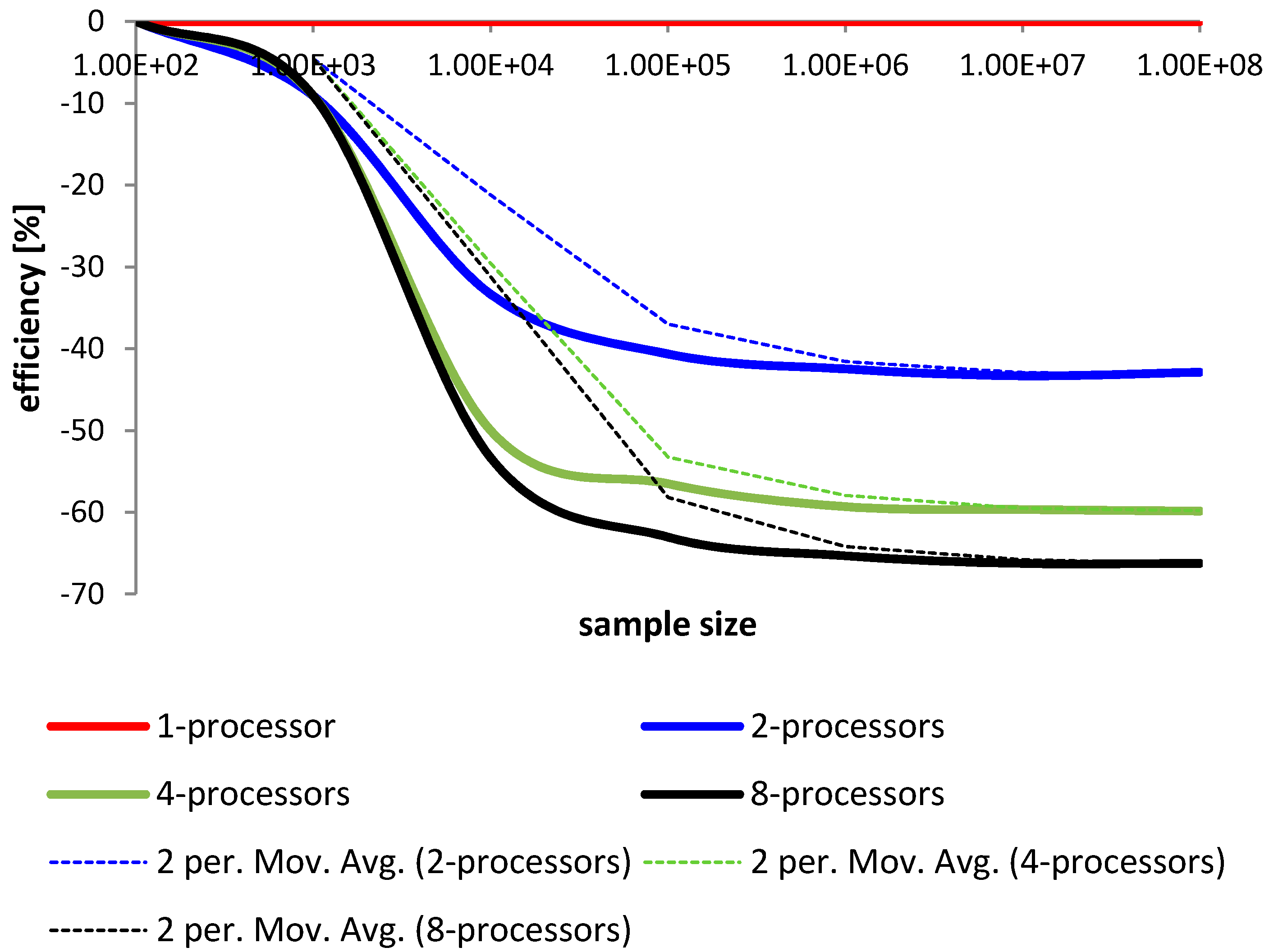
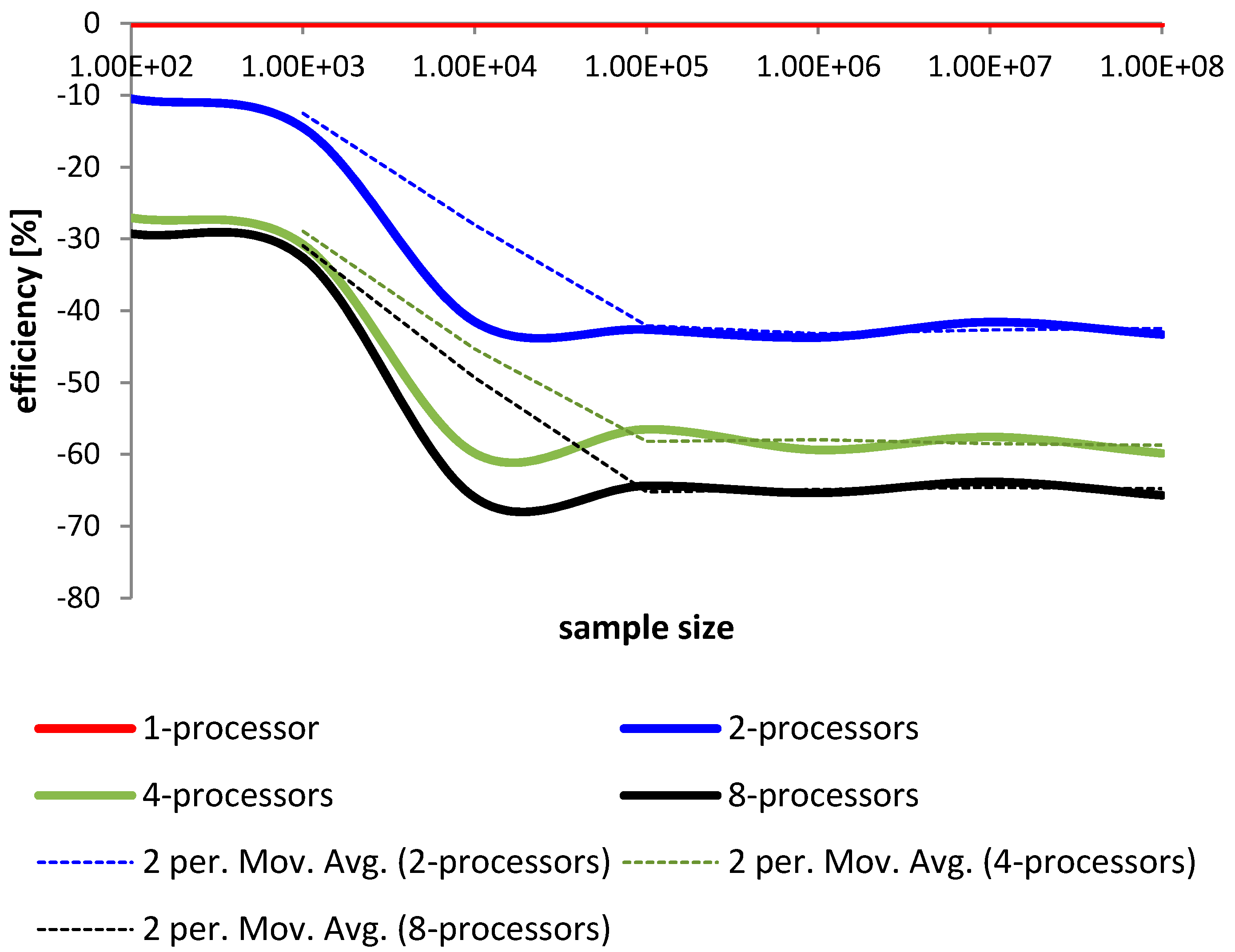
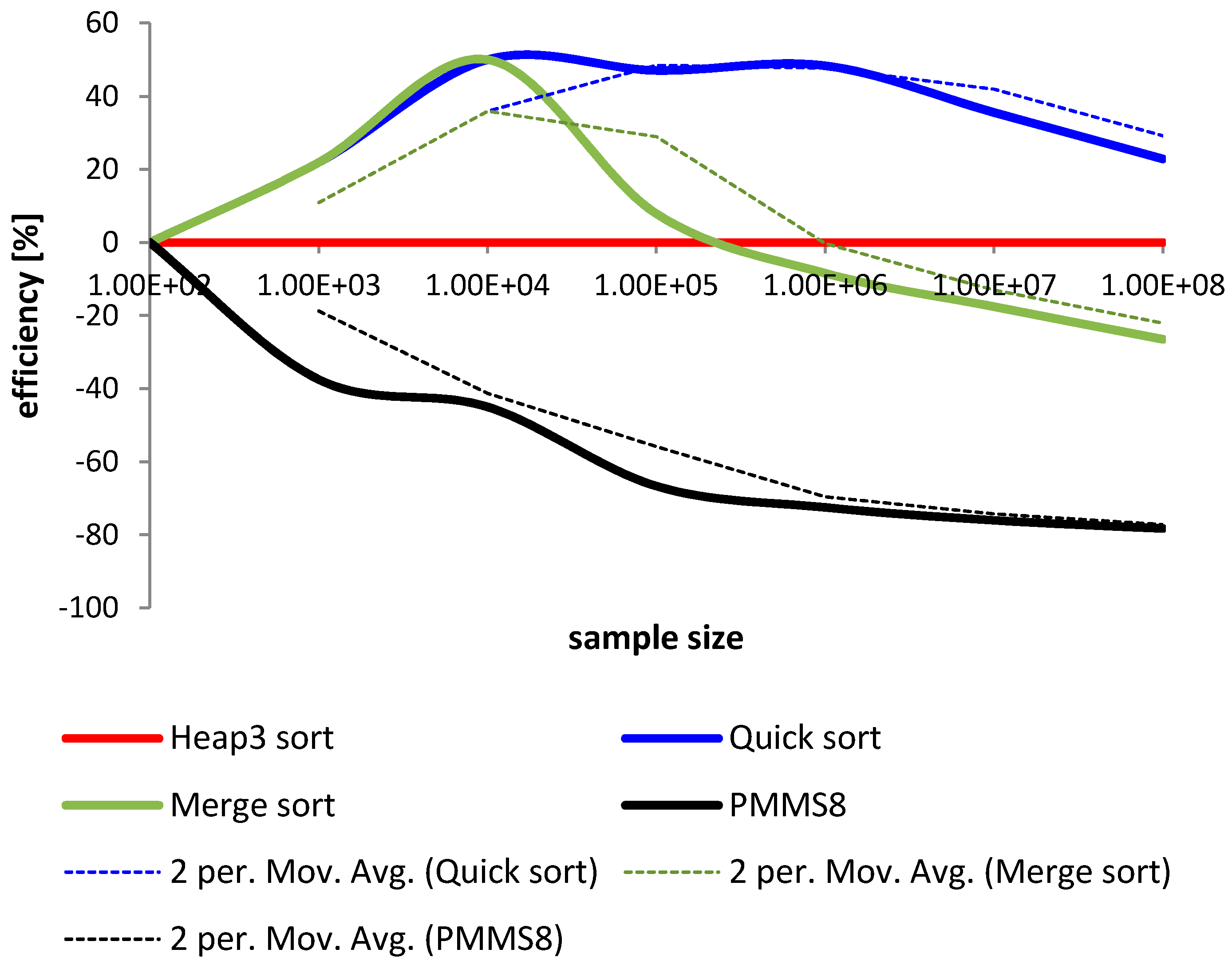
4.1. Comparison and Analysis
4.2. Conclusions
5. Final Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Aho, I.; Hopcroft, J.; Ullman, J. The Design and Analysis of Computer Algorithms; Addison-Wesley Publishing Company: Boston, MA, USA, 1975. [Google Scholar]
- Knuth, D. The Art of Computer Programming Vol.3: Sorting and Searching; Addison-Wesley: Boston, MA, USA, 1998. [Google Scholar]
- Bing-Chao, H.; Knuth, D. A one-way, stack less quick sort algorithm. BIT 1986, 26, 127–130. [Google Scholar] [CrossRef]
- Francis, R.; Pannan, L. A parallel partition for enhanced parallel quick sort. Parallel Comput. 1992, 18, 543–550. [Google Scholar] [CrossRef]
- Rauh, A.; Arce, G. A fast weighted median algorithm based on quick select. In Proceedings of the IEEE 17th International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 105–108. [Google Scholar]
- Tsigas, P.; Zhang, Y. A simple, fast parallel implementation of quick sort and its performance evaluation on SUN enterprise 10,000. In Proceedings of the Euromicro Workshop on Parallel, Distributed and Network-Based Processing, Genova, Italy, 5–7 February 2003; pp. 372–381. [Google Scholar]
- Daoud, A.; Abdel-Jaber, H.; Ababneh, J. Efficient non-quadratic quick sort (NQQuickSort). In Proceedings of the International Conference on Digital Enterprise and Information Systems, London, UK, 20–22 July 2011. [Google Scholar]
- Edmondson, J. Pivot sort—Replacing quick sort. In Proceedings of the 2005 International Conference on Algorithmic Mathematics and Computer Science, Las Vegas, NV, USA, 20–23 June 2005; pp. 47–53. [Google Scholar]
- Kushagra, S.; López-Ortiz, A.; Munro, J.; Qiao, A. Multi-pivot quicksort: Theory and experiments. In Proceedings of the Meeting on Algorithm Engineering & Experiments. Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, 10–12 January 2016; pp. 47–60. [Google Scholar]
- Ben-Or, M. Lower bounds for algebraic computation trees. In Proceedings of the 15th ACM Symposium on Theory of Computing (STOC), Boston, MA, USA, 25–27 April 1983; pp. 80–86. [Google Scholar]
- Doberkat, E. Inserting a new element into a heap. BIT Numer. Math. 1983, 21, 255–269. [Google Scholar] [CrossRef]
- Lutz, M.; Wegner, L.; Teuhola, J. The external heap sort. IEEE Trans. Softw. Eng. 1989, 15, 917–925. [Google Scholar]
- Sumathi, S.; Prasad, A.; Suma, V. Optimized heap sort technique (OHS) to enhance the performance of the heap sort by using two-swap method. In Proceedings of the 3rd International Conference on Frontiers of Intelligent Computing: Theory and Applications (FICTA-2014), Bhubaneswar, India, 14–15 November 2014; pp. 693–700. [Google Scholar]
- Roura, S. Digital access to comparison-based tree data structures and algorithms. J. Algorithms 2001, 40, 123–133. [Google Scholar] [CrossRef]
- Abrahamson, K.; Dadoun, N.; Kirkpatrick, D.; Przytycka, T. A simple parallel tree construction algorithm. J. Algorithms 1987, 10, 287–302. [Google Scholar] [CrossRef]
- Carlsson, S.; Levcopoulos, C.; Petersson, O. Sublinear merging and natural merge sort. Algorithms 1990, 450, 251–260. [Google Scholar] [CrossRef]
- Cole, R. Parallel merge sort. SIAM J. Comput. 1988, 17, 770–785. [Google Scholar] [CrossRef]
- Gedigaa, G.; Duntschb, I. Approximation quality for sorting rules. Comput. Stat. Data Anal. 2002, 40, 499–526. [Google Scholar] [CrossRef]
- Gubias, L. Sorting unsorted and partially sorted lists using the natural merge sort. Softw. Pract. Exp. 2006, 11, 1339–1340. [Google Scholar] [CrossRef]
- Huang, B.; Langston, M. Merging sorted runs using main memory. Acta Inform. 1989, 27, 195–215. [Google Scholar] [CrossRef]
- Huang, B.; Langston, M. Practical in-place merging. Commun. ACM 1989, 31, 348–352. [Google Scholar] [CrossRef]
- Zhang, W.; Larson, P. Speeding up external merge sort. IEEE Trans. Knowl. Data Eng. 1996, 8, 322–332. [Google Scholar] [CrossRef]
- Zhang, W.; Larson, P. Dynamic memory adjustment for external merge sort. In Proceedings of the Very Large Data Bases Conference, San Francisco, CA, USA, 25–29 August 1997; pp. 376–385. [Google Scholar]
- Zhang, W.; Larson, P. Buffering and read-ahead strategies for external merge sort. In Proceedings of the Very Large Data Bases Conference, New York, NY, USA, 24–27 August 1998; pp. 523–533. [Google Scholar]
- Vignesh, R.; Pradhan, T. Merge sort enhanced in place sorting algorithm. In Proceedings of the 2016 International Conference on Advanced Communication Control and Computing Technologies (ICACCCT), Ramanathapuram, India, 25–27 May 2016; pp. 698–704. [Google Scholar]
- Cheema, S.; Sarwar, N.; Yousaf, F. Contrastive analysis of bubble & merge sort proposing hybrid approach. In Proceedings of the 2016 International Conference on Innovative Computing Technology (INTECH), Dublin, Ireland, 24–26 August 2016; pp. 371–375. [Google Scholar]
- Smita, P.; Sourabh, C.; Safikul, A.S. Enhanced merge sort—A new approach to the merging process. Procedia Comput. Sci. 2016, 93, 982–987. [Google Scholar]
- Alanko, T.; Erkio, H.; Haikala, I. Virtual memory behavior of some sorting algorithm. IEEE Trans. Softw. Eng. 1984, 10, 422–431. [Google Scholar] [CrossRef]
- Larson, P.-Å.; Graefe, G. Memory management during run generation in External Sorting. In Proceedings of the SIGMOD, Seattle, WA, USA, 2–4 June 1998; pp. 472–483. [Google Scholar]
- LaMarca, A.; Ladner, R. The influence of caches on the performance of sorting. J. Algorithms 1999, 31, 66–104. [Google Scholar] [CrossRef]
- Crescenzi, P.; Grossi, R.; Italiano, G.F. Search data structures for skewed strings. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2647, pp. 81–96. [Google Scholar]
- Estivill-Castro, V.; Wood, D. A survey of adaptive sorting algorithms. Comput. Surv. 1992, 24, 441–476. [Google Scholar] [CrossRef]
- Choi, S.; Seo, J.; Kim, M.; Kang, S.; Han, S. Chrological big data curation: A study on the enhanced information retrieval system. IEEE Access 2017, 5, 11269–11277. [Google Scholar] [CrossRef]
- Axtmann, M.; Bigmann, T.; Schulz, C.; Sanders, P. Practical massively parallel sorting. In Proceedings of the 27th ACM Symposium on Parallelism in Algorithms and Architectures (SPAA’15), Portland, OR, USA, 13–15 June 2015; pp. 13–23. [Google Scholar]
- Shen, Z.; Zhang, X.; Zhang, M.; Li, W.; Yang, D. Self-sorting-based MAC protocol for high-density vehicular Ad Hot networks. IEEE Access 2017, 5, 7350–7361. [Google Scholar] [CrossRef]
- Abdel-Hafeez, S.; Gordon-Ross, A. An efficient O(N) comparison-free sorting algorithm. IEEE Trans. Very Large Scale Integr. Syst. 2017, 25, 1930–1942. [Google Scholar] [CrossRef]
- Saher, M.A.; Emrah, A.S.; Celebi, F. Bidirectional conditional insertion sort algorithm; An efficient progress on the classical insertion sort. Future Gener. Comput. Syst. Int. J. ESci. 2017, 71, 102–112. [Google Scholar]
- Woźniak, M.; Marszałek, Z.; Gabryel, M.; Nowicki, R. Preprocessing large data sets by the use of quick sort algorithm. Adv. Intell. Syst. Comput. KICSS’2013 2015, 364, 111–121. [Google Scholar] [CrossRef]
- Woźniak, M.; Marszałek, Z.; Gabryel, M.; Nowicki, R. Triple heap sort algorithm for large data sets. In Looking into the Future of Creativity and Decision Support Systems; Skulimowski, A.M.J., Ed.; Progress & Business Publishers: Cracow, Poland, 2015; pp. 657–665. [Google Scholar]
- Woźniak, M.; Marszałek, Z.; Gabryel, M.; Nowicki, R. Modified merge sort algorithm for large scale data sets. In Proceedings of the International Conference on Artificial Intelligence and Soft Computing, Zakopane, Poland, 9–13 June 2013; pp. 612–622. [Google Scholar]
- Marszałek, Z.; Woźniak, M.; Borowik, G.; Wazirali, R.; Napoli, C.; Pappalardo, G.; Tramontana, E. Benchmark tests on improved merge for big data processing. In Proceedings of the Asia-Pacific Conference on Computer Aided System Engineering (APCASE’2015), Quito, Ecuador, 14–16 July 2015; pp. 96–101. [Google Scholar]
- Czerwiński, D. Digital filter implementation in Hadoop data mining system. In Proceedings of the International Conference on Computer Networks, Brunow, Poland, 16–19 June 2015; pp. 410–420. [Google Scholar]
- Marszałek, Z. Novel recursive fast sort algorithm. In Proceedings of the 22nd International Conference on Information and Software Technologies (ICIST), Druskininkai, Lithuania, 13–15 October 2016; pp. 344–355. [Google Scholar]
- Uyar, A. Parallel merge sort with double merging. In Proceedings of the 2014 IEEE 8th International Conference on Application of Information and Communication Technologies (AICT), Astana, Kazakhstan, 15–17 October 2014; pp. 490–494, Book Series: International Conference on Application of Information and Communication Technologies. [Google Scholar]
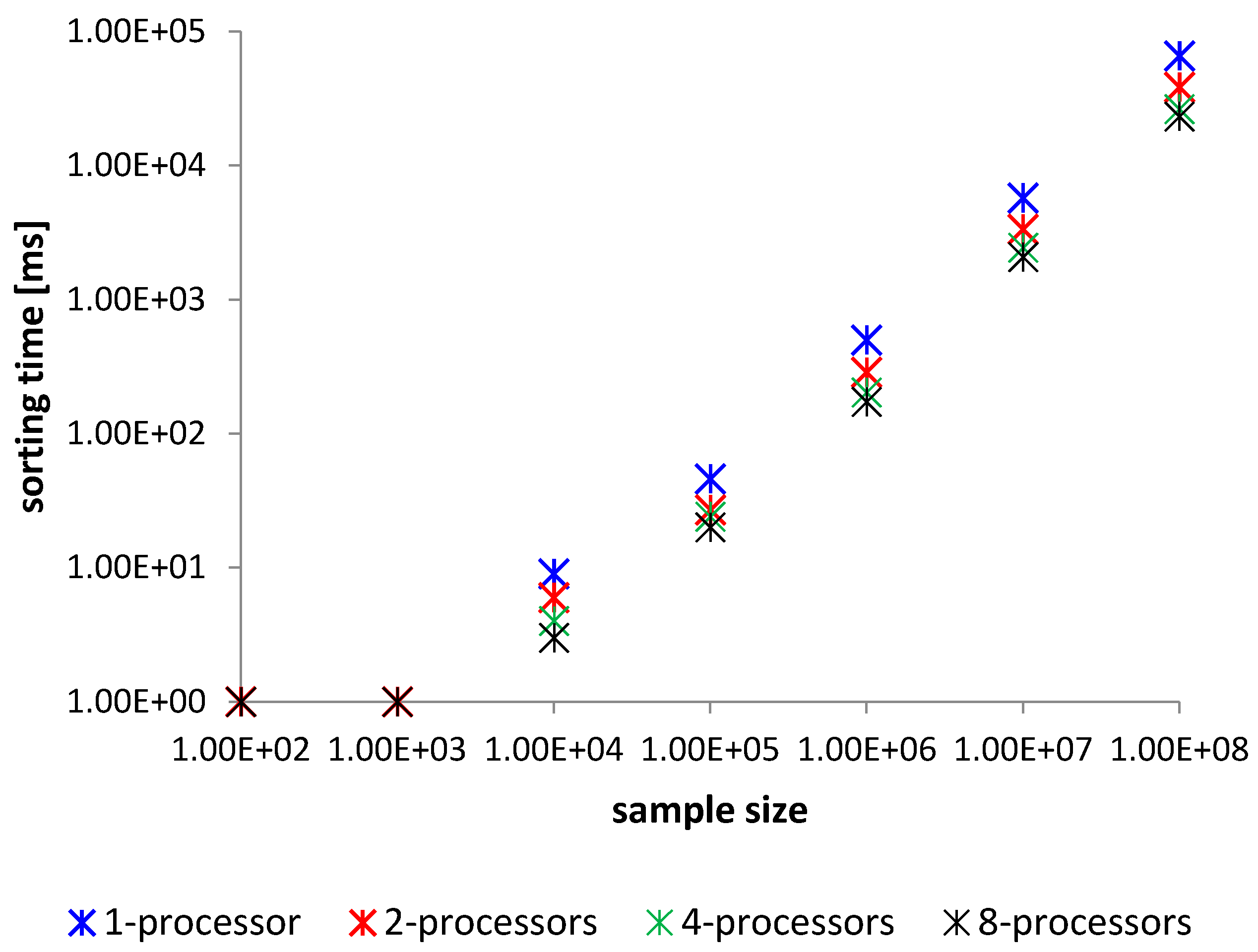
| Method—Average Time Sorting for 100 Samples in [ms] | ||||
|---|---|---|---|---|
| Elements | 1—Processor | 2—Processors | 4—Processors | 8—Processors |
| 100 | 1 | 1 | 1 | 1 |
| 1000 | 1 | 1 | 1 | 1 |
| 10,000 | 6 | 4 | 3 | 3 |
| 100,000 | 46 | 27 | 20 | 17 |
| 1,000,000 | 499 | 287 | 203 | 173 |
| 10,000,000 | 5745 | 3256 | 2317 | 1938 |
| 100,000,000 | 65,730 | 37,542 | 26,382 | 23,186 |
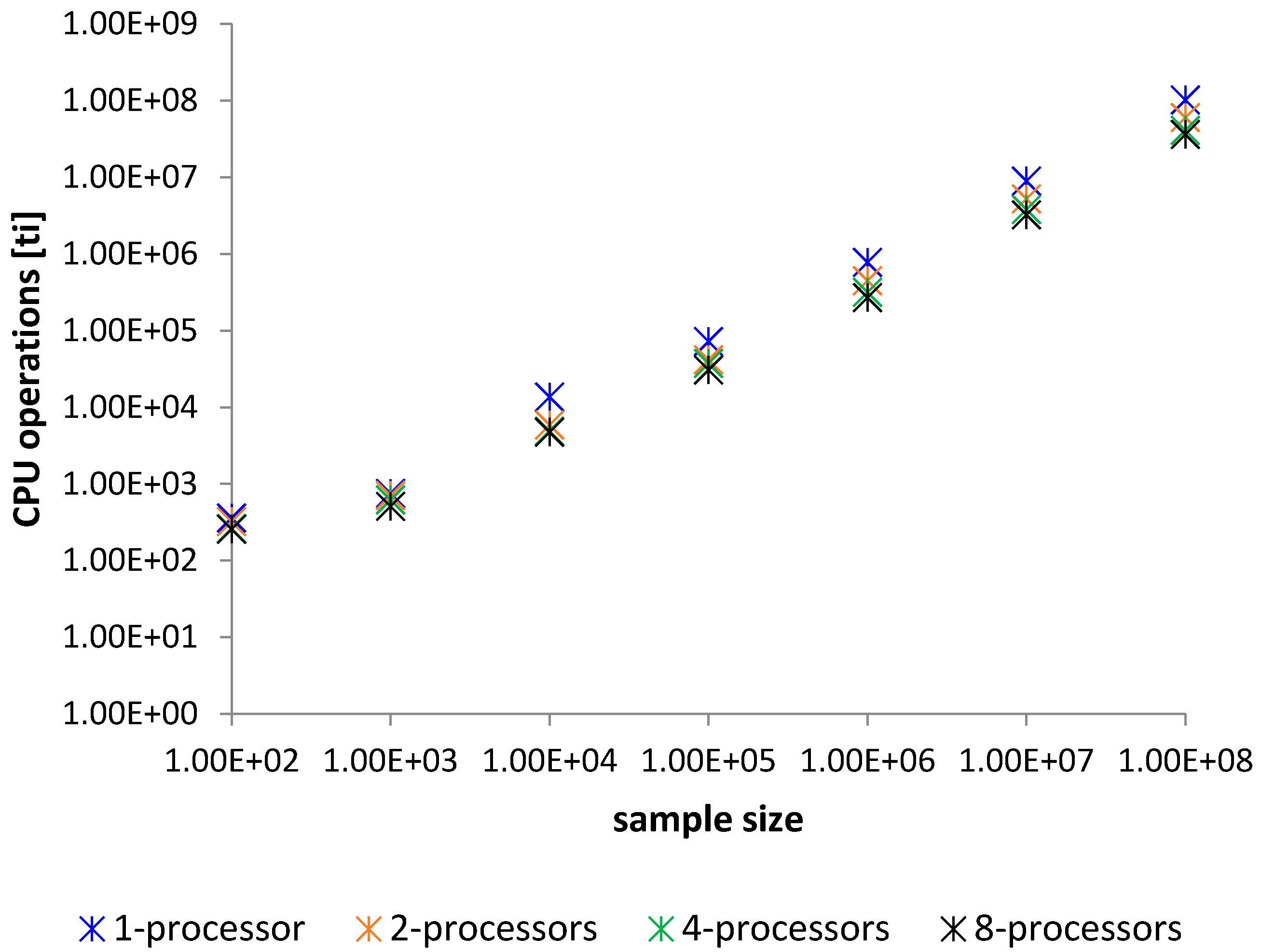
| Method—Average Time Sorting for 100 Samples in [ti] | ||||
|---|---|---|---|---|
| Elements | 1—Processor | 2—Processors | 4—Processors | 8—Processors |
| 100 | 362 | 324 | 264 | 256 |
| 1000 | 757 | 647 | 524 | 510 |
| 10,000 | 13,672 | 7993 | 5490 | 4647 |
| 100,000 | 72,291 | 41,473 | 31,437 | 25,748 |
| 1,000,000 | 777,903 | 437,706 | 315,924 | 269,424 |
| 10,000,000 | 8,954,448 | 5,230,931 | 3,798,070 | 3,238,545 |
| 100,000,000 | 102,449,603 | 58,073,015 | 41,119,351 | 35,138,937 |
| Coefficient of Variation [ms] | ||||
|---|---|---|---|---|
| Elements | 1—Processor | 2—Processors | 4—Processors | 8—Processors |
| 100 | 0.3821615 | 0.43268856 | 0.42831802 | 0.44107100 |
| 1000 | 0.3643562 | 0.40356701 | 0.41257718 | 0.36173402 |
| 10,000 | 0.2743689 | 0.36596252 | 0.21821789 | 0.34069257 |
| 100,000 | 0.1661708 | 0.17707090 | 0.17747680 | 0.14015297 |
| 1,000,000 | 0.1919563 | 0.21309771 | 0.14367983 | 0.15528751 |
| 10,000,000 | 0.2029680 | 0.21077261 | 0.16998284 | 0.17756993 |
| 100,000,000 | 0.2089429 | 0.20919211 | 0.20167919 | 0.16278364 |
| Coefficient of Variation [ti] | ||||
|---|---|---|---|---|
| Elements | 1—Processor | 2—Processors | 4—Processors | 8—Processors |
| 100 | 0.40505154 | 0.26224710 | 0.15192519 | 0.17000328 |
| 1000 | 0.36725132 | 0.28016626 | 0.20075293 | 0.254527489 |
| 10,000 | 0.28111613 | 0.31917443 | 0.23101516 | 0.212133586 |
| 100,000 | 0.16516246 | 0.17583523 | 0.12684148 | 0.132691392 |
| 1,000,000 | 0.19185991 | 0.21235997 | 0.15981887 | 0.155664995 |
| 10,000,000 | 0.20295364 | 0.21077453 | 0.16344274 | 0.177647028 |
| 100,000,000 | 0.20894325 | 0.20918928 | 0.15855142 | 0.162786764 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marszałek, Z. Parallelization of Modified Merge Sort Algorithm. Symmetry 2017, 9, 176. https://doi.org/10.3390/sym9090176
Marszałek Z. Parallelization of Modified Merge Sort Algorithm. Symmetry. 2017; 9(9):176. https://doi.org/10.3390/sym9090176
Chicago/Turabian StyleMarszałek, Zbigniew. 2017. "Parallelization of Modified Merge Sort Algorithm" Symmetry 9, no. 9: 176. https://doi.org/10.3390/sym9090176
APA StyleMarszałek, Z. (2017). Parallelization of Modified Merge Sort Algorithm. Symmetry, 9(9), 176. https://doi.org/10.3390/sym9090176





