1. Introduction
In the modern business environment, the performance of a company largely depends on the competitiveness of its supply chain. Supply chain management is a process that covers raw material procurement, the production of finished products, and distributing the finished good to consumers through distributors and retailers [
1]. Suppliers are the foundation of the supply chain operation, which have a great potential to enhance the competitiveness of the supply chain for a focal firm [
2]. In this regard, selecting the most appropriate supplier can reduce the cost of production, decrease the time for bringing products to the market, improve the quality of products, and increase customer satisfaction and profitability [
3,
4]. Thus, to increase business performance and competitive advantage, supplier selection is a crucial strategic decision in supply chain management and has become a very fundamental component of the viable benefits of firms and industries.
When selecting appropriate suppliers, various criteria are often involved, including price, quality, delivery time, service, and reputation. It is clear that supplier selection for an organization is a complex, multiple criteria decision-making (MCDM) problem due to the presence of conflicting and competing factors, such as quality and cost. VIKOR (VIsekriterijumska optimizacija i KOmpromisno Resenje), initially proposed by Opricovic [
5], is an effective MCDM method for handling discrete multi-criteria problems with conflicting and noncommensurable criteria. It focuses on ranking and choosing from a set of alternatives, and determines compromise solutions which can help decision-makers to reach a final decision [
6,
7]. In view of its features and capabilities, the VIKOR approach has been successfully implemented in lots of real-world decision-making problems. For example, Hafezalkotob and Hafezalkotob [
8] proposed an interval target-based VIKOR model supported on interval distance and preference degree to solve machine selection problems. Canto-Perello et al. [
9] proposed a hybrid model combining Delphi, an analytical hierarchy process (AHP), and the VIKOR technique for the selection of a rehabilitation project considering social, economic, and landscape indicators. Büyüközkan and Karabulut [
10] presented a combination approach integrating AHP and VIKOR for energy project performance evaluation with a sustainability perspective. Xu et al. [
11] used a VIKOR-based method to evaluate the service performance of electric vehicle sharing programs in Beijing, China. Soner et al. [
12] applied AHP and VIKOR methods within an interval type-2 fuzzy context for selecting a hatch cover type for bulk carriers. Sharma et al. [
13] employed a novel Entropy-VIKOR approach for optimizing the performance of discrete V obstacles in a solar air flow channel. Ghorabaee et al. [
14] presented an extended VIKOR method with interval type-2 fuzzy sets for solving the multi-criteria project selection problem. In Sari [
15], a decision framework based on Monte Carlo simulation, AHP, and the VIKOR method under a fuzzy environment was reported for evaluating green supply chain management practices. Moreover, the use of the VIKOR for supplier selection is practical and has demonstrated satisfactory results [
4,
16,
17,
18,
19]. Therefore, it is natural to utilize the the VIKOR approach to manage supplier selection problems involving comprehensive criteria.
On the other hand, it is often hard to precisely assess the performance of each alternative in the supplier selection process, as human judgments are imprecise and vague under many circumstances [
20]. As a result, a lot of supplier selection methods under a fuzzy environment have been suggested in the literature [
18,
21,
22]. In many real-life situations, however, the information obtained is not enough for the exact definition of a membership degree for a certain element [
23]. That is, there may be some amount of a hesitation degree among membership and non-membership. To address this problem, Atanassov [
24] introduced the concept of intuitionistic fuzzy sets (IFSs) as an extension of fuzzy set theory [
25]. Each IFS is described by a membership function and a non-membership function. Because of insufficiency in information availability, the IFS theory has been widely used to solve many MCDM problems. For instance, Rodríguez et al. [
26] presented an intuitionistic fuzzy method for the selection of the most suitable risk management option in information technology projects. Mehlawat and Grover [
27] developed an MCDM method using triangular intuitionistic fuzzy numbers to handle the critical path selection problem. Liu et al. [
28] proposed a method based on sentiment analysis technique and IFSs to rank products through online reviews. In Botía et al. [
29], a method based on fuzzy cellular automata and IFSs was used for analyzing optical frequency comb behavior and the spectral shape in terms of phase and intensity. In Atalay and Can [
30], a hybrid approach combining intuitionistic fuzzy AHP and intuitionistic fuzzy multi-objective optimization by ratio analysis (MOORA) was proposed for new product selection. In addition, other intuitionistic fuzzy decision-making approaches have been proposed by researchers for radio frequency identification technology selection [
31], failure mode and effect analysis [
32], construction site layout [
33], and so on. Therefore, the IFSs are more flexible and precise for tackling imprecise and uncertain decision information in supplier selection due to their capability of accommodating hesitation in a decision-making process.
Given the strengths and wide applications of the VIKOR method and IFSs, this paper extends the classical VIKOR to develop a new method, called intuitionistic fuzzy hybrid VIKOR (IFH-VIKOR), for solving supplier selection problems. The primary contributions of this study are summarized as follows: (1) to deal with the uncertainty and vagueness in supplier selection, performance ratings of alternatives are taken as linguistic terms denoted by intuitionistic fuzzy numbers (IFNs); (2) to combine the merits of both subjective and objective weighting methods, a combination weighting method is proposed to define criteria weights in solving the supplier selection problem; and (3) to identify the most appropriate supplier, an extended VIKOR method is developed for the ranking of the considered alternatives. Furthermore, two empirical examples of supplier selection are provided to illustrate the applicability and effectiveness of our proposed hybrid method.
The remaining part of this paper is set out as follows. The current supplier selection approaches are reviewed in
Section 2 to show the research gaps. In
Section 3, the preliminaries about IFS theory and the objective weighting method are introduced. In
Section 4, we develop the IFH-VIKOR method to solve supplier selection problems with intuitionistic fuzzy information.
Section 5 investigates two practical supplier selection problems to demonstrate the proposed method. Finally, we conclude this paper with some observations in
Section 6.
3. Preliminaries
3.1. Intuitionistic Fuzzy Set Theory
In what follows, some basic concepts of IFSs are introduced.
Definition 1. Let X be a fixed set, then an IFS A in X is given as the following [
24]:
where and are membership function and non-membership function, respectively, satisfying .
The numbers and represent, respectively, the membership degree and the non-membership degree of the element to A, for all . Besides, denotes the hesitation degree of , which is the degree of indeterminacy or the degree of hesitancy of x to A. It is obvious that .
For an IFS, the pair is called an intuitionistic fuzzy number (IFN), and each IFN is represented by , where and . In addition, and are the score and accuracy degrees of , respectively.
Definition 2. Given any three IFNs , , and , the operations of IFNs can be shown as follows [
48,
49]:
- (1)
- (2)
- (3)
- (4)
Definition 3. For comparing any two IFNs and , the method based on score function and accuracy function was proposed [
51,
52]:
- (1)
If , then ;
- (2)
If , and
If , then ;
If , then .
Definition 4. Suppose that and are two IFNs, then the distance between and is computed by [
53]:
Definition 5. For a collection of IFNs is the weight vector of with and if , andthen the function is called the symmetric intuitionistic fuzzy weighted averaging (SIFWA) operator [
54].
The concept of a linguistic variable is of vital importance for dealing with circumstances which are too complex or too ill-defined to be reasonably described via conventional quantitative expressions [
55]. In this study, the relative weights of criteria and the ratings of alternatives concerning each criterion are taken as linguistic terms represented using IFNs. For instance, these linguistic terms can be denoted by IFNs as depicted in
Table 1 and
Table 2. Note that the IFNs can be defined based on historical data and/or a questionnaire responded to by domain experts.
3.2. Objective Weighting Method
The entropy concept [
56] is able to measure information uncertainty formulated in line with probability theory. It is very useful in determining the relative contrast in intensities of criteria to express the average intrinsic information conveyed to the decision-maker. The entropy method utilizes the probabilistic discrimination among data to obtain the importance weights of evaluation criteria [
57,
58]. If all alternatives are the same in relation to a specific criterion, then that criterion should be eliminated because it transmits no information about decision-makers’ preferences. On the opposite, the criterion that discriminates the data more effectively should be given a higher weight.
Different from the traditional entropy method, intuitionistic fuzzy entropy (IFE) focuses on the credibility of the input data to determine criteria weights. It measures the extent of separation of the IFSs from fuzzy sets rather than from ordinary sets as in the traditional entropy method. Vlachos and Sergiadis [
59] presented an approach to discrimination measures for IFSs based on information theory, and derived an entropy measure for IFSs as follows:
Here, if then and respectively.
In this research, the IFE measure is applied to compute the objective weights for supplier selection criteria, and the procedural steps are explained as below:
Step 1: Establish the intuitionistic fuzzy decision matrix.
Suppose that there are
m alternatives
Ai (
i = 1, 2,...,
m) to be performed over
n criteria
Cj (
j = 1, 2,...,
n). The intuitionistic fuzzy decision matrix
R is constructed as:
where
,
i = 1, 2,...,
m and
j = 1, 2 ,...,
n.
Step 2: Calculate the IFE values.
The following equation is applied for the calculation of the IFE value
Ej for each criterion:
Step 3: Obtain the objective weights of criteria by:
where
and
.
4. The Proposed Supplier Selection Method
To address a supplier selection problem, the decision-maker must evaluate alternatives pertaining to each criterion, address criteria weights, and determine the optimum one from the generated set of alternatives. This section extends the VIKOR method to the intuitionistic fuzzy setting for supplier selection and a combination weighting method is utilized for assigning the weights of the evaluation criteria. In the proposed method, the ratings of alternatives are taken as linguistic terms, which can be represented by IFNs as given in
Table 1. The subjective weights of the criteria are evaluated by decision-makers with the linguistic terms shown in
Table 2. The objective criteria weights are obtained by using the IFE method as presented in
Section 3.2. Thus, the proposed intuitionistic fuzzy hybrid VIKOR (IFH-VIKOR) method can not only benefit from IFSs but also combine the strengths of the two kinds of weighting methods.
Suppose that a group supplier selection problem has l decision-makers , m alternatives and n evaluation criteria . Each of the l decision-makers is specified a weight to reflect his/her relative importance in the supplier selection process. Then, the steps of the proposed IFH-VIKOR method for the ranking of suppliers can be defined as follows:
Step 1: Aggregate the decision-makers’ individual assessments.
In the group supplier selection process, the decision-makers’ individual opinions need to be aggregated into group evaluations to build a collective intuitionistic fuzzy decision matrix. Let
be the IFN given by
DMk on the assessment of
Ai with respect to C
j. Then, the aggregated intuitionistic fuzzy ratings (
) of alternatives with regard to each criterion can be acquired through the SIFWA operator as:
Hence, we can express a group supplier selection problem in matrix format as seen below:
where
,
i = 1, 2, ...,
m and
j = 1, 2 ,...,
n are linguistic terms which can be expressed in IFNs.
Step 2: Compute the subjective weights of criteria.
Assume that the weight of the criterion
Cj is provided as
by the decision-maker
DMk. Then, the collective intuitionistic fuzzy weights (
) of the criteria are computed using the SIFWA operator, as:
where
,
j = 1, 2, ...,
n is the importance weight of the
jth criterion.
Based on the collective weights of criteria
, the normalized subjective weight of each criterion is obtained by Equation (10) [
32,
60].
where
and
.
Step 3: Calculate the objective weights of the criteria.
The objective criteria weights can be calculated using the objective weighting method described in
Section 3.2.
Step 4: Determine the intuitionistic fuzzy positive ideal solution
and the intuitionistic fuzzy negative ideal solution
of all criteria ratings,
j = 1, 2,...,
n.
Step 5: Determine the normalized intuitionistic fuzzy differences , i = 1, 2,..., m, j = 1, 2,..., n.
The normalized intuitionistic fuzzy differences
are determined as:
where
Step 6: Obtain the values
Si and
Ri, i = 1, 2,...,
m, by using the formulas:
where
are the combination weights of the criteria, and
denotes the relative importance between subjective weights and objective weights. The value of
φ can be taken to be any value from 0 to 1and it set as 0.5 in this study for simplicity.
Step 7: Determine the values
Qi, i = 1, 2,...,
m, with Equation (18).
where
;
v and 1-
v are the weights for the strategy of maximum group utility and the individual regret, respectively. Usually, the value of
v can be assumed to be 0.5.
Step 8: Rank the alternative suppliers according to the values of S, R, and Q in increasing order. The results are three ranking lists.
Step 9: Propose a compromise solution, the alternative (A(1)), which is the best ranked by the measure Q (minimum) if the following two conditions are satisfied:
C1. Acceptable advantage: where is the alternative with second position in the ranking list by Q.
C2. Acceptable stability: The alternative A(1) must also be in the first place by S or/and R. This compromise solution is stable within a decision-making process, which could be: “voting by majority rule” (when v >0.5 is needed), or “by consensus” , or “with veto” (v <0.5).
The following compromise solutions can be proposed if one of the above conditions is not fulfilled:
Alternatives A(1) and A(2) if only condition C2 is not satisfied; or
Alternatives A(1), A(2),..., A(M) if condition C1 is not satisfied; A(M) is calculated by the equation for maximum M.
5. Illustrative Examples
Two practical examples are presented in this section for illustrating the applicability of the proposed IFH-VIKOR method for supplier evaluation and selection.
5.1. Supplier Selection for a General Hosptial
A university teaching hospital located in Shanghai, China intends to buy a new information management system in order to increase work productivity. After pre-elimination, four software companies A1, A2, A3, and A4 have been determined as alternatives for further assessment. To perform the evaluation, a group composed of four decision-makers DM1, DM2, DM3, and DM4 has been established. Five evaluation criteria for the software are considered, which include Functionality (C1), Reliability (C2), Usability (C3), Maintainability (C4), and Price (C5).
The committee employ the linguistic terms expressed in
Table 1 and
Table 2 to assess the importance weights of the criteria and the suppliers with regard to each criterion. The evaluation results obtained are as shown in
Table 3 and
Table 4. In the supplier selection process, the following weights are given to the four decision makers:
λ1 = 0.15,
λ2 = 0.20,
λ3 = 0.30, and
λ4 = 0.3 owing to their different domain knowledge backgrounds and expertise.
Next, we use the IFH-VIKOR method being proposed to provide a solution for the supplier selection problem, and the computational process is described as follows:
Step 1: After quantifying the linguistic evaluations by corresponding IFNs, the collective intuitionistic fuzzy decision matrix can be created using the SIFWA operator as given in Equation (8). The results are shown in
Table 5.
Step 2: The assessments of decision-makers on criteria weights are fused by Equation (9) as listed in the last row of
Table 5. Then, using Equation (10), the normalized subjective weights of criteria are obtained as displayed in
Table 6.
Step 3: Based on the objective weighting method, the IFE value of each criterion is obtained by Equation (6) and the objective criteria weights are calculated based on Equation (7). The results of these calculations are displayed in
Table 7.
Step 4: Functionality, reliability, usability, and maintainability are benefit criteria, and price is a cost criterion. Hence, we can determine the intuitionistic fuzzy positive ideal solution and the intuitionistic fuzzy negative ideal solution of all criteria ratings as seen below:
Step 5: The normalized intuitionistic fuzzy differences are calculated by applying Equation (13) and outlined in
Table 6.
Step 6: The values of
S,
R, and
Q are calculated by Equations (16)–(18) for the four alternatives and summarized in
Table 8.
Step 7: The rankings of the four alternatives by the
S,
R, and
Q values in increasing order are presented in
Table 9.
Step 8: Based on
Table 9, the ranking of the four alternatives is
in accordance with the values of
Q. Thus,
A2 is the most suitable company among the alternatives to provide the required software for this hospital.
To validate the effectiveness of the method being proposed, the intuitionistic fuzzy TOPSIS (IF-TOPSIS) suggested by Boran et al. [
60] is applied for the given case study. With the use of the evaluation of criteria weights and the ratings of alternative suppliers in
Table 3 and
Table 4, the four alternatives are ranked as
. It is found that the most desirable supplier obtained by the IFH-VIKOR and the IF-TOPSIS methods is exactly the same. This demonstrates the validity of our proposed method.
5.2. Supplier Selection for a Car Manufacturer
To further demonstrate the proposed IFH-VIKOR method, an example of resilient supplier selection from Sahu et al. [
18] is considered. An automobile manufacturer desires to develop a proactive resiliency strategy for selecting suppliers as its commitment to the global market. Five potential suppliers, named as
A1,
A2, …,
A5, are identified for the analysis. For assessing the suppliers, five decision-makers, i.e.,
DM1,
DM2,
…,
DM5, from different departments are invited. The following criteria have been considered in the supplier evaluation and selection: Quality (
C1), Reliability (
C2), Functionality (
C3), Customer satisfaction (
C4), and Cost (
C5). By using the seven-member linguistic term set in
Table 1, the assessments of the alternative suppliers given by the decision-makers are shown in
Table 10. Similarly, the decision-makers are asked to use another seven-member linguistic term set (
Table 2) to rate the importance weights against individual criteria. The linguistic assessments regarding the criteria weights are given in
Table 11. Note that
λ1 =
λ2 = ... =
λ5 = 0.2 in this case, since the same weights are allocated to the five decision-makers.
With the help of the proposed IFH-VIKOR model, the values of
S,
R, and
Q acquired for the five suppliers are presented in
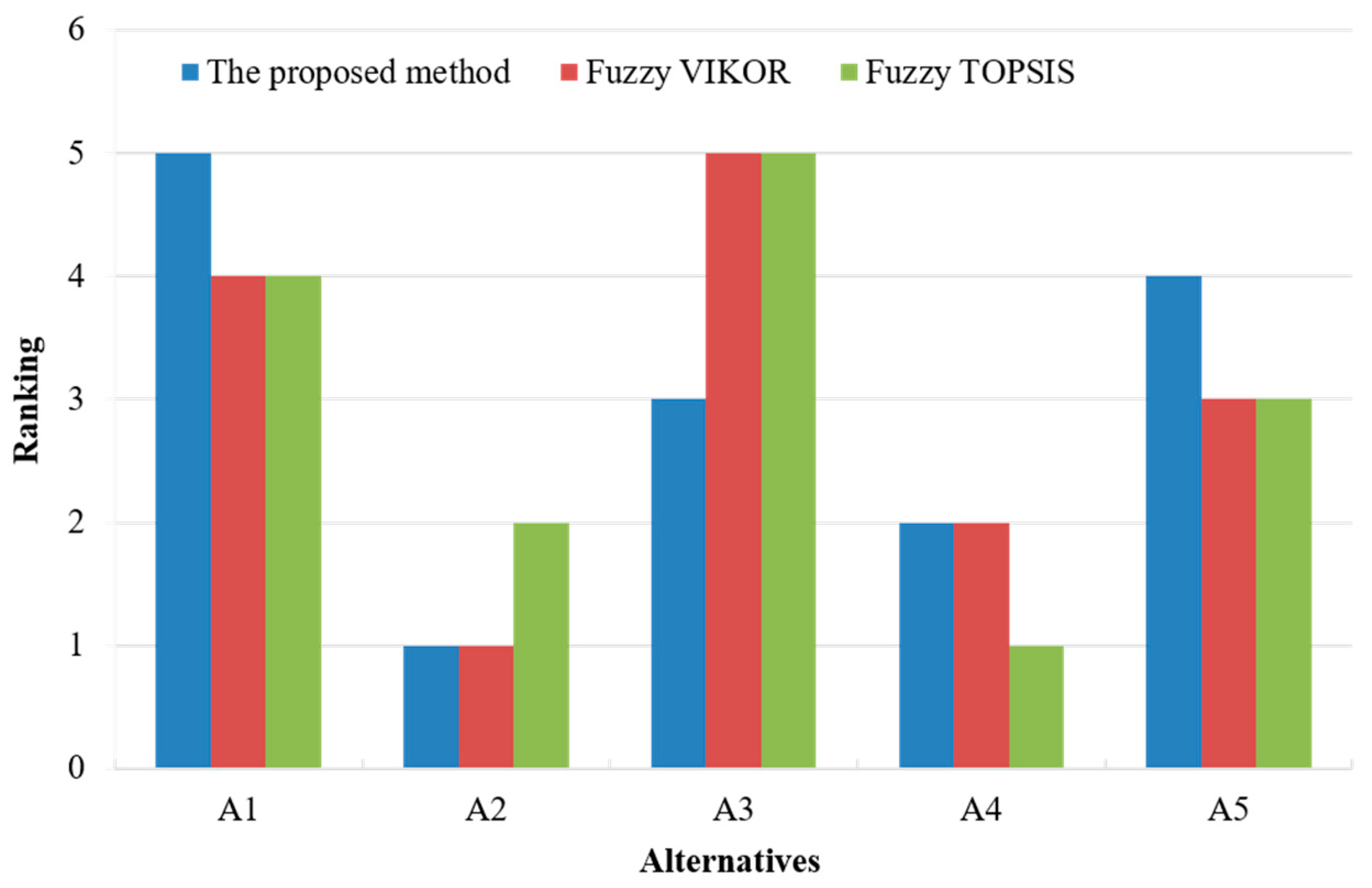
Table 12. It is clear that the ranking order for the five alternatives is
and
A2 is the most suitable supplier. The above supplier selection problem was also solved by the fuzzy VIKOR [
18] and the fuzzy TOPSIS [
21] methods. The ranking results of the candidate suppliers as derived via the application of these methods and the proposed IFH-VIKOR method are shown in
Figure 1.
The ranking results show that the first choice of supplier remains the same, i.e., A2, using the proposed approach and the fuzzy VIKOR method. Nevertheless, according to the fuzzy TOPSIS method, A4 has a higher priority as compared to A2, and is the best option for the considered supplier selection case. The ranking orders of the other alternatives (A1, A3, A5,) obtained by the proposed IFH-VIKOR method are different from those produced by the fuzzy VIKOR and the fuzzy TOPSIS approaches. The main reasons that brought about the inconsistencies are as follows: (1) fuzzy set theory is used by the two compared methods to handle the ambiguity information that arises in the supplier selection process. However, there is no means to incorporate the hesitation or uncertainty in the fuzzy set. In contrast, the theory of IFSs adopted in this study is helpful for addressing the uncertainty of supplier evaluation and for quantifying the ambiguous nature of subjective assessments in a convenient way; (2) only subjective weights of criteria are taken into account in the fuzzy VIKOR and the fuzzy TOPSIS methods. In the proposed IFH-VIKOR approach, both subjective and objective criteria weights are considered in the prioritization of alternative suppliers, which makes the method here proposed more realistic and more flexible; and (3) the ranking lists determined by using the proposed model and the fuzzy TOPSIS method are greatly different. This is mainly because the aggregation approaches employed in the two approaches are dissimilar. The IFH-VIKOR approach is based on an aggregating function which represents the distance from the ideal solution. The fuzzy TOPSIS method, in contrast, is based on the idea that the optimum alternative should have the shortest distance from the positive ideal solution and the farthest from the negative ideal solution.
6. Conclusions
In this paper, we presented an IFH-VIKOR approach to deal with those supplier selection problems in which the preference ratings of alternatives and the importance of criteria are given as linguistics terms characterized by IFNs. The SIFWA operator was used to aggregate the ratings of decision-makers into collective assessments. In particular, both subjective and objective weights of criteria were considered during the supplier evaluation and selection, which can avoid the subjectivity in the decision-maker’s knowledge and is helpful to reflect the essential characteristics of a supplier selection problem. To illustrate the feasibility and effectiveness of the proposed IFH-VIKOR method, two application examples were examined, and the obtained results were demonstrated. Moreover, comparative analyses with some relevant representative methods were made to indicate the advantages of our developed supplier selection methodology.
In future research, we will focus on the following directions. First, the subjective weights and objective weights were assumed to be equally important in the case study. However, in real applications, decision-makers may be challenged to determine a weight restriction φ that is practically reasonable for a supplier selection problem. Therefore, an optimization method to obtain the weight restriction objectively should be developed in the future. Second, the inter-relationships among criteria are not considered in the proposed method when determining criteria weights. Hence, future research may be conducted in applying the DEMATEL method for assigning the subjective weights of criteria. In addition, the proposed IFH-VIKOR method for supplier selection is a general method, which can be used for other areas of management decision-making problems, such as robot selection, health-care waste management, green material selection, and factory location selection.