An Agent-Based Co-Evolutionary Multi-Objective Algorithm for Portfolio Optimization
Abstract
:1. Introduction
1.1. Multi-Objective Optimization
1.2. Evolutionary Multi-Objective Algorithms
1.3. Maintaining Population Diversity in Evolutionary Multi-Objective Algorithms
1.4. Agent-Based Co-Evolutionary Algorithms
2. Previous Research
- The idea, design and realization of the agent-based multi-objective co-evolutionary algorithm for portfolio optimization. As compared to our previous research, we propose here different architectures, algorithms and a modified technique for maintaining population diversity. The proposed algorithm utilizes two co-evolving sexes and the competition for limited resources mechanism (dominating agents obtain resources from the dominated ones) in order to obtain high quality solutions and maintain population diversity. The number of the sexes corresponds with the number of objectives of the problem being solved. Each sub-population (sex) is optimized with the use of different objectives. The agents choose partners for the reproduction from the opposite sex and the decision is made on the basis of the quality of the solutions and also on the basis of the resources possessed by the agents.
- Design (including the adjustments needed for solving the multi-objective portfolio optimization problem) and realization of a genetic algorithm and co-evolutionary algorithm (including the fitness function, all genetic operators and the diversity maintaining mechanisms) for multi-objective portfolio optimization.
- Experimental comparison of evolutionary, co-evolutionary, proposed agent-based co-evolutionary and trend-following algorithms with the use of historical data dating two years prior (2010 and 2008) with quite different stock market trends.
3. Evolutionary, Co-Evolutionary and Agent-Based Algorithms for Portfolio Optimization
3.1. Genetic Algorithm
- mutation—the mutation operator changes exactly one value, , representing the percentage share of a specific stock i (each time the value i is chosen randomly) to ( (0,1) is chosen randomly). After that, we have to normalize the vector. Mutation_coefficient determines which part of the population will be subjected to the mutation operator.
- selection—the breeding_coefficient determines which part of the population will be subjected to crossover operator. Selection is based on the fitness function (only the fittest part of the population will be selected);
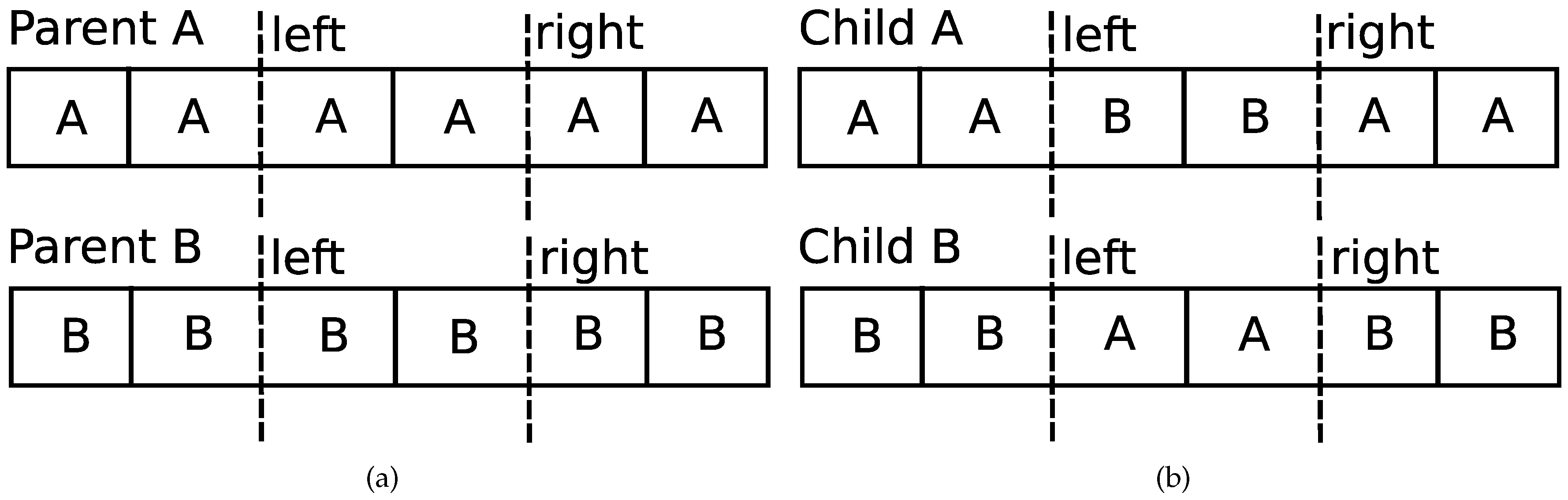
- crossover—after selecting chromosomes eligible for the reproduction, each pair of chromosomes is subjected to crossover operator. As a result, new chromosomes are created (each pair produces two new chromosomes) and added to the population. Crossover chooses left and right points (both are chosen randomly) which cut parents’ chromosomes in the way presented in the Figure 2a. Children are created according to the process shown in the Figure 2b.
3.1.1. Pseudo-code
| Algorithm 1: GA pseudo-code |
 |
3.1.2. Fitness Function
- is the value of the portfolio’s fitness calculated for specific ;
- is the percentage share of a specific stock i in the whole portfolio;
- returns the price of the stock i for the specific .
3.2. Co-Evolutionary System
3.2.1. Maintaining Population Diversity
- crossover is allowed only between the fittest chromosomes from different sub-populations;
- mutations introduce random genetic change;
- migration allows chromosomes to travel to different nodes.
3.2.2. Pseudo-Code
| Algorithm 2: Co-evolutionary algorithm (CEA) pseudo-code |
 |
3.3. The Co-Evolutionary Multi-Agent System
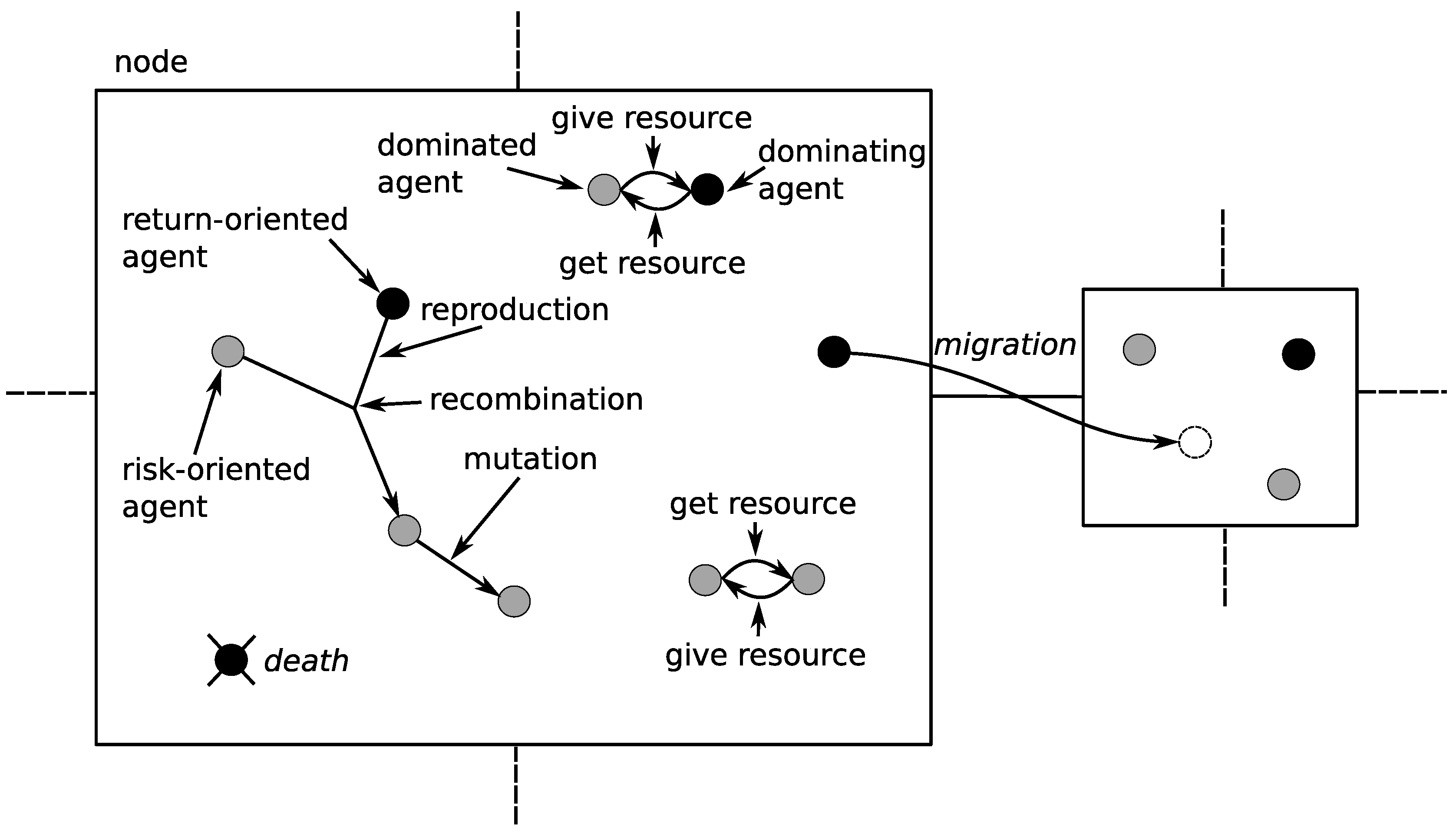
- sex1—tries to achieve the lowest risk possible;
- sex2—tries to achieve the highest expected return possible.
3.3.1. CoEMAS Model
- is the set of environment types in the time t;
- is the set of environments of the in the time t;
- is the set of types of elements that can exist within the system in time t;
- is the set of vertice types that can exist within the system in time t;
- is the set of object (not an object in the sense of object-oriented programming but an object as an element of the simulation model) types that may exist within the system in time t;
- is the set of agent types that may exist within the system in time t;
- is the set of resource types that exist in the system in time t; the amount of resource of type will be denoted by ;
- is the set of information types that exist in the system, the information of type will be denoted by ;
- is the set of relations between sets of agents, objects, and vertices;
- is the set of attributes of agents, objects, and vertices; and
- is the set of actions that can be performed by agents, objects, and vertices.
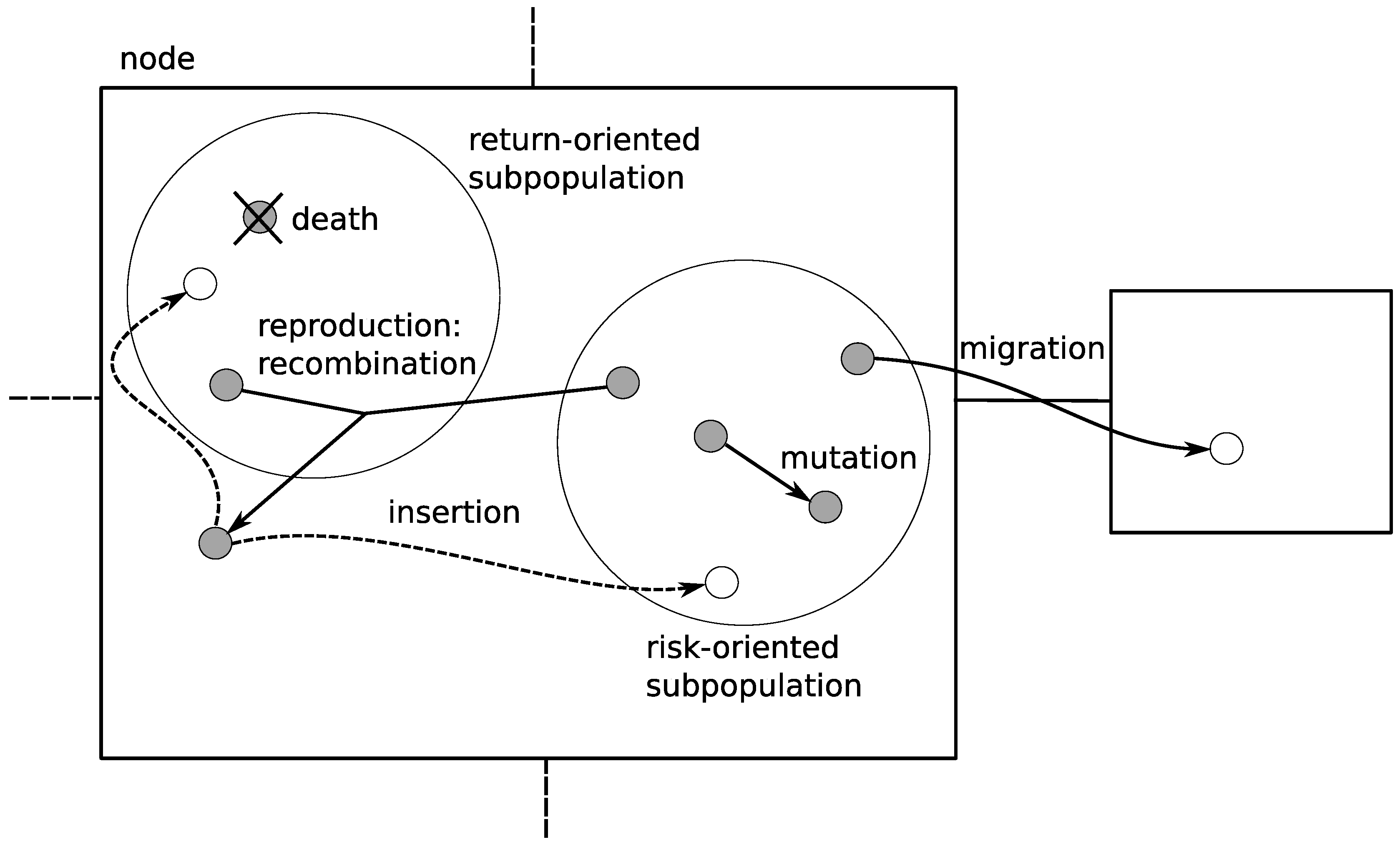
- death—if the amount of the resource that an agent possesses is lower than the threshold value, the agent dies;
- mig—the agent is allowed to migrate but the probability of this action is low;
- rep—the agents from different sexes are allowed to reproduce provided that they both exceed the minimum amount of resource allowing to reproduce;
- give/get—the agent can get a resource from other, dominated agents;
- rec—agents produce offspring by means of recombination;
- mut—a mutation introduces random change to the potential solution, and normalization of the solution vector is then required;
- seek—agents appropriate to the rep as well as get operations can be found thanks to this action.
- is the set of attributes of the vertice at the beginning of its existence;
- is the set of actions which the vertice can perform at the beginning of its existence, when asked for it;
- is the set of resource types which can exist within the vertice at the beginning of its existence;
- is the set of information types which can exist within the vertice at the beginning of its existence;
- is the set of types of vertices that can be connected with the vertice at the beginning of its existence;
- is the set of types of objects that can be located within the vertice at the beginning of its existence; and
- is the set of types of agents that can be located within the vertice at the beginning of its existence.
- is the set of attributes of vertice —it can change during its lifetime;
- is the set of actions, which vertice can perform when asked for it—it can change during its lifetime;
- is the set of resources of types from that exist within the ;
- is the set of information of types from that exists within the — is the information about agents of sex1 that are located within the given vertice and is the information about the agents of sex2;
- is the set of vertices of types from connected with the vertice —in our case it is the set of four vertices (see Figure 4);
- is the set of objects of types from that are located in the vertice ;
- is the set of agents of types from that are located within the vertice .
- is the set of goals of the agent at the beginning of its existence;
- is the set of attributes of the agent at the beginning of its existence;
- is the set of actions which the agent can perform at the beginning of its existence;
- is the set of resource types which can be used by the agent at the beginning of its existence;
- is the set of information types which can be used by the agent at the beginning of its existence;
- is the set of types of objects that can be located within the agent at the beginning of its existence; and
- is the set of types of agents that can be located within the agent at the beginning of its existence.
- is the set of goals, which agent tries to realize—it can change during its lifetime;
- is the set of attributes of agent —it can change during its lifetime;
- is the set of actions which agent can perform in order to realize its goals—it can change during its lifetime;
- is the set of resources of types from , which are used by agent ;
- is the set of information of types from which agent can possess and use—an agent uses information about the other agents located within the same vertice;
- is the set of objects of types from that are located within the agent ;
- is the set of agents of types from that are located within the agent .
- co-evolution is implemented as a sequence of turns;
- in each turn every agent performs its action (the action to perform at any particular turn is chosen with a well defined probability, e.g., there is a 10% chance that the agent will try to find a partner for reproduction, and a 60% chance that the agent will try to obtain some resources from the dominated agent);
- after every agent performes some action the turn ends and the entire population of agents is checked as to whether some of them should die (when not enough resources are left after other agents take resource from them).
3.3.2. Pseudocode
- —with probability 0.6;
- —with probability 0.2;
- —with probability 0.1;
- —with probability 0.1.
| Algorithm 3: CoEMAS pseudocode |
 |
4. Trend Following
4.1. Types of Trends
- Short-term trend: any price movement that occurs over a few hours or days.
- Intermediate-term trend: general movement in price data that lasts from three weeks to six months.
- Long-term trend: any price movement that occurs over a significant period of time, often over one year or several years.
4.2. Designing Trading System Based on Trend Following
- how much money are we willing to put on a single trade;
- when to exit (what kind of losses are acceptable);
- when to enter (when the trend has started);
- which markets are we interested in and how to split the money between them (we would like to have a diverse portfolio: stocks, gold, etc.).
- Simple moving average (SMA) of the last N days is greater than SMA of last M days ();
- Current stock price is maximal of the last N days (that is usually a good indicator of lucrative opportunity on the market).
- Losses on a single trade are greater than 2% (this rule is used to quickly abandon an investment where we were wrong about its trend direction; the amount of tolerable loss solely depends on our strategy and does not have to be exactly 2%);
- The simple moving average (SMA) of the last N days is lesser than the SMA of last M days ().
4.3. Pseudo-Code
- SMA(i,N) calculates the simple moving average for stock i, N last days are taken into account;
- go_short(i) sell stock i;
- go_long(i) buy stock i;
- get_current_stock_price(i, day) returns stock i price for specific ;
- get_most_recent_trade_price(i) returns the price we paid for stock i (we have stock i in our portfolio);
- max(i,N) returns the maximum price for stock i in the last N days;
- N, M, maximal_value_loss modifiable parameters.
| Algorithm 4: The trend-following pseudo-code |
 |
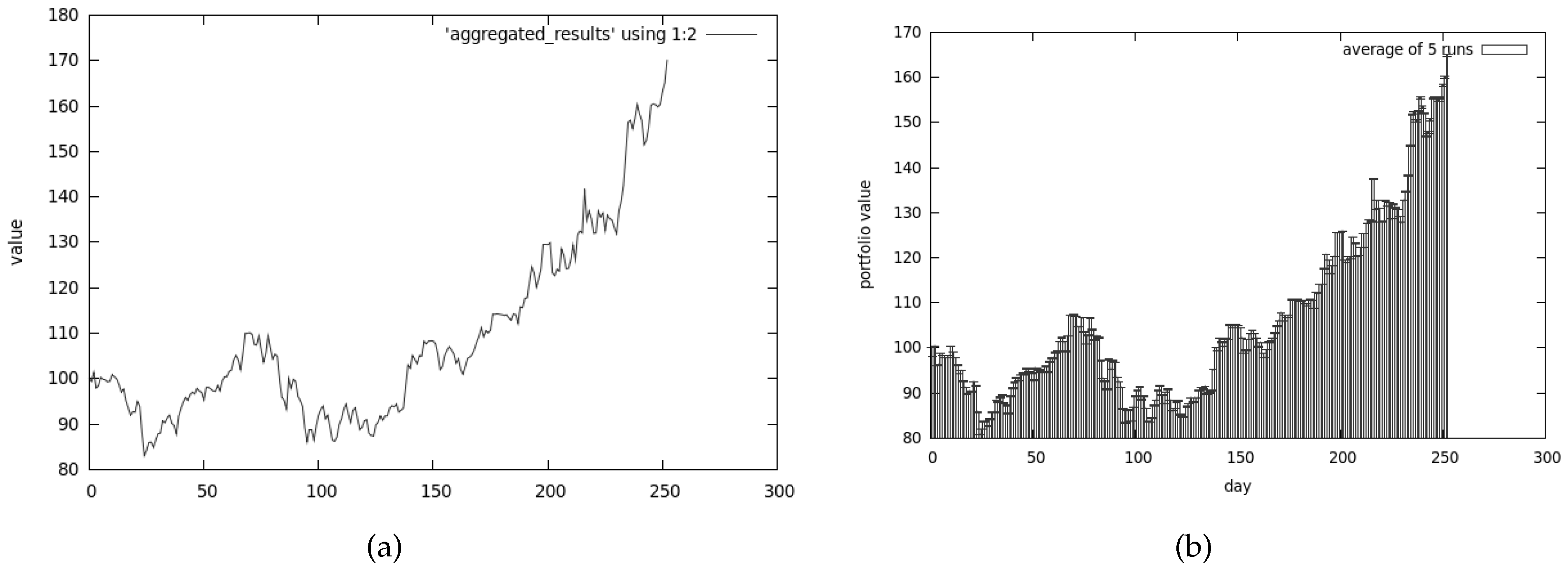
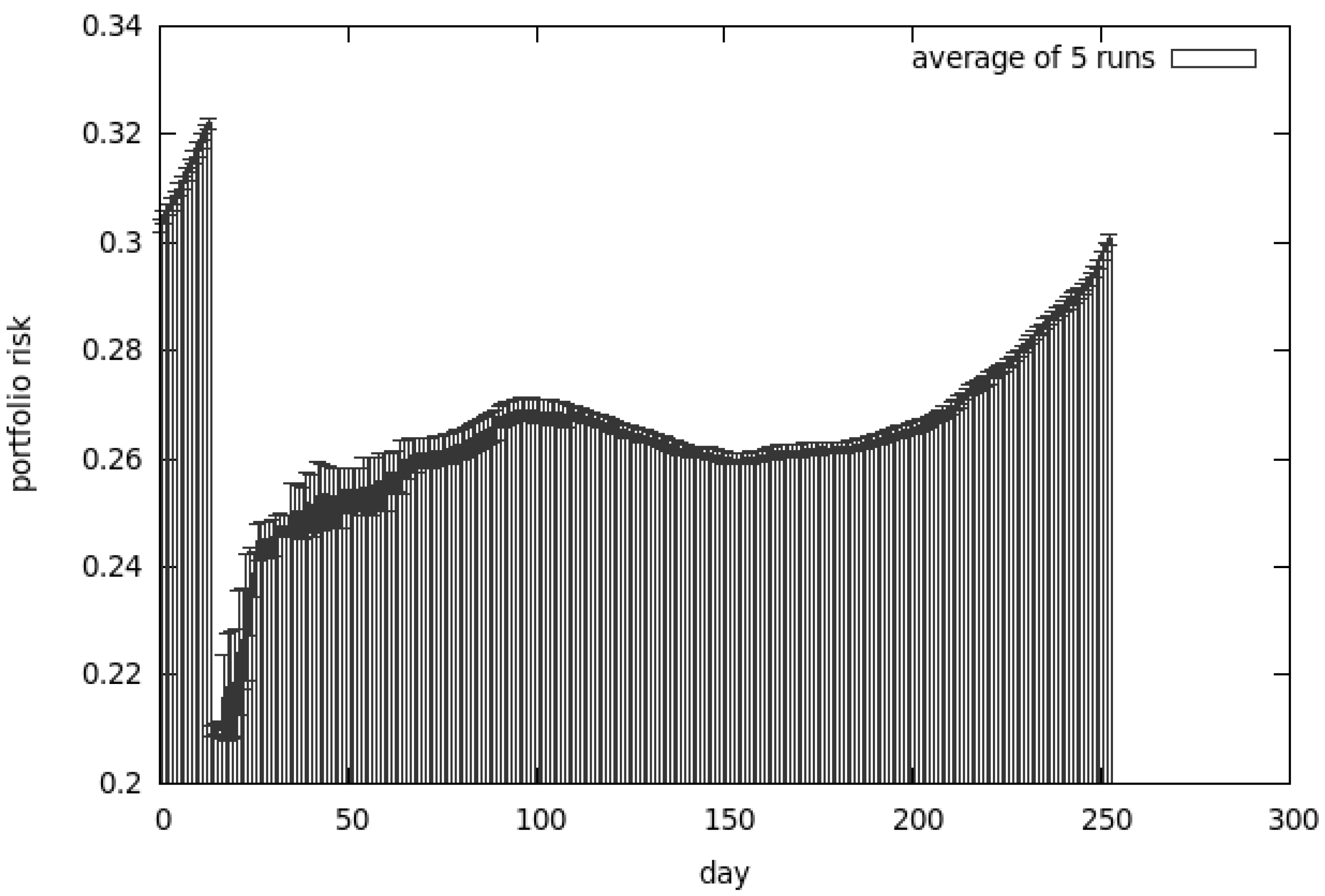
5. Experimental Results
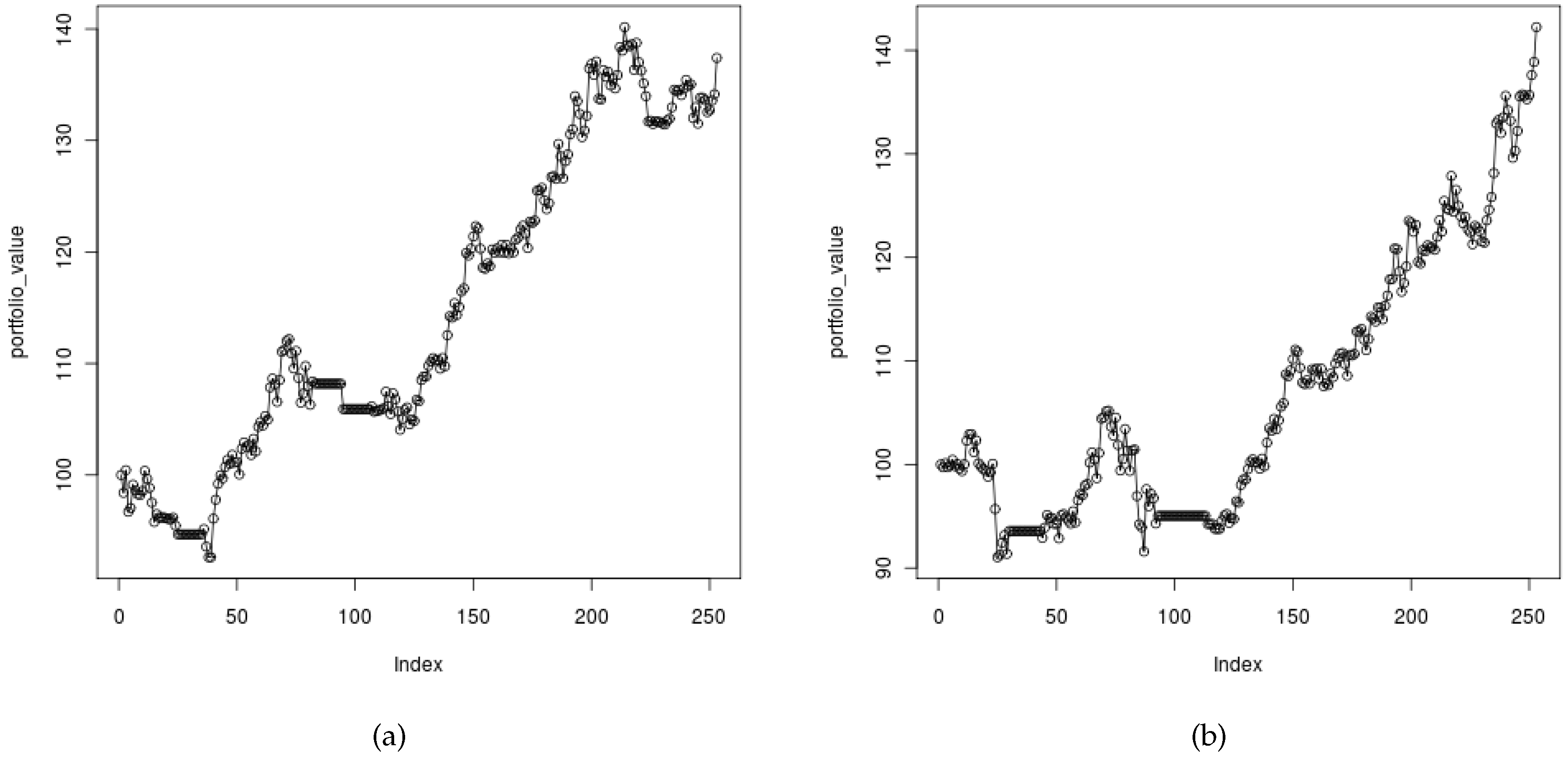
5.1. First Set of Tests
- KGHM Polska Miedź S.A. (KGHM)—mining sector company;
- Telekomunikacja Polska (TPSA)—telecommunication sector company;
- PKO Bank Polski (PKOBP)—finance and insurance sector company.
- using a simulation of the trading strategy throughout the entire year 2010;
- all investing decisions have been based solely on the results from the implemented algorithms;
- the migration mechanism between computing nodes has been enabled;
- two computing nodes (with the appropriate algorithms) have been used to obtain results.
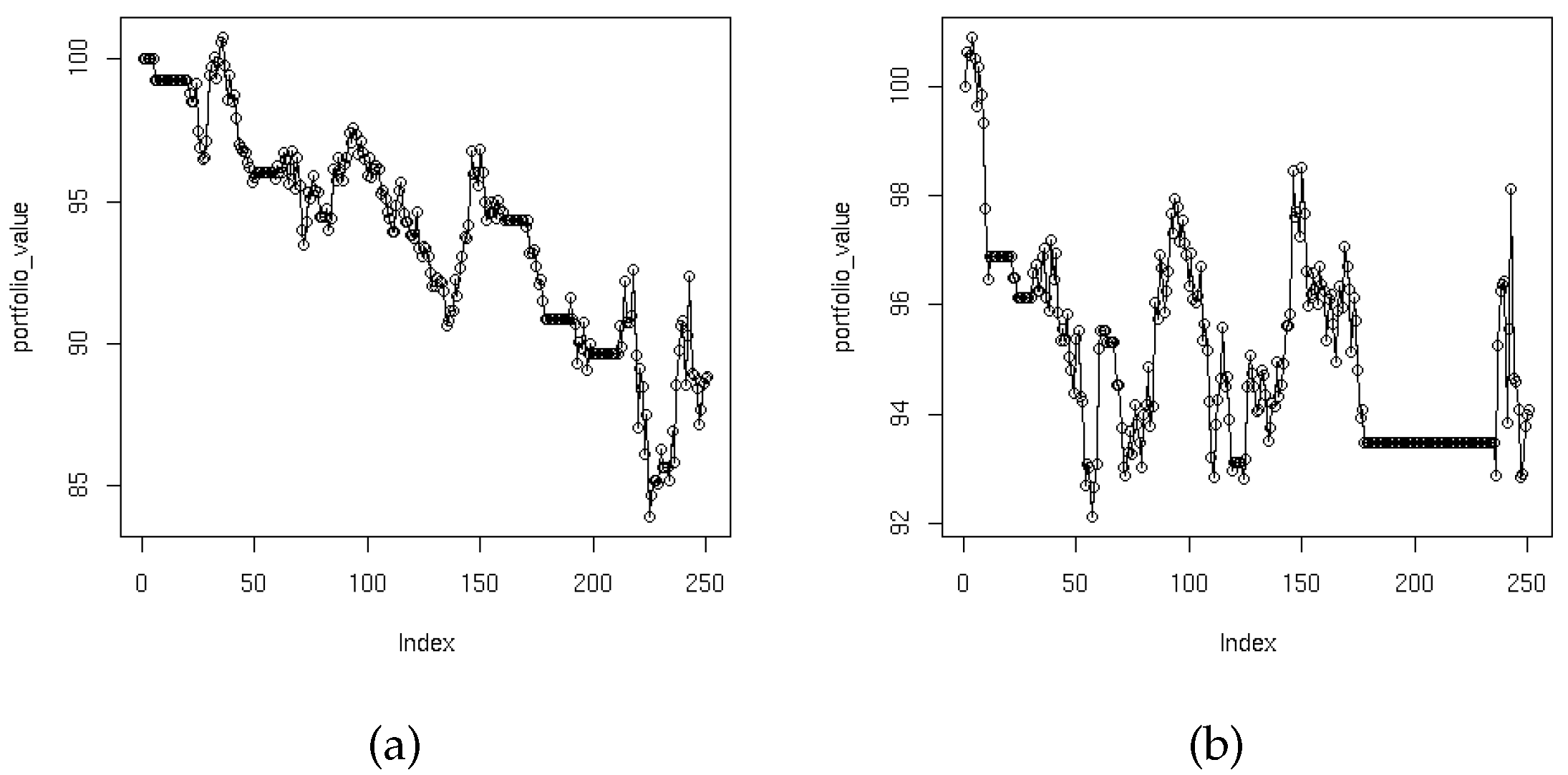
5.1.1. Trend Following
5.1.1.1. Short-Term Trend Results
5.1.1.2. Intermediate-Term Trend Results
5.1.2. Genetic Algorithm
- reproduction_coeff was set to 0.2;
- population size was 512;
- mutation_coeff was set to 0.1;
- extinction_coeff was set to 0.3.
5.1.3. Co-Evolutionary Algorithm
- reproduction_coeff was set to 0.2;
- sub-population size in each computing node was set to 64;
- number of computing nodes was set to 2;
- mutation_coeff was set to 0.1;
- extinction_coeff was set to 0.3.
5.1.4. CoEMAS
- reproduction_coeff was set to 0.2;
- each sex was represented initially by 64 agents (in each computing node);
- number of computing nodes was set to 2;
- mutation_coeff was set to 0.1;
- extinction_coeff was set to 0.3.
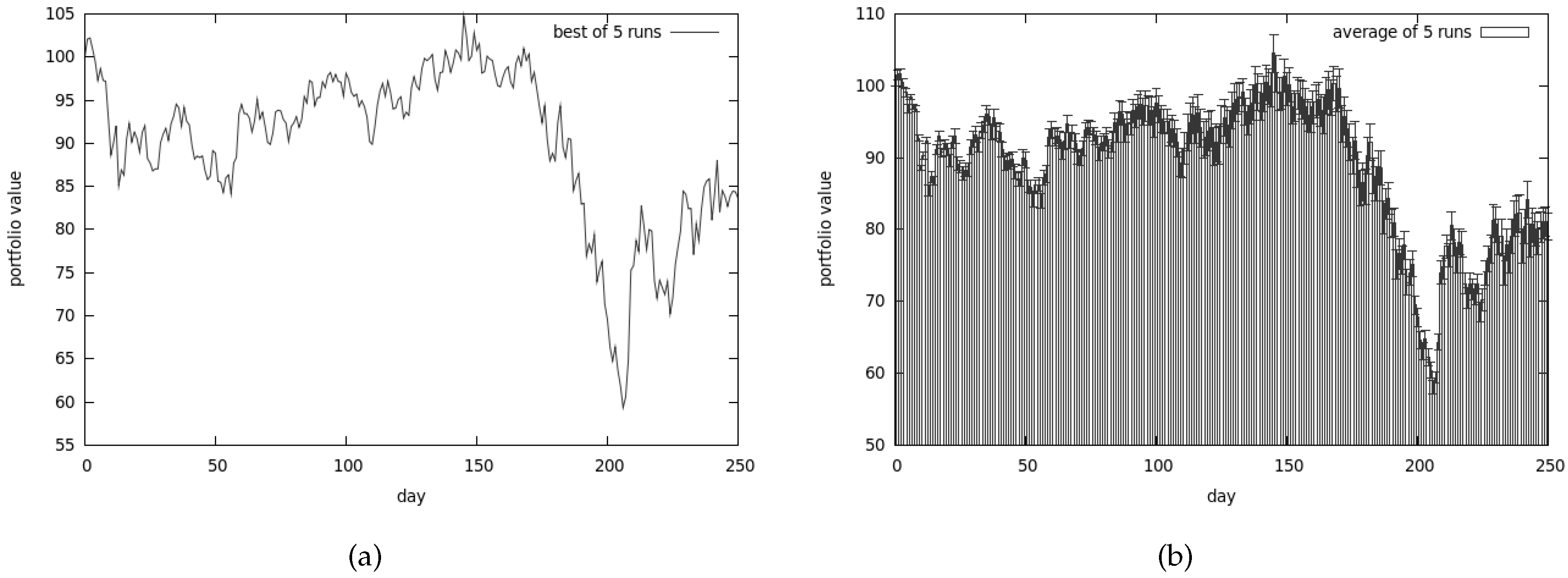
5.1.5. Conclusions from the First Set of Tests
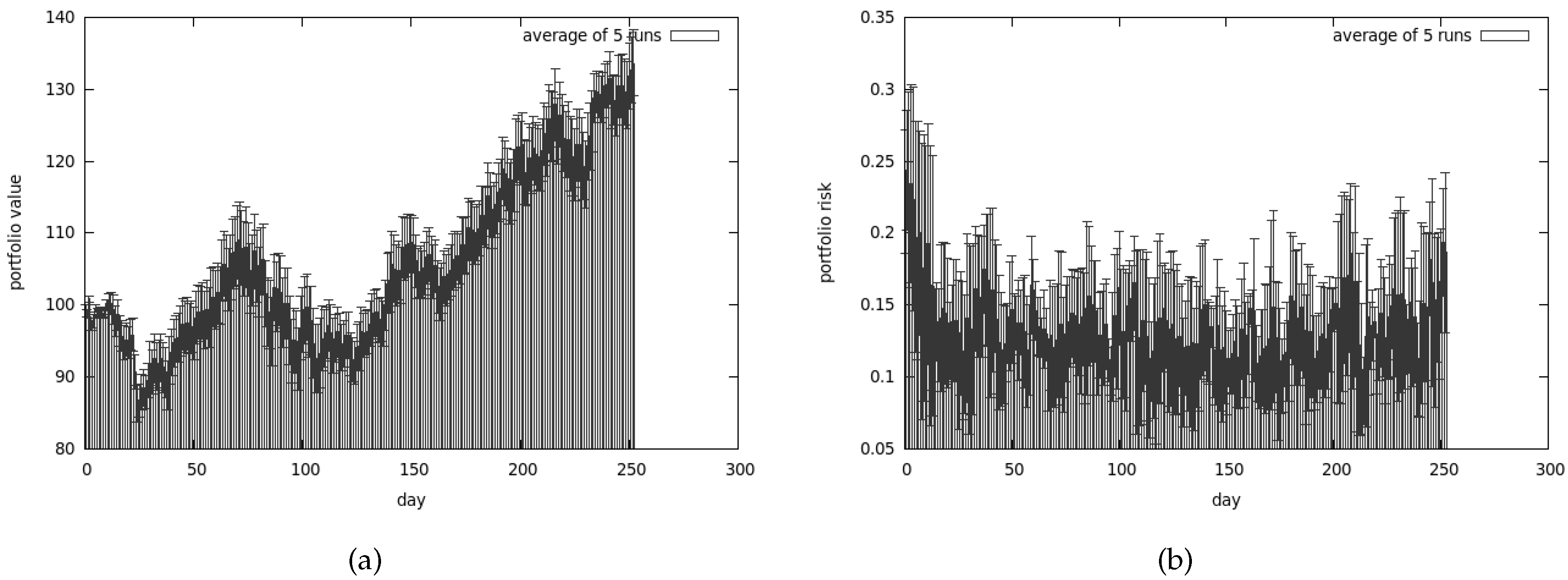
5.2. Second Set of Tests
5.2.1. Trend Following
5.2.2. Genetic Algorithm
- reproduction_coeff was set to 0.2;
- population size was 512;
- mutation_coeff was set to 0.1;
- extinction_coeff was set to 0.3.
5.2.3. Co-Evolutionary Algorithm
- was set to 0.2;
- sub-population size in each computing node was set to 64;
- number of computing nodes was set to 2;
- was set to 0.1;
- was set to 0.3.
5.2.4. CoEMAS
- was set to 0.2;
- each sex was represented initially by 64 agents (in each computing node);
- number of computing nodes was set to 2;
- was set to 0.1;
- was set to 0.3.
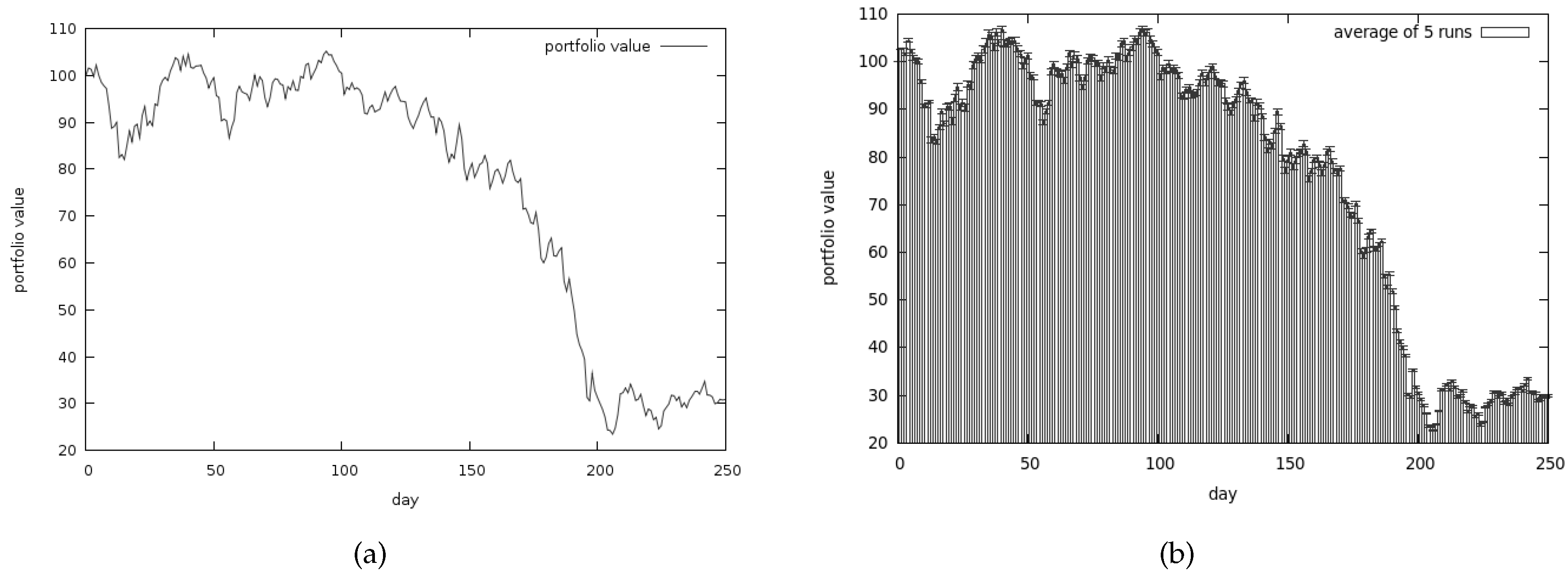
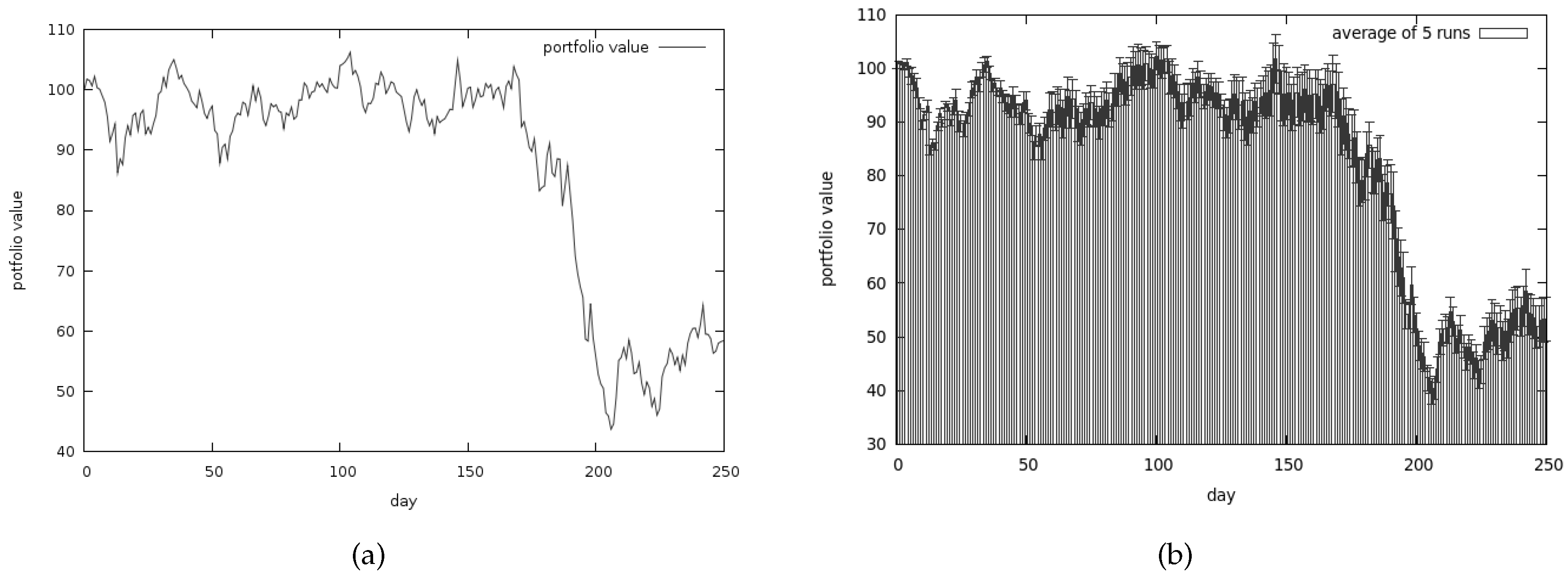
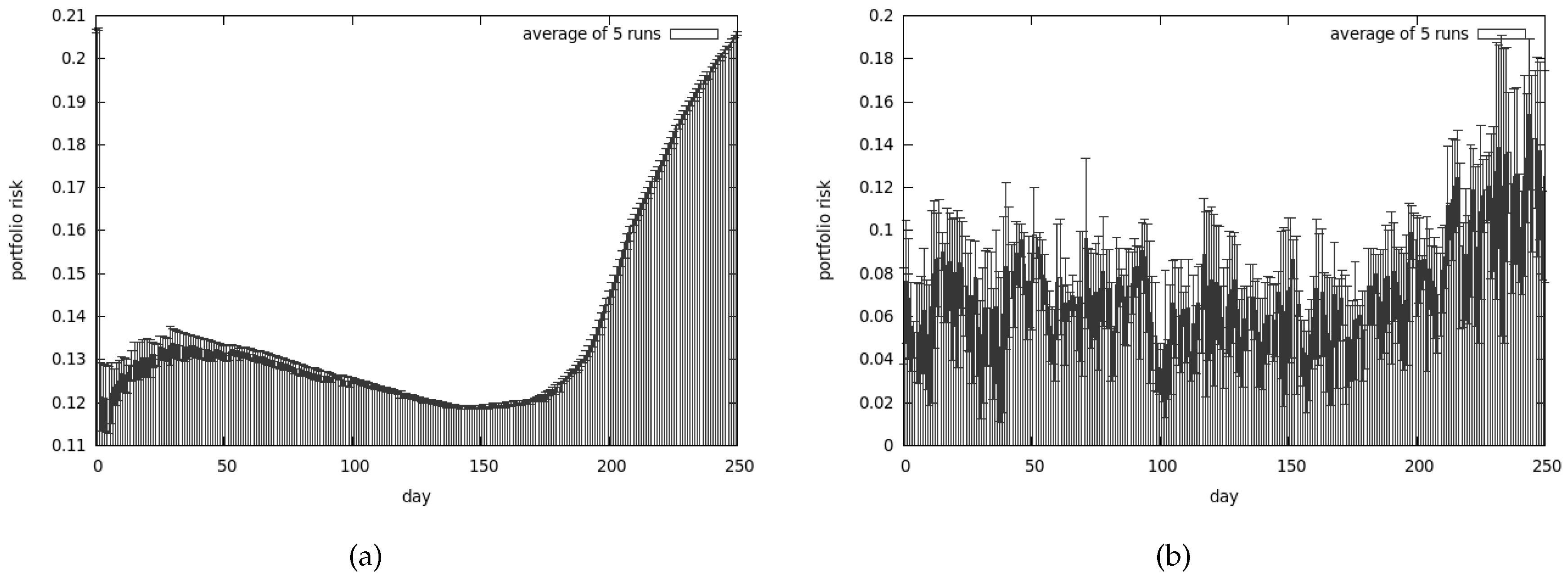
5.2.5. Conclusions from the Second Set of Tests
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rom, B.M.; Ferguson, K.W. Post-Modern Portfolio Theory Comes of Age. J. Investig. 1994, 3, 11–17. [Google Scholar] [CrossRef]
- Zitzler, E. Evolutionary Algorithms for Multiobjective Optimization: Methods and Applications. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 1999. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Coello Coello, C.A.; Van Veldhuizen, D.A.; Lamont, G.B. Evolutionary Algorithms for Solving Multi-Objective Problems; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Osyczka, A. Evolutionary Algorithms for Single and Multicriteria Design Optimization; Physica Verlag: Heidelberg, Germany, 2002. [Google Scholar]
- Tan, K.C.; Khor, E.F.; Lee, T.H. Multiobjective Evolutionary Algorithms and Applications; Springer: London, UK, 2005. [Google Scholar]
- Villalobos, M.A. Analisis de Heuristicas de Optimizacion para Problemas Multiobjetivo. Ph.D. Thesis, Centro de Investigacion y de Estudios Avanzados del Instituto Politecnico Nacional, Mexico City, Mexico, 2005. [Google Scholar]
- Toscano, G. On the Use of Self-Adaptation and Elitism for Multiobjective Particle Swarm Optimization. Ph.D. Thesis, Centro de Investigacion y de Estudios Avanzados del Instituto Politecnico Nacional, Mexico City, Mexico, 2005. [Google Scholar]
- Rudolph, G. Evolutionary Search under Partially Ordered Finite Sets. In Proceedings of the International NAISO Congress on Information Science Innovations (ISI 2001), Dubai, UAE, 17–21 March 2001; Sebaaly, M.F., Ed.; ICSC Academic Press: Dubai, UAE, 2001; pp. 818–822. [Google Scholar]
- Osyczka, A.; Kundu, S. A new method to solve generalized multicriteria optimization problems using the simple genetic algorithm. Struct. Multidiscip. Optim. 1995, 10, 94–99. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. An Evolutionary Algorithm for Multiobjective Optimization: The Strength Pareto Approach; Technical Report 43; Swiss Federal Institute of Technology: Zurich, Switzerland, 1998. [Google Scholar]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; Technical Report 103; Swiss Federal Institute of Technology: Zurich, Switzerland, 2001. [Google Scholar]
- Knowles, J.; Corne, D. Approximating the Nondominated Front Using the Pareto Archived Evolution Strategy. Evol. Comput. 2000, 8, 149–172. [Google Scholar] [CrossRef] [PubMed]
- Van Veldhuizen, D.A. Multiobjective Evolutionary Algorithms: Classifications, Analyses and New Innovations. Ph.D. Thesis, Graduate School of Engineering of the Air Force Institute of Technology Air University, Dayton, OH, USA, 1999. [Google Scholar]
- Coello Coello, C.; Toscano, G. Multiobjective Structural Optimization using a Micro-Genetic Algorithm. Struct. Multidiscip. Optim. 2005, 30, 388–403. [Google Scholar] [CrossRef]
- Kursawe, F. A Variant of Evolution Strategies for Vector Optimization. In Parallel Problem Solving from Nature; 1st Workshop, PPSN I; Schwefel, H., Manner, R., Eds.; Springer: Berlin, Germany, 1991; Volume 496, pp. 193–197. [Google Scholar]
- Murata, T.; Ishibuchi, H. MOGA: Multi-objective genetic algorithms. In Proceedings of the IEEE International Conference on Evolutionary Computation, Perth, Australia, 29 November–1 December 1995; IEEE Service Center: Piscataway, NJ, USA, 1995; Volume 1, pp. 289–294. [Google Scholar]
- Hajela, P.; Lee, E.; Lin, C. Genetic algorithms in structural topology optimization. In Topology Design of Structures; Bendsøe, M.P., Soares, C.A.M., Eds.; Springer: Amsterdam, The Netherlands, 1993; Volume 1, pp. 117–133. [Google Scholar]
- Horn, J.; Nafpliotis, N.; Goldberg, D.E. A Niched Pareto Genetic Algorithm for Multiobjective Optimization. In Proceedings of the First IEEE Conference on Evolutionary Computation, IEEE World Congress on Computational Intelligence, Orlando, FL, USA, 27–29 June 1994; IEEE Service Center: Piscataway, NJ, USA, 1994; Volume 1, pp. 82–87. [Google Scholar]
- Srinivas, N.; Deb, K. Multiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Fonseca, C.; Fleming, P. Genetic Algorithms for Multiobjective Optimization: Formulation, Discussion and Generalization. In Proceedings of the Fifth International Conference on Genetic Algorithms, Urbana-Champaign, IL, USA, 17–21 July 1993; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993; pp. 416–423. [Google Scholar]
- Hiroyasu, T.; Miki, M.; Watanabe, S. Distributed Genetic Algorithms with a New Sharing Approach. In Proceedings of the Conference on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; IEEE Service Center: Piscataway, NJ, USA, 1999; Volume 1. [Google Scholar]
- Mahfoud, S.W. Crowding and preselection revisited. In Parallel Problem Solving from Nature—PPSN-II; IlliGAL Report No. 92004; Männer, R., Manderick, B., Eds.; Elsevier: Amsterdam, The Netherlands, 1992; pp. 27–36. [Google Scholar]
- Goldberg, D.E.; Richardson, J. Genetic algorithms with sharing for multimodal function optimization. In Proceedings of the 2nd International Conference on Genetic Algorithms, Cambridge, MA, USA, 29–31 July 1987; Grefenstette, J.J., Ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1987; pp. 41–49. [Google Scholar]
- Ratford, M.; Tuson, A.L.; Thompson, H. An Investigation of Sexual Selection as a Mechanism for Obtaining Multiple Distinct Solutions; Technical Report 879; Department of Artificial Intelligence, University of Edinburgh: Edinburgh, UK, 1997. [Google Scholar]
- Jelasity, M.; Dombi, J. GAS, a concept of modeling species in genetic algorithms. Artif. Intell. 1998, 99, 1–19. [Google Scholar] [CrossRef]
- Adamidis, P. Parallel Evolutionary Algorithms: A Review. In Proceedings of the 4th Hellenic-European Conference on Computer Mathematics and Its Applications (HERCMA 1998), Athens, Greece, 24–26 September 1998. [Google Scholar]
- Cantú-Paz, E. A Survey of Parallel Genetic Algorithms. Calc. Paralleles Reseaux Syst. Repartis 1998, 10, 141–171. [Google Scholar]
- Hajela, P.; Lin, C. Genetic search strategies in multicriterion optimal design. Struct. Optim. 1992, 4, 99–107. [Google Scholar] [CrossRef]
- Paredis, J. Coevolutionary Computation. Artif. Life 1995, 2, 355–375. [Google Scholar] [CrossRef] [PubMed]
- Potter, M.A.; De Jong, K.A. Cooperative Coevolution: An Architecture for Evolving Coadapted Subcomponents. Evol. Comput. 2000, 8, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Darwen, P.J.; Yao, X. On evolving robust strategies for iterated prisoner’s dilemma. In Process in Evolutionary Computation; AI’93 and AI’94 Workshops on Evolutionary Computation, Selected Papers; Yao, X., Ed.; Springer: Berlin/Heidelberg, Germany, 1995; Volume 956. [Google Scholar]
- Laumanns, M.; Rudolph, G.; Schwefel, H.P. A Spatial Predator-Prey Approach to Multi-objective Optimization: A Preliminary Study. In Parallel Problem Solving from Nature—PPSN V; Eiben, A.E., Bäck, T., Schoenauer, M., Schwefel, H.P., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1498. [Google Scholar]
- Li, X. A Real-Coded Predator-Prey Genetic Algorithm for Multiobjective Optimization. In Evolutionary Multi-Criterion Optimization, Proceedings of the Second International Conference (EMO 2003), Faro, Portugal, 8–11 April 2003; Fonseca, C.M., Fleming, P.J., Zitzler, E., Deb, K., Thiele, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2632. [Google Scholar]
- Iorio, A.; Li, X. A Cooperative Coevolutionary Multiobjective Algorithm Using Non-dominated Sorting. In Genetic and Evolutionary Computation—GECCO 2004; Deb, K., Poli, R., Banzhaf, W., Beyer, H.G., Burke, E.K., Darwen, P.J., Dasgupta, D., Floreano, D., Foster, J.A., Harman, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3102–3103, pp. 537–548. [Google Scholar]
- Todd, P.M.; Miller, G.F. Biodiversity through sexual selection. In Artificial Life V: Proceedings of the Fifth International Workshop on the Synthesis and Simulation of Living Systems; Bradford Books; Langton, C.G., Shimohara, K., Eds.; The MIT Press: Cambridge, MA, USA, 1997; pp. 289–299. [Google Scholar]
- Gavrilets, S. Models of speciation: What have we learned in 40 years? Evolution 2003, 57, 2197–2215. [Google Scholar] [CrossRef] [PubMed]
- Allenson, R. Genetic Algorithms with Gender for Multi-Function Optimisation; Technical Report EPCC-SS92-01; Edinburgh Parallel Computing Centre: Edinburgh, UK, 1992. [Google Scholar]
- Lis, J.; Eiben, A.E. A Multi-Sexual Genetic Algorithm for Multiobjective Optimization. Proceedings of 1997 IEEE International Conference on Evolutionary Computation (ICEC'97), Indianapolis, IN, USA, 13–16 April 1997; IEEE Press: Piscataway, NJ, USA, 1997; pp. 59–64. [Google Scholar]
- Bonissone, S.; Subbu, R. Exploring the Pareto Frontier Using Multi-Sexual Evolutionary Algorithms: An Application to a Flexible Manufacturing Problem; Technical Report 2003GRC083; GE Global Research: Schenectady County, NY, USA, 2003. [Google Scholar]
- Dreżewski, R. Co-Evolutionary Multi-Agent System with Speciation and Resource Sharing Mechanisms. Comput. Inform. 2006, 25, 305–331. [Google Scholar]
- Cetnarowicz, K.; Kisiel-Dorohinicki, M.; Nawarecki, E. The application of Evolution Process in Multi-Agent World to the Prediction System. In Proceedings of the 2nd International Conference on Multi-Agent Systems (ICMAS 1996), Kyoto, Japan, 9–13 December 1996; Tokoro, M., Ed.; AAAI Press: Menlo Park, CA, USA, 1996; pp. 26–32. [Google Scholar]
- Cetnarowicz, K.; Dreżewski, R. Maintaining Functional Integrity in Multi-Agent Systems for Resource Allocation. Comput. Inform. 2010, 29, 947–973. [Google Scholar]
- Dreżewski, R. A Model of Co-evolution in Multi-agent System. In Multi-Agent Systems and Applications III, Proceedings of the 3rd International Central and Eastern European Conference on Multi-Agent Systems, Prague, Czech Republic, 16–18 June 2003; Marik, V., Muller, J., Pechoucek, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2691, pp. 314–323. [Google Scholar]
- Dreżewski, R.; Siwik, L. Multi-objective Optimization Using Co-evolutionary Multi-agent System with Host-Parasite Mechanism. In Computational Science—ICCS 2006, Proceedings of the 6th International Conference on Computational Science, Reading, UK, 28–31 May 2006; Part III; Alexandrov, V.N., van Albada, G.D., Sloot, P.M.A., Dongarra, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3993, pp. 871–878. [Google Scholar]
- Dreżewski, R.; Siwik, L. Multi-objective Optimization Technique Based on Co-evolutionary Interactions in Multi-agent System. In Applications of Evolutionary Computing, Proceedings of the 2007 EvoWorkshops EvoCoMnet, EvoFIN, EvoIASP, EvoINTERACTION, EvoMUSART, EvoSTOC and EvoTransLog, Valencia, Spain, 11–13 April 2007; Giacobini, M., Brabazon, A., Cagoni, S., Di Caro, G.A., Drechsler, R., Farooq, M., Fink, A., Lutton, E., Machado, P., Minner, S., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4448, pp. 179–188. [Google Scholar]
- Dreżewski, R.; Siwik, L. Agent-Based Co-Operative Co-Evolutionary Algorithm for Multi-Objective Optimization. In Artificial Intelligence and Soft Computing—ICAISC 2008, Proceedings of the 9th International Conference, Zakopane, Poland, 22–26 June 2008; Rutkowski, L., Tadeusiewicz, R., Zadeh, L.A., Zurada, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5097, pp. 388–397. [Google Scholar]
- Dreżewski, R.; Siwik, L. Techniques for Maintaining Population Diversity in Classical and Agent-Based Multi-objective Evolutionary Algorithms. In Computational Science—ICCS 2007, Proceedings of the 7th International Conference, Beijing, China, 27–30 May 2007; Part II; Shi, Y., van Albada, G.D., Dongarra, J., Sloot, P.M.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4488, pp. 904–911. [Google Scholar]
- Dreżewski, R. Agent-Based Modeling and Simulation of Species Formation Processes. In Multi-Agent Systems—Modeling, Interactions, Simulations and Case Studies; Alkhateeb, F., Al Maghayreh, E., Abu Doush, I., Eds.; InTech: Rijeka, Croatia, 2011; pp. 3–28. [Google Scholar]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Markowitz, H. The early history of portfolio theory: 1600–1960. Financ. Anal. J. 1999, 55, 5–16. [Google Scholar] [CrossRef]
- Tobin, J. Liquidity preference as behavior towards risk. Rev. Econ. Stud. 1958, 25, 65–86. [Google Scholar] [CrossRef]
- Brabazon, A.; O’Neill, M. Biologically Inspired Algorithms for Financial Modelling; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Brabazon, A.; O’Neill, M. (Eds.) Natural Computation in Computational Finance; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Brabazon, A.; O’Neill, M. (Eds.) Natural Computation in Computational Finance; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Brabazon, A.; O’Neill, M. (Eds.) Natural Computation in Computational Finance; Springer: Berlin/Heidelberg, Germany, 2010; Volume 3. [Google Scholar]
- Brabazon, A.; O’Neill, M.; Maringer, D. (Eds.) Natural Computation in Computational Finance; Springer: Berlin/Heidelberg, Germany, 2011; Volume 4. [Google Scholar]
- Kassicieh, S.K.; Paez, T.L.; Vora, G. Investment Decisions Using Genetic Algorithms. In Proceedings of the 30th Hawaii International Conference on System Sciences, Maui, Hawaii, USA, 7–10 January 1997; IEEE Computer Society: Los Alamitos, CA, USA, 1997; Volume 5, pp. 484–490. [Google Scholar]
- Pictet, O.V.; Dacorogna, M.M.; Dave, R.D.; Chopard, B.; Schirru, R.; Tomassini, M. Genetic Algorithms with Collective Sharing for Robust Optimization in Financial Applications; Technical Report; Olsen & Associates: Zurich, Switzerland, 1995. [Google Scholar]
- Yin, X.; Germay, N. A Fast Genetic Algorithm with Sharing Scheme Using Cluster Analysis Methods in Multimodal Function Optimization. In Artificial Neural Nets and Genetic Algorithms, Proceedings of the International Conference in Innsbruck, Austria, 1993; Albrecht, R.F., Reeves, C.R., Steele, N.C., Eds.; Springer: Vienna, Austria, 1993; pp. 450–457. [Google Scholar]
- Allen, F.; Karjalainen, R. Using Genetic Algorithms to Find Technical Trading Rules. J. Financ. Econ. 1999, 51, 245–271. [Google Scholar] [CrossRef]
- Alfaro-Cid, E.; Sharman, K.; Esparcia-Alcázar, A.I. A Genetic Programming Approach for Bankruptcy Prediction Using a Highly Unbalanced Database. In Applications of Evolutionary Computing, Proceedings of the 2007 EvoWorkshops on EvoCoMnet, EvoFIN, EvoIASP, EvoINTERACTION, EvoMUSART, EvoSTOC and EvoTransLog, Valencia, Spain, 11–13 April 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 169–178. [Google Scholar]
- Azzini, A.; Tettamanzi, A.G.B. Evolutionary Single-Position Automated Trading. In Applications of Evolutionary Computing. EvoWorkshops 2008: EvoCOMNET, EvoFIN, EvoHOT, EvoIASP, EvoMUSART, EvoNUM, EvoSTOC, and EvoTransLog; Giacobini, M., Brabazon, A., Cagnoni, S., Di Caro, G.A., Drechsler, R., Ekart, A., Esparcia-Alcazar, A.I., Farooq, M., Fink, A., McCormack, J., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 4974, pp. 62–72. [Google Scholar]
- Fan, K.; Brabazon, A.; O’Sullivan, C.; O’Neill, M. Quantum-Inspired Evolutionary Algorithms for Calibration of the VG Option Pricing Model. In Applications of Evolutionary Computing, Proceedings of the 2007 EvoWorkshops EvoCoMnet, EvoFIN, EvoIASP, EvoINTERACTION, EvoMUSART, EvoSTOC and EvoTransLog; Giacobini, M., Brabazon, A., Cagoni, S., Di Caro, G.A., Drechsler, R., Farooq, M., Fink, A., Lutton, E., Machado, P., Minner, S., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4448, pp. 189–198. [Google Scholar]
- Lipinski, P.; Winczura, K.; Wojcik, J. Building Risk-Optimal Portfolio Using Evolutionary Strategies. In Applications of Evolutionary Computing, Proceedings of the 2007 EvoWorkshops EvoCoMnet, EvoFIN, EvoIASP, EvoINTERACTION, EvoMUSART, EvoSTOC and EvoTransLog, Valencia, Spain, 11–13 April 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 208–217. [Google Scholar]
- García, S.; Quintana, D.; Galván, I.; Isasi, P. Extended mean-variance model for reliable evolutionary portfolio optimization. AI Commun. 2014, 27, 315–324. [Google Scholar]
- Ke, J.; Yu, Y.; Yan, B.; Ren, Y. Asset Risk Diversity and Portfolio Optimization with Genetic Algorithm. In Recent Advances on Applied Mathematics and Computational Methods in Engineering, Proceedings of the International Conference on Applied Mathematics and Computational Methods in Engineering (AMCME 2015), Barcelona, Spain, 7–9 April 2015; Mastorakis, N.E., Rudas, I., Shitikova, M.V., Shmaliy, Y.S., Eds.; pp. 54–57.
- Ibrahim, M.A.; El-Beltagy, M.; Khorshid, M. Evolutionary Multiobjective Optimization for Portfolios in Emerging Markets: Contrasting Higher Moments and Median Models. In Applications of Evolutionary Computation, Proceedings of the 19th European Conference (EvoApplications 2016), Porto, Portugal, 30 March–1 April 2016; Part I; Squillero, G., Burelli, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9597, pp. 73–87. [Google Scholar]
- Dreżewski, R.; Siwik, L. Co-evolutionary Multi-Agent System for Portfolio Optimization. In Natural Computing in Computational Finance; Brabazon, A., O’Neill, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 1, pp. 271–299. [Google Scholar]
- Dreżewski, R.; Sepielak, J. Evolutionary System for Generating Investment Strategies. In Applications of Evolutionary Computing, Proceedings of the EvoWorkshops 2008: EvoCOMNET, EvoFIN, EvoHOT, EvoIASP, EvoMUSART, EvoNUM, EvoSTOC, and EvoTransLog, Naples, Italy, 26–28 March 2008; Giacobini, M., Brabazon, A., Cagnoni, S., Di Caro, G.A., Drechsler, R., Ekart, A., Esparcia-Alcazar, A.I., Farooq, M., Fink, A., McCormack, J., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 4974, pp. 83–92. [Google Scholar]
- Dreżewski, R.; Sepielak, J.; Siwik, L. Classical and Agent-Based Evolutionary Algorithms for Investment Strategies Generation. In Natural Computing in Computational Finance; Brabazon, A., O’Neill, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2, pp. 181–205. [Google Scholar]
- Dreżewski, R.; Siwik, L. Co-Evolutionary Multi-Agent System with Sexual Selection Mechanism for Multi-Objective Optimization. In Proceedings of the IEEE World Congress on Computational Intelligence (WCCI 2006), Vancouver, BC, Canada, 16–21 July 2006; pp. 769–776. [Google Scholar]
- Dreżewski, R.; Siwik, L. Agent-Based Multi-Objective Evolutionary Algorithm with Sexual Selection. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC 2008), Hong Kong, China, 1–6 June 2008; pp. 3679–3684. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Fama, E.F. Risk, Return and Equilibrium: Some Clarifying Comments. J. Financ. 1968, 23, 29–40. [Google Scholar] [CrossRef]
- Covel, M.W. Trend Following (Updated Edition); FT Press: Upper Saddle River, NJ, USA, 2009. [Google Scholar]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dreżewski, R.; Doroz, K. An Agent-Based Co-Evolutionary Multi-Objective Algorithm for Portfolio Optimization. Symmetry 2017, 9, 168. https://doi.org/10.3390/sym9090168
Dreżewski R, Doroz K. An Agent-Based Co-Evolutionary Multi-Objective Algorithm for Portfolio Optimization. Symmetry. 2017; 9(9):168. https://doi.org/10.3390/sym9090168
Chicago/Turabian StyleDreżewski, Rafał, and Krzysztof Doroz. 2017. "An Agent-Based Co-Evolutionary Multi-Objective Algorithm for Portfolio Optimization" Symmetry 9, no. 9: 168. https://doi.org/10.3390/sym9090168
APA StyleDreżewski, R., & Doroz, K. (2017). An Agent-Based Co-Evolutionary Multi-Objective Algorithm for Portfolio Optimization. Symmetry, 9(9), 168. https://doi.org/10.3390/sym9090168





